Matematika Teknik 1, Bab 3 BAB III LIMIT. (Pertemuan ke 4)

(1)

s. johanes, dtm sv ugm 22

BAB III LIMIT

(Pertemuan ke 4)

PENDAHULUAN

Diskripsi singkat

Pada bab ini dibahas tentang limit, antara lain mengenai pengertian limit secara intuisi/tak formal, pengertian persis tentang limit, pengkajian mendalam tentang limit, teorema limit utama dan teorema subtitusi.

Manfaat

Pengertian limit memberikan gagasan baru, yang membedakan kalkulus dengan matematika lainnya. Kalkulus dapat didefinisikan sebagai pengkajian tentang limit. Jadi fungsi limit merupakan andil yang sangat dominan ketika mendalami kalkulus.

Relevansi

Untuk mempelajjari kalkulus dengan baik, maka pengertian tentang limit sangat diperlukan, karena pemahaman tentang limit akan mendasari pemahaman tentang kalkulus. .

Learning Outcomes

Mahasiswa dapat mengenal, mamahami arti limit serta terapannya dalam bidang-bidang terkait, dan dapat mengerjakan soal-soal limit dengan baik.

(2)

PENYAJIAN

Pengertian limit memberikan gagasan baru, yang membedakan kalkulus dengan matematika lainnya. Kalkulus dapat didefinisikan sebagai pengkajian tentang limit.

Contoh 1: Pandang fungsi yang ditentukan oleh rumus berikut.

Fungsi tersebut tak terdefinisi pada x = 1, karena di titik ini berbentuk , yang tanpa arti. Sebuah pertanyaan: “Apa yang terjadi pada bila x mendekati 1?”.

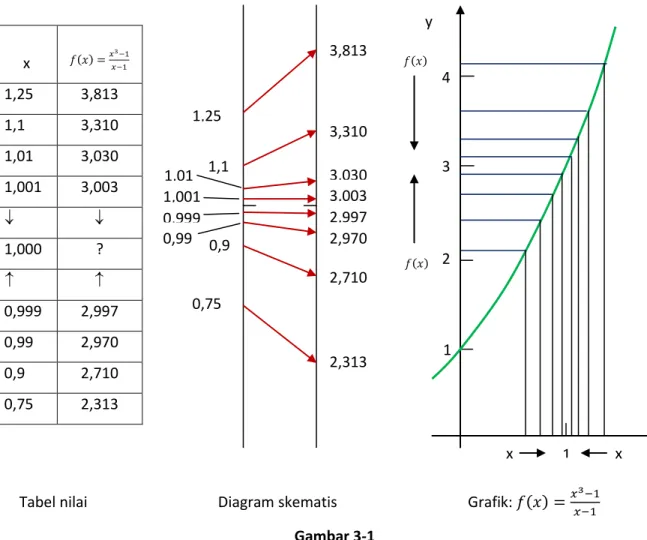
x 1,25 3,813 1,1 3,310 1,01 3,030 1,001 3,003 1,000 ? 0,999 2,997 0,99 2,970 0,9 2,710 0,75 2,313

Tabel nilai Diagram skematis Grafik:

Gambar 3-1 4 3 2 1 1 y x x x 1,25 1,1 1,01 1,001 0,999 0,99 0,9 0,75 3,813 3,310 3,030 3,003 2,997 2,970 2,710 2,313

Definisi (pengertian limit secara intuisi/tak formal)

Untuk mengatakan bahwa , berarti bahwa bilamana x dekat tetapi berlainan dari c (atau ) , maka f(x) dekat ke L.

(3)

s. johanes, dtm sv ugm 24 Telah dihitung beberapa nilai f(x) untuk x dekat 1 (lihat tabel), dan telah dibuat diagram skematisnya, serta telah disketsakan garfik (Gambar 1).

Semua informasi tampaknya menunjuk ke kesimpulan yaitu f(x) mendekati 3 bila x mendekati 1. Dalam lambang matematis ditulis sebagai:

dibaca: “limit dari untuk x mendekati 1 adalah 3”.

Berikut adalah definisi yang menurut sementara orang disebut definisi terpenting dalam kalkulus.

Perhatikan bahwa tidak disyaratkan agar sesuatu tepat benar di c. Fungsi f bahkan tidak perlu terdefinisi di c. Pemikiran limit dihubungkan dengan perilaku suatu fungsi dekat c, bukannya di c.

Pertanyaan: seberapa dekat ?

Contoh 1. Cari limit berikut :

Bila x dekat 3, maka 4x – 5 dekat terhadap 4.3 – 5 = 7. Ditulis sebagai berikut:

Contoh 2. Cari limit berikut:

Penyelesaian. Perhatikan bahwa tidak terdefinisi di x = 3, tetapi tak masalah (sama dengan contoh sebelumnya). Untuk mendapatkan gagasan tentang apa yang terjadi bila x mendekati 3, dapat memakai kalkulator untuk menghitung ungkapan yang diberikan, misalnya di 3,1; 3,01; 3,001,dan seterusnya.Tetapi adalah jauh lebih baik memakai sedikit aljabar untuk menyederhanakan persoalan. Maka

Definisi (pengertian persis tentang limit)

Mengatakan bahwa , berarti bahwa untuk tiap > 0 yang diberikan (betapapun kecilnya), terdapat δ > 0 yang berpadanan sedemikian

sehingga asalkan bahwa , yakni,

(4)

s. johanes, dtm sv ugm 25 Contoh 3. Cari limit berikut :

Penyelesaian.

Penyelesaian. Tidak ditemukan cara unttuk menyederhanakan limit tersebut secara aljabar. Kalkulator akan menolong memperoleh bayangan tentang nilai itu (lihat tabel). Kesimpulannya (walau tak kuat) adalah:

x -1,0 -0,5 -0,1 -0,01 0 0,01 0,1 0,5 1,0

0,84147 0,95885 0,99833 0,99998 ? 0,99998 0,99833 0,95885 0,84147

Tanda Peringatan

Ternyata keadannya tidak semudah apa yang kelihatan. Kalkulator mungkin mengecoh, demikian juga dengan intuisi kita. Contoh berikut mengetengahkan jebakan yang mungkin terjadi. Contoh 5. Cari limit berikut :

Dengan seperti yang terdahulu, maka disusun tabel nilai seperti terlihat pada Gambar.

x 1 0,99995 0,5 0,24991 0,1 0,00990 0,01 0,000000005 0 ?

Dengan melihat angka-angka yang ada pada tabel, nampaknya kesimpulan nilai limit tersebut mengarah pada harga = 0. Tetapi itu

salah. Jika diingat bahwa grafik ,

nilainya 1 untuk x mendekati 0. Maka :

Penyelesaian. Contoh ini mengetengahkan pertanyaan paling rumit tentang limit. Untuk itu perhatikan dua hal berikut:

(5)

s. johanes, dtm sv ugm 26 1. Ambil sebarisan nilai x yang mendekati

0, jika anda beruntung maka

menemukan angka-angka yang

berakibat nilai akan berayun secara liar (lihat tabel).

2. Jika menggambarkan gafik

, siapapun tidak akan menghasilkan gafik yang sangat baik, tetapi dengan bantuan nilai-nilai yang

ada pada tabel, nampaknya

memberikan petunjuk yang baik, tentang apa yang tejadi. Di sekitar titik asal grafik bergoyang ke atas dan ke bawah di antara harga -1 dan 1 berulang kali secara tak hingga. Jelas

bahwa tidak berada pada

suatu bilangan unik L bila x dekat 0.

Kesimpulannya tidak ada. x 1 0 -1 0 1 0 -1 0 1 0 -1 0 0 ? y x -1 1 Gambar 3-2

(6)

s. johanes, dtm sv ugm 27 Soal-soal. Carilah limit berikut.

1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20.

Pengkajian mendalam tentang limit

Seharusnya tidak mudah percaya terhadap apa yang dikatakan orang, dalam arti bijaksana dalam menyikapinya. Kehati-hatian menerima pernyataan orang menjadi hal penting, sambil memeriksanya. Jika mengatakan kepada seorang matematikawan bahwa sesuatu adalah benar, maka wajar jika kemungkinan mendapat tanggapan: ”buktikan!”. Untuk membuktikan, maka haruslah memahami arti kata-kata yang digunakan dengan sejelas-jelasnya, terutama yang menyangkut kata limit, karena kalkulus semuanya bersandar pada arti kata tersebut.

Untuk mengatakan bahwa , berarti selisih antara f(x) dan L dapat dibuat sekecil mungkin, dengan mensyaratkan bahwa x cukup dekat tetapi tidak sama dengan c. Untuk mengemukakan buktinya, menggunakan huruf Yunani yaitu ε (epsilon) dan δ (delta) untuk menggantikan bilangan-bilangan kecil positif.

Mengatakan bahwa f(x) berbeda dari L dan lebih kecil dari ε, sama saja mengatakan bahwa:

Ini berarti bahwa f(x) terletak dalam selang terbuka (L-ε, L+ε). Selanjutnya ucapan bahwa x cukup dekat tetapi berlainan dengan c, sama saja mengatakan bahwa untuk suatu δ, x terletak dalam selang terbuka (c-δ, c+δ), dengan c tidak diikutkan. Untuk mengatakan ini, dapat ditulis:

(7)

s. johanes, dtm sv ugm 28 Definisi yang menurut sementara orang disebut definisi yang terpenting dalam kalkulus adalah sebagai berikut.

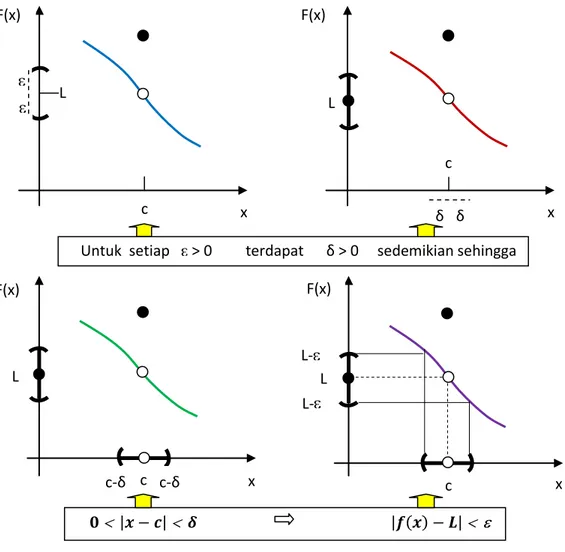
Gambar 3-3, kiranya dapat membantu untuk memahami pengertian definisi tersebut di atas.

Untuk setiap > 0 terdapat δ > 0 sedemikian sehingga

L L F(x) F(x) c _x c x δ δ F(x) F(x) L c c-δ c-δ x x L- L- L c Gambar 3-3 Definisi (pengertian persis tentang limit)

Mengatakan bahwa , berarti bahwa untuk setiap ε>0 yang deberikan (betapapun kecilnya), terdapat δ>0 yang berpadanan sedemikian sehingga

asalkan bahwa ;

(8)

s. johanes, dtm sv ugm 29 Teorema Limit Contoh 1. Carilah Penyelesaian. Contoh 2. Carilah Penyelesaian. 3 8 2 5 5 3 8 2

Teorema A (Teorema Limit Utama)

Andaikan n bilangan bulat positif, k konstanta, f dan g adalah fungsi-fungsi yang mempunyai limit di c. maka :

1. 2. 3. 4. 5. 6. 7. , asalkan 8.

(9)

s. johanes, dtm sv ugm 30 Contoh 3. Carilah Penyelesaian. Contoh 5. Carilah Penyelesaian. Contoh 6. Carilah

Penyelesaian. Baik Teorema B ataupun pernyataan 7 Teorema A tidak berlaku, karena limit dari penyebut 0. Tetapi karena limit pembilang adalah 11, jika dibagi oleh bilangan positif dekat dengan 0, hasilnya sebuah bilangan positif yang besar (dapat dibuat sekehendak). Dikatakan bahwa limitnya tidak ada (atau + ).

Contoh 7. Carilah

Penyelesaian. Lagi-lagi teorema B tak dapat diterapkan. Tetapi kali ini hasil baginya mengambil bentuk tanpa arti ( ) di x = 2. Harus disederhanakan dulu secara aljabar (faktorisasi), sebelum menentukan limitnya. Maka

7 5

9 4

8,1 ₂

Teorema B (Teorema Subtitusi)

Jika f suatu fungsi polinom atau fungsi rasional, maka:

(10)

Kekontinuan Fungsi

Dalam arti umum, kata kontinu digunakan untuk memberikan suatu proses yang berkelanjutan tanpa perubahan yang mendadak. Gagasan inilah yang berkenaan fungsi, yang sekarang ingin dibuat persis. Pandang tiga grafik yang diperlihatkan dalam Gambar 1. Hanya grafik yang ketiga memperlihatkan kekontinuan di c.

Gambar 1

Dengan definisi ini, bermaksud mensyaratkan 3 hal:

1. ada,

2. ada, 3.

Jika salah satu dari ketiga hal tersebut tak dipenuhi, maka f tak kontinu (diskontinu) di c.

y y _y x x x c c c F(x) F(x) F(x) ada, tetapi tidak ada

Definisi (kekontinuan di satu titik)

Dikatakan bahwa f kontinu di c jika beberapa selang terbuka di sekitar c tekandung dalam daerah asal f dan

Gambar 3-4

(11)

Contoh 1. Andaikan , x 2.

Bagaimana seharusnya f didefinisikan di x = 2, agar kontunu di titik it?

Penyelesaian:x

Karena itu definisikan f(2) = 4. Grafik dari fungsi yang dihasilkan, diperlihatkan pada Gambar 3-5. Kenyataannya dapat dilihat bahwa f(x) = x + 2, kontinu untuk semua x.

Soal-soal. Nyatakan apakah fungsi yang ditunjukkan kontinu di 2? Jika tak kontinu jelaskan sebabnya ! 21. 22. 23. 24. 25. 26.

Dalam soal nomer 28 s/d 30 tak terdifinisi di suatu titik tertentu. Bagaimana mendifinisikannya di sana, agar kontinu pada titik itu.

27. 28. 29. 30. y x 2 2 3 1 4 1 3 _{, x 2} , x = 2 Gambar 3-5