1
BAB I
PENDAHULUAN
1.1Latar Belakang Masalah
Manusia tidak lepas dari berbagai macam permasalahan dalam kehidupan di dunia. Permasalahan – permasalahan tersebut menyangkut berbagai aspek, dimana dalam penyelesaiannya diperlukan sebuah pemahaman melalui suatu metode dan ilmu bantu tertentu. Salah satu ilmu bantu yang dapat digunakan adalah matematika.
Matematika merupakan alat untuk menyederhanakan penyajian dan pemahaman masalah. Matematika mempunyai bahasa dan aturan yang jelas, sistematis dan keterkaitan antar konsep yang kuat. Oleh karena itu, banyak permasalahan di luar bidang matematika yang bisa diselesaikan dengan mudah menggunakan matematika. Salah satu cabang dari ilmu matematika adalah pemodelan matematika. Model matematika adalah himpunan dari rumus dan atau persamaan berdasarkan fenomena nyata dan dibuat dengan harapan bisa merepresentasikan dengan baik fenomena nyata tersebut menurut ilmu yang melatarbelakanginya. Melalui model matematika, matematika berusaha merepresentasikan berbagai fenomena yang terjadi di alam ini. Dalam perkembangannya, model matematika telah digunakan dalam ilmu fisika, biologi, kesehatan dan bahkan ilmu-ilmu sosial.
Salah satu persoalan paling penting di dunia adalah proyeksi populasi. Ukuran dan pertumbuhan populasi dalam suatu negara secara langsung mempengaruhi keadaan ekonomi, politik, budaya, pendidikan dan lingkungan dari negara tersebut dan menentukan eksplorasi dan kebutuhan sumber daya alam. Tidak ada yang ingin menunggu sampai sumber daya ini habis karena ledakan populasi.
Dengan dibentuknya sebuah model matematika, proyeksi populasi tiap tahun dapat dilakukan berdasar data sensus penduduk yang sudah ada, sehingga tidak perlu melaksanakan sensus penduduk tiap tahun. Pemerintah dan sektor perusahaan selalu membutuhkan gambaran akurat tentang ukuran yang akan
2
datang dari bermacam entitas seperti populasi, sumber daya, kebutuhan dan konsumsi untuk perencanaan kegiatan.
Salah satu model matematika untuk pertumbuhan populasi adalah model logistik pertumbuhan populasi (model Verhults). Model ini memasukkan batas untuk populasinya sehingga jumlah populasi dengan model ini tidak akan tumbuh secara tak terhingga. Laju pertumbuhan penduduk akan terbatas akan ketersediaan makanan, tempat tinggal, dan sumber hidup lainnya. Dengan asumsi tersebut, jumlah populasi dengan model ini akan selalu terbatas pada suatu nilai tertentu. Pada masa tertentu jumlah populasi akan mendekati titik kesetimbangan (equilibrium), pada titik ini jumlah kelahiran dan kematian dianggap sama. Laju pertumbuhan, yaitu nilai yang menggambarkan daya tumbuh suatu populasi diasumsikan positif, karena mengingat setiap populasi memiliki potensi untuk berkembang biak.
Indonesia adalah Negara besar dengan jumlah penduduk yang banyak. Agar tidak terjadi ledakan populasi yang dapat menimbulkan bencana, maka diperlukan perencanaan untuk pengendalian jumlah populasi, salah satunya bisa dimulai dengan memprediksi pertumbuhan populasi penduduk Indonesia.
Berdasarkan uraian diatas, maka penulis mengambil judul ”Penerapan Model Verhults pada Populasi Penduduk Indonesia”.
1.2Rumusan Masalah
Berdasarkan latar belakang yang diuraikan diatas, permasalahan yang akan dibahas dalam penelitian ini adalah :
Bagaimana memprediksi jumlah populasi menggunakan model logistik pertumbuhan populasi?
Bagaimana menentukan daya tampung dan laju pertumbuhan intrinsik berdasarkan model logistik pertumbuhan populasi ?
1.3Batasan Masalah
Adapun batasan masalah yang digunakan dalam penelitian ini adalah : Model pertumbuhan populasi yang dibahas adalah model logistik
3
1.4Tujuan Penelitian
Berdasarkan rumusan masalah diatas maka tujuan dari penelitian ini adalah : Mengetahui hasil prediksi populasi berdasarkan perhitungan model logistik
pertumbuhan populasi (Verhulst).
Menentukan daya tampung dan laju pertumbuhan intrinsik dari suatu populasi menggunakan model logistik pertumbuhan populasi (model Verhults).
1.5Metode Penelitian
Penelitian ini dilakukan dengan pendekatan teoritis, dimana penulis menganalisa jurnal, mengeksplor apa yang ada didalam jurnal dan kemudian menarik kesimpulan dari penelitian ini.
1.6Sistematika Penulisan
Adapun sistematika yang dipakai dalam penyusunan studi literatur ini, adalah sebagai berikut :
BAB I PENDAHULUAN
Bab ini meliputi Latar Belakang Masalah, Rumusan masalah, Batasan Masalah, Tujuan Penelitian, Metode Penelitian, Sistematika Penulisan dan Kerangka Berfikir dari studi literatur.
BAB II LANDASAN TEORI
Bab ini akan menguraikan dasar teori yang akan digunakan dalam penyusunan studi literatur, yang meliputi Persamaan Diferensial dan Model Pertumbuhan Populasi (model eksponensial pertumbuhan populasi (model Malthus) dan model logistik pertumbuhan populasi (Verhulst)).
BAB III
Bab ini merupakan bab pembahasan yang merupakan aplikasi teori yaitu model logistik pertumbuhan populasi (model Verhults) menggunakan studi kasus pertumbuhan populasi Indonesia.
BAB IV KESIMPULAN DAN SARAN
Dalam bab ini, berisi kesimpulan dan saran yang merupakan hasil yang telah didapatkan.
4
DAFTAR PUSTAKA
1.7Kerangka Berfikir
Ledakan pertumbuhan populasi manusia dan penggunaan sumberdaya secara besar-besaran merupakan penyebab utama kerusakan lingkungan. Kedua kekuatan utama yang mempengaruhi pertumbuhan populasi, yaitu angka kelahiran dan angka kematian, dapat diukur dan digunakan untuk memprediksi bagaimana ukuran populasi akan berubah menurut waktu.
Model eksponensial pertumbuhan populasi menjelaskan suatu pertumbuhan populasi ideal dalam lingkungan yang tidak terbatas. Model ini memprediksi bahwa semakin besar suatu populasi akan semakin cepat populasi tersebut tumbuh. Namun, pertumbuhan eksponensial tidak dapat dipertahankan tanpa batas dalam populasi apapun. Model logistik, merupakan model yang lebih realistis membatasi pertumbuhan dengan menyertakan daya tampung, ukuran populasi yang dapat didukung oleh sumberdaya yang tersedia.
BAB II
LANDASAN TEORI
2.1Persamaan Diferensial
Banyak hukum-hukum alam yang mendasari perubahan-perubahan di alam ini dinyatakan dalam bentuk persamaan yang memuat laju perubahan dari suatu kuantitas, yang tak lain adalah berupa persamaan diferensial.
Persaman diferensial adalah suatu persamaan yang memuat satu atau beberapa turunan dari suatu fungsi, dengan satu atau lebih peubah yang tak diketahui. Jika fungsi yang tidak diketahui itu hanya bergantung pada satu peubah saja, maka persamaan diferensial tersebut dinamakan persamaan diferensial biasa. Sedangkan jika fungsinya bergantung pada dua atau lebih peubah, maka persamaan diferensial tersebut dinamakan persamaan diferensial parsial.
Orde dari persamaan diferensial didefinisikan sebagai orde turunan tertinggi yang terkandung pada persamaan tersebut. Persamaan diferensial orde
5
pertama hanya mengandung 𝑦′. bentuk umum dari persamaan diferensial pertama dapat dituliskan sebagai 𝑓 𝑥, 𝑦, 𝑦′ = 0, atau biasa di tulis 𝑦′= 𝑓(𝑥, 𝑦). Arti fisis diferensial adalah, laju perubahan sebuah peubah terhadap peubah lain.
Banyak kegunaan praktis persamaan diferensial biasa dapat diturunkan kedalam bentuk
𝒈 𝒚 𝒚′ = 𝒇(𝒙) ...(2.1)
dengan manipulasi aljabar murni. Maka dapat diintegralkan kedua sisi terhadap 𝑥, diperoleh
𝒈 𝒚 𝒚′𝒅𝒙 = 𝒇 𝒙 𝒅𝒙 + 𝒄 …(2.2)
Dikiri dapat dapat diubah kepada 𝑦 sebagai variabel dari pengintegralan. Dengan kalkulus, 𝑦′𝑑𝑥 = 𝑑𝑦, maka
𝒈 𝒚 𝒅𝒚 = 𝒇 𝒙 𝒅𝒙 + 𝒄 …(2.3)
Jika 𝑓 dan 𝑔 adalah fungsi kontinu, integral di (2.3) ada, dan dengan mengevaluasinya diperoleh solusi umum dari (2.1). Metode penyelesaian persamaan direfensial biasa ini disebut metode variabel terpisah , dan (2.1) disebut persamaan terpisah , karena di (2.3) variabel sekarang terpisah : 𝑥 hanya muncul dikanan dan 𝑦 hanya dikiri. [6]
2.2Model Pertumbuhan Populasi
Kedua kekuatan utama yang mempengaruhi pertumbuhan populasi, yaitu angka kelahiran dan angka kematian, dapat diukur dan digunakan untuk memprediksi bagaimana ukuran populasi akan berubah menurut waktu. [8]
2.2.1 Model Eksponensial
Model eksponensial merupakan model pertumbuhan yang sangat sederhana. Model eksponensial pertumbuhan populasi menjelaskan suatu populasi ideal dalam lingkungan yang tidak terbatas. Pada model ini individu berkembang tidak dibatasi oleh lingkungan seperti kompetisi dan keterbatasan akan suplai makanan. Laju perubahan populasi dapat dihitung jika banyaknya kelahiran, kematian dan migrasi diketahui.
Prediksi bahwa jumlah populasi akan tumbuh secara eksponensial pertama kali dicetuskan oleh Malthus (1798) [1]. Populasi yang tumbuh secara
6
eksponensial pertama kali diamati terjadi di alam bebas. Dinamika populasi dapat di aproksimasi dengan model ini hanya untuk periode waktu yang pendek saja.
Mengasumsikan bahwa laju pertumbuhan populasi terhadap waktu berbanding lurus dengan jumlah populasi yang ada. [2]
Misalkan 𝑁(𝑡) menyatakan jumlah populasi pada saat 𝑡 dan diketahui bahwa jumlah populasi saat 𝑡 = 0 = 𝑡0 adalah 𝑁0 , maka model matematikanya
dapat dituliskan :
𝝏𝑵
𝝏𝒕 = 𝒂𝑵 ; dimana 𝑎 konstan …(2.4)
Berikut ini adalah solusi jumlah populasi 𝑁 pada saat 𝑡 atau 𝑁(𝑡) berdasarkan (2.4) : 𝜕𝑁 𝑁 = 𝑎 𝜕𝑡 ln 𝑁 = 𝑎𝑡 + 𝑐 𝑁(𝑡) = 𝑒𝑎𝑡+𝑐 𝑁(𝑡) = 𝑒𝑎𝑡. 𝑒𝑐 𝑁(𝑡) = 𝐶1𝑒𝑎𝑡 Karena 𝑁 𝑡0 = �𝑁0 =𝐶1𝑒𝑎(0) = 𝐶1 , maka : 𝑵 𝒕 = 𝑵𝟎𝒆𝒂(𝒕−𝒕𝟎) ...(2.5) dimana
𝑎 : daya tumbuh suatu populasi (intrinsic growth rate) / perbedaan antara angka kelahiran dan kematian per kapita (𝑎 = angka kelahiran tahunan perkapita – angka kematian tahunan per kapita) / laju pertumbuhan populasi per kapita.
Persamaan (2.5) dikenal sebagai Model Eksponensial pertumbuhan populasi/ Model pertumbuhan populasi Malthus.
Dari (2.5) dapat diperoleh : 𝑒𝑎(𝑡−𝑡0)
=
𝑁𝑡 𝑁0ln
𝑒𝑎(𝑡−𝑡0)= 𝑙𝑛
𝑁 𝑡 𝑁0𝒂 =
(𝒕−𝒕𝟏 𝟎)𝒍𝒏
𝑵 𝒕 𝑵𝟎…(2.6)
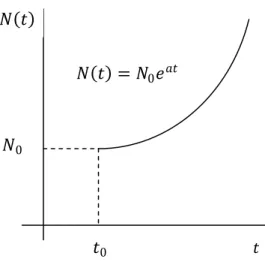
Jika solusi (2.5) ditampilkan dalam bentuk grafik, maka didapatkan dua grafik berikut :
7
Dari Gambar.2.1 jelas bahwa untuk 𝑎 > 0 diperoleh lim𝑡→∞𝑁 𝑡 = ∞. Jika hasil ini dikaitkan dengan jumlah suatu populasi, maka akan menimbulkan pertanyaan : dapatkah suatu populasi berkembang sampai pada jumlah tak-hingga?
𝑁 𝑡 = 𝑁0𝑒𝑎𝑡
𝑁 𝑡
𝑁0
𝑡0 𝑡
Gambar.2.1
Grafik Pertumbuhan Eksponensial Grafik untuk 𝑎 > 0 𝑁 𝑡 = 𝑁0𝑒𝑎𝑡 𝑁 𝑡 𝑁0 𝑡0 𝑡 Gambar.2.2
Grafik Pertumbuhan Eksponensial Grafik untuk 𝑎 < 0
8
Gambar.2.2, untuk 𝑎 < 0 akan didapatkan lim𝑡→∞𝑁 𝑡 = 0, yang mana jika dikaitkan dengan jumlah populasi nampaknya hasil ini cukup logis. Suatu populasi akan mendekati kepunahan (akan habis) jika laju pertumbuhannya negatif.
Model ini memprediksi bahwa semakin besar suatu populasi akan semakin cepat populasi tersebut tumbuh.
2.2.2 Model Logistik
Model ini merupakan penyempurnaan dari model eksponensial dan pertama kali diperkenalkan oleh Pierre Verhulst pada tahun 1838. [1]
Model pertumbuhan eksponensial mengasumsikan sumberdaya yang tidak terbatas, model ini merupakan kasus yang tidak pernah ditemukan di dunia nyata ini. Karena setiap populasi tumbuh dan tumbuh sehingga jumlahnya semakin besar, peningkatan kepadatan populasi bisa mempengaruhi kemampuan individu untuk mengambil sumberdaya yang mencukupi untuk pemeliharaan, pertumbuhan, dan reproduksi. Populasi hidup dari jumlah sumberdaya yang terbatas, dan ketika populasi menjadi semakin padat, masing-masing individu mendapat bagian sumberdaya yang semakin kecil. Akhirnya, terdapat suatu batas dari jumlah individu yang dapat menempati suatu habitat. Para ahli ekologi mendefinisikan daya tampung (carrying capacity) sebagai ukuran populasi maksimum yang dapat ditampung oleh suatu lingkungan tertentu tanpa ada pertambahan atau penurunan ukuran populasi selama periode waktu yang relatif lama. [8] Daya tampung yang disimbolkan dengan 𝑎𝑏 adalah ciri lingkungan, dengan demikian daya tampung bervariasi terhadap waktu dan ruang dengan keberlimpahan sumberdaya yang terbatas.
Kepadatan dan keterbatasan sumberdaya dapat mempunyai dampak yang besar pada laju pertumbuhan populasi. Jika individu tidak mendapatkan sumberdaya yang mencukupi untuk bereproduksi, angka kelahiran per kapita akan menurun. Jika mereka tidak memperoleh cukup energi untuk mempertahankan diri mereka sendiri, angka kematian per kapita akan meningkat. Suatu penurunan dalam angka kelahiran tahunan per kapita atau suatu peningkatan dalam angka kematian tahunan per kapita akan mengakibatkan laju pertumbuhan populasi yang lebih kecil.
9
Model ini memasukkan batas untuk populasinya sehingga jumlah populasi dengan model ini tidak akan tumbuh secara tak terhingga. Laju pertumbuhan penduduk akan terbatas akan ketersediaan makanan, tempat tinggal, dan sumber hidup lainnya. Dengan asumsi tersebut, jumlah populasi dengan model ini akan selalu terbatas pada suatu nilai tertentu. Pada masa tertentu jumlah populasi akan mendekati titik kesetimbangan (equilibrium), pada titik ini jumlah kelahiran dan kematian dianggap sama. [5]
Verhulst menunjukkan bahwa pertumbuhan populasi tidak hanya bergantung pada ukuran populasi tetapi juga pada sejauh mana ukuran ini dari batas atasnya seperti daya tampung. Dia memodifikasi model Malthus (eksponensial) untuk membuat ukuran populasi sesuai baik untuk populasi sebelumnya dengan syarat 𝑎−𝑏𝑁𝑎 , dimana 𝑎 dan 𝑏 disebut koefisien vital dari populasi.
Suatu model logistik diawali dengan model pertumbuhan eksponensial dan menciptakan suatu ekspresi yang mengurangi nilai 𝑎 ketika 𝑁 meningkat. Jika ukuran populasi maksimum yang dapat dipertahankan adalah 𝑎𝑏 , maka 𝑎𝑏− 𝑁 akan memberikan petunjuk berapa banyak individu tambahan yang dapat ditampung oleh lingkungan tersebut, dan
𝑎 𝑏−𝑁
𝑎 𝑏
=𝑎−𝑏𝑁𝑎 memberikan petunjuk berapa fraksi 𝑎𝑏 yang masih tersedia untuk pertumbuhan populasi.
Persamaan yang telah dimodifikasi menggunakan syarat baru adalah :
𝜕𝑁 𝜕𝑡 = 𝑎𝑁 𝑎−𝑏𝑁 𝑎 = 𝑎2𝑁−𝑎𝑏𝑁2 𝑎 = 𝑎𝑁 − 𝑏𝑁 2 𝝏𝑵 𝝏𝒕 =𝒂𝑵 − 𝒃𝑵𝟐 …(2.7)
Model ini merupakan persamaan diferensial nonlinear yang mempunyai solusi :
𝜕𝑁 𝑎𝑁−𝑏𝑁2= 𝜕𝑡 1 𝑎 1 𝑁+ 𝑏 𝑎−𝑏𝑁 𝑑𝑁 = 𝑑𝑡 1 𝑎 1 𝑁𝑑𝑁 + 𝑏 𝑎−𝑏𝑁𝑑𝑁 = 𝑡 + 𝑐 𝟏 𝒂(𝐥𝐧 𝑵 − 𝐥𝐧(𝒂 − 𝒃𝑵)) = 𝒕 + 𝒄 …(2.8)
Diketahui bahwa jumlah populasi saat 𝑡 = 0 = 𝑡0 adalah 𝑁0 , maka:
10
Dengan mensubstitusi nilai 𝑐, persamaan (2.8) menjadi :
1 𝑎(ln 𝑁 − ln(𝑎 − 𝑏𝑁)) = 𝑡 + 1 𝑎(ln 𝑁0− ln(𝑎 − 𝑏𝑁0)) 1 𝑎 (ln 𝑁 − ln(𝑎 − 𝑏𝑁)) − (ln 𝑁0− ln(𝑎 − 𝑏𝑁0)) = 𝑡 𝑙𝑛𝑎−𝑏𝑁𝑁 − 𝑙𝑛 𝑁0 𝑎−𝑏𝑁0 = 𝑎𝑡 𝑙𝑛𝑁(𝑎−𝑏𝑁0) 𝑁0(𝑎−𝑏𝑁)= 𝑎𝑡
Dengan melakukan pengeksponensialan pada kedua ruas, diperoleh :
𝑁(𝑎−𝑏𝑁0) 𝑁0(𝑎−𝑏𝑁)= 𝑒 𝑎𝑡 𝑁0 𝑎 − 𝑏𝑁 𝑒𝑎𝑡 =𝑁(𝑎 − 𝑏𝑁 0) 𝑎𝑁0𝑒𝑎𝑡− 𝑏𝑁𝑁 0𝑒𝑎𝑡 =𝑁(𝑎 − 𝑏𝑁0) 𝑎𝑁0𝑒𝑎𝑡 =𝑁 𝑎 − 𝑏𝑁0 + 𝑁(𝑏𝑁0𝑒𝑎𝑡) 𝑎𝑁0𝑒𝑎𝑡 =𝑁(𝑎 − 𝑏𝑁0+ 𝑏𝑁0𝑒𝑎𝑡) 𝑁 = 𝑎𝑁0𝑒𝑎𝑡 𝑎−𝑏𝑁0+𝑏𝑁0𝑒𝑎𝑡 (bagi dengan 𝑏𝑁0𝑒 𝑎𝑡) = 𝑎 𝑏 1+ 𝑎−𝑏𝑁0𝑏𝑁0 𝑒𝑎𝑡1 = 𝑎 𝑏 1+ 𝑎 𝑏𝑁0−1 1 𝑒𝑎𝑡 𝑵(𝒕) = 𝒂 𝒃 𝟏+ 𝒂 𝒃 𝑵𝟎 −𝟏 𝒆−𝒂𝒕 …(2.9)
Persamaan (2.9)dikenal sebagai Model Logistik pertumbuhan populasi / Model pertumbuhan populasi Verhulst .
Jika persamaan (2.9) dilimitkan sebagai 𝑡 → ∞ , didapatkan (untuk 𝑎 > 0) :
𝑵𝒎𝒂𝒙= 𝐥𝐢𝐦𝒕→∞𝑵 = 𝒂𝒃 ..(2.10)
Verhulst menjelaskan bagaimana parameter 𝑎 dan 𝑎𝑏 dapat diperkirakan dari populasi 𝑁(𝑡) dalam tiga yang berlainan tetapi dengan jarak tahun yang sama. [1] Jika 𝑁0 adalah populasi pada saat 𝑡 = 0 , 𝑁1 pada saat 𝑡 = 1 dan 𝑁2 pada saat 𝑡 = 2, maka dari persamaan (2.9) dapat diperoleh :
Ambil 𝑡 = 1, sehingga 𝑁 adalah 𝑁1
𝑁
1=
𝑎 𝑏 1+ 𝑎 𝑏 𝑁0 −1 𝑒−𝑎(1)11
=
𝑎 𝑏 1+ 𝑏𝑁0𝑎 −1 𝑒−𝑎=
𝑎 𝑏 1+ 𝑎−𝑏𝑁0𝑏𝑁0 𝑒−𝑎=
𝑎 𝑏 𝑏𝑁0+𝑎𝑒−𝑎 −𝑏𝑁0𝑒−𝑎 𝑏𝑁0=
𝑎𝑏𝑁0 𝑏(𝑏𝑁0+𝑎𝑒−𝑎−𝑏𝑁0𝑒−𝑎)𝑁
1 = �𝑎𝑁0 𝑏𝑁0+𝑎𝑒−𝑎−𝑏𝑁0𝑒−𝑎1 𝑁1 =𝑏𝑁0+𝑎𝑒 −𝑎−𝑏𝑁 0𝑒−𝑎 𝑎𝑁0
=𝑏 𝑎+ 𝑒−𝑎 𝑁0 − 𝑏𝑁0𝑒−𝑎 𝑎𝑁0
1 𝑁1= 𝑏 𝑎 1 −
𝑒
−𝑎 + 𝑒−𝑎 𝑁0 𝒃 𝒂 𝟏 −𝒆
−𝒂 = 𝟏 𝑵𝟏− �𝑪−𝒂 𝑵𝟎 ..(2.11)Ambil 𝑡 = 2, sehingga 𝑁 adalah 𝑁2 dengan cara yang sama diperoleh :
𝒃 𝒂 𝟏 −
𝒆
−𝟐𝒂 = 𝟏 𝑵𝟐−𝒆 −𝟐𝒂 𝑵𝟎 ..(2.12)Bagi (2.12) oleh (2.11) untuk mengeliminasi 𝑏𝑎 , diperoleh : 𝑏 𝑎 1−𝑒−2𝑎 = 1 �𝐶2− 𝑒−2𝑎 𝑁0 𝑏 𝑎 1−𝑒−𝑎 = 1 𝑁1− 𝑒−𝑎 𝑁0
1 + 𝑒
−𝑎=
1 𝑁2− 𝑒−2𝑎 𝑁0 1 𝑁1− 𝑒−𝑎 𝑁0=
𝑁0−𝑁2𝑒−2𝑎 𝑁0𝑁2 𝑁0−𝑁1𝑒−𝑎 𝑁0𝑁1=
𝑁0𝑁1(𝑁0−𝑁2𝑒−2𝑎) 𝑁0𝑁2(𝑁0−𝑁1𝑒−𝑎)=
𝑁1(𝑁0−𝑁2𝑒−2𝑎) 𝑁2(𝑁0−𝑁1𝑒−𝑎)=
𝑁0𝑁1−𝑁1𝑁2𝑒−2𝑎 𝑁0𝑁2−𝑁1𝑁2𝑒−𝑎12
𝑒
−𝑎=
𝑁0𝑁1−𝑁1𝑁2𝑒−2𝑎 𝑁0�𝑁2−𝑁1𝑁2𝑒−𝑎−
𝑁0𝑁2−𝑁1𝑁2𝑒−𝑎 𝑁0𝑁2−𝑁1𝑁2𝑒−𝑎𝑒−𝑎 𝑁 0𝑁2− 𝑁1𝑁2𝑒−𝑎 = 𝑁0𝑁1− 𝑁1𝑁2𝑒−2𝑎− (𝑁0𝑁2− 𝑁1𝑁2𝑒−𝑎) 𝑁0𝑁2𝑒−𝑎− 𝑁 1𝑁2𝑒−2𝑎= 𝑁0𝑁1− 𝑁1𝑁2𝑒−2𝑎− 𝑁0𝑁2+ 𝑁1𝑁2𝑒−𝑎 𝑁0𝑁2𝑒−�𝑎− 𝑁1𝑁2𝑒−𝑎= 𝑁0𝑁1− 𝑁0𝑁2 −𝑁0𝑁2𝑒−�𝑎+ 𝑁 1𝑁2𝑒−𝑎= −𝑁0𝑁1+ 𝑁0𝑁2 𝑒−�𝑎(𝑁 1𝑁2− 𝑁0𝑁2) = −�𝐶0𝑁1+ 𝑁0𝑁2
𝑒
−�𝑎=
𝑁0𝑁2−𝑁0𝑁1 𝑁1𝑁2−𝑁0𝑁2𝒆
−�𝒂=
𝑵𝟎(𝑵𝟐−𝑵𝟏) 𝑵𝟐(𝑵𝟏−𝑵𝟎)..(2.13) Substitusi (2.13) ke (2.11), maka : 𝑏 𝑎
1 −
𝑁0(𝑁2−𝑁1) 𝑁2(𝑁1−𝑁0)=
1 𝑁1−
𝑁0(𝑁2−𝑁1) 𝑁2(𝑁1−𝑁0) 𝑁0𝑏 𝑎 𝑁2(𝑁1−𝑁0) 𝑁2(𝑁1−𝑁0)
−
𝑁0(𝑁2−𝑁1) 𝑁2(𝑁1−𝑁0)=
𝑁2(𝑁1−𝑁0)−𝑁1(𝑁2−𝑁1) 𝑁1𝑁2(𝑁1−𝑁0)𝑏 𝑎
=
𝑁2(𝑁1−𝑁0)−𝑁1(𝑁2−𝑁1) 𝑁1𝑁2(𝑁1−𝑁0) 𝑁2(𝑁1−𝑁0)−𝑁0(𝑁2−𝑁1) 𝑁2(𝑁1−𝑁0)=
𝑁2(𝑁1−𝑁0) 𝑁2(𝑁1−𝑁0)−𝑁1(𝑁2−𝑁1) 𝑁1𝑁2(𝑁1−𝑁0) 𝑁2(𝑁1−𝑁0)−𝑁0(𝑁2−𝑁1)=
𝑁1𝑁2−𝑁0𝑁2−𝑁1𝑁2+𝑁12 𝑁1(𝑁1𝑁2−𝑁0𝑁2−𝑁0𝑁2+𝑁0𝑁1)=
𝑁12−𝑁0𝑁2 𝑁1(𝑁0𝑁1−2𝑁0𝑁2+𝑁1𝑁2)𝒂 𝒃
=
𝑵𝟏(𝑵𝟎𝑵𝟏−𝟐𝑵𝟎𝑵𝟐+𝑵𝟏𝑵𝟐) 𝑵𝟏𝟐−𝑵𝟎𝑵𝟐..(2.14)
Dengan mensubstitusi (2.14) ke (2.10), diperoleh :
𝑵𝒎𝒂𝒙= 𝐥𝐢𝐦𝒕→∞𝑵 = 𝒂𝒃 =𝑵𝟏(𝑵𝟎𝑵𝟏−𝟐𝑵𝟎𝑵𝟐+𝑵𝟏𝑵𝟐)
𝑵𝟏𝟐−𝑵𝟎𝑵𝟐
..(2.15) Ketika ukuran suatu populasi berada dibawah daya tampungnya, pertumbuhan populasi akan berjalan cepat menurut model logistik, akan tetapi ketika 𝑁 mendekati 𝑎𝑏 , pertumbuhan populasi akan menjadi lambat.
13
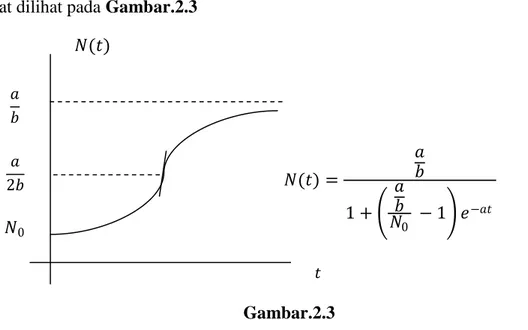
Untuk 𝑎 > 0 berlaku lim𝑡→∞𝑁 = 𝑎𝑏 , sehingga disimpulkan bahwa grafik dari (2.9) mempunyai asimtot mendatar 𝑁 𝑡 =𝑎𝑏 . Grafik solusi untuk kasus dapat dilihat pada Gambar.2.3
Dapat dilihat bahwa kurva logistik adalah 𝑆-shaped dan mempunyai titik infleksi ketika 𝑁 = 𝑎
2𝑏 . (dihasilkan dari 𝜕2𝑁
𝜕𝑡2 =𝑎𝑁
′ − 𝑏𝑁𝑁′=0). [3]
Sedangkan untuk 𝑎𝑏< 𝑁0 , 𝑎 > 0 grafik solusinya adalah :
𝑁(𝑡) = 𝑎 𝑏 1 + 𝑎 𝑏 𝑁0 − 1 𝑒−𝑎𝑡 𝑁(𝑡) = 𝑎 𝑏 1 + 𝑎 𝑏 𝑁0 − 1 𝑒−𝑎𝑡 𝑁0 𝑁0 𝑁(𝑡) 𝑎 𝑏 Gambar.2.3
Grafik pertumbuhan logistik yang Naik 𝑡 𝑎 2𝑏 𝑁(𝑡) = 𝑎 𝑏 1 + 𝑎 𝑏 𝑁0 − 1 𝑒−𝑎𝑡 𝑡 𝑁0 𝑁(𝑡) 𝑎 𝑏 Kasus 𝑎𝑏< 𝑁0 , 𝑎 > 0 Gambar.2.4
14
Untuk 𝑎 < 0 didapatkan solusi yang tidak stabil, yaitu tidak mengarah pada titik kesetimbangan tertentu. Himpunan grafik solusinya adalah sebagai berikut :
Dari (2.9) dapat diperoleh nilai 𝑡∗ dengan cara sebagai berikut : 𝑁(𝑡) = 𝑎 𝑏 1+ 𝑎 𝑏 𝑁0 −1 𝑒−𝑎𝑡 𝑒−𝑎𝑡= 𝑎 𝑏 𝑁−1 𝑎 𝑏 𝑁0−1 −𝑎𝑡 = 𝑙𝑛 𝑎 𝑏 𝑁−1 𝑎 𝑏 𝑁0−1 𝒕∗= 𝒍𝒏 𝒂 𝒃 𝑵−𝟏 𝒂 𝒃 𝑵𝟎−𝟏 −𝒂 ..(2.16)
Persamaan (2.16) adalah nilai 𝑡∗ yang menunjukkan waktu ketika 𝑁 mencapai setengah dari batas populasi maksimum. [1]
Gambar.2.5
Solusi Model Pertumbuhan Logistik dengan 𝑎 < 0 𝑁(𝑡) = 𝑎 𝑏 1 + 𝑎 𝑏 𝑁0 − 1 𝑒−𝑎𝑡 𝑎 𝑏 𝑡 𝑁(𝑡) Kasus 𝑎 < 0
15
Model pertumbuhan logistik memberikan pengertian akan jumlah populasi maksimum atau minimum sebagai titik jenuh pertumbuhannya.
BAB III
PENERAPAN MODEL VERHULTS
PADA POPULASI PENDUDUK INDONESIA
Salah satu persoalan paling penting di dunia adalah proyeksi populasi. Ukuran dan pertumbuhan populasi dalam suatu negara secara langsung mempengaruhi keadaan ekonomi, politik, budaya, pendidikan dan lingkungan dari negara tersebut dan menentukan eksplorasi dan kebutuhan sumber daya alam. Tidak ada yang ingin menunggu sampai sumber daya ini habis karena ledakan populasi.
Dengan dibentuknya sebuah model matematika, proyeksi populasi tiap tahun dapat dilakukan berdasar data sensus penduduk yang sudah ada, sehingga tidak perlu melaksanakan sensus penduduk tiap tahun. Pemerintah dan sektor perusahaan selalu membutuhkan gambaran akurat tentang ukuran yang akan datang dari bermacam entitas seperti populasi, sumber daya, kebutuhan dan konsumsi untuk perencanaan kegiatan.
Indonesia merupakan Negara kepulauan yang berdasarkan posisi garis lintang dan garis bujur berada diantara 60 LU – 110 LS dan 950 BT – 1410 BT. Secara geografis Indonesia terletak diantara dua samudera dan dua benua, yaitu Samudera Pasifik dan Samudera Hindia, serta Benua Asia dan Benua Australia. Topografi wilayah Indonesia sangat bervariasi, hal tersebut berpengaruh pada kehidupan masyarakatnya. Masyarakat Indonesia merupakan masyarakat yang majemuk, dimana Indonesia memiliki berbagai macam bahasa, agama, mata pencaharian, suku bangsa dan lain-lain.
Indonesia juga merupakan Negara besar dengan jumlah penduduk yang banyak. Agar tidak terjadi ledakan populasi yang dapat menimbulkan bencana, maka diperlukan perencanaan untuk pengendalian jumlah populasi, salah satunya bisa dimulai dengan memprediksi pertumbuhan populasi pendudukIndonesia.
16
Studi literatur ini memusatkan pada aplikasi model logistik pertumbuhan populasi (model Verhults) untuk memprediksi pertumbuhan populasi Indonesia menggunakan data dari tahun 1987 sampai 2010.
Data jumlah penduduk Indonesia dari tahun 1987 sampai dengan 2010 berdasarkan katalog BPS (Badan Pusat Statistik) : 3101015. [4]
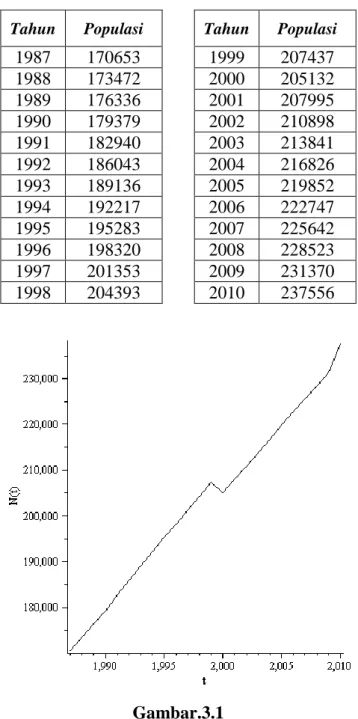
Tabel.3.1Jumlah penduduk Indonesia (ribu), 1987-2010 Sumber : Badan Pusat Statistik
Tahun Populasi Tahun Populasi
1987 170653 1999 207437 1988 173472 2000 205132 1989 176336 2001 207995 1990 179379 2002 210898 1991 182940 2003 213841 1992 186043 2004 216826 1993 189136 2005 219852 1994 192217 2006 222747 1995 195283 2007 225642 1996 198320 2008 228523 1997 201353 2009 231370 1998 204393 2010 237556 Gambar.3.1
17
Berdasarkan pada populasi dari tahun 1987 sampai 2010 pada Tabel.3.1 , misal 𝑡 = 0,1,2 mewakili masing-masing tahun 1987, 1988 dan 1989 . Maka 𝑁0, 𝑁1, 𝑁2 berturut-turut adalah 170653, 173472 dan 176336.
Substitusi 𝑁0, 𝑁1dan 𝑁2 kedalam persamaan (2.15) diperoleh :
𝑁𝑚𝑎𝑥 = lim𝑡→∞𝑁 = 𝑎𝑏
=
𝑁1(𝑁0𝑁1−2𝑁0𝑁2+𝑁1𝑁2)𝑁12−𝑁0𝑁2
=
173472( 170653 (173472173472)−22−( 170653170653 176336 176336+(173472)( 176336))=
1.446928564 ×10267376 12= 5411587.293
ini merupakan prediksi daya tampung (carring capacity) atau ukuran populasi penduduk maksimum yang dapat ditampung Indonesia.
Dari persamaan (2.13), dengan mensubstitusi 𝑁0, 𝑁1dan 𝑁2diperoleh :
𝑒
−�𝑎=
𝑁0(𝑁2−𝑁1) 𝑁2(𝑁1−𝑁0)= 170653(176336−173472)176336(173472−170653) =488750192 497091184 = 0.9832220398 𝑎 = − ln 0.9832220398 = 0.016920304 = 1.692030459%
ini mengimplikasikan bahwa laju pertumbuhan populasi penduduk Indonesia diperkirakan 1.692030459% pertahun.
Untuk memperoleh prediksi populasi, substitusi nilai 𝑁0, 𝑒−�𝑎 dan 𝑎𝑏 kedalam
persamaan (2.9) sebagai berikut :
𝑁 𝑡 =
𝑎 𝑏 1+ 𝑎 𝑏 𝑁0 −1 𝑒−𝑎𝑡=
5411587.293 1+ 5411 587 .293170653 −1 (0.9832220398 )𝑡18
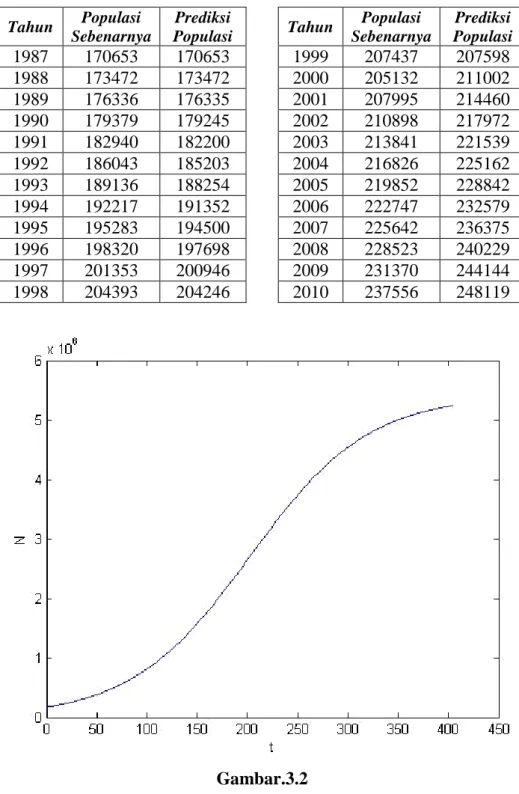
Tabel.3.2Jumlah penduduk Indonesia (ribu), 1987-2010
Populasi sebenarnya dan populasi prediksi berdasarkan model Verhults.
Tahun Populasi Sebenarnya Prediksi Populasi Tahun Populasi Sebenarnya Prediksi Populasi 1987 170653 170653 1999 207437 207598 1988 173472 173472 2000 205132 211002 1989 176336 176335 2001 207995 214460 1990 179379 179245 2002 210898 217972 1991 182940 182200 2003 213841 221539 1992 186043 185203 2004 216826 225162 1993 189136 188254 2005 219852 228842 1994 192217 191352 2006 222747 232579 1995 195283 194500 2007 225642 236375 1996 198320 197698 2008 228523 240229 1997 201353 200946 2009 231370 244144 1998 204393 204246 2010 237556 248119 Gambar.3.2
Grafik jumlah populasi prediksi berdasarkan model Verhults
Kurva logistik mempunyai titik infleksi ketika 𝑁 = 𝑎
2𝑏 . [3] 𝑎
19
Dari persamaan (2.16) diperoleh nilai 𝑡∗ sebagai berikut :
𝑡∗ = 𝑙𝑛 𝑎 𝑏 𝑁−1 𝑎 𝑏 𝑁0−1 −𝑎
=
𝑙𝑛 5411 587.2932705793.647 −1 5411 587.293170653 −1 −0.016920304=−3.424622827−0.016920304 = 202.3972399 ≈ 202
Jadi, populasi penduduk Indonesia diprediksikan menjadi 2705793.647 pada tahun 2202.
BAB IV
KESIMPULAN DAN SARAN
4.1Kesimpulan
Dari kajian studi literatur yang telah dilakukan, maka dapat disimpulkan bahwa sebagai berikut :
Model logistik pertumbuhan populasi (model Verhults) adalah : 𝑁(𝑡) = 𝑎 𝑏 1+ 𝑎 𝑏 𝑁0 −1 𝑒−𝑎𝑡 (9) dimana :
𝑁(𝑡) : jumlah populasi pada saat 𝑡
𝑎
𝑏 : daya tampung / carrying capacity (ukuran populasi maksimum yang dapat
ditampung oleh suatu lingkungan tertentu tanpa ada pertambahan atau penurunan ukuran populasi selama periode waktu yang relatif lama).
𝑎 : daya tumbuh suatu populasi (intrinsic growth rate) / perbedaan antara angka kelahiran dan kematian per kapita (𝑎 = angka kelahiran tahunan perkapita – angka
20
kematian tahunan per kapita) / laju pertumbuhan populasi per kapita dan diasumsikan positif.
Dengan model logistik pertumbuhan populasi (model Verhults) diprediksikan daya tampung untuk populasi Indonesia adalah 5411587.293 . Berdasarkan model ini, laju pertumbuhan populasi Indonesia adalah
1.692030459% pertahun, dan populasi akan mencapai 2705793.647 pada tahun
2202.
4.2Saran
Dalam kajian studi literatur ini, penulis hanya membahas model logistik pertumbuhan populasi (model Verhults) untuk prediksi pertumbuhan populasi di Indonesia. Dari kajian studi literatur yang telah dilakukan, pembaca dapat memperhatikan kelebihan dan kekurangan dari model logistik pertumbuhan populasi (model Verhults), sehingga diharapkan bagi yang akan menyusun studi literatur mengenai pemodelan matematika khususnya model matematika untuk pertumbuhan populasi, modifikasi dari pertumbuhan logistik pertumbuhan populasi atau model pertumbuhan populasi lainnya dapat dijadikan sebagai bahan penulisan selanjutnya.