Skripsi
Diajukan Untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Teknik Program Studi Teknik Informatika
Oleh:
SASONGKO HADI
065314062
PROGRAM STUDI TEKNIK INFORMATIKA
JURUSAN TEKNIK INFORMATIKA
FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA
YOGYAKARTA
A Thesis
Presented as a Partial Fulfillment of the Requirements To Obtain The Sarjana Teknik Degree
In Informatics Engineering
By :
Sasongko Hadi 065314062
INFORMATICS ENGINEERING STUDY PROGRAM
INFORMATICS ENGINEERING DEPARTMENT
FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY
v
mendapatkan sebuah rangka yang memenuhi syarat one-pixel thickness dan connectivity. Tujuan penelitian ini adalah untuk mengetahui apakah algoritma Nagendraprasad-Wang-Gupta dapat menghasilkan kerangka yang baik jika diaplikasikan kepada sejumlah citra aksara jawa. Berdasarkan dokumentasi Nagendraprasad-Wang-Gupta, algoritma ini telah diketahui dapat digunakan untuk penipisan citra aksara latin dan memiliki kecepatan yang relatif lebih baik dari algoritma Wang-Zang.
Penelitian dilakukan dengan menganalisa citra rangka yang dihasilkan oleh algoritma Nagendraprasad-Wang-Gupta menurut beberapa parameter yaitu connectivity, one-pixel thickness, kecepatan proses penipisan, persentase jumlah piksel yang dihapus, ukuran file input dan output penipisan dan kompleksitas waktu algoritma. Selain itu sebagai tambahan disebarkan kuisioner kepada 50 orang responden untuk melihat kemiripan citra hasil penipisan dengan citra asli, dimana algoritma Rosenfeld digunakan sebagai pembanding karena algoritma ini telah diuji oleh Kristi Krisnawati dan menghasilkan rangka yang relatif baik ketika diaplikasikan pada citra aksara jawa. Penipisan dan pengujian secara otomatis dilakukan dengan membangun aplikasi berbasis Matlab.
vi
recognition. This thesis proposed Nagendraprasad-Wang-Gupta thinning algorithm to obtain skeleton of a digital image because this algorithm has proven generating a thin and connected skeleton. The aim of this research was finding whether Nagendraprasad-Wang-Gupta thinning algorithm can produces skeleton if using Javanese character image. Based on the documentation of Nagendraprasad-Wang-Gupta, this algorithm had been known that it was able to use in reducing thickness of character images. Besides, this algorithm has rapidity better than Wang-Zang algorithm.
This research was done by analyzing skeleton image which was produced by Nagendraprasad-Wang-Gupta algorithm. It was according to several parameters; connectivity, one-pixel thickness, rapidity of thinning process, and percentage of pixel which was deleted, file input dimension and output of the thinning, and algorithm time complexity. Besides, questionnaires as the instrument of this research were also distributed to 50 respondents to observe the resemblance of the result and the original images, which Rosenfeld algorithm was used to compare, in as much as this algorithm was tested by Kristi Krisnawati and produced skeletons which good quality when it applied to Javanese character images. Thinning and testing were done by building the application which had a Matlab-based application.
vii
MOTTO
“Kalau Kamu Mau Pasti Mampu!”
(Doraemon: Petualangan Negeri Robot)
“Doing What You Can Doing!”
(Center Stage: Turn It Up)
“Believe!”
x
Puji syukur kepada Allah SWT yang telah memberikan kesempatan, waktu, tenaga dan pikiran serta rasa, sehingga penulis dapat menyelesaikan tugas akhir yang berjudul “Penipisan Citra Aksara Jawa Menggunakan Algoritma Negendraprasad-Wang-Gupta” ini dengan baik.
Dalam pengerjaan tugas akhir ini, penulis tidak lepas dari bantuan sejumlah pihak, oleh karena itu penulis ingin mengucapkan terimakasih kepada:
1. Bapak dan Ibu tercinta, atas diberikannya kesempatan dan dukungan. 2. Anastasia Rita Widiarti, S.Si., M.Kom., selaku dosen pembimbing
tugas akhir, atas kesabarannya dalam membimbing penulis, memberikan waktunya, dukungan, serta saran yang sangat membantu penulis.
3. Ermilinda Y. Pati, Bayu Sanjaya dan Tulus Wardoyo, atas bantuan selama mengalami hambatan.
4. Responden Kuisioner, atas kerjasamannya dalam mengerjakan kuisioner pengamatan visual.
xi
bermanfaat bagi kemajuan dan perkembangan ilmu pengetahuan serta berbagai pengguna pada umumnya.
Yogyakarta, 24 Agustus 2010
xii
HALAMAN PERSETUJUAN PEMBIMBING……….. iii
HALAMAN PENGESAHAN……… iv
ABSTRAK……… v
ABSTRACT………. vi
MOTTO……… vii
PERNYATAAN KEASLIAN KARYA………. viii
PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS……….. ix
KATA PENGANTAR………. x
1.5 Metodologi Penelitian………... 3
1.6 Sistematika Penulisan………... 5
BAB II : LANDASAN TEORI……….. 7
2.1 Citra………... 7
2.1.1 Pengertian Citra……….. 7
2.1.2 Format Citra……… 8
2.2 Pemrosesan Citra………... 11
2.3 Penipisan/Thinning………... 13
xiii
2.4.1.3 Analisa menurut Jang dan Chin (1990). 23
2.4.2 Kompleksitas Waktu……….. 29
2.4.2.1 Kompleksitas Waktu Asimtotik…… 29
2.5 Algoritma Rosenfeld………. 36
2.6 Aksara Jawa……… 37
BAB III : ANALISA DAN PERANCANGAN SISTEM………. 38
3.1 Gambaran Umum Sistem………. 38
3.2 Analisa Kebutuhan Proses……… 39
3.2.1 Proses Binerisasi………. 39
3.2.2 Proses Penipisan……….. 40
3.3 Perancangan Pengujian……… 41
3.5.1 Pengamatan Ukuran Citra……….. 41
3.5.2 Sum Template A dan Sum Not Critical Point…. 42
3.5.3 One-pixel Thickness………. 44
3.5.4 Sum of Pixel Object………. 46
3.5.5 Sum of Remove Pixel………... 47
3.5.6 Running Time………... 48
3.5.7 Connectivity………. 49
3.5.8 Waktu Asimtotik Algoritma……….. 50
3.5.9 Pengamatan Visual………. 50
3.4 Perancangan Tampilan Antarmuka………. 50
xiv
4.1 Implementasi Algoritma Nagendraprasad-Wang-Gupta…. 57
4.2 Implementasi Binerisasi……… 59
4.3 Implementasi Pengujian……… 59
4.3.1 Implementasi Pengamatan Ukuran Citra…….. 60
4.3.2 Implementasi Sum Template A dan Sum Not Critical Point………... 60
4.3.3 Implementasi One-pixel thickness……….. 61
4.3.4 Implementasi Sum of Pixel Object………. 62
4.3.5 Implementasi Sum of Remove Pixel... 62
4.3.6 Implementasi Running Time……… 63
4.3.7 Implementasi Connectivity………. 63
4.3.8 Implementasi Waktu Asimtotik Algoritma….. 64
4.3.9 Implementasi Pengamatan Visual………. 65
4.4 Implementasi Interface………. 65
4.1.1 Halaman Utama……….. 66
4.1.2 Halaman Input Citra………... 67
4.1.3 Halaman Simpan Citra……… 68
4.1.4 Halaman About………... 69
4.1.5 Halaman Help………. 70
4.5 Implementasi Error-Handling……….. 71
4.2.1 Error-Handling Thining………. 71
4.2.2 Error-Handling Clear……….. 72
4.2.3 Error-Handling Save……… 73
4.2.4 Error-Handling Exit……… 73
BAB V: HASIL DAN PEMBAHASAN……… 76
5.1. Analisa Citra Hasil Penipisan……… 76
xv
5.1.5. Pengujian Connectivity……… 96
5.2. Pengamatan Visual………. 108
5.3. Kompleksitas Waktu……….. 112
5.4. Rangkuman Perbandingan Algoritma Nagendraprasad-Wang-Gupta dengan Algoritma Rosenfeld. 117 BAB VI : PENUTUP……….. 118
6.1 Kesimpulan……… 118
6.2 Saran……….. 120
DAFTAR PUSTAKA……….. 121
xiv
Gambar 2.2: Komposisi Citra Warna... 9
Gambar 2.3: Contoh Citra Grayscale... 10
Gambar 2.4: Contoh Citra Warna, Citra Grayscale dan Citra Biner... 10
Gambar 2.5: Hasil sebelum dan sesudah thinning... 14
Gambar 2.6: Gambar 8-tetangga... 15
Gambar 2.7: Nilai c(p)……….. 16
Gambar 2.8: Citra Angka 3………... 17
Gambar 2.9: Algoritma Nagendraprasad-Wang-Gupta ……… 19
Gambar 2.10: B(p) bernilai 1 jika dilakukan penghapusan……….. 20
Gambar 2.11: B(p) bernilai 7 jika dilakukan penghapusan……….. 21
Gambar 2.18: (a) citra T. (b) 4-connected- component juga 8-connected- component dari S dan SC adalah
Gambar 2.20: (a) citra T, yang memuat anggota S (b) Bacground dari S. (c) Holes dari S……… 29
Gambar 2.21: Flowchart algoritma Rosenfeld (Krinawati, 2009)……….. 35
xv
Gambar 4.1: Gambar citra asli, citra rangka sebelum ada D dan E dan citra rangka sesudah ada D dan E (Carasco,-)………. 58
Gambar 4.7: Error-Handling Thinning………. 72
Gambar 4.8: Error-Handling Thinning 2……….. 72
Gambar 4.9: Error-Handling Thinning 3……….. 73
xvi
Gambar 5.4: Gambar Citra Ca_2 sesudah Binerisasi…………..………… 101
Gambar 5.5: Gambar Citra Ca_2 Asli/ Sebelum Binerisasi ……… 103
Gambar 5.6: Gambar Citra Da_2.JPG Asli/ Sebelum Binerisasi………… 105
Gambar 5.7: Gambar Citra Da_2.JPG Sesudah Binerisasi……….. 106
xvii
DAFTAR TABEL
Tabel 2.1: Pengelompokan Algoritma Berdasarkan Notasi O-Besar…… 34
Tabel 5.1: Data Citra Input dan Output ……… 76
Tabel 5.2: Hasil Pengamatan Ukuran Citra ……….. 86
Tabel 5.3: Hasil Pengamatan Jumlah Piksel Terhapus………... 88
Tabel 5.4: Hasil Pengamatan Waktu Komputasi ………... 91
Tabel 5.5: Hasil Pengujian One-Pixel Thickness ………. 93
Tabel 5.6: Hasil Pengamatan Visual ……….. .. 108
Tabel 5.7: Persentase Hasil Pengamatan Visual ………….……….. 110
1
1.1 Latar Belakang
Bangsa Indonesia telah mengenal tulisan sejak waktu yang lampau. Salah satu tulisan lampau itu adalah tulisan aksara Jawa, seperti umumnya tulisan kuno, aksara jawa banyak ditulis pada buku, kertas dan lontar. Sebuah media yang memiliki kemungkinan untuk mengalami kerusakan, baik oleh rayap, sobek dan basah serta termakan oleh zaman. Selain itu, huruf-huruf kuno seiring perkembangan zaman menjadi sebuah huruf asing yang sudah tidak lagi dikenali oleh orang-orang sehingga banyak naskah-naskah kuno jawa tidak dapat dipahami.
Proses digitalisasi merupakan salah satu langkah penting yang dapat digunakan untuk mempermudah mengungkap isi dari naskah-naskah kuno dan melindungi naskah-naskah kuno jawa dari kemungkinan kerusakan. Salah satu bagian dari proses digitalisasi naskah-naskah kuno jawa adalah dengan penipisan. Proses penipisan adalah salah satu tahap untuk mendapatkan rangka/skeleton dari aksara jawa. Rangka ini memiliki fungsi sebagai informasi esensial dari aksara jawa agar dapat menjadi acuan untuk proses pengenalan karakter aksara jawa.
menggunakan algoritma Nagendraprasad-Wang-Gupta. Algoritma ini salah satu algoritma yang dapat digunakan untuk melakukan proses penipisan yang memiliki keunggulan dalam kecepatan yang lebih baik dibandingkan algoritma Wang-Zang ketika diuji cobakan pada huruf latin (Nagendraprasad, 1993). Sehingga algoritma Nagendraprasad-Wang-Gupta patut untuk di uji coba terhadap data citra aksara jawa utuk mendapatkan hasil skeleton yang lebih baik. Dalam hal ini penulis melakukan pengujian connectivity, ketebalan (One-pixel thickness), pengamatan ukuran citra, pengamatan jumlah piksel terhapus, pengamatan waktu komputasi, kompleksitas waktu dan pengamatan visual dengan menggunakan pembanding algoritma Rosenfeld yang telah terbukti dengan baik untuk melakukan penipisan citra aksara jawa (Krisnawati, 2009).
1.2 Rumusan Masalah
Dari latar belakang di atas, masalah dapat dirumuskan sebagai berikut: 1. Bagaimana cara kerja algoritma Nagendraprasad-Wang-Gupta?
2. Bagaimana mengimplementasikan algoritma Nagendraprasad-Wang-Gupta pada penipisan citra aksara jawa dengan matlab?
3. Apakah algoritma Nagendraprasad-Wang-Gupta dapat menghasilkan kerangka citra aksara jawa yang memenuhi kriteria operasi penipisan?
1.3 Tujuan
data citra berupa aksara jawa dengan membuat aplikasi Matlab, serta untuk mengetahui apakah algoritma Nagendraprasad-Wang-Gupta merupakan algoritma yang efektif untuk melakukan proses penipisan citra aksara jawa, sesuai dengan syarat-syarat penipisan yaitu connectivity, ketebalan (One-pixel thickness), dengan tambahan pengamatan ukuran citra, pengamatan
jumlah piksel terhapus, pengamatan waktu komputasi, kompleksitas waktu dan pengamatan visual dengan menggunakan pembanding algoritma Rosenfeld yang telah terbukti dengan baik untuk melakukan penipisan citra aksara jawa (Krisnawati, 2009).
1.4 Batasan Masalah
Dalam membuat program implementasi algoritma Nagendraprasad-Wang-Gupta pada penipisan citra aksara jawa ini ditentukan beberapa batasan masalah sebagai berikut:
1. Citra yang diproses adalah citra biner atau citra skala keabuan (grayscale) dengan ekstensi *.jpg.
2. Program dibuat dengan matlab.
3. Proses yang dilakukan program adalah proses penipisan sebagai proses tambahan adalah proses binerisasi. Proses ini dilakukan sebagai preprocessing dari citra masukan yang bukan biner sehingga dapat diproses oleh program.
4. Pengujian hasil penipisan yang dilakukan adalah pengujian connectivity, one-pixel thickness, pengamatan ukuran citra hasil
waktu komputasi/ running time, kompleksitas waktu dan pengamatan visual dengan pembanding algoritma Rosenfeld.
1.5 Metodologi Penelitian
Metodologi penelitian dilakukan sebagai berikut:
1. Studi pustaka yang bertujuan untuk mempelajari teori citra dan proses pengolahan citra digital untuk penipisan menggunakan algoritma Nagendraprasad-Wang-Gupta.
2. Pengembangaan program aplikasi menggunakan model Waterfall (Pressman, 1997).
Gambar 1.1: Model Waterfall
Tahapan:
- System Enginering
System Enginering adalah tahap untuk mengumpulkan dan
menentukan semua kebutuhan elemen sistem. - Analisis
Analisis adalah tahap untuk menentukan analisis terhadap permasalahan yang dihadapi dan menentukan kebutuhan software.
Kebutuhan tersebut meliputi performance dan interfacing. - Desain
Desain adalah proses menterjemahkan kebutuhan sistem ke dalam sebuah gambaran program.
- Implementasi
Implementasi merupakan proses penterjemahan desain ke dalam bentuk yang dapat dieksekusi.
- Pengujian
Pengujian memastikan apakah semua fungsi-fungsi program berjalan dengan baik dan menghasilkan output yang sesuai dengan yang dibutuhkan.
3. Menganalisa hasil yang diperoleh dari penipisan dengan syarat-syarat hasil penipisan citra yang sudah ditentukan sebelumnya dan mengambil kesimpulan dari percobaan yang telah dilakukan.
1.6 Sistematika Penulisan
Berikut ini akan dijabarkan sistematika penulisan sebagai berikut:
BAB I: PENDAHULUAN
Bab ini berisi tentang latar belakang masalah, rumusan masalah, tujuan penelitian, batasan masalah, metodologi penelitian dan sistematika penulisan.
BAB II : LANDASAN TEORI
BAB III : ANALISA DAN PERANCANGAN SISTEM
Bab ini berisi rancangan aplikasi yang akan dibuat. Hal-hal yang akan dirancang seperti algoritma program, diagram alir dari algoritma program dan desain user interface aplikasi yang akan dibuat.
BAB IV : IMPLEMENTASI
Berisi tentang implementasi hasil dari analisis dan perancangan sistem dalam bentuk program (proses, interface dan cara kerja program).
BAB V : HASIL DAN PEMBAHASAN
Bab ini menyajikan hasil penelitian berupa hasil percobaan dan kuisioner, dan analisa terhadap hasil penelitian tersebut yang ditinjau dari syarat-syarat penipisan citra.
BAB VI : PENUTUP
7
Dalam bab ini dituliskan landasan teori yang menjadi acuan pengerjaan
skripsi:
2.1 Citra
2.1.1 Pengertian Citra
Citra adalah gambar pada bilangan dwi matra (dua dimensi)
(Munir, 1994). Citra terbagi menjadi dua yaitu citra kontinyu dan citra
diskrit, agar semua citra dapat diolah dengan komputer digital, maka
suatu citra harus direpresentasikan secara numerik dengan nilai-nilai
diskrit. Representasi citra dari fungsi malar (kontinyu) menjadi
nilai-nilai diskrit disebut dengan digitalisasi citra dan citra yang dihasilkan
disebut dengan citra digital. Pada umumnya citra digital terbentuk
empat persegi panjang dengan dimensi ukuran dinyatakan sebagai
tinggi x lebar (atau lebar x panjang) (Munir, 2004) seperti yang
ditunjukkan pada gambar Gambar 2.1.
Gambar 2.1: Bentuk citra digital Tinggi
Lebar
Lebar
2.1.2 Format Citra Digital
Menurut intensitas warna format citra digital dapat dikategorikan
seperti berikut:
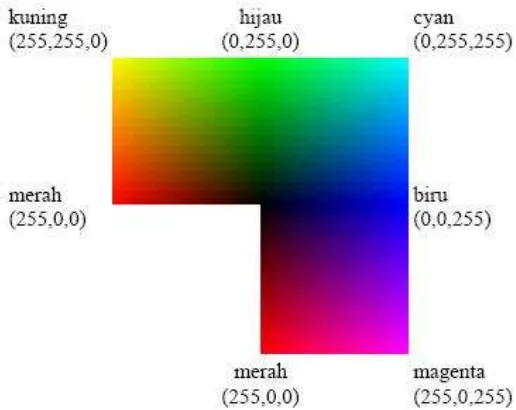
1. Citra RGB (True Color)
Citra RGB merupakan citra yang memiliki 3 komponen
channel yaitu Red, Green dan Blue. Setiap channel memiliki nilai
intensitas yang berbeda, tergantung warna yang direpresentasikan.
Untuk monitor komputer, nilai rentang paling kecil = 0 dan paling
besar = 255. Pilihan skala 256 ini didasarkan pada cara mengungkap
8 digit bilangan biner yang digunakan oleh mesin komputer.
Dengan cara ini, akan diperoleh warna campuran sebanyak 256 x
256 x 256 = 1677726 jenis warna. Sebuah jenis warna, dapat
dibayangkan sebagai sebuah vektor di ruang 3 dimensi yang
biasanya dipakai dalam matematika, koordinatnya dinyatakan dalam
bentuk tiga bilangan, yaitu komponen-x, komponen-y dan
komponen-z. Misalkan sebuah vektor dituliskan sebagai r = (x,y,z).
Untuk warna, komponen-komponen tersebut digantikan oleh
komponen R(ed), G(reen), B(lue). Jadi, sebuah jenis warna dapat dituliskan sebagai berikut: warna = RGB (30, 75, 255). Putih =
Gambar 2.2: Komposisi Citra Warna
(Sumber: www.ittelkom.ac.id)
2. Citra Grayscale
Citra grayscale merupakan citra menggunakan fungsi
intensitas untuk menentukan warna. Fungsi intensitas yang
digunakan adalah fungsi intensitas warna keabuan (hitam-putih).
Fungsi intensitas warna yang digunakan pada citra grayscale
memiliki kedalaman piksel yang berbeda-beda. Namun, pada
kebanyakan aplikasi, citra grayscale dikuantisasi pada level 256
dan membutuhkan 1 byte (8 bit) untuk merepresentasikan setiap
Gambar 2.3: Contoh Citra Grayscale
(Sumber: www.ittelkom.ac.id)
3. Citra Biner
Citra biner atau citra monokrom merupakan citra yang
memiliki 2 kemungkinan warna pada setiap pikselnya. Citra biner
hanya dikuantisasikan pada 2 level yaitu 0 dan 1, sehingga setiap
piksel pada citra cukup direpresentasikan dengan 1 bit (0 dan 1).
Gambar 2.4: Contoh Citra Warna, Citra Grayscale dan Citra Biner
(Sumber: www.ittelkom.ac.id)
Jika =0 dan = 1, maka operasi ini akan
mentransformasikan suatu citra menjadi citra biner. Misal suatu
citra memiliki gray level 256, dipetakan menjadi citra biner, maka
fungsi trasformasinya adalah sebagai berikut:
piksel-pikselyang nilai intensitasnya di bawah 128 diubah menjadi
hitam (nilai intensitas = 0), sedangkan piksel-piksel yang nilai
intensitasnya di atas 128 diubah menjadi putih (nilai intensitas =1).
2.2 Pemrosesan Citra
Analisa dokumen citra memiliki tujuan untuk mengenali komponen
tulisan dan gambar yang terkandung dalam citra serta mengambil informasi
yang ada dalam citra. Analisa citra dokumen mempunyai 2 komponen penting
yaitu tekstual dan pemrosesan grafis.
Pemrosesan citra merupakan salah satu tahap dalam analisa dokumen
citra yang berfungsi untuk mempersiapkan citra untuk dianalisa. Pemrosesan
citra sendiri mempunyai tujuan agar citra dapat lebih mudah untuk diproses.
Dalam pemrosesan citra, beberapa tahap yang akan dilakukan dapat
dijabarkan sebagai berikut:
1. Grayscaling
Citra grayscale merupakan citra dimana representasi setiap piksel
diwakili dengan hanya satu jenis atau satu nilai warna dalam skala
keabuan. Untuk mendapatkan nilai intensitas keabuan, maka dapat
dihitung dengan menjumlahkan 30% dari nilai channel red pada citra
RGB, 59% channel green, dan 11% channel blue. Hasil penjumlahan dari
setiap elemen tersebut yang kemudian direpresentasikan dalam setiap
channel red, green dan blue dengan intensitas yang sama.
2. Tresholding
Tresholding yang disebut juga dengan gray-level segmentation
(pemisahan warna dalam skala keabuan) merupakan proses pengubahan
dari sebuah citra dengan skala keabuan menjadi citra biner atau citra
dengan 2 intensitas warna yaitu hitam dan putih.
Salah satu algoritma yang digunakan untuk tresholding adalah
algoritma Otsu. Tujuan dari metode Otsu adalah membagi histogram citra
gray level ke dalam dua daerah yang berbeda secara otomatis tanpa
membutuhkan bantuan user untuk memasukkan nilai ambang. Pendekatan
yang dilakukan oleh metode Otsu adalah dengan melakukan analisis
diskriminan yaitu menentukan suatu variabel yang dapat membedakan
antara dua atau lebih kelompok yang muncul secara alami. Analisis
Diskriminan akan memaksimumkan variable tersebut agar dapat membagi
piksel citra on (foreground) dan latarbelakang (background).
Formulasi dari metode Otsu adalah sebagai berikut. Nilai Ambang
yang akan dicari dari suatu citra gray level dinyatakan dengan k. Nilai k
berkisar antara 1 sampai dengan L, dengan nilai L = 255. Probabilitas
dengan :
ni menyatakan jumlah piksel pada level ke i
N menyatakan total jumlah piksel pada citra.
Nilai Zeroth Cumulative Moment, First Cumulative Moment, dan total
nilai mean berturut-turut dapat dinyatakan dengan rumus berikut:
Nilai ambang k dapat ditentukan dengan memaksimumkan
persamaan :
2.3 Penipisan
Secara umum penipisan dapat dinyatakan sebagai proses pereduksian
wilayah dari tepi objek berupa citra hingga yang tersisa merupakan garis
……….. (2.3)
……….. (2.4)
tengahnya saja atau dapat disebut juga sebagai rangka atau skeleton.
Penipisan memiliki definisi sebagai proses pengurangan pola (pattern) yang
secara umum diperpanjang (elongated) ke representasi yang menyerupai garis
(Lam et al.,1992). Sedangkan menurut Rinaldi Munir, penipisan adalah
operasi pemrosesan citra biner dimana piksel citra on direduksi menjadi
rangka yang menghampiri garis sumbu piksel citra (Munir, 2004). Skeleton
atau kerangka menurut J.R. Perker (1997), diasumsikan sebagai representasi
bentuk dari suatu piksel citra on dalam jumlah piksel on yang relatife kecil,
yang dimana kesemuanya merupakan bagian yang struktural dan oleh karena
itu representasi itu dibutuhkan. Sebuah kerangka diharapkan dapat
memberikan representasi bentuk dari piksel citra on dalam jumlah piksel on
yang lebih kecil.
Dalam konsep yang telah dikembangkan oleh banyak orang, J.R. Parker
(1997), mengatakan bahwa tidak semua piksel citra dapat dikenai operasi
penipisan, dan hasil dari operasi penipisan yang disebut sebagai kerangka
mempunyai kemungkinan untuk tidak berfungsi di semua situasi. Contoh
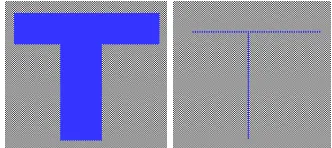
rangka/skeleton hasil dari proses penipisan ditunjukkan pada Gambar 2.5.
Gambar 2.5: Hasil sebelum dan sesudah penipisan
2.4 Algoritma Nagendraprasad-Wang-Gupta
Algoritma Nagendraprasad-Wang-Gupta merupakan algoritma penipisan
yang dikembangkan dari algoritma Wang-Zhang (1989) yang memiliki fungsi
untuk membentuk rangka yang memiliki konektivitas dari suatu citra yang
dibentuk kerangkanya (Carasco, -). Algoritma ini merupakan algoritma
penipisan paralel, dimana nilai baru yang diberikan untuk sebuah titik pada
iterasi sekarang (iterasi ke-n) tergantung pada nilai yang dihasilkan pada
iterasi sebelumnya (iterasi ke-(n-1)), dimana seluruh titik yang mewakili citra
tersebut diproses secara serentak, dengan asumsi bahwa setiap piksel
terhubung dengan 8 titik tetangga seperti pada gambar Gambar 2.6.
Gambar 2.6: Gambar 8-tetangga
Dalam melakukan pemrosesan, citra akan disimpan dalam matrik
Q dan mengikuti fungsi yang diberikan melalui algoritma dengan langkah
sebagai berikut:
1. awal: fungsi bahwa:
a. menghitung jumlah contour loop m;
b. menghitung contour point pertama FIRST[k], dan titik sebelumnya,
PREV[ k], untuk setiap contour loop L[k], (k = 1, 2,..., m); dan
c. set nilai awal dari variabel loop decision untuk h [k] =1. h[k]= 1 berarti
2. loop-end-test (k): fungsi untuk uji coba apakah k contour loop diakhiri.
3. Countour (p): sebuah fungsi untuk melihat dimana sebuah titik ada pada
garis atau tepi citra atau tidak.
4. Successor (z,p): fungsi yang menghitung titik penerus dari titik
sebelumnya (x) sesuai dengan urutan searah jarum jam sekitar tetangga p
untuk memenuhi titik gelap pertama.
5. Deletion (Q,p): sebuah fungsi yang digunakan untuk menghapus sebuah
titik p di dalam Q (merubah piksel 1 menjadi 0) jika memenuhi 2 kondisi:
a. 1<B(p)<7; dan
b. (A(p) = 1 or C(p) = 1) and (p[2] +p[4])*p[0]*p[6] =0 atau (A(p) = i or
C(p) = 1) and ( p[0] + p[6])*p[2]* P[4] =0),
Dimana B(p) adalah jumlah tetangga dari p yang tidak bernilai 0. Untuk
A(p) adalah total piksel disekitar p dari off ke on transisi dimana tetangga
diambil dari perputaran disekitar p, dengan nilai c(p) sebagai berikut:
Gambar 2.7: Nilai c(p)
Dalam algoritma NWG dikenal pula contour, yang disebut dengan
contour adalah piksel-piksel yang berada di tepi suatu citra atau memiliki
ketetanggaan putih seperti yang ditunjukan pada Gambar 2.8 berupa citra
contour adalah piksel-piksel a hingga g. Piksel-piksel tersebut adalah piksel
yang akan dilakukan penghapusan terlebih dahulu, jika piksel-piksel tersebut
telah berhasil dihapus barulah piksel “1” dilakukan penghapusan, tentu dalam
hal ini yang memenuhi nilai B(p), A(p) atau C(p).
Gambar 2.8: Citra angka 3
Algoritma Nagendraprasad-Wang-Gupta diberikan pada Gambar
2.9.
Definisi dan Notasi Dasar yang digunakan pada algoritma
Nagendraprasad-Wang-Gupta adalah sebagai berikut:
Definisi 1: tetangga piksel, p: [i, j], diidentifikasikan oleh delapan arah, [-i 1,
j], [i-1,] tl, [i, j +1], [i-tl,] tl, [i-tl, j], [i-tl, 11, [i, 11, [i-1,
j-11, k = 0,. . . , 8, p [8] = p [O], seperti ditunjukkan pada Gambar
2.6.
Definisi 2: countour point dari beberapa pola digital piksel didefinisikan
sebagai tetangga yang setidaknya satu tetangga putih seperti pada
Gambar 2.8 berupa piksel a hingga g.
loop c; adalah tetangga ci+1 untuk 1 ≤ i < n dan cn adalah tetangga
c1. Kami menggunakan L (1),..., L (m) untuk label contour loop
yang berbeda dari pola, di mana m adalah jumlah contour loop,
pada Gambar 2.8 nilai m=1.
Definisi 4: Ketika sebuah countour point U diproses, countour point untuk
diproses, v, disebut sebagai countour point penerus U dan U
disebut countour point sebelumnya v.
Definisi 5: Misalkan p menjadi countour point yang sedang diproses. Biarkan
x menjadi countour point sebelumnya p, dan z menjadi penerus
countour point. Maka s akan disebut fungsi pengganti jika z = s
(x, p) adalah fungsi dari x sesuai dengan urutan searah jarum jam
Gambar 2.9: Algoritma Nagendraprasad-Wang-Gupta
(Sumber: Algoritma For Thinning and Rethickening Binary Digital
Patern.pdf)
Keterangan Gambar 2.9:
1. g adalah sebuah variable untuk menentukan case suatu piksel yang akan
dilakukan penipisan. Nilai g akan berubah-ubah dari 0 ke 1 dan 1 ke 0.
Untuk pertamakali nilai g akan menjadi 0, atau dalam hal ini penipisan
pada iterasi pertama akan menggunakan penipisan yang ada pada case 0,
jika iterasi pertama sudah dilakukan maka nilai g akan menjadi 1, yang
artinya penipisan berikutnya atau iterasi kedua akan dilakukan pada
ditipiskan sesudah iterasi kedua selesai dan iterasi ketiga dijalankan maka
kondisi penghapusan akan kembali pada case 0.
2. h adalah variable penentu sampai kapan pemeriksaan tiap-tiap piksel
dilakukan, dalam hal ini pemeriksaan akan dihentikan jika sudah tidak ada
satupun piksel yang dapat dihapus atau nilai h=0, selama ada piksel yang
dihapus nilai h adalah 1.
3. Q dan Q1 adalah matrik citra, dengan Q adalah citra asli dan Q1 adalah
citra yang ditipiskan atau yang mengalami penghapusan piksel.
4. B(p) adalah jumlah tetangga dari piksel p yang bernilai on, nilai B(p)
harus lebih besar dari satu dan kurang dari 7. Hal ini dikarenakan jika
bernilai 1 seperti pada Gambar 2.10 jika dilakukan penghapusan maka
akan membuat piksel menjadi tidak bersisa yang akan mengakibatkan
bentuk kerangka kurang terjaga atau juga jika B(p) bernilai 0 maka akan
membuat semua piksel akan terhapus. Demikian pula jika B(p) bernilai 7
akan memberikan hasil kerangka yang kurang baik seperti pada Gambar
2.11 yaitu citra akan menjadi berlubang, hal ini juga akan terjadi jika nilai
B(p) adalah 8.
5. A(p) adalah variabel yang digunakan untuk menemukan jumlah transisi
piksel on ke off dari tetangga p. Dalam algoritma nilai A(p) harus
bernilai 1 agar piksel p dapat dilakukan penghapusan. Hal ini
dikarenakan jika nilai A(p) lebih dari 1 misal berjumlah 4 seperti pada
Gambar 2.12 dapat memberikan hasil kerangka yang kurang baik, karena
ada kemungkinan p adalah critical point seperti pada gambar Gambar
2.12.
6. c(p) adalah nilai suatu piksel agar dapat dihapus selain nilai A(p), jika
nilai A(p) tidak terpenuhi. Untuk melakukan penghapusan piksel, nilai
c(p) harus 1. Untuk nilai c(p) bernilai 1 dpat dilihat pada Gambar 2.7.
Gambar 2.11: B(p) bernilai 7 jika dilakukan penghapusan p
Gambar 2.12: A(p) bernilai 4 jika dilakukan penghapusan,
Hal ini dikarenakan saat c(p) bernilai 1, p adalah critical point sehingga
perlu dilakukan penghapusan seperti pada Gambar 2.13.
2.4.1 Analisa Algoritma Penipisan
Suatu algoritma penipisan dapat dinyatakan baik jika memenuhi
beberapa syarat seperti One-pixel thickness dan connectivity oleh karena itu
diperlukan suatu analisa untuk membuktikan, hal ini dilakukan untuk
menunjukan suatu algoritma penipisan selalu menghasilkan rangka yang
saling terhubung seperti bentuk citra yang asli serta memiliki ketebalan
sebesar 1 piksel (Jang dan Chin, 1990). Oleh karena itu algoritma
Nagendraprasad-Wang-Gupta yang akan digunakan sebagai algoritma
penipisan citra aksara jawa, perlu dilakukan analisis sebagai berikut: p
Gambar 2.13: c(p) bernilai 1
2.4.1.1. Connectivity: Suatu kerangka hasil penipisan (I) yang memiliki
Connectivity dengan citra asli (S) harus memiliki homotopy yang
sama (dua himpunan berhingga dikatakan homotopy jika terdapat
koresponden satu-satu antara connected component dari S dan I ).
Maka dari itu I adalah 8-connected dan komplemennya mengandung
4-connected component.
2.4.1.2. One-Piksel Thickness: Sebuah kerangka yang dibentuk dari proses
penipisan harus memiliki kriteria one-pixel thickness, atau memiliki
ketebalan 1 piksel. Syarat sebuah kerangka dapat disebut one-pixel
thickness adalah sebagai berikut:
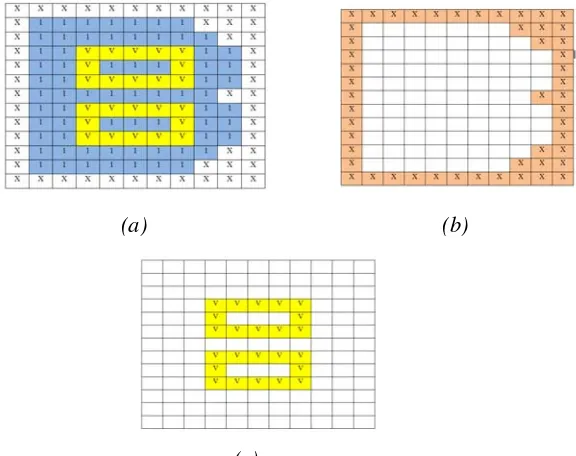
1. Bila tidak memuat templates A= { A1, A2, A3 , A4 } yang
berukuran 2x2 dengan struktur ditunjukkan pada Gambar 2.10.
A1 A2 A3 A4
Gambar 2.14: Struktur template A
Susunan Gambar 2.14 adalah susunan pola yang ditemukan
dalam komponen-komponen terhubung yang bukan merupakan
rangka.
2. Apabila satu atau lebih templates A (A1, A2, A3 , A4 ) terdapat
tersebut bukan rangka dengan ketebalan 1 piksel atau rangka
merupakan critical point atau jika piksel-piksel tersebut dihapus
akan menyebabkan piksel-piksel yang lain menjadi tidak
terhubung atau menghasilkan lubang. Suatu kerangka dikatakan
critical point bila sekurang-kurangnya memenuhi struktur
templates B yang memiliki struktur B = ( B1, B2, B3 , B4), ataupun
C yang membuat struktur ke empat templates A seperti pada
Gambar 2.15.
B1 B2 B3 B4
C
Gambar 2.15: Struktur template B dan C
2.4.1.3. Analisa menurut Jang dan Chin (1990):
• Sebuah titik p memiliki 4 tetangga yaitu atas, bawah, kiri dan
kanan, yang diinisialisasikan sebagai a, b, c dan d seperti pada
Gambar 2.16: Gambar Inisialisasi a, b, c, d
Titik-titik ini disebut 4-neigbors dari p (atau 4-adjacent dari p).
Jika U,V ⊆S dan beberapa titik dari U adalah 4-adjacent
terhadap beberapa titik dari V, maka U dikatakan 4-adjacent dari
V.
• Sebuah titik p mempunyai 4 tetangga diagonal, yaitu titik e, f, g
dan h seperti pada Gambar 2.16. Ke empat titik tersebut,
bersama dengan titik 4-neigbors seperti yang disebutkan pada
Gambar 2.16 , maka akan disebut 8-neigbors dari p ( atau
8-neigbors dari p). Misal U,V ⊆S dan beberapa titik dari U adalah
8- adjacent terhadap beberapa titik dari V, maka U dikatakan 8-
adjacent terhadap V.
• Sebuah 8-path ataupun 4-path yang disebut πn (x,y) yaitu
panjang n dari x ke y adalah sebuah urutan dari titik-titik (x = x0,
x1, x2, …, xn = y ), dimana xi adalah 8-neigbors atau 4-neigbors
Gambar 2.17: 8-path ataupun 4-path
πn (x,y) merupakan 8-path atau 4-path dengan panjang n = 6
dari x ke y dengan urutan x0, x1, x2, …, x6 dimana xi merupakan
8-neigbors dari x1, x3 merupakan dari x4, begitu seterusnya
hingga x6.
• Misal x dan y adalah 2 titik yang berbeda dalam S. Titik x
disebut merupakan 8-path-connected atau 4-path-connected
terhadap y, jika terdapat sebuah 8-path ataupun 4-path, πn
(x,y), dalam S. Definisi ini menyiratkan bahwa x adalah
4-path-connected terhadap y, maka x juga 8-path-connected terhadap y.
Namun keadaan sebaliknya tidak selalu terpenuhi.
• Misalkan x ∈ S, 8-component (terkadang disebut juga sebagai
8-connected-component atau 4- component dari S, KS (x),
dedefinisikan sebagai: KS (x)= { y∈S: y adalah 8-path-connected
ataupun 4-path-connected terhadap x}, seperti pada Gambar
(a) (b)
(c)
Gambar 2.18: (a) citra T. (b) 4-connected- component juga 8-connected-
component dari S dan SC adalah 4-connected. (c) 8-connected- component
juga 8-connected- component dari S dan SC adalah 4-connected
• S adalah 8-connected ataupun 4-connected jika S hanya
mempunyai satu 8-component ataupun 4-component.
• Border dari S disebut ∂S, yang definisikan oleh S = { x : x
adalah 4-adjacent terhadap y, x ∈S, y ∈SC }. Interior dari S
didefiniskan sebagai himpunan perbedaan antara S dan
(a) (b)
(c)
Gambar 2.19: (a) citra T, yang memuat anggota S (b) Border dari S. (c)
Interior dari S
Pada (a) piksel-piksel objek bernilai ‘1’ adalah anggota S, maka
(b) piksel-piksel objek yang termasuk border dan merupakan
4-adjacent terhadap piksel berwarna putih (SC), sedangkan (c)
piksel-piksel objek yang termasuk interior dari S, yaitu
piksel-piksel yang merupakan anggota S tetapi bukan border.
• Komponen dari SC, K Sc yang mengandung baris-baris teratas
dan dasar (baris pertama dan baris terakhir) maupun kolom
paling kiri dan paling kanan (kolom pertama dan terakhir) dari
disebut latar dari S. Seperti yang ditunjukkan pada Gambar
2.20.
(a) (b)
(c)
Gambar 2.20: (a) citra T, yang memuat anggota S (b) Bacground dari
S. (c) Holes dari S
Pada gambar (a) piksel-piksel objek bernilai ‘1’ adalah anggota
S, maka (b) piksel-piksel latar berwarna putih, diluar piksel
objek bernilai ‘1’ adalah background dari S, sedangkan (c)
piksel-piksel berwarna kuning adalah lubang dari S dan bukan
latar.
2.4.2 Kompleksitas Waktu
Kompleksitas waktu diperlukan dalam menganalisis algoritma, hal ini
melakukan proses tetapi juga diketahui tingkat efektifitasnya. Dalam hal ini
algoritma diukur dari jumlah waktu dan ruang (space) memori yang
dibutuhkan untuk menjalankannya.
Algoritma dikatakan efisien jika suatu algoritma mampu
meminimumkan kebutuhan waktu dan ruang. Kebutuhan waktu dan ruang
suatu algoritma bergantung pada ukuran masukan (n), yang menyatakan
jumlah data yang diproses. Dalam praktik, dapat diukur waktu yang
diperlukan oleh sebuah algoritma dengan menghitung banyaknya
operasi/instruksi yang dieksekusi. Jika mengetahui besaran waktu (dalam
satuan detik) untuk melaksanakan sebuah operasi tertentu, maka dapat
dihitung berapa waktu sesungguhnya untuk melaksanakan algoritma tersebut.
Dalam melakukan perhitungan perlu diperhatikan model abstrak
pengukuran waktu/ruang yang harus independen dari pertimbangan mesin dan
compiler apapun. Besaran yang dipakai untuk menerangkan model abstrak
pengukuran waktu/ruang ini adalah kompleksitas algoritma. Ada dua macam
kompleksitas algoritma, yaitu: kompleksitas waktu dan kompleksitas ruang.
Kompleksitas waktu, T(n), diukur dari jumlah tahapan komputasi yang
dibutuhkan untuk menjalankan algoritma sebagai fungsi dari ukuran masukan
n. Kompleksitas ruang S(n), diukur dari memori yang digunakan oleh struktur
data yang terdapat di dalam algoritma sebagai fungsi dari ukuran masukan n.
Dengan menggunakan besaran kompleksitas waktu/ruang algoritma, kita dapat
menentukan laju peningkatan waktu (ruang) yang diperlukan algoritma
Dalam praktek, kompleksitas waktu dihitung berdasarkan jumlah
operasi abstrak yang mendasari suatu algoritma, dan memisahkan analisis dari
implementasi.
2.4.2.1 Kompleksitas Waktu Asimptotik
Kompleksitas waktu detail dari sebuah algoritma, terkadang
tidak terlalu diperlukan yang diperlukan adalah besaran dari kompleksitas
waktu yang mendekati besarnya kompleksitas waktu yang sebenarnya.
Kompleksitas waktu yang demikian disebut dengan kompleksitas waktu
asimtotik yang dinotasikan dengan notasi “O” disebut notasi “O-Besar”
(Big-O).
Aturan Untuk Menentukan Kompleksitas Waktu Asimptotik
adalah sebagai berikut:
1. Jika kompleksitas waktu T(n) dari algoritma diketahui,
(iv) pada algoritma selection_sort
Penjelasannya adalah sebagai berikut:
T(n) = (n + 2) log(n2 + 1) + 5n2
2. Menghitung O-Besar untuk setiap instruksi di dalam algoritma
dengan panduan di bawah ini, kemudian menerapkan teorema O
-Besar.
(a) Pengisian nilai (assignment), perbandingan, operasi aritmetik,
read, write membutuhkan waktu O(1).
(b) Pengaksesan elemen larik atau memilih field tertentu dari sebuah
……….. (2.10)
record membutuhkan waktu O(1).
(e) if C then S1 else S2; membutuhkan waktu
(d) Kalang for. Kompleksitas waktu kalang for adalah jumlah
pengulangan dikali dengan kompleksitas waktu badan (body)
kalang.
Kompleksitas waktu asimptotik:
nO(n) = O(n.n) = O(n2)
(e) While C do S; dan repeat S until C; Untuk kedua buah kalang,
kompleksitas waktunya adalah jumlah pengulangan dikali
dengan kompleksitas waktu badan C dan S.
jumlah:=jumlah + a[i]; O(1)
Pengelompokan Algoritma Berdasarkan Notasi O-Besar
Tabel 2.1: Pengelompokan Algoritma
Berdasarkan Notasi O-Besar
Kelompok Algoritma Nama
O(1)
Urutan spektrum kompleksitas waktu algoritma adalah :
O1(41)4<O4(log44n4)<4O4(n4)<4O4(n2log44n)4<O4(4n24)<4O4(n43)4<4...3<O1(4 22n4)<4 3O4(n!)
algoritma polinomial algoritma eksponensial
2.5 Algoritma Penipisan Rosenfeld
Menurut (Toussaint, -), algoritma Rosenfeld merupakan algoritma paralel
yang bekerja dengan secara berturut-turut membuang subset dari boundary /
batas dari region objek atau yang disebut juga contour pixelatau contour point
(piksel luar / tepi). Algoritma ini digunakan sebagai pembanding untuk
pengamatan visual, algoritma ini dipilih dikarenakan telah teruji untuk
melakukan penipisan citra aksara jawa dengan terpenuhinya syarat
connectivity dan One-pixel thickness sebesar 99.98% (Krinawati, 2009).
Keterangan :
Pada subiterasi 1 kondisi yang harus dipenuhi adalah : Citra[i,j] adalah obyek
Citra[i,j] bukan isolate atau end pixel, yaitu B(b)>1 Citra[i,j] adalah simple, yaitu XH(p) = 1
Citra[i,j] adalah north border
Pada subiterasi 2 kondisi yang harus dipenuhi adalah : Citra[i,j] adalah obyek
Citra[i,j] bukan isolate atau end pixel, yaitu B(b)>1 Citra[i,j] adalah simple, yaitu XH(p) = 1
Citra[i,j] adalah east border
Pada subiterasi 3 kondisi yang harus dipenuhi adalah : Citra[i,j] adalah obyek
Citra[i,j] bukan isolate atau end pixel, yaitu B(b)>1 Citra[i,j] adalah simple, yaitu XH(p) = 1
Citra[i,j] adalah south border
Pada subiterasi 4 kondisi yang harus dipenuhi adalah : Citra[i,j] adalah obyek
Citra[i,j] bukan isolate atau end pixel, yaitu B(b)>1
iterasi tidak terdapat perubahan nilai piksel dari obyek ke latar maka nilai
variabel n ini akan tetap sama dengan 0. Iterasi akan dilakukan selama masih
ada piksel yang diubah dari piksel objek menjadi piksel latar (nilai n>0).
Dengan kata lain iterasi akan dihentikan jika tidak ada lagi piksel obyek yang
berubah menjadi piksel, yaitu nilai variabel n=0.
2.6 Aksara Jawa
Aksara jawa dalam lafalan (wanda) baku memiliki urutan tertentu yang
diwakili oleh 20 aksara dasar (Ha, Na, Ca, Ra, Ka, Da, Ta, Sa, Wa, La, Pa,
Dha, Ja, Ya, Nya, Ga, Ba, Tha, Nga) seperti yang ditunjukkan pada gambar
Gambar 2.16.
Gambar 2.21: Aksara Jawa
40
Analisa dan perancangan sistem digunakan untuk menggambarkan sistem yang akan dibangun, dalam hal ini adalah proses-proses yang dibutuhkan dalam penelitian, perangkat lunak yang dibutuhkan dalam pengerjaan program, informasi perangkat keras yang digunakan untuk melakukan penelitian serta rancangan interface yang akan dibangun dalam sistem.
3.1 Gambaran Umum Sistem
Secara umum sistem yang akan dibangun adalah sistem yang menitik-beratkan pada operasi algoritma Nagendraprasad-Wang-Gupta terhadap citra masukan berupa citra aksara jawa yang akan dikenai penipisan. Sistem yang dibangun menggunakan user interface Matlab sebagai tempat pengoperasian penipisan.
Aktivitas yang dilakukan oleh sistem ditunjukkan pada Gambar 3.1.
Gambar 3.1: Diagram Konteks
Sistem Penipisan
Citra Aksara User
3.2 Analisa Kebutuhan Proses
Dari uraian mengenai gambaran umum sistem pada Gambar 3.1, terdapat beberapa proses yang harus dilakukan oleh sistem yaitu proses melakukan pengubahan citra menjadi citra biner (jika citra bukan merupakan citra biner), kemudian melakukan proses penipisan.
Dari penjelasan proses pada Gambar 3.1 maka didapatkan Data Flow Diagram(DFD) level 1 ditunjukkan pada Gambar 3.2.
Gambar 3.2: DFD level 1
3.2.1 Proses Binerisasi
Proses binerisasi adalah salah satu proses yang harus dilakukan, hal ini dikarenakan untuk melakukan proses penipisan citra masukan yang diperlukan berupa citra biner (bernilai 0 dan 1 dalam piksel gambar). Proses binerisasi yang dirancang dapat dilihat pada Gambar 3.3.
User
1
Binerisasi Citra Biner Penipisan Citra 2 Citra Tipis
Informasi Hasil Penipisan
Gambar 3.3: Proses Binerisasi
Keterangan:
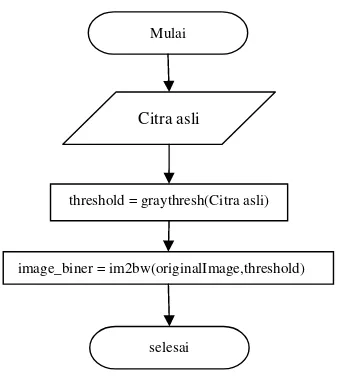
• Proses binerisasi dilakukan pada citra asli menggunakan
perintah yang sudah ada di dalam matlab yaitu im2bw yang digunakan untuk melakukan proses binerisasi atau mengubah piksel citra menjadi 0 atau 1. Sebelum proses im2bw dilakukan, proses graythresh dilakukan terlebih dahulu.
Graythresh adalah perintah yang sudah ada di dalam matlab yang dapat digunakan untuk menentukan nilai ambang piksel citra untuk diubah menjadi 0 atau 1.
3.2.2 Proses Penipisan
Proses penipisan adalah proses utama yang dilakukan, dalam hal ini penipisan yang dilakukan adalah penipisan
Mulai
Citra asli
threshold = graythresh(Citra asli)
image_biner = im2bw(originalImage,threshold)
Nagendraprasad-Wang-Gupta. Hasil penipisan inilah yang akan disimpan oleh user berupa citra penipisan, selain itu disertai pula informasi mengenai hasil penipisan seperti persentase One-Pixel Thickness (persentase memenuhi syarat One-pixel thickness), Sum
Of Object (jumlah piksel on citra sebelum ditipiskan), Sum Of
Remove Pixel (jumlah piksel citra yang dihapus), Sum Of
Templates A (jumlah piksel citra yang mengandung Templates A),
Sum Of Not Critical Point (jumlah piksel citra yang merupakan Not Critical Point) dan Running Time (lama waktu proses
penipisan) yang dapat dilihat oleh user.
3.3 Perancangan Pengujian Sistem
Salah satu syarat utama sebuah kerangka adalah keterhubungan/connectivity dan one-pixel thickness. Untuk mengetahui apakah citra hasil penipisan memiliki hasil yang baik atau tidak diperlukan pengujian, berikut adalah pengujian yang dilakukan:
3.3.1 Pengamatan Ukuran Citra
benar-benar mengalami penipisan atau tidak. Jika ukuran semakin bertambah besar atau tetap maka dapat dipastikan piksel citra tidak mengalami penghapusan piksel.
3.3.2 Sum Template A dan Sum Not Critical Point
Sum Template A dan Sum Not Critical Point digunakan untuk
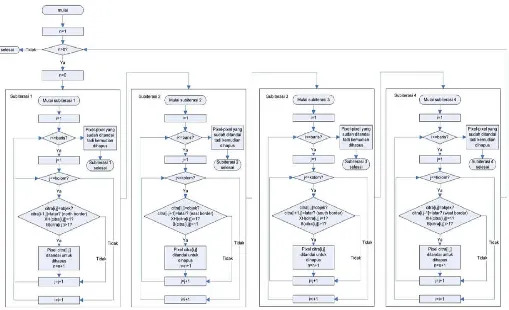
mendeteksi dan mencari jumlah citra hasil penipisan yang memiliki templateA dan bukan merupakan critical point. Flow cart dapat
Gambar 3.4: Pengujian Sum Template A dan Sum Not Critical Point
Keterangan:
• Pencarian piksel yang mengandung templateA dilakukan dengan
yaitu dengan melihat apakah piksel memiliki karakter seperti yang ada dalam Gambar 2.9, jika kondisi dalam gambar
Gambar 2.9 terpenuhi maka “TemplateA=TemplateA+1” akan
dieksekusi sehingga nilai TemplateA akan bertambah.
• Jika TemplateA telah diketahui maka selanjutnya dilakukan
eksekusi apakah TemplateA tersebut mengandung TemplateB atau TemplateC seperti yang ada pada Gambar 2.10. Jika kondisi template pada Gambar 2.10 tidak terpenuhi maka piksel adalah piksel not critical point.
3.3.3 One-pixel Thickness
One-pixel thickness digunakan untuk melihat apakah citra
Gambar 3.5: One-pixel thickness
Keterangan:
• One-pixel thickness didapatkan dari jumlah piksel citra hasil
penipisan dikurangi dengan jumlah piksel yang merupakan not critical point yang didapat seperti pada Gambar 3.4. Dari hasil pengurangan tersebut akan diketahui jumlah piksel yang merupakan critical point atau memenuhi syarat ketebalan satu piksel (One-pixel thickness).
• Setelah diketahui jumlah piksel yang memenuhi syarat ketebalan
satu piksel (One-pixel thickness) selanjutnya jumlah tersebut dirata-rata dengan cara dibagi dengan jumlah piksel keseluruhan pada citra hasil penipisan yang didapat seperti pada Gambar 3.6. Selanjutnya jumlah yang didapat dikalikan 100, jumlah inilah
Mulai
yang menjadi persentase dari One-pixel thickness yang berhasil dipenuhi pada citra hasil penipisan.
3.3.4 Sum of Pixel Object
Pengujian Sum of Pixel Object digunakan untuk mengetahui jumlah piksel citra sebelum dilakukan penipisan. Untuk mendapatkan Sum of Pixel Object ditunjukkan pada Gambar 3.6.
Gambar 3.6: Sum of Pixel Object
Keterangan:
• Proses Sum of Pixel Object dilakukan pada citra asli yang telah
dahulu, selanjutnya dilakukan eksekusi pada piksel citra yang “on” dengan membaca setiap baris dan kolom dari citra. Jika piksel adalah piksel “on” maka dilakukan eksekusi pada count sehingga nilainya bertambah, begitu seterusnya hingga seluruh piksel dieksekusi.
3.3.5 Sum of Remove Pixel
Pengujian Sum of Remove Pixel digunakan untuk mengetahui jumlah piksel citra sebelum dilakukan penipisan. Untuk mendapatkan Sum of Remove Pixel ditunjukkan pada Gambar 3.7.
Gambar 3.7: Sum of Remove Pixel
Mulai
Result= Sum of Pixel Object-count
Keterangan:
• Proses Sum of Remove Pixel dilakukan pada citra asli yang telah
dikenai proses binerisasi. Citra ini dibaca dimensinya terlebih dahulu, selanjutnya dilakukan eksekusi piksel citra yang “on” dengan membaca setiap baris dan kolom dari citra. Jika piksel adalah piksel “on” maka dilakukan eksekusi pada count sehingga nilainya bertambah, begitu seterusnya hingga seluruh piksel dieksekusi.
• Hasil eksekusi yang berupa nilai count, kemudian digunakan
untuk operasi pengurangan dengan mengurangi Sum of Pixel Object yang didapat dengan cara pada Gambar 3.8. Hasil dari operasi ini adalah Sum of Remove Pixel.
3.3.6 Running Time
Pengujian Running Time digunakan untuk melihat kecepatan yang dilakukan oleh algoritma dalam melakukan proses penipisan. Proses dalam melakukan pengujian Running Time diberikan pada
Gambar 3.8: Running Time
Keterangan:
• Pengujian Running Time menggunakan perintah yang sudah ada
di dalam matlab yaitu tic sebagai awal dimulai waktu dan toc sebagai akhir dari waktu eksekusi.
3.3.7 Connectivity
Pengujian Connectivity digunakan untuk melihat apakah citra hasil rangka serupa dengan bentuk asli dari citra masukan. Misal jika suatu citra aksara memiliki lubang maka citra hasil juga harus memiliki lubang, demikian juga jika citra asli tidak memiliki suatu piksel yang tidak putus maka citra rangka juga tidak boleh putus.
Pengujian Connectivity dilakukan dengan melakukan pengamatan langsung dari tiap-tiap citra rangka dan citra masukan secara langsung.
Mulai
tic
Prose Penipisan
tac Time=tac;
3.3.8 Waktu Asimtotik Algoritma
Pengujian Waktu Asimtotik Algoritma digunakan untuk mengetahui keefektifan algoritma. Pengujian dilakukan dengan melakukan perhitungan tiap-tiap bagian algoritma NWG dengan menggunakan ketentuan yang ada pada 2.4.2.1 Kompleksitas
Waktu Asimptotik pada halaman 29.
3.3.9 Pengamatan Visual
Pengujian dengan pengamatan visual dilakukan dengan membagi 50 kuisioner berisikan citra hasil penipisan dan citra asli algoritma NWG dengan pembanding algoritma Rosenfeld yang telah terbukti menghasilkan rangka yang memenuhi One-pixel thickness dan connectivity (Krisnawati, 2009). Kuisoner dibagikan secara random kepada 50 responden, dari hasil 50 responden ini dilakukan perhitungan jumlah citra yang dianggap mirip dan citra yang dianggap lumayan serta citra yang dianggap tidak mirip.
3.4 Perancangan Tampilan Antar-Muka
Rancangan tampilan antar-muka pada program ini adalah sebagai berikut:
3.4.1Halaman Utama
Gambar 3.9: Halaman Utama
Pada halaman utama yang merupakan halaman tempat dilakukan proses penipisan dilakukan, akan memiliki 3 buah tombol yaitu tombol thinning yang digunakan untuk melakukan proses penipisan, tombol clear yang digunakan untuk melakukan reset dan tombol Save yang digunakan untuk menyimpan citra hasil penipisan serta terdapat menu file, about dan help.
3.4.2Halaman About
Rancangan halaman About dapat dilihat pada Gambar 3.10.
File About Help
Thinning Clear Save
Gambar 3.10: Halaman About
Halaman about digunakan untuk memberikan informasi mengenai pembuat program dan kontak yang dapat dihubungi. Pada halaman ini hanya akan berisi informasi mengenai pembuat program.
3.4.3Halaman Help
Rancangan halaman help dapat dilihat pada Gambar 3.11. About
PENIPISAN CITRA AKSARA JAWA MENGGUNAKAN ALGORITMA NWG
OLEH : SASONGKO HADI NIM : 065314062
PEMBIMBING: A.RITA WIDIARTI
TEKNIK INFORMATIKA FAK.SAINS DAN TEKNOLOGI
UNIVERISTAS SANATA DHARMA YOGYAKARTA
Gambar 3.11: Halaman Help
Halaman Help digunakan untuk memberikan informasi mengenai program, dalam halaman ini hanya akan ada informasi mengenai program.
3.4.4Halaman Input Citra
Rancangan halaman input citra dapat dilihat pada Gambar 3.12. Help
Cara penggunaan Aplikasi:
1. Pilihlah sebuah citra aksara jawa.
2. Kemudian lakukan proses penipisan dengan menekan tombol ‘Proses Penipisan’. Maka hasil penipisan akan muncul di area ‘Citra Hasil Penipisan’.
3. Untuk menyimpan citra hasil penipisan, anda dapat lakukan denganmenekan tombol ‘Save’. Tentukan direktori dan nama file yanganda ingini.
4. Untuk keluar dari program tekanlah tombol ‘Keluar’.
Gambar 3.12: Halaman Input Citra
Halaman Input citra digunakan untuk memilih citra yang akan diproses di halaman utama. Dalam halaman ini terdapat dua buah tombol, cancel jika user tidak jadi memasukan citra dan open jika user jadi memilih sebuah citra yang akan diproses.
3.4.5Halaman Simpan Citra
Rancangan halaman simpan citra dapat dilihat pada Gambar 3.13. LOOK UP
File Name File Type
Open
Gambar 3.13: Halaman Simpan Citra
Halaman Input citra digunakan untuk menyimpan citra yang telah diproses dalam halaman utama. Dalam halaman ini terdapat dua buah tombol, cancel jika user tidak jadi menyimpan citra dan Save jika user jadi menyimpan sebuah citra yang telah diproses.
3.4.6Halaman Keluar Aplikasi
Rancangan halaman keluar aplikasi dapat dilihat pada Gambar 3.14.
Gambar 3.14: Halaman Keluar Aplikasi
Save Is
File Name File Type
Save
Cancel
Anda Yakin Untuk Keluar?
Halaman ini adalah halaman berupa pesan konfirmasi apakah user benar-benar ingin keluar dari program atau tidak. Dalam konfirmasi terdapat dua buah tombol, yes jika user benar-benar ingin keluar dari program dan program akan keluar. Cancel jika user tidak jadi keluar dari program.
3.5 Kebutuhan Perangkat Lunak dan Kebutuhan Perangkat Keras
Spesifikasi yang digunakan untuk membuat tugas akhir ini adalah sebagai berikut:
• Processor : AMD Atlon 64 X2 2.01 GHz
• Memory : RAM 2.5 GB
• Operating System : Windows Xp versi 2
59
Dalam bab ini akan dibahas mengenai implementasi yang telah dilakukan sebagai berikut:
4.1 Implementasi Algoritma Nagendraprasad-Wang-Gupta
Implementasi algoritma Nagendraprasad-Wang-Gupta digunakan untuk melakukan proses penipisan citra, berikut adalah pseudocode untuk proses penipisan mengunakan algoritma Nagendraprasad-Wang-Gupta:
Implementasi algoritma Nagendraprasad-Wang-Gupta: 1. Input/Q = array citra biner
2. Inisialisasi g sama dengan 1, dan h sama dengan 1
3. Jika nilai h lebih besar dari 0 lakukan langkah 4, jika tidak lakukan langkah 5.
4. Untuk setiap piksel (p) pada baris dan kolom pada input lakukan langkah 4.1 dan 4.2.
4.1 Set nilai h menjadi 0, g =1-g dan Q=Q1 dengan Q1 adalah array citra biner yang ditipiskan.
4.2 Uji apakah p = 0 (merupakan piksel obyek) jika ya lakukanlangkah 4.3 sampai 4.8 jika tidak lakukan langkah 4. 4.3 Hitung B atau jumlah 8-tetangga p yang “on”
4.4 Hitung A atau jumlah piksel 8-tetangga p dari “on” ke “off” 4.5 Hitung C atau jumlah piksel 8-tetangga p yang memiliki nilai
sebagai berikut:
(P(1)+P(2)+P(3)+P(6)==0)&(P(5)==1)&(P(7)==1)) atau
((P(3)+P(4)+P(5)+P(8)==0) & (P(7)==1) & (P(1)==1))
4.6 Hitung D atau jumlah piksel 8-tetangga p yang memiliki nilai
sebagai berikut:
((P(2)+P(5)+P(6)+P(7)==0)&(P(1)==1)&(P(3)==1)) atau
((P(1)+P(4)+P(7)+P(8)==0) & (P(3)==1) & (P(5)==1))
4.8 Uji apakah g bernilai 0 atau bernilai 1, jika bernilai 0 lakukan langkah 4.8.1 dan jika bernilai 1 lakukan langkah 4.8.2
4.8.1Jika B bernilai lebih besar dari 1 dan kurang dari 7 dan A
bernilai 1 atau E bernilai 1 dan
((P(3)+P(5))*P(1)*P(7))==0) maka lakukan langkah
4.8.1.a, jika tidak lakukan langkah 4.8.1.b.
a. Lakukan penghapusan pada piksel p pada citra Q1 dan set nilai h dengan h+1.
b. Kembali lakukan langkah 4.
4.8.2Jika B bernilai lebih besar dari 1 dan kurang dari 7 dan A
bernilai atau E bernilai 1 dan
((P(7)+P(1))*P(3)*P(5))==0) maka lakukan langkah
4.8.2.a jika tidak lakukan langkah 4.8.2.b.
a. Lakukan penghapusan pada piksel p pada citra Q1 b. Kembali lakukan langkah 4 dan set nilai h dengan h+1.
5. Proses penipisan selesai
(1-4.2 Implementasi Binerisasi
Implementasi Binerisasi dilakukan dengan menggunakan metode Otsu, metode ini telah ada dalam matlab sehingga tinggal menggunakan fungsi yang ada di dalam matlab. Implementasi binerisasi terdapat pada pseudocode berikut:
Implementasi Binarisasi:
1. Cari nilai intensitas citra terbesar (max)
2. Bandingkan nilai max dengan 1, jika max=1 proses binarisasi selesai, jika max > 1 lakukan langkah 3
3. Cari varian antar kelas terbesar dari nilai intensitas citra (sigma)
4. Bandingkan tiap nilai intensitas pada citra (intens_citra) dengan sigma, jika intents_citra > sigma maka intents_citra = 1, jika tidak maka intents_citra = 0
Proses binerisasi dilakukan pada citra asli menggunakan perintah yang sudah ada di dalam matlab yaitu im2bw yang digunakan untuk mengubah nilai piksel menjadi 0 dan 1. Input dari im2bw didapat dari variabel threshold yang berisikan perintah graythresh dengan inputan citra asli yang
digunakan untuk mendapatkan nilai ambang batas dari piksel citra. Nilai ambang batas yang didapatkan digunakan untuk menentukan piksel yang akan diubah menjadi bernilai 1 atau 0.
4.3 Implementasi Pengujian
Implementasi pengujian yang dilakukan meliputi Running Time yang digunakan untuk menghitung lama waktu proses penipisan, Sum of Remove
Pixel yang digunakan untuk menghitung jumlah piksel sesudah proses
piksel citra sebelum penipisan, One-pixel thickness yang digunakan untuk mengetahui persentase piksel yang memenuhi syarat One-pixel thickness, Sum Template A yang digunakan untuk mengetahui jumlah Template A dan
Sum Not Critical Point yang digunakan untuk mengetahui jumlah piksel
yang bukan critical point.
4.3.1 Implementasi Pengamatan Ukuran Citra
Implementasi Pengamatan Ukuran Citra tidak dilakukan dengan
coding matlab, namun dilakukan dengan pengamatan secara
langsung terhadap tiap-tiap citra asli dan citra rangka. Setelah melakukan pengamatan, data yang dihasilkan dilakukan perhitungan dan mendapatkan rata-rata ukuran citra asli dan citra rangka.
4.3.2 Implementasi Sum Template A dan Sum Not Critical Point
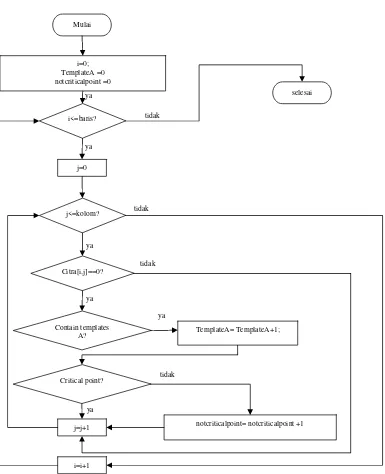
Implementasi Sum Template A dan Sum Not Critical Point ditunjukkan pada pseudocodeberikut ini:
Implementasi Sum Template A dan Sum Not Critical Point: 1. Inisialisasi variabel contain_A = 0
2. Untuk setiap titik obyek pada citra rangka lakukan langkah 3 3. Uji apakah merupakan template A1, jika ya lakukan langkah
3.a jika tidak lakukan langkah 4.
a.Uji apakah merupakan template B1 atau C,
i. Jika ya, not critical point bertambah 1dan lakukan langkah 4.
ii. Jika tidak , nilai contain_A bertambah 1, lakukan langkah 4 4. Uji apakah merupakan template A2, jika ya lakukan langkah
4.a jika tidak, lakukan langkah 5.
i. Jika ya not critical point bertambah 1 lakukan langkah 5
ii. Jika tidak nilai contain_A bertambah 1, lakukanlangkah 5
5. Uji apakah merupakan template A3, jika ya lakukan langkah 5.a jika tidak lakukan langkah 6.
a. Uji apakah merupakan template B3 atau C
i. Jika ya not critical point bertambah 1 dan lakukan langkah 6
ii. Jika tidak nilai contain_A bertambah 1, lakukan langkah 6
6. Uji apakah merupakan template A4, jika ya lakukan langkah 6.a
a. Uji apakah merupakan template B4 atau C, i. Jika ya nilai not critical point bertambah 1 ii. Jika tidak nilai contain_A bertambah 1
4.3.3 Implementasi One-pixel thickness
Implementasi One-pixel thickness akan menghasilkan persentase piksel citra hasil penipisan yang memenuhi syarat One-pixel
thickness. Implementasi One-pixel thickness ditunjukkan pada
pseudocodeberikut ini:
Implementasi One-pixel thickness:
1. Hitung jumlah piksel citra rangka (SumOfPixelSkeleton) dengan cara yang sama pada Implementasi Sum of Pixel Object 2. Hitung jumlah notCriticalPoint seperti pada Implementasi
Sum Template A dan Sum Not Critical Point.
3. Hitung Onepixelthickness dengan cara SumOfPixelSkeleton dikurangi notCriticalPoint.
4. Hitung persentase OnePixelThickness dengan cara
OnePixelThickness dibagi SumOfPixelSkeleton dikali 100%.
Selanjutnya dari Implementasi Sum Template A dan Sum Not Critical
Point dimana akan diketahui jumlah piksel yang merupakan Not Critical Point, piksel ini akan dijadikan pengurang pada jumlah
piksel citra hasil penipisan. Hasil perhitungan tersebut kemudian diketahui persentasenya dengan cara pengurangan antara jumlah piksel citra hasil penipisan dan piksel Not Critical Point dibagi dengan jumlah piksel citra hasil penipisan.
4.3.4 Implementasi Sum of Pixel Object
Implementasi Sum of Pixel Object ditunjukkan pada pseudocode berikut ini:
Implementasi Sum of Pixel Object:
1. Inisialisasi temp dengan array citra biner 2. Inisialisasi dimensi citra
3. Inisialisasi count dengan 0
4. Untuk setiap piksel(p) pada baris dan kolom pada input lakukan langkah 4.1.
4.1Uji apakah piksel(p) bernilai 0, jika ya lakukan langkah a, jika tidak lakukan langkah a, jika tidak kembali lakukan langkah 4.
a. Nilai count bertambah 1.
Proses Sum of Pixel Object dilakukan dengan membaca dimensi citra terlebih dahulu, dimensi ini digunakan untuk menentukan batas perulangan for. Jika terdapat piksel 0 atau “on”, maka count akan ditambah satu hingga semua piksel pada citra dieksekusi.
4.3.5 Implementasi Sum of Remove Pixel