ANALISA TORSI, LENTUR, LENDUTAN DAN LINTANG PADA TAMPANG I

(1)

ANALISA TORSI, LENTUR, LENDUTAN DAN LINTANG

PADA TAMPANG I

TUGAS AKHIR

Diajukan untuk Melengkapi tugas-tugas dan Memenuhi Syarat untuk Menempuh Ujian Sidang Sarjana Teknik Sipil

Disusun oleh

DAPOT H MALAU

03 0303 060

SUB JURUSAN STRUKTUR

JURUSAN TEKNIK SIPIL

FAKULTAS TEKNIK

UNIVERSITAS SUMATERA UTARA

2009

(2)

KATA PENGANTAR

Puji syukur penulis ucapkan atas kehadirat Tuhan Yang Maha Esa yang telah memberikan rahmat dan hidayat-Nya hingga selesainya tugas akhir ini dengan judul “ANALISA TORSI, LENTUR, LENDUTAN DAN LINTANG PADA PROFIL I”

Tugas akhir ini disusun untuk diajukan sebagai syarat dalam ujian sarjana teknik sipil bidang studi struktur pada Fakultas Teknik Universitas Sumatera Utara Medan. Penulis menyadari bahwa isi dari tugas akhir ini masih banyak kekurangannya dan jauh dari kata sempurna. Hal ini penulis akui karena keterbatasan pengetahuan dan kurangnya pemahaman penulis. Untuk penyempurnaannya, saran dan kritik dari bapak dan ibu dosen serta rekan mahasiswa sangatlah penulis harapkan.

Penulis juga menyadari bahwa tanpa bimbingan, bantuan dan dorongan dari berbagai pihak, tugas akhir ini tidak mungkin dapat diselesaikan dengan baik. Oleh karena iu pada kesempatan ini penulis menyampaikan rasa terimakasih yang sebesar-besarnya kepada kedua orang tua yang senantiasa penulis muliakan yang dalam keadaan sulit telah mau memperjuangkan hingga penulis dapat menyelesaikan perkuliahan dan sampai saat ini.

Penulis juga tidak lupa mengucapkan terima kasih kepada :

1. Bapak Prof.Dr. Ing. Johannes Tarigan, IPU selaku ketua jurusan departemen teknik sipil Universitas Sumatera Utara.

2. Bapak Ir. Terunajaya M.Sc. selaku wakil ketua jurusan departemen teknik sipil Universitas Sumatera Utara.

3. Bapak Prof.Dr. Ing. Johannes Tarigan, dan Bapak Ir. Sanci Barus M.T, selaku dosen pembimbing dan co-pembimbing yang telah banyak meluangkan waktu,

(3)

tenaga dan pikiran untuk memberikan bimbingan dalam menyelesaikan tugas akhir ini.

4. Bapak Ir. Syahrizal M.T, selaku dosen wali sekaligus dosen pengajar selama menempuh studi.

5. Bapak/ Ibu dosen pengajar departemen teknik sipil Universitas Sumatera Utara. 6. Seluruh pegawai administrasi yang telah memberikan bantuan dalam kemudahan

penyelesaian administrasi.

7. Rekan-rekan mahasiswa departemen teknik sipil Universitas Sumatera Utara khususnya buat Himsar, Ronald, Tony, Masana, Ganda, Marshal dan lain lain yang telah membantu penulis didalam mencari bahan untuk menyelesaikan tugas akhir ini.

Sekali lagi penulis memohon maaf yang sebesar-besarnya apabila terdapat kesalahan penulisan dan penyusunan tugas akhir ini. Akhir kata penulis berharap tugas akhir ini berguna bagi semua pihak yang memerlukan.

Medan, Februari 2009 030404060 Dapot H Malau

(4)

Tugas akhir ini aku persembahkan kepada Ayah dan Ibu

Sebagai tanda hormat dan terima kasih Atas segala kasih sayang dan doa

(5)

ABSTRAK

Pada bangunan teknik sipil banyak dijumpai struktur balok bersilang/grid. Struktur Grid adalah struktur yang elemen batangnya hanya menerima gaya dalam lentur satu arah (dengan arah vektor, momen lentur searah bidang grid), lintang dan torsi. Keadaan istimewa pada struktur grid adalah beban yang bekerja mengarah tegaklurus bidang grid, deformasi aksial pada elemen grid diabaikan dan tidak terjadi twisting (putaran) dengan arah vektor yang tegak bidang grid. Struktur grid biasanya ditemui pada struktur jembatan, rangka pelat lantai dan sejenisnya. biasanya struktur balok bersilang ini dikombinasikan dengan pelat beton sehingga merupakan satu kesatuan struktur.

Pada struktur balok bersilang/grid tersebut dapat terjadi gaya torsi sebagai akibat dari gaya luar yang bekerja di samping juga gaya lentur dan gaya geser, Gaya torsi tersebut dapat menimbulkan tegangan torsi dan tegangan warping, Tegangan torsi pada balok bersilang dapat terjadi di badan profil dan pada sayap atau flens profil sedangkan untuk tegangan warping terjadi pada flens akibat dari flens yang melintir ke arah lateralnya. Tegangan-tegangan yang terjadi ini harus diperhitungkan karena dapat mengakibatkan kelebihan tegangan (overstress) pada struktur apabila dikombinasikan antara tegangan yang satu dengan yang lainnya sehingga dapat melampaui tegangan baja yang diijinkan.

Dari hasil perhitungan balok bersilang maka dapat dilihat akibat beban terpusat maka akan timbul momen torsi dimana momen torsi pada batang utama (main girder) merupakan momen lentur pada batang pengaku (stiffner), harga momen torsi maksimum yang terjadi sekitar 0.1%-0.2 % dari momen lentur maksimum. Akibat momen torsi maka akan timbul tegangan torsi pada badan dan flens serta tegangan warping akibat flens melentur ke arah lateral, tegangan warping dikombinasikan dengan tegangan lentur dan geser akibat lentur murni. Pertambahan tegangan akibat torsi dibandingkan akibat lentur murni untuk tegangan geser pada badan profil sekitar 20% sedangkan pada flens sekitar 50-100%, tegangan geser pada flens akibat warping < 1% sedangkan tegangan lentur akibat warping sekitar 5-10 %,

Lendutan yang maksimum yang terjadi masih di bawah lendutan yang diijinkan untuk struktur baja yaitu L/250

(6)

DAFTAR ISI

KATA PENGANTAR ...i

ABSTRAK ...iv

DAFTAR ISI...vi

DAFTAR NOTASI ...ix

BAB I. PENDAHULUAN ...11 1.1. Latar belakang ...11 1.2. Permasalahan ...12 1.3. Tujuan ...13 1.4. Pembatasan Masalah ...13 1.5. Metodologi... ...14

BAB II. TEORI DASAR ...15

2.1 Jenis-jenis Struktur pada Bangunan Teknik Sipil ... 15

2.1.1 Truss (rangka) ... 15

2.1.2. Grid (Balok Silang) ... 15

2.1.3. Frame (Portal) ... 16

2.2 Jenis-jenis balok bersilang ... 16

2.3 Struktur pada balok bersilang ... 17

2.4 Gaya-gaya pada balok bersilang ... 17

2.5 Bidang Torsi ... 18

2.5.1 Perletakan Torsi ... 18

2.5.2 Penggambaran bidang Torsi ... 19

2.6 Momen Primer dan Sekunder Akibat Torsi Pada Tampang I ... 21

(7)

2.6.2 Torsi pada tampang I ... 21

2.7 Gaya torsi pada penampang I pada balok bersilang ... 22

2.8 Torsi Murni ... 23

2.9 Torsi terpilin ... 23

2.10 Tegangan geser akibat torsi ... 32

2.10.1 Akibat torsi murni ... 32

2.10.2 Akibat warping ... 33

BAB III. METODE ANALISA ... 35

3.1.Dasar-dasar Metode Elemen Hingga... 35

3.2 Metode Element Hingga berdasarkan usaha Virtual ... 36

3.3 Fungsi dan Bentuk dan Peralihan Umum ... 43

3.4. Struktur Balok (Beam Element) ... 51

3.4.1 Fungsi bentuk dan koefisien kekakuan ... 51

3.4.2 Matriks kekakuan elemen ... 54

3.5 Rangka batang bidang (Plane truss) ... 56

3.5.1 Matriks kekakuan pada koordinat lokal ... 56

3.5.2 Matriks kekakuan elemen pada koordinat global ... 60

3.6 Portal Bidang (Plane Frame) ... 62

3.6.1 Matriks kekakuan elemen portal (frame) ... 63

3.6.2 Matriks kekakuan elemen ... 66

3.6.3 Transformasi koordinat ... 69

3.7 Struktur Grid (Grid Element) ... 72

3.7.1 Pengaruh torsi ... 72

(8)

3.7.3 Transformasi koordinat ... 75

3.8 Kompatibilitas, Keseimbangan, Penentuan Dari Matriks Kekakuan... 78

3.9 Syarat keseimbangan ... 82

3.10 Beban Nodal Ekuivalen ... 83

BAB V. APLIKASI... 86

4.1 Contoh balok silang/grid ... 86

4.2 Beban yang dipikul oleh bekerja/dipikul grid baja ... 86

4.3 Perhitungan ... 87

BAB V. KESIMPULAN DAN SARAN ... 120

5.1. Kesimpulan... ... 120

5.2. Saran... ... 121

DAFTAR PUSTAKA... 122 LAMPIRAN

(9)

DAFTAR NOTASI

E = Modulus elastis bahan (Modulus Young)

G = Modulus geser bahan

µ = Poisson ratio x,y,z = Koordinat kartesian

σ = Tegangan

τ = Tegangan geser

M = Momen lentur

Mz = Momen torsi total Ms = Momen torsi murni

W

M = Momen torsi akibat warping J = Konstanta torsi

w

C = Konstanta torsi terpilin

s

τ = Tegangan geser akibat torsi murni

P = Beban terpusat

L = Panjang bentang

{u} = Matriks perpindahan [T] = Matriks Transformasi

(10)

[B] = Matriks regangan-perpindahan [K] = Matriks kekakuan

Δ = Lendutan

(11)

BAB

I PENDAHULUAN

1.1 Latar Belakang.

Suatu balok dibebani akan timbul resultante tegangan yang secara umu tediri dari tiga gaya dan tiga kopel. Gaya gaya tersebut adalah gaya aksial Nx,gaya geser Dy, Dz dan kopelnya adalah momen punter Mx dan momen lentur My dan Mz..Deformasi batang dapat dianalisa dengan meninjau masing-masing resultante tegangan secara terpisah dan menentukan pengaruhnya pada elemen batang.

Saat ini sangat dibutuhkan ruangan yang relatif luas pada bangunan bertingkat.Sehingga untuk memenuhi hal ini maka dibutuhkan balok silang untuk menahan beban luar, dan juga terkadang untuk memperindah nilai arsitektur maka diperlukan balok silang. Dan balok silang ini mengalami gaya gaya dalam yang akan mengakibatkan deformasi struktur.

Untuk profil yang simetris maka tidak akan mengalami torsi jika tidak ada gaya luar.Jadi dalam hal ini balok silang digunakan profil I yang simetris.

Balok silang adalah struktur bidang yang dibentuk oleh balok menerus yang saling bertemu atau bersilang dimana pertemuan dari sambungan tersebut adalah kaku.Berbeda dari portal bidang yang gaya luarnya berada dalam bidang struktur, gaya luar pada balok silang tegak lurus bidang struktur, dan vektor momen semua kopel berada dalam bidang balok. Arah beban seperti ini dapat mengakibatkan puntir dan lenturan pada sejumlah batang. Penampang lintang setiap batang memiliki dua sumbu simetri, sehingga lenturan dan puntir tidak saling bergantungan.

P

(12)

Gbr 1.1 Balok silang yang mengalami beban terpusat

Bila suatu struktur diberi beban , batangnya akan mengalami deformasi (perubahan bentuk yang kecil)sehingga titik titik pda struktur akan berpindah keposisi yang baru.Umumnya semua titik kecuali tumpuan yang tidak dapat bergerak akan mengalami perpindahan. Deformasi tersebut menimbulkan respons gaya dalam.

1.2 Permasalahan

Pada struktur balok bersilang/grid dapat terjadi gaya torsi sebagai akibat dari gaya luar P yang bekerja, juga gaya lentur dan gaya geser.Gaya torsi tersebut dapat menimbulkan tegangan torsi dan warping.Tegangan torsi pada balok bersilang I dapat terjadi dibadan profil dan pada sayap atau flens profil, sedangkan untuk tegangan warping terjadi pada flens yang melintir kearah

(13)

lateralnya.Tegangan-tegangan yang terjadi ini harus diperhitungkan karena dapat mengakibatkan kelebihan tegangan (over stress) pada struktur apabila dikombinasikan antara ysng satu dan yang lainnya sehingga dapat melampaui tegangan baja yang diijinkan.

Gbr 1.2 Profil I yang mengalami torsi

1.3.Tujuan

Adapun tujuan penulisan dari tugas akhir ini adalah untuk mengetaui tegangan torsi dan tegangan warping pada flens dan badan pada balok bersilang dengan menggunakan profil I sebagai akibat dari gaya dalam.

1.4 Pembatasan Masalah

Yang menjadi batasan masalah adalah : 1. Perletakan yang dipakai adalah jepit-jepit 2. Profil yang digunakan adalah satu jenis 3. Menentukan lendutan maksimum pada grid

4. Menentukan besar gaya gaya dalam pada balok bersilang 5. Menentukan tegangan lentur dan geser pada badan dan flens

(14)

6. Menentukan tegangan torsi 7. menentukan tegangan warping

8. Contoh perhitungan dilakukan terhadap balok bersilang

1.1. Metodologi

Metode yang digunakan dalam penulisan tugas akhir ini adalah literatur yaitu dengan mengumpulkan data-data dan keterangan dari buku-buku yang berhubungan dengan pembahasan pada tugas akhir ini serta masukan-masukan dari dosen pembimbing. Untuk perhitungan dilakukan dengan metode elemen hingga,dengan perhitungan manual.

(15)

BAB II

TEORI DASAR

2.1 Jenis-jenis Struktur pada Bangunan Teknik Sipil 2.1.1 Truss (rangka)

Definisi truss (rangka) adalah konstruksi yang tersusun dari batang-batang tarik dan batang-batang tekan saja, umumnya dari baja, kayu, atau paduan ringan guna mendukung atap atau jembatan, umumnya dapat menahan gaya aksial saja.

Truss 2 dimensi adalah truss yang dapat menahan beban pada arah datar saja (sumbu x, y) umumnya beban yang bekerja adalah beban terpusat nodal.

Truss 3 dimensi adalah truss yang dapat menahan beban pada semua arah (sumbu x, y dan z) umumnya beban yang bekerja adalah beban terpusat nodal.

2.1.2. Grid (Balok Silang)

Definisi grid (balok silang) adalah kerangka yang terdiri dari dua atau lebih bagian konstruksi yang disambungkan secara kaku (guna stabilitas) pada arah mendatar, umumnya dapat menahan gaya yang bekerja tegak lurus (sumbu y) terhadap bidang datarnya (sumbu x), struktur seperti sistem lantai, sistem atap dan lantai jembatan dapat dianalisis sebagai grid atau balok silang.

(16)

2.1.3. Frame (Portal)

Definisi frame (portal) adalah kerangka yang terdiri dari dua atau lebih bagian konstruksi yang disambungkan guna stabilitas, umumnya dapat menahan gaya momen, gaya geser dan aksial.

Frame 2 dimensi adalah frame yang dapat menahan beban pada arah datar saja (sumbu x, y) umumnya beban yang bekerja adalah beban terpusat nodal dan beban batang. Frame 3 dimensi adalah frame yang dapat menahan beban pada semua arah (sumbu x, y dan z) umumnya beban yang bekerja adalah beban terpusat nodal dan beban batang.

2.2 Jenis-jenis balok bersilang

Balok bersilang/grid banyak terdapat pada struktur bangunan sipil seperti pada bangunan gedung, rangka atap, pelat lantai, jembatan dan lain-lain Beberapa jenis atau pola pada balok bersilang dapat dilihat pada gambar 2.1 dimana arah balok bersilang dapat horizontal, vertikal maupun diagonal

(17)

2.3 Struktur pada balok bersilang

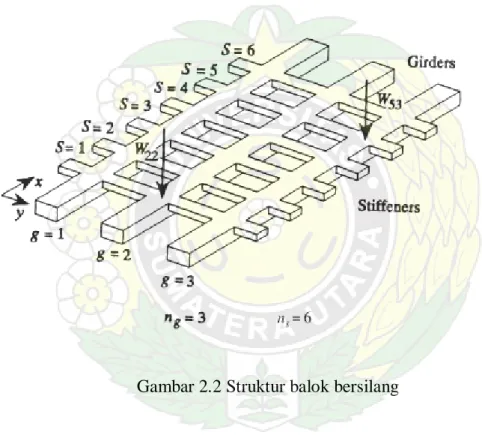
Pada balok bersilang strukturnya terdiri dari 2 bagian dimana terdapat balok utama (main girder) dan pengaku (stiffner), biasanya penampang pada balok bersilang dapat mempunyai ukuran yang sama ataupun berbeda dalam hal ini ukuran balok utama lebih besar dibandingkan pengakunya seperti pada gambar 2.2

Gambar 2.2 Struktur balok bersilang

2.4 Gaya-gaya pada balok bersilang

Pada balok bersilang karena bebannya pada arah sumbu z maka gaya-gaya yang terjadi adalah momen akibat lentur murni, gaya geser serta torsi . Untuk momen dan geser sama seperti pada balok baja biasa

(18)

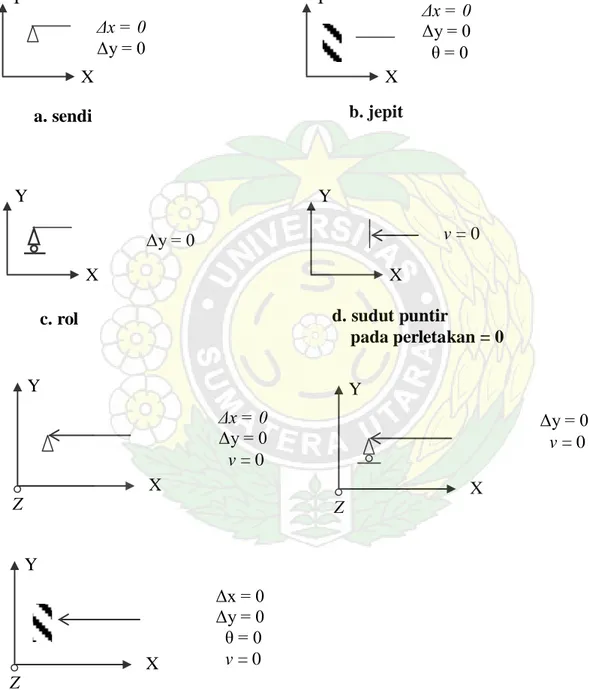
2.5 Bidang Torsi 2.5.1 Perletakan Torsi

Pada jenis perletakan tanpa torsi dikenal dengan sendi, jepit dan rol (lihat gambar 2.3). Khusus pada torsi maka diadakan simbol perletakan seperti pada gambar 2.3. d.

Y X Δx = 0 Δy = 0 Y X Δx = 0 Δy = 0 θ = 0 a. sendi b. jepit Y X Y X Δy = 0 v = 0

c. rol d. sudut puntir

pada perletakan = 0 Δx = 0 Δy = 0 v = 0 Y X Z Δy = 0 v = 0 Y X Z Δx = 0 Δy = 0 θ = 0 v = 0 Y X Z

Gambar 2.3 Perletakan torsi

(19)

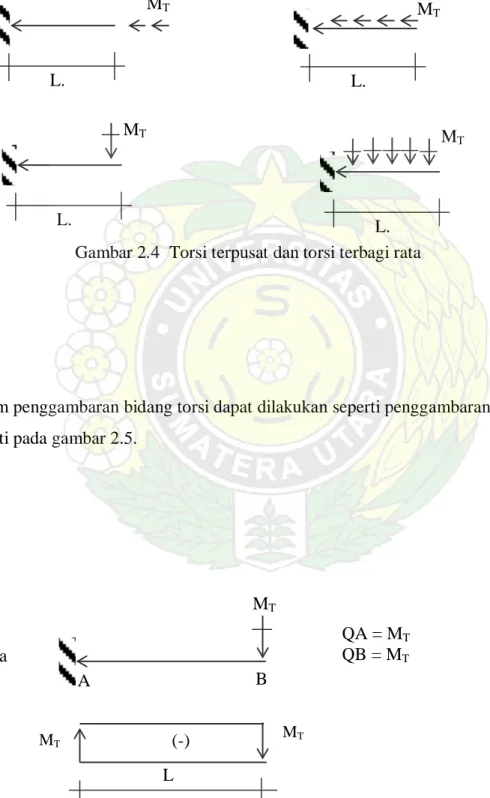
2.5.2 Penggambaran bidang Torsi

Momen torsi dapat dibuat dengan simbol seperti pada gambar 2.4 (a), tetapi dapat juga dibuat analog dengan gambar 2.4 b (seperti gaya terpusat atau beban terbagi rata).

Dalam penggambaran bidang torsi dapat dilakukan seperti penggambaran gaya lintang seperti pada gambar 2.5.

a. MT L. MT L. b. MT L. MT L. Gambar 2.4 Torsi terpusat dan torsi terbagi rata

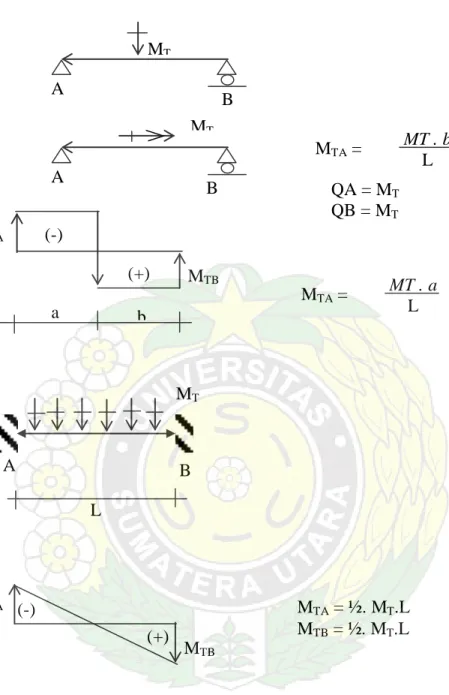
a MT A B MT (-) MT QA = MT QB = MT L

(20)

Gambar 2.5. Gambar bidang Torsi

Penggambaran tanda bidang momen sama seperti menutup dan membuka skrup. Kalau arah Momen Torsi kearah menutup maka digambarkan negatif dan kalau kearah membuka maka digambar positif.

MT A _B c. L (-) (+) MTA MTB MTA = ½. MT.L MTB = ½. MT.L MT A B b. QA = MT QB = MT MTA = MT . b L MTA MTB (-) (+) a _b MTA = MT . a L MT A B

(21)

2.6 Momen Primer dan Sekunder Akibat Torsi Pada Tampang I 2.6.1 Inertia Polar pada tampang I

Inertia polar pada tampang I adalah seperti pada gambar 2.9, inersia torsi didapat dihitung :

...2.1

2.6.2 Torsi pada tampang I

Jika suatu konstruksi dengan profil dibebani dengan MT seperti pada gambar 2.7a,

maka bidang torsinya adalah paa gambar 2.7.b, IT =

Σ

n i = ⅓ . an . b 3 n A B C a. GIT 2 MT (-) (+) b. MT MT L/2 L/2

b33 IT = a1 a2 a3 b1 b2 b3

Gambar 2.6 Inertia polar

(22)

2.7.Gaya torsi pada penampang I pada balok bersilang Gaya torsi pada penampang I terdiri dari dua jenis :

Torsi murni (Pure Torsion) Torsi terpilin (Warping Torsion)

Gambar 2.8 Struktur yang mengalami torsi

2.7.1 Torsi Murni (Pure Torsion)

Terjadi jika penampang melintang yang rata tetap menjadi rata setelah torsi bekerja dan penampang hanya mengalami rotasi selama torsi bekerja.dengan kata lain torsi murni hanya mengakibatkan perputaran profil karena tidak adanya penahan profil

(23)

Misalkan pada balok memikul torsi murni sebesar Ms maka besarnya torsi tersebut adalah dz d GJ Ms= φ ...(2.2) dimana Ms = momen torsi murni

G = modulus geser = ) 1 ( 2 +µ E

dimana J = konstanta torsi

2.7.2 Torsi terpilin (Warping Torsion)

Keadaanya sama dengan balok yang mengalami lentur ke luar bidang gambar akibat beban lateral . Jadi torsi terpilin ini flens balok berpindah secara lateral selama terpuntir .

(24)

Jika balok memikul torsi terpilin, maka flens tekan balok akan melengkung ke salah satu arah lateral dan flens tariknya akan melengkung ke arah lateral lainnya Penampang balok menjadi tidak rata lagi, flens akan melendut sebesar uf , lendutan ini menimbulkan tegangan lentur dan geser pada flens tersebut.

Torsi terpilin/warping terdiri atas 2 bagian yaitu :

1. Torsi murni (Pure Torsion), menyebabkan rotasi elemen (=φ).

2. Translasi yang menyebabkan balok melentur secara lateral (akibat warping). Penurunan persamaan diferensial untuk torsi penampang I

Vf = gaya geser yang bekerja pada flens akibat balok melendut secara lateral, pada saat balok melendut lateral badan balok tetap datar.

untuk φ sangat kecil maka tanφ ≈φ φ = 2 h U_f maka 2 h Uf =φ ...(2.3) dz d h dz dUf φ 2 = ...(2.4) 2 2 2 2 2 dz d h dz U d _f φ = ...(2.5) 3 3 3 3 2 dz d h dz U d _f φ = ...(2.6)

Dari mekanika teknik diketahui

f f f EI M dz U d − = 2 2 ...(2.7) f

(25)

f

M = Momen lentur lateral pada flens

Gaya lintang _f f f EI_f dz U d dz dM V ₃ 3 − = = ...(2.8) atau f f f EI V dz U d − = 3 3 dimana ₃ 3 3 3 2 dz d h dz U d _f φ = . ...(2.9) atau ) 2 ( ₃ 3 dz d h EI V_f =− _f φ . ...(2.10) Kita mengetahui bahwa komponen momen torsi M yang menimbulkan lenturan _w pada flens = Vf.h = ₃ 3 2 2 dz d h EI_f φ − ...(2.11) dengan 2 .h2 I

C_w = f C = konstanta torsi terpilin (warping coefficient) _w

Momen torsi total = momen torsi akibat rotasi (M_S)+ momen toris akibat lentur lateral (M_W) W S Z M M M = + ...(2.12) 3 3 dz d EC dz d GJ M_Z = φ − _W φ ...(2.13)

Persamaan diferensial dari akan dicari penyelesaiannya, ruas kiri dan kanan dibagi dengan E.C_W maka dz d C E GJ dz d C E M W W Z φ φ . . 3 3 − = − ...(2.14)

(26)

misalkan 2 .CW =λ E GJ sehingga W Z C E M dz d dz d . 2 3 3 − = −λ φ φ ...(2.15)

Persamaan diferensial tersebut adalah homogen maka ada 2 jawaban yaitu jawaban umum PD homogen dan jawaban khusus PD non homogen

Jawaban PD homogen ₃ 2 0 3 = − dz d dz d φ _λ φ ...(2.16) Misalkan φ = A.emz mz e m A dz d . . = φ .. ...(2.17) mz e m A dz d . . 2 2 2 = φ . ...(2.18) mz e m A dz d . . 3 3 3 = φ ...(2.19) 0 . . . .m3emz − 2Amemz = A λ ...(2.20) 0 ) (m2 −λ2 = m  m₁ =0 m₂ =0 dan m₃ =−λ Jadi A1.e A2.e A3 Z Z + + = λ −λ φ . ...(2.21) Dalam fungsi hiperbolikus dapat ditulis :

C z B z A + + = λ λ φ₁ .sinh .cosh ...(2.22) dimana W EC GJ = λ

(27)

Jawaban khusus dari W Z C E M dz d dz d . 2 3 3 − = −λ φ φ ...(2.23) ) ( 1 2 = f z φ dan M_Z = f(z) ) ( . 1 ) ( ) ( 2 1 3 1 3 z f C E dz z df dz z f d W − = −λ ...(2.24) diperoleh f₁(z)

Maka jawaban total φ =φ₁+φ₂ dengan φ = sudut torsi

Sekarang kita tinjau balok 2 perletakan dengan profil I dimana ujung-ujung berupa sendi. Momen torsi bekerja di tengah bentang, maka akan ditentukan persamaan untuk sudut torsi φ dan besar tegangan geser akibat torsi murni dan warping serta tegangan normal yang terjadi akibat lendutan arah lateral, di sini langkah –langkahnya adalah sebagai berikut : Distribusi momen torsi total M_Z =M_S +M_Wyang menyebabkan geser pada flens. Distribusi momen torsi M akibat torsi murni _Z

dz d GJ

M_S = φ.

Distribusi momen torsi ₃

3 . dz d C E MW W φ − =

Karena M bernilai konstan maka _Z φ dapat berbentuk A+B.z

A adalah jawaban umum persamaan diferensial homogen sedangkan B jawaban khusus persamaan diferensial homogen

Kembali ke persamaan diferensialnya

w Z w EC M dz d EC GJ dz d . 3 3 − = − φ φ ...(2.25) Bz A+ = φ

(28)

B dz dφ ₌ 0 2 2 = dz d φ Maka w w EC T EC GJ B /2 0− =− . ...(2.26) GJ T B 2 =

Jadi jawaban umum PD homogen adalah

z GJ T C z B z A 2 . cosh . sinh + + + = λ λ φ ...(2.27) Syarat batas 1 φ =0 pada z=0 dan z=L 0 = φ 0 = z maka 0=B+C. ...(2.28) 2. ₂ 0 2 = dz d φ pada z=0 dan z=L GJ T z B z A dz d 2 . sinh . . . cosh . . + +− =λ λ λ λ φ z B z A dz d cosh . . sinh . . 2 2 2 2 λ λ λ φ ₌₋ ₊ B + = 0 0 diperoleh B =0 . ...(2.29) Harga 2.29 disubstitusikan ke 2.28 diperoleh C= 0

0 =

dz dφ

pada z=L/2 ...(2.30)

(29)

GJ T L A 2 2 cosh 0= λ + ) 2 cosh 1 ( 2GJ L T A λ λ − = ...(2.31)

Dari harga A, B dan C diperoleh persamaan untuk jawaban total

z GJ T z L GJ T 2 sinh ) 2 cosh 1 ( 2 + − = _λ λ λ φ ...(2.32) ) 2 cosh sinh ( 2 L z z GJ T λ λ λ λ φ = − ...(2.33)

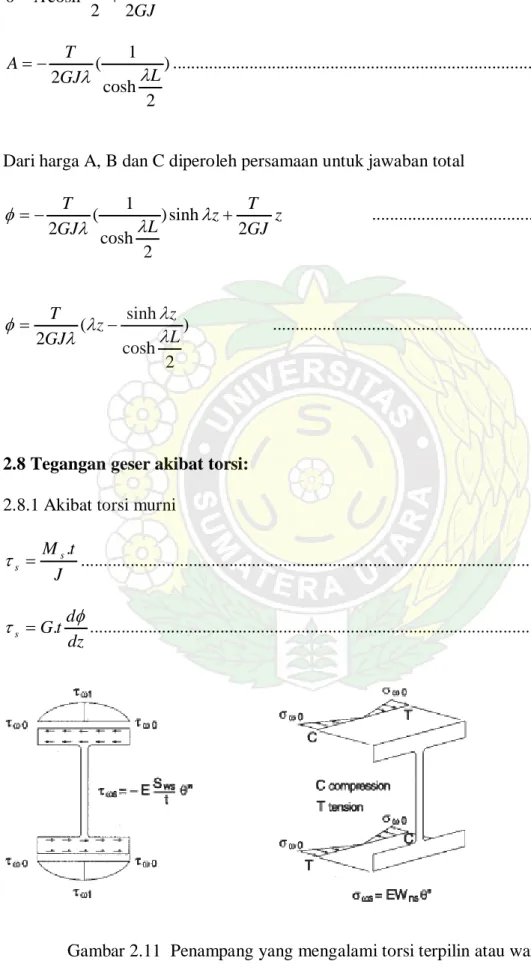
2.8 Tegangan geser akibat torsi: 2.8.1 Akibat torsi murni

J t M_s s . = τ ...(2.34) dz d t G s φ τ = . ...(2.35)

(30)

2.8.2 Akibat warping

Pada gambar 2.6 penampang yang mengalami warping maka

f f f t b b t b Q . 8 4 . . 2 2 = = ...(2.36) f f f f s t I Q V . . = τ ...(2.37) f f f f w t I dz d h EI t b . / ). 2 / .( ).( . 8 / ( 2 3φ 3 τ = − ...(2.38) 3 3 2 16 dz d h b E w ϕ τ = ...(2.39) f f bw I E M . = σ ...(2.40) f f f I E M dz U d . 2 2 = ...(2.41) dimana 2 .h Uf =φ 2 2 2 2 2 dz d h dz U d _f φ = f f I E M dz d h . 2 2 2 − = φ 2 2 . dz d h C E M w f φ = ...(2.42) dimana 2 .h2 If Cw=

(31)

Tegangan normal maksimum terjadi pada x=b/2 ) 2 ( ) 2 ( . ₂ 2 f f bw I b dz d h I E φ σ = ...(2.43) 2 2 4 dz d Ebh bw φ σ = ...(2.45)

(32)

BAB III

METODE ANALISA

3.1 Dasar-dasar Metode Elemen Hingga

Struktur dalam istilah teknik sipil adalah rangkaian elemen-elemen yang sejenis maupun yang tidak sejenis. Elemen adalah susunan materi yang mempunyai bentuk relatif teratur. Elemen ini akan mempunyai sifat-sifat tertentu yang tergantung kepada bentuk fisik dan materi penyusunnya. Bentuk fisik dan materi penyusun elemen tersebut akan menyebutkan totalitas element tersebut. Totalitas sifat elemen inilah disebut dengan kekakuan elemen. Jika diperinci maka sebuah struktur mempunyai Modulus elastis (E), Modulus geser (G), Luas penampang (A), Panjang (L) dan Inersia (I). Hal inilah yang salah satu yang perlu dipahami didalam pemahaman elemen hingga nantinya, bahwa kekakuan adalah fungsi dari E,G,A,L,I.

Sebagaimana telah didefinisikan para pendahulu-pendahulu, bahwa energi itu adalah kekal dan jika aksi (energi) dilakukan terhadap suatu materi, maka materi akan melakukan suatu reaksi sebesar aksi tersebut. Reaksi dari materi ini akan disebut dengan gaya dalam.”GAYA DALAM “ yang ada dalam struktur didefinisikan yaitu, Gaya Normal, Gaya Lintang, dan Gaya Momen yang akan mempengaruhi bentuk fisik materi tersebut. Perubahan bentuk fisik materi ini disebut dengan peralihan (displacement). Metode elemen hingga adalah suatu metode pemaparan bagaimana

(33)

perjalanan aksi hingga timbul reaksi dalam materi, atau metode untuk meramal besar reaksi dan reaksi apa yang timbul dari materi tersebut.

3.2 Metode Element Hingga berdasarkan usaha Virtual

Ambil contoh sebuah elemen tiga dimensi yang terletak pada salib sumbu Cartesius dalam kordinat X,Y dan Z peralihan umum (generic displacement) yang terjadi pada sembarangan titik dalam elemen dinyatakan dalam vektor kolom u :

u =

{

u ,,v w

}

...(3.1) dimana u,v dan w berturut-turut merupakan translasi dalam arah x,y dan z

Bila pada elemen dikerjakan gaya tubuh (Body force), gaya-gaya ini akan dimasukkan kedalam vektor b, seperti sebagai berikut :

b =

{

b_x,b_y,b_z

}

………(3.2)

Notasi b ,_x b_y, dan b mewakili kokponen-komponen gaya (persatuan volume, _z luas atau panjang) yang bekerja pada sembarangan titik sesuai dengan arah x,y dan z.

Sementara ini, peralihan titik nodal (nodal displacement) q yang diperhitungkan hannyalah berupa translasi dalam arah x,y dan z. Bila n = jumlah _en titik nodal elemen , maka:

q =

{ }

q ( i = 1,2,3,... ₁ n ) _en ...(3.3) dimana :

i

q =

{

q_xi_,q_yi,q_zi

}

=

{

ui,vi,wi

}

...(3.3b)

Demikian pula untuk gaya titik nodal ( nodal action) p sementara ini hanya diambil dalam arah x,ydan z saja

(34)

i

q =

{

p_xi,p_yi,p_zi

}

Hubungan antara peralihan umum dan peralihan titik nodal dinyatakan oleh fungsi bentuk peralihan (displacement shape function) dalam tulisan ini digunakan persamaan:

u = fq ...(3.5) dalam hal ini notasi f adalh matriks segiempat yang menunjukan bahwa u sepenuhnya tergantung pada q. Hubungan regangan-peralihan diperoleh dengan menurunkan matriks peralihan umum.proses ini ditunjukkan dalam pembentukan matriks d yang disebut diferensial linier dan dapat dibentuk dalam perkalian matriks:

ε = d u ...(3.6) dalam persamaan ini operator d menyatakan hubungan antra vektor regangan ε dngan vertor peralihan umum (vektor u). Dengan mensubsitusikan persamaan (3.5) kedalam persamaan (3.6) akan diperoleh:

ε = b q ...(3.7) dimana B = d f ...(3.8) Matriks B menunjukan regangan yang terjadi pada sembarangan titik dalam elemen akibat satu satuan peralihan tititk nodal.

Dari persamaan (2.3) dalam bab II.2 telah diperoleh hubungan tegangan-regangan dalam bentuk sebagai berikut.

σ = E ε ...(3.9) dimana E adalah matrik yang menghubungkan antara vektor tegangan σ dan regangan ε. Jika persamaan (3.7) disubsitusikan kedalam persamaan (3.9) menghasilkan:

(35)

dimana perkalian matriks E B menunjukan tegangan pada sembarang titik bila terjadi satu-satun peralihan titik nodal.

Prinsip usaha virtuil : bila ada struktur dalam keadaan setimbang, dikerjakan suatu peralihan virtual yang kecil dalam batas-batas devormasi yang masih dapat diterima , maka usaha virtual dari beban luar tadi sama dengan enegi regangan virtual dari tegangan dalamnya.

Bila perinsip diatas kita terapkan pada elemen hingga, akan diperoleh:

δUe= δWe ...(3.11a)

dimana δU adalah energi regangan virtual dari regangan dalam dan δW merupakan usaha virtual beban luar yang bekerja pada elemen. Untuk memperoleh kedua nilai tersebut, kita asumsikan adanya peralihan virtual kecil yang dinyatakan dalm vektor δq. Jadi,

δq = { δqi} ( i = 1,2,3,... n ) en ...(3.11b)

kemudian peralihan umum virtual akan menjadi [lihat persamaan (3.5)]

δu = f δ q ...(3.11c)

Dengn menggunakan hubungan regangan-peralihan dalam persamaan (3.7) didapat: δε = B δq ...(3.11d) Maka enegi regangan virtual dalam δU dapat ditulis sebagai berikut:

δUe=

∫

v T dv . σ δε ...(3.11e)

selanjutnya usaha virtual dari gaya titik nodal dan gaya tubuh menjadi :

_ = +      v T v T dv d b f p q dv EB B . . . . ………(3.11i)

persamaan ( j ) dapat dituliskan kembali menjadi :

K q = p - p_b ...(3.12) Dimana K =

∫

v BTE B dv ...(3.13) Dan p_b =

∫

v fTb dv ………..(3.14)

Matriks K dalam persamaan (3.13) adalah matriks kekakuan elemen, yaitu gaya yang terjadi pada titik nodal akibat adanya satu-satuan peralihan titik nodal. Sedangka n titik vektor Pb pada persamaan (3.14) menunjukan gaya nodal ekuivalen akibat bekerjanya gaya tubuh dalam vektor b.

Tegangan dan regangan yang diturunkan diatas hanya bergantung pada peralihan titik nodal. Bila terjadi regangan awal ε , maka regangan total dapat o

dituliskan sebagai berikut :

ε = ε + Cσ o ...(3.15)

dimana C adalah matriks hubungan regangan-tegangan. Dari persamaan terdahulu telah kita dapatkan :

(37)

C = E−1 ...(3.16) Dengan menyelesaikan vektor tegangan σ pada persamaan (3.13) akan diperoleh :

σ = E (ε -εo) ...(3.17)

bila persamaan ini digunakan untuk menggantikan s dalam persamaan (h), maka akhirnya rumus tersebut menghasilkan:

K q = p + p_b + p₀ ...(3.18)

Dimana p0 =

∫

v

BTE εodv ...(3.19a)

Kita dapat menganggap vektor p0merupakan beban titik nodal ekivalen akibat

regangan awal, sama halnya dengan yang ditimbulkan oleh perubahan temperatur. gambar 2.2 melakiskan sebuah sebuah elemen aksial , yang kini akan diselesaikan dengan metode elemen hingga. Dalam gambar hanya ditunjukkan hanya ada satu peralihan umum, yaitu u dalam arah x. jadi persamaan (3.1) akan diperoleh :

u = u

Gaya tubuh yang memungkinkan adalah komponen tunggal b_x

Peralihan titik nodal q1 dan q2 menunjukan translasi arah x pada nodal 1 dan 2 (gambar 2.2). Jadi persamaan (3.3) menjadi :

q = { q1,q2} = { u1,u2 }

gaya nodal yang terjadi pada titik 1 dan 2 adalah (persamaan 3.4)

p = {p1,p2} = (px1,px2}

diasumsikan peralihan u disembarangan titik pada elemen merupakan fungsi linier dari x, seperti berikut:

(38)

q2 q1 2 1 u 1 1 (c) (b) (a) f2 f1 L x

gambar 3.1 Elemen aksial

persamaan ini dikenal sebagai fungsi peralihan. Persamaan ini dapat dinyatakan dalam fungsi bentuk peralihan [ persamaan (3.5)], dengan mencari kedua konstanta, yaitu c ₁ dan c . Pada x = 0 didapat ₂ c = ₁ q ; dan untuk x = L akan diperoleh ₁ q = ₂ c + ₁ c L. ₂ Jadi

2

c = q - ₂ q /L. Bila konstanta ini disubsitusikan ke dalam persamaan (k), akan ₁ diperoleh :     ₋ − = x L q q q u 2 1 1 ...( 3.19c)

sekarang persamaan ini bukan lagi merupakan merupakan fungsi dari konstanta, melainkan fungsi dari peralihan titik nodal. Bila persamaan digabungkan dengan persamaan (3.5),maka akan didapat :

    − = L x L x u 1 = f g ...(3.19d)

(39)

dimana f =

[

]

    − L x L x f f₁ ₂ 1

kedua fungsi bentuk peralihan ini diperlihatkan dalam gambar2.2 b dan c

Hubungan regangan peralihan [persamaan 3.6, 3.7 dan 3.8] untuk elemen aksial hanya terdiri dari turunan saja:

ε = ε = d u = x dx du = q dx df = Bq maka B = dx df = 1 −

[

1 1

]

L ...( 3.19e) dengan cara yang sama kita dapatkan hubungan tegangan-regangan [persamaan 3.9 dan 3.10] sebagai berikut: σ = σ = Eε = x Eε = E Bq x jadi E = E dan E B =

[

−1 1

]

L E ...(3.19f)

kemudian kekakuan elemen dapat dihitung dari persamaan 3.13 sebagai berikut :

K =

∫

v BTE B DV = _

[

−

]

∫

    − A L dx dA L E . 1 . 1 1 1 0 2 ...(3.19g) = L EA       − − 1 1 1 1

dengan mengasumsikan luas penampang A besarnya konstan.

Gambar 2.5 (a) dan (b) melukiskan beban merata b yang bervariasi secara _x linier (beban persatuan panjang) dan didefinisikan sebagai berikut:

x b = b + ₁

(

)

L x b b₂ − ₁

akibat gaya tubuh ini, persamaan 3.14 akan menghasilkan beban titik nodal ekivalen sebesar :

(40)

(

)

      + + =     − +           − = =

∫

2 1 2 1 1 2 1 0 0 2 2 6 . 1 . b b b b L dx L x b b b L x L x dx b f p L L x T b ...(3.19g) 2 1 u (a) L bx Pb2 Pb1 x b1 b2 (b) dx bx

Gambar 3.2 Beban merata aksial

Sebaliknya, jika elemen dibebani perubahan temperatur yang serangan ΔT , regangan awal akibat ini besarnya :

3.3 Fungsi dan Bentuk dan Peralihan Umum

Asumsikan bahwa fungsi peralihan dinyatakan sebagai perkalian antara matrik geometri q dengan matrik vektor dari konstanta sembarang c sebagai berikut :

U = g c ...(3.20) Kemudian dicari operator g untuk setiap titik nodal sehingga :

(41)

dimana h = {g} ( i = 1,2,3,…n ) _en ………(3.22) dan g menunjukkan matriks g yang dihitung pada titik nodal i, dengan mengasumsikan bahwa matriks h adalah matriks bujur sangkar dan non singula, kemudian konstanta c dapat dicari

c = h−1q ...(3.23a)

subsitusikan persamaan 4.3 kedalam persamaan 4.1, sehingga diperoleh :

u = g c = h−1q ...(3.23b )

jika persamaan ( b ) ini dibandingkan dengan persamaan (3.5), dapat dilihat bahwa fungsi bentuk yang diinginkan adalah :

f = g h−1 ... (3.24a)

untuk elemen aksial, pertama kali dipasang fungsi peralihan asumsi [ persamaan (k) dari bab II.3 ] kedalam persamaan (4.1)

jadi u =

[

]

_      2 1 1 c c x ... ( 3.24b) diperoleh g =

[ ]

1 x ... (3.24c) perkatikan, matriks h terdiri dari dua bahagian yang dipisahkan oleh garis pembagi seperti pada persamaan dibawah ini:

h = _            2 1 1 0 1 g g L ...(3.24d) invers dari h adalah:

h−1=     − L x L x 1 ...(3.24e)

(42)

kemudian dari persamaan terdahulu kita peroleh :

f = g h−1=

[

1−x L x L

]

... ( 3.24f)

dengan koefisien sembarang c , ₁ c , ₂ c , ... ₃ c , dengan fungsi peralihan asumsi tadi n

dapat dianggap sebagai peralihan umum ( generalized displacement ), kemudian dapat pula diturunkan hubungan antara peralihan titik nodal, gaya ( aksi ), kekakuan, dengan besaran-besaran “umum“-nya. Akhirnya, persamaan dapat dituliskan tanpa tergantung kepada gaya tubuh ataupun regangan awal :

K q = p ...(3.24g)

(43)

Gambar 2.6(a) melukiskan sebuah elemen torsi yang dapat berupa tongkat pada mesin atau batang pada struktur grid. Elemen ini juga memiliki peralihan umum tunggal θ , yaitu rotasi kecil dalam arah x. Jadi, _x

u = θ_x

akibat adanya peralihan elastis ini ( rotasi kecil tadi ) akan dihasilkan gaya tubuh:

b = m _x

berupa momen ( persatuan panjang ) yang bekerja dalam arah x positif.

Peralihan titik nodal [lihat gambar 3.6 (a)] terdiri dari rotasi aksial yang kecil pada titik pada nodal 1 dan 2. maka:

q =

{

q₁,q₂

} {

+ φx₁,θx₂

}

Gaya titik nodal yang dihasilkan pada titik 1 dan 2 adalah:

p =

{

p₁,p₂

} {

= M_x₁,M_x₂

}

berupa momen ( atau torsi ) dalam arah x

f2 f1 q1 (c) Pb1 q2 (b) (a) x L 1 2 z x

(44)

Karena hanya ada dua peralihan titik nodal pada elemen torsi ini, maka dapat digunakan fungsi peralihan yang linier yaitu :

2

1 c

c

x = +

φ ... ( 3.28b)

seperti halnya pada elemen aksial, fungsi bentuk peralihan pada elemen torsi ini akan menjadi: f = g h−1 =

[

]

    − L x L x f f₁ ₂ 1 ... ( 3.28c)

seperti yang diperlihatkan gambar 3.3(b) dan (c).

Kita dapat menurunkan hubungan regangan-peralihan untuk elemen torsi dengan penampang lingkaran seperti yang terlihat pada gambar 3.4. Asumsikan bahwa jari-jari penampang tetap lurus selama terjadi deformasi torsi. Disini dapat kita simpulkan bahwa regangan geser γ akan bervariasi linier terhadap panjang jari-jari r seperti berikut: ω φ γ r dx d r x = = ... ( 3.28d ) dimana ω adalah putaran (twist), yaitu besarnya perubahan dari putaran sudut, jadi :

dx dθ_x

(45)

z y dx T ymax x R r

gambar 3.4 Deformasi Torsi

dari persamaan (s) dapat dibuktikan bahwa nilai maksimum regangan geser terjadi pada permukaan. Jadi,

ω γmax =R

dimana R adalah jari-jari penampang (lihat gambar 3.4). selanjutnya, pada persamaan (s)jelas terlihat bahwa operator diferensial d yang menghubungkan γ denganθ adalah _x

d = dx

d

r ... (3.28f)

maka, matriks regangan-peralihan B akan menjadi:

B = d f =

[

−1 1

]

L r

... ( 3.29g)

Yang mirip dengan matriks B pada elemen aksial, kecuali muncul nilai r.

Pada elemen torsi, hubungan antara tegangan geser τ ( lihat gambar 3.4) dengan regangan gesernya γ dinyatakan dengan

(46)

dimana simbol G menunjukka n modulus geser material. Jadi,:

E = G dan E B = G B ... (3.29i )

Kekakuan torsi sekarang dapat diperoleh dengan menurunkan persamaan (3.13) sebagai berikut: K =

∫

Ε v T BdV B ... (3.29j)

[

]

rdrd dx L Gr L R . . . 1 1 1 1 0 2 0 0 2 2 θ π −      − =

∫ ∫∫

= _      − − 1 1 1 1 L GJ

dengan GJ konstan. Momen inersia polar J didefenisikan sebagai berikut:

J =

∫∫

= π _π θ 2 0 0 4 3 2 . . . R R d dr r ... (3.29k )

Untuk penampang yang bukan lingkaran, momen inersia polar digantikan oleh konstanta torsi.

Gambar 2.8 menunjukkan elemen torsi dengan dua jenis penampang lingkaran; sengah bentang yang lain mempunyai jari-jari R. Untuk memperoleh kekakuan struktur ini, kita dapat menggunakan persamaan (3.13), hasilnya:

K = _x L R L L R d dx dr r dx dr r L G π _θ

∫ ∫ ∫

∫ ∫

_      +       − − 2 0 2 0 2 0 2 0 3 3 2 . . . 1 1 1 1 = _      − 1 1 1 1 2 17 L GJ ... (3.30)

jika persamaan (3.30) dibandingkan dengan (3.31); disini terlihat bahwa perbedaan kedua persamaan tersebut hannya terletak pada konstanta pengalinya saja.

(47)

beban titik nodal ekivalen akibat torsi terpusat M yang berjarak x = L/G dari titik _x nodal 1 [gambar 3.8(a)] menjadi:

( )

_      =       − = = ₌ 1 5 6 6 1 6 1 1 6 x x L x T x x M M f M P ... (3.31 )

untuk masalah tersebut hasilnya dapat diperoleh dengan menghitung besarnya fungsi bentuk peralihan pada titik sejauh x = L/G . perhitungan ini sama sekali tidak membutuhkan proses integrasi [pada persamaan (3.13)]. Selanjutnya, hasil perhitungan dari elemen torsi dengan penampang kombinasi ini akan sama dengan elemen biasa (ukan kombinasi) karena kedua elemen ini menggunakan fungsi bentuk yang sama. Gambar 2.8(b) memperlihatkan torsi aksial merata berbentuk parabolik (persatuan panjang) yang ditentukan sebagai berikut:

2 2 2 L x m m_x = _x ... (3.32 ) ( b ) mx mx2 dx x Mx ( a ) L 2 L 2 L 5 2 1 Pb1 4R 2R Pb 2 x

(48)

akibat pengaruh torsi ini, beban titik nodal ekivalen yang dihitung dari persamaan (3.14) adalah :

∫

= dx L x m f P_b T _x ₂ . 2 2 ………. (3.33)

∫

          − = L x L x L x L m 0 2 1 12       = 3 1 12 2L m_x

yang sekali lagi tidak tergantung kepada perbedaan luas penampang.

3.4. Struktur Balok (Beam Element)

Balok adalah struktur yang dimodelkan secara bidang datar dimana beban yang bekerja pada arah longitudinalnya.

3.4.1 Fungsi bentuk dan koefisien kekakuan

Pada Gambar 3.6 kita mengambil satu elemen dari balok. titik koordinat pada kedua ujung dari elemen ini ditandai dengan δ₁,δ₂,δ dan ₃ δ₄(perpindahan linier dan sudut). Pada gambar ini juga menunjukkan gaya (atau momen) P ,₁ P ,₂ P dan ₃ P akibat ₄

(49)

perpindahan titik elemen δ Koordinat sistem elemen atau lokal x ,_i ydan zyang dikekang pada titik awal di sebelah kiri ujung

Gambar 3.6 Balok dengan koordinat titik δ₁ sampai δ₁ dan gaya titik P ₁

Koefisisen kekakuan k_ij didefinisikan sebagai gaya pada titik koordinat i ketika satu satuan perpindahan diberikan pada titik koordinat j . Gambar 3.10 menunjukkan koefisien kekakuan untuk elemen balok akibat satu satuan perpindahan pada koordinat 1

(50)

Gambar 3.7 Koefisien kekakuan balok akibat satu satuan perpindahan pada titik koordinat

Perhitungan dari koefisien k_i_,_jdan fungsi bentuk N₁(x), N₂(x),N₃(x)dan )

(

4 x

N untuk kurva seperti yang ditunjukkan pada gambar 3.10 maka

EI x w dx y d ( ) 4 2 = ………...………....…. (3.34) dimana w(x)= gaya luar persatuan panjang.

E= modulus elastisitas

I = momen inersia penampang

Untuk balok seperti pada gambar 3.10 dengan tidak ada beban untuk w(x)= 0, maka

persamaan menjadi 0 4 4 = dx y d ………. ...…. (3.35)

Dengan mengintegralkan persamaan 3.35 empat kali, persamaan untuk perpindahan pada balok pada suku dari keempat konstanta integrasi, C ,₁ C ,C₂ ₃danC ₄

4 3 2 2 3 1 2 1 6 1 C x C x C x C y= + + + ………...…. (3.36)

Konstanta integrasi dari C sampai ₁ C dihitung dari syarat batas . Untuk balok seperti ₄ pada gambar 3.9 maka syarat batas adalah :

(51)

Pada x=0 y(0)=1 dan (0) =0 dx dy ………...……… (3.37) Pada x= L y(L)=1 dan ( ) =0 dx L dy …………....………. (3.38)

Dengan mensubstitusikan syarat batas pada persamaan untuk memperoleh

1

C ,C ,C₂ ₃dan C maka hasil persamaan dari fungsi bentuk untuk balok adalah ₄ 3 2 1( ) 1 3 2       +       − = L x L x x N ………...…...…. (3.39)

dimana N₁(x) sebagai pengganti dari y(x)akibat kondisi δ₁ =1 terhadap balok. Kita memperoleh untuk fungsi bentuk yang lain adalah

2 2( ) 1       − = L x x x N ………...………..…. (3.40) 3 2 3( ) 3 2       −       = L x L x x N ………...………. (3.41)       − = 1 ) ( 2 4 L x L x x N ………...………. (3.42)

Total perpindahan y(x)pada koordinat x akibat perpindahan δ₁,δ₂,δ dan ₃ δ₄ pada titik koordinat dari elemen balok dapat dituliskan :

4 4 3 3 2 2 1 1( ). ( ). ( ). ( ). ) (x N x δ N x δ N x δ N x δ y = + + + ……….…………...…. (3.43)

3.4.2 Matriks kekakuan elemen

(52)

dx x N x N EI k _j i L j i ( ) ( ) 0 , ″ ″ =

∫

………..………. (3.44)

dimana N_i″(x)dan N_j″(x) adalah turunan kedua dari fungsi bentuk persamaan 3.39 sampai 3.42 yang berhubungan dengan x , Eadalah modulus elastisitas dan Iadalah momen inersia penampang balok, sebagai contoh untuk menghitung k , kita ₁₂ memasukkan persamaan 3.39 dan 3.40 ke persamaan 3.44 kita peroleh :

2 12 6 L EI k = ………...………. (3.45) 4 14 3 13 2 12 1 11 1 k δ k δ k δ k δ P = + + + …..………..………. (3.46)

Secara analog maka untuk koordinat lain diperoleh

4 24 3 23 2 22 1 21 2 k δ k δ k δ k δ P = + + + …..………. (3.47) 4 34 3 33 2 32 1 31 3 k δ k δ k δ k δ P = + + + …..………. (3.48) 4 44 3 43 2 42 1 41 4 k δ k δ k δ k δ P = + + + …..………. (3.49)

atau dalam bentuk matiks dapat ditulis

            =             44 43 42 41 43 33 32 31 42 32 22 21 14 13 12 11 4 3 2 1 k k k k k k k k k k k k k k k k P P P P …..………... (3.50)

Dengan menggunakan persamaan 3.42 ke dalam persamaan 3.43 maka koefisien kekakuan dapat diperoleh sebagai berikut :

                        − − − − − − =             4 3 2 1 2 2 2 2 3 4 3 2 1 4 6 2 6 6 12 6 12 2 6 4 6 6 12 6 12 δ δ δ δ L L L L L L L L L L L L L EI P P P P ………... (3.51)

(53)

atau dalam bentuk sederhana

( )

P =

[ ]

k

( )

δ ………...……... (3.52)

3.5 Rangka batang bidang (Plane truss)

Rangka batang bidang adalah struktur rangka batang yang dimodelkan dan dianalisis secara bidang datar dengan beban yang bekerja terletak pada bidang datar tersebut, Arah beban yang bekerja :

1. Beban terpusat arah vertikal yang bekerja di titik buhul. 2. Beban terusat arah horizontal yang bekerja di titik buhul.

Gambar 3.11 Rangka batang bidang dengan perpindahan titik dan gaya

3.5.1 Matriks kekakuan pada koordinat lokal

Suatu batang truss (rangka batang) bidang mempunyai empat titik koordinat dengan dua titik koordinat pada masing-masing titik hubungnya seperti pada Gambar 3.11. Untuk perpindahan kecil, dapat diasumsikan bahwa hubungan gaya

(54)

Gambar 3.8 Perpindahan penampang pada rangka batang bidang

dan perpindahan untuk titik koordinat sepanjang sumbu batang (koordinat 1 dan 3 pada gambar 3.11, tidak bergantung pada perpindahan transversal sepanjang koordinat. Asumsi ini adalah ekivalen untuk menyatakan bahwa perpindahan sepanjang titik koordinat 1 dan 3 tidak menghasilkan gaya sepanjang titik koordinat 2 dan 4. Seperti pada gambar 3.12 jika u=u(x) adalah perpindahan pada potongan x , perpindahan pada potongan x+dxakan menjadi u+du. Elemen dx pada posisinya

yang baru telah berubah panjangnya sebesar du dan karena itu regangan menjadi dx du

.,

karena hukum Hooke maka rasio tegangan terhadap regangan sama dengan modulus elastisitas E , dapat ditulis menjadi

AE P dx

du = ………...……... (3.53) Dengan mengintegralkan persamaan terhadapx diperoleh

C x AE P x u( )= + ………...……... (3.54) dimana C adalah konstanta integrasi. Dengan syarat batas u =1 pada x=0 dan u =0 pada x= , kita memperoleh fungsi perpindahan L u₁ =u₁(x)akibat δ₁ =1, karena

(55)

L x x

u1( )= 1− ………...…...…... (3.55)

Secara analog maka fungsi perpindahan

L x x

u₂( )= ………...…...…... (3.56)

Koefisien kekakuan akibat aksial di titik koordinat mungkin diperoleh menggunakan persamaan dx x u x u AE k _j i L j i, ₀ ( ) ( ) ′ ′ =

_∫

...…...….... (3.57)

Penggunaan dari persamaan ini untuk elemen menghasilkan koefisien sebagai berikut :

L AE k k₁₁ = ₃₃ = dan L AE k k₁₃ = ₃₁ =− …...…... (3.58) dimana E= modulus elastisitas

I = momen inersia penampang L= panjang batang

Koefisien kekakuan untuk ujung sendi elemen, akibat titik koordinat 2 dan 4 semua sama dengan nol, karena gaya tidak menghasilkan perpindahan pada titik ini. Karena itu dengan menyusun koefisien pada persamaan 3.56 kita memperoleh persamaan kekakuan untuk batang truss menjadi

                        − − =             3 3 2 1 4 3 2 1 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 1 δ δ δ δ L AE P P P P …...…... (3.59)

(56)

atau dengan notasi yang sederhana

( )

[ ]

T juga membuat transformasi dari vektor perpindahan titik

3.5.2 Matriks kekakuan elemen pada koordinat global

δ ... (3.69)

k adalah pada sistem sumbu global koordinat

Gaya ujung P pada sistem sumbu lokal kemudian dihitung dengan persamaan 3.62. Akan tetapi dapat juga menghitung gaya elemen (tekan dan tarik) dengan menentukan pertama kali deformasi aksial dan gaya aksial pada elemen.

(59)

Perpindahan dari elemen ini sepanjang sumbu x longitudinal dapat dituliskan sebagai berikut : θ δ δ θ δ δ )cos ( )sin ( 3 − 1 + 4 − 2 = ∆ ... (3.70) Regangannya menjadi L ∆ =

ε dan tegangan σ =Eε =E∆/Ldan gaya aksial L

EA A

P = σ = ∆/ ... (3.71) atau dengan menggunakan persamaan

[

(δ₃ −δ₁)cosθ +(δ₄ −δ₂)sinθ

]

= L EA P ... (3.72) Dimana E= modulus elastisitas

I = momen inersia penampang L= panjang batang

θ = sudut antara sumbul global X dan sumbu lokal x

3.6 Portal Bidang (Plane Frame)

Portal bidang adalah struktur portal yang dimodelkan dan dianalisa secara bidang datar dengan beban yang bekerja terletak pada bidang tersebut. Struktur portal bidang dapat pula berbentuk balok menerus terletak di atas beberapa tumpuan dan sering disebut sebagai struktur balok Arah beban yang bekerja merupakan :

(60)

1. Beban terpusat /terbagi rata arah vertikal (berat sendiri, beban gerak sesuai dngen peraturan muatan).

2. Beban terpusat/terbagi rata arah horizontal (beban angin, beban gempa dengan statis ekivalen).

3. Beban terpusat arah putaran se arah atau berlawanan arah jarum jam.

3.6.1 Matriks kekakuan elemen portal (frame)

Matriks kekakuan pada koordinat titik dari suatu elemen dari portal bidang diperoleh dari kombinasi antar matriks kekakuan akibat pengaruh aksial dan matriks kekakuan akibat pengaruh lentur. Hasil matriks dari kombinasi hubungan P dan perpindahan _i δ _i pada koordinat titik adalah seperti pada Gambar 3.14 :

Gambar 3.10 Elemen portal bidang

Pada Gambar 3.14 kita mengambil satu elemen dari portal .dengan titik koordinat pada kedua ujung dari elemen ini ditandai dengan δ₁,δ₂,δ₃dan δ₄(perpindahan linier dan sudut). Pada gambar ini juga menunjukkan gaya (atau momen) P ,₁ P ,₂ P dan ₃ P akibat ₄ perpindahan titik elemen δ Koordinat sistem elemen atau lokal x ,i ydan zyang

dikekang pada titik awal di sebelah kiri ujung seperti pada Gambar 3.14. Koefisisen kekakuan kij didefinisikan sebagai gaya pada titik koordinati ketika satu satuan

(61)

perpindahan diberikan pada titik koordinat j . Gambar menunjukkan koefisien kekakuan untuk elemen balok akibat satu satuan perpindahan pada koordinat 1

Gambar 3.11 Koefisien kekakuan portal bidang akibat satu satuan perpindahan pada titik koordinat

Perhitungan dari koefisien ki,jdan fungsi bentuk N1(x), N2(x),N3(x)dan N4(x)

(62)

EI x w dx y d ( ) 4 2 = ... (3.73) dimana w(x)= gaya luar persatuan panjang.

E= modulus elastisitas

I = momen inersia penampang

Untuk balok seperti pada gambar 3.15 dengan tidak ada beban untuk w(x)= 0,

persamaan menjadi : 0 4 4 = dx y d ... (3.74)

Dengan menintegralkan persamaan empat kali, persamaan untuk perpindahan pada balok pada suku dari keempat konstanta integrasi, C ,₁ C ,C₂ ₃dan C ₄

4 3 2 2 3 1 2 1 6 1 C x C x C x C y= + + + ... (3.75) Konstanta integrasi dari C sampai ₁ C dihitung dari syarat batas . Untuk portal bidang ₄ seperti pada gambar 3.15 maka syarat batas adalah :

Pada x=0 y(0)=1 dan (0) =0 dx dy ... (3.76) Pada x= L y(L)=1 dan ( ) =0 dx L dy ... (3.77)

Dengan mensubstitusikan syarat batas pada persamaan untuk memperoleh

1

C ,C ,C₂ ₃dan C maka hasil persamaan dari fungsi bentuk untuk portal bidang adalah ₄ 3 2 1( ) 1 3 2       +       − = L x L x x N ... (3.78)

dimana N₁(x) sebagai pengganti dari y(x)akibat kondisi δ₁ =1 terhadap balok. Kita memperoleh untuk fungsi bentuk yang lain adalah

(63)

2 2( ) 1       − = L x x x N ... (3.79) 3 2 3( ) 3 2       −       = L x L x x N ... (3.80)       − = 1 ) ( 2 4 L x L x x N ... (3.81)

Total perpindahan y(x)pada koordinat x akibat perpindahan δ₁,δ₂,δ dan 3 δ4 pada

titik koordinatdari elemen balok dapat dituliskan :

4 4 3 3 2 2 1 1( ). ( ). ( ). ( ). ) (x N x δ N x δ N x δ N x δ y = + + + ... (3.82)

3.6.2 Matriks kekakuan elemen

Persamaan umum untuk menghitung koefisien kekakuan untuk balok adalah dx x N x N EI k _j i L j i, ₀ ( ) ( ) ″ ″ =

∫

...(3.83) dimana N_i″(x)dan Nj (x) ″

adalah turunan kedua dari fungsi bentuk persamaan yang berhubungan dengan x , Eadalah modulus elastisitas dan Iadalah momen inersia penampang balok, sebagai contoh untuk menghitung k , kita memasukkan persamaan ₁₂ ke persamaan dan persamaan kita peroleh :

2 12 6 L EI k = ...(3.84) 4 14 3 13 2 12 1 11 1 k δ k δ k δ k δ P = + + + ...(3.85) Secara analog maka untuk koordinat lain diperoleh

4 24 3 23 2 22 1 21 2 k δ k δ k δ k δ P = + + + ...(3.86) 4 34 3 33 2 32 1 31 3 k δ k δ k δ k δ P = + + + ...(3.87)

(64)

4 44 3 43 2 42 1 41 4 k δ k δ k δ k δ P = + + + ...(3.88) atau dalam bentuk matiks dapat ditulis

            =             44 43 42 41 43 33 32 31 42 32 22 21 14 13 12 11 4 3 2 1 k k k k k k k k k k k k k k k k P P P P ...(3.89)

Dengan menggunakan persamaan ke dalam persamaan maka koefisien kekakuan dapat diperoleh sebagai berikut

                        − − − − − − =             4 3 2 1 2 2 2 2 3 4 3 2 1 4 6 2 6 6 12 6 12 2 6 4 6 6 12 6 12 δ δ δ δ L L L L L L L L L L L L L EI P P P P ...(3.90)

Matriks kekakuan pada koordinat titik dari suatu elemen dari portal bidang diperoleh dari kombinasi antar matriks kekakuan akibat pengaruh aksial dan matriks kekakuan akibat pengaruh lentur.maka diperoleh

                      − − − − − − − − =                     2 2 2 2 2 2 2 2 3 6 5 4 3 2 1 4 6 0 2 6 0 6 12 0 6 12 0 0 0 0 0 2 6 0 4 6 0 6 12 0 6 12 0 0 0 0 0 6 L L L L L L I AL I AL L L L L L L I AL I AL L EI P P P P P P ...(3.91)