IMPLEMENTASI FUNGSI PEMBANGKIT NUMERIK DENGAN METODE PIECEWISE POLYNOMIAL

IMPLEMENTASI FUNGSI PEMBANGKIT NUMERIK DENGAN METODE

PIECEWISE POLYNOMIAL

Munjiah Nur Sa’adah1, Yudhi Purwananto2, Rully Soelaiman3

Teknik Informatika, Fakultas Teknologi Informasi, Institut Teknologi Sepuluh Nopember Email: mociymociy@gmail.com1, purwananto@yahoo.com2, rully130270@gmail.com3

ABSTRAK

Fungsi numerik, seperti trigonometri, logaritmik, dan akar kuadrat banyak digunakan dalam computer graphics, digital signal processing, communication systems, robotics, dan lain-lain. Khusus dalam aplikasi grafis, sekitar setengah dari total waktu pemrosesan digunakan untuk menghitung fungsi numerik. Dengan demikian untuk aplikasi numerik intensif atau real-time dan akselerator hardware sering diperlukan fungsi pembangkit numerik.

Beberapa algoritma segmentasi piecewise polynomial untuk fungsi pembangkit numerik dibangun untuk menyelesaikan permasalahan ini. Namun, algoritma-algoritma tersebut masih kurang efektif untuk menemukan jumlah segmen optimal. Dengan menggunakan metode segmentasi piecewise polynomial beserta pengecekan yang ada di dalamnya dibangunlah algoritma baru untuk mendapatkan jumlah segmen optimal.

Hasil uji coba pada Tugas Akhir ini menunjukkan bahwa metode segmentasi piecewise polynomial untuk fungsi pembangkit numerik lebih mudah diimplementasikan dan lebih efektif dalam hal mendapatkan jumlah segmen optimal.

Kata kunci : fungsi numerik, fungsi pembangkit numerik, algoritma segmentasi, segmentasi piecewise polynomial

1.

PENDAHULUAN

Fungsi numerik, seperti trigonometri, logaritmik, akar kuadrat, dan kombinasi dari beberapa fungsi secara luas telah bayak digunakan dalam computer graphics, digital signal processing, communication systems, robotics, dan lain-lain. Khusus dalam aplikasi grafis, sekitar setengah dari total waktu pemrosesan digunakan untuk menghitung fungsi numerik. Dengan demikian untuk aplikasi numerik intensif atau real-time dan akselerator hardware sering diperlukan fungsi pembangkit numerik.

Function generator adalah bagian dari peralatan elektronik atau perangkat lunak yang digunakan untuk menghasilkan berbagai jenis bentuk gelombang listrik melalui berbagai frekuensi. Salah satu kelebihan dari function generator adalah kemampuannya untuk mengunci fase gelombang ke sumber sinyal eksternal atau function generator lain. Beberapa bentuk gelombang yang paling umum dihasilkan oleh function generator adalah sinus, persegi, segitiga, dan bentuk gelombang gigi gergaji.

Piecewise function adalah fungsi yang definisinya tergantung pada variabel independennya. Polinomial sendiri adalah ekspresi terbatas yang dibangun dari beberapa variabel dan konstanta menggunakan hanya operasi penjumlahan, pengurangan, perkalian, dan pangkat non-negatif bilangan bulat. Jadi, piecewise polynomial adalah

fungsi polinomial yang definisinya tergantung pada variabel independen.

Beberapa algoritma segmentasi fungsi polinomial yang telah ada sebelum algoritma ini adalah algoritma segmentasi Douglas–Peucker dan algoritma segmentasi Frenzen. Algoritma segmentasi fungsi polinomial dibagi menjadi dua jenis, yaitu segmentasi non-uniform dan segmentasi uniform. Pada Tugas Akhir ini digunakan metode segmentasi piecewise polynomial yang tidak mengacu pada segmentasi uniform maupun non-uniform karena metode ini merupakan metode perbaikan dari metode-metode segmentasi yang telah disebutkan sebelumnya yang kurang efektif.

Metode segmentasi piecewise polynomial adalah metode yang keseluruhan proses segmentasinya dilakukan dalam tiga tahapan utama, yaitu ESTIMATE, LOCATE, dan PINPOINT. Keuntungan menggunakan metode ini adalah dalam hal kesalahan dalam perkiraan polinomial di masing-masing segmen tidak lebih besar daripada kesalahan yang telah ditetapkan. Selain itu, dalam hal waktu komputasi metode ini berjalan lebih cepat daripada algoritma sebelumnya yang tela ada sekaligus mampu menghasilkan jumlah segmen terkecil.

2.

DASAR TEORI

2.1.

Fungsi Pembangkit Numerik

Fungsi pembangkit numerik adalah sebuah rangkaian logika dari fungsi aritmatika, seperti = sin selama beberapa interval tertentu ≤ ≤ . Gambaran fungsi pembangkit numerik dapat dilihat pada Gambar 2.1. Berdasarkan gambaran tersebut, fungsi f(x) yang diberikan dianggap sebagai satu set segmen atau potongan, dimana f memperkirakan masing-masing segmen dengan persamaan linear (2-1).

≈ + (2-1)

Nilai dari c1 dan c0 disimpan dalam Coefficients Memory seperti pada Gambar 2.1 di lokasi yang alamatnya ditentukan oleh Segment Index Encoder. Dalam merancang rangkaian ini, salah satu pembagian interval ≤ ≤ menjadi segmen, dimana koefisien nilai c1 dan c0 adalah sama di tiap segmen dan mendekati fungsi f(x) dalam beberapa kesalahan tertentu.

Sebuah rangkaian biasanya merealisasikan segmentasi non-uniform karena secara umum, tiap segmen memiliki lebar yang berbeda. Oleh karena itu dipilih lebar segmen selebar mungkin yang menyebabkan aprosimasi kesalahan tidak lebih besar dari aproksimasi kesalahan yang telah didefinisikan.

Sebaliknya, terdapat pula segmentasi uniform. Pada kasus ini, semua segmen memiliki lebar segmen yang sama. Jika lebar segmen adalah 2 maka segment index encoder dapat dihapus dan order yang lebih tinggi − bit digunakan untuk mendapatkan alamat pada segment index encoder, dimana n adalah jumlah bit untuk mengodekan x. Pada kasus ini, rangkaian menjadi lebih kecil dan lebih cepat.

2.2.

Metode Segmentasi Piecewise Polynomial Metode segmentasi piecewise polynomial terdiri dari beberapa tahap, yaitu mencari titi-titik awal yang sesuai dengan batasan domain fungsi f(x), tahapan untuk mencari lebar segmen optimal, tahap ESTIMATE, tahap LOCATE, dan tahap PINPOINT.

2.2.1

Mencari Titik-Titik Sesuai Batasan Domain Tahap pertama dalam implementasi fungsi pembangkit numerik dengan metode segmentasi piecewise polynomial adalah mencari titik-titik awal yang sesuai dengan batasan domain fungsi f(x). Terdapat beberapa jenis batasan dalam domain fungsi, seperti yang ada pada Tabel 2.1.

Tabel 2.1 Jenis batasan dalam domain fungsi f(x)

Batasan Domain Fungsi f(x) Keterangan , ≤ ≤ , ! "! ≤ < $ , ! ! < ≤ $ , " < <

Berdasarkan Tabel 2.1 terdapat empat jenis batasan domain fungsi f(x). Secara umum dapat dijelaskan seperti ini. Jika terdapat kurung siku buka (“[“) atau kurung siku tutup (“]”) pada batasan domain fungsi f(x) maka artinya kurang dari atau sama dengan untuk kurung siku buka (“[“) dan lebih dari atau sama dengan untuk kurung siku buka (“]”). Jika terdapat kurung buka (“(“) atau kurung tutup (“)”) pada batasan domain fungsi f(x) maka artinya kurang dari untuk kurung buka (“(“) dan lebih dari untuk kurung tutup (“)”).

2.2.2

Tahapan Mencari Lebar Segmen Optimal Bagian penting dari algoritma segmentasi piecewise polynomial adalah asal mula dari pekiraan lebar segmen. Perkiraan yang akurat merupakan hal penting karena kemudian pencarian harus dilakukan untuk mendapatkan lebar segmen yang tepat.

Segmen yang dicari dalam n-order pendekatan polinomial adalah dalam rentang [e, s]. Aproksimasi kesalahan maksimum dari aproksimasi Chebyshev ditunjukkan pada persamaan (2-2).

% =_-& '()*+,_{./ !}*+,max)454'6 ./ 6 (2-2) Persamaan (2-2) diselesaikan hingga mendapatkan lebar segmen 7 − 8. Sehingga didapatkan persamaan (2-3) yang merupakan persamaan untuk mendapatkan lebar segmen.

7 − 8 = 4 :_{& <=>?@A@B}./ !;_6C*+, _{5 6} *+,

(2-3)

Untuk dua kasus perkiraan polinomial linear dan perkiran kuadratik, didapatkan persamaan (2-4) dan (2-5). 7 − 8| .'EF= 4:_<=>?@A@B;_|CGG_{5 |}= 4:_6CGG ;

BH?5∗ 6 (2-4)

7 − 8|JKELFEM N= 4:O _<=>?@A@B;_|CGGG_{5 |}= 4:_6CGGG ; BH?5∗ 6

O _(2-5)

dimana 7 − 8| _.'EF dan 7 − 8|_{JKELFEM N} adalah lebar segmen untuk perkiraan liner dan perkiraan kuadratik. Berdasarkan persamaan di atas bagian max_)454'6 ./ 6 dan max)454'6 ′′′ 6 diganti dengan yang lebih singkat

6 ′′

'() ∗ 6 dan 6

′′′

'() ∗ 6 secara berturut-turut dapat

mengenali jika turunan yang tepat adalah kontinu pada interval tertutup, maka maxima di atas, masing-masing akan dicapai di beberapa titik x* dalam interval tersebut.

Namun, pada Tugas Akhir ini hanya fokus pada perkiraan linear. Sehingga persamaan yang digunakan untuk mencari lebar segmen adalah persamaan (2-4).

2.2.3

Tahap ESTIMATE

Setelah mendapatkan lebar segmen pada proses sebelumnya, maka masuk ke tahap ESTIMATE yang mampu mendapatkan perkiraan titik akhir segmen sementara 7')M dengan persamaan (2-5).

7')M= + 7 − 8| .'EF (2-5)

Begitu pula dengan perkiraan kesalahan untuk titik 7')M yang dinotasikan %_')M dapat diketahui dengan mengurangi titik xi yang telah dimasukkan pada fungsi f(x) yang dinotasikan sebagai yi dengan titik 7')M yang telah dimasukkan pada fungsi f(x) yang dinotasikan sebagai P'B?Qseperti pada persamaan (2-6), (2-7), dan (2-8).

= P (2-6)

7')M = P')M (2-7)

%')M= |P − P')M| (2-8)

Setelah diketahui lebar segmen, perkiraan titik akhir segmen 7_')M, dan perkiraan kesalahan untuk titik 7_')M yang dinotasikan %_')M kemudian dilakukan pengecekan jika 7')M> maka ditetapkan sebagai 7_')M. Jika 7')M= dan %_')M ≤ % maka 7_')M ditetapkan sebagai titik akhir segmen 7 dan proses berhenti.

Proses ini diakhiri dengan ditetapkannya H dan L sebagai 7_')M.

2.2.4

Tahap LOCATE

Tahap LOCATE adalah tahap setelah ESTIMATE. Jika pada tahap ESTIMATE belum menemukan titik akhir segmen 7 maka pada tahap ini titik akhir segmen 7 dicari lagi dengan membandingkan perkiraan kesalahan ε dengan perkiraan kesalahan titik 7_')M, perkiraan kesalahan titik H, dan perkiraan kesalahan titik L.

Tahap ini diawali dengan membandingkan perkiraan kesalahan untuk titik 7_')M yang dinotasikan %_')M dengan perkiraan kesalahan ε. Jika %_')M< % maka titik H dinaikkan dengan angka tertentu yang dinotasikan sebagai i sebagai batas atas titik 7_')M.

S = S + T (2-9)

Setelah menaikkan titik H dilakukan pengecekan kembali jika %_U≤ % < %_V maka dapat melanjutkan ke proses selanjutnya, yaitu PINPOINT. Jika tidak memenuhi syarat %U≤ % < %V maka dilakukan pengecekan kembali jika

7V≤ % dan S = maka 7_')M ditetapkan sebagai titik akhir segmen 7 dan proses berhenti. Namun, jika %_')M≥ % maka menurunkan titik L dengan angka tertentu yang dinotasikan j sebagai batas bawah 7_')M.

X = X + Y (2-10)

2.2.5

Tahap PINPOINT

Jika sampai pada tahap LOCATE belum ditemukan titik akhir segmen 7 maka akan diproses kembali pada tahap PINPOINT hingga menemukan titik akhir segmen 7 .

Pada tahap PINPOINT dibentuk satu titik baru dari persamaan

Z =V/U_& (2-11) yang merupakan titik tengah antara titik H dan titik L, yaitu titik A. Kemudian titik A ditetapkan sebagai perkiraan titik akhir segmen yang baru menggantikan 7_')M. Lalu dihitung perkiraan kesalahan antara titik xi dengan titik A sebagai perkiraan titik akhir segmen yang baru. Perkiraan kesalahan tersebut dinotasikan %_[ dapat diketahui dengan mengurangi titik xi yang telah dimasukkan pada fungsi f(x) yang dinotasikan sebagai yi dengan titik A yang telah dimasukkan pada fungsi f(x) yang dinotasikan sebagai P_[. Jika %_[ > % maka titik H digantikan oleh titik A. Namun, jika %_[ ≤ % maka titik L digantikan oleh titik A.

Titik H atau L yang digantikan oleh titik A diangap sebagai titik Hpp atau Lpp. Langkah selanjutnya adalah menghitung perkiraan kesalahan Hpp yang dinotasikan %_V\\ dan perkiraan kesalahan Lpp yang dinotasikan %_U\\. Langkah-langkah untuk mencari %_V\\ dan %_U\\ sama seperti mencari %_[. Kemudian jika %_U\\≤ % < %_V\\ maka titik Lpp ditetapkan sebagai titik akhir segmen 7 .

3.

IMPLEMENTASI

Secara umum, sistem perangkat lunak ini mengimplementasikan fungsi pembangkit numerik dengan metode piecewise polynomial. Diagram alir perancangan sistem secara umum dapat dilihat pada Gambar 3.1.

Gambar 3.1 Diagram alir sistem secara umum

Langkah-langkah untuk mengimplementasikan fungsi pembangkit numerik dengan metode segmentasi piecewise polynomial diatas adalah sebagai berikut:

1. Tahap pertama dalam implementasi fungsi pembangkit numerik dengan metode segmentasi piecewise polynomial adalah mencari titik-titik awal yang sesuai dengan batasan domain fungsi f(x) [xlow, xhigh].

2. Selanjutnya mendapatkan asal mula dari pekiraan lebar segmen. Perkiraan yang akurat merupakan hal penting karena kemudian pencarian harus dilakukan untuk mendapatkan lebar segmen yang tepat.

3. Setelah mendapatkan lebar segmen pada proses sebelumnya, maka masuk ke tahap ESTIMATE yang mampu mendapatkan perkiraan titik akhir segmen sementara 7_')Mdan perkiraan kesalahan untuk titik 7_')M yang dinotasikan %_')M.

4. Jika pada tahap ESTIMATE belum menemukan titik akhir segmen 7 maka masuk tahapLOCATE. Tahap ini diawali dengan membandingkan perkiraan kesalahan untuk titik 7_')M yang dinotasikan %_')M dengan perkiraan kesalahan ε. Jika %_')M< % maka titik H dinaikkan dengan angka tertentu yang dinotasikan sebagai i sebagai batas atas titik 7_')M. Namun, jika %')M≥ % maka menurunkan titik L dengan angka

tertentu yang dinotasikan j sebagai batas bawah 7_')M. 5. Jika sampai pada tahap LOCATE belum ditemukan

titik akhir segmen 7 maka akan diproses kembali pada tahap PINPOINT hingga menemukan titik akhir segmen 7 . Pada tahap PINPOINT dibentuk satu titik baru yang merupakan titik tengah antara titik H dan

titik L, yaitu titik A. Jika %_[ > % maka titik H digantikan oleh titik A. Namun, jika %_[ ≤ % maka titik L digantikan oleh titik A. Titik H atau L yang digantikan oleh titik A diangap sebagai titik Hpp atau Lpp. Langkah selanjutnya adalah menghitung perkiraan kesalahan Hpp yang dinotasikan %_V\\ dan perkiraan kesalahan Lpp yang dinotasikan %_U\\. Jika %U\\≤ % < %V\\ maka titik Lpp ditetapkan sebagai titik akhir segmen 7 .

4.

UJI COBA DAN EVALUASI

4.1.

Skenario 1

Pada skenario pertama, fungsi f(x) yang digunakan adalah 25. Domain , untuk fungsi ini adalah [0, 1). Sedangkan nilai aproksimasi kesalahan ε yang digunakan adalah 2( ] dan jumlah titik N adalah 2^.

Gambar 4.1 Kurva fungsi _ ` = a`untuk titik x

Gambar 4.2 Kurva fungsi _ ` = a`untuk titik hasil segmentasi e

Gambar 4.3 Kurva fungsi _ ` = a`untuk untuk

titik-titik x dan titik-titik-titik-titik hasil segmentasi e Tabel 4.1 Percobaan nilai i dan j pada skenario 1

Uji Coba i j Jumlah Segmen Keterangan 1 0.01114959 2427677 0.01114959 2427677 74 Tidak Optimal 2 0.01114952 2499485 0.01114952 2499485 75 Optimal 3 0.01114938 2351940 0.01114938 2351940 78 Tidak Optimal

4.2.

Skenario 2

Pada skenario kedua, fungsi f(x) yang digunakan adalah

5. Domain , untuk fungsi ini adalah [1,

2). Sedangkan nilai aproksimasi kesalahan ε dan jumlah titik N yang digunakan tetap, yaitu 2( ] dan 2^.

Gambar 4.4 Kurva fungsi _ ` =b

` untuk titik x

Gambar 4.5 Kurva fungsi _ ` =b<sub>`</sub> untuk titik hasil segmentasi e

Gambar 4.6 Kurva fungsi _ ` =b<sub>`</sub> untuk untuk titik-titik x dan titik-titik-titik-titik hasil segmentasi e Tabel 4.2 Percobaan nilai i dan j pada skenario 2

Uji Coba I j Jumlah Segmen Keterangan 1 0.0078020 0.0078020 78 Tidak Optimal 2 0.0078015 0.0078015 75 Optimal 3 0.0078011 0.0078011 73 Tidak Optimal

4.3.

Skenario 3

Pada skenario ketiga, fungsi f(x) yang digunakan adalah √ . Domain , untuk fungsi ini adalah [1, 2). Sedangkan nilai aproksimasi kesalahan ε dan jumlah titik N yang digunakan tetap, yaitu 2( ] dan 2^.

Gambar 4.7 Kurva fungsi _ ` = √` untuk titik x

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1 1.2 1.4 1.6 1.8 2 x = Domain[0, 1) y = 2 x

Plot of 2x in standart point 2^standart point 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1 1.2 1.4 1.6 1.8 2 x = Domain[0, 1) y = 2 x

Plot of 2x in yield point 2^yield point 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1 1.2 1.4 1.6 1.8 2 x = Domain[0, 1) y = 2 x

Plot of 2x between standart point and yield point 2^titik standart 2^titik hasil 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 0.5 0.6 0.7 0.8 0.9 1 x = Domain[1, 2) y = 1 /x

Plot of 1/x in standart point

1/standart point 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 0.5 0.6 0.7 0.8 0.9 1 x = Domain[0, 1) y = 1 /x

Plot of 1/x in yield point

1/yield point 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 0.5 0.6 0.7 0.8 0.9 1 x = Domain[1, 2) y = 1 /x

Plot of 1/x between standart point and yield point

1/titik standart 1/titik hasil 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 1 1.05 1.1 1.15 1.2 1.25 1.3 1.35 1.4 1.45 x = Domain[1, 2) y = s q rt (x )

Plot of sqrt(x) in standart point

Gambar 4.8 Kurva fungsi _ ` = √` untuk titik hasil segmentasi e

Gambar 4.9 Kurva fungsi _ ` = √` untuk untuk

titik-titik x dan titik-titik-titik-titik hasil segmentasi e Tabel 4.3 Percobaan nilai i dan j pada skenario 3

Uji Coba i j Jumlah Segmen Keteran gan 1 -0.00002500000 0000 + 0.02209058691 2080i -0.000025000 000000 + 0.022090586 912080i 21 Tidak Optimal 2 -0.00001500000 0000 + 0.02209058691 2080i -0.000015000 000000 + 0.022090586 912080i 35 Optimal 3 -0.00001000000 0000 + 0.02209058691 2080i -0.000010000 000000 + 0.022090586 912080i 31 Tidak Optimal

4.4.

Skenario 4

Pada skenario keempat, fungsi f(x) yang digunakan adalah

√5. Domain , untuk fungsi ini adalah [1,

2). Sedangkan nilai aproksimasi kesalahan ε dan jumlah titik N yang digunakan tetap, yaitu 2( ] _{dan 2}^_.

Gambar 4.10 Kurva fungsi _ ` = b

√` untuk titik x

Gambar 4.11Kurva fungsi _ ` = b

√` untuk titik hasil

segmentasi e

Gambar 4.12 Kurva fungsi _ ` = b

√` untuk untuk

titik-titik x dan titik-titik-titik-titik hasil segmentasi e Tabel 4.4 Percobaan nilai i dan j pada skenario 4

Uji Coba I j Jumlah Segmen Keterangan 1 0.0127340 0.0127340 40 Tidak Optimal 2 0.0127363 0.0127363 50 Optimal 3 0.0127350 0.0127350 44 Tidak Optimal

4.5.

Skenario 5

Pada skenario kelima, fungsi f(x) yang digunakan adalah log_& . Domain , untuk fungsi ini adalah [1, 2). Sedangkan nilai aproksimasi kesalahan ε dan jumlah titik N yang digunakan tetap, yaitu 2( ] dan 2^.

Gambar 4.13 Kurva fungsi _ ` = ghi<sub>a</sub>` untuk titik x

Gambar 4.14 Kurva fungsi _ ` = jkl<sub>a</sub>`untuk titik

hasil segmentasi e 1 1.0001 1.0002 1.0003 1.0004 1.0005 1.0006 1 1.0001 1.0002 1.0003 x = Domain[1, 2) y = s q rt (x )

Plot of sqrt(x) in yield point

sqrt(yield point) 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 1 1.05 1.1 1.15 1.2 1.25 1.3 1.35 1.4 1.45 x = Domain[1, 2) y = s q rt (x )

Plot of sqrt(x) between standart point and yield point

sqrt(standart point) yield point 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 0.7 0.75 0.8 0.85 0.9 0.95 1 x = Domain[1, 2) y = 1 /s q rt (x )

Plot of sqrt(x) in standart point

1/sqrt(standart point) 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 0.7 0.75 0.8 0.85 0.9 0.95 1 x = Domain[1, 2) y = 1 /s q rt (x )

Plot of 1/sqrt(x) in yield point

1/sqrt(yield point) 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 0.7 0.75 0.8 0.85 0.9 0.95 1 x = Domain[1, 2) y = 1 /s q rt (x )

Plot of 1/sqrt(x) between standart point and yield point

1/sqrt(standart point) 1/sqrt(yield point) 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 0 0.2 0.4 0.6 0.8 1 x = Domain[1, 2) y = l o g 2 (x )

Plot of log2(x) in standart point log2(standart point) 1.0102 1.0104 1.0106 1.0108 1.011 1.0112 1.0114 1.0116 1.0118 1.012 1.0122 0.0148 0.015 0.0152 0.0154 0.0156 0.0158 0.016 0.0162 0.0164 0.0166 x = Domain[1, 2) y = l o g 2 (x )

Plot of log2(x) in yield point

Gambar 4.15 Kurva fungsi _ ` = jkl<sub>a</sub>` untuk untuk titik-titik x dan titik-titik hasil segmentasi e Tabel 4.5 Percobaan nilai i dan j pada skenario 5

Uji Coba i j Jumlah Segmen Keteran gan 1 -0.000010000 000000 + 0.009298515 800902i -0.0000100000 00000 + 0.0092985158 00902i 14 Tidak Optimal 2 -0.000016000 000000 + 0.009298515 800902i -0.0000160000 00000 + 0.0092985158 00902i 76 Optimal 3 -0.000020000 000000 + 0.009298515 800902i -0.0000200000 00000 + 0.0092985158 00902i 36 Tidak Optimal

4.6.

Skenario 6

Pada skenario keenam, fungsi f(x) yang digunakan adalah m . Domain , untuk fungsi ini adalah [1, 2). Sedangkan nilai aproksimasi kesalahan ε dan jumlah titik N yang digunakan tetap, yaitu 2( ] dan 2^.

Gambar 4.16 Kurva fungsi _ ` = jn ` untuk titik x

Gambar 4.17 Kurva fungsi _ ` = jn ` untuk titik hasil segmentasi e

Gambar 4.18 Kurva fungsi _ ` = jn ` untuk untuk

titik-titik x dan titik-titik hasil segmentasi e Tabel 4.6 Percobaan nilai i dan j pada skenario 6

Uji Coba i j Jumlah Segmen Ketera ngan 1 -0.000010000 0000 + 0.011051543 456040i -0.000010000000 0 + 0.011051543456 040i 51 Tidak Optima l 2 -0.000016160 0000 + 0.011051543 456040i -0.000016160000 0 + 0.011051543456 040i 63 Optima l 3 -0.000020000 0000 + 0.011051543 456040i -0.000020000000 0 + 0.011051543456 040i 54 Tidak Optima l

4.7.

Skenario 7

Pada skenario ketujuh, fungsi f(x) yang digunakan adalah sin 75. Domain , untuk fungsi ini adalah [0, 2). Sedangkan nilai aproksimasi kesalahan ε dan jumlah titik N yang digunakan tetap, yaitu 2( ] dan 2^.

Gambar 4.19 Kurva fungsi _ ` = opn q` untuk titik x

Gambar 4.20 Kurva fungsi _ ` = opn q` untuk titik hasil segmentasi e 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 0 0.2 0.4 0.6 0.8 1 x = Domain[1, 2) y = l o g 2 (x )

Plot of log2(x) between standart point and yield point

log2(standart point) log2(yield point) 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 x = Domain[1, 2) y = l o g (x )

Plot of log(x) in standart point

log(standart point) 1 1.0001 1.0002 1.0003 1.0004 1.0005 1.0006 1.0007 1.0008 1.0009 1.001 0 0.2 0.4 0.6 0.8 1x 10 -3 x = Domain[1, 2) y = l o g (x )

Plot of log(x) in yield point

log(yield point) 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 x = Domain[1, 2) y = l o g (x )

Plot of log(x) between standart point and yield point

log(standart point) log(yield point) 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 -1 -0.5 0 0.5 1 x = Domain[0, 2) y = s in (e x p (x ))

Plot of sin(exp(x)) in standart point

sin(exp(standart point)) 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 -1 -0.5 0 0.5 1 x = Domain[0, 2) y = s in (e x p (x ))

Plot of sin(exp(x)) in yield point

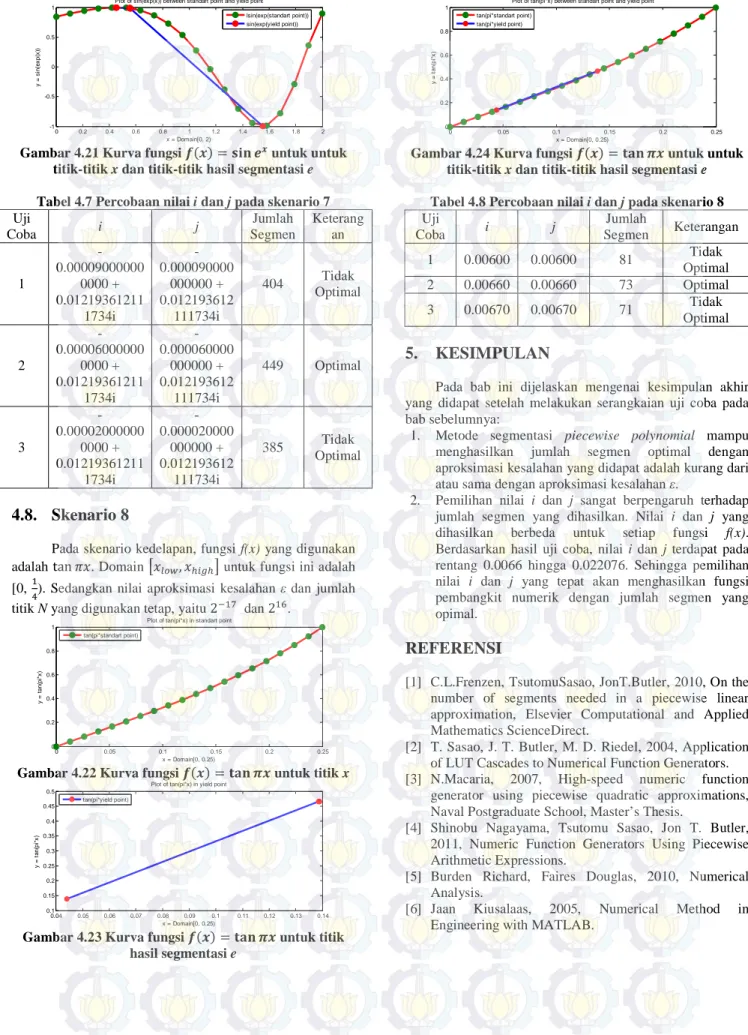
Gambar 4.21 Kurva fungsi _ ` = opn q` untuk untuk titik-titik x dan titik-titik hasil segmentasi e Tabel 4.7 Percobaan nilai i dan j pada skenario 7

Uji Coba i j Jumlah Segmen Keterang an 1 -0.00009000000 0000 + 0.01219361211 1734i -0.000090000 000000 + 0.012193612 111734i 404 Tidak Optimal 2 -0.00006000000 0000 + 0.01219361211 1734i -0.000060000 000000 + 0.012193612 111734i 449 Optimal 3 -0.00002000000 0000 + 0.01219361211 1734i -0.000020000 000000 + 0.012193612 111734i 385 Tidak Optimal

4.8.

Skenario 8

Pada skenario kedelapan, fungsi f(x) yang digunakan adalah tan . Domain , untuk fungsi ini adalah [0, _-). Sedangkan nilai aproksimasi kesalahan ε dan jumlah titik N yang digunakan tetap, yaitu 2( ] dan 2^.

Gambar 4.22 Kurva fungsi _ ` = stn u` untuk titik x

Gambar 4.23 Kurva fungsi _ ` = stn u` untuk titik

hasil segmentasi e

Gambar 4.24 Kurva fungsi _ ` = stn u` untuk untuk

titik-titik x dan titik-titik hasil segmentasi e Tabel 4.8 Percobaan nilai i dan j pada skenario 8

Uji Coba i j Jumlah Segmen Keterangan 1 0.00600 0.00600 81 Tidak Optimal 2 0.00660 0.00660 73 Optimal 3 0.00670 0.00670 71 Tidak Optimal

5.

KESIMPULAN

Pada bab ini dijelaskan mengenai kesimpulan akhir yang didapat setelah melakukan serangkaian uji coba pada bab sebelumnya:

1. Metode segmentasi piecewise polynomial mampu menghasilkan jumlah segmen optimal dengan aproksimasi kesalahan yang didapat adalah kurang dari atau sama dengan aproksimasi kesalahan ε.

2. Pemilihan nilai i dan j sangat berpengaruh terhadap jumlah segmen yang dihasilkan. Nilai i dan j yang dihasilkan berbeda untuk setiap fungsi f(x). Berdasarkan hasil uji coba, nilai i dan j terdapat pada rentang 0.0066 hingga 0.022076. Sehingga pemilihan nilai i dan j yang tepat akan menghasilkan fungsi pembangkit numerik dengan jumlah segmen yang opimal.

REFERENSI

[1] C.L.Frenzen, TsutomuSasao, JonT.Butler, 2010, On the number of segments needed in a piecewise linear approximation, Elsevier Computational and Applied Mathematics ScienceDirect.

[2] T. Sasao, J. T. Butler, M. D. Riedel, 2004, Application of LUT Cascades to Numerical Function Generators. [3] N.Macaria, 2007, High-speed numeric function

generator using piecewise quadratic approximations, Naval Postgraduate School, Master’s Thesis.

[4] Shinobu Nagayama, Tsutomu Sasao, Jon T. Butler, 2011, Numeric Function Generators Using Piecewise Arithmetic Expressions.

[5] Burden Richard, Faires Douglas, 2010, Numerical Analysis.

[6] Jaan Kiusalaas, 2005, Numerical Method in Engineering with MATLAB.

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 -1 -0.5 0 0.5 1 x = Domain[0, 2) y = s in (e x p (x ))

Plot of sin(exp(x)) between standart point and yield point

lsin(exp(standart point)) sin(exp(yield point)) 0 0.05 0.1 0.15 0.2 0.25 0 0.2 0.4 0.6 0.8 1 x = Domain[0, 0.25) y = t a n (p i* x )

Plot of tan(pi*x) in standart point tan(pi*standart point) 0.04 0.05 0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13 0.14 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 x = Domain[0, 0.25) y = t a n (p i* x )

Plot of tan(pi*x) in yield point

tan(pi*yield point) 0 0.05 0.1 0.15 0.2 0.25 0 0.2 0.4 0.6 0.8 1 x = Domain[0, 0.25) y = t a n (p i* x )

Plot of tan(pi*x) between standart point and yield point

tan(pi*standart point) tan(pi*yield point)