KESTABILAN MODEL MANGSA PEMANGSA DENGAN FUNGSI RESPON TIPE HOLLING II DAN WAKTU TUNDA
Teks penuh
Gambar
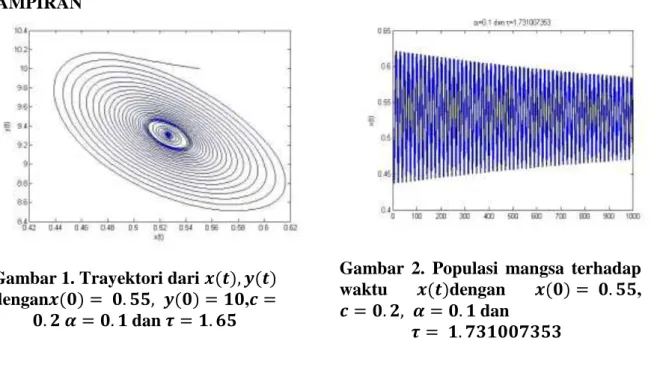
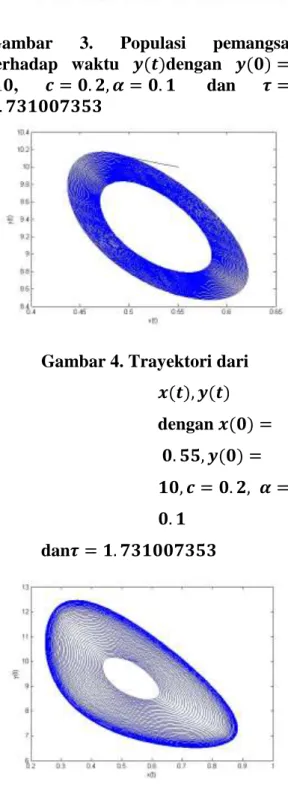
Dokumen terkait
Hasil pengukuran kelelahan tenaga kerja yang bekerja di Industri Gamelan Supoyo menunjukan bahwa dari 30 orang tenaga kerja, 15 orang tenaga kerja yang bekerja
Pelaporan dan Analisis Transaksi Keuangan (PPA TK) yaitu transaksi yang mencurigakan; transaksi tunai dalam jumlah kumulatif Rp. - kewajiban pelaporan tersebut tidak berlaku
Harahap, Sofyan Syafri, 2002, Akuntansi Aktiva Tetap, Edisi 1, Penerbit PT Raja Grafindo Persada, Jakarta.. Ikatan Akuntan Indonesia, 2011, Standar Akuntansi Keuangan, Penerbit
Strategi diferensiasi terdiri dari diferensiasi produk (produk yang dipasarkan), diferensiasi pelayanan (pelayanan kepada konsumen), diferensiasi citra (pembentukan citra perusahaan
Mini market Jekulo yaitu Indomaret dan Alfamart, untuk Indomart sendiri berjarak kurang lebih 100 meter dari pasar tradisional Jekulo dan sudah mulai buka pada pagi
Observasi merupakan suatu proses yang kompleks, suatu proses yang tersusun dari berbagai proses biologis dan psikologis. Proses pengambilan data ini dilakukan dalam penelitian
Sisingamangaraja XII bergerilya didaerah Pakpak selama lebih dari 20 tahun sejak 1887 sampai beliau wafat di Sindeas, Si Ennem Koden, beliau membina hubungan baik
13 Siti Nakiyah, Kekerasan Terhadap Istri Dalam Rumah Tangga Sebagai Alasan Perceraian , (Studi Kasus di Pengadilan Agama Salatiga ) Skripsi untuk mempereh gelar S-1 pada
