Pengaruh Filter Pasif Double Tuned Pada Motor Induksi 3 Phasa Chapter III V

(1)

BAB III

METODE PENELITIAN

3.1Umum

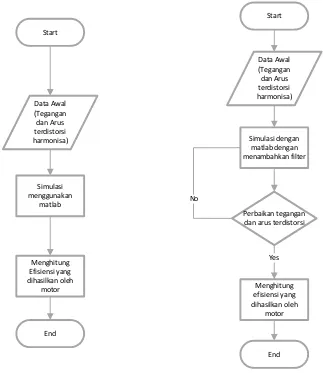
Proses simulasi yang akan dirancang memiliki beberapa tahapan dimulai dari menentukan parameter-parameter harmonisa yang telah diperoleh dari hasil pengukuran yang telah dilakukan oleh peniliti sebelumnya hingga penentuan nilai dari filter pasif yang akan digunakan untuk mengurangi harmonisa tersebut. Secara keseluruhan tahapan perancangan simulasi ini dapat dilihat pada diagram alir /

flowchart pada Gambar 3.1.

(2)

Untuk proses simulasi ini akan dilakukan dalam dua tahap. Tahap pertama adalah simulasi harmonisa tanpa penambahan filter, hal ini dimaksudkan untuk melihat pengaruh harmonisa pada sistem dan menentukan tegangan dan arus yang terdistorsi. Pada tahap kedua adalah simulasi harmonisa dengan penambahan filter, hal ini dimaksudkan untuk memperbaiki tegangan dan arus yang terdistorsi.

3.2 Menentukan Parameter -Parameter Simulasi

Untuk menentukan parameter-parameter dalam simulasi ini, penulis mengambil data-data dari hasil penelitian yang telah dilakukan oleh peneliti sebelumnya.

3.2.1 Data Harmonisa

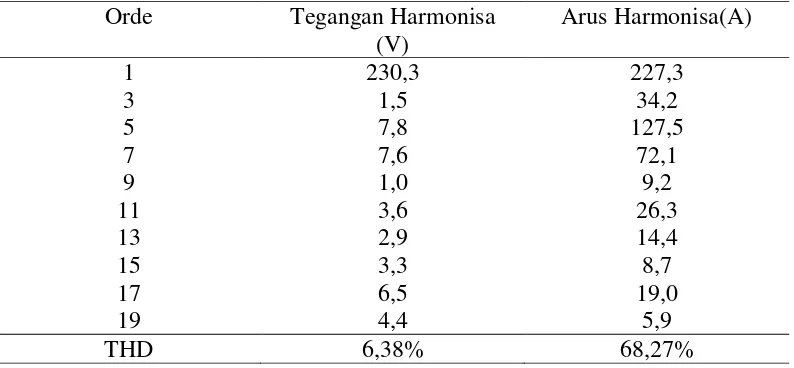
Pengambilan data harmonisa dilakukan dengan pengukuran , berikut adalah data hasil pengukuran .

Tabel 3.1 Hasil Pengukuran Tegangan Harmonisa, Arus Harmonisa Dan THD Orde Tegangan Harmonisa

(3)

3.2.2 Perancangan Simulasi

Dalam perancangan simulasi diperlukan beberapa data tambahan untuk mensimulasikan sistem tenaga listrik pada PT.Growth Sumatera Industry Ltd Medan. Namun penulis tidak mengambil keseluruhan data dari hasil penelitian yang telah dilakukan oleh peneliti sebelumnya, tetapi hanya beberapa data yang diperlukan untuk proses simulasi. Diantaranya dapat dilihat pada tabel 3.2

Tabel 3.2 Data Sistem Tenaga PT. Growth Sumatera Industry Ltd.

Tegangan Sumber(V) Impedansi Sumber(Ω) Impedansi Beban(Ω)*

231 0,001392+j0,0112 0,212423+j20,3718

Rs = 0,001392 Ω

Ls = 0,0112/314

= 0,000035668 RL = 0.21242300 LL = 20.3718/314

= 0.06487843

* nilai impedansi beban yang digunakan disesuaikan pada proses simulasi, agar memperoleh harmonisa sesuai data hasil pengukuran

Dimana : Rs = Tahanan Sumber

Ls = Induktansi Sumber RL= Tahanan Beban LL= Induktansi Beban

3.3 Perancangan Filter Pasif Double T une d

(4)

penelitian ini hanya akan digunakan dua buah double tuned passive filter.yang akan dituning pada orde 3, 5 dan 7.

3.3.1 Perhitungan Komponen R,L,C dari Doubl e T une d Fi lte r

Untuk menentukan kapasitas dari nilai kapasitor yang akan digunakan pada double tuned filter diperlukan langkah-langkah sebagai berikut:

1. Menentukan nilai kapasitansi ∆Q untuk memperbaiki faktor daya, perbaikan faktor daya umumnya berkisar antara 0.95-0.99.

∆Q = P(tanθa wa l – tanθt a r g et)

Daya aktif untuk beban penuh;

P =

x 0,88 = 469,3333 Watt

Saat kondisi beban 90%

P = 469,3333 x 0,9 = 422,4

Perbaikan faktor daya yang di kehendaki adalah 0,97 maka nilai kapasitansi nya adalah

∆Q = P(tanθa wa l – tanθt a r g et)

∆Q = 422,4(tan 28,35 – tan 14,07)

(5)

Sehingga kapasitas kapasitor yang dipilih adalah

∆Q = 123 kvar

2. Menghitung reaktansi kapasitor pada frekuensi fundamental

XCa = � ∆Q

XCa = ,

, = 0,71148 Ω

Sehingga nilai Ca diperoleh:

Ca =

� . � � , = 0,004476181 F

Untuk nilai XCb diperoleh:

XCb = ,

, = 1.116875 Ω

Sehingga nilai Cb diperoleh:

Cb =

� , � � , = 0,00285145 F

C1 = 0,007327631 F

3. Menghitung nilai reaktor yang digunakan untuk meredam harmonisa ke-n.

(6)

Sehingga nilai XL dicari berdasarkan orde harmonisa yang akan direduksi yaitu orde 5 (XLa) dan orde 7 (XLb), maka:

� = , = 0,0284592 Ω

� = . = 0,0227933 Ω

Nilai induktansi masing-masig orde harmonisa yaitu:

� =��_��

� = ��

Maka:

� = _{� , �}, = 0,000090634 H

� = _{� , �}, = 0,00007259 H

Sehingga diperoleh nilai L1 pada rangkaian ekivalen double tuned yaitu:

� = _{� +�}� �

Maka :

(7)

4. Menghitung tahanan reaktor untuk menentukan nilai faktor kualitas Q, dimana:

R = �

Maka:

� = , x = 0,00142296 Ω

� = , x = 0,001595531 Ω

Maka untuk menentukan nilai tahanan R1 yaitu:

� = ��

Sehingga :

� = � . = 0.000126563 Ω

Untuk nilai Q antara 35-100

Nilai a dan x diperoleh dari:

=

�_� = .

. = 1.57

� = √

� �_{� �} =

√

. .

(8)

Untuk menentukan nilai R2 dari rangkaian ekivalen double tuned yaitu:

R2 = � [ ] − � [ ] + � [ ] Dimana:

A = .

. = 0,178672646

B = .

. = 0,07286772

C =− .

. = -0,064868412

Sehingga:

� = � [ , ] − � [ , ] + � [− , ]

� = 0,000129773 Ω

5. Nilai kapasitas C2

=

� � � +� � +�

� � −� �

Maka:

C2 = . . .

. − .

(9)

6. Nilai �

L2 = � � −� �

� +� � +�

Maka

L2 =

( . � − 4)

. . = 0.00000495 H

7. Nilai R3

R2 = -� [ ] + � [ ] + � [ ]

Dimana:

A = .

. = 0.096866683

B = .

. = 0.151895314

C = .

. = 0.030596593

Sehingga :

� = −� [ . ] + � [ . ] + � [ . ]

(10)

Berikut ini rancangan filter yang telah dibuat pada simulasi simulink matlab

Gambar 3.2 Rangkaian ekivalen filter pasif double tuned

8. Menghitung nilai reaktor yang digunakan untuk meredam harmonisa orde 3 dan orde 5.

� = , = 0,079053333 Ω

� = . = 0,044675 Ω

Nilai induktansi masing-masig orde harmonisa yaitu:

� =��_��

Maka:

� = , _{� , �} = 0.000251762 H

(11)

9. Menghitung tahanan reaktor untuk menentukan nilai faktor kualitas Q, dimana:

R = �

Maka:

� = . x = 0,00142296 Ω

� = , x = 0,001595531 Ω

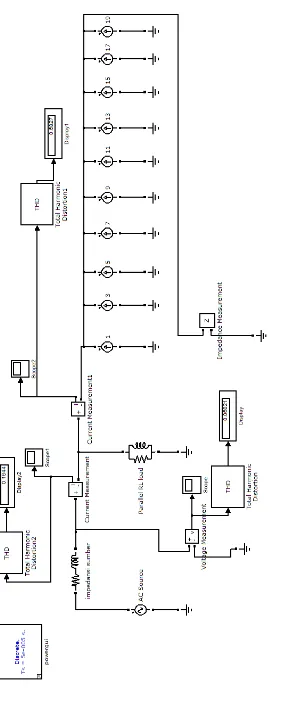
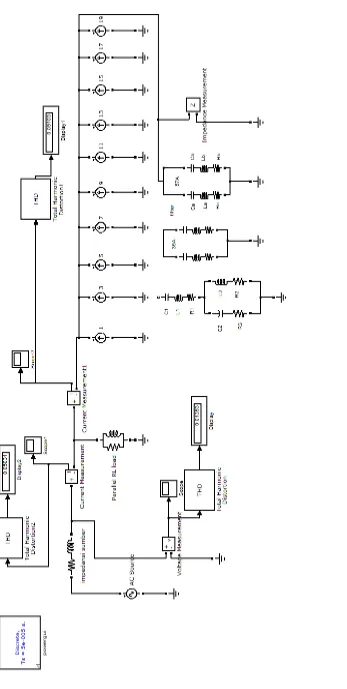
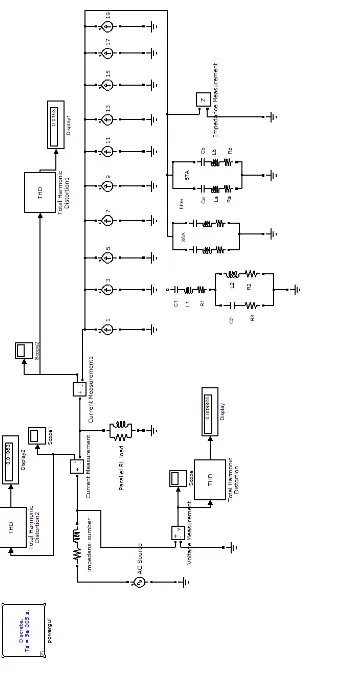
3.4 Simulasi Sistem tanpa filter

(12)

G

am

ba

r 3.3 Ra

ng

ka

ia

n s

im

ul

as

i t

anpa

f

il

te

(13)

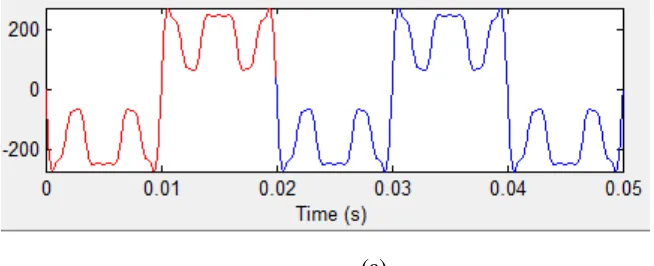
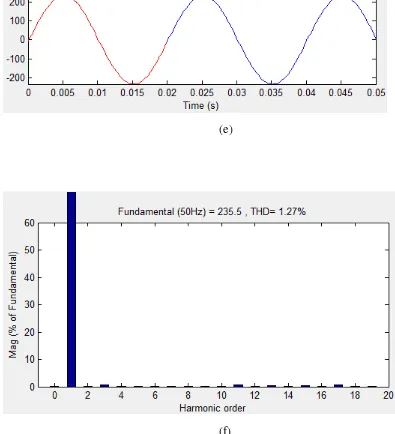
Berikut ini merupakan grafik dan spektrum hasil simulasi,

(a)

(b)

(14)

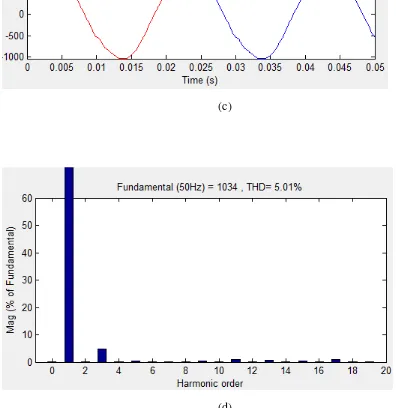
(c)

(d)

(15)

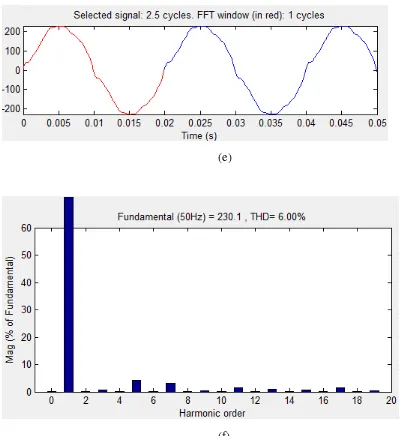
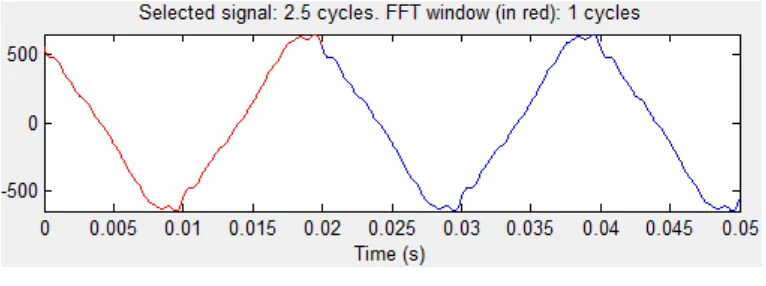
(e)

(f)

Gambar 3.6 (e) Gelombang tegangan, (f) Spektrum tegangan

3.5 Simulasi dengan penambahan filter pada orde 5 dan orde 7

(16)

G

am

ba

r 3.7 Ra

ng

ka

ia

n s

im

ul

as

i d

eng

an fi

lt

er pa

d

a orde

5 d

(17)

Berikut ini merupakan grafik dan spektrum hasil simulasi, dengan filter orde 5 dan 7

(a)

(b)

(18)

(c)

(d)

(19)

(e)

(f)

Gambar 3.10 (e) Gelombang tagangan, (f) Spektrum tegangan

3.6 Simulasi Dengan Penambahan Filter Pada Orde 3,5 Dan 7

(20)

(21)

Berikut ini merupakan grafik dan spektrum hasil simulasi, dengan filter orde 5 dan 7

(a)

(b)

(22)

(c)

(d)

(23)

(e)

(f)

(24)

BAB IV

ANALISIS DAN PEMBAHASAN

4.1 Pendahuluan

Pada bab ini dibahas hasil simulasi yang telah dilakukan secara keseluruhan, mulai simulasi tanpa penambahan filter dan simulasi setelah penambahan filter serta pengaruh hasil simulasi terhadap motor induksi tiga phasa.

4.2 Hasil rancangan filter pasif doubl e t une d

Hasil perancangan filter dapat dilihat pada tabel 4.1

Tabel 4.1 Data komponen filter pasif orde 5 dan 7

Kode Komponen R (Ω) Komponen L (H) Komponen C (F)

A 0,00142296 0,000090634 0,004476181

B 0,001595531 0,00007259 0,00285145

1 0.000126563 0.000040307 0,007327631

2 0,000129773 0.00000495 0.061402146

3 0.000108308 - -

Tabel 4.2 Data komponen filter pasif orde 3 dan 5

Kode Komponen R (Ω) Komponen L (H) Komponen C (F)

A 0,00142296 0.000251762 0,004476181

B 0,001595531 0.000142277 0,00285145

4.3 Hasil simulasi tanpa filter

Hasil dar simulasi tanpa filter dapat dilihat pada tabel 4.3 Tabel 4.3 Hasil simulasi tanpa filter

Orde harmonisa

(25)

17

4.4 Hasil simulasi dengan penambahan filter pada orde 5 dan 7

Hasil dari simulasi tanpa filter dapat dilihat pada tabel 4.4 Tabel 4.4 Hasil simulasi dengan penambahan filter

Orde harmonisa

Tegangan harmonisa Arus harmonisa 1

4.5 Hasil simulasi dengan penambahan filter pada orde 3,5 dan 7

Hasil dari simulasi tanpa filter dapat dilihat pada tabel 4.5

Tabel 4.5 Hasil simulasi dengan penambahan filter Orde

harmonisa

(26)

4.6 Analisis Pada Motor Induksi 3 Phasa

Pada bagian ini akan dibahas mengenai pengaruh dari harmonisa pada effisiensi motor induksi tiga phasa.

Spesifikasi dari motor induksi yang akan di analisis • 29,502 hp, 22kW, 400V, pf = 0,88 A. Kondisi tanpa harmonisa

1. Impedansi motor S =

� = , = 25 kVA = 0,025 MVA

= � �� + √ − ��

= _,, , + √ − , = , + ,

2. Perhitungan arus beban penuh

= � ℎ

� = � ,

,

= ,

3. Perhitungan Arus pada kondisi tanpa beban (no-load)

= , = , ,

= ,

4. Perhitungan rugi � pada kondisi tanpa beban

� = � = , � ,

= , = ,

5. Effisiensi motor induksi

(27)

B. Kondisi terdistorsi harmonisa 1. Impedansi motor

S =

� = , = 25 kVA = 0,025 MVA

= � �� + √ − �� )

= _,, , + √ − , = , + ,

= � ℎ

� = � ,

,

= ,

= , = , ,

= ,

4. Perhitungan Irms (pada kondisi terdistorsi harmonisa)

= . √ + � �

= . √ + , = 23,078 x 1,3 = 30 A

� = � = � ,

= , = ,

Ƞ = �_{� �} %

(28)

C. Kondisi setelah penambahan filter pada orde 5 dan 7 1. Impedansi motor

S =

� = , = 25 kVA = 0,025 MVA

= � �� + √ − �� )

= _,, , + √ − , = , + ,

= � ℎ

� = � ,

,

= ,

= , = , ,

= ,

= . √ + � �

= . √ + . = 23,078 x 1,004123 = 23,1731506 A

� = � = , � ,

= , = ,

Ƞ = �_{� �} %

(29)

D. Kondisi setelah penambahan filter pada orde 3, 5 dan 7 1. Impedansi motor

S =

� = , = 25 kVA = 0,025 MVA

= � �� + √ − �� )

= _,, , + √ − , = , + ,

= � ℎ

� = � ,

,

= ,

= , = , ,

= ,

= . √ + � �

= . √ + . = 23,078 x 1,000106574 = 23,08046 A

� = � = , � ,

= , = ,

Ƞ = �_{� �} %

(30)

Tabel 4.6 Hasil analisis pada motor induksi 3 phasa

No Kondisi rugi � (kW) Effisiensi motor

induksi (%) 1 Tanpa Terdistorsi Harmonisa 2,9995698 86,36

2 Terdistorsi Harmonisa 5,0607000 76,99

3 Setelah Penambahan Filter (5,7) 3,0243553 86,25 4 Setelah Penambahan Filter (3,5,7) 3,0002090 86,36

4.7 Pembahasan

Pada Tabel 4.1 memperlihatkan nilai-nilai dari komponen filter pasif double tuned dimana nilai-nilai tersebut diperoleh berdasarkan perhitungan matematis. Tabel 4.1 juga menunjukkan orde-orde dimana filter tersebut akan dituning,lebih tepatnya filter ini akan digunakan atau ditempatkan pada orde 5 dan orde 7. Dan diharapkan mampu menurunkan harmonisa mencapai standar IEEE 512-1992.

Pada Tabel 4.2 memperlihatkan nilai-nilai dari komponen filter pasif double

tuned yang dituning atau ditempatkan pada orde 3 dan orde 5. sehingga orde-orde yang difilter adalah orde 3,5 dan7. Pada tabel 4.3 menunjukkan nilai dari tegangan dan arus yang terdistorsi oleh harmonisa. Pada tabel juga memperlihatkan nilai dari THDi serta THDv. Terlihat dari tabel kondisi dari Harmonisa arus yang terjadi pada orde 3,5 dan 7 melebihi standar yang ditetapkan.

Pada Tabel 4.4 menunjukkan nilai-nilai dari arus dan tegangan terdistorsi yang mengalami perbaikan setelah pemberian filter pada orde 5 dan orde 7. Namun harmonisa arus yang terjadi masih belum sesuai standart IEEE 512-1992.

(31)

BAB V

KESIMPULAN DAN SARAN

5.1 Kesimpulan

Setelah dilakukan proses simulasi dan analisis terhadap motor induksi maka dapat diambil kesimpulan sebagai berikut:

1. Pemasangan fiter pasif double tuned orde 5 dan orde 7 dapat mereduksi harmonisa, walaupun belum sesuai dengan standar yang telah ditentukan yaitu standar IEEE 512-1992. hal ini dapat dilihat pada tabel 4.4.

2. Pemasangan filter pasif double tuned orde 3,5 dan 7 mampu mereduksi harmonisa sesuai standar IEEE 512-1992, dan mampu meningkatkan efisiensi motor induksi sebesar 9,37%

5.2 Saran

1. Pada simulasi diperlukan dua buah filter pasif double tuned untuk mereduksi harmonisa hingga mencapai standar IEEE 512-1992, hal ini kurang efisien, mengingat fisik dari filter tersebut cukup besar. Untuk itu sebaiknya percobaan selanjutnya dilakukan dengan jenis filter yang lain. 2. Percobaan untuk mereduksi harmonisa dengan filter pasif double tuned