LAPORAN PRAKTIK SISTEM KENDALI II Operas

(1)

LAPORAN PRAKTIK SISTEM KENDALI II

Operasi Logika dalam Himpunan Fuzzy

DISUSUN OLEH :

ANDRI DEWANTORO

12507134012

JURUSAN PENDIDIKAN TEKNIK ELEKTRONIKA

FAKULTAS TEKNIK

UNIVERSITAS NEGERI YOGYAKARTA

(2)

FAKULTAS TEKNIK

UNIVERSITAS NEGERI YOGYAKARTA LAPORAN SISTEM KENDALI II

Semester 5 Operasi Logika dalam Himpunan Fuzzy 4x50 menit Tgl : 02 Oktober 2014

A. Kompetensi

Mahasiswa dapat menjelaskan dasar – dasar Fuzzy Logic

B. Sub Kompetensi

 Mahasiswa dapat menjelaskan bagaimana mengoperasikan logika pada himpunan Fuzzy

 Mahasiswa dapat menjelaskan pengaruh berbagai Operasi Logika (biasa/himpunan crsip) yang berlaku dan tidak berlaku dalam himpunan fuzzy

C. Dasar Teori

Tidak seperti logika Boolean (biner – digital) yang memiliki dua buah nilai true (1) dan false (0), fuzzy logic mempunyai nilai input bilangan real antara 0 dan 1 tergantung pada derajat keanggotaannya. Bagaimana cara kita melakukan operasi logika dalam fuzzy? Untuk operasi AND kita menggunakan operasi min. Dengan menggantikan A AND B dengan min (A,B) kita akan mendapatkan operasi yang kita inginkan. Sementara itu operasi logika A OR B digantikan dengan operasi max (A,B). Akhirnya operasi NOT A digantikan dengan I-A.

Lebih luas lagi dalam fuzzy logic kita mengenal ini sebagai: fuzzy intersection atau conjunction (AND), fuzzy union or disjunction (OR), dan fuzzy complement (NOT). Intersection dari dua buah set fuzzy A dan B dikenal dengan istilah T norm,

μ A ∩ B(x)=T(μ A(x), μ B(x))

Sebagaimana fuzzy intersection, fuzzy union operator dikenal dengan S-norm(T-co norm):

μ A∪B(x)=S(μ A(x), μ B(x))

(3)

1. Komputer atau Laptop 2. Program MATLAB 3. Buku dan Alat tulis

E. Keselamatan Kerja

 Memastikan personal computer (PC) telah terinstall dengan baik  Tidak mengubah- ubah setting pada system operasi PC

F. Langkah Kerja

1. Menghidupkan komputer dan menyiapkan software matlab, fuzzy logic toolbox 2. Memilih new M-file. Dan mengetik perintah dibawah :

 Untuk Membership Function Bell dan Gaussian :

x = (0:1:100)';

A = gbellmf (x, [20, 4, 40]); B = gaussmf (x, [70, 20]); Subplot(221); plot(x, A, x, B);

%set(gca, 'xticklabel', []);

Lalu menyimpan dengan nama tertentu

3. Membuka kembali command window matlab, eksekusi file 4. Mengamati dan menggambar hasil eksekusi

5. Menyimpan file dan mengeksekusi 6. Menggambar hasil eksekusi

(4)

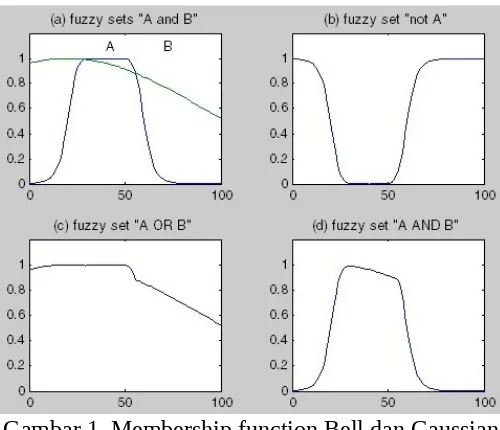
 Membership Function Bell dan Gaussian

Gambar 1. Membership function Bell dan Gaussian

Dalam membership function Bell dan Gaussian ini menggunakan program seperti dibawah ini :

x = (0:1:100)';  menunjukan batasan sumbu x dan y

A = gbellmf (x, [20, 4, 40]);  mengatur jenis MF

B = gaussmf (x, [70, 20]);  mengatur jenis MF

Subplot(221); plot(x, A, x, B);

axis ([-inf inf 0 1.2]);

title ('(a) Fuzzy sets "A and B"'); Program untuk grafik (a)

text(40, 1.1, 'A'); text(70, 1.1, 'B');

subplot (222); plot(x, 1-A);

axis ([-inf inf 0 1.2]); Program untuk grafik (b)

title ('(b) Fuzzy sets "not A"'); subplot (223); plot(x, max(A,B));

axis ([-inf inf 0 1.2]); Program untuk grafik (c) title ('(c) Fuzzy sets "A OR B"');

subplot (224); plot(x, min(A,B));

axis ([-inf inf 0 1.2]); Program untuk grafik (d) title ('(d) Fuzzy sets "A AND B"');

(5)

Subplot(221); plot(x, A, x, B);  mengeset fuzzy

axis ([-inf inf 0 1.2]);  mengatur batas min max sumbu y

title ('(a) Fuzzy sets "A and B"');  memberi judul grafik

text(40, 1.1, 'A');  memberi label pada posisi tertentu

text(70, 1.1, 'B');  memberi label pada posisi tertentu

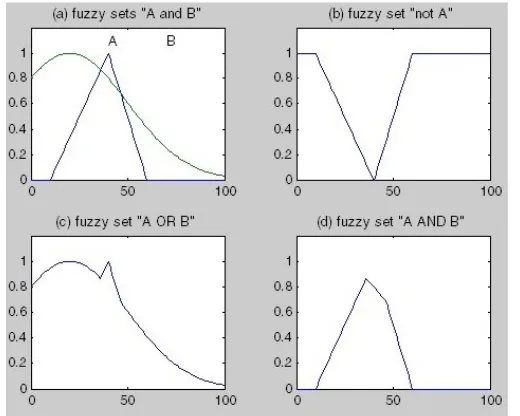
 Membership Function Triangular dan Gaussian

Gambar 2. Membership Function Triangular dan Gaussian

Untuk menghasilkan membership function triangular dan gaussian ini programnya sama dengan membership function bell dan Gaussian hanya saja pada pengaturan jenis Mfnya diganti menjadi :

A = trimf(x, [10, 40, 60]); B = gaussmf(x, [30, 20]);

(6)

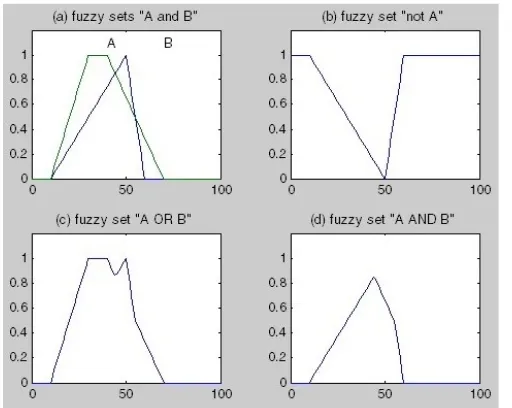
Gambar 3. Membership Function Triangular dan Trapezoid

Untuk menghasilkan membership function triangular dan trapezouid ini programnya sama dengan membership function bell dan Gaussian hanya saja pada pengaturan jenis Mfnya diganti menjadi :

A = trimf(x, [10, 50, 60]); B = trapmf(x, [10, 30,40,70]);

H. Bahan Diskusi

Buktikan dengan gambar (menggunakan matlab ) bahwa operasi berikut berlaku pada fuzzy logic :

a. A ∩ A'

=∅ b. A∪A'=1

c. A ∩B=B ∩ A

d. A ∩(B∪C)=(A ∩ B)∪(A ∩ C) e. A∪(B ∩C)=(A∪B)∩(A∪C)

f. A∪(A ∩ B)=A

g. (A ∩B)'=A'_∪_B' h. (A∪B)'=A'_{∩ B '}

Simpulkan operasi diatas mana yang berlaku pada fuzzy logic dan mana yang tidak

(7)

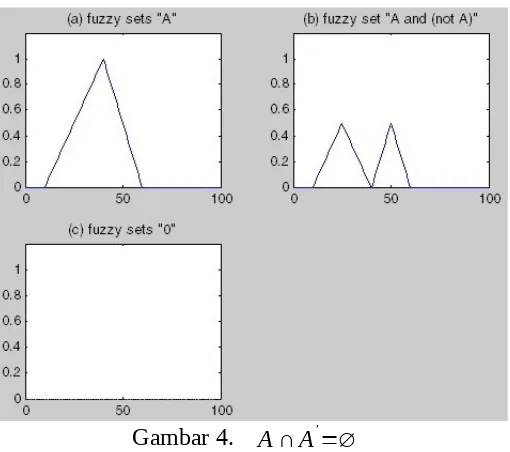
a. A ∩ A'=∅

Gambar 4. A ∩ A'=∅

Dari gambar 4 dapat disimpulkan bahwa operasi A ∩ A'=∅ tidak berlaku pada fuzzy karena pada gambar 4 bagian (b) terlihat bahwa A ∩ A’ tidak sama dengan ∅ . Ini terbukti ketika fuzzy diset 0 akan seperti pada bagian (c). Karena gambar bagian (b) dan (c) berbeda maka operasi tersebut tidak sama.

b. A∪A'

=1

Gambar 5. A ∪ A’ = 1

Dari gambar 5 dapat disimpulkan bahwa operasi A ∪ A’ = 1 tidak berlaku pada fuzzy karena pada gambar 5 bagian (b) terlihat A ∪ A’ tidak sama dengan 1. Ini terbukti ketika fuzzy diset 1 maka gambarnya akan seperti pada bagian (c). Karena gambar bagian (b) dan (c) berbeda maka operasi tersebut tidak sama.

(8)

Gambar 6. A∩B = B∩A

Dari gambar 6 dapat disimpulkan bahwa operasi diatas berlaku pada fuzzy. ini terbukti hasil gambar A∩B sama dengan hasil gambar B∩A.

d. A ∩(B∪C)=(A ∩ B)∪(A ∩ C)

Gambar 7. A ∩(B∪C)=(A ∩ B)∪(A ∩ C)

Dari gambar 7 dapat disimpulkan bahwa operasi diatas berlaku pada fuzzy. ini terbukti hasil gambar A ∩(B∪C) sama dengan hasil gambar (A ∩B)∪(A ∩C) . e. A∪(B ∩C)=(A∪B)∩(A∪C)

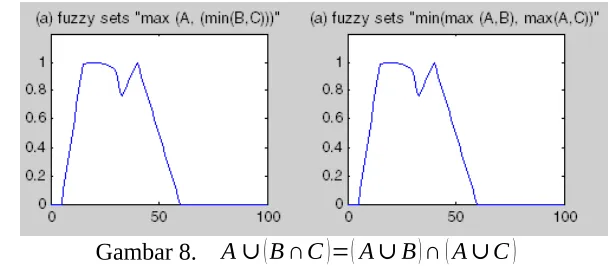
Gambar 8. A∪(B ∩C)=(A∪B)∩(A∪C)

Dari gambar 8 dapat disimpulkan bahwa operasi diatas berlaku pada fuzzy. ini terbukti hasil gambar A∪(B ∩C) sama dengan hasil gambar (A∪B)∩(A∪C) .

(9)

Gambar 9. A∪(A ∩ B)=A

Dari gambar 9 dapat disimpulkan bahwa operasi diatas berlaku pada fuzzy. ini terbukti hasil gambar A∪(A ∩ B) sama dengan hasil gambar A.

g. (A ∩B)'=A'_∪_B'

Gambar 10. (A ∩B)'=A'∪B'

Dari gambar 10 dapat disimpulkan bahwa operasi diatas berlaku pada fuzzy. ini terbukti hasil gambar (A ∩B)' sama dengan hasil gambar A'_∪_B' _.

h. (A∪B)'=A'_{∩ B '}

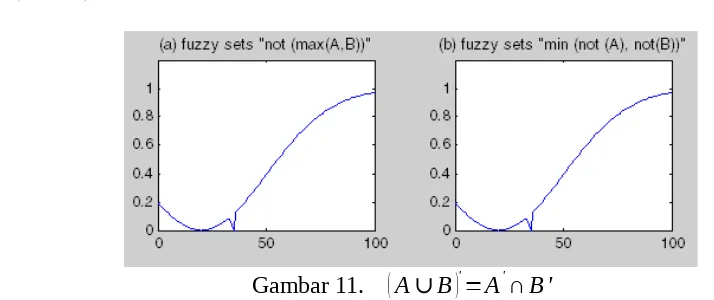
Gambar 11. (A∪B)'=A'∩ B '

(10)

J. Kesimpulan

Setelah melakuikan praktikum operasi logika dalam himpunan fuzzy ini dapat disimpulkan bahwa :

1. Untuk mengetahui operasi logika yang berlaku pada himpunan fuzzy dapat dibuktikan dengan memasukan operasi tersebut dalam bentuk gambar.

2. Dari operasi logika diatas hanya terdapat dua operasi logika yang tidak termasuk dalam himpunan fuzzy, yaitu pada point a dan b.

(11)