SIMULASI TOTAL KERUGIAN ASURANSI MENGGUNAKAN
DEDUCTIBLE DAN LIMITED COVERAGE
SYAMSUL
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2016
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Simulasi Total Kerugian Asuransi Menggunakan Deductible dan Limited Coverage adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, November 2016
Syamsul
ABSTRAK
SYAMSUL. Simulasi Total Kerugian Asuransi Menggunakan Deductible dan
Limited Coverage. Dibimbing oleh BERLIAN SETIAWATY dan RUHIYAT. Polis asuransi adalah kontrak yang dibuat oleh perusahaan asuransi dengan peserta asuransi. Pada tugas akhir ini, perusahaan asuransi menerapkan kebijakan
deductible dan limited coverage. Untuk mendesain polis, perusahaan asuransi harus memperkirakan total kerugian yang akan ditanggung oleh perusahaan tersebut. Pemodelan total kerugian dilakukan dengan cara menggabung sebaran frekuensi kerugian yang menyebar Poisson dan sebaran tingkat keparahannya yang menyebar Pareto. Dalam penelitian ini digunakan metode simulasi untuk memperkirakan total kerugian, menentukan premi, menghitung keuntungan yang diperoleh perusahaan asuransi, dan membandingkan hasil perkiraan total kerugian antara metode simulasi dengan hasil secara analitik. Menggunakan data yang dibangkitkan melalui
software Mathematica 11.0, dapat disimpulkan bahwa metode simulasi adalah metode yang cukup baik untuk memperkirakan total kerugian perusahaan asuransi. Kata kunci: sebaran gabungan Poisson-Pareto, simulasi, total kerugian
ABSTRACT
SYAMSUL. Simulation of Aggregate Loss of Insurance Using Deductible and Limited Coverage. Supervised by BERLIAN SETIAWATY and RUHIYAT.
Policy is a contract made by insurer with insurance participants. In this research, insurer implements deductibleandlimited coverage policy. To design the policy, the insurer must know the approximation of aggregate loss that will be paid by insurer itself. The modeling of aggregate loss is created by compounding the distributions of loss frequency which has Poisson distribution and distribution of loss severity which has Pareto distribution. Simulation method is used to approximate the aggregate loss distribution, to determine the premium, to calculate the insurer benefits, and to compare the results of the approximation aggregate loss using the method of simulation and the analytic results. Using data which are generated by software Mathematica 11.0, it can be concluded that the simulation method is quite good to approximate aggregate loss of the insurer.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
SIMULASI TOTAL KERUGIAN ASURANSI MENGGUNAKAN
DEDUCTIBLE DAN LIMITED COVERAGE
NAMA PENULIS
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2016
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Maret 2016 ini ialah keuangan dan aktuaria, dengan judul Simulasi Total Kerugian Asuransi Menggunakan Deductible dan Limited Coverage.
Terima kasih penulis ucapkan kepada:
1. Dr Berlian Setiawaty, MS dan Ruhiyat, SSi, MSi sebagai pembimbing yang telah memberikan ilmu, arahan dan menyediakan waktu untuk membimbing penulis dalam menyelesaikan karya ilmiah ini serta Dr I Gusti Putu Purnaba, DEA yang telah banyak memberikan saran.
2. Seluruh dosen dan staf karyawan/karyawati Departemen Matematika.
3. Orang tua beserta keluarga yang selalu memberikan do’a, kasih sayang dan dukungannya.
4. PT. Adaro Indonesia selaku penyandang dana Beasiswa Utusan Daerah yang telah memberikan kesempatan kepada penulis untuk kuliah di IPB.
5. Ibu Susi yang senantiasa memberi nasehat dan saran.
6. Aulia, Ulfa, Amri, Afif, Umam dan keluarga IGAF LC IPB yang selalu memberikan semangat dan motivasi.
7. Kholis, Kemal, Idham, Norma, Fredy, Rivanu, serta semua teman-teman Matematika 49 yang selalu ada dan membantu penulis.
8. Fai, Hami, Indra, Upik, Dilah, dan seluruh Dangsanak Adaro, serta semua pihak yang telah memberikan bantuan maupun dukungan kepada penulis dalam menyelesaikan skripsi ini.
Semoga karya ilmiah ini bermanfaat.
Bogor, November 2016
DAFTAR ISI
DAFTAR TABEL vi DAFTAR GAMBAR vi DAFTAR LAMPIRAN vi PENDAHULUAN 1 Latar Belakang 1 Tujuan Penelitian 2 LANDASAN TEORI 2Ruang Contoh, Kejadian, dan Peluang 2
Peubah Acak dan Fungsi Sebaran 3
Polis Asuransi 7
Premi 9
Keuntungan Perusahaan Asuransi 9
METODE 9
Deskripsi Data 9
Prosedur Pemrograman Data 10
HASIL DAN PEMBAHASAN 10
Identifikasi dan Simulasi Sebaran Frekuensi 10
Identifikasi dan Simulasi Sebaran Tingkat Keparahan 11 Identifikasi dan Simulasi Sebaran Total Kerugian 12
Premi dan Keuntungan Perusahaan Asuransi 16
Galat dari Rata-Rata dan Simpangan Baku 17
SIMPULAN 18
DAFTAR PUSTAKA 18
LAMPIRAN 19
DAFTAR TABEL
1 Premi dan keuntungan yang didapatkan perusahaan asuransi 16
2 Rata-rata dan simpangan baku 17
3 Galat mutlak dan galat relatif 17
DAFTAR GAMBAR
1 Histogram peluang dari frekuensi kerugian berdasarkan hasil simulasi 11 2 Histogram peluang dari tingkat keparahan kerugian berdasarkan hasil
simulasi 11
3 Histogram peluang dari total kerugian yang harus ditanggung oleh perusahaan asuransi (𝑆𝑎) berdasarkan hasil simulasi 12 4 Histogram peluang dari total kerugian yang harus ditanggung oleh
pemegang polis (𝑅𝑏) berdasarkan hasil simulasi, dengan 𝑑 =
Rp2 000 000 dan 𝑢 = Rp8 000 000 13
5 Histogram peluang dari total kerugian yang harus ditanggung perusahaan asuransi (𝑆𝑏) berdasarkan hasil simulasi, dengan 𝑑 = Rp2 000 000 dan
𝑢 = Rp8 000 000 13
6 Histogram peluang dari total kerugian yang harus ditanggung oleh seluruh pemegang polis (𝑅𝑐) berdasarkan hasil simulasi, dengan 𝑑*= Rp60 000 000 dan 𝑢*= Rp240 000 000 14 7 Histogram peluang dari total kerugian yang harus ditanggung oleh
perusahaan asuransi (𝑆𝑐) berdasarkan hasil simulasi, dengan 𝑑*= Rp60 000 000 dan 𝑢*= Rp240 000 000 14 8 Histogram peluang dari total kerugian yang harus ditanggung oleh
seluruh pemegang polis (𝑅𝑐) berdasarkan hasil simulasi, dengan 𝑑*=
Rp100 000 000 dan 𝑢*= Rp300 000 000 15 9 Histogram peluang dari total kerugian yang harus ditanggung oleh
perusahaan asuransi (𝑆𝑐) berdasarkan hasil simulasi, dengan 𝑑*=
Rp100 000 000 dan 𝑢*= Rp300 000 000 15
DAFTAR LAMPIRAN
1 Pembuktian nilai harapan dan ragam sebaran Poisson 19 2 Pembuktian nilai harapan dan ragam sebaran Pareto 20
3 Pembuktian nilai harapan total kerugian 22
4 Pembuktian ragam total kerugian 23
5 Pemrograman simulasi menggunakan software Mathematica 11.0 25 6 Menghitung keuntungan perusahaan menggunakan software
Mathematica 11.0 30
7 Rata-rata dan simpangan baku secara analitik dari tiga sebaran yang
PENDAHULUAN
Latar BelakangSetiap orang memiliki risiko yang merupakan sebuah ketidakpastian di masa mendatang yang bisa menimbulkan suatu kerugian seperti kecelakaan, kebakaran, kebanjiran dan lainnya. Jumlah dari semua kerugian dalam periode waktu tertentu disebut total kerugian (aggregate loss). Total kerugian terdiri atas banyaknya peristiwa merugikan (frekuensi) dan tingkat keparahan kerugian tersebut (severity). Untuk mengantisipasi kerugian dari peristiwa tersebut maka diperlukan jaminan perlindungan dari jasa asuransi.
Berdasarkan Undang-Undang Republik Indonesia Nomor 40 Tahun 2014 tentang Usaha Perasuransian, Usaha Asuransi Umum adalah usaha jasa pertanggungan risiko yang memberikan penggantian kepada tertanggung atau pemegang polis karena kerugian, kerusakan, biaya yang timbul, kehilangan keuntungan, atau tanggung jawab hukum kepada pihak ketiga yang mungkin diderita pemegang polis karena terjadi suatu peristiwa yang tidak pasti. Jaminan terhadap risiko atau kerusakan yang terjadi oleh perusahaan asuransi kepada pemegang polis disebut klaim, sedangkan biaya yang harus dibayarkan pemegang polis kepada perusahaan asuransi disebut premi. Besarnya premi dan klaim setiap pemegang polis bisa berbeda-beda. Besarnya premi dan klaim dipengaruhi beberapa faktor seperti, masa asuransi, besarnya uang pertanggungan, kebijakan perusahaan asuransi dan lainnya.
Setiap perusahaan asuransi biasanya memiliki kebijakan polis masing-masing, dan beberapa di antaranya menerapkan kebijakan deductible dan limited coverage. Untuk membuat kebijakan yang menyangkut berbagai aspek polis asuransi, perusahaan asuransi harus bisa menggambarkan perilaku risiko seorang pemegang polis terkait total kerugian yang dialaminya. Oleh karena itu, diperlukan suatu model aktuaria yang dapat digunakan untuk mempelajari pola klaim pemegang polis. Salah satu cara yang dapat dilakukan adalah membuat pemodelan, kemudian mengestimasi frekuensi kerugian dalam waktu tertentu dan mengukur seberapa besar kerugian yang akan ditanggung oleh pihak perusahaan, sehingga dapat melakukan penghitungan total kerugian.
Pemodelan total kerugian dilakukan dengan menggabung sebaran frekuensi kerugian dan sebaran tingkat keparahan kerugiannya. Sebaran frekuensi kerugian merupakan sebaran yang bersifat diskret seperti sebaran binomial, sebaran multinomial, sebaran hipergeometrik dan sebaran Poisson sedangkan sebaran tingkat keparahan kerugian memiliki sifat yang kontinu seperti sebaran beta, sebaran eksponensial, sebaran lognormal, sebaran gamma, sebaran Pareto dan lainnya. Gabungan antara sebaran frekuensi kerugian dan sebaran tingkat keparahan tersebut akan menghasilkan sebaran baru yang disebut sebaran gabungan (compound), sebaran inilah yang akan digunakan untuk memproyeksikan total kerugian di masa depan.
Ada banyak metode yang dapat digunakan untuk memperkirakan total kerugian seperti metode fourier inversion, metode panjer recursion, dan fast fourier transform. Pada penelitian ini akan digunakan metode lainnya yaitu metode simulasi. Metode simulasi dilakukan untuk meniru suatu peristiwa nyata dengan
2
menggunakan model matematika sehingga dapat menggambarkan kejadian yang sebenarnya, kemudian hasil yang diperoleh digunakan untuk meramalkan dampak kejadian tersebut di masa depan. Keuntungan utama dari metode simulasi adalah selain dapat digunakan untuk memperkirakan total kerugian secara umum, juga dapat memperkirakan total kerugian jika perusahaan menerapkan kebijakan
deductible dan limited coverage baik secara individu maupun secara keseluruhan. Menurut Napitupulu (2009), sebaran yang paling baik untuk menggambarkan pola frekuensi kerugian adalah sebaran Poisson, maka dalam penelitian ini akan diperkirakan total kerugian menggunakan sebaran gabungan Poisson-Pareto melalui pendekatan simulasi dan mempelajari efeknya jika perusahaan menerapkan kebijakan deductible dan limited coverage, dengan data frekuensi kerugian menyebar Poisson dan tingkat keparahan kerugiannya menyebar Pareto.
Rujukan utama penelitian ini bersumber pada tulisan Mohamed et al.(2010) yang berjudul “Approximation of Aggregate Losses Using Simulation”.
Tujuan Penelitian
Tujuan dari karya ilmiah ini yaitu:
1. Memperkirakan total kerugian perusahaan asuransi dan menyelidiki efeknya jika perusahaan asuransi menetapkan kebijakan deductible dan limited coverage dengan menggunakan metode simulasi.
2. Menentukan premi yang harus dibayar pemegang polis. 3. Menghitung keuntungan yang diperoleh perusahaan asuransi.
4. Membandingkan hasil prediksi total kerugian perusahaan asuransi menggunakan metode simulasi dan secara analitik.
LANDASAN TEORI
Ruang Contoh, Kejadian, dan Peluang Definisi 1 (Percobaan Acak)
Dalam suatu percobaan seringkali dilakukan pengulangan dengan kondisi yang sama. Semua kemungkinan hasil yang akan muncul dapat diketahui, akan tetapi hasil pada percobaan berikutnya tidak dapat diduga dengan tepat. Percobaan semacam ini, yang dapat diulang dalam kondisi sama, disebut percobaan acak (Hogg et al. 2014).
Definisi 2 (Ruang Contoh dan Kejadian)
Himpunan semua hasil yang mungkin dari suatu percobaan acak disebut ruang contoh, dinotasikan dengan Ω. Suatu kejadian 𝐴 adalah himpunan bagian dari Ω
(Grimmet dan Stirzaker 2001).
Definisi 3 (Medan-σ)
Medan-σ adalah suatu himpunan ℱ yang anggotanya terdiri atas himpunan bagian dari ruang contoh Ω yang memenuhi kondisi sebagai berikut:
3 2. Jika 𝐴1, 𝐴2, … ∈ ℱ, maka ⋃∞𝑖=1𝐴𝑖 ∈ ℱ
3. Jika 𝐴 ∈ ℱ maka 𝐴𝐶 ∈ ℱ (Grimmet dan Stirzaker 2001).
Definisi 4 (Ukuran Peluang)
Misalkan ℱ adalah medan-σ dari ruang contoh Ω. Ukuran peluang adalah suatu fungsi 𝑃: ℱ → [0,1] yang memenuhi:
1. 𝑃(Ø) = 0, 𝑃(Ω) = 1
2. Jika 𝐴1, 𝐴2, … ∈ ℱ adalah himpunan yang saling lepas yaitu 𝐴𝑖 ∩ 𝐴𝑗 = Ø untuk setiap pasangan 𝑖 ≠ 𝑗 maka 𝑃(⋃∞𝑖=1𝐴𝑖) = ∑∞𝑖=1𝑃(𝐴𝑖).
Pasangan (Ω, ℱ, 𝑃) disebut ruang peluang (Grimmet dan Stirzaker 2001).
Peubah Acak dan Fungsi Sebaran Definisi 5 (Peubah Acak)
Misalkan (Ω, ℱ, 𝑃) adalah ruang peluang. Peubah acak adalah fungsi 𝑋: Ω → ℝ
dengan sifat {𝜔 ∈ Ω: 𝑋(𝜔) ≤ 𝑥} ∈ ℱ untuk setiap 𝑥 ∈ ℝ (Grimmet & Stirzaker 2001).
Definisi 6 (Fungsi Sebaran)
Misalkan X adalah peubah acak. Fungsi sebaran dari peubah acak 𝑋 adalah fungsi 𝐹𝑋: ℝ → [0,1] yang diberikan oleh 𝐹𝑋(𝑥) = 𝑃(𝑋 ≤ 𝑥). Fungsi 𝐹𝑋 disebut fungsi sebaran dari peubah acak 𝑋 (Grimmet & Stirzaker 2001).
Definisi 7 (Peubah Acak Diskret)
Peubah acak 𝑋 dikatakan diskret jika nilainya berada pada himpunan bagian yang terhitung dari ℝ (Grimmet & Stirzaker 2001).
Definisi 8 (Peubah Acak Kontinu)
Peubah acak 𝑋dikatakan kontinu jika fungsi sebaran 𝐹𝑋(𝑥) adalah fungsi kontinu
untuk seluruh 𝑥 ∈ ℝ(Hogg et al. 2014). Definisi 9 (Fungsi Massa Peluang)
Misalkan (Ω, ℱ, 𝑃) adalah ruang peluang. Fungsi massa peluang dari peubah acak diskret 𝑋 adalah suatu fungsi 𝑝𝑋 : ℝ → [0,1] yang didefinisikan oleh
𝑝𝑋 (𝑥) = 𝑃(𝑋 = 𝑥) (Grimmet & Stirzaker 2001).
Definisi 10 (Fungsi Kepekatan Peluang)
Misalkan 𝑋 adalah peubah acak kontinu, maka 𝑓𝑋(𝑥) adalah fungsi kepekatan
peluang dari 𝑋 dengan syarat sebagai berikut: 1. 𝑓𝑋(𝑥) ≥ 0,∀𝑥 ∈ ℝ 2. ∫−∞∞ 𝑓𝑋(𝑥)𝑑𝑥 = 1 3. 𝑃(𝑎 < 𝑋 < 𝑏) =∫ 𝑓𝑋(𝑥)𝑑𝑥 𝑏 𝑎 (Hogg et al. 2014).
4
Definisi 11 (Nilai Harapan Sebaran Diskret)
Jika 𝑋 adalah peubah acak diskret dengan fungsi massa peluang 𝑝𝑋(𝑥) maka nilai harapan dari 𝑋, dinotasikan dengan 𝐸(𝑋), adalah
𝐸(𝑋) = ∑ 𝑥𝑝𝑋(𝑥) ∀𝑥
asalkan jumlah tersebut konvergen mutlak (Hogg et al. 2014).
Definisi 12 (Nilai Harapan Sebaran Kontinu)
Jika 𝑋 adalah peubah acak kontinu dengan fungsi kepekatan peluang 𝑓𝑋(𝑥) maka nilai harapan dari 𝑋 adalah
𝐸(𝑋) = ∫ 𝑥𝑓𝑋(𝑥) 𝑑𝑥 ∞
−∞
asalkan integral tersebut konvergen mutlak (Hogg et al. 2014).
Definisi 13 (Nilai Harapan Bersyarat)
Misalkan 𝑋 dan 𝑌 adalah peubah acak kontinu dan 𝑓𝑋|𝑌 (𝑥|𝑦) adalah fungsi kepekatan peluang bersyarat dari 𝑋 dengan syarat 𝑌 = 𝑦. Nilai harapan dari 𝑋
dengan syarat 𝑌 = 𝑦 adalah
𝐸(𝑋|𝑌 = 𝑦) = ∫ 𝑥𝑓𝑋|𝑌 (𝑥|𝑦) 𝑑𝑥
∞
−∞ (Hogg et al. 2014).
Definisi 14 (Ragam dan Simpangan Baku)
Ragam dari suatu peubah acak 𝑋adalah nilai harapan dari kuadrat selisih antara
𝑋 dengan nilai harapannya, didefinisikan sebagai berikut
𝜎𝑋2 = var(𝑋) = 𝐸(𝑋 − 𝐸(𝑋)) 2
= 𝐸(𝑋2) − (𝐸(𝑋))2
(Hogg et al. 2014).
Misalkan 𝜎𝑋2adalah ragam dari suatu peubah acak 𝑋, maka simpangan bakunya adalah akar kuadrat positif dari ragam, didefinisikan sebagai berikut
𝜎𝑋 = √𝜎𝑋2 (Hogg et al. 2014).
Definisi 15 (Sebaran Poisson)
Suatu peubah acak 𝑁 dikatakan menyebar Poisson dengan parameter ,> 0, jika memenuhi fungsi massa peluang
𝑝𝑁(𝑛;) =
𝑛
𝑒−
𝑛! , 𝑛 = 0,1,2, …
(Grimmet & Stirzaker 2001).
Lema 1 (Nilai Harapan dan Ragam Sebaran Poisson)
Jika peubah acak 𝑁 menyebar Poisson dengan parameter ,> 0, maka
𝐸(𝑁) = var(𝑁) = (1)
(Ghahramani 2005). Bukti: Lihat Lampiran 1.
5
Definisi 16 (Sebaran Pareto)
Suatu peubah acak 𝑋 dikatakan menyebar Pareto dengan parameter 𝛼 dan 𝛽 jika memenuhi fungsi kepekatan peluang, sebagai berikut
𝑓𝑋(𝑥; 𝛼,𝛽) =
𝛼𝛽𝛼
(𝛽+ 𝑥)𝛼+1, 𝛼> 0 dan 𝛽 > 0
(Grimmet & Stirzaker 2001).
Teorema 1 (Nilai Harapan dan Ragam Sebaran Pareto)
Jika peubah acak 𝑋 menyebar Pareto dengan parameter 𝛼, 𝛽 > 0, maka
𝐸(𝑋) = 𝛽
𝛼 − 1
var(𝑋) = 𝛼𝛽
2
(𝛼 − 1)2(𝛼 − 2),𝛼 >2 (2) (Grimmet & Stirzaker 2001).
Bukti: Lihat Lampiran 2.
Definisi 17 (Kesalingbebasan Peubah Acak)
Peubah acak 𝑋1, 𝑋2, … , 𝑋𝑛 dikatakan saling bebas jika untuk semua i dari 𝑋𝑖 memenuhi persamaan berikut
𝑃(𝑋1 ≤𝑥1, … ,𝑋𝑛 ≤ 𝑥𝑛) = 𝑃(𝑋1 ≤ 𝑥1)… 𝑃(𝑋𝑛 ≤𝑥𝑛) (Grimmet & Stirzaker 2001).
Definisi 18 (Bebas Stokastik Identik)
Misalkan 𝑋1, 𝑋2, … , 𝑋𝑛 adalah 𝑛 peubah acak yang memiliki fungsi kepekatan yang sama yaitu 𝑓(𝑥) maka 𝑋1, 𝑋2, … , 𝑋𝑛 disebut bebas stokastik identik jika
𝑓1(𝑥1) = 𝑓(𝑥1)
𝑓2(𝑥2) = 𝑓(𝑥2)
⋮
𝑓𝑛(𝑥𝑛) = 𝑓(𝑥𝑛)
sehingga fungsi kepekatan bersamanya adalah
𝑓(𝑥1, 𝑥2, … , 𝑥𝑛) = 𝑓(𝑥1)𝑓(𝑥2) … 𝑓(𝑥𝑛) (Hogg et al. 2014).
Definisi 19 (Fungsi Sebaran Bersama Dua Peubah Acak)
Fungsi sebaran dari dua peubah acak 𝑋 dan 𝑌 adalah fungsi 𝐹𝑋𝑌 : ℝ2 → [0,1] yang diberikan oleh
𝐹𝑋𝑌 (𝑥, 𝑦) = 𝑃(𝑋 ≤ 𝑥, 𝑌 ≤ 𝑦),∀𝑥, 𝑦 ∈ ℝ. (Grimmet & Stirzaker 2001).
Definisi 20 (Total Kerugian)
Jumlah dari semua kerugian yang dialami oleh pemegang polis yang harus ditanggung oleh perusahaan asuransi dalam suatu periode waktu tertentu disebut total kerugian. Total kerugian terdiri atas banyaknya peristiwa merugikan (frekuensi) dan tingkat keparahan kerugian tersebut. Misalkan𝑁 adalah peubah
6
acak yang menyatakan banyaknya kerugian yang terjadi dan 𝑋𝑖 adalah peubah acak yang menunjukkan tingkat keparahannya, maka total kerugian dapat diperoleh dengan menjumlahkan kerugian yang dialami oleh semua pemegang polis tersebut, sehingga untuk 𝑖 = 1, … , 𝑁 total kerugian adalah sebesar 𝑆, di mana 𝑆 adalah peubah acak dengan nilai sebagai berikut
𝑆 = 𝑋1+ 𝑋2+ … + 𝑋𝑁. (3) Model ini mengasumsikan bahwa 𝑋𝑖 bersifat bebas stokastik identik dengan asumsi sebaran frekuensi kerugian (𝑁) saling bebas terhadap sebaran tingkat keparahannya (𝑋𝑖) (Klugman et al. 2012).
Teorema 2 (Nilai Harapan Total Kerugian)
Misalkan 𝑋1,𝑋2, …adalah peubah acak yang bebas stokastik identik dengan nilai harapan 𝐸(𝑋), dan jika 𝑁 > 0 yang merupakan peubah acak dengan nilai integer
dan saling bebas dengan 𝑋𝑖, 𝑖 = 1, … , 𝑁 dengan nilai harapan 𝐸(𝑁) < ∞, maka
𝐸 (∑ 𝑋𝑖
𝑁
𝑖=1
) = 𝐸(𝑁) 𝐸(𝑋) (4)
(Ghahramani 2005). Bukti: Lihat Lampiran 3.
Berdasarkan persamaan (4), jika 𝑁 adalah peubah acak yang menyebar Poisson dengan parameter dan (𝑋1, 𝑋2, … , 𝑋𝑁) merupakan peubah acak yang menyebar Pareto dengan parameter α dan 𝛽, maka nilai harapan dari total kerugian 𝑆 di mana
𝑆 = 𝑋1+ 𝑋2+ ⋯ + 𝑋𝑁 dari sebaran gabungan Poisson-Pareto adalah
𝐸(𝑆) = 𝐸(𝑁) 𝐸(𝑋) = ( 𝛽
𝛼 − 1)
= 𝛽
𝛼 − 1,𝛼 > 1. (5)
Teorema 3 (Ragam Total Kerugian)
Misalkan 𝑋1,𝑋2, …adalah peubah acak yang bebas stokastik identik dengan nilai harapan 𝐸(𝑋) dan ragam var(𝑋). Misalkan diberikan 𝑁 > 0 yang merupakan peubah acak dengan nilai integer dan saling bebas dengan 𝑋𝑖, 𝑖 = 1, … , 𝑁 dengan nilai harapan 𝐸(𝑁) < ∞ dan var(𝑁) < ∞, maka
var (∑ 𝑋𝑖
𝑁
𝑖=1
) = 𝐸(𝑁) var(𝑋) + var(𝑁) (𝐸(𝑋))2 (6) (Ghahramani 2005).
Bukti: Lihat Lampiran 4.
Berdasarkan persamaan (6), jika 𝑁 merupakan peubah acak yang menyebar Poisson dengan parameter dan (𝑋1, 𝑋2, … , 𝑋𝑁) peubah acak yang menyebar Pareto dengan parameter α dan 𝛽, serta sebaran Poisson saling bebas dengan sebaran Pareto, maka ragam dari total kerugian 𝑆 di mana 𝑆 = 𝑋1+ 𝑋2+ ⋯ + 𝑋𝑁
7
var(𝑆) = 𝐸(𝑁) var(𝑋) + var(𝑁) (𝐸(𝑋))2 = ( 𝛼 𝛽 2 (𝛼 − 1)2( 𝛼 − 2)) + ( 𝛽 𝛼 − 1) 2 = 𝛼𝛽 2 (𝛼 − 1)2( 𝛼 − 2)+ 𝛽2 (𝛼 − 1)2 = 𝛼𝛽 2 (𝛼 − 1)2( 𝛼 − 2)+ 𝛽2( 𝛼 − 2) (𝛼 − 1)2( 𝛼 − 2) = 𝛽 2(2𝛼 − 2) (𝛼 − 1)2(𝛼 − 2), 𝛼 > 2. (7) Polis Asuransi
Polis asuransi adalah kontrak yang dibuat oleh perusahaan asuransi dengan peserta asuransi. Setiap perusahaan asuransi biasanya memiliki kebijakan polis masing-masing, dan beberapa di antaranya menerapkan kebijakan deductible dan
limited coverage.
Deductible
Deductible adalah ketentuan kebijakan umum yang mengharuskan pemegang polis untuk membayar sebagian dari kerugian yang dialami. Tujuan kebijakan
deductible adalah menghilangkan klaim yang nilai kerugiannya lebih kecil dari batas deductible yang diterapkan oleh perusahaan asuransi, mengurangi premi yang dibayarkan oleh pemegang polis, dan mengurangi kerugian yang dilakukan pemegang polis secara sengaja, karena beberapa pemegang polis mungkin akan sengaja menyebabkan kerugian dalam rangka untuk mendapatkan keuntungan dari perusahaan asuransi. Kebijakan deductible akan mendorong pemegang polis untuk lebih berhati-hati agar tidak mengalami kerugian karena mereka harus ikut menanggung bagian dari kerugian tersebut.
Misalkan 𝑋 adalah peubah acak yang menunjukkan besar kerugian seorang pemegang polis. Ketika sebuah perusahaan asuransi menerapkan kebijakan
deductible sebesar 𝑑, maka kerugian yang harus ditanggung pemegang polis karena peristiwa merugikan yang dialami adalah sebesar 𝑌, di mana 𝑌 adalah peubah acak dengan nilai sebagai berikut
𝑌 = { 𝑋, 𝑋 ≤ 𝑑
𝑑, 𝑋 > 𝑑 (8) sedangkan kerugian pemegang polis yang ditanggung oleh perusahaan asuransi dapat diwakili oleh peubah acak Z, dengan nilai sebagai berikut
𝑍 = { 0, 𝑋 ≤ 𝑑
𝑋 − 𝑑, 𝑋 > 𝑑 . (9)
Limited Coverage
Limited coverage adalah batas dana maksimum yang akan ditanggung oleh perusahaan asuransi jika pemegang polis melakukan klaim. Misalkan 𝑋 adalah peubah acak yang menunjukkan besar kerugian seorang pemegang polis. Ketika sebuah perusahaan asuransi menerapkan kebijakan limited coverage sebesar 𝑢,
8
maka dana yang harus ditanggung pemegang polis jika mengalami kerugian adalah sebesar 𝑌, di mana 𝑌 adalah peubah acak dengan nilai sebagai berikut
𝑌 = { 0, 𝑋 ≤ 𝑢
𝑋 − 𝑢, 𝑋 > 𝑢 (10) sedangkan kerugian pemegang polis yang ditanggung oleh perusahaan asuransi dapat diwakili oleh peubah acak Z, dengan nilai sebagai berikut
𝑍 = {𝑋, 𝑋 ≤ 𝑢
𝑢, 𝑋 > 𝑢. (11)
Polis Asuransi tanpa Deductible dan Limited Coverage
Misalkan 𝑋𝑖, 𝑖 = 1,2, … , 𝑁 adalah peubah acak yang menunjukkan besar kerugian pemegang polis ke 𝑖. Ketika polis asuransi tidak menerapkan deductible
dan limited coverage, maka tidak ada kerugian yang harus ditanggung pemegang polis, apabila kerugian yang ditanggung pemegang polis dinotasikan dengan 𝑅𝑎, maka 𝑅𝑎 = 0 untuk setiap kerugian yang terjadi. Total kerugian pemegang polis yang ditanggung oleh perusahaan asuransi karena peristiwa merugikan yang terjadi dapat diwakili oleh peubah acak 𝑆𝑎, dengan nilai sebagai berikut
𝑆𝑎 = 𝑆 =𝑋1+ 𝑋2+ … + 𝑋𝑁. (12)
Polis Asuransi dengan Deductible dan Limited Coverage
Misalkan 𝑋𝑖, 𝑖 = 1,2, … , 𝑁 adalah peubah acak yang menunjukkan besar kerugian pemegang polis ke 𝑖. Jika polis asuransi mengandung deductible sebesar d dan limited coverage sebesar u, maka kerugian yang harus ditanggung pemegang polis ke 𝑖 jika mengalami peristiwa merugikan adalah sebesar 𝑌𝑖, 𝑖 = 1,2, … , 𝑁, di mana 𝑌𝑖 adalah peubah acak dengan nilai sebagai berikut
𝑌𝑖 = {
𝑋𝑖, 𝑋𝑖 ≤ 𝑑 𝑑, 𝑑 <𝑋𝑖 ≤ 𝑢
𝑋𝑖 + 𝑑 − 𝑢, 𝑋𝑖 > 𝑢
(13)
sehingga total kerugian yang ditanggung pemegang polis adalah sebesar 𝑅𝑏, di mana 𝑅𝑏 adalah peubah acak dengan nilai sebagai berikut
𝑅𝑏= 𝑌1+ 𝑌2+ … + 𝑌𝑁 (14) sedangkan kerugian yang harus ditanggung oleh perusahaan asuransi karena klaim dari pemegang polis ke 𝑖 dapat diwakili oleh peubah acak 𝑍𝑖, 𝑖 = 1,2, … , 𝑁, di mana
𝑍𝑖 adalah peubah acak dengan nilai sebagai berikut
𝑍𝑖 = {
0, 𝑋𝑖 ≤ 𝑑 𝑋𝑖− 𝑑, 𝑑 < 𝑋𝑖 ≤ 𝑢 𝑢 − 𝑑, 𝑋𝑖 > 𝑢
(15)
sehingga total kerugian yang ditanggung oleh perusahan asuransi, adalah sebesar
𝑆𝑏, di mana 𝑆𝑏 adalah peubah acak dengan nilai sebagai berikut
𝑆𝑏 =𝑍1+ 𝑍2+ … + 𝑍𝑁. (16) Misalkan 𝑆𝑎 adalah peubah acak yang menunjukkan total kerugian yang dialami seluruh pemegang polis. Jika polis asuransi menerapkan aggregate deductible sebesar d* dan aggregate limited coverage sebesar u*, maka total kerugian yang harus ditanggung seluruh pemegang polis karena peristiwa merugikan yang dialami adalah sebesar 𝑅𝑐, di mana 𝑅𝑐 adalah peubah acak dengan nilai sebagai berikut
9 𝑅𝑐 = { 𝑆𝑎, 𝑆𝑎 ≤ 𝑑∗ 𝑑∗, 𝑑∗ < 𝑆 𝑎 ≤ 𝑢∗ 𝑆𝑎+ 𝑑∗− 𝑢∗, 𝑆𝑎 > 𝑢∗ (17)
sedangkan total kerugian yang ditanggung oleh perusahaan asuransi dapat diwakili oleh peubah acak 𝑆𝑐 sebagai berikut
𝑆𝑐 = { 0, 𝑆𝑎 < 𝑑∗ 𝑆𝑎− 𝑑∗, 𝑑∗ ≤𝑆 𝑎 ≤ 𝑢∗ 𝑢∗− 𝑑∗, 𝑆 𝑎 > 𝑢∗ . (18) Premi
Penghitungan premi simulasi didasarkan pada nilai harapan dari total biaya yang harus ditanggung oleh perusahaan asuransi, ditambah 15% dari biaya tersebut dan beban tetap sebesar Rp100 000. Jika premi dinotasikan dengan P, maka
𝑃𝑖 = 1.15𝐸 (𝑆𝑖
𝑁) + 100 000, 𝑖 = 𝑎, 𝑏, 𝑐 (19)
dengan:
𝑎 = polis asuransi tanpa menggunakan deductible dan limited coverage 𝑏 = polis asuransi dengan menggunakan deductible dan limited coverage 𝑐 = polis asuransi dengan menggunakan aggregate deductible dan aggregate
limited coverage.
Keuntungan Perusahaan Asuransi
Keuntungan perusahaan asuransi adalah nilai yang diperoleh dari pembayaran premi dari seluruh pemegang polis dikurangkan dengan total kerugian yang ditanggung perusahaan tersebut. Jika keuntungan yang diperoleh perusahaan asuransi dinotasikan dengan 𝛱, maka
𝛱𝑖 = 𝑀 𝑃𝑖 − 𝑆𝑖, 𝑖 = 𝑎, 𝑏, 𝑐 (20) dengan:
𝑀 = banyaknya pemegang polis.
METODE
Deskripsi DataData pada penelitian ini dibangkitkan menggunakan software Mathematica
11.0 dengan sebaran frekuensi kerugian menyebar Poisson () dan tingkat keparahan kerugian menyebar Pareto (α, 𝛽), dengan asumsi nilai = 30, α =10,
𝛽 = 45 000 000, d= Rp2 000 000, u= Rp8 000 000, d* yang pertama sebesar
Rp100 000 000 dan d* yang kedua sebesar Rp60 000 000, u* yang pertama sebesar Rp300 000 000 dan u* yang kedua sebesar Rp240 000 000, serta banyaknya pemegang polis adalah 500 orang.
10
Prosedur Pemrograman Data
Simulasi total kerugian dapat dilakukan dengan langkah-langkah sebagai berikut:
1. Bangkitkan frekuensi kerugian (𝑁) dengan menggunakan sebaran Poisson (). 2. Untuk 𝑖 = 1 sampai 𝑖 = 𝑁, bangkitkan kerugian individu (𝑋𝑖) dengan
menggunakan sebaran Pareto (α, 𝛽).
3. Untuk 𝑖 = 1 sampai 𝑖 = 𝑁, dengan menggunakan nilai 𝑋𝑖 yang sudah dibangkitkan, tentukan kerugian yang ditanggung pemegang polis (𝑌𝑖) dan kerugian yang ditanggung oleh perusahaan asuransi (𝑍𝑖).
4. Menentukan total kerugian (𝑆𝑎) dengan menjumlahkan semua 𝑋𝑖, 𝑖 = 1,2, … , 𝑁.
5. Jika perusahaan menerapkan deductible dan limited coverage, maka tentukan total besar kerugian yang ditanggung seluruh pemegang polis (𝑅𝑏) dan kerugian yang ditanggung oleh perusahaan asuransi (𝑆𝑏).
6. Jika perusahaan menerapkan aggregate deductible dan aggregate limited coverage, maka dengan menggunakan nilai 𝑆𝑎yang sudah diperoleh, tentukan kerugian yang ditanggung seluruh pemegang polis (𝑅𝑐) dan kerugian yang ditanggung oleh perusahaan asuransi (𝑆𝑐).
7. Menentukan premi yang harus dibayar pemegang polis jika perusahaan tidak menerapkan deductible dan limited coverage (𝑃𝑎) dengan 𝑃𝑎 = 1.15 (
𝑆𝑎 𝑁) +
100 000.
8. Menentukan premi yang harus dibayar pemegang polis jika perusahaan menerapkan deductible dan limited coverage (𝑃𝑏) dengan 𝑃𝑏= 1.15 (𝑆𝑏
𝑁) +
100 000.
9. Menentukan premi yang harus dibayar pemegang polis jika perusahaan menerapkan aggregate deductible dan aggregate limited coverage (𝑃𝑐) dengan
𝑃𝑐 = 1.15 (𝑆𝑐
𝑁) + 100 000.
10. Langkah 1 sampai 9 diulang sebanyak 1000 kali.
11. Tentukan rata-rata, ragam, simpangan baku, kuartil 1, kuartil 2, dan kuartil 3
dari 𝑆𝑘 dan 𝑅𝑘serta rata-rata 𝑃𝑘, 𝑘 = 𝑎, 𝑏, 𝑐.
HASIL DAN PEMBAHASAN
Identifikasi dan Simulasi Sebaran Frekuensi
Sebaran frekuensi menunjukkan banyaknya kejadian merugikan pada kurun waktu tertentu. Sebaran frekuensi merupakan sebaran diskret, dalam penelitian ini sebaran yang digunakan adalah sebaran Poisson. Nilai peluang sebaran Poisson hanya bergantung pada nilai tengahnya, yang menyatakan rata-rata dari banyaknya peristiwa merugikan yang terjadi pada pemegang polis selama selang waktu tertentu.
Melalui software Mathematica 11.0 dilakukan 1000 simulasi menggunakan sebaran Poisson (= 30). Hasil simulasi menunjukkan bahwa rata-rata pemegang polis yang mengalami kerugian adalah sebanyak 30 orang pada jangka waktu yang
11 ditentukan, dengan histogram peluang dari frekuensi kerugian yang disajikan pada Gambar 1 dan Lampiran 5.
Gambar 1 Histogram peluang dari frekuensi kerugian berdasarkan hasil simulasi
Identifikasi dan Simulasi Sebaran Tingkat Keparahan
Sebaran tingkat keparahan kerugian menggambarkan pola penyebaran yang menunjukkan seberapa besar kerugian yang diderita oleh pemegang polis jika mengalami suatu peristiwa merugikan dalam kurun waktu tertentu. Sebaran tingkat keparahan memiliki sifat yang kontinu, sehingga bisa menjelaskan pola data yang berbentuk pecahan. Melalui software Mathematica 11.0 dilakukan 1000 simulasi dengan menggunakan sebaran Pareto (α = 10, 𝛽=45 000 000). Hasil simulasi menunjukkan bahwa rata-rata kerugian yang dialami pemegang polis adalah sebesar Rp5 001 040 dan simpangan bakunya adalah Rp5 593 430, histogram
peluang dari tingkat keparahan kerugian yang disajikan pada Gambar 2 dan Lampiran 5.
Gambar 2 Histogram peluang dari tingkat keparahan kerugian berdasarkan hasil simulasi
Peluang Peluang
Besar kerugian Frekuensi kerugian
12
Identifikasi dan Simulasi Sebaran Total Kerugian
Sebaran total kerugian dilakukan dengan menggabung sebaran frekuensi kerugian dan sebaran tingkat keparahan kerugiannya. Sebaran frekuensi kerugian didasarkan pada sebaran Poisson sedangkan sebaran tingkat keparahan kerugian adalah sebaran Pareto. Gabungan antara kedua sebaran tersebut akan menghasilkan sebaran baru yang disebut sebaran gabungan Poisson-Pareto, sebaran inilah yang akan digunakan untuk memproyeksikan total kerugian. Menggunakan software Mathematica 11.0 dilakukan 1000 simulasi yang didasarkan pada sebaran gabungan tersebut, dengan = 30, α =10 dan 𝛽 = 45 000 000.
Total Kerugian tanpa Deductible dan Limited Coverage
Jika polis asuransi tidak mengandung deductible dan limited coverage, maka tidak ada kerugian yang harus ditanggung pemegang polis, sehingga semua kerugian yang terjadi harus ditanggung oleh perusahaan asuransi. Berdasarkan hasil simulasi, diperoleh histogram peluang dari total kerugian (𝑆𝑎) yang disajikan pada Gambar 3.
Gambar 3 Histogram peluang dari total kerugian yang harus ditanggung oleh perusahaan asuransi (𝑆𝑎) berdasarkan hasil simulasi
Hasil simulasi pada Gambar 3, menunjukkan bahwa rata-rata total kerugian yang dialami pemegang polis adalah sebesar Rp149 966 946, simpangan bakunya adalah Rp41 074 198, kuartil pertama sebesar Rp121 396 378, median sebesar
Rp145 951 962, dan kuartil ketiganya sebesar Rp173 301 752. Penghitungan hasil simulasi tersebut dapat dilihat pada Lampiran 5.
Total kerugian dengan Deductible dan Limited Coverage
Jika polis asuransi mengandung deductible sebesar Rp2 000 000 dan limited coverage sebesar Rp8 000 000, maka akan ada kerugian yang harus ditanggung pemegang polis jika mengalami peristiwa yang merugikan. Berdasarkan hasil simulasi, diperoleh total kerugian yang harus ditanggung pemegang polis (𝑅𝑏) dan total kerugian yang harus ditanggung perusahaan asuransi (𝑆𝑏) dengan histogram peluang yang dapat dilihat pada Gambar 4 dan Gambar 5.
Peluang
13
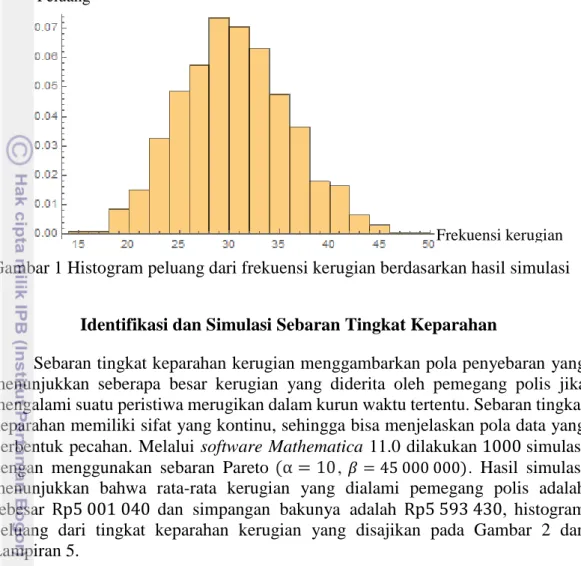
Gambar 4 Histogram peluang dari total kerugian yang harus ditanggung oleh pemegang polis (𝑅𝑏) berdasarkan hasil simulasi, dengan
𝑑 = Rp2 000 000 dan 𝑢 = Rp8 000 000
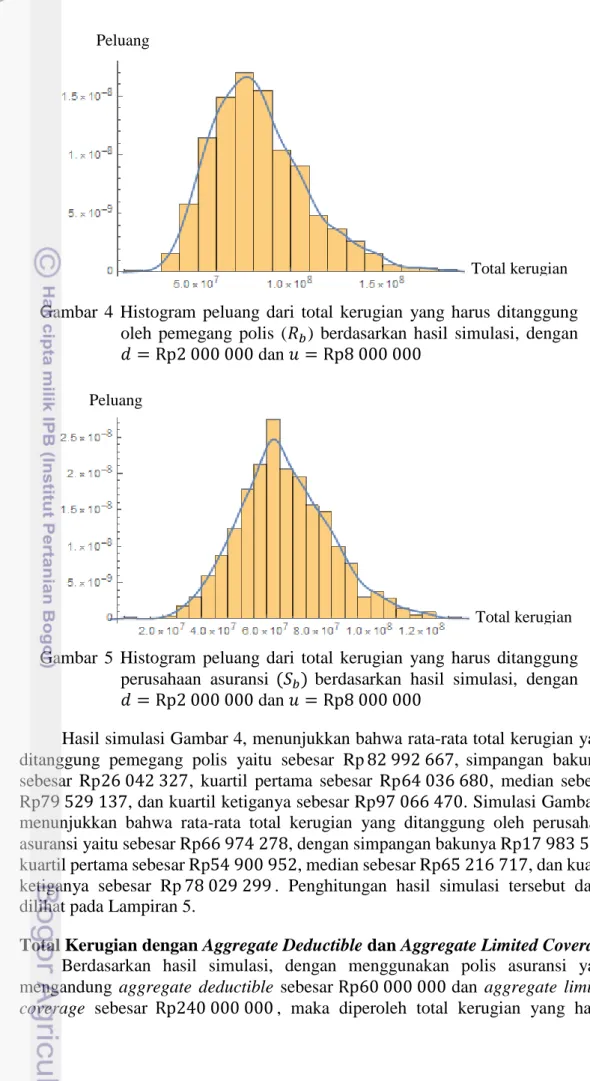
Gambar 5 Histogram peluang dari total kerugian yang harus ditanggung perusahaan asuransi (𝑆𝑏) berdasarkan hasil simulasi, dengan
𝑑 = Rp2 000 000 dan 𝑢 = Rp8 000 000
Hasil simulasi Gambar 4, menunjukkan bahwa rata-rata total kerugian yang ditanggung pemegang polis yaitu sebesar Rp82 992 667, simpangan bakunya sebesar Rp26 042 327, kuartil pertama sebesar Rp64 036 680, median sebesar Rp79 529 137, dan kuartil ketiganya sebesar Rp97 066 470. Simulasi Gambar 5 menunjukkan bahwa rata-rata total kerugian yang ditanggung oleh perusahaan asuransi yaitu sebesar Rp66 974 278, dengan simpangan bakunya Rp17 983 521, kuartil pertama sebesar Rp54 900 952, median sebesar Rp65 216 717, dan kuartil ketiganya sebesar Rp78 029 299. Penghitungan hasil simulasi tersebut dapat dilihat pada Lampiran 5.
Total Kerugian dengan Aggregate Deductible dan Aggregate Limited Coverage
Berdasarkan hasil simulasi, dengan menggunakan polis asuransi yang mengandung aggregate deductible sebesarRp60 000 000 dan aggregate limited coverage sebesar Rp240 000 000, maka diperoleh total kerugian yang harus
Peluang Peluang
Total kerugian Total kerugian
14
ditanggung seluruh pemegang polis (𝑅𝑐) dan total kerugian yang harus ditanggung perusahaan asuransi (𝑆𝑐), dengan histogram peluang yang disajikan pada Gambar 6 dan Gambar 7.
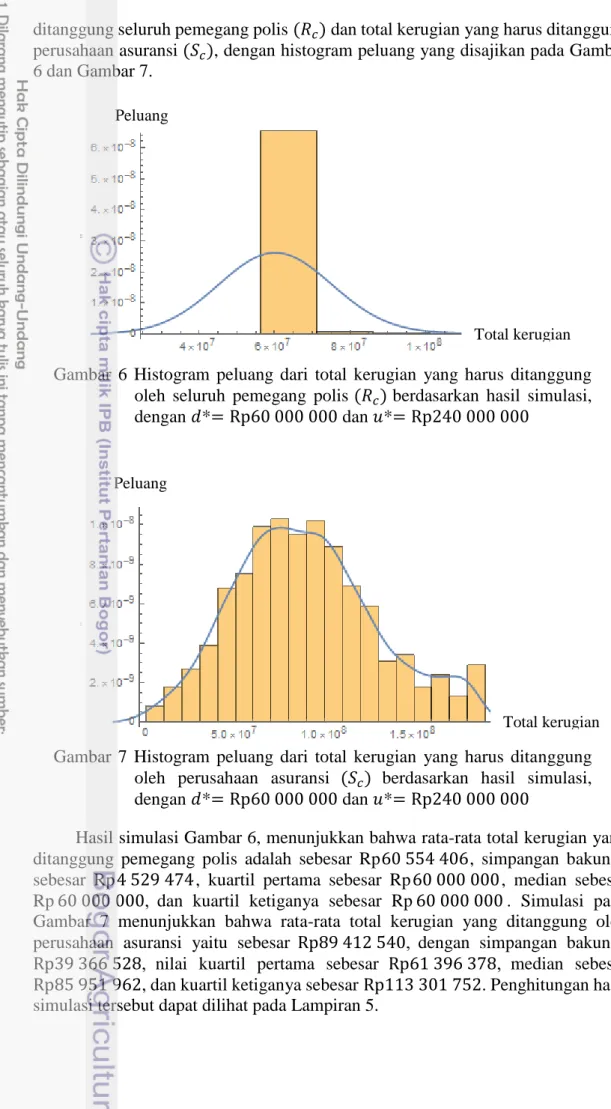
Gambar 6 Histogram peluang dari total kerugian yang harus ditanggung oleh seluruh pemegang polis (𝑅𝑐) berdasarkan hasil simulasi, dengan 𝑑*= Rp60 000 000 dan 𝑢*= Rp240 000 000
Gambar 7 Histogram peluang dari total kerugian yang harus ditanggung oleh perusahaan asuransi (𝑆𝑐) berdasarkan hasil simulasi, dengan 𝑑*= Rp60 000 000 dan 𝑢*= Rp240 000 000
Hasil simulasi Gambar 6, menunjukkan bahwa rata-rata total kerugian yang ditanggung pemegang polis adalah sebesar Rp60 554 406, simpangan bakunya sebesar Rp4 529 474, kuartil pertama sebesar Rp60 000 000, median sebesar Rp60 000 000, dan kuartil ketiganya sebesar Rp60 000 000. Simulasi pada Gambar 7 menunjukkan bahwa rata-rata total kerugian yang ditanggung oleh perusahaan asuransi yaitu sebesar Rp89 412 540, dengan simpangan bakunya
Rp39 366 528, nilai kuartil pertama sebesar Rp61 396 378, median sebesar
Rp85 951 962, dan kuartil ketiganya sebesar Rp113 301 752. Penghitungan hasil simulasi tersebut dapat dilihat pada Lampiran 5.
Peluang
Total kerugian Total kerugian Peluang
15 Berdasarkan hasil simulasi, dengan menggunakan polis asuransi yang mengandung aggregate deductible sebesar Rp100 000 000 dan aggregate limited coverage sebesar Rp300 000 000, maka diperoleh total kerugian yang harus ditanggung seluruh pemegang polis (𝑅𝑐) dan total kerugian yang harus ditanggung perusahaan asuransi (𝑆𝑐), dengan histogram peluang yang disajikan pada Gambar 8 dan Gambar 9.
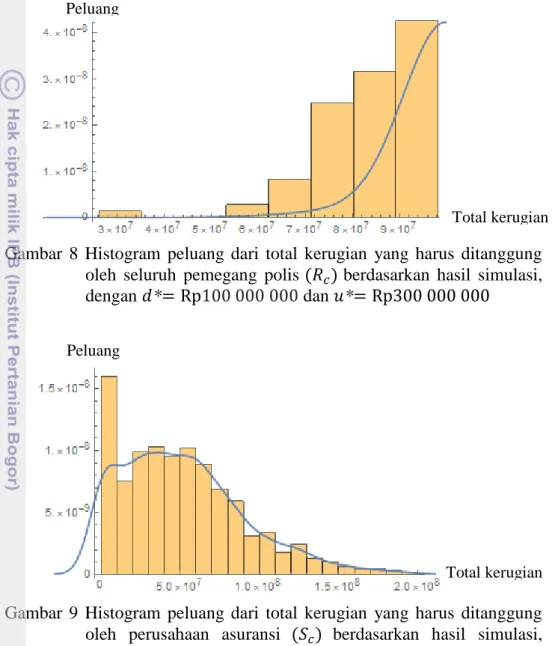
Gambar 8 Histogram peluang dari total kerugian yang harus ditanggung oleh seluruh pemegang polis (𝑅𝑐) berdasarkan hasil simulasi, dengan 𝑑*= Rp100 000 000 dan 𝑢*= Rp300 000 000
Gambar 9 Histogram peluang dari total kerugian yang harus ditanggung oleh perusahaan asuransi (𝑆𝑐) berdasarkan hasil simulasi, dengan 𝑑*= Rp100 000 000 dan 𝑢*= Rp300 000 000
Hasil simulasi Gambar 8, menunjukkan bahwa rata-rata total kerugian yang ditanggung pemegang polis adalah sebesar Rp98 672 294, simpangan bakunya sebesar Rp5 651 025, kuartil pertama sebesar Rp100 000 000, median sebesar Rp100 000 000, dan kuartil ketiganya sebesar Rp100 000 000. Simulasi pada Gambar 9 menunjukkan bahwa rata-rata total kerugian yang ditanggung oleh perusahaan asuransi yaitu sebesar Rp51 294 651, dengan simpangan bakunya
Rp38 971 924, nilai kuartil pertama sebesar Rp21 396 378, median sebesar Total kerugian Peluang
Peluang
16
Rp45 951 962, dan kuartil ketiganya sebesar Rp73 301 752. Penghitungan hasil simulasi tersebut dapat dilihat pada Lampiran 5.
Premi dan Keuntungan Perusahaan Asuransi
Setelah diperoleh total kerugian yang ditanggung perusahaan asuransi dari masing-masing polis asuransi, maka dapat ditentukan masing-masing premi yang harus dibayarkan oleh pemegang polis. Pada Tabel 1 disajikan besar premi dan keuntungan yang didapatkan perusahaan asuransi.
Tabel 1 Premi dan keuntungan yang didapatkan perusahaan asuransi No Polis Deductible Limited Coverage Premi Keuntungan
Perusahaan
1 - - Rp5 849 170 Rp2 775 400 322
2 𝑑=Rp2 000 000 𝑢=Rp8 000 000 Rp2 668 060 Rp1 274 693 184 3 c 𝑑*=Rp60 000 000 𝑢*=Rp240 000 000 Rp3 453 012 Rp1 636 474 965
𝑑*=Rp100 000 000 𝑢*=Rp300 000 000 Rp1 952 430 Rp930 551 186 Tabel 1 menunjukkan hasil dari 4 polis asuransi yang berbeda. Pada polis pertama, perusahaan asuransi tidak menetapkan kebijakan deductible dan limited coverage dan nilai premi yang harus dibayarkan oleh pemegang polis adalah sebesar Rp5 849 170. Pada polis yang kedua, perusahaan menetapkan deductible Rp2 000 000 dan limited coverage sebesar Rp8 000 000 serta premi sebesar
Rp2 668 060. Dengan demikian, jika pemegang polis membayar premi sebesar
Rp2 668 060, maka untuk kerugian kurang dari Rp2 000 000 kerugian tersebut akan ditanggung oleh pemegang polis, tetapi jika kerugian diatas Rp8 000 000 maka kerugian akan ditanggung oleh pemengang polis sebesar Rp2 000 000 dan sisanya ditanggung oleh perusahaan asuransi dengan batas penanggungan maksimal sebesar Rp6 000 000. Polis ketiga menetapkan aggregate deductible sebesar
Rp60 000 000 dan aggregate limited coverage sebesar Rp240 000 000 dengan premi sebesar Rp3 453 012. Dengan kata lain, jika seorang pemegang polis membayar premi sebesar Rp3 453 012, maka apabila total kerugian yang dialami seluruh pemegang polis kurang dari Rp60 000 000, kerugian tersebut akan ditanggung oleh pemegang polis, tetapi jika total kerugian yang terjadi diatas
Rp60 000 000 maka kerugian akan ditanggung oleh seluruh pemengang polis sebesar Rp60 000 000 dan sisanya ditanggung oleh perusahaan asuransi dengan batas penanggungan maksimal sebesar Rp180 000 000. Polis terakhir menetapkan
aggregate deductible sebesar Rp100 000 000 dan aggregate limited coverage
sebesar Rp3 00 000 000 dengan premi sebesar Rp1 952 430. Dengan kata lain, jika seorang pemegang polis membayar premi sebesar Rp1 952 430, maka apabila total kerugian yang dialami seluruh pemegang polis kurang dari Rp100 000 000, kerugian tersebut akan ditanggung oleh pemegang polis, tetapi jika total kerugian yang terjadi diatas Rp100 000 000 maka kerugian akan ditanggung oleh seluruh pemengang polis sebesar Rp100 000 000 dan sisanya ditanggung oleh perusahaan asuransi dengan batas penanggungan maksimal sebesar Rp200 000 000.
Penentuan kebijakan deductible dan limited coverage sangat berpengaruh terhadap besar premi yang harus dibayar pemegang polis, semakin kecil deductible
17 yang diterapakan maka premi yang harus dibayar akan semakin besar. Hal tersebut berkebalikan dengan limited coverage karena semakin kecil limited coverage yang diterapkanmaka nilai premi akan semakin kecil.
Setelah mendapatkan nilai premi untuk masing-masing polis asuransi, maka selanjutnya dilakukan sekali simulasi lagi untuk mendapatkan total kerugian yang baru, kemudian dihitung besar keuntungan yang akan didapatkan oleh perusahaan asuransi pada masing-masing polis. Keuntungan yang diperoleh dari polis 1 sampai polis 4 adalah Rp2 775 400 322, Rp1 274 693 184, Rp1 636 474 965, dan
Rp930 551 186. Penghitungan keuntungan perusahaan asuransi disajikan pada Lampiran 6.
Galat dari Rata-Rata dan Simpangan Baku
Galat adalah selisih antara nilai perkiraan dengan nilai yang sebenarnya. Ada dua macam galat yaitu galat mutlak dan relatif. Galat mutlak adalah nilai mutlak suatu galat yang diperoleh dari selisih hasil analitik dan hasil pendektannya, sedangkan galat relatif adalah perbandingan antara galat mutlak dan nilai analitiknya. Tabel 2 menunjukkan rata-rata dan simpangan baku dari tiga sebaran yang diperoleh menggunakan metode simulasi dan hasil secara analitik, dari hasil Tabel 2 kemudian dilakukan penghitungan galat mutlak dan relatif yang disajikan pada Tabel 3.
Tabel 2 Rata-rata dan simpangan baku
Sebaran Hasil Simulasi Hasil analitik
E 𝜎 E 𝜎
Frekuensi kerugian 29.9990 5.4778 30 5.4772 Tingkat keparahan
kerugian Rp5 001 040 Rp5 593 430 Rp5 000 000 Rp5 590 169 Total kerugian (𝑆𝑎) Rp149 966 946 Rp41 074 198 Rp150 000 000 Rp41 079 191
Tabel 3 Galat mutlak dan galat relatif
Sebaran Galat mutlak Galat relatif
E 𝜎 E 𝜎 Frekuensi kerugian 0.0010 0.0006 0.0033% 0.0109% Tingkat keparahan kerugian Rp1 040 Rp3 261 0.0208% 0.0583% Total kerugian (𝑆𝑎) Rp33 054 Rp4 993 0.0220% 0.0121% dengan: 𝐸 = Rata-rata 𝜎 = Simpangan baku
Berdasarkan Tabel 3, dapat dilihat bahwa dari tiga sebaran yang digunakan diperoleh galat mutlak dan galat relatif yang cukup kecil, sehingga bisa dikatakan bahwa metode simulasi merupakan metode yang cukup baik untuk memperkirakan total kerugian. Penghitungan nilai rata-rata dan simpangan baku secara analitik disajikan pada Lampiran 7.
18
SIMPULAN
Melalui metode simulasi dapat diperkirakan total kerugian dengan cara mendekati sebaran gabungan dari frekuensi dan tingkat keparahannya, diperoleh tiga total kerugian yang ditanggung oleh pemegang polis dan perusahaan asuransi. Total kerugian terbesar yang ditanggung oleh pemegang polis adalah pada polis asuransi dengan kebijakan aggregate deductible dan aggregate limited coverage, sedangkan total kerugian yang paling besar bagi perusahaan asuransi adalah pada polis asuransi tanpa deductible dan limited coverage. Besar premi yang harus dibayarkan oleh pemegang polis berbeda-beda pada setiap polis asuransi, karena nilai premi sangat dipengaruhi oleh penentuan deductible dan limited coverage. Keuntungan perusahaan asuransi sangat dipengaruhi dari premi yang dibayarkan oleh pemegang polis, diperoleh keuntungan yang paling besar adalah pada polis asuransi tanpa deductible dan limited coverage. Hasil perkiraan total kerugian menggunakan simulasi tidak jauh berbeda dibanding secara analitik, sehingga dapat disimpulkan bahwa metode simulasi dapat digunakan untuk memperkirakan total kerugian.
DAFTAR PUSTAKA
Ghahramani S. 2005. Fundamentals of Probability with Stochastic Processes. Ed ke-3. New Jersey (US): Prentice Hall.
Grimmet GR, Stirzaker DR. 2001. Probability and Random Process. Ed ke-3. Oxford (GB): Clarendon Press.
Hogg RV, Craig AT, McKean JW. 2014. Introduction to Mathematical Statistics. Ed ke-7. New Jersey (US): Prentice Hall.
Klugman AK, Panjer HH, Willmot GE. 2012. Loss Models from Data to Decisions.
Ed ke-4. New York (US): John Wiley & Sons.
Mohamed MA, Ahmad MR, Noriszura I. 2010. Approximation of Aggregate Losses Using Simulation. Journal of Mathematics and Statistics 6 (3): 233-239. Napitupulu SJ. 2009. Pengukuran Risiko Operasional dengan Metode Aggregating
Value At Risk [skripsi]. Medan (ID): Universitas Sumatera Utara.
Pemerintah Republik Indonesia. 2014. Undang-Undang Republik Indonesia Nomor 40 Tahun 2014 tentang Usaha Perasuransian. Jakarta (ID): Sekretariat Negara.
19
LAMPIRAN
Lampiran 1 Pembuktian nilai harapan dan ragam sebaran Poisson
Misalkan 𝑁 adalah peubah acak yang menyebar Poisson dengan parameter > 0, dan fungsi massa peluang sebagai berikut
𝑝𝑁(𝑛;) =
𝑛𝑒−
𝑛! , 𝑛 = 0,1,2, …
akan dibuktikan bahwa 𝐸(𝑁) = var(𝑁) =.
Bukti: 𝐸(𝑁) = ∑ 𝑛 ∞ 𝑛=0 𝑝𝑁(𝑛;) = ∑ 𝑛 ∞ 𝑛=0 𝑛𝑒− 𝑛! = ∑ 𝑛 ∞ 𝑛=1 𝑛𝑒− 𝑛! = ∑ 𝑛 ∞ 𝑛=1 𝑛−1𝑒− 𝑛(𝑛 − 1)! = 𝑒−∑ 𝑛−1 (𝑛 − 1)! ∞ 𝑛=1 = 𝑒−∑ 𝑛 𝑛! ∞ 𝑛=0 = 𝑒−𝑒= .
Jadi terbukti bahwa 𝐸(𝑁) =.
𝐸(𝑁2) = ∑ 𝑛2 ∞ 𝑛=0 𝑝𝑁(𝑛;) = ∑ 𝑛2 ∞ 𝑛=0 𝑛 𝑒− 𝑛! = ∑ 𝑛 2 ∞ 𝑛=1 𝑛 𝑒− 𝑛! = 𝑒 −∑ 𝑛 𝑛−1 (𝑛 − 1)! ∞ 𝑛=1 = 𝑒−∑ 1 (𝑛 − 1)! ∞ 𝑛=1 𝑑 𝑑(𝑛) = 𝑒− 𝑑 𝑑(∑ 𝑛 (𝑛 − 1)! ∞ 𝑛=1 ) = 𝑒− 𝑑 𝑑(∑ 𝑛−1 (𝑛 − 1)! ∞ 𝑛=1 ) = 𝑒− 𝑑 𝑑( 𝑒) = 𝑒−(𝑒+ 𝑒) =+2. var(𝑁) = 𝐸(𝑁2) − (𝐸(𝑁))2 = (+2) −2 =.
20
Lampiran 2 Pembuktian nilai harapan dan ragam sebaran Pareto
Misalkan 𝑋 adalah peubah acak yang menyebar Pareto dengan parameter 𝛼 dan
𝛽 yang memenuhi fungsi kepekatan peluang, sebagai berikut
𝑓𝑋(𝑥; 𝛼, 𝛽) = 𝛼𝛽
𝛼
(𝛽 + 𝑥)𝛼+1, 𝛼 > 0 dan 𝛽 > 0 akan dibuktikan bahwa:
𝐸(𝑋) = 𝛽 𝛼 − 1 var(𝑋) = 𝛼𝛽 2 (𝛼 − 1)2(𝛼 − 2), 𝛼 > 2. Bukti: 𝐸(𝑋) = ∫ 𝑥𝑓𝑋(𝑥) 𝑑𝑥 ∞ −∞ = ∫ 𝑥 𝛼𝛽 𝛼 (𝛽 + 𝑥)𝛼+1 𝑑𝑥 ∞ 0 = 𝛼𝛽𝛼∫ 𝑥 (𝛽 + 𝑥)𝛼+1 𝑑𝑥 ∞ 0 misalkan 𝑢 = 𝑥 + 𝛽 Jika 𝑥 = 0 maka 𝑢 = 𝛽 𝑢 − 𝛽 = 𝑥 Jika 𝑥 = ∞ maka 𝑢 = ∞ 𝑑𝑢 = 𝑑𝑥 sehingga 𝐸(𝑋) = 𝛼𝛽𝛼∫ 𝑢 − 𝛽 𝑢𝛼+1 𝑑𝑢 ∞ 𝛽 = 𝛼𝛽𝛼(∫ 𝑢 𝑢𝛼+1 𝑑𝑢 ∞ 𝛽 − ∫ 𝛽 𝑢𝛼+1 𝑑𝑢 ∞ 𝛽 ) = 𝛼𝛽𝛼(∫ 1 𝑢𝛼 𝑑𝑢 ∞ 𝛽 − ∫ 𝛽 𝑢𝛼+1 𝑑𝑢 ∞ 𝛽 ) = 𝛼𝛽𝛼([ 1 (1 − 𝛼)𝑢𝛼−1 ] 𝛽 ∞ + [ 𝛽 𝛼𝑢𝛼 ] 𝛽 ∞ ) = 𝛼𝛽𝛼((0 − 1 (1 − 𝛼)𝛽𝛼−1) + (0 − 𝛽 𝛼𝛽𝛼)) = − 𝛼𝛽 𝛼 (1 − 𝛼)𝛽𝛼−1− 𝛽 = − 𝛼𝛽 1 − 𝛼− 𝛽 = −𝛼𝛽 + 𝛽(1 − 𝛼) 1 − 𝛼 = 𝛽 𝛼 − 1.
Jadi terbukti bahwa 𝐸(𝑋) = 𝛽 𝛼 − 1.
21 𝐸(𝑋2) = ∫ 𝑥2𝑓 𝑋(𝑥) 𝑑𝑥 ∞ −∞ = ∫ 𝑥2 𝛼𝛽 𝛼 (𝛽 + 𝑥)𝛼+1 𝑑𝑥 ∞ 0 = 𝛼𝛽𝛼∫ 𝑥 2 (𝛽 + 𝑥)𝛼+1 𝑑𝑥 ∞ 0 misalkan 𝑢 = 𝑥 + 𝛽 Jika 𝑥 = 0 maka 𝑢 = 𝛽 𝑢2− 2𝑢𝛽 + 𝛽2 = 𝑥2 Jika 𝑥 = ∞ maka 𝑢 = ∞ 𝑑𝑢 = 𝑑𝑥 sehingga 𝐸(𝑋2) = 𝛼𝛽𝛼∫ 𝑢 2− 2𝑢𝛽 + 𝛽2 𝑢𝛼+1 𝑑𝑢 ∞ 𝛽 = 𝛼𝛽𝛼(∫ 𝑢 2 𝑢𝛼+1 𝑑𝑢 ∞ 𝛽 − ∫ 2𝑢𝛽 𝑢𝛼+1 𝑑𝑢 ∞ 𝛽 + ∫ 𝛽 2 𝑢𝛼+1 𝑑𝑢 ∞ 𝛽 ) = 𝛼𝛽𝛼(∫ 1 𝑢𝛼−1 𝑑𝑢 ∞ 𝛽 − ∫ 2𝛽 𝑢𝛼 𝑑𝑢 ∞ 𝛽 + ∫ 𝛽 2 𝑢𝛼+1 𝑑𝑢 ∞ 𝛽 ) = 𝛼𝛽𝛼([ 1 (2 − 𝛼)𝑢𝛼−2 ] 𝛽 ∞ − [ 2𝛽 (1 − 𝛼)𝑢𝛼−1 ] 𝛽 ∞ − [ 𝛽 2 𝛼𝑢𝛼 ] 𝛽 ∞ ) = 𝛼𝛽𝛼((0 − 1 (2 − 𝛼)𝛽𝛼−2) − (0 − 2𝛽 (1 − 𝛼)𝛽𝛼−1) + (0 − 𝛽2 𝛼𝛽𝛼)) = − 𝛼𝛽 2 2 − 𝛼+ 2𝛼𝛽2 1 − 𝛼+ 𝛽 2 =−𝛼𝛽 2(1 − 𝛼) + 2𝛼𝛽2(2 − 𝛼) + 𝛽2(2 − 3𝛼 + 𝛼2) 2 − 3𝛼 + 𝛼2 = 2𝛽 2 2 − 3𝛼 + 𝛼2. var(𝑋) = 𝐸(𝑋2) − (𝐸(𝑋))2 = 2𝛽 2 2 − 3𝛼 + 𝛼2− ( 𝛽 𝛼 − 1) 2 = 2𝛽 2 (𝛼 − 1)(𝛼 − 2)− 𝛽2 (𝛼 − 1)2 =2𝛽 2(𝛼 − 1) − 𝛽2(𝛼 − 2) (𝛼 − 1)2(𝛼 − 2) = 2𝛼𝛽2− 2𝛽2− 𝛼𝛽2+2𝛽2 (𝛼 − 1)2(𝛼 − 2) = 𝛼𝛽 2 (𝛼 − 1)2(𝛼 − 2).
Jadi terbukti bahwa var(𝑋) = 𝛼𝛽
2
22
Lampiran 3 Pembuktian nilai harapan total kerugian
Misalkan 𝑋1,𝑋2, …adalah peubah acak yang bebas stokastik identik dengan nilai harapan 𝐸(𝑋), dan jika 𝑁 > 0 yang merupakan peubah acak dengan nilai integer
dan saling bebas dengan 𝑋𝑖, 𝑖 = 1, … , 𝑁 dengan nilai harapan 𝐸(𝑁) < ∞, maka
𝐸 (∑ 𝑋𝑖 𝑁 𝑖=1 ) = 𝐸(𝑁) 𝐸(𝑋) Bukti: 𝐸 (∑ 𝑋𝑖 𝑁 𝑖=1 | 𝑁 = 𝑛) = 𝐸 (∑ 𝑋𝑖 𝑛 𝑖=1 | 𝑁 = 𝑛) = 𝐸 (∑ 𝑋𝑖 𝑛 𝑖=1
) , karena X1,X2,…, Xnbebas stokastik, maka
= ∑ 𝐸(𝑋𝑖) 𝑛 𝑖=1 = 𝑛 𝐸(𝑋). 𝐸 (∑ 𝑋𝑖 𝑁 𝑖=1 ) = 𝐸 (𝐸 (∑ 𝑋𝑖 𝑁 𝑖=1 | 𝑁 = 𝑛)) = ∑ 𝐸 (∑ 𝑋𝑖 𝑁 𝑖=1 | 𝑁 = 𝑛) ∞ 𝑛=1 𝑃(𝑁 = 𝑛) = ∑ 𝑛 𝐸(𝑋) ∞ 𝑛=1 𝑃(𝑁 = 𝑛) = 𝐸(𝑋) ∑ 𝑛 𝑃(𝑁 = 𝑛) ∞ 𝑛=1 = 𝐸(𝑋)𝐸(𝑁).
Jadi terbukti bahwa 𝐸 (∑ 𝑋𝑖
𝑁
𝑖=1
23 Lampiran 4 Pembuktian ragam total kerugian
Misalkan 𝑋1,𝑋2, …adalah peubah acak yang bebas stokastik identik dengan nilai harapan 𝐸(𝑋) dan ragam var(𝑋). Misalkan diberikan 𝑁 > 0 yang merupakan peubah acak dengan nilai integer dan saling bebas dengan 𝑋𝑖, 𝑖 = 1, … , 𝑁 dengan nilai harapan 𝐸(𝑁) < ∞ dan var(𝑁) < ∞, maka
var (∑ 𝑋𝑖
𝑁
𝑖=1
) = 𝐸(𝑁) var(𝑋) + var(𝑁) (𝐸(𝑋))2 Bukti:
Misalkan 𝑋 adalah suatu peubah acak, maka ragam dari peubah acak 𝑋, dinotasikan dengan var(𝑋) = 𝐸(𝑋2) − [𝐸(𝑋)]2. Misalkan X dan N adalah dua peubah acak, maka ragam dari 𝑋 dengan syarat 𝑁 adalah var(𝑋|𝑁) = 𝐸(𝑋2|𝑁) − (𝐸(𝑋|𝑁))2. Teorema:
var(𝑋) = 𝐸[var(𝑋|𝑁)] + var(E[𝑋|𝑁]) Bukti: 𝐸[var(𝑋|𝑁)] = 𝐸 [𝐸(𝑋2|𝑁) − (𝐸(𝑋|𝑁))2] = 𝐸[𝐸(𝑋2|𝑁)] − 𝐸[𝐸(𝑋|𝑁)2] = 𝐸(𝑋2) − 𝐸[𝐸(𝑋|𝑁)2]. var(E[𝑋|𝑁]) = 𝐸[𝐸(𝑋|𝑁)2] − (𝐸[𝐸(𝑋|𝑁)])2 = 𝐸[𝐸(𝑋|𝑁)2] − [𝐸(𝑋)]2. 𝐸[var(𝑋|𝑁)] + var(E[𝑋|𝑁]) = 𝐸(𝑋2) − 𝐸[𝐸(𝑋|𝑁)2] + 𝐸[𝐸(𝑋|𝑁)2] − [𝐸(𝑋)]2 = 𝐸(𝑋2) − [𝐸(𝑋)]2 = var(𝑋).
Terbukti bahwa var(𝑋) = 𝐸[var(𝑋|𝑁)] + var(E[𝑋|𝑁]). Dengan menggunakan teorema di atas, maka
var (∑ 𝑋𝑖 𝑁 𝑖=1 ) = 𝐸 [var (∑ 𝑋𝑖 𝑁 𝑖=1 | 𝑁)] + var [𝐸 (∑ 𝑋𝑖 𝑁 𝑖=1 | 𝑁)]
24 dengan 𝐸 [var (∑ 𝑋𝑖 𝑁 𝑖=1 | 𝑁)] = 𝐸 [var (∑ 𝑋𝑖 𝑁 𝑖=1 | 𝑁 = 𝑛)] = 𝐸 [var (∑ 𝑋𝑖 𝑛 𝑖=1 | 𝑁 = 𝑛)] = 𝐸 [var (∑ 𝑋𝑖 𝑛 𝑖=1 )] = 𝐸 [∑ var(𝑋𝑖) 𝑛 𝑖=1
] , karena 𝑋1, 𝑋2, … , 𝑋𝑛saling bebas, maka
= 𝐸[𝑛 var(𝑋)] = 𝐸[𝑁 var(𝑋)] = var(𝑋) 𝐸(𝑁).
var [𝐸 (∑ 𝑋𝑖 𝑁 𝑖=1 | 𝑁)] = var [𝐸 (∑ 𝑋𝑖 𝑁 𝑖=1 | 𝑁 = 𝑛)] = var [𝐸 (∑ 𝑋𝑖 𝑛 𝑖=1 | 𝑁 = 𝑛)] = var [𝐸 (∑ 𝑋𝑖 𝑛 𝑖=1 )] = var [∑ 𝐸(𝑋𝑖) 𝑛 𝑖=1
] , karena 𝑋1, 𝑋2, … , 𝑋𝑛saling bebas, maka
= var[𝑛 𝐸(𝑋)] = var[𝑁 𝐸(𝑋)] = (𝐸(𝑋))2 var(𝑁).
sehingga var (∑ 𝑋𝑖 𝑁 𝑖=1 ) = 𝐸 [var (∑ 𝑋𝑖 𝑁 𝑖=1 | 𝑁)] + var [𝐸 (∑ 𝑋𝑖 𝑁 𝑖=1 | 𝑁)] = var(𝑋) 𝐸(𝑁) + (𝐸(𝑋))2 var(𝑁) = 𝐸(𝑁) var(𝑋) + var(𝑁) (𝐸(𝑋))2.
Jadi terbukti bahwa var (∑ 𝑋𝑖
𝑁
𝑖=1
) = 𝐸(𝑁) var(𝑋) + var(𝑁) (𝐸(𝑋))2.
25 Lampiran 5 Pemrograman simulasi menggunakan software Mathematica 11.0 Membangkitkan Sebaran Poisson (𝛌)
λ=30; n=1000; SeedRandom[39071];poisson=RandomVariate[PoissonDistribution[λ],n]; Mean[poisson]//N StandardDeviation[poisson]//N Histogram[poisson,Automatic,"PDF"] 29.999 5.4778
Membangkitkan Sebaran Pareto (𝜶, 𝜷) SeedRandom[96081]; pareto=RandomVariate[ParetoDistribution[45000000,10,0],30]; Mean[pareto]//N StandardDeviation[pareto]//N Histogram[pareto,Automatic,"PDF"] Show[Histogram[pareto,{Min[pareto],Max[pareto],2500000},"PDF"], SmoothHistogram[pareto,2500000,"PDF"]] 5001041.81 5593427.50
Membangkitkan Sebaran Gabungan Poisson-Pareto, sebanyak n simulasi
SeedRandom[1774];X=Table[RandomVariate[ParetoDistribution[45000000 ,10,0],poisson[[i]]],{i,n}];
26
Total Kerugian Tanpa Deductible dan Limited Coverage
Kerugian yang ditanggung pemegang polis
(* tidak kerugian yang ditanggung pemegang polis, Ra=0 *)
Kerugian yang dibayarkan oleh perusahaan Asuransi
Sa=Table[Total[X[[i]]],{i,n}];
Show[Histogram[Sa,Automatic,"PDF"],SmoothHistogram[Sa,Automatic, "PDF"]]
Total Kerugian dengan Deductible dan Limited Coverage d=2000000; u=8000000;
Kerugian yang ditanggung pemegang polis
Y=Table[If[X[[i,j]]<=d,X[[i,j]],If[d<X[[i,j]]<=u,d,X[[i,j]]+d-u]], {i,n},{j,Length[X[[i]]]}];
Total kerugian yang ditanggung pemegang polis
Rb= Table[Total[Y[[i]]],{i,n}];
Show[Histogram[Rb,Automatic,"PDF"],SmoothHistogram[Rb,Automatic, "PDF"]]
Kerugian yang dibayarkan oleh perusahaan
Z=Table[If[X[[i,j]]<=d,0,If[d<X[[i,j]]<=u,X[[i,j]]-d,u-d]],{i,n}, {j,Length[X[[i]]]}];
27
Total kerugian yang dibayarkan perusahaan
Sb= Table[Total[Z[[i]]],{i,n}];
Show[Histogram[Sb,Automatic,"PDF"],SmoothHistogram[Sb,Automatic, "PDF"]]
Total Kerugian dengan Aggregate Deductible dan Aggregate Limited Coverage
Kasus 1 (* dengan 𝑑*=Rp60000000 dan 𝑢*=240000000 *)
Da=60000000; (* Da = Nilai aggregate deductible*)
Ua=240000000; (* Ua = Nilai aggregate limited coverage*)
Kerugian yang ditanggung seluruh pemegang polis
Rc=Table[If[Sa[[i]]<=Da,Sa[[i]],If[Da<Sa[[i]]<=Ua,Da,Sa[[i]]+Da-Ua]],{i,n}];
Show[Histogram[Rc,{Min[Rc],Max[Rc],9000000},"PDF"], SmoothHistogram[Rc,9000000,"PDF"]]
Kerugian yang dibayarkan oleh perusahaan
Sc=Table[If[Sa[[i]]<=Da,0,If[Da<Sa[[i]]<=Ua,Sa[[i]]-Da,Ua-Da]],{i,n}];
Show[Histogram[Sc,Automatic,"PDF"],SmoothHistogram[Sc,Automatic, "PDF"]]
28
Kasus 2 (* dengan 𝑑*=Rp100000000 dan 𝑢*=300000000 *)
Da2=100000000; (* Da2 = Nilai aggregate deductible*)
Ua2=300000000; (* Ua2 = Nilai aggregate limited coverage*)
Kerugian yang ditanggung seluruh pemegang polis
Rc2=Table[If[Sa[[i]]<=Da2,Sa[[i]],If[Da2<Sa[[i]]<=Ua2,Da2,Sa[[i]]+ Da2-Ua2]],{i,n}];
Show[Histogram[Rc2,{Min[Rc2],Max[Rc2],15000000},"PDF"], SmoothHistogram[Rc2,15000000,"PDF"]]
Kerugian yang dibayarkan oleh perusahaan
Sc2=Table[If[Sa[[i]]<=Da2,0,If[Da2<Sa[[i]]<=Ua2,Sa[[i]]-Da2,Ua2-Da2]],{i,n}];
Show[Histogram[Sc2,Automatic,"PDF"],SmoothHistogram[Sc2,Automatic, "PDF"]]
29 Menghitung Premi
Premi Tanpa Deductible dan Limited Coverage
Pa=Table[100000+1.15*Sa[[i]]/poisson[[i]],{i,n}]; Mean[Pa] 5849168.47
Premi Dengan Deductible dan Limited Coverage
Pb=Table[100000+1.15*Sb[[i]]/poisson[[i]],{i,n}]; Mean[Pb] 2668062.52
Premi dengan Aggregate Deductible dan Aggregate Limited Coverage
Pc=Table[100000+1.15*Sc[[i]]/poisson[[i]],{i,n}]; Mean[Pc] 1952434.19
Pc2=Table[100000+1.15*Sc2[[i]]/poisson[[i]],{i,n}]; Mean[Pc2] 3453012.44
Rataan, Simpangan Baku, Kuartil dari 𝑺 dan 𝑹
Rataan RataRataS=List[Mean[Sa],Mean[Sb],Mean[Sc],Mean[Sc2]] RataRataR=List[Mean[Rb],Mean[Rc], Mean[Rc2]] {1.49967×108, 6.69743×107, 5.12946×107, 8.94125×107} {8.299267×107, 9.86723×107, 6.05544×107} Simpangan Baku SimpanganBakuS=List[StandardDeviation[Sa],StandardDeviation[Sb], StandardDeviation[Sc],StandardDeviation[Sc2]] SimpanganBakuR=List[StandardDeviation[Rb],StandardDeviation[Rc], StandardDeviation[Rc2] {4.10742×107, 1.79835×107, 3.89719×107, 3.93665×107} {2.60423×107, 5.65102×106, 4.52974×106} Kuartil KuartilS=List[Quartiles[Sa],Quartiles[Sb],Quartiles[Sc], Quartiles[Sc2]] KuartilR=List[Quartiles[Rb],Quartiles[Rc],Quartiles[Rc2]] {{1.21396×108,1.45952×108,1.73302×108}, {5.49009×107,6.52167×107,7.80293×107}, {2.13964×107,4.59519×107,7.33017×107} {6.13964×107, 8.59520×107, 1.13302×108}} {{6.40367×107,7.95291×107,9.70665×107}, {1.×108,1.×108,1.×108}, {6.×107, 6.×107, 6.×107}}
30
Lampiran 6 Menghitung keuntungan perusahaan menggunakan software Mathematica 11.0
Membangkitkan Sebaran Poisson (𝛌) λ=30;n=1;
SeedRandom[3];poisson=RandomVariate[PoissonDistribution[λ],n];
Membangkitkan Sebaran Gabungan Poisson-Pareto, dengan 1 kali simulasi SeedRandom[677];
X=RandomVariate[ParetoDistribution[135000,10,0],poisson[[1]]]; Total Kerugian Perusahaan
Kerugian perusahaan Asuransi tanpa Deductible dan Limited Coverage
Sa=Total[X] 453373.
Kerugian perusahaan denggan Deductible dan Limited Coverage
d=2000000;u=8000000;
Z=Table[If[X[[i]]<=d,0,If[d<X[[i]]<=u,X[[i]]-d,u-d]], {i,poisson[[1]]}];
Sb= Total[Z] 1.50031×108
Kerugian perusahaan dengan Aggregate Deductible dan Aggregate Limited Coverage
(* dengan d*=Rp60000000 dan u*=240000000 *)
Da=100000000; (* Da = nilai Aggregate Deductible*)
Ua=300000000; (* Ua = Nilai aggregate limited coverage*) Sc=If[Sa<=Da,0,If[Da<Sa<=Ua,Sa-Da,Ua-Da]]
5.003125×107
(* dengan d*=Rp60000000 dan u*=240000000 *)
Da2=60000000; (* Da2 = nilai Aggregate Deductible*)
Ua2=240000000; (* Ua2 = Nilai aggregate limited coverage*) Sc2=If[Sa<=Da2,0,If[Da2<Sa<=Ua2,Sa-Da2,Ua2-Da2]]
9.00313×107
Keuntungan Perusahaan
(*Dengan menggunakan asumsi banyaknya pemegang polis sebanyak 50 orang*) M=500; Pa=5849168.47; Pb=2668062.52; Pc=1952434.19; Pc2=3453012.44; Πa=M*Pa-Sa Πb=M*Pb-Sb Πc=M*Pc-Sc Πc2=M*Pc2-Sc2 2.77540×109 1.27469×109 9.30551×108 1.63647×109
31 Lampiran 7 Rata-rata dan simpangan baku secara analitik dari tiga sebaran yang
diidentifikasi
Sebaran Frekuensi Kerugian
Menggunakan persamaan (1) dengan =30 diperoleh rata-rata sebaran frekuensi sebagai berikut:
𝐸(𝑁) = var(𝑁) == 30 dan simpangan bakunya adalah
𝜎𝑁 = √var(𝑁) = √30 = 5.4778.
Sebaran Tingkat Keparahan Kerugian
Menggunakan persamaan (2) dengan 𝛼=10 dan 𝛽=135 000 diperoleh rata-rata sebaran tingkat keparahan kerugian sebagai berikut:
𝐸(𝑋) = 𝛽
𝛼 − 1
= 45 000 000
10 − 1
= 5 000 000
dan simpangan bakunya adalah
𝜎𝑋= √var(𝑋) = √ 𝛼𝛽2 (𝛼 − 1)2(𝛼 − 2) = √10 (45 000 000) 2 (10 − 1)2(10 − 2) = 5 590 169.
Sebaran Total Kerugian
Menggunakan persamaan (5) dan (7) dengan =30, 𝛼=10, dan 𝛽=135 000 diperoleh rata-rata sebaran total kerugian sebagai berikut:
𝐸(𝑆) = 𝛽
𝛼 − 1
= (30)45 000 000
10 − 1
= 150 000 000
dan simpangan bakunya adalah
𝜎𝑆 = √var(𝑆) = √ 𝛽 2 (2𝛼− 2) (𝛼 − 1)2(𝛼 − 2) = √10 (45 000 000) 2(20 − 2) (10 − 1)2(10 − 2) = 41 079 191.
32
RIWAYAT HIDUP
Penulis dilahirkan pada tanggal 01 Desember 1994 di Balangan, Kalimantan Selatan. Penulis merupakan putra ketiga dari Bapak Saini dan Ibu Masrupah. Tahun 2012 penulis lulus dari SMA Negeri 01 Paringin di kabupaten Balangan, Kalimantan Selatan. Pada tahun yang sama penulis lulus seleksi masuk Institut Pertanian Bogor melalui Jalur Beasiswa Utusan Daerah (BUD). Penulis diterima di Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam. Selain mengikuti perkuliahan pada Mayor Matematika, penulis juga mengikuti perkuliahan minor Statistika Terapan.
Selama mengikuti perkuliahan, penulis aktif dalam kegiatan berorganisasi di antaranya, penulis menjadi Ketua Himpunan Mahasiswa Penerima Beasiswa Utusan Daerah (BUD) PT. Adaro Indonesia, menjadi Anggota Badan Pengawas di Gugus Mahasiswa Matematika (Gumatika) IPB, menjadi anggota Divisi Internal di Unit Kegiatan Mahasiswa Indonesian Green Action Forum Local Comitte IPB (IGAF LC IPB), anggota divisi Agriculture and Environment di Forum For
Indonesia (FFI) Bogor, dan anggota divisi Action Plan di Hilo Green Community
(HGC) Bogor. Penulis juga pernah menjadi panitia di beberapa kegiatan, di antaranya menjadi Anggota DDD pada acara Youth Consultation 2016, Anggota Divisi Humas IPB Green Living movement 2015, Anggota Divisi Logistik dan Transportasi The4th IPB Mathematics Challenges 2015, Anggota Divisi Logistik dan Transportasi Matematika Ria 2014, dan menjadi anggota divisi pada beberapa kegiatan Gumatika IPB.
Penulis menjadi asisten dosen matakuliah Matematika Ekonomi semester genap tahun ajaran 2016/2017, dan menjadi delegasi IGAF pada acara konferensi
United Nation Habitat 3 ASIA-PACIFIC Regional Meeting di Jakarta. Penulis juga pernah juara 2 lomba puisi “Anti Narkoba” tingkat kampus IPB kemudian menjadi perwakilan IPB pada Tingkat Nasional. Penulis aktif dalam beberapa kegiatan pengabdian masyarakrat dengan melakukan Bina Desa pada tahun 2015-2016, menjadi volunteerUnilever Bright Future pada tahun 2015, volunteer Rakpungpah pada tahun 2015 dan menjadi volunteer di beberapa acara lainnya.
Selama kuliah, penulis mendapatkan beasiswa Utusan Daerah (BUD) yang diberikan oleh PT. Adaro Indonesia yang bekerja sama dengan Pemerintah Daerah Kabupaten Balangan.