MODEL FIXED EFFECT PADA ANALISIS DATA POOLING

MODEL FIXED EFFECT

PADA ANALISIS DATA POOLING

SKRIPSI

Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta

untuk memenuhi sebagian persyaratan guna memperoleh gelar Sarjana Sains

Disusun oleh:

Musringatun

NIM. 013114757

PROGRAM STUDI MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI YOGYAKARTA

ii

MODEL FIXED EFFECT PADA ANALISIS DATA POOLING Telah disetujui dan disahkan pada tanggal

2008

untuk dipertahankan di depan Tim Penguji Skripsi Fakultas Matematika dan Pengetahuan Alam

Universitas Negeri Yogyakarta

Disetujui oleh

Pembimbing I, Pembimbing II,

Endang Listyani, M.S Elly Arliani, M.Si NIP. 131 569 343 NIP. 131 993 532

iii

Nama : Musringatun

NIM : 013114757

Program Studi : Matematika

Fakultas : Matematika dan Ilmu Pengetahuan Alam Judul Skripsi : Model Fixed Effect pada Analisis Data Pooling

Menyatakan bahwa skripsi ini adalah hasil pekerjaan saya sendiri dan sepanjang pengetahuan saya tidak berisi materi yang telah dipublikasikan atau ditulis oleh orang lain atau telah dipergunakan dan diterima sebagi persyaratan penyelesaian studi pada universitas lain, kecuali pada bagian-bagian tertentu yang telah dinyatakan dalam teks. Apabila ternyata terbukti hal ini tidak benar, sepenuhnya menjadi tangggung jawab saya.

Yogyakarta, 2008 Yang menyatakan,

Musringatun NIM. 013114757

iv Disusun oleh Musringatun NIM. 013114757

Telah dipertahankan di depan Tim Penguji skripsi Jurusan Pendidikan Matematika Dan Ilmu Pengetahuan Alam

Universitas Negeri Yogyakarta

pada tanggal 2008 dan dinyatakan telah memenuhi syarat guna memperoleh gelar Sarjana Sains.

Tim Penguji

Nama Tanda Tangan

Ketua Penguji Endang Listyani, MS ……….. NIP. 131569343

Sekretaris Penguji Elly Arliani, M.Si ……….. NIP. 131993532

Penguji I M.Susanti, M.Si ………...

NIP.131808672

Penguji II Kismiantini, M.Si ………

NIP.132296139

Yogyakarta, 2008 Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Negeri Yogyakarta Dekan,

Dr. Ariswan NIP. 130791367

v

manusia, jika kamu sanggup menembus(melintasi) penjuru langit dan bumi, maka lintasilah, kamu tidak dapat menembusnya, melainkan dengan kekuatan.

(Ar Rahman 32-33)

Hanya kepada Engkaulah kami menyembah dan hanya kepadaEngkaulah kami mohon pertolongan. (Al fatikhah:5)

Hidup ini adalah rangkaian pembelajaran Tanpa batas waktu

Suatu kejadian beralih ke kejadian yang lain Adalah guru kehidupan yang menukarkan Hikmah tanpa henti

Tangkaplah setiap tetes hikmah

karena ialah milik kita yang amat berharga jangan sia-siakan pelajaran yang Alloh berikan lewati kegagalan dan kesalahan

vi

panjatkan ke hadirat Allah SWT yang

telah melimpahkan rahmat, hidayah dan

kenikmatan sehingga penulis dapat

menyelesaikan penulisan skripsi ini.

Kupersembahkan karya kecil ini untuk: Bapak, Mama atas cinta, pengorbanan, doa serta kasih sayang yang tulus. Saudaraku: Moko, Desi, Nur, Janah, Damar, Linda, Putri.

vii

Mas Aris sekeluarga, Nizar sekeluarga, keluarga besar Jati Mulyo, Bi Lah & Bu Ipong sekeluarga.

Teman-Teman Ulya (Umi, Nurha, Dewi, Anik, Ica, Arna, Nita, Yunan, Alfi, Ihat, Asri, Deedee, Mb Rini), Fatiya, Tasnim, Nadia, TM Munawwar & Adek2 TPA.

Destri, Dwi, Ida, Asri, Eni, Nurika, Ristina, Noenk, Mien, Siti, Hasti, Reni, Hesti, Didi, Ica, Yuni, Sulis, Yuli, Isti, Anggi, Neli, Lia, Eko, Anggra, Ami, Febi, Audi, Ika terima kasih atas nasihat,doa dan tawaran persahabatannya.

Murobbi, Guruku dan ikhwafillah terima kasih atas pembelajaran tuk berbagi pada sesama dan pandangan masa depan.

viii Musringatun NIM. 013114757

ABSTRAK

Penulisan ini bertujuan untuk mengestimasi parameter model fixed effect pada data pooling serta menerapkan model fixed effect pada data pooling.

Data pooling merupakan data gabungan antara data cross section dan data

time series). Data time series adalah data yang dikumpulkan dari waktu ke waktu

terhadap suatu individu. Sedangkan data cross section adalah data yang dikumpulkan dalam satu waktu saja terhadap banyak individu. Salah satu model regresi pada data pooling adalah model fixed effect pada data pooling. Bentuk umum model fixed effect pada data pooling:

∑

∑

= = + + = N j K k it kit k jt j it D X Y 1 2 1

β

ε

β

, dengan Yit adalah variabel dependen, Xkit adalah

variabel independen dan D adalah variabel dummy,

ε

_it= error untuk individu ke-i dan waktu ke-t dengan E

( )

ε_it =0,E

( )

ε_it2 =σ_ε2. Pada model fixed effect pada data pooling, diasumsikan diasumsikan intersep β_1iberbeda antar individu namun intersep antar waktu sama sedangkan slope β_ktetap sama antar individu dan antar waktu. Untuk menghitung b1 dan bs digunakan rumus berikut:

(

)

(

X I D X

)

X

(

I D

)

Y b_s = ′_{s N}⊗ _{T s} −1 ′_{s N} ⊗ _T dan s i i 1i Y Xb b = − ′ , b =(b₂ b₃ L b_K)′

s . Pengujian hipotesis model fixed effect

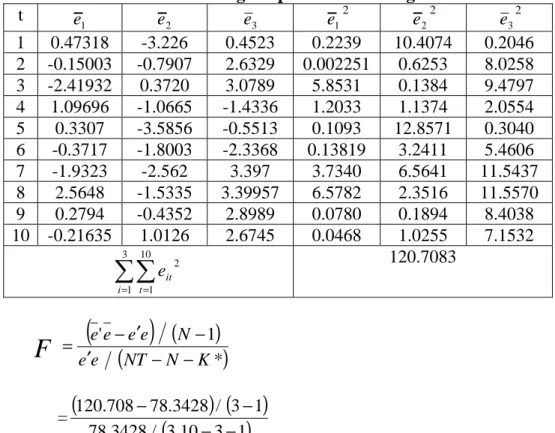
pada data pooling menggunakan uji F.

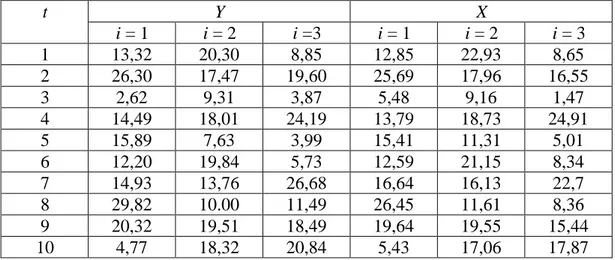
Penerapan model fixed effect dalam skripsi ini adalah investasi (Yit) tiga

perusahaan yang dipengaruhi oleh keuntungan perusahaan (X2it) selama sepuluh

tahun dengan model fixed effect dugaannya:

it t

t t

it D D D X

Yˆ =−1.5138 1 +−2.8463 2 +0.1137 3 +1.1028 2 . Model fixed effect pada

data pooling mampu menjelaskan perbedaaan investasi ketiga perusahaan tersebut. Sedangkan penerapan yang lain adalah mengenai bantuan pembangunan (Yit) di 5

Daerah Tingkat II Propinsi Daerah Istimewa Yogyakarta yang dipengaruhi Pendapatan Asli Daerah (X2it) dan Subsidi Daerah Otonom (X3it) selama 7 tahun

dengan model fixed effect dugaannya:

it it t t t t t it X X D D D D D Y 3 2 5 4 3 2 1 696397 . 2 55312 . 0 6448748 1628601 2549787 2742149 3103601 + − − − − − − = .

ix

Alhamdulillah, puji syukur penulis panjatkan kepada Allah SWT yang telah melimpahkan rahmat, hidayah dan kenikmatan sehingga penulis dapat menyelesaikan penyusunan skripsi ini.

Skripsi ini disusun untuk memenuhi sebagian persyaratan memeperoleh gelar Sarjana Sains Program Studi Matematika di Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta. Skripsi ini terselesaikan berkat bantuan dan dukungan dari berbagai pihak. Oleh karena itu, pada kesempatan ini penulis menyampaikan ucapan terima kasih kepada :

1. Bapak Dr. Ariswan, selaku Dekan Fakultas MIPA Universitas Negeri Yogyakarta

2. Bapak Dr. Hartono, selaku ketua jurusan Matematika yang telah memberikan kelancaran kelancaran pelayanan dalam urusan akademik 3. Ibu Atmini Dhoruri, M.Si selaku Ketua Program Studi Matematika

FMIPA Universitas Negeri Yogyakarta yang telah memberikan kelancaran kelancaran pelayanan dalam urusan akademik

4. Ibu Endang Listyani, M.S, selaku Dosen Pembimbing I dan penasehat akademik yang telah memberikan pengarahan, bimbingan serta nasehat yang diberikan kepada penulis.

5. Ibu Elly Arliani, M.Si, selaku Pembimbing II yang telah memberikan pengarahan, bimbingan serta nasehat yang diberikan kepada penulis.

x memberikan ilmu kepada penulis.

8. Semua pihak yang telah membantu dan memberikan dukungan sehingga dapat memperlancar proses penyelesaian skripsi ini.

Penulis menyadari bahwa skripsi ini masih banyak kekurangan, oleh karena itu kritik dan saran yang membangun dari berbagai pihak sangat penulis harapkan. Penulis berharap semoga karya ini dapat bermanfaat bagi dunia pendidikan dan perkembangan ilmu pengetahuan.

Yogyakarta, 2008 Penulis

xi

Halaman

HALAMAN JUDUL... i

HALAMAN PERSETUJUAN... ii

HALAMAN PERNYATAAN... iii

HALAMAN PENGESAHAN... iv MOTTO... v PERSEMBAHAN... vi ABSTRAK... viii KATA PENGANTAR... ix DAFTAR ISI………..…… xi

DAFTAR TABEL... xiii

DAFTAR LAMPIRAN... xiv

BAB I PENDAHULUAN A. Latar Belakang ……… 1

B. Rumusan Masalah …………..………. 5

C. Tujuan Penulisan……… 5

D. Manfaat Penulisan ……….. 5

BAB II DASAR TEORI A. Matriks...……….. 7

B. Model Regresi Linier Ganda ………... 15

1. Estimasi Parameter………..………. 17

2. Estimasi Variansi ………...………. 23

3. Matrik Variansi Kovariansi b.………..………...…….. 25

C. Variabel Dummy ………...….. 26

BAB III PEMBAHASAN A. Model fixed effect pada data pooling ...……….……….. 27

1. Estimasi Parameter.……….……….. 31

xii BAB IV PENUTUP A. Kesimpulan ……….. 57 B. Saran ……….. 60 DAFTAR PUSTAKA ……… 61 LAMPIRAN ……….. 63

xiii

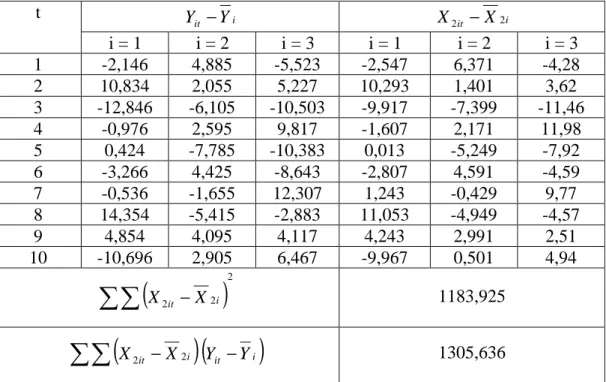
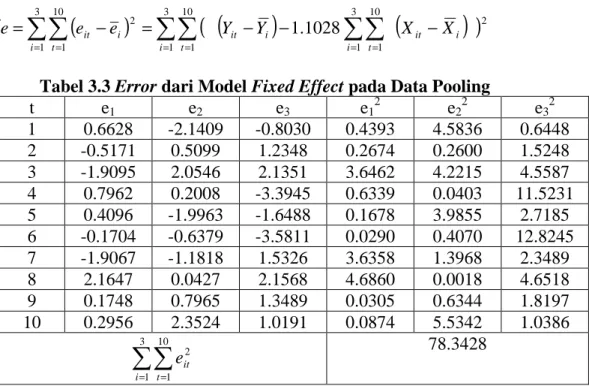
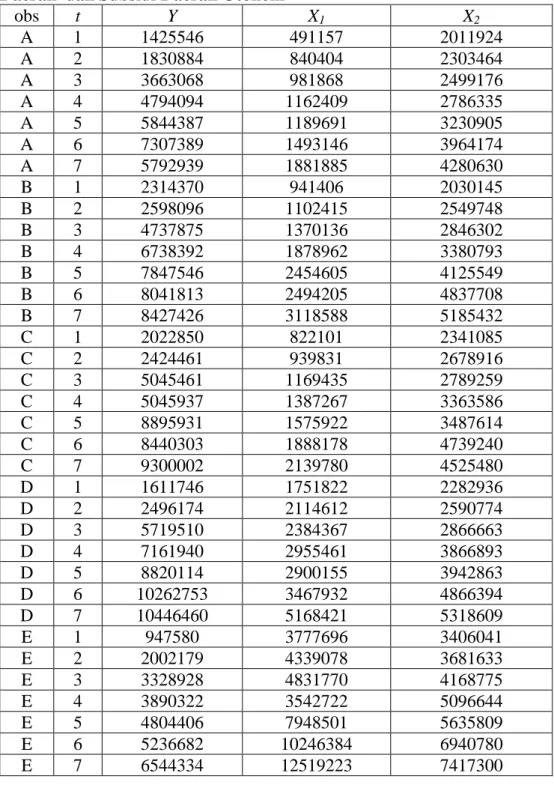
1. Tabel 3.1 Investasi dan Keuntungan dari 3 Perusahaan ……...…… 44 2. Tabel 3.2 Bentuk Deviasi Rata-Rata …..………...…… 45 3. Tabel 3.3 Sum Squared Resid dari Model Fixed Effect Pada

Data Pooling….……… 47 4. Tabel 3.4 Sum Squared Resid dari Model Regresi Data Pooling.….. 50 5. Tabel 3.5 Perkembangan bantuan pembangunan pada semua

Daerah Tingkat II di Propinsi Daerah Istimewa Yogyakarta,

xiv

Lampiran 1 Output Tabel 3.1Investasi dan Keuntungan dari

3 Perusahaan………..… 64 Lampiran 2 Output Tabel 3. 5 Perkembangan Bantuan Pembangunan pada

semua Daerah Tingkat II di Propinsi Daerah Istimewa Yogyakarta, Pendapatan Asli Daerah dan Subsidi Daerah

BAB 1 PENDAHULUAN

A. Latar Belakang

Dalam kehidupan sehari-hari sering dijumpai adanya hubungan antara satu variabel dengan variabel lain. Sebagai contoh di bidang ekonomi, adanya penghasilan yang diperoleh berhubungan dengan tingkat pendidikan seseorang, di bidang pertanian, adanya hubungan antara dosis pupuk yang diberikan dengan hasil yang diperoleh. Hubungan antara dua variabel atau lebih umumnya dinyatakan dalam bentuk persamaan matematika yang menyatakan hubungan fungsional antara variabel-variabel. Persamaan ini disebut dengan persamaan regresi. Dalam persamaan regresi dibedakan dua jenis variabel yaitu variabel bebas (independen) dan variabel terikat (dependen).

Regresi pertama kali diperkenalkan oleh Sir Francis Galton pada tahun 1886. Galton menemukan adanya kecenderungan bahwa orang tua yang memiliki tubuh tinggi memiliki anak yang tinggi, orang tua yang pendek memiliki anak-anak yang pendek. Kendati demikian, diamati juga ada kecenderungan tinggi anak-anak cenderung bergerak menuju rata-rata tinggi populasi secara keseluruhan. Dengan kata lain, ketinggian anak yang tinggi atau orang tua yang amat pendek cenderung bergerak ke arah rata-rata tinggi populasi. Inilah yang disebut hukum Galton mengenai regresi universal (Mudrajat Kuncoro, 2001: 91). Sedangkan analisis regresi dalam pengertian modern adalah studi bagaimana variabel dependen dipengaruhi oleh satu atau lebih dari variabel independen dengan tujuan untuk mengestimasi atau memprediksi nilai rata-rata variabel dependen didasarkan pada

nilai variabel independen yang diketahui. Keberhasilan dari setiap analisis regresi tergantung dari ada tidaknya ketersediaan data.

Data dapat dibagi menjadi (Supramono, 1993: 10): 1. Menurut sifatnya: a. Data kualitatif b. Data kuantitatif 2. Menurut sumbernya: a. Data internal b. Data eksternal

3. Menurut cara memperolehnya: a. Data primer

b. Data sekunder

4. Menurut waktu pengumpulannya:

a. Data time series (data runtut waktu) b. Data cross section (data seksi silang)

Data yang sering digunakan dalam analisis regresi adalah data time series (data runtut waktu) dan data cross section (data seksi silang). Data time series adalah data yang dikumpulkan dari waktu ke waktu terhadap suatu individu. Sedangkan data cross section adalah data yang dikumpulkan dalam satu waktu saja terhadap banyak individu. Namun terkadang ditemukan data yang merupakan gabungan dari data time series dan data cross section. Gabungan data ini disebut dengan data pooling. Dengan kata lain data pooling adalah data beberapa individu yang pengamatannya dilakukan dari waktu ke waktu, misalnya data pertumbuhan

perekonomian propinsi-propinsi di Indonesia. Data ini merupakan kumpulan informasi tentang perkembangan perekonomian di semua propinsi di Indonesia, dan dikumpulkan selama beberapa kurun waktu. Analisis regresi dengan menggunakan data pooling disebut analisis regresi data poling. Untuk selanjutnya analisis regresi data pooling dalam skripsi ini ditulis regresi data pooling.

Data pooling merupakan gabungan data cross section dan data time series mempunyai observasi lebih banyak dibandingkan dengan data cross section atau data time series saja. Pada data pooling ini, hasil regresi data pooling cenderung lebih baik dibanding regresi yang hanya menggunakan data cross section atau data

time series saja (Nachrowi, 2006: 312).

Beberapa keuntungan menggunakan data pooling (Indrawati, 2006) :

1. dengan menggabungkan data cross section dan data time series, data pooling lebih informatif, bervariasi, degree of freedom lebih besar dan lebih efisien.

2. dengan menggabungkan data data cross section dan data time series, data pooling dapat menghindari masalah multikolinearitas.

3. data pooling lebih dapat mendeteksi dan mengukur pengaruh-pengaruh yang tidak dapat diobservasi pada data cross-section murni atau

time-series murni.

4. dengan menggunakan beberapa ribu unit data cross section dan data time

Bentuk umum model regresi data pooling adalah

∑

= + + = K k it kit k i it X Y 2 1

β

ε

β

(1.1) t = 1,2…,T i = 1,2…,N k= 2,3…,K dengan

Yit = variabel terikat untuk unit cross section (unit individu ) ke-i dan waktu

ke-t

Xkit = variabel bebas ke-k untuk unit cross section ke-i dan waktu ke-t

i

1

β

= intersep untuk unit cross section ke-i

k

β

= slope bersama untuk semua unit

it

ε

= error untuk individu ke-i dan waktu ke-t dengan

( )

ε 0 E it = ,

( )

2 2 ε

σ

= it ε E

Beberapa model regresi pada data pooling menurut Pindyick dan Rubinfield (1998: 202) adalah

1. model dengan menggabungkan data cross section dan data time series.

2. model fixed effect / model kovarian / pendekatan Least Square Dummy

Variable. Model ini menambahkan variabel dummy untuk mengetahui variabel

yang menyebabkan perbedaan intersep antar unit individu.

3. model random effect / error component model. Model ini menghitung faktor error (error term) yang menimbulkan korelasi antar unit waktu dan unit individu.

Estimasi parameter model regresi data dengan menggabungkan data cross

section dan data time series digunakan metode kuadrat terkecil. Pada model ini

tidak dapat diketahui perbedaan intersep dan slope baik antar waktu maupun antar individu. Salah satu metode untuk mengatasi permasalahan tersebut dengan menggunakan model fixed effect data pooling. Model fixed effect pada data

pooling adalah model regresi data pooling dengan menggunakan variabel dummy untuk menjelaskan adanya perbedaan intersep antar individu. Parameter model

fixed effect pada data pooling diestimasi dengan menggunakan metode kuadrat

terkecil. Oleh karena itu model fixed effect disebut juga pendekatan Least Square

Dummy Variable. Salah satu kelebihan dari model fixed effect pada data pooling

adalah dapat mengetahui adanya perbedaan karakteristik dalam setiap individu. Sebagai contoh karakteristik dalam hal ini pada perusahaan adalah budaya perusahaan, gaya manajerial.

B. Rumusan Masalah

Rumusan masalah yang dapat disusun adalah sebagai berikut:

1. Bagaimana mengestimasi parameter-parameter model fixed effect pada data pooling?

2. Bagaimana penerapan model fixed effect pada data pooling?

C. Tujuan Penulisan Tujuan dari penulisan ini adalah:

1. Menjelaskan langkah-langkah mengestimasi parameter-parameter model

fixed effect pada data pooling.

2. Menjelaskan penerapan model fixed effect pada data pooling.

D. Manfaat Penulisan

1. Memberikan gambaran dan penjelasan konsep dasar model fixed effect data pooling yang sering ditemui dalam observasi.

2. Dapat menerapkan model fixed effect pada data pooling di bidang ekonomi.

BAB II DASAR TEORI

Pada bab II pada model fixed effect pada data pooling ini memerlukan beberapa teori tentang matriks, regresi linier ganda dan variabel dummy sebagai landasan dalam pembahasan model fixed effect pada data pooling.

A. Matriks

Pada skripsi ini model regresi linier dituliskan dalam notasi matriks. Matriks memberikan metode yang ringkas untuk menyelesaikan model regresi yang terdiri dari banyak variabel.

Definisi 2.1 Matriks (Anton, 1987: 22)

Matriks adalah susunan segi empat siku-siku dari bilangan-bilangan. Bilangan-bilangan dalam susunan tersebut dinamakan entri dalam matriks.

Contoh:       = 2 4 3 7 1 2 A

Definisi 2.2 Transpos suatu matriks (Searle, 1982: 23)

Transpos suatu matriks adalah matriks yang dibentuk dari matriks semula dengan mengubah entri-entri baris menjadi entri-entri kolom dan entri-entri kolom menjadi entri-entri baris. Transpos suatu matriks biasanya dituliskan dengan tanda

( )

' pada notasi matriks aslinya.

Contoh:             = 4 11 9 9 14 6 6 13 19 11 17 18 A dan           = ′ 4 9 6 11 11 14 13 17 9 6 19 18 A

Sifat-sifat transpos suatu matriks (Anton, 1987: 37) : 1.

( )

A′ ′ =A

2.

(

A+B

)

′ =A′+B′

3.

( )

kA′ =k A′, dengan k adalah sebarang skalar. 4.

( )

AB ′ =B′A′

Definisi 2.3 Matriks Persegi (Dumairy, 1999: 292)

Matriks persegi adalah matriks yang banyaknya baris sama dengan banyaknya kolom. Contoh:           = 0 5 4 1 3 7 8 5 3 B

Definisi 2.4 Matriks Diagonal (Dumairy, 1999: 300)

Matriks diagonal adalah matriks persegi yang semua entrinya nol kecuali pada diagonal utamanya. Contoh:       = 3 0 0 2 A

Definisi 2.5 Matriks Identitas (Anton, 1987: 33)

Matriks identitas adalah matriks persegi yang semua entri pada diagonal utamanya adalah bilangan satu sedangkan entri yang lain bilangan nol. Matriks identitas berukuran n × n biasa dinyatakan dengan In.

Contoh:       = 1 0 0 1 2 I

Definisi 2.6 Matriks Skalar (Dumairy, 1999: 303)

Matriks skalar adalah matriks diagonal yang entri-entrinya sama atau seragam (λ). Apabila λ= 1 matriks skalar menjadi matriks identitas.

Contoh:       = 3 0 0 3 A

Definisi 2.7 Matriks Simetris (Dumairy, 1999: 302)

Matriks simetris adalah matriks persegi yang sama dengan transposnya. Matriks A dikatakan simetris apabila A′=A.

Contoh:       = 7 3 3 1 A dan _      = ′ 7 3 3 1 A

Apabila sebuah matriks simetris dikalikan dengan matriks transposnya hasilnya berupa kuadrat dari matriks tersebut yaitu AA′=AA=A2.

Definisi 2.8 Invers suatu Matriks (Anton, 1987: 34)

Jika A dan B adalah matriks-matriks persegi, sedemikian sehingga

I BA

AB= = , maka Adikatakan mempunyai invers dan B disebut invers

Adan dinotasikan B= A . −1

Sifat invers suatu matriks (Anton, 1987: 37):

1. jika B dan C invers suatu matriks A maka B= C .

2. Jika A dan B adalah matriks-matriks yang mempunyai invers dan berordo sama , maka

a. AB mempunyai invers b.

( )

A−1 −1 =A

c.

( )

AB −1 =B−1A−1)

d.

( ) ( )

An −1 = A−1 n untuk n = 0,1,2...N Untuk sebarang skalar k≠0 maka

( )

kA −1 =

k

1 1

A−

Definisi 2.9 Determinan (Dumairy, 1999: 313)

Setiap matriks persegi A, selalu ada suatu skalar yang disebut determinan matriks A dengan simbol det(A) atau A .

Nilai dari suatu determinan dapat dilakukan dengan cara mengalikan unsur-unsurnya secara diagonal.

      = 22 21 12 11 a a a a A determinannya adalah

( )

11 22 21 12 22 21 12 11 det a a a a a a a a − = = A

Contoh: 4 24 28 7 6 4 4 ) det( , 7 6 4 4 = − = =       = A A

Matriks berdimensi tiga:

          = 33 32 31 23 22 21 13 12 11 a a a a a a a a a A determinan A adalah

( )

32 23 11 33 12 21 13 22 31 32 21 13 31 23 12 33 22 11 33 32 31 23 22 21 13 12 11 det a a a a a a a a a a a a a a a a a a a a a a a a a a a − − − + + = = A Contoh:           = 9 8 7 6 5 4 3 2 1 A

( )

1.5.9 2.6.7 3.8.4 7.5.3 4.2.9 1.6.7 0 9 8 7 6 5 4 3 2 1 det A = = + + − − − =

Sifat-sifat determinan (Anton, 1987: 71-75):

a. Jika A adalah sebarang matriks persegi, maka det(A) = det

( )

A′

b. Jika A dan B adalah matriks-martiks persegi yang ordonya sama, maka det(AB) = det(A)det(B)

c. Sebuah matriks persegi A mempunyai invers jika dan hanya jika det(A)≠0

d. Jika A mempunyai invers maka

) det( 1 ) det( A A−1 =

Contoh:      ₋ = 3 4 6 1 A dan _     ₋ = − 27 1 27 4 9 2 9 1 1 A

Definisi 2.10 Trace suatu Matriks (Searle, 1982: 27)

Trace suatu matriks persegi A berordo n adalah jumlah n elemen diagonal

utama matriks tersebut, ditulis:

( )

∑

= = + + + = n i ij nn a a a a tr 1 22 11 L A dengan i = j Contoh : 4 8 3 1 8 2 4 9 3 8 6 7 1 − = − + =           − − tr

Beberapa hal yang berlaku (Intriligator, 1978: 579): 1. tr(A′)=tr(A)

2. tr(c)=c, c adalah skalar

3. tr(cA) = c [tr(A)]

4. tr(In) = n

5. tr(A+B) = tr(A) + tr(B)

6. Apabila AB = BA, maka tr(AB) = tr(BA) Definisi 2.11 Matriks Nol (Dumairy, 1999: 301)

Matriks nol adalah matriks yang semua entri-entrinya nol. Contoh:       = × 0 0 0 0 0 0 3 2 0

Definisi 2.12 Matriks Idempoten (Maddala, 1977: 445 )

Matriks A adalah matriks idempoten jika dan hanya jika A2 = A Definisi 2.13 Kronecker Product (Muirhead, 2005: 73)

Jika A adalah matriks dengan ukuran n×m dan B adalah matriks dengan

ukuran k×l maka Kronecker Product dari A dan B adalah

            = ⊗ B B B B B B B B B B A MN M M N N a a a a a a a a a L M M M L L 2 1 2 22 21 1 12 11

dengan A ⊗ B adalah matriks dengan ukuran mk×nl.

Contoh:       = 0 2 3 1 A , _      = 3 0 1 0 2 2 B

Untuk kronecker product A dan B adalah

                                    = ⊗ 3 0 1 0 2 2 0 3 0 1 0 2 2 2 3 0 1 0 2 2 3 3 0 1 0 2 2 1 B A             = 0 0 0 6 0 2 0 0 0 0 4 4 9 0 3 3 0 1 0 6 6 0 2 2                                                 = ⊗ 0 2 3 1 3 0 2 3 1 0 0 2 3 1 1 0 2 3 1 0 0 2 3 1 2 0 2 3 1 2 A B

            = 0 6 0 0 0 2 9 3 0 0 3 1 0 0 0 4 0 4 0 0 6 2 6 2

Sifat-sifat dari Kronecker Product adalah

1. A⊗B≠B⊗A

2.

(

A⊗B

)(

C⊗D

)

=AC⊗BD 3.

(

A⊗B

)

−1 =A−1⊗B−1

4.

(

A⊗B

)

′ =A′⊗B′

5. A⊗

(

B+C

)

=A⊗B+A⊗C

Definisi 2.14 Vektor dan matriks dengan semua elemen 1 (Neter, 1985: 198) Vektor kolom dengan semua elemen 1 ditulis dengan

            = × 1 1 1 M 1 r1

dan matriks persegi yang semua elemennya 1 dapat ditulis dengan

            = × 1 1 1 1 1 1 1 1 1 L M M M L L r rJ Contoh:           = × 1 1 1 1 31           = × 1 1 1 1 1 1 1 1 1 3 3J

[

]

=

[ ]

n =n             = ′ × 1 1 1 1 1 1 M L 1 11 1

[

]

n n n n1 J 1 × × =             = ′ 1 1 1 1 1 1 L M

B. Model Regresi Linier Ganda

Secara umum model regresi linier ganda (Judge, 1988: 926) dapat ditulis:

i ki k i i i X X X Y =

β

+

β

+

β

+L+

β

+

ε

3 3 2 2 1 i = 1,2,...n dengan 1 β = intersep k

β

β

β

₂, _3...., = slope i

ε

= error,

ε

_i~ N(0,

σ

2)

i = observasi (pengamatan) ke-i n = banyaknya observasi

Oleh karena i menunjukkan observasi maka terdapat n persamaan:

n kn k n n n k k k k X X X Y X X X Y X X X Y

ε

β

β

β

β

ε

β

β

β

β

ε

β

β

β

β

+ + + + + = + + + + + = + + + + + = L M L L 3 3 2 2 1 2 2 32 3 22 2 1 2 1 1 31 3 21 2 1 1

Model regresi dapat ditulis dalam matriks sebagai berikut :

ε Xβ Y= + dengan ε β + =X

                    = k i

β

β

β

β

M M 2 1 β                     = n i

ε

ε

ε

ε

M M 2 1 ε             = kn n n k k X X X X X X X X X L M M M M L L 3 2 2 32 22 1 31 21 1 1 1 X

Beberapa asumsi yang penting dalam regresi linier ganda (Widarjono, 2005: 78) antara lain :

1. Hubungan antara Y (variabel dependen) dan X (variabel independen)

adalah linier dalam parameter.

2. Tidak ada hubungan linier antara variabel independen atau tidak ada multikolinieritas antara varibel independen.

3. Nilai rata-rata dari ε adalah nol.

( )

ε 0 E = ,

Dalam bentuk matriks:

E

( )

ε =0                     =                     = 0 0 0 0 ) ( ) ( ) ( ) ( 2 1 M M M M n i E E E E

ε

ε

ε

ε

= vektor nol

4. Tidak ada korelasi antara

( )

ε

_i dan

( )

ε

_j . E(

ε

_i

ε

_j) = 0 , i≠j, 5. Variansi setiap

ε

adalah sama (homoskedastisitas)

E

( )

ε2 =

σ

_ε2

E

( )

ε2 = E(εε′) =

(

n

)

n E

ε

ε

ε

ε

ε

ε

L M 1 2 2 1            

( )

(

)

(

)

( )

(

)

( ) (

)

(

)

(

) (

)

( )

                   = 2 2 1 2 1 2 2 2 1 2 1 2 1 2 1 ( ) n n n n i i i n n E E E E E E E E E E E E

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

ε

L M M M L M M M L L                     = 2 2 2 2 0 0 0 0 0 0 0 0 0 0 0 0 ε ε ε ε

σ

σ

σ

σ

L L L L L L L L = In 2 ε

σ

1. Estimasi Parameter

Persamaan regresi linier ganda dugaan (Makridakis, 1999: 282)

ki k i i i b b X b X b X Y = + + +L+ 3 3 2 2 1 ˆ

Persamaan regresi linier ganda dugaan ditulis dalam matriks sebagai berikut: Xb Yˆ = dengan                     = n i Y Y Y Y ˆ ˆ ˆ ˆ ˆ 2 1 M M Y                     = k i b b b b M M 2 1 b             = kn n n k k X X X X X X X X X L M M M M L L 3 2 2 32 22 1 31 21 1 1 1 X εβ + =X

Salah satu cara yang digunakan untuk mengestimasi β adalah metode kuadrat terkecil. Metode kuadrat terkecil adalah suatu metode untuk menghitung b sebagai estimator β dengan meminimalkan jumlah variabel error (Widarjono,

2005: 32). Misalkan b sebagai estimatorβ dan persaman hasil estimasi adalah Xb Yˆ = dan Y Y e= − ˆ Selanjutnya ) Y (Y ) Y (Y e e′ = − ˆ ′ − ˆ

(

Y Xb

) (

Y Xb

)

e e′ = − ′ −

(

Y bX

)(

Y Xb

)

e e′ = ′− ′ ′ − Xb X b Y X b Xb Y Y Y e e′ = ′ − ′ − ′ ′ + ′ ′

Oleh karena b′X′Yadalah suatu matriks skalar maka matriks transposnya adalah Y X b′ ′ =Y′Xb sehingga Xb X b Y X b 2 Y Y e e′ = ′ − ′ ′ + ′ ′

Di dalam matematika, untuk mendapatkan nilai minimal dalam sebuah fungsi syaratnya turunan pertama dari fungsi tersebut sama dengan nol. Oleh karena itu untuk mendapatkan

∑

e sekecil mungkin adalah dengan cara melakukan _i2 penurunan

∑

e terhadap komponen b dapat ditulis 2i 0

b e2i = ∂ ∂

∑

.

∑

2 i

e diturunkan terhadap komponen b:

Xb X 2 Y X 2 b e e ′ + ′ − = ∂ ′ ∂ dengan e′e=Y′Y−2b′X′Y+b′X′Xb 0 Xb X Y X′ +2 ′ = 2 atau Xb X Y X′ = ′

(

XX

)

XY b= ′ −1 ′

Teorema 3.1 Gauss Markov (Widarjono, 2005: 36)

Metode Kuadrat Terkecil menghasilkan estimator parameter yang bersifat

Best Linear Unbiased Estimator (BLUE) yaitu linier, tidak bias, dan

memiliki variansi minimum.

Akan dibuktikan b merupakan estimator yang linier, tidak bias, memiliki variansi yang minimum. a. Linier

(

XX

)

XY b= ′ −1 ′

(

X′X

)

1X′

(

Xβ+ε

)

= −

( )

X′X 1X′Xβ+

( )

X′X 1X′ε = − −

( )

XX Xε β+ ′ 1 ′ = − karena (X′X)−1X′X=I

Persamaan diatas menunjukan b adalah fungsi linier dari β dan ε . b. Tidak Bias

( )

b E

[

β

(

XX

)

Xε

]

E = + ′ −1 ′

( ) ( ) ( )

b Eβ E XX Xε

=β+

(

X′X

)

−1X′E

( )

ε

=β, sebab X= konstan dan E

( )

ε =0

Terbukti bahwa b merupakan estimator kuadrat terkecil yang tidak bias. c. Memiliki variansi yang minimum

Diketahui

(

)

[

2

]

β b E Var(b)= − atau

(

)(

)

_   _{− −} ′ =E b β b β Var(b) Dengan mensubstitusikan

( )

X X X ε 1 ′ ′ −

untuk (b−β ) maka akan diperoleh

(

)

{

}

{

( )

}

_   ′ ′ ′ ′ ′ = − − ε X X X ε X X X E Var(b) 1 1

(

)

( )

[

1 1

]

X X X ε ε X X X E Var(b)= ′ − ′ ′ ′ −

(

)

1

( ) (

)

1 X X X ε ε E X X X′ − ′ ′ ′ − =

(

)

1

(

)

1 X X X I σ X X′ − ′ − = n 2 ε

(

)

1

(

)

1 X X X X X X σ ′ − ′ ′ − = 2 ε

(

)

1 X X σ ′ − = 2 ε

(

)

1 X X σ Var(b)= _ε2 ′ −

Untuk menunjukkan bahwa semua b adalah estimator-estimator terbaik, akan dibuktikan bahwa variansi yang diperoleh yaitu

(

)

1 2

ε XX

σ

lain yang mungkin linear dan tidak bias, yaitu dengan mengasumsikan sebuah estimator alternatif yang linear dan tidak bias, dan akan dibuktikan bahwa variansinya lebih besar daripada variansi estimator model regresi.

Misalkan b* adalah estimator alternatif yang linear dan tidak bias bagi β. Anggaplah b*=

[

(X′X)−1X′+B

]

Y dengan B adalah matriks

konstanta berukuran k×n yang diketahui. Diperoleh

[

(XX) X B

]

Y b*= ′ −1 ′ +

[

(XX) X B

]

[

Xβ ε

]

b*= ′ −1 ′ + +

(

)

(

)

[

(XX) X Xβ ε B Xβ ε

]

b*= ′ −1 ′ + + +

( )

b* E

[

(XX) X

(

Xβ ε

)

B

(

Xβ ε

)

]

E = ′ −1 ′ + + +

( )

b* E

[

(XX) X Xβ

(

XX

)

Xε BXβ Bε

]

E = ′ −1 ′ + ′ −1 ′ + + dengan I X X X) (X′ −1 ′ = , E

( )

ε =0

(

b*

)

β BXβ E = +

Dari persamaan diatas diasumsikan b* merupakan estimator yang tidak bias bagi β maka seharusnya E

(

b*

)

=β atau BXβ merupakan matriks nol dengan BX= 0 .

Variansi dari estimator alternatif adalah

(

)(

)

_   _{− −} ′ =E b* β b* β Var(b*)

[

]

{

}

{

[

( )

]

}

_   ′ − + ′ ′ − + ′ ′ = − − β Y B X X X β Y B X ) X X ( 1 1 E

[

]

(

)

{

}

{

[

( )

]

(

)

}

_   ′ − + + ′ ′ − + + ′ ′ = − − β ε Xβ B X X X β ε Xβ B X ) X X ( 1 1 E

[

{

( )

( )

}

{

( )

( )

′ ′ + + −

}

′

]

+ ′ ′ − + + ′ ′ + ′ ′ = − − − − β Bε BXβ ε X X X Xβ X X X β Bε BXβ ε X X X Xβ X X X E 1 1 1 1

( )

{

}

{

( )

}

_   ′ − + ′ ′ + − + ′ ′ + = − − β Bε ε X X X Iβ β Bε ε X X X Iβ E 1 1 Karena (X′X)−1X′X=I,BX=0

( )

{

}

{

( )

}

_   ′ + ′ ′ + ′ ′ = − − Bε ε X X X Bε ε X X X E 1 1

( )

{

}

{

( )

}

[

XX Xε Bε εX XX εB

]

E ′ 1 ′ + ′ ′ 1 + ′ ′ = − −

( )

{

}

{

( )

}

[

XX X B εε X XX B

]

E ′ 1 ′+ ′ ′ 1 + ′ = − −

( )

{

}

[ ]

{

( )

}

[

X′X 1X′+B εε′ X X′X 1 +B′

]

= − − E

{

′ ′ ₊

}{

′ ₊ ′

}

=_σ2_{I (X X)}−1_{X B X(XX)}−1 _B ε n

( )

( ) ( )

{

(X X) X XX XX BX XX XX XB BB

}

I σε2 ′ 1 ′ ′ ′ 1 + ′ 1 + ′ 1 ′ ′+ = − − − − n

{

(X X) BB

}

I σ_ε2 ′ 1 + ′ = − n karena Bε=0

( )

XX σ I BB I σ_ε2 ′ 1 + 2_ε ′ = − n n

( )

b*

Var lebih besar daripada Var

( )

b yaitu dengan kelebihan sebesar σ_ε2 I_nBB′, sehingga terbukti bahwa b merupakan estimator terbaik.

2. Estimasi Variansi

Menurut Judge et al. (1988: 205), estimator yang tidak bias untuk

σ

_ε2 adalah

2 ˆ_ε σ dengan k n e e − ′ = 2 σˆ_ε Pembuktian

Model regresi linier ganda ditulis dalam persamaan matriks :

ε

Xβ Y= +

akan digunakan sebagai dasar mengestimasi σ_ε2 dengan σ_ε2 adalah variansi dari

error.

Misalkan b sebagai estimator β dan persaman hasil estimasi adalah Xb Yˆ = =X

(

X′X

)

−1X′Y dan Y Y e= − ˆ

( )

XX XY X Y− ′ 1 ′ = −

(

)

(

I −X X′X 1X′

)

Y = − n

( )

(

I −X X′X 1X′

)

(

Xβ+ε

)

= − n

(

)

(

I −X X′X 1X′

)

ε = − n Mε =

M M MM M M ′= = 2 =

(

)

(

I −X X′X 1X′

)

(

I −X

(

X′X

)

1X′

)

=

(

I −X

(

X′X

)

1X′

)

= − − − n n n

Matriks yang memenuhi sifat di atas disebut matriks idempoten.

(

)

(

I X XX X

)

(

I X

(

XX

)

X

)

ε ε e e′ = ′ n − ′ −1 ′ n − ′ −1 ′ Mε ε Mε M ε′ ′ = ′ =

(

)

(

I X XX X

)

ε ε − ′ 1 ′ = − n

Karena ε′Mε adalah skalar maka

[ ]

ee E

[

tr

(

εMε

)

]

E

[

tr

(

Mεε

)

]

E ′ = ′ = ′

[ ]

ee tr

{

ME

[ ]

εε

}

tr

[

M

( )

σ I

]

σ tr

( )

M E ′ = ′ = _ε2 n = _ε2

(

)

[

I X XX X

]

tr σ 2 − ′ 1 ′ = − n ε

( )

(

(

)

)

[

tr I tr X XX X

]

σ 2 − ′ 1 ′ = − n ε

( )

(

(

)

)

[

1

]

2 X X X X tr I tr σ − ′ ′ − = ε n karena(X X) X X I 1 ′ = ′ −

( ) ( )

[

k

]

2 I tr I tr σ − = ε n

(

n−k

)

= 2 σ_ε

[ ]

e′e =σ 2

(

n−k

)

E _ε Akibatnya

(

)

2 2 σ σ 1 e e E  − = _ε      − =     − ′ k n k n k n Untuk _{n k} e e − ′ = 2 σˆ_{ε maka} E

[ ]

σˆ_ε2 =σ_ε2

3. Matrik Variansi Kovariansi b

Definisi 2.15 Matrik Variansi-Kovariansi dari b (Gujarati, 1978: 137).

Var-cov(b)=E

{

[

b−E(b)

][

b−E(b)

]

′

}

Diketahui E(b)=βsehingga

[

][

]

{

_{b−E(b) b−E(b)}′

}

_=E

{

[

_b−β

][

_b−β

]

′

}

E               ′             − − −             − − − = k k k k b b b b b b E

β

β

β

β

β

β

M M 2 2 1 1 2 2 1 1

[

]

              − − −             − − − = k k k k b b b b b b E

β

β

β

β

β

β

L M 1 1 2 2 2 2 1 1

[

]

[

]

[

]

[

]

[

]

[

]

[

] [

]

[

]

             − − − − − − − − − − − − − − − = 2 2 2 1 2 2 2 2 2 2 1 2 2 1 1 2 2 1 1 2 1 1 ) ( ) )( ( ) )( ( ) )( ( ) ( ) )( ( ) )( ( ) )( ( ) ( k k k k k k k k k k k b E b b E b b E b b E b E b b E b b E b b E b E

β

β

β

β

β

β

β

β

β

β

β

β

β

β

β

L M M M M L L             = ) ( ) , cov( ) , cov( ) , cov( ) ( ) , cov( ) , cov( ) , cov( ) ( 2 1 2 2 1 2 1 2 1 1 k k k k k b Var b b b b b b b Var b b b b b b b Var L M M M L L

Matriks diatas adalah matriks simetris yang mengandung variansi dari estimator b di sepanjang diagonal utama dan kovariansi pada elemen yang lain. Oleh karena itu matriks ini disebut matriks variansi-kovariansi dari estimator kuadrat terkecil

Var-cov

( )

b =E

{

(b−β)(b−β)′

}

Dengan mensubstitusikan

( )

X X X ε

1 ′

′ −

untuk (b−β) maka akan diperoleh

Var-cov (b)=E_

{

(

X′X

)

−1X′ε

}

{

(

X′X

)

−1X′ε

}

′ _

(

)

( )

[

1 1

]

X X X ε ε X X X E ′ − ′ ′ ′ − =

(

)

1

( ) (

)

1 X X X ε ε E X X X′ − ′ ′ ′ − =

(

)

1

(

)

1 X X X I σ X X X′ − ′ ′ − = n 2 ε

(

)

1

(

)

1 2 X X X X X X σ ′ − ′ ′ − = _ε

(

)

1 X X σ ′ − = 2 ε Var-cov (b)=σ_ε2(X′X)−1

C. Variabel Dummy (Sumodiningrat, 1996: 345)

Variabel dummy adalah variabel kualitatif dalam model regresi. Variabel kualitatif tidak dapat diukur, tetapi hanya dapat ditandai sifatnya antara ada dan tidak ada. Nilai variabel dummy dalam model bernilai 1 atau 0 untuk masing-masing kategori. Misalkan untuk kategori jenis kelamin pria adalah 1 dan untuk kategori jenis kelamin wanita adalah 0.

BAB III PEMBAHASAN

Data pooling adalah data beberapa individu yang pengamatannya dilakukan dari waktu ke waktu. Regresi dengan menggunakan data pooling disebut regresi data poling.

Bentuk umum model regresi data pooling adalah

∑

= + + = K k it kit k i it X Y 2 1

β

ε

β

(3.1) t = 1,2…T ; i = 1,2…N; k = 2,3…K dengan:

Yit = variabel terikat untuk unit cross section (unit individu ) ke-i dan waktu

ke-t

Xkit = variabel bebas ke-k untuk unit cross section ke-i dan waktu ke-t

i

1

β

= intersep untuk unit cross section ke-i

k

β

= slope bersama untuk semua unit

it

ε

= error untuk individu ke-i dan waktu ke-t dengan

( )

ε 0

E _it = ,E

( )

ε_it2 =

σ

_ε2

A. Model Fixed Effect Pada Data Pooling

Model fixed effect pada data pooling adalah model regresi data pooling dengan menggunakan variabel dummy yang digunakan untuk menjelaskan adanya perbedaan intersep antar individu. Sebagai contoh perbedaan intersep antar individu, perbedaan karakteristik pada perusahaan budaya perusahaan adalah gaya manajerial. Model fixed effect pada data pooling dapat dituliskan dalam bentuk berikut ini:

∑

∑

= = + + = N j K k it kit k jt j it D X Y 1 2 1

β

ε

β

(3.2)

dengan Djt adalah variabel dummy dan mengambil nilai 0 atau 1. Dapat juga ditulis

berikut ini: Djt = i j jika i j jika ≠ =    0 1

Jadi variabel dummy akan bernilai 1 untuk observasi yang sama dengan individu ke- j dan bernilai 0 untuk observasi individu yang lain. Pada model fixed effect untuk data pooling, diasumsikan bahwa intersep

β

_1iberbeda antar individu namun intersep antar waktu sama sedangkan slope

β

_k tetap sama antar individu dan antar waktu. Model fixed effect pada data pooling terdapat N persamaan dengan masing-masing T observasi dapat dituliskan berikut ini:

Nt kNt K k k jt N j j t N t t k K k k jt N j j t t t k K k k jt N j j t X D Y X D Y X D Y

ε

β

β

ε

β

β

ε

β

β

+ + = + + = + + =

∑

∑

∑

∑

∑

∑

= = = = = = 2 1 1 2 2 2 1 1 2 1 1 2 1 1 1 M

Untuk i = 1 dan t = 1,2,...,T, model fixed effect pada persamaan (3.2) dapat ditulis dalam bentuk matriks berikut ini:

            +                         +                         =             T K T K T T K K N NT T T N N T X X X X X X X X X D D D D D D D D D Y Y Y 1 12 11 3 2 1 31 21 12 312 212 11 311 211 1 12 11 2 1 2 22 12 1 21 11 1 12 11

ε

ε

ε

β

β

β

β

β

β

M M L M M M L L L M M M L L ) 1 (T× (T×N) (N×1) (T×K)

(

K×1

)

(T×1)

            +                         +                         =             T K T K T T K K N T X X X X X X X X X Y Y Y 1 12 11 3 2 1 31 21 12 312 212 11 311 211 1 12 11 1 12 11 0 0 1 0 0 1 0 0 1

ε

ε

ε

β

β

β

β

β

β

M M L M M M L L L M M M L L Dimisalkan =

(

1 1 L 1

)

′ T

j adalah vektor matriks berukuran

(

T×1

)

maka untuk individu ke-1 persamaan ( 3.2 ) dapat ditulis dengan notasi matriks berikut ini: 1t k k1t T 11 1t β j X β ε Y = + +

Untuk i = 2 dan t = 1,2,...,T, model fixed effect pada persamaan (3.2) dapat ditulis dalam bentuk matriks berikut ini:

            +                         +                         =             T K T K T T K K N NT T T N N T X X X X X X X X X D D D D D D D D D Y Y Y 2 22 21 3 2 2 32 22 22 322 222 21 321 221 1 12 11 2 1 2 22 12 1 21 11 2 22 21

ε

ε

ε

β

β

β

β

β

β

M M L M M M L L M L M M M L L M             +                         +                         =             T K T K T T K K N T X X X X X X X X X Y Y Y 2 22 21 3 2 2 32 22 22 322 222 21 321 221 1 12 11 2 22 21 0 1 0 0 1 0 0 1 0

ε

ε

ε

β

β

β

β

β

β

M M L M M M L L M L M M M L L M Dimisalkan =

(

1 1 L 1

)

′ T

j adalah vektor matriks berukuran

(

T×1

)

maka untuk individu ke-2 persamaan ( 3.2 ) dapat ditulis dengan notasi matriks berikut ini: t k t k T 1 t β j X β ε Y₂ = ₂ + ₂ + ₂

Untuk i = N dan t = 1,2,...,T, model fixed effect pada persamaan (3.2) dapat ditulis dalam bentuk matriks berikut ini:

            +                         +                         =             NT N N K KNT NT NT KN N N KN N N N NT T T N N NT N N X X X X X X X X X D D D D D D D D D Y Y Y

ε

ε

ε

β

β

β

β

β

β

M M L M M M L L M L M M M L L M 2 1 3 2 3 2 2 2 3 2 2 1 1 3 1 2 1 12 11 2 1 2 22 12 1 21 11 2 1             +                         +                         =             NT N N K KNT NT NT KN N N KN N N N NT N N X X X X X X X X X Y Y Y

ε

ε

ε

β

β

β

β

β

β

M M L M M M L L M L M M L L M 2 1 3 2 3 2 2 2 3 2 2 1 1 3 1 2 1 12 11 2 1 1 0 0 1 1 0 0 1 0 0 Dimisalkan =

(

1 1 L 1

)

′ T

j adalah vektor matriks berukuran

(

T×1

)

maka untuk individu ke-N, persamaan ( 3.2 ) dapat ditulis dengan notasi matriks berikut ini: t k t k T 1 t β j X β ε Y_N = _N + _N + _N

Untuk i = 1,2...N dan t = 1,2,...,T, persamaan (3.2) dapat ditulis dalam bentuk matriks berikut ini:

i s si T 1i i β j X β ε Y = + + dengan i= 1,2...N (3.3) dengan             = iT i i Y Y Y M 2 1 i Y             = KiT iT iT Ki i i Ki i i X X X X X X X X X L M M M L L 3 2 2 2 3 2 2 1 1 3 1 2 si X             = iT i i

ε

ε

ε

M 2 1 i ε dan ) ( _{2 3} ′ =

β

β

L

β

K s β .

Secara lengkap NT observasi dapat ditulis sebagai berikut:

            +                         +                         =             N K sN s s N T T T N X X X j j j Y Y Y

ε

ε

ε

β

β

β

β

β

β

M M M M L M M M L L M 2 1 3 2 2 1 1 12 11 2 1 0 0 0 0 0 0

            +                             =             N N N T T T N j j j Y Y Y

ε

ε

ε

β

β

β

M M L M O M M L L M 2 1 1 12 11 2 1 0 0 0 0 0 0 s s s2 s1 β X X X (3.4)

dengan menggunakan notasi Kronecker product akan ekivalen dengan

[

]

ε β β X j I Y s 1 s T N +      ⊗ = (3.5) dengan N 2 1,Y , ,Y Y Y′= ′ ′ L ′ _,

(

s1 s2 sN

)

s X ,X , , X X′ = ′ ′ K ′

(

ε1,ε2, ,εN

)

ε′= ′ ′ K ′ _,

(

β

11,

β

12,K,

β

1N

)

= ′₁ β dan T N j

I ⊗ adalah matriks dari variabel dummy berukuran (NT x N).

            = ⊗ T T T j j j L M O M M L L 0 0 0 0 0 0 T N j I 1. Estimasi Parameter

Model fixed effect pada data pooling dalam bentuk matriks dinyatakan sebagai berikut:

[

]

ε β β X j I Y s 1 s T N +      ⊗ =

Misalkan b sebagai estimator β dan persamaan model fixed effect pada data pooling dugaan adalah

[

]

      ⊗ = s 1 s T N b b X j I Yˆ (3.6)

Estimasi parameter dengan menggunakan metode kuadrat terkecil adalah

(

XX

)

XY b= ′ −1 ′ Apabila X=

[

I_N ⊗j_T X_s

]

, _      = s 1 b b

b maka b=

(

X′X

)

−1X′Ydapat ditulis sebagai berikut:

(

I j X

) (

I j X

) (

I j X

)

Y b b s T N 1 s T N s T N s 1 _{ ⊗} ′      _⊗ ′ _⊗ =       −

(

_{) (}

_{) (}

)

_Y X j I X j I X j I b b s T N 1 s T N s T N s 1         ′ ′ ⊗         ⊗         ′ ′ ⊗ =       −

(

) (

) (

)

(

)

(

)

_      ′ ′ ⊗         ′ ⊗ ′ ′ ⊗ ⊗ ′ ⊗ =       − Y X Y j I X X j I X X j I j I j I b b s T N s s T N s s T N T N T N s 1 1

dan

(

I_N⊗j_T

) (

′ I_N ⊗j_T

)

=I_N ⊗j′_Tj_T =TI_N disubtitusikan dalam persamaan

(

) (

) (

)

(

)

(

)

_      ′ ′ ⊗         ′ ⊗ ′ ′ ⊗ ⊗ ′ ⊗ =       − Y X Y j I X X j I X X j I j I j I b b s T N s s T N s s T N T N T N s 1 1 sehingga

dapat dituliskan sebagai berikut:

(

)

(

)

(

)

_      ′ ′ ⊗         ′ ⊗ ′ ′ ⊗ =       − Y X Y j I X X j I X X j I TI b b s T N 1 s T N s s T N N s 1 s (3.7)

Walaupun secara teori tidak ada masalah dalam memperoleh

(

b₁′,b_s′

)

namun dapat menjadi masalah perhitungan yang disebabkan kesulitan dalam perhitungan invers. Alternatif yang dapat digunakan untuk menghitung bs dan b1i

adalah sebagai berikut ini:

dengan

(

)

                        = ⊗ sN s2 s1 T T T s T N X X X D 0 0 0 D 0 0 0 D X D I M L M O M M L L             = sN T s2 T s1 T X D X D X D M dan

(

)

                        = ⊗ N 2 1 T T T T N Y Y Y D 0 0 0 D 0 0 0 D Y D I M L M O M M L L             = N T 2 T 1 T Y D Y D Y D M

Akan ditunjukkan bahwa DT adalah matriks idempoten, sehingga IN×DT

juga idempoten. T j j I D T T T T ′ − =       ′ −       ′ − = T j j I T j j I D D T T T T T T T T 2 T T T T T T T T j j j j T j j I − ′ + ′ ′ = 2 T j j I T T T ′ − =