Bab 3 Terapan Integral Ganda

KK-Astronomi Page 3-1

Bab 3

Terapan Integral Ganda

__________________________________________________________________________

3.1 Integral Ganda dalam koordinat Kartesis dan Polar

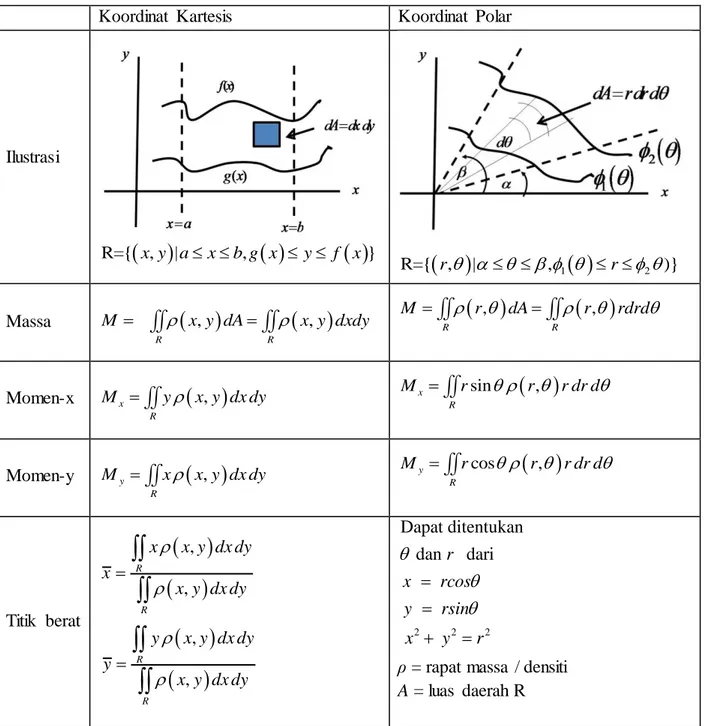
Koordinat Kartesis Koordinat Polar

Ilustrasi





 

 

R={ ,x y a|  x b g x,  y f x}

_{ }

_{ }

1 2 R={ ,r      |   ,  r   )} Massa



,





,



R R x y dA x y dxdy M 

∬

 

∬

 M 

∬

_R 

 

,r  dA

∬

_R  ,

 

r  rdrd Momen-x _x ,





R M 

∬

y x y dx dy Mx 

∬

_Rrsin , 

 

r  r r d d  Momen-y ,





R y x x y d dy M 

∬

 x y cos ,

 

R r r r dr M 

∬

   d Titik berat

 

 

, , R R x x y dx dy x x y dx dy 





 

 

 

, , R R y x y dx dy y x y dx dy 





  2 2 2 Dapat ditentukan dan dari r x rcos y rsin x y r       

ρ = rapat massa / densiti A = luas daerah R

KK-Astronomi Page 3-2 Jika ρ konstan titik pusat massa disebut Sentroid

1 R R R x dx dy x x dx dy A dx dy 









1 R R R y dx dy y y dx dy A dx dy 









3.2 Momen Inersia

1. Momen inersia terhadap suatu garis L, pada kurva

2

( , ) ( , ) L

R

I 



 x y  x y dxdy

Dalam hal ini,



x, y



 = jarak titik (x,y) dari garis L 2. Momen inersia terhadap sumbu x dan sumbu y

2 ( , ) x R I 



y  x y dxdy , _y 2 ( , ) R I 



x  x y dxdy

KK-Astronomi Page 3-3



2 2



0 x y I I I ( , ) R x y x y dxdy   



 

Contoh

1. Diketahui: Suatu lamina berbentuk daerah yang dapat didefinisikan sebagai himpunan

 

2

3

R  { x, y | 0 x 8, 0 y x } dengan rapat massa



x y,



xy Ditanya:M, Mx, My dan ( , )x y , dan lain-lain

Jawab : _R  _{{ x, y | 0}

 

 _{x 8, 0} _{y x}23_} Jadi 2 2 3 3 2 3 8 8 8 2 0 0 0 0 0 0 8 7 3 0 1 ( ) ( , ) 2 1 768 2 5 x x x R

M R x y dxdy xy dxdy xydy dx xy dx

x dx   _{ }      _{  }          _{ }   



 

 







Jadi massanya adalah 768/5 satuan massa

Untuk pertanyaan lain dapat diselesaikan, dengan menggunakan pernyataan Moment terhadap sumbu x

 





( , ) x

R

M R y  x y dxdy

Moment terhadap sumbu y

 





( , ) y

R

M R x  x y dxdy

Koordinat pusat massa

( ) ( ) , ( ) ( )  My R  M Rx x y M R M R

3.3 Studi kasus Nebula Cincin

Lingkaran konsentris berikut adalah model ideal dari sebuah ”ring- nebula” berjari- jari a dan b, dan mempunyai rapat massa yang tetap( , )x y c. Pertanyaannya;

a. Deskripsikan daerah R dari cincin ini b. Hitung momen inersia polarnya

KK-Astronomi Page 3-4 Simulasi Ring Nebulae “Fomalhaut”, suatu

nebula yang berjarak 25 pc, massa 2,3 massa matahari dan radiusnya 1,85 radius matahari. Suhunya 8500 K dan berumur 200 juta tahun. Noktah merah menunjukkan planet, noktah putih adalah bintang dan cincin bagian dalam

berwarna kecoklatan menyatakan serpihan piringan. Jarak planet ke bintang 15 au

Nebula terletak pada rasi Piscis Austrinus dengan h m s o

22 57 39 ,1 dan 29 37 ' 20"

    

Penyelesaian

Persamaan lingkaran dengan jejari a dan b adalah;

2 2 2

x y b sebut dareah R1

2 2 2

x y a sebut dareah R2

Jadi daerah cincin tersebut adalah R1-R2

Momen inersia cincin dengan jejari a dan b adalah;

2

0 _R

I 



r dA dalam hal ini, r – jarak elemen massa/luas ke pusat koordinat,  = rapat massa dan dA elemen luas dalam daerah R

Cara 1

Daerah cincin adalah selisih R dan ₁ R . Luas daerah ini merupakan 4 kali luas daerah yang ₂

terletak pada kuadran I



x0 dan y0





2 2



1 4 ( , ) | 0 , 0 ( ) R  x y  x b  y b x dan R₂ 4 ( , ) |



x y o x a, 0 y (a2x2)



Jadi : 2 0 2 ( ) ( , ) R x y x y dxdy I 



  1 2 2 2 2 2 0 1 1 4 4 4 ( ) 4 ( ) R R I 



x y cdxdy



x y cdxdy

KK-Astronomi Page 3-5









2 2 2 2 2 2 2 2 0 0 0 0 0 4 4 4 4 4( ) b b x a a x b a b a I x y cdxdy x y cdxdy I I I I   

 

 

 

     Misalkan;













2 2 2 2 1 3 2 2 2 3 2 2 2 ₂ 2 2 ₂ 0 0 0 0 0 1 1 3 3 a x a a x a a a I x y dxdy x y y dx x a x a x dx c   _{ }      _  _  _    _   _{ }

 





Misalkan;

 

sin cos 0 0 arcsin 1 2 x a dx a d x x a                

Jadi diperoleh bentuk integral yang baru;





1





3

2

2 2 2 2 2 ₂ 2 2 2 ₂

0

1

sin sin sin cos

3 a I a a a a a a d c    _    _  



      2 2 4 2 2 4 4 2 2 4 0 0 / 2 2 4 2 4 4 2 4 0 0 1 1

sin cos cos (1 cos ) cos cos

3 3 2 2 cos cos 3 3 a I a d a d c a d a C C      _  _  _   _          _  _  _  _    







              

Gunakan rumus rekursif;









1

2

1

cos n cos n sin ( 1)

n n C d n C n     

_

   _    _ Diperoleh; /2 _{4 4} 4 2 4 0 2 3 8 8 a a I a a c a C C I c       _  _     

Dengan cara yang sama, diperoleh;

/2 4 4 4 2 4 0 2 3 8 8 b b I b b c b C C I c  _{ }    _  _     

KK-Astronomi Page 3-6





4 4



4 4



0 4 2 2 b a c b a b c a c I  I I     Cara 2

Persamaan ini lebih mudah diselesaikan dengan koordinat polar dalam hal ini daerah yang ditinjau adalah ;



( , ) , dan 0 2



R r  a r b    sedangkan elemen luas dArdrd

Jadi kita harus menghitung;



4 4



2 2 3 3 0 0 2 ( , ) 4 b R R a c b a I r r rdrd r cdrd c r drd         

_



_



_{ }

 Atau;



4 4



0 2 c b a I  

3.4 Studi Kasus Inti Komet

1) Inti sebuah komet memperlihatkan daerah berbentuk mirip elips. Inti ini dapat dianggap sebagai suatu lamina dengan rapat massa tetap. Model ideal untuk inti komet digambarkan sebagai sebuah daerah yang dibatasi oleh dua kurva. Pertanyaannya, tentukan sentroid dari lamina S yang dibatasi kurva berikut:

2 3 y  x dan 2 5 y  x Penyelesaian

Apabila kurva berpotongan artinya, titik potong antara dua kurva memenuhi

3 5 1 x    x x Dengan demikian 2 5 4 2 y      x y

Jadi titik potongnya adalah (1,-2) dan (1,2)

Misal rapat massa lamina homogen tersebut ρ. Maka massa dari lamina tersebut adalah

 

R R

KK-Astronomi Page 3-7 y R R x R R xdxdy M x A dxdy ydxdy M y A dxdy    









Jawab: Hitung luas daerah R

 









2 2 2 2 2 5 2 2 2 2 5 _{2 2 2 3} 3 2 2 3 2 2 2 2 5 3 8 2 8 3 16 16 32 64 16 16 32 3 3 3 3 y y y R y A dxdy dxdy x dy y y dy y dy y y                     _  _       _  _{ }   _      



 







Titik beratnya dapat dicari

2 2 2 2 5 5 2 2 2 2 4 4 2 2 3 2 3 2 2 2 2 2 3 2 2 1 3 3 1 3 25 10 6 9 64 64 2 64 2 2 3 16 4 3 2 3 16 16 3 64 8 16 16 1 64 2 64 3 64 3 3 64 3 y y R y y y y y y x x dxdy x dxdy x dy dy A y dy y y                     _{ }  _  _                 _{ }  _  _  _  _{ }  _ _{ }          

 







∬

dan

 





 













 





2 2 2 2 5 2 2 2 5 _{3 3} 3 2 3 2 2 2 2 3 2 4 2 2 1 3 3 3 5 3 64 64 64 3 3 1 3 8 2 4 16 8 16 8 0 64 64 2 64 y y y R _y y y dxdy y dxdy xy dy y y y y dy A y y dy y y                      _  _       

 







∬

2) . Suatu daerah dibatasi oleh kurva ylogx , garisy0 dan 1 x a

Carilah massa dan sentroid dari lamina tersebut ?

KK-Astronomi Page 3-8 Jawab:

 



, 1 , 0 log



R x y  x a  y x ln log ln10 x x

 

log log 0 1 0 1 1 1 ln log ln10 x a a x R a a A dxdy dydx y dx x xdx dx     

 







∬

Tinjau 1 ln a xdx



Mis : u lnx du 1dx, dv dx v x x      

Gunakan integrasi parsial



u dvuv



v du





₁



  

₁ 1 1 1 ln ln ln ln1 ln 1 a a a a xdx x x x dx a a x a a a x        





Jadi luas daerah yang dibatasi adalah

ln 1

ln10

a a a

A  

Titik berat dapat dicari dari pernyataan

 

log log 0 1 0 1 1 1 1 1 1 1 1 ln log ln10 x a a a a x R x x x dxdy x dydx xy dx x xdx x dx A A A A A 

_∬



 













Tinjau 1 ln a x xdx



Mis : u lnx du 1dx x    dan 1 2 2 dvxdx v x

Gunakan integrasi parsial



u dvuv



v du

2 2 2 2 1 1 1 1 1 1 1 1 1 ln ln ln 0 2 2 2 4 a a a a x x dx x x x dx a a x x       _{ }  _  __{ }      





KK-Astronomi Page 3-9 2 2 2 2 1 1 1 2 ln 1 ln ln 2 4 4 4 a a a a a x x dx a a    



Untuk titik berat hitung dari pernyataan

2 2 2 2 2 2 1 (2 1) ln10 (2 1) (2 1) (4 ln10) ( ln 1) 4 ln10 4( ln 1 n ln ) ln l a a a a a a a a a x A a a a a a a             





2 log 2 log 2 0 1 0 1 1 1 log 1 1 1 1 1 1 ln 2 2 2 ln10 x x a a a a R x x y y dxdy y dydx y dx dx dx A A A A A        _{ }   _{ }    

 







∬

Tinjau integral

 

2 1 ln a I 



x dx Mis : u lnx du 1dx x    dan dvln x dx v xlnxx

 





 

2 2 2 1 1 1 1 2 2 ( ln ) (ln ) [ (ln ) ln ] ( (ln ) ln ) [ ln ] ln ln ln 2 0 2 ln 2 ln 2 2 a a a a udv uv vdu x x x I x dx x x x x dx a a a a x x x x x a a a a a a a a a a a a                      









Jadi

 

2

 

ln

_

2 2 ln 2

_

2

 

ln

_

2 2 ln 2

_

2 1 ln10 ln 2 ln 2 2 2 2 ln 1 ln10 2 ln 1 a a a a a a a a a a y a a a a a A a a a a a a                

Kesimpulan, titik beratnya adalah;

2 2 (2 1) 4( ln n 1 l ) a a a x a a a      dan

 





2 ln 2 ln 2 2 2 ln 1 a a a a a y a a a      

3.5 Menentukan titik berat inti asteroid / komet

Untuk menentukan titik berat inti asteroid / komet. Bayangan dibagi dalam empat persegi panjang kecil dengan luas yang sama. Pengukuran dilakukan dengan densitometer. Masing masing empat persegi panjang diukur densitasnya. Pelat potret bergerak maju mundur, ke kiri dan ke kanan

x

y (xi,yi)

y

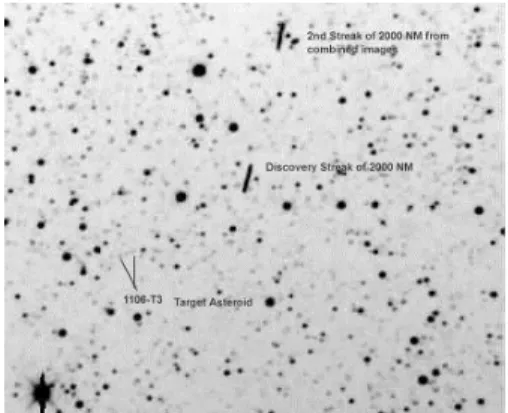
KK-Astronomi Page 3-10 Plat potret Schmidt, memperlihatkan

jejak asteroid/komet. Problem utama adalah menentukan posisi yang tepat memilih inti komet/asteroid. Aplikasi mencari titik berat dapat digunakan untuk menentukan inti komet/asteroid

Gambar Low activity comet P/2006 HR30 bayangan kasar komet dan model koma dipotret 4 Agustus 2006 Palomar 200 inch. Komet ini mirip asteroid tipe D

Titik berat dapat dicari dari formula.

1 1 n i i i n i i x x y x x y         





dan 1 1 n i i i n i i y x y y x y         





dengan _irapat massa pada tiap empat persegi panjang dengan dimensi yang sama, sedangkan n jumlah empat persegi panjang.

3.6 Soal latihan

Tentukan sentroid dari lamina S berikut, jika daerah S dibatasi oleh kurva yang bersangkutan

1. yx x2,  y 2 [x  1/ 2,y 8 / 5]

2. y2  x 3,y2  5 x [x 1,y0]

x

dengan rapat “massa” pada tiap empat persegi panjang dengan dimensi yang sama, sedangkan n jumlah empat persegi panjang.

KK-Astronomi Page 3-11 3. x2y 8 0, x3y 5 0, x 2, x4

18, 50 13 39 x y  _{ }      4. 2 , 0, 0 ysin x y  x  [x  / 2,y / 8] 5. sin , cos , 0 4 y x y x  x  2 2 (log ) ( 2 1) 1 ; 4 2( log 1) a a x y a a a           _ _{  }        6. ylog , x y0, 1 x a 2 2 2 2 log 1 (log ) ; 4( log 1) 2( log 1) a a a a a x y a a a a a a  _   _   _{   }    7. x y 1, x0,y0

[

1 5 x  y ] 8. _x23_y23 _{1, x}_{0, y}_{0 pada kuadran I [} 256 _] 315 x y   

KK-Astronomi Page 3-12 Daftar Isi

Bab 3 ... 1

Terapan Integral Ganda... 1

3.1 Integral Ganda dalam koordinat Kartesis dan Polar ... 1

3.2 Momen Inersia ... 2

3.3 Studi kasus Nebula Cincin ... 3

3.4 Studi Kasus Inti Komet ... 6

3.5 Menentukan titik berat inti asteroid / komet ... 9