) = HASIL DAN PEMBAHASAN METODE PENELITIAN = = 1 (48) d u d. du du. du du. du du

(47) (48) (49) (50) (51) (52) (53) fungsi dikenal dalam matematik sebagai fungsi eliptik Jacobi[8,9,13].

sn u

Mirip dengan fungsi trigonometrik, dapat pula didefinisikan fungsi eliptik Jacobi cn   melalui hubungan:

u

(54) 2

cnu= 1 sn− u =cosϕ 

kemudian tinjau kembali integral eliptik versi Legendre pada persamaan (41), jelas terlihat:

2 2 1 1 sin du dϕ = _{−k ϕ}  

dan berdasarkan hubungan (48) dapat pula didefinisikan fungsi melalui perumusan berikut ini yaitu:

dn u 2 2 dnu d 1 k sn u du ϕ   = = −

dengan demikian, jelas bahwa fungsi fungsi tersebut memenuhi hubungan:

2 2

cn u+sn u=1 

2 2 2

dn u+k sn u=  1

kemudian, untuk mengetahui turunan pertama bagi masing-masing fungsi terhadap variabel

, maka diperoleh hasil sebagai berikut: u

(

sn

)

(

sin

)

d u d du du ϕ = =   cos d cn dnu u du ϕ ϕ =  

(

cn

)

(

cos

)

d u d du du ϕ = = sin d sn dnu u du ϕ ϕ − = −

(

dn

)

₍

₁ 2_sin d u d k du =du − ϕ

)

=   2 2 2 sin cos sn cn 1 sin k d k u u du k ϕ ϕ ϕ ϕ − = − −  

METODE PENELITIAN

1. Waktu dan Tempat Penelitian

Penelitian ini dilaksanakan pada bulan Februari 2009 sampai dengan bulan Desember 2009. Dan tempat penelitian dilakukan di Laboratorium Fisika Teori dan Komputasi Departemen Fisika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor (IPB).

2. Peralatan

Pada penelitian kali ini alat yang digunakan berupa laptop milik pribadi dengan processor Intel (R) Core (TM) 2 Duo CPU

dengan memory 2GB dan menggunakan Windows Vista Home Basic. Lalu pada penelitian ini juga menggunakan bantuan Software Mapple 11 dan Mathematica 7.

3. Metode Penelitian

3.1 Studi Pustaka

Pada penelitian ini studi pustaka dimulai dari pemecahan solusi satu persamaan NLS melalui pendekatan analisis sistem dinamik. Kemudian dengan proses yang sama maka persamaan modus tergandeng yang didapatkan dari perluasan persamaan NLS dapat diselesaikan secara eksak pula. Dan dengan bantuan ketiga fungsi eliptik, maka dapat diketahui perilaku trayektori solusinya dalam bidang fasa.

3.2 Penurunan Solusi Secara Eksak

Proses ini dilakuakan untuk mengetahui perilaku persamaan 55 dan 56 secara analitik, melalui pendekatan sistem dinamik.

3.3 Analisa Solusi Dengan Mapple 11 dan Mathematica 7

Proses ini dilakukan untuk menganalisis hasil visualisasi gambar trayektori solusi yang didapatkan oleh kedua software yang digunakan. Sebenarnya dalam menunjukan bentuk trayektori solusi beserta aliran trayektorinya akan lebih baik menggunakan software Mathematica, namun dalam teknis pengerjaannya lebih mudah dikerjakan pada software Mapple, karena dalam Mapple sintaks yang digunakan lebih sederhana. Berbeda sekali dengan software Mathematica yang menggunakan algoritma pemrograman. Namun demikian hasil gambar yang diperoleh akan sama saja bentuknya, perbedaanya hanya dari segi tampilannya saja.

HASIL DAN PEMBAHASAN

1. Solusi Eksak Soliton Optik Nonlinier Melalui Metode Sistem Dinamik

Adanya propagasi gelombang soliter dalam modulasi nonlinier kisi Bragg optik yang menimbulkan ketidakseragaman distribusi medan listrik melintang sepanjang sumbu x telah dipelajari sebelumnya untuk pilihan yang lebih spesifik pada sistem parameternya[10] dengan mengabaikan efek pembendung yang disebabkan oleh kondisi batas konvensional yang nantinya sangat diperhitungkan dalam proses pemebentukan gelombang. Ketidakseragaman proses distribusi medan transversal muncul dari

  2 * * 2 2 ˆ f f f N b N f b N f b P U −ηU +c U +b U U +b U U

(

2 2

)

(

2

)

0 f 2 b f N b 2 f b 0 b U U U b U U U + + + + = 2 * * 2 2 ˆ b b b N f N b f N b f 2 PU −ηU +c U +b U U +b U U

(

2 2

)

(

2 2

)

0 b 2 f b N f 2 b f 0 b U U U b U U U + + + + = (55) (56) (57) (58)

(

)

2 2 N d F AD K A c B F dx −⎡⎣η− − ⎤⎦

(

2 2

)

(

2 2

)

2 3 0 2 N 3 2N 0 b A A B b B A B b AB F ⎡ ⎤ +_⎣ + + + + _⎦ =

(

)

2 2 N d F BD K B c A F dx −⎡⎣η+ − ⎤⎦

(

2 2

)

(

2 2

)

2 3 0 2 N 3 2N 0 b B A B b A A B b BA F ⎡ ⎤ +_⎣ + + + + _⎦ = (59) (60)

(

K A c B F

)

N

(

K B

)

c A FN AD BD η η ⎡ − − ⎤ ⎡ + − ⎤ ⎣ ⎦ ₌⎣ ⎦ 2 2 2 N A B c K AB ⎡ − ⎤ ⎣ ⎦ = (61) (62)

[

]

[

]

2 ₂ 0 2 0 2 4 2 N N N N A b b A b b b b ± ⎡ ⎤ − + ± _⎣ + − _⎦ = B

istilah difraksi yang telah diperkenalkan sebelumnya dalam model. berikut ini akan ditinjau model persamaan diferensial parsial yang terkopel, berikut persamaannya[11]:

(

)

(

)

(

)

(

)

2 2 2 2 2 3 0 2 2 2 2 2 2 3 0 2 2 3 2 3 N N N N b A A B b B A B b AB F AD b B A B b A A B b BA F BD ⎡ + + + + ⎤ ⎣ ⎦ ⎡ + + + + ⎤ ⎣ ⎦ = (63) (64)

[

]

2 ₂ 0 2N 4 N b b b ⎡ _{+ −} ⎤_{= Γ} ⎣ ⎦ (65)

[

0 2

]

2 N N b b B A b ±_{= ⎨}⎧⎪− + ± Γ⎫⎪ ± ⎬ ⎪ ⎪ ⎩ ⎭ (66)

[

0 2

]

2 N N b b b α±₌⎡_⎢− + ± Γ⎤_⎥ ⎢ ⎥ ⎣ ⎦ (67) persamaan (55) dan (56) merupakan set

persamaan diferensial parsial yang terkopel, pada persamaan tersebut nilai ˆ

f

P dan

merupakan operator persamaan diferensial yang didefinisikan oleh sebuah persamaan   dan sebuah persamaan , dengan parameter x dan z yang mengimplikasikan keadaan transversal dan longitudinal pada sistem koordinat masing-masing. Sementara itu parameter   yang dirumuskan sebagai

ˆ b P 2 ˆ _{/ /} f P = ∂ ∂ + ∂ ∂i z D x 2 ˆ _/ b P = − ∂ ∂ + ∂ ∂i z D D / 2 2 2 / x B

D=k Nk   menunjukan kekuatan dari efek

difraksi yang timbul. Sedangkan parameter η  merupakan frekuensi spasial yang dirumuskan sebagai η=k Nk/ _B 1

N

c

− . Kemudian parameter   adalah parameter yang nilainya sebanding dengan besarnya komponen Fourier N−th  berdasarkan fungsi suseptibilitas linier. Sedangkan parameter nonlinier

mempunyai nilai sebanding dengan nilai   yang merupakan komponen Fourier gabungan dari fungsi suseptibilitas nonlinier.

0, N,dan b2N

b b

0 th,− N−th, dan 2N−th

Untuk menyelesaikan persamaan (55) dan persamaan (56), maka akan diperkenalkan sebuah fungsi Ansatz yakni:

( )

iK zf f U =AF x e iK z −  

( )

b b U =BF x e  

Dimana F merupakan fungsi real, sedangkan untuk A B, , dan K_{f b( )} merupakan parameter

yang konstan. Untuk menemukan dua buah set persamaan diferensial biasa orde dua, misal dengan menggunakan hubungan

b f

K =K

ternyata didapatkan solusi yang trivial artinya

nilai akibatnya jika

menggunakan hubungan tersebut maka penyelesaian persamaan diferensial yang didapatkan akan bernilai nol. Untuk

menghindari hal tersebut gunakan hubungan berikutnya yaitu , ternyata persamaan (55) dan (56) memilki solusi yang non-trivial[12], dengan memasukan hubungan tersebut ke persamaan fungsi Ansatz (57) dan (58) lalu masukan ke persamaan (55) dan (56)

an hasil: 2 n b_N=0 0, 0, da N N c = b = b f K = −K = K maka didapatk F 3 F    

Dari kedua persamaan tersebut, maka akan direduksi sehingga hanya menghasilkan sebuah persamaan diferensial biasa orde dua. Caranya dengan menyamakan kedua persamaan tersebut berdasarkan order fungsinya masing-masing. Ketika fungsi berorder disamakan didapatkan hubungan

Sedangkan ketika fungsi berorder didapatkan sebuah hubungan:

pada persamaan (64) untuk bagian yang berada dalam fungsi akar bisa didefinisikan sebagai berikut:

sehingga persamaan (64) bisa dituliskan menjadi sebagai berikut:

kemudian untuk membuat persamaan (66) terlihat lebih sederhana maka akan dimisalkan sebuah fungsi α yaitu:

1 2 F =F 3 2 1 1 2 1 F =βF −β F (76) (77) B±=α±A± (68)

(

2

)

(

3

)

2 2 3 0 1 2 N 3 2N b b b A F D α α± α α ⎡ + + + + ⎤ ⎣ ⎦ (69)

(

2

)

(

3

)

0 2 2 1 2 _N 3 _N b b b D α α α α β ± ⎡ 2 2 A + + + + ⎣ = ⎤⎦ (70) 2 1 2 N c K α α± ⎡ − ⎤ ⎣ ⎦ = (71)

(

_{2 1} 2

)

2 N c F D αη α α± ⎡ _{− +⎡⎣ ⎤⎦} ⎤ ⎣ ⎦ (72)

(

2

)

1 2 1 2 N c D αη α β α± ⎡ _{− +⎡⎣ ⎤⎦} ⎤ ⎣ = ⎦ (73) 2 3 1 2 2 0 d F F F dx −β +β = (74) 1 0 F = 1 1 F 2 β β = ± (78) (79) 1 0 F=βF→λ =β1 (80) 1 1,2 1 2 F 2 F = − β →λ = − β (81) sehingga persamaan (66) akan terlihat menjadi

sebuah persamaan yang cukup sederhana yaitu: 2 3 2 2 1 1 1 0 d F F F dx β β β − + + = (75)

setelah mendapatkan persamaan (68), maka substitusikan persamaan (68) ke persamaan (59) untuk order fungsi 3

F saja. Sehingga

akan didapatkan persamaan sebagai berikut:

berdasarkan persamaan (69), akan dimisalkan sebuah parameter β₂ yang dirumuskan:

kemudian substitusikan persamaan (68) ke persamaan (62) maka akan didapatkan:

setelah itu substitusikan persamaan (71) ke persamaan (59) untuk order fungsi saja. Sehingga akan didapatkan persamaan: F

dan berdasarkan persamaan (72), akan dimisalkan sebuah parameter β₁  yang dirumuskan sebagai berikut:

dengan demikian PDB orde dua yang didapatkan dan nantinya akan dianalisa secara sistem dinamik yaitu:

dengan mengatur kembali persamaan (74) akan didapatkan persamaan:

dimana nilai 1/ β₁ dapat dipandang sebagai “effective diffraction strength”, sedangkan nilai β β dapat dipandang sebagai ₂/ ₁ “effective cubic nonlinier coeffisient” atau disebut juga suseptibilitas orde ketiga _{χ .} ( )3

Kemudian dengan memisalkan F=F₁  dan

2

F F

•

=  akan didapatkan sebuah aan diferensial biasa orde satu yaitu:

bifurkasi apa yang terjadi, coba tinjau persamaan Be rkan persamaan (77) didapatkan

tik kritis yaitu:

Dari kedua titik itis tersebut, engan mudah dibuktikan bahwa untuk kas

1 0, 2 0 dan 1 0, 2 0

set persam

 

Setelah itu untuk mengetahui proses

(77). set rdasa ti   dapat kr d us β < β > β > β < hanya ter atu dapat s buah titik kritis yaitu F₁=0 dengan persamaan linier yang terkait diberikan oleh:

dengan λ₀=β₁, sedangkan k kasus 1 0, 2 0 dan 1 0, 2 0

untu

β < β < β > β > terdapat tiga buah titik kritis yaitu F1=0 dan ₁ 1

2 F β β = ± an oleh: untuk  den persamaan liniernya diberik

gan 1 1 2 F β β

= ± denganλ1,2= −2β1dan untuk

1 0 dengan 0 1 F = λ =β memilki persam ma denga aan (80). dasarkan aan (80 kondisi 0 d aan yang sa n persam

Ber persam ), untuk

1 0, 2 an 1 0, 2 0

β < β > β > β

kondisi < titik kritis yang terkait merupakan titik Sadel yang bersifat stabil. Sedangkan untuk

1 0, 2 0 dan 1 0, 2 0

β < β < β > β >   titik Sadel

tersebut b di lain

pihak untuk titik kritis

ersifat tidak stabil, tetapi 1 1 F 2 β β = ± berdasarkan persamaan (81) keduanya bersifat stabil. Berikut ilustrasi diagram bifurkasinya untuk satu dimensi:

ambar 20 Diagram Bifurkasi satu dimensi untuk Persamaan (77)

edangkan untuk diagram bifurkasi dua di ensi dibagi tiga kondisi yakni untuk nilai

1 G s m 2 0, 0

β > β < lalu β β₁, ₂=0  dan yang terakhir F

  _{1 1} 0 1 f f F F ∂ ∂ ⎛ ⎞ ⎜ ⎟ _{⎛ ⎞} ⎝ ⎠ 1 2 2 1 2 1 2 2 3 0 A A F f f F F β β ⎜ ⎟ = _{→ = ⎜ ⎟} ⎜∂ ∂ ⎟ _⎝ − _⎠ ⎜ ⎟ 1 2 (82) 1 0, 2 0 F = F = 1 1 2 2 , 0 F F β β = ± = (83) (84) 1 1 λ = ± β 2 2 1 λ = ± − β (85) (86) 1 1 λ = ± −β 2 2 1 λ = ± β (87) (88) -4 -2 0 2 4 -4 -2 0 2 4 F1HtL F2 H t L

Plot Bidang Fase

F1 F2 F1 F2 F1 F2

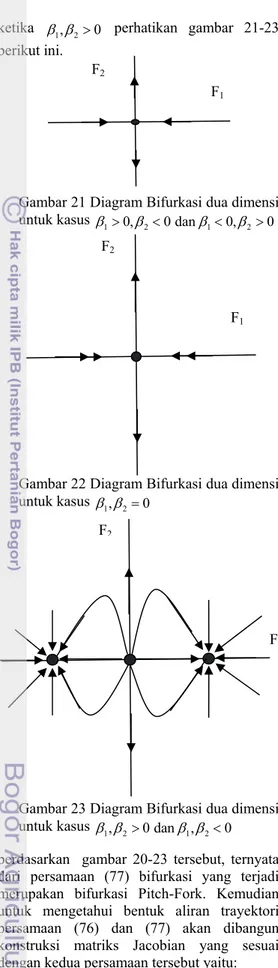
ketika β β₁, ₂>0 perhatikan gambar 21-23 berikut ini.

ambar 21 Diagram Bifurkasi dua dimensi ntuk kasus ₁ 0, ₂ 0 dan ₁ 0, ₂ 0 G

u β > β < β < β >

Gambar 22 Diagram Bifurkasi dua dimensi untuk kasus β β₁, ₂=0 

 

Gambar 23 Diagram Bifurkasi dua dimensi

untuk kasus 0                 1, 2 0 dan ,1 2 β β > β β < er dari

me rkasi Pitch-Fork. Kemudian

edangkan set titik kritis yang didapat dari ersamaan (76) dan (77) yaitu:

b dasarkan gambar 20-23 tersebut, ternyata persamaan (77) bifurkasi yang terjadi rupakan bifu

untuk mengetahui bentuk aliran trayektori persamaan (76) dan (77) akan dibangun konstruksi matriks Jacobian yang sesuai dengan kedua persamaan tersebut yaitu:

s p  

untuk kasus β₁>0 harga eigen yang terkait ngan masing- titik kritis diber eh kedua nilai berikut:

itis (83) merupakan ebuah titik Sade titik kritis (

erupakan titik

Kemudian unt 0

g- titik kritis diber eh kedua nilai berikut:

itis (83) merupakan ebuah titik Sade titik kritis (

erupakan titik

Kemudian unt 0

de

ll masingmasing ikan ikan o

  o  

dari kedua nilai tersebut dapat dengan mudah disimpulkan bahwa titik k

dari kedua nilai tersebut dapat dengan mudah disimpulkan bahwa titik k

ss l, sedangkan 84) 84) ter. l, sedangkan ter. m m Cen uk kasus Cen uk kasus β₁₁< harga ei merupakan

titi ter, sed kritis

merupakan titik

Dengan demi peroleh ba

gen yang terkait dengan masing-masing titik kritis diberikan oleh kedua nilai berikut:

 

Dari kedua nilai tersebut dapat dengan mudah disimpulkan bahwa titik kritis (83)

k Cen angkan titik (84)

Sadel.

hwa kian, dapat di

kedua persamaan (76) dan(77) memilki hubungan simultan yang sama artinya jika

1 0

β < maka β₂<0begitu pula sebaliknya, sebab jika hubungannya kontradiktif maka hanya menimbulkan satu buah titik kritis saja. ilustrasi gambar trayektori terkait dengan menggunakan “Mathematica dan Mapple11

kan pada ar 24-27 diberi gamb

ambar 24 Plot kasus ₁ 0, ₂ 0

G β < β <  

engan menggunakan Mathematica d

-4 -2 0 2 4 -4 -2 0 2 4 F1HtL F2 H t L

Plot Bidang Fase

(

)

(

)

(

)

(

)

2 2 2 2 2 2 3 1 2 sn , 2 sn , 0 sn , sn , x k k x k k x k x k ζ ζ ζ ζ ζ β ζ β ζ ⎧ ⎡_{− + −} ⎤⎫ ⎪ ⎣ _{⎦ =}⎪ ⎨ ⎬ ⎪− + ⎪ ⎩ ⎭ (89)

(

)

(

)

(

)

2 2 2 2 2 2 2 2 sn , sn , 0 sn , k x k x k k x k ζ ζ ζ ζ ζ β β ζ ⎧ ⎡_{− + −}⎤⎫ ⎪ _{⎢ ⎥}⎪ 1 2 = ⎨ ⎬ ⎢ _{− +} ⎥_⎪ ⎣ ⎦ ⎪⎩ ⎭ (90)

(

)

2 2 2 2 2 2 2 1 2ζ k β sn ζx k, ζ ζ k β 0 ⎡ + ⎤ − − − = ⎣ ⎦ (91) 2 2 2 k β ζ − = ± 2 1 2 4 2 β β ζ = ± − (92) (93)   2 2 k β 2 1 β β − = − (94)

ambar 25 Trayektori Kasus

G β₁<0,β₂<0  dengan menggunakan Mapple

ambar 26 Plot untuk kasus

G β₁>0,β₂>0

Dengan menggunakan Mathematica

ambar 27 Trayektori Kasus

G β₁>0,β₂>0  dengan menggunakan Mapple

Unt jenis tipe

F  2.

te

nalisa Sistem Dinamik Fungsi Eliptik acobi Pada Soliton Optik Nonlinear

ada pembahasan sebelumnya fungsi F

rs sembarang.

A J

P

ebut masih berupa fungsi uk soliton spasial punya dua

soliton yakni “Bright Soliton” dan “Dark Soliton”. Pada kasus “Bright Soliton” fungsi

merupakan fungsi sech

( )

ζ . Sedangka x

untuk “Dark Soliton” fungsi Fmerupakan

fungsi

n

( )

tanh ζ . Namun untuk penelitian x

kali ini akan digunakan fungsi Fyang

erupakan fungsi d

m ari Jacobian Eliptik

(

)

(

)

(

)

sn ζx k, , cn ζx k, ,dandn ζx k, . Dimana parame   nunjukan modulus yang terkontr kan parameter zeta ( )

ter k me

ol, sedang ζ

dapat dipandang sebagai frekuensi sudut. Untuk mendapatkan nilai kedua parameter tersebut, Pertama-tama substitusikan fungsi

(

)

sn ζx k, k persamaan (74) maka diperoleh: e

den an mengatur kembali persamaan (89) ma diperoleh:

aan (90), ternyata ersamaan tersebut bisa dikelompokan

enurut fungsi g ka erdasarkan persam b p

(

)

2 sn , m ζx k sehingga ersamaan (90) menjadi: erlihat, ba (91) secara aljabar nilai dari koefisien eta

p

dari persamaan (91) t hwa dengan meyelesaikan persamaan

iasa maka akan diperoleh b

( )

z ζ  dan koefisien k. Berikut hasilnya:

emudian substitusikan persamaan (93) ke ersamaan (92), dalam hal ini gunakan ertanda positif, sehingga diperoleh:  

k

p nilai

 

(

)

2 2

(

)

2 2

(

)

1 , 2 sn , cn 0 x k k x k x ζ ζ ζ ζ β ζ β ⎧ ⎡ ₋ ⎤₋ ⎫ ⎣ ⎦ ⎪ ⎪

(

)

(

)

(

2

)

cn ζx k, 1 sn ζx k, 2 cn , k = ⎨ ⎬ ⎪ ⎩+ − ⎡⎣− + ⎤⎦ ⎪⎭ (95)

(

)

(

)

(

)

2 2 2 2 2 1 2 2 2 sn , cn , 0 sn , k x k x k x k ζ ζ ζ ζ β β β ζ ⎧ ⎡ ₋ ⎤⎫ ⎪ _{⎢ ⎥ =}⎪ ⎨ ⎬ ⎢_{− + −} ⎥ ⎪ _{⎣ ⎦}⎪ ⎩ ⎭ (96)

(

)

2 2 2 2 2 1 2 2ζ k β sn ζx k, ζ β β 0 ⎡ − ⎤ − − + = ⎣ ⎦ (97) 2 2 k 2 β ζ = ± 2 1 ζ = ± β −β (98) (99) 2 2 1 2 2 k β β −β = (100)

(

)

(

)

(

)

)

2 2 dn , 2 sn , dn , 1 x k k x k k x k k x k ζ ζ ζ ζ ζ ⎫ − ⎣ ⎦ ⎛− ⎞ ⎜ _⎟⎪ − + _{⎡ ⎤ ⎟} − + ⎪ β1dn

(

ζx k,

)

β2⎜ sn

(

ζ , _{⎦ ⎠⎭}⎪ ⎣ ⎝ ⎩ 2 2 2 2 2 ⎡ ⎤ 0 = ⎬ ⎧ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ (101

(

)

(

)

(

)

2 2 2 2 2 2 2 1 2 2 2 sn , dn , 0 sn , k x k k x k k x k ζ ζ ζ ζ β β β ζ ⎧ ⎡ ₋ ⎤⎫ ⎪ _{⎢ ⎥}⎪ ) = ⎨ ⎬ ⎢_{− + −} ⎥ ⎪ _{⎣ ⎦}⎪ ⎩ ⎭ (102)

(

)

2 2 2 2 2 2 2 1 2ζ k β k sn ζx k, ζ k β β2 0 ⎡ − ⎤ − − + = ⎣ ⎦ (103) 2 1 k β −β ζ = ± 2 2 2 β ζ = ± (104) (105) 2 1 2 k 2 β −β = β (106) 2 1 2 2 4 2 1 1 1 4 2 2 H = F −β F +β F ₍₁₀₇₎ 1 2 H F F ∂ = ∂ 2 1 H F F ∂ = − ∂ (108) Langkah berikutnya, substitusikan fungsi

(

)

cn ζx k, ke persamaan (74) maka akan idapatkan hasil:

(109) d

den an mengatur kembali persamaan (95), maka akan diperoleh:

g

dari persamaan (96) dapat diperoleh, bahwa persamaan (96) ternyata bisa dikelompokan

erdasarkan fungsi b

(

)

2 sn ζx k,   sehingga ersamaanya menjadi: ikan pers m ka akan diperoleh ni p

dengan demikian, dari persamaan (97) terlihat, bahwa dengan meyelesa a aan (97) secara aljabar biasa ma lai dari koefisien zeta

_{( )}

ζ  dan koefisien

erikut hasilnya:

alam hal ini gunakan nilai ehingga diperoleh:

Setelah fu

k.

B  

kemudian substitusikan persamaan (99) ke persamaan (98), d

ertanda positif, s b

ngsi sn

(

ζx k,

)

dan cn

(

ζx k,

)

,

berikut akan disubstitusikan fungsi dn

(

ζx k,

)

ke persamaan (74), sehingga diperoleh:

(101), ma akan diperoleh:

sebelumnya, ternyata 02) bisa pula dikelompokan n fungsi

(

dengan mengatur kembali persamaan ka

sama halnya dengan cara yang diterapkan pada kedua fungsi

persamaan (1 b

)

2 sn , erdasarka ζx k sehingga iperoleh hasil: bar nilai dari koefisien zeta d

dengan demikian, dari persamaan (103) terlihat, bahwa dengan meyelesaikan persamaan (103) secara alja biasa maka

akan diperoleh

_{( )}

ζ  

an koefisien k. Berikut hasilnya:

ke kan nilai ertanda positif, sehingga diperoleh:

engan didapatkannya keseluruhan nila d

 

kemudian substitusikan persamaan (105) persamaan (104), dalam hal ini guna b

d i dari

parameter k dan zeta ( )ζ untuk keseluruhan

fungsi sn

₍

ζx k, , cn

_{) (}

ζx k, ,

₎

dandn

₍

ζx k,

₎

, maka kan bisa dianalisa secara satu per satu nil

a ai

edua parameter tersebut yang cocok ngsinya masing-masing.

k pada

fu

Untuk fungsi sn

(

ζx k,

)

nilai parameter keduanya arus meme hi syarat h nu β β₁, ₂<0 agar nilai dari parameter k dan zeta ( )ζ   bernilai real, kemudian untuk fungsi cn

(

ζx k,

)

nilai dari parameter k dan zeta ( )ζ  harus memenuhi syarat β β1, 2>0→β1<β2 atau

1 0, 2 0

β < β > . Sedangkan untuk fungsi dn

(

ζx k,

)

0 syarat yang harus dipenuhi yaitu β₁<0,β₂   atau ₁, ₂ 0

> β β > . Dengan memasukan

tersebut ke parameter untuk fung asing masing, maka bisa ditinjau bentuk yektori solusi dari masing-masing fungsi.

ini tinjau kembali persama ) dan (77), Hamiltonian yang co

persamaan tersebut yaitu:

dimana persamaan (75) dan (76) memenuhi per syarat si m tra Berikut an (76 cok dengan samaan kanonik:

mengingat pada titik (0,0) merupakan titik Sadel untuk syarat β β₁, ₂>0, maka nilai Hamiltonian untuk trayektori yang terkait

gan titik kritis tersebut

den adalah H=0.

Dengan demikian, sambil memperhatikan enyataan terdapat dua buah titik Center dan

d ksud d

Gambar 28 Trayektori untuk k

sebuah titik Sadel di titik asal, maka bentuk trayektori yang ima iberikan pada gambar 28.

0

H=  

 

Sedangkan untuk titik kritis (0,0) yang erupakan titik Center untuk syarat m

1, 2 0

β β < engan titi

, maka nilai hamiltonian yang terkait k kritis tersebut yaitu

d 2_{/ 4}

H= −β1 β2.

De empe atikan

kenyataan terdapat dua titik Sadel dan sebuah titi

gambar 2

ambar 29 Trayektori untuk ngan demikian, sambil m rh k Center di titik asal, maka bentuk trayektori yang dimaksud diberikan pada

9.

G 2

1 / 4 2

H= −β β

Berikut ini tinjau kembali persamaan (107), dengan mensubstitusikan fungsi eliptik Jacobi sn

(

ζx k, , cn

) (

ζx k, ,

)

dandn

(

ζx k,

)

secara bergantian ke parameter F₁, kemudian turunan

pertam ngsi Jacobian

elip eter F, lal

a dari masing-masing fu

tik secara bergantian ke param ₂ u pilih nilai x=0. Maka akan didapatkan betuk trayektori solusi yang terkait ketiga fungsi eliptik t

Untuk fungsi eliptikal Jacobi ersebut. sn

₍

ζx k,

₎

  syarat parameter yang harus dipenuhi yaitu

1, 2 0

β β < . Sehingga bentuk trayektor yang dapat diper diberikan pada gambar 30.

i oleh

ambar 30 Trayektori fungsi

(

)

G sn ζx k,

engan kondisi k 1 dan h 0

d < >

dari gambar 30, dapat diketahui ternyata fungsi sn

(

ζx k,

)

berada di dalam trayektori yang terkait untuk Hamiltonian 2

1 / 4 2

H= −β β

yan 9. Pada

gam ketahui pula ondisi yang ip ar ketika nilai h>0, nilai h

1dan 2

F F d

bi

(

g ditunjukan pada gambar 2

bar 30 dapat di k

nuhi dari gamb d e

disini menyatakan Fungsi hamiltonian ketika fungsi igantikan oleh fungsi eliptik.

Kemudian untuk fungsi Jaco cn ζx k,

)

syarat parameter yang harus dipenuhi yaitu

1, 2 0 1 2

β β > →β <β . Dimana dalam koefisien 2

β ada parameter yang bersifat bebas yaitu parameter A yang secara fisis melambangkan

amplitudo pada persamaan. Dengan demikian ika parameter A dipilih secara bebas dan

berpengaruh langsung terhadap parameter ₂ ket

β   cul dua buah kondisi yaitu 0 dan h 0

mengakibatkan mun

h> < . Untuk kondisi h>0 ternyata

 

trayektori untuk H=0, sedangkan kondisi 0

h<  gambar trayektori solusinya berada di

dalam. Artinya dengan memvariasikan nilai parameter β₂ yang terkait dengan parameter bebas A maka akan didapatkan dua kondisi

berbe Namun kondisi tersebut tidak bisa ditebak secara bebas artinya ketika nilai

0

h>  bukan berarti berada di luar trayektori

untuk gambar 28, sebab pada fungsi

(

yang

solusi

da.

Untuk fungsi Jacobi dn

(

ζx k,

)

sama halnya engan fungsi jacobi

(

)

)

sn ζx k, kondisi yang diperoleh berada di 0

h> dan ternyata berada di dalam trayektori

solusi ntuk 2

1 / 4 2

H

u = −β β . Berikut ini ilustrasi yang didapat untuk kedua kondisi tersebut pada fungsi cn

(

ζx k,

)

.

a

mb

G ar 31 Trayektori fungsi cn

(

ζx k,

)

  dengan kondisi h<0 dan k>1

d cn ζx k, , namun syarat ang harus dipenuhi , 0 ₂

y β β_{1 2}> → <β β₁ . Untuk

me mbar 33

dan

Gambar 33 Trayektori fungsi dn

(

,

)

mahaminya, perhatikan ilustrasi ga

34 berikut.

x k

ζ  

dengan kondisi h<0 dan k<1

Gambar 34 Trayektori fungsi dn

(

ζx k,

)

  dengan kondisi h>0 dan k>1

erdasarkan gambar 31-34, ternyata memiliki keu ikan tersendiri yaitu untuk gambar 31-32 unt fungsi

b n

uk cn

(

ζx k,

)

antara nilai h dan k 

me n untuk

gam dan  memiliki

ubungan kesebandingan (lurus). miliki hibungan terbalik, sedangka

bar 33-34 antara nilai h k

Gambar 32 Trayektori fungsi cn

(

ζx k,

)

  dengan kondisi h>0 dan k<1 h

Untuk lebih memahami bentuk dari ketiga fungsi eliptik, maka berikut ini akan diilustrasikan fungsi eliptik

masing-masing terhadap sumbu x pada koordinat cartesian dengan memenuhi kondisi syaratnya masing-masing.

bentuk secara

Gambar 35 Plot Fungsi sn

(

ζx k,

)

isi 1 dan

 terhadap sumbu x dengan kond

Gambar 36 Plot Fungsi

0 k< h>

(

)

cnζx k,   0 h> dan terhadap sumbu x dengan kondisi k<1

Gambar 37 Plot Fungsi cn

(

ζx k,

)

  0

h< dan

terhadap sumbu x dengan kondisi

 

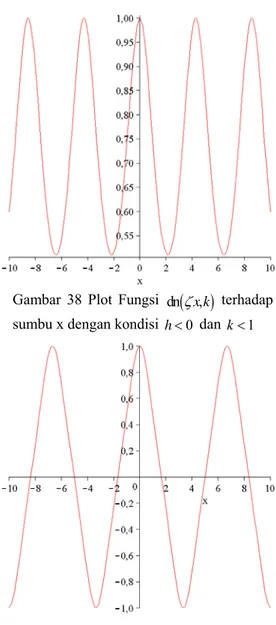
Gambar 38 Plot Fu gsi dn

(

,

)

1

k>  

n ζx k   terhadap

sumbu x dengan ko isi h<0 dan k<1

ambar 39 Plot Fungsi dn

(

,

)

nd

G ζx k   terhadap

mbu x dengan kondisi h>0 dan k>1

dasarkan gambar 3 -39 dapat dinyatakan pula bahwa untuk gam 36 dan 39, ternyata plot yang dihasilkan berpotongan dengan

sum ambar plo ak ton n terha dem su ber 5 bar

bu x, sedangkan untuk g 37 dan 38 t yang dihasilkan tid berpo ga

dap sumbu x. Dengan ikian untuk mendapatkan plot yang berpotongan dengan sumbu x maka kondisi yang harus dipenuhi yaitu ketikah>0. Kemudian berdasarkan gambar 35 jika dilihat secara mendalam ternyata serupa dengan bentuk grafik fungsi sinus pada fungsi trigonometri yang terkait dengan fungsi ganjil. Sedangkan untuk gambar 36 dan 39 ternyata serupa dengan grafik fungsi cosinus pada fungsi trigonometri yang terkait dengan fungsi genap.

Untuk lebih memahami bentuk trayektori solusi ketiga fungsi eliptik yang telah ditunjukan pada gambar sebelumnya, maka

 

berikut ini akan diilustrasikan pada gambar 40 bentuk trayektori solusi gabungan ketiga fungsi eliptik. Gambar tersebut didapatkan dengan cara memplotkan ketiga fungsi eliptik yang direpresentasikan pada sumbu x terhadap fungsi turunan pertama dari ketiga fungsi eliptik masing-masing pada sumbu y. Lalu untuk membedakannya digunakan warna yang berbeda-beda, yaitu fungsi sn

(

ζx k,

)

berwarna biru, fungsi cn

(

ζx k,

)

berwarna hitam, dan fungsi dn

(

ζx k,

)

berwarna merah.

Gambar 40 Gabungan Trayektori untuk fungsi sn

₍

ζx k, , cn

_{) (}

ζx k, , dan dn

₎

₍

ζx,k

₎

berdasarkan ilustrasi gambar 40, dapat d etahui bahwa untuk trayektori fungsi ik

(

)

sn ζx k,   tr

(

(biru)  cocok dengan bentuk di titik asal. Sedangkan untuk fungsi ayektori dua titik sadel dan satu titik Center

)

cn ζx k, dan dn

(

ζx k,

)

(hitam dan merah)

asal. De

Kemudian berdasar

terkait dengan bentuk trayektori dua titik Center dan satu titik Sadel yang berada di titik

ngan demikian bentuk trayektori masing-masing fungsi cocok dengan bentuk trayektori gabungan yang diilustrasikan pada gambar 40 di atas.

kan gambar 40, fungsi

(

)

cn ζx k, dan dn

(

ζx k,

)

dapat diklasifikasikan

secara dua jenis, yaitu untuk jenis pertama terkait dengan kondisik<1yang diilustrasikan

pada gambar 41. Sedangkan untuk jenis kedua terkait dengan kondisi k>1 yang ditunjukan pada gambar 42.

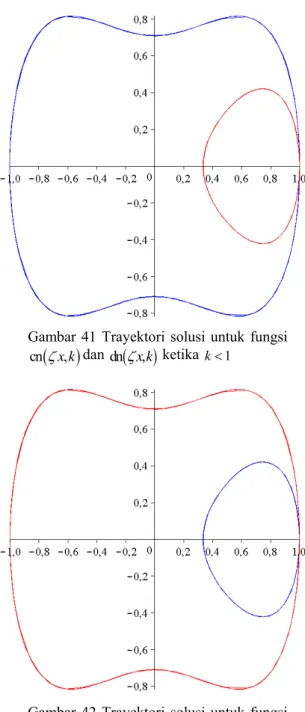
ambar 41 Trayektori solusi untuk fungsi G

(

)

dn

(

,

)

cnζx k, dan ζx k ketika k<1

Gambar 42 Trayektori solusi untuk fungsi

(

)

dn

(

,

)

cnζx k, dan ζx k ketika k>1

Berdasarkan gambar 41 untuk kondisi

1

k<  trayektori solusi fungsi cn

(

ζx,k

)

 berada

diluar trayektori gambar 28 yang ditunjukan oleh wa

fun

rna biru, sedangkan trayektori solusi gsi dn

(

ζx k,

)

  berada di dalam trayektori

ang dit n oleh wa a m gam

Ke bar 28 y unjuka rn erah. keba

mudian untuk gambar 42 berlaku likannya yakni fungsi cn

(

ζx k,

)

  yang ditunjukan warna biru berada di dalam trayektori solusi gambar 28, sedangkan untuk fungsi dn

(

ζx k,

)

  yang ditunjukan oleh warna merah berada di luar trayektori solusi gambar 28. Dengan demikian berdasarkan kedua

kondisi tersebut antara fungsi cn

(

ζx k,

)

dan

(

)

dnζx k, memiliki hubungan alikan, yang artinya untuk kondisi k berbeda maka

trayektori sinya akan saling bertukar tempat. nantinya akan ada satu kondisi yang membuat kedua bentuk trayektori solusi memiliki bentuk yang sama. Kondisi yang dimaksud yakni ketika k=1.

KESIMPULAN DAN SARAN

1. Kesimpulan

Pada penelitian ini dapat disimpulkan beberapa hal penting yakni, yang pertama bifurkasi yang terjadi p

m rupakan proses bifurka itch-F berkeb rsamaan (74 ork, hal i 1 2 solu amun e ) ni tik N di kriti pad si P a e

tandai dengan kemunculan dua buah ti s bersifat stabil ketika kondisi β >0,β >0

dua ang

Kemudian yang ke

didapat memilki syarat simultan yang artinya bentuk trayektori y nilai β β₁, ₂>0 dan ,β β_{1 2}<0, sebab jika kedua parameter tersebut berbeda tanda maka hanya memilki satu buah titik kritis saja.

Kemudian untuk trayektori solusi fungsi

(

)

sn ζx k, kondisi yang harus dipenuhi yaitu

1, 2 0

β β < kemudian untuk fungsi cn

(

ζx k,

)

kondisi yang harus dipenuhi adalah

1, 2 0 1 2

β β > →β <β . dan untuk fungsi dn

(

ζx k,

)

  kondisinya sama dengan fungsi cn

(

ζx k,

)

 yaitu

1, 2 0 1 2

β β > → <β β. Kemudian berdasarkan 40 dapat dilihat bahwa trayektori

(

gambar

fungsi sn ζx k,

)

terkait dengan titik

yang berada di titik asal, sedangkan untuk Center fungsi cn

(

ζx k,

)

dan dn

(

ζx k,

)

terkait dengan

titik Sadel yang berada di titik as

Berdasarkan gambar trayektori solusi gsi eliptik ada beberapa hal yang perlu diingat yaitu yang pertama ketiga fungsi m kondisi h yang berbeda-beda.

Dalam hal ini tidak selalu bisa dipastikan untuk < ber da di da rayektori solusi Hamiltonian, begitu pula sebaliknya. Faktor yang menyebabkan nilai h<0 atau h>

al. ketiga bua h h fun emiliki a 0 lam t 0berasal dari pemilihan parameterβ yang di dalamnya ₂ terkait dengan suatu parameter bebas yakni parameter A  yang secara fisis dapat

dipandang sebagai amplitudo persamaan. Dan nilai A yang dipilih harus selalu lebih besar

dari nol, andaikan β bernilai negatif hal itu ₂ terjadi bukan karena pemilihan nilai A,

melainkan faktor paramet lain di dalam er β₂ 

fungsi

yang bernilai negatif. Kemudian yang kedua

(

)

cn ζx k, dan dn

(

ζx k,

)

  terkait dengan

kondisi k yang berbeda yakni untuk k<1 

ditunjukan pada gambar 41, sedangkan untuk kondisi k>1 ditunjukan pada gambar 42. 2. Saran

Penelitian ini perlu dikembangkan leb lanjut, terutama secara kajian teoritik. Ada beberapa hal y ng mung dilakukan yakni menggan fungsi Eliptik Jacobi den fungsi-fungsi khusus lainnya seperti fungsi Beta, Gamma, dan Bassel. Dan untuk lebih menarik lagi dalam proses penelusura

ih

a kin

ti gan

n cara eksak, bisa digunakan per maan se

persamaan sa untuk solion Temporal, sehingga dalam hal ini dapat dilihat pengaruh waktu dalam proses penjalaran gelombang soliton.