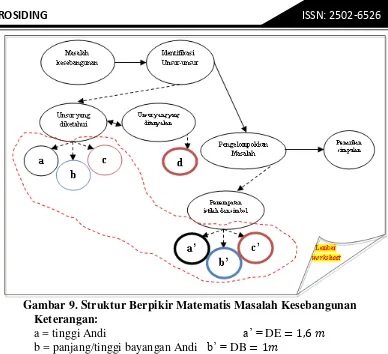
PM 34 Sriyanti Mustafa dan Vernita Sari hal 546 554
Teks penuh
Gambar



Dokumen terkait
Pada penelitian ini didapatkan sebagian besar responden mendapatkan dukungan keluarga yang tinggi, hal tersebut dapat terbentuk karena adanya kerjasama keluarga dan tenaga
Gambaran Ken semasa Satrio melakukan kampanye menunjukkan bahwa Satrio berusaha memenuhi kebutuhannya akan aktualisasi diri, dalam hal ini menjadi seorang
(8A) Walau apa pun apa-apa jua dalam Perlembagaan ini, jika di dalam mana- mana Universiti, Kolej dan institusi pendidikan lain yang memberikan pendidikan selepas Malaysian
Akuisisi citra adalah tahap untuk mendapatkan citra digital. Citra yang didapat terbagi atas citra latih dan citra uji. Proses pengambilan citra telur ayam negeri adalah
Norma moral adalah peraturan/kaidah hidup yang bersumber dari hati nurani dan merupakan perwujudan nilai – nilai moral yang mengikat manusia.. Perilaku yang baik adalah
Berdasarkan hasil penelitian dan interpretasi data setelah diadakan pengujian hipotesis dengan judul yang berbunyi “Pengaruh Pendapatan Dan Pengelolaan Dana Keluarga
Berdasarkan hasil penelitian yang dilakukan, menunjukkan adanya peningkatan aktivitas enzim katalase pada kelenjar submandibularis Rattus norvegicus strain wistar akibat
Satuan Polisi Pamong Praja (Satpol PP) merupakan salah satu instansi yang membantu Camat dalam melaksanakan penertiban hewan ternak ini. Tugas Satpol PP melakukan