BAB 2 LANDASAN TEORI

BAB 2

LANDASAN TEORI

2.1 Analisis Numerik

Analisis numerik merupakan bagian dari bahan pelajaran mutakhir mengenai pengolahan informasi (information processing). Data yang diberikan adalah informasi masukan (input information), dan hasil yang diperlukan adalah informasi keluaran (output information), sedangkan metode perhitungan tersebut dikenal sebagai algoritma (algorithm). Unsur-unsur pokok ini yang terkandung di dalam sebuah diagram alir, yakni:

Gambar 2.1. Diagram alir pengolahan informasi.

2.1.1 Metode Numerik

Metode numerik adalah salah satu alternatif pencarian jawaban dalam permasalahan matematika yang tidak dapat diselesaikan secara analisis. Tujuan dari metode ini adalah mencari metode yang terbaik untuk memperoleh jawaban yang berguna dari persoalan matematika dan untuk menarik informasi yang berguna dari berbagai jawaban yang dapat diperoleh.

Input Information

Algorithm Output

Menurut Djojodihardjo (2000, p2) dalam mengerjakan metode numerik terdapat beberapa cara pendekatan, yaitu:

a. Pendekatan atau penyederhanaan perumusan persoalan sehingga dapat dipecahkan secara eksak.

b. Mengusahakan diperolehnya jawab pendekatan dari persoalan yang perumusannya eksak.

c. Gabungan dari kedua cara pemecahan diatas.

Pada umumnya metode numerik tidak mengutamakan diperolehnya jawaban yang tepat, tetapi mengusahakan perumusan metode yang menghasilkan jawab pendekatan yang memiliki selisih sebesar suatu nilai yang ditentukan berdasarkan kesepakatan dari jawab eksak.

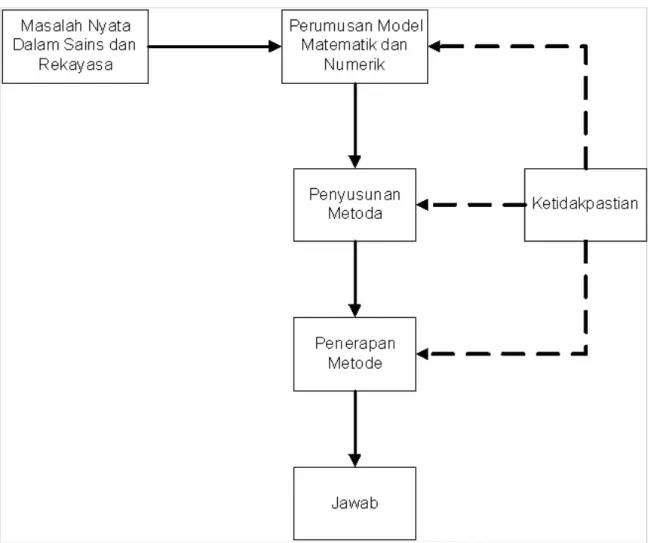
Menurut Djojodihardjo (2000, p12) proses pemecahan persoalan, pada umumnya berlangsung dalam tiga tahap, yaitu:

a. Perumusan secara tepat dari model matematik dan model numerik yang berkaitan b. Penyusunan metode untuk memecahkan persoalan numerik

8

Gambar 2.2 Proses pemecahan persoalan dalam metode numerik. Metode Numerik memiliki 2 pengertian, dari segi:

1. Sains, Metode Numerik merupakan proses penyelesaian masalah matematik

menggunakan operasi aritmetik.

2. Seni, Metode Numerik merupakan suatu cara bagaimana memilih prosedur /

algoritma penyelesaian masalah yang paling sesuai.

Model matematik suatu sistem / proses fisis tidak selalu dapat diselesaikan secara

analitk, sedangkan penyelesaian analitik tidak selalu mudah dicari. Oleh karena itu,

diperlukan kemampuan berhitung dalam penyelesaian matematik. Akhir-akhir ini, operasi

9 Numerik.

Penggunaan Metode Numerik untuk analisis, simulasi, dan desain teknik pemrosesan dan sistem telah berkembang pada tahap yang sangat cepat pada beberapa tahun belakangan ini. Ketersediaan tenaga perhitungan yang sangat cepat membuat solusi numerik dari masalah-masalah teknis yang rumit, secara ekonomis dapat diselesaikan.

Penggunaan Metode Numerik dalam perteknikan dapat dianggap sebagian sains, sebagian seni. Prosedur yang sesuai buku tidak akan efektif dalam mempelajari metode tersebut. Oleh karena itu, penulis harus menyelesaikan masalah menggunakan pendekatan yang berbeda dan berbagai sistem piranti lunak dan percobaan dengan berbagai parameter-parameter masalah tersebut.

Hasil berbeda yang didapatkan melalui proses ini akan membentuk dasar percobaan untuk memilih metode yang sosok dan menafsirkan hasil-hasil bagi sebuah masalah baru. .

Kebanyakan masalah-masalah analisis perteknikan melibatkan:

1. Pengembangan sebuah model matematika untuk merepresentasikan semua karakteristik-karakteristik penting dari sistem fisis.

2. penurunan persamaan-persamaan utama dari model dengan menggunakan hukum-hukum fisis, seperti persamaan ekuilibrium, hukum gerak Newton, konservasi massa dan konservasi energi.

3. solusi persamaan-persamaan utama; dan 4. interpretasi solusi tersebut.

Berdasarkan sistem yang telah dianalisis dan model matematika yang digunakan, persamaan-persamaan utama mungkin merupakan sebuah himpunan peraamaanpersamaan aljabar linear atau non linear, sebuah himpunan

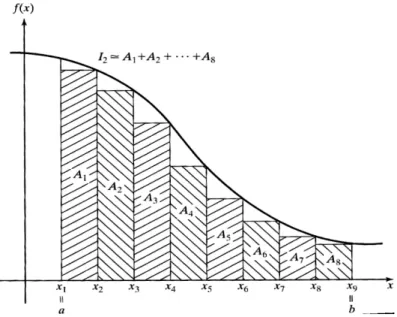
persamaan-persamaan transenden, sebuah himpunan persamaan-persamaan-persamaan-persamaan diferensial biasa atau parsial, sebuah himpunan persamaan-persamaan homogen yang menuju masalah nilai eigen, atau sebuah persamaan yang melibatkan integral atau turunan. Kita mungkin bisa, atau mungkin tidak bisa untuk menemukan solusi persamaan utama secara analitik. Jika solusinya dapat direpresentasikan dalam bentuk sebuah ekspresi matematika yang tertutup, hal ini disebut sebuah solusi analitik. Solusi analitik menandakan solusi-solusi tepat yang dapat digunakan untuk mempelajari kebiasaan sistem dengan berbagai macam parameter-parameter. Sayangnya, hanya sedikit sistem praktis yang mengarah ke solusi analitik, oleh karena itu solusi analitik penggunaannya terbatas. Dalam beberapa masalah-masalah yang bertipe khusus, solusi grafis dapat ditemukan untuk mempelajari kebiasaan sistem. Bagaimanapun juga, solusi grafis biasanya kurang akurat, penggunaannya kaku, hanya dapat diimplementasikan jika dimensi masalahnya kurang atau sama dengan tiga, dan membutuhkan waktu yang lebih lama. Solusi-solusi numerik adalah hal-hal yang tidak dapat diekspresikan dalam bentuk ekspresi-ekspresi matematika.. solusi ini hanya dapat ditemukan menggunakan jenis proses perhitungan intensif yang cocok, yang dikenal sebagai Metode Numerik. Sebagai contoh, anggap integral ₌

∫

b − a x dx xe I₁ 2 . (2.1)

nilai dari integral ini dapat diekspresikan secara analitik sebagai

2 2 2

(

2 2

)

2 1 2 1 2 1 2 1 1 b a a b b a x e e e e e I − ⎟ =− − + − = − − − ⎠ ⎞ ⎜ ⎝ ⎛ − = (2.2)

=

∫

=

∫

− b a x b a dx e dx x f I₂ ( ) 2 . (2.3)

tidak memiliki solusi (analitik) tertutup.integral ini hanya dapat dievaluasi secara numerik. Karena integral sama dengan daerah dibawah kurva f(x), maka nilainya bisa diestimasi dengan memecah-mecah daerah di bawah kurva menjadi persegi-persegi kecil dan menambah daerah-daerah persegi-persegi tersebut. (lihat Gambar2.3.). Karena metode numerik melibatkan sejumlah besar perhitungan aritmatik monoton, penggunaannya dan popularitas telah meningkat karena pengembangan dan keberadaan komputer yang sangat bagus dan murah harganya. Metode Numerik dapat digunakan untuk mencari solusi dari masalah teknik yang bahkan sangat rumit. Ketika solusi analitik biasanya membutuhkan beberapa asumsi sederhana dari sistem fisis, solusi numerik tidak membutuhkan asumsi-asumsi tersebut. Walaupun solusi numerik tidak dapat menyediakan pendekatan yang cepat pada kebiasaan sistem fisis yang disederhanakan, solusi ini dapat digunakan untuk mempelajari kebiasaan sistem fisis yang sebenarnya.

2.2 Integrasi Numerik

Solusi dari banyak masalah-masalah teknik membutuhkan evaluasi sebuah integral. Jika fungsi yang diintegralkan terlalu rumit atau jika nilai fungsinya hanya diketahui pada nilai diskrit dari variabel independen, maka teknik integrasi numerik digunakan. Pada dasarnya, variasi fungsi (yang diintegralkan) diasumsikan sebagai sebuah polinomial sederhana daripada sebuah interval diskrit, dan lalu integral tersebut dievaluasi sebagai jumlah daerah-daerah di bawah polinomial yang diasumsikan daripada berbagai macam interval diskrit. Sebagai contoh, jika integral pasti seperti yang terlihat pada Pers. (2.3), integral numeriknya dapat dievaluasi sebagai (Gambar 2.3) I₂ ≈ A₁ + A₂ + A₃ +_L+ A₈ (2.4) pentingnya integrasi numerik dapat dipahami dengan memperlihatkan berapa sering perumusan soal-soal di dalam analisis terapan akan melibatkan turunan-turunan. Maka wajarlah untuk menduga sebelumnya bahwa pemecahan soal-soal seperti itu akan melibatkan integral. Untuk kebanyakan integral maka tidak ada representasi yang mungkin dinyatakan dalam fungsi-fungsi elementer, sehingga aproksimasi akan menjadi perlu.

Seringkali, banyak masalah-masalah teknik membutuhkan evaluasi dari integral =

∫

b a dx x f I ( ) . (2.5)

dimana fungsi f(x) disebut integrand dan a dan b disebut limit dari integrasi. Jika fungsi f(x) kontinu, terbatas, dan berada di antara jangkauan integrasi a ≤ x ≤b, integral (I)

dapat di evaluasi menggunakan teknik matematika yang tersedia. Jika f(x) merupakan fungsi sederhana seperti sebuah fungsi polinomial, sebuah fungsi eksponensial, atau sebuah fungsi trigonometri, integral-integral ini terkenal dari kalkulus. Jika f(x)

melibatkan fungsi-fungsi yang lebih rumit, seringkali, tabel standar integral dapat digunakan untuk mengevaluasi integral (I) dalam bentuk tertutup. Jika tersedia ekspresi analitik atau bentuk tertutup untuk integral-integral, maka akan sangat berharga, karena ekspresi tersebut pasti dan tidak ada kesalahan yang terlibat dalam evaluasinya. Sebagai tambahan, akibat dari berubahnya beberapa parameter fisis dari masalah teknik pada integral dapat dipelajari secara mudah. Ekspresi bentuk tertutup integral (I) dapat digunakan untuk memverifikasi keakuratan integrasi numerik.

Di lain pihak, fungsi f(x) mungkin merupakan sebuah fungsi kontinu rumit yang sulit atau tidak mungkin diintegrasi dalam bentuk tertutup; mungkin diketahui hanya dalam sebuah bentuk tabel/daftar, dimana nilai x dan f(x) tersedia pada sejumlah titik-titik diskrit pada interval a ke b. limit dari integrasi mungkin tak tebatas atau fungsi f(x) mungin diskontinu atau mungkin menjadi tak terbatas pada beberapa titik pada interval a ke b. pada semua kasus ini, integral (I) dapat dievaluasi hanya secara numerik.

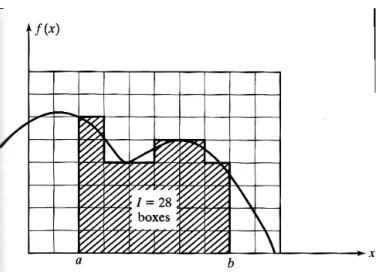
Gambar 2.5 Evaluasi dari sebuah integral menggunakan jaring atau kertas grafik.

Integral dari sebuah fungsi f(x) diantara limit-limit a dan b pada dasarnya menunjukkan daerah di bawah kurva f(x) diantara a dan b seperti yang diperlihatkan pada Gambar 2.4. integrasi juga dikenal sebagai kuadratur. Sebuah pendekatan sederhana, perseptif untuk mengevaluasi integral dalam Pers.(2.5) adalah dengan meletakkan fungsi f(x) pada sebuah jaring atau kertas grafik dan hitung jumlah kotak atau persegi yang mengestimasi daerah di bawah kurva f(x). (lihat Gambar 2.5). Hasil dari banyaknya kotak-kotak dan daerah dari setiap kotak memberikan sebuah estimasi dari seluruh jumlah daerah di bawah kurva (mis, integral, I). pengestimasian ini dapat di buktikan, jika perlu, mengguanakan sebuah jaring yang lebih baik. Bagaimanapun juga metode yang digunakan sangat tidak praktis dan tidak akurat di alam banyak kasus.

2.3 Sumber-sumber Kesalahan

Di dalam integrasi numerik, maka akan ada sumber-sumber kesalahan yang biasa. Akan tetapi, kesalahan-kesalahan masukan di dalam nilai-nilai data y0,…,yn tidak akan diperbesar oleh kebanyakan rumus integrasi, sehingga sumber kesalahan ini hampir

tidak begitu menyusahkan seperti halnya di dalam diferensiasi numerik. Kesalahan pemotongannya, yang sama dengan

∫

− b a dx x p x y( ) ( )] [ (2.6) untuk rumus-rumus yang paling sederhana, dan suatu komposit yang terdiri dari potongan-potongan yang serupa untuk kebanyakan rumus lain, adalah penyumbang kesalahan yang utama sekarang. Berbagai macam usaha telah dibuat untuk memperkirakan kesalahan ini, tetapi kita masih mungkin memperbaiki perkiraan tersebut. Sebuah pertanyaan yang berkaitan dengan ini adalah pertanyaan mengenai konvergensi. Pertanyaan ini menanyakan apakah dihasilkan sebuah urutan untuk mana

limit kesalahan pemotongannya sama dengan nol, jika polinomial-polinomial yang berderajat lebih tinggi digunakan secara terus menerus atau jika interval-interval hn yang lebih kecil di antara titik-titik data dengan lim hn = 0 digunakan secara terus menerus. Di dalam banyak kasus, di mana kaidah trapesoida dan kaidah Simpson adalah contoh-contohnya yang istimewa, maka konvergensinya dapat dibuktikan. Juga, kesalahan pembulatan akan mempunyai pengaruh yang kuat. Sebuah interval h yang kecil, berarti akan merupakan perhitungan yang cukup banyak dan pembulatan yang cukup banyak. Kesalahan-kesalahan algoitma ini akhirnya akan membuat konvergensi menjadi kabur yang secara teoritis harus terjadi, dan di dalam praktek telah didapatkan bahwa pengurangan h di bawah suatu tingkat tertentu akan menghasilkan kesalahan yang lebih besar dan bukannya akan menghasilkan kesalahan yang lebih kecil. Jika kesalahan pemotongannya menjadi dapat diabaikan, maka kesalahan-kesalahan pembulatan akan mengumpul, yang akan membatasi ketelitian yang dapat diperoleh oleh sebuah metode yang diberikan.

2.4 Rumus Newton-Cotes

Rumus-rumus Newton-Cotes adalah yang paling umum digunakan dalam metode integrasi numerik. Rumus-rumus tersebut berdasarkan menempatkan kembali sebuah fungsi rumit atau data tabel dengan beberapa fungsi yang mirip fungsi aslinya yang dapat diintegrasikan secara mudah, yaitu,

=

∫

( ) ≈

∫

( ) ,. b a m b a dx x p dx x f I (2.7)

dimana pm(x) merupakan fungsi yang mirip fungsi aslinya, biasanya diambil sebagai derajat polinomial ke-m

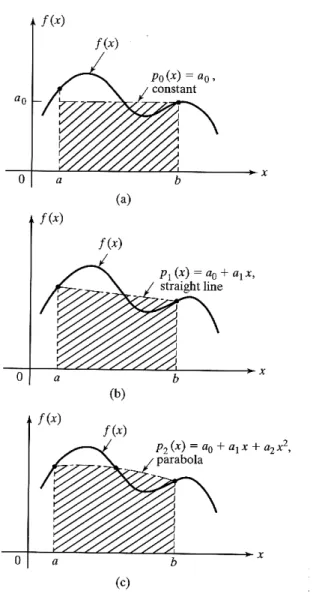
( ) 2 _{1 0}, 2 1 1x a x a x a a x a x p_m = _m m + _m− m− +_L+ + + (2.8) dimana koefisien dari polinomial (konstan) a_m,a_m−1,_L,a₁,a₀ diselesaikan seperti f(x) dan pm(x) memiliki nilai yang sama pada sejumlah titip yang terbatas. Gbr 2.6 memperlihatkan pendekatan f(x) menggunakan 3 polinomial sederhana, yaitu, sebuah konstan, sebuah garis lurus, dan sebuah parabola.

Gambar 2.6 Tipe-tipe yang berbeda dari pendekatan f(x).

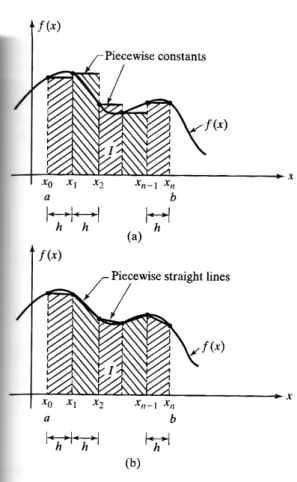
2.4.1 Aturan Persegi

fungsi atau data dari f(x) juga dapat didekat menggunakan sebuah deret polinomial bagian per bagian seperti yang ditunjukkan dalam Gambar 2.7.. Pada pendekatan ini, jangkauan integrasi a≤ x ≤b pertama kali dibagi menjadi sejumlah interval-interval

yang terbatas (n) atau strip-strip yang lebar tiap intervalnya adalah n a b x h =Δ = − (2.9)

titik-titik diskrit di dalam jangkauan interval tersebut didefinisikan sebagai 1 2 1 0 = a,x ,x ,....,xn− x , dan xn =b dengan xi = a+ih;i=0,1,2,...,n (2.10) nilai dari fungsi f(x) pada titik diskrit xi diasumsikan diketahui sebagai fi (i=0,1,2,…,n). Seperti yang diperlihatkan pada Gambar 2.7(a), pendekatan paling sederhana ke fungsi f(x) adalah bagian polinomial dengan order 0 (mis, sebuah deret konstan) jelasnya, dari

Gambar 2.7(a) fungsi f(x) dapat didekati melalui interval xi ≤ x ≤ xi₊₁ baik dengan nilai fi atau fi+1. Jika nilai dari fi digunakan (mis, f(x) didekati oleh nilainya pada awal setiap

interval), daerah dibawah kurva f(x) dalam interval xi ≤ x ≤ xi₊₁ diambil sebagai (fih) dan maka dari itu, integral (I) dievaluasi sebagai

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ≈ =

∫

∑

− = 1 0 ) ( n i i b a f h dx x f I (2.11)

di lain pihak, jika nilai fi+1 digunakan (mis, f(x) didekati oleh nilainya pada akhir setiap

interval), daerah di bawah kurva f(x) dalam interval xi ≤ x≤ xi₊₁ diambil sebagai (fi+1h) an maka dari itu, integral (I) dievaluasi sebagai

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ≡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ≈ =

_∫

∑

∑

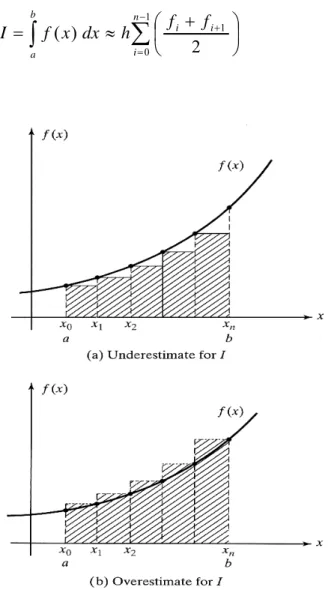
= − = + n i i n i i b a f h f h dx x f I 1 1 0 1 ) ( (2.12)

Gambar 2.7 Pendekatan f(x) oleh bagian dari polinomial berderajat 0 dan 1. Untuk sebuah fungsi naik monoton, Pers. (2.11) merendahkan dan Pers. (2.12) meninggikan nilai integral yang sebenarnya. Dalam praktek, aturan persegi menuju kesalahan pemotongan yang besar untuk fungsi nonlinear umum f(x) dan, maka dari itu, aturan ini tidak biasa digunakan. Bagaimanapun juga, metode ini disajikan untuk mengilustrasikan konsep dasar yang digunakan dalam integrasi numerik dan rumus-rumus Newton-Cotes. Sebuah bukti dalam keakuratan dari pendekatan bagian yang konstan (aturan persegi) dapat diambil dengan menggunakan rata-rata nilai dari fi dan fi+1

dalam interval xi ≤ x ≤ xi₊₁seperti yang ditunjukkan pada Gambar 2.9 dalam kasus ini, integral (I) dievaluasi sebagai

∫

∑

− = + _⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ≈ = 1 0 1 2 ) ( n i i i b a f f h dx x f I (2.13)

Gambar 2.8 Estimasi atas dan estimasi bawah dari I.

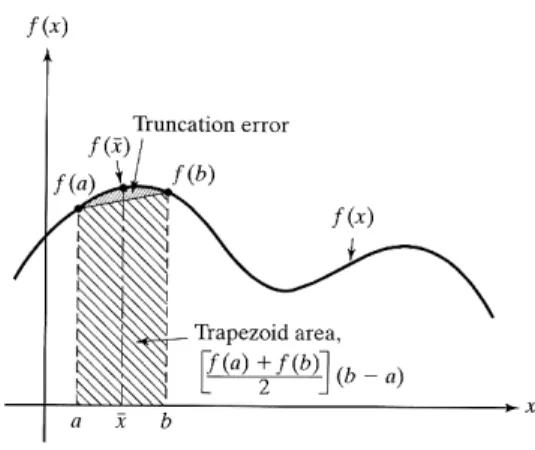
2.4.2 Aturan Trapezoidal

Aturan trapezoidal sering digunakan dalam aplikasi-aplikasi teknik karena kesederhanaannya dalam mengembangkan sebuah program komputer. Metode ini berhubungan dengan pendekatan ke f(x) oleh bagian polinomial dengan order satu {p1(x)

= c1x+c0}, yang dengan segmen-segmen garis lurus seperti yang ditunjukkan pada

Gambar2.7(b). pada kasus ini, daerah di bawah kurva f(x) di dalam interval

1

+ ≤ ≤ i

i x x

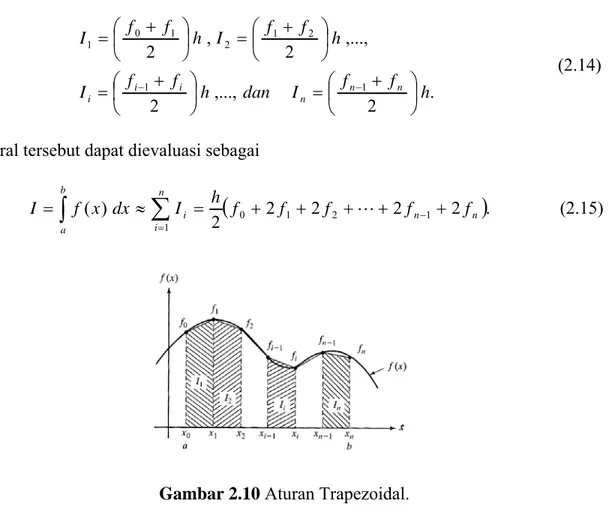
x sama dengan daerah dari trapezoid, maka dari itu dinamakan aturan trapezoidal. Dengan mengindikasikan daerah-daerah trapezoid sebagai I1,I2,…,In, maka (Gambar 2.10) . 2 ,..., 2 ,..., 2 , 2 1 1 2 1 2 1 0 1 h f f I dan h f f I h f f I h f f I n n n i i i ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + = − − (2.14)

integral tersebut dapat dievaluasi sebagai

(

2 2 2 2

)

. 2 ) ( _{0 1 2 1} 1 n n n i i b a f f f f f h I dx x f I = ≈ = + + + + ₋ + =

∑

∫

L (2.15)

Gambar 2.11 Kesalahan pemotongan Aturan Trapezoidal.

2.4.3 Kesalahan Pemotongan dalam Aturan Trapezoidal

Dasar kesalahan pemotongan dari aturan trapezoidal telah diberikan sebagai E f x dx f a f b

(

b a

)

b a − ⎥⎦ ⎤ ⎢⎣ ⎡ + − =

_∫

2 ) ( ) ( ) ( (2.16) dimana bagian pertama dari sebelah kanan Pers. (2.16) menyatakan integral yang tepat dan bagian kedua merepresentasikan integral pendekatan yang diberikan oleh aturan trapezoidal. Perhatikan bahwa hanya ada satu segmen yang dianggap dalam interval untuk kemudahan. (lihat Gambar 2.11). Untuk menurunkan ekspresi yang lebih baik untuk kesalahannya, kita menggunakan perpanjangan deret Taylor dari f(x) tentang titik tengah dari jangkauan,

2 b a x = + : ( ) . ! 2 ) ( ) ( ) ( 2 L + ′′ + ′ + = f x yf x y f x x f (2.17)

disini y= x−x., sebuah garis diatas menunjukkan sebuah turunan, dan fungsi f(x) diasumsikan analitik dalam interval a ≤ x≤b. Persamaan (2.17) dapat digunakan untuk

( ) , ! 2 ) ( ) ( ) ( /2 2 / 2 dy x f y x f y x f dx x f h h b a

∫

∫

− _⎭⎬ ⎫ ⎩ ⎨ ⎧ + ′′ + ′ + = _L (2.18)

dimana y = -h/2 dan y = +h/2 dapat dilihat untuk berhubungan dengan x = a dan x = b. dengan membawa keluar integrasi dalam Pers. (2.18), kita dapatkan

L L + ′′ + = + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ′′ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ′ + = _{− − −}

∫

) ( 24 1 ) ( 3 ) ( 2 1 2 ) ( ) ( ) ( ) ( 3 2 / 2 / 3 2 / 2 / 2 2 / 2 / x f h x hf y x f y x f y x f dx x f hh h h h h b a (2.19)

substitusi x = a dan x = b ke Pers (2.17) didapat

( ) ; 2 2 1 ) ( 2 ) ( ) ( 2 L − ′′ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ′ − = f x h f x h f x a f (2.20) ( ) ; 2 2 1 ) ( 2 ) ( ) ( 2 L + ′′ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + ′ + = f x h f x h f x b f (2.21)

dimana nilai y pada x = a dan x = b diambil sebagai ;

2 h x a x x− = − =− dan 2 h x b x

x− = − = + . Tak ada (b – a) = h, bagian kedua pada sebelah kanan Pers.(2.16) dapat diekspresikan sebagai

L L L + ′′ + = ⎥⎦ ⎤ + ′′ + ′ + + − ′′ + ′ ⎢⎣ ⎡ ₋ = ⎥⎦ ⎤ ⎢⎣ ⎡ + − ) ( 8 1 ) ( ) ( 8 1 ) ( 2 ) ( ) ( 8 1 ) ( 2 ) ( 2 2 ) ( ) ( ) ( 3 2 2 x f h x hf x f h x f h x f x f h x f h x f h b f a f a b (2.22)

Substitusikan Pers. (2.19) dan (2.22) ke Pers. (2.16) dan potong bagian turunan yang berorder lebih tinggi, menjadi

) ( 12 1 ) ( 8 1 ) ( ) ( 24 1 ) ( 3 3 3 x f h x f h x hf x f h x hf E ′′ − ≈ ⎥⎦ ⎤ ⎢⎣ ⎡ _{+ ′′ +} − ⎥⎦ ⎤ ⎢⎣ ⎡ _{+ ′′ +} = _L r _L (2.23)

Ini menunjukkan bahwa kesalahan dari aturan Trapezoidal ( per segmen atau langkah) proposional dengan f ′′(x)dan h3. maka, kesalahan dapat dikecilkan dengan mengecilkan nilai h = b – a.

Kesalahan dalam aturan trapezoidal banyak segmen, Pers. (2.15) dapat dicari dengan menjumlahkan kesalahan-kesalahan dari segmen individual (x0,x1), (x1,x2),…,(x n-1,xn). karena jangkauan integrasi dibagi menjadi n segmen-segmen yang sama, kita

mendapat

n a b

h= − dan maka itu

( ), 12 1 1 3

∑

= ′′ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − ≈ n i i x f n a b E (2.24) dimanaxiadalah titik tengah antara xi dan xi+1. Dengan mendeskripsikan sebuah nilai rata-rata dari turunan kedua,

1 ( ), 1

∑

= ′′ = ′′ n i i x f n f (2.25) Pers. (2.24) dapat ditulis sebagai

(

)

(

)

( ). 12 1 12 1 2 2 2 h O f h a b f n a b a b E ⎟ ′′=− − ′′ = ⎠ ⎞ ⎜ ⎝ ⎛ − − − ≈ (2.26)

Ini menunjukkan bahwa kesalahan dari aturan trapezoidal banyak segmen, Pers. (2.15), proposional dengan h2 _{(karena (b - a) tetap).}

2.4.4 Kesalahan Pemotongan pada Aturan Persegi

Prosedur yang telah ada dapat digunakan untuk mengevaluasi kesalahan pemotongan dalam aturan persegi. Kesalahannya dapat diekspresikan, untuk segmen sederhana a ≤ x ≤b, sebagai

E f x dx f a h b a ) ( ) ( − =

∫

, untuk Pers. (2.11) (2.27) dan E f x dx f b h b a ) ( ) ( − =

∫

, untuk Pers. (2.12) (2.28) dimana bagian pertama sebelah kanan dari Pers. (2.27) dan (2.28) menyatakan integral yang sebenarnya dan bagian kedua merepresentasikan integral pendekatan yang diberikan oleh aturan khusus persegi. Perpanjangan deret Taylor dari f(x) sekitar a diberikan oleh = + − ′ + − ′′( )+_L ! 2 ) ( ) ( ) ( ) ( ) ( 2 a f a x a f a x a f x f (2.29)

integrasi dari Pers. (2.29) memunculkan

, 6 ) ( 2 ) ( ) ( 6 ) ( 2 ) ( ) ( ) ( ! 2 ) ( ) ( ) ( 3 2 0 3 0 2 0 0 2 L L L + ′′ + ′ + = + ′′ + ′ + = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ′′ + ′ + =

∫

∫

h a f h a f h a f y a f y a f y a f dy a f y a f y a f dx x f h h h h b a (2.30)

dimana y = x – a dan h = b – a. Maka Pers. (2.27) memberikan . 6 ) ( 2 ) ( 3 2 L + ′′ + ′ = f a h f a h E (2.31) Secara sama, perpanjangan deret Taylor dari f(x) sekitar b dapat diekspresikan sebagai = − − ′ + − ′′( )−_L ! 2 ) ( ) ( ) ( ) ( ) (x f b b x f b b x 2 f b f (2.32)

, 6 ) ( 2 ) ( ) ( 6 ) ( 2 ) ( ) ( ) ( ! 2 ) ( ) ( ) ( 3 2 0 3 0 2 0 0 2 L L L − ′′ + ′ − = − ′′ + ′ − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ − ′′ + ′ − =

∫

∫

h b f h b f h b f y b f y b f y b f dy b f y b f y b f dx x f h h h h b a (2.33)

dimana y = b - x dan h = b – a. Maka Pers. (2.28) memberikan . 6 ) ( 2 ) ( 3 2 L − ′′ + ′ − = f b h f b h E (2.34) Pers. (2.31) dan (2.34) mengindikasikan bahwa kesalahan dari aturan persegi per langkah proposional ke h2 dan f′(a) atau f′(b). Dengan melanjutkan seperti pada kasus aturan trapezoidal, kesalahan dalam sebuah aturan persegi banyak langkah dapat diekspresikan sebagai

(

)

f

(

b a

)

hf n a b a b E ⎟ ′= − ′ ⎠ ⎞ ⎜ ⎝ ⎛ − − = 2 1 2 1 , untuk Pers.(2.27) (2.35) dan

(

)

f

(

b a

)

hf n a b a b E ⎟ ′=− − ′ ⎠ ⎞ ⎜ ⎝ ⎛ − − − = 2 1 2 1 , untuk Pers.(2.28) (2.36) dimana f′ da;am Pers. (2.35) dan (2.36) menyatakan nilai rata-rata dari turunan pertama pada titik diskrit masing-masing a,x₁,x₂,_K,x_n−1 dan x₁,x₂,_K,x_n−1,b . Ini menunjukkan bahwa kesalahan dalam aturan persegi banyak langkah, Pers. (2.11) dan (2.12) proposional ke h karena (b – a) tetap.

2.4.5 Aturan Simpson

Keakuratan aturan trapezoidal dapat dibuktikan dengan menurunkan besar langkah h ( atau menaikkan banyaknya segmen n). bagaimanapun juga, kesalahan

pembulatan menaik dengan sebuah penurunan dalam besar langkah h. Cara lain mendapatkan estimasi yang lebih akurat dari sebuah integral adalah dengan menggunakan polinomial dengan order lebih tinggi untuk pendekatan fungsi f(x).

2.4.6 Aturan Simpson 1/3

Seperti yang sebelumnya integral =

∫

b a dx x f I ( ) . (2.37)

dievaluasi menggunakan sebuah parabola atau polinomial berorder dua untuk pendekatan f(x). asumsikan bahwa a ≤ x_i−1 ≤ x_i ≤ x_i+1 ≤b, ketiga titik (xi-1,fi-1), (xi,fi)

dan (xi+1,fi+1), seperti yang diperlihatkan pada Gambar 2.12, digunakan untuk mendeskripsikan sebuah polinomial berderajat dua, p2(x). Dengan membuat polinomial

2 _{1 0} 2

2(x) c x c x c

p = + + (2.38)

Gambar 2.12 Aturan Simpson 1/3.

melewati tiga titik yang ditunjukkan pada Gambar 2.12, konstantanya c0, c1, dan c2 dapat

berhubungan dengan –h dan +h. pemilihan titik asal seperti ini tidak mempengaruhi hasil akhir. Dengan menggunakan hubungan

Untuk xi-1, ( ) ( ) ( ) 2 _{1 0}; 2 0 1 2 2 1 2 x h f c h c h c c h c h c p = − = _i− = − + − + = − + (2.39) Untuk xi, ( 0) (0)2 ₁(0) _{0 0}; 2 2 x f c c c c p = = i = + + = (2.40) Untuk xi+1, 2 _{1 0} 2 0 1 2 2 1 2(x h) f c (h) c (h) c c h c h c p = = i+ = + + = + + (2.41)

solusi dari Pers. (2.39) hingga (2.41) dapat ditemukan, yaitu

, . 2 , 2 2 0 1 1 1 2 1 1 2 i i i i i i f c dan h f f c h f f f c = − − + + = + − − = (2.42)

Daerah dibawah polinomial berderajat dua p2(x) di antara xi-1 dan xi+1 dapat diditemukan sebagai berikut:

(

)

. 2 3 2 ) ( ) ( 2 ) ( 3 ) ( 0 3 2 0 2 1 3 2 0 1 2 2 2 1 1 h c h c x c x c x c dx c x c x c dx x p I h h h h h h h h x x i i + = + + = + + = = − − − −

∫

∫

+ − (2.43)

Dengan mensubstitusikan untuk c2 dan c0 dari Pers. (2.42), Pers. (255) memberikan

( 4 ). 3 2 2 2 3 2 1 1 1 1 3 + − + − _{⎟+ = + +} ⎠ ⎞ ⎜ ⎝ ⎛ − + = i i i _{i i i i} f f f h hf h f f f h I (2.44) bentuk “ 3 1

” dalam aturan Simpson 1/3 berdasarkan keberadaan faktor “ 3 1

” dalam Pers. (2.44). Perhatikan bahwa dua segmen digunakan untuk menurunkan Pers. (2.44). maka, untuk sebuah aplikasi banyak tingkat dari aturan Simpson 1/3, kita perlu membagi

jangkauan a ≤ x ≤bke dalam n segmen-segmen dengan lebar yang sama

n a b h = − . Banyaknya segmen harus merupakan angka genap jadi Pers. (2.44) dapat diaplikasikan untuk kelompok-kelompok dua segmen. Integral dalam Pers. (2.37) bisa dievaluasi sebagai ( ) . /2( ) , 1

∑

∫

= ≈ = n j j b a I dx x f I (2.45)

dimana (I)_j menyatakan nilai dariI berhubungan dengan j jumlah pasangan segmen dan diberikan oleh Pers. (2.44) dengan i = 2j – 1. Pers. (2.44) dan (2.45) menuju ke 4 2 . 3 2 ,... 6 , 4 , 2 1 ,... 5 , 3 , 1 0 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + + ≈

∑

−

∑

− = n n i i n i i f f f f h I (2.46) 2.4.7 Aturan Simpson 3/8

Dalam metode ini, integral dievaluasi dengan pendekatan fungsi f(x) oleh sebuah polinomial berderajat tiga, p3(x), seperti yang ditunjukkan pada Gambar 2.13. Dengan

mengasumsikan polinomial p3(x) sebagai

2 _{1 0} 2 3 3 3(x) c x c x c x c p = + + + (2.47) konstantanya c0, c1, c2 dan c3 dapat dicari. Dengan membuat polinomial tersebut

melewati empat titik (xi-1,fi-1), (xi,fi), (xi+1,fi+1) dan (xi+2,fi+2). Dengan mengambil titik

asal pada xi (x=0 pada xi) jadi xi-1, xi+1 dan xi+2 dapat diasumsikan masing-masing

berhubungan dengan x = –h, h, dan 2h. pemilihan titik asal seperti ini tidak mempengaruhi hasil akhir. Dengan menggunakan hubungan

Untuk xi-1,

( ) 3 3 2 _{2 1 0};

1

3 x h f h c h c hc c

Untuk xi, p₃(x= 0) = fi = c₀; (2.49) Untuk xi+1, ( ) 2 _{2 1 0}; 3 3 1 3 x h f h c h c hc c p = = _i+ = + + + (2.50) Untuk xi+2, 2 _{2 1 0} 3 3 2 3(x 2h) f 8h c 4h c 2hc c p = = _i+ = + + + (2.51)

Gambar 2.13 Aturan Simpson 3/8.

Solusi dari Pers. (2.48) sampai (2.51) dapat dinyatakan sebagai

c₀ = fi; (2.52)

(

6 3 2

)

; 6 1 1 1 2 1 = − fi+ + fi+ − fi − fi− h c (2.53)

(

2

)

; 2 1 1 1 2 2 = fi− − fi + fi+ h c (2.54) _{3 3}

(

₂ 3 ₁ 3 ₁

)

6 1 − + + − + − = fi fi fi fi h c (2.55)

Daerah ( I ) dibawah polinomoal berderajat tiga p3(x) diantara xi-1 dan xi+2 dapat

diditemukan sebagai berikut:

(

)

). 3 ( ) 3 ( 2 ) 9 ( 3 ) 15 ( 4 ) ( ) ( 2 ) ( 3 ) ( 4 ) ( 0 2 1 3 2 4 3 2 0 2 2 1 2 3 2 2 4 3 2 0 1 2 2 3 3 3 2 1 h c h c h c h c x c x c x c x c dx c x c x c x c dx x p I h h h h h h h h h h x x i i + + + = + + + = + + + = = − − − − −

∫

∫

+ − (2.56)

Dengan mensubstitusikan dari c0 hingga c3 dari Pers. (2.52) hingga (2.55), Pers. (2.56)

memberikan ). 3 3 ( 8 3 3 6 2 3 6 2 3 2 2 3 6 3 3 4 15 1 1 2 1 1 2 2 1 1 3 3 1 1 2 4 − + + − + + − + − + + + + + = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− + − − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + − = i i i i i i i i i i i i i i i i f f f f h hf h f f f f h h f f f h h f f f f h I (2.57) bentuk “ 8 3

” dalam aturan Simpson 3/8 berdasarkan keberadaan faktor “ 8 3

” dalam Pers. (2.57). Perhatikan bahwa tiga segmen digunakan untuk menurunkan Pers. (2.57). maka, untuk sebuah aplikasi banyak tingkat dari aturan Simpson 3/8, kita perlu membagi jangkauan a ≤ x ≤bke dalam n segmen-segmen dengan lebar yang sama

n a b h = − . Banyaknya segmen harus merupakan kelipatan 3 jadi Pers. (2.57) dapat diaplikasikan untuk kelompok-kelompok tiga segmen. Integral dalam Pers. (2.37) bisa dievaluasi sebagai ( ) . /3( ) , 1

∑

∫

≈ ₌ = n j j b a I dx x f I (2.58)

dimana (I)_j merepreentasikan nilai dariI berhubungan dengan j jumlah kelompok tiga segmen dan diberikan oleh Pers. (2.57) dengan i = 3j – 2. Pers. (2.57) dan (2.58) menuju ke 3 ( ) 2 . 8 3 3 ,... 9 , 6 , 3 2 ,... 7 , 4 , 1 1 0 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + + + + ≈

∑

−

∑

− = + n n i i n i i i f f f f f h I (2.59)

dapat ditunjukkan bahwa kesalahan pemotongan dalam penggunaan Pers. (2.59) dengan order yang sama sengan aturan Simpson 1/3. tetapi penggunaan Pers. (2.59) memerlukan banyaknya segmen merupakan kelipatan 3. maka, Pers. (2.59) jarang digunakan sendiri. Seringkali kedua aturan Simpson 1/3 dan 3/8 digunakan bersamaan jadi banyaknya segmen n, tidak perlu dibatasi sesuatu. Di lain pihak, bila banyaknya segmen ganjil, aturan Simpson 3/8 dapat digunakan, misalnya, untuk tiga segmen pertama dan aturan Simpson 1/3 dapat digunakan untuk banyaknya segmen genap sisanya.

2.4.8 Kesalahan Pemotongan pada Aturan Simpson

Seperti pada kasus trapzoidal, dasar kesalahan pemotongan dari aturan Simpson 1/3, melibatkan hanya dua segmen dalam interval a ke b, yang diberikan oleh

[

( ) 4 ( ) ( )

]

, 6 ) (x dx b a f a f x f b f E b a ⎟⎠ + + ⎞ ⎜ ⎝ ⎛ − − =

_∫

(2.60)

dimana bagian pertama dari sisi sebelah kanan Pers.(2.60) menyatakan integral yang sebenarnya, dimana bagian kedua merepresentasikan integral pendekatan yang diberikan oleh aturan Simpson 1/3 (lihat Gambar 2.14). kita dapat memperluas f(x) menggunakan deret Taylor mengenai titik tengah dari jangkauan, x1, yaitu

, ) ( ! 5 ) ( 4 ) ( ! 3 ) ( ! 2 ) ( ) ( ) ( ₁ 5 1 4 1 3 1 2 1 1 + ′ + ′′ + ′′′ + ′′′′ + ′′′′′ +L = f x yf x y f x y f x y f x y f x x f

(2.61) dimana y = x – x1. Pers. (2.61) dapat digunakan untuk mengekspresikan integral dari f(x)

sebagai , ) ( ! 120 ) ( 24 ) ( 6 ) ( 2 ) ( ) ( ) ( 1 5 1 4 1 3 1 2 1 1 dy x f y x f y x f y x f y x f y x f dx x f h h b a ⎭ ⎬ ⎫ + ′′ ′′′ + ′′ ′′ + ⎩ ⎨ ⎧ _′′′ + ′′ + ′ + =

∫

∫

− L (2.62)

dimana y = -h dan y = h masing-masing berhubungan dengan x = a dan x = b. dengan mengeluarkan integrasi dari Pers. (2.62), kita dapatkan

. ) ( 6 ) ( 3 ) ( 2 720 ) ( 120 ) ( 24 ) ( 6 ) ( 2 ) ( ) )( ( ) ( 1 5 1 3 1 6 1 5 1 4 1 3 1 2 1 1 L L + ′′ ′′ + ′′ + = + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ′′ ′′′ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ′′ ′′ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ′′′ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ′′ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ′ + = − − − − − −

∫

x f h x f h x hf y x f y x f y x f y x f y x f y x f dx x f h h h h h h h h h h h h b a (2.63)

Gambar 2.14 Kesalahan pemotongan Aturan Simpson.

Substitusikan x = a (y = -h), x = x1 (y = 0), dan x = b (y = h) ke Pers. (2.61)

; ) ( 120 ) ( 24 ) ( 6 ) ( 2 ) ( ) ( ) ( 1 5 1 4 1 3 1 2 1 1 L + ′′ ′′′ − ′′ ′′ + ′′′ − ′′ + ′ − = x f h x f h x f h x f h x f h x f a f (2.64) f(x₁)= f(x₁); (2.65) . ) ( 120 ) ( 24 ) ( 6 ) ( 2 ) ( ) ( ) ( 1 5 1 4 1 3 1 2 1 1 L + ′′ ′′′ + ′′ ′′ + ′′′ + ′′ + ′ − = x f h x f h x f h x f h x f h x f b f (2.66)

sekarang bagian kedua dari sisi sebelah kanan dari Pers. (2.60) dapat diekspresikan, menggunakan Pers. (2.64) hingga (2.66), menjadi

. ) ( 12 ) ( ) ( 6 6 . ) ( 120 ) ( 24 ) ( 6 ) ( 2 ) ( ) ( ) ( 4 ) ( 120 ) ( 24 ) ( 6 ) ( 2 ) ( ) ( 6 1 4 1 2 1 1 5 1 4 1 3 1 2 1 1 1 1 5 1 4 1 3 1 2 1 1 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ + ′′ ′′ + ′′ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = ⎥ ⎦ ⎤ + ′′ ′′′ + ′′ ′′ + ′′′ + ′′ + ′ − + + + + ′′ ′′′ − ′′ ′′ + ⎢ ⎢ ⎢ ⎣ ⎡ _′′′ − ′′ + ′ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − L L L x f h x f h x f a b x f h x f h x f h x f h x f h x f x f x f h x f h x f h x f h x f h x f a b (2.67)

Substitusikan Pers. (2.63) dan (2.67) ke dalam Pers. (2.60) dan potong bagian yang melibatkan turunan yang lebih tinggi daripada pemberian kelima

). ( 90 1 ) ( ) ( 2880 1 ) ( 2 12 1 6 ) ( 2 6 ) ( ) ( ) ( 2 60 1 ) ( 2 3 1 ) ( 2 2 . 1 5 1 5 1 4 1 2 1 1 5 1 3 1 x f h x f a b x f a b a b x f a b a b x f a b x f a b x f a b x f a b E ′′ ′′ − ≈ ′′ ′′ − − ≈ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ′′ ′′ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + ′′ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + − − ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ′′ ′′ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + ′′ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ≈ (2.68)

ini menandakan bahwa kesalahan aturan Simpson 1/3 (per setiap pasangan segmen) proposional ke h5 dan f ′′′′(x₁) . Maka kesalahan akan jadi nol jika f(x) merupakan

sebuah polinomial berorder tiga, karena f ′′′′=0.

kesalahan dalam aturan Simson 1/3 banyak segmen, Pers. (2.59), dapat ditemukan dengan menjumlahkan kesalahan-kesalahan dari pasangan segmen individual (x0,x2),

(x2,x4), …, (xn-2,xn): ( ). 90 1 ,... 5 , 3 , 1 5

∑

− = ′′ ′′ − ≈ n j j x f h E (2.69) dengan mendeskripsikan sebuah nilai rata-rata dari turunan keempat, f ′′′′, sebagai _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ′′ ′′ = ′′ ′′

∑

− = 1 ,... 5 , 3 , 1 ) ( 2 n j j x f n f (2.70)

Pers. (2.69) dapat diekspresikan sebagai berikut:

). ( ) ( 180 1 2 90 1 4 4 5 h O f a b h f n h E ≈ ′′ ′′ − − ≈ ′′ ′′ − ≈ (2.71)

Ini mengindikasikan bahwa kesalahan dalam aturan Simpson banyak segmen, Pers. (2.46), proposional dengan h4, karena (b - a) tetap.

Dengan mengikuti pendekatan yang sama, kesalahan pemotongan dalam sebuah aturan Simpson 3/8 banyak segmen juga dapat diperlihatkan proposional dengan h4.

2.5 Aturan Boole

Dalam metode ini, integral dievaluasi dengan pendekatan fungsi f(x) oleh sebuah polinomial berderajat empat, p4(x). Dengan mengasumsikan polinomial p4(x) sebagai

2 _{1 0} 2 3 3 4 4 4(x) c x c x c x c x c p = + + + + (2.72) konstantanya c0, c1, c2, c3 dan c4 dapat dicari. Dengan membuat polinomial tersebut

melewati lima titik (xi-2,fi-2), (xi-1,fi-1), (xi,fi), (xi+1,fi+1) dan (xi+2,fi+2). Dengan mengambil

titik asal pada xi (x=0 pada xi) jadi xi-2, xi-1, xi+1 dan xi+2 dapat diasumsikan masing-masing berhubungan dengan x = –2h, -h, h, dan 2h. pemilihan titik asal seperti ini tidak mempengaruhi hasil akhir. Dengan menggunakan hubungan

Untuk xi-2, ( 2 ) 16 8 4 2 ₂ 2 _{1 0}; 3 3 4 4 2 4 x h f h c h c h c hc c p = − = _i− = − + − + (2.73) Untuk xi-1, ( ) 3 3 2 _{2 1 0}; 4 4 1 4 x h f h c h c h c hc c p = − = i− = − + − + (2.74) Untuk xi, p₄(x =0)= fi =c₀; (2.75) Untuk xi+1, ( ) 2 _{2 1 0}; 3 3 4 4 1 4 x h f h c h c h c hc c p = = _i+ = + + + + (2.76) Untuk xi+2, 2 _{2 1 0} 3 3 4 4 2 4(x 2h) f 16h c 8h c 4h c 2hc c p = = _i+ = + + + + (2.77)

Solusi dari Pers. (2.73) sampai (2.77) dapat dinyatakan sebagai c0 = fi (2.78)

(

)

; 3 1 1 1 1 = fi+ − fi− h c (2.79)

(

16 30 16

)

; 24 1 2 1 1 2 2 2 = − fi− + fi− − fi + fi+ − fi+ h c (2.80) _{3 3}

(

_{2 2} 2 ₁ 2 ₁

)

12 1 + − − + − + − = fi fi fi fi h c (2.81) _{4 4}

(

₂ 4 ₁ 6 4 _{1 2}

)

24 1 + + − − − + − + = fi fi fi fi fi h c (2.82)

Daerah (I ) dibawah polinomial berderajat empat p4(x) diantara xi-2 dan xi+2 dapat

diditemukan sebagai berikut:

(

)

). 4 ( ) 16 ( 3 ) 64 ( 5 ) ( ) ( 2 ) ( 3 ) ( 4 ) ( 5 ) ( 0 3 2 5 4 2 2 0 2 2 2 1 2 2 3 2 2 2 4 3 2 2 5 4 2 2 0 1 2 2 3 3 4 4 4 2 2 h c h c h c x c x c x c x c x c dx c x c x c x c x c dx x p I h h h h h h h h h h h h x x i i + + = + + + + = + + + + = = − − − − − −

∫

∫

+ − (2.83)

Dengan mensubstitusikan dari c0 hingga c3 dari Pers. (2.78) hingga (2.82), Pers. (2.83)

memberikan ). 7 32 12 32 7 ( 45 2 4 24 16 30 16 16 24 4 6 4 5 64 2 1 1 2 2 2 1 1 2 3 3 2 1 1 2 4 + + − − + + − − + + − − + + + + = + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛− + − + − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + − + = i i i i i i i i i i i i i i i i f f f f f h hf h f f f f f h h f f f f f h I (2.84)

Formula Newton-Cotes untuk polinomial berderajat empat ini sering disebut dengan aturan Boole.

2.5.1 Rumus Newton-Cotes secara Umum

Seperti yang telah dinyatakan sebelumnya, rumus-rumus Newton-Cotes diturunkan dengan menggunakan sebuah polinomial dengan order m untuk pendekatan fungsi f(x), maka,

∫

( ) .≈

∫

b ( ) ,. a m b a dx x p dx x f (2.85) dimana ( ) 2 _{1 0}. 2 1 1x c x c x c c x c x p m m m m m = + + + + + − − L (2.86)

Rumus-rumus integrasi numerik yang berhubungan dengan m = 0 (aturan persegi), m = 1 (aturan trapezoidal), m = 2 (aturan Simpson 1/3), m = 3 (aturan Simpson 3/8), dan m = 4 (aturan Boole) telah diturunkan di Bagian 2.4 dan 2.5. Rumus-rumus yang berhubungan dengan polinomial berorder lebih tinggi juga dapat diturunkan. Estimasi kesalahan yang berhubungan dengan rumus mana saja juga dapat diturunkan seperti yang telah dilakukan sebelumnya. Sebuah ringkasan dari beberapa rumus-rumus Newton-Cotes, bersama dengan estimasi keslahan yang berhubungan, diberikan pada tabel 2.1

Tabel 2.1 Tabel beberapa rumus Newton-Cotes beserta estimasi kesalahannya.

2.6 Kuadratur Gauss

Sementara metode-metode dianggap memerlukan evaluasi dari integrand pada interval yang sama, kuadratur Gauss dianggap memerlukan evaluasi integrand pada interval tertentu, tapi tidak sama. kuadratur Gauss merupakan metode integrasi numerik yang kuat dan keakuratannya jauh lebih tinggi daripada rumus-rumus Newton-Cotes. Walau begitu, kuadratur Gauss tidak begitu berguna untuk mengintegrasikan fungsi yang diberikan dalam bentuk tabel dengan interval equispace. Bentuk yang paling terkenal dari kuadratur Gauss, dikenal sebagai kuadratur Gauss-Legendre, menggunakan polinomial Legendre untuk pendekatan fungsi f(x). Metode ini menggunakan akar-akar polinomial Legendre untuk melokasikan titik dimana integrand dievaluasi. Dalam integrasi Gauss, integral dievaluasi dengan menggunakan rumus

( ) . ( ), 1

∑

∫

= = n i i b a x f wi dx x f (2.87)

Dimana n disebut banyaknya titik-titik Gauss, wi adalah koefisien yang tidak diketahui, disebut juga weight, dan xi adalah nilai khusus dari x, disebut juga titik Gauss, dimana integrand dievaluasi. Untuk n tertentu, nilai dari wi dan xi dipilih sehingga rumusnya akan tepat untuk polinomial ke atas, termasuk derajat (2n – 1). Misalnya untuk n = 2, nilai dari w1, w2, x1, dan x2 dipilih agar rumusnya memberikan nilai tepat

dari integral untuk polinomial hingga derajat tiga.

2.6.1 Perubahan Koordinat

Seperti yang terlihat pada Pers. (2.87), integrasi Gauss memerlukan jangkauan integrasi dari -1 hingga +1. untuk kenyamanan notasi, anggap saja, koordinat asli y dan jangkauan integrasi f(y) dari a ke b. Maka perubahan

a b b a y x − − − = 2 (2.88) Memberikan koordinat yang dinormalisasi x = -1, ketika y = a dan x = +1, ketika y = b. Perubahan dari x ke y menjadi

2 )

(b a x a b

y = − + + (2.89)

Dengan memperhatikan bahwa dy b a⎟dx ⎠ ⎞ ⎜ ⎝ ⎛ − = 2 , integral aslinya

∫

b a dy

f(y) dapat ditulis kembali sebagai

∫

∫

∑

= − − = = n i i i b a y f w a b dx dx dy y f dy y f 1 1 1 ), ( 2 ) ( ) ( (2.90)

Jika xi adalah titik Gauss dari koordinat yang dinormalisasi, nilai yang berhubungan dengan yi dapat dinyatakan, menggunakan Pers. (2.89), sebagai

. 2 ) (b a x a b y i i + + − = (2.91) Karena weight, wi , tetap sama, integral dapat dievaluasi menggunakan ekspresi sisi sebelah kanan Pers. (2.90).

2.6.2 Ciri sebuah rumus Gauss

Pemikiran utama di belakang integrasi Gauss adalah bahwa di dalam pemilihan sebuah rumus

∫

∑

= n i i i b a x y A dx x y 1 ) ( ~ ) ( (2.92) Maka mungkin merupakan hal yang bijaksana untuk tidak menetapkan argumen-argumen xi yang tak berjarak antara sama. Banyak integral yang melibatkan fungsi-fungsi analitik yang cukup dikenal yang dapat dihitung untuk sembarang argumen dan dengan ketelitian yang cukup besar. Di dalam kasus-kasus seperti itu, maka akan berguna bagi kita untuk menanyakan pilihan xi dan Ai yang manakah yang bersama-sama akan memberikan ketelitian maksimum. Terbukti bahwa akan memudahkan kita untuk membicarakan rumus yang sedikit lebih umum, yakni

∫

∑

= n i i i b a x y A dx x y x w 1 ) ( ~ ) ( ) ( (2.93) dimana w(x) adalah fungsi bobot yang akan ditentukan kelak. Bila w(x) = 1 maka kita memperoleh rumus asli yang lebih sederhana.

Satu pendekatan kepada rumus Gauss seperti itu adalah dengan mencari ketelitian yang sempurna bila y(x) adalah salah satu dari fungsi-fungsi pangkat 1, x, x2, ..., x2n-1. Ini menyediakan 2n persyaratan untuk menentukan 2n bilangan, yakni xi dan Ai. Ternyata, =

∫

b a i i w x L x dx A ( ) ( ) (2.94)

Dimana Li(x) adalah fungsi pengali Langrangre. Argumen-argumen x1, ..., xn adalah titik-titik nol dari polinomial pn(x) yang berderajat n yang termasuk pada sebuah kelompok yang mempunyai sifat ortogonalitas

_∫

w(x)p (x)p (x)dx=0

b a

m

n untuk m≠n (2.95) Polinomial-polinomial ini bergantung pada w(x). Dengan demikian maka fungsi bobot tersebut akan mempengaruhi keduanya Ai dan xi tetapi tidak akan muncul secara eksplisit di dalam rumus Gauss.

2.6.3 Rumus Gauss-Legendre

Rumus ini diperoleh bila w(x) = 1. inilah prototip metode Gauss. Sudah lazim menormalisasikan interval (a,b) menjadi (-1,1). Maka polinomial-polinomial ortogonal tersebut adalah polinomial-polinomial Legendre

n n n n n x dx d n x P ( 1) ! 2 1 ) ( ₌ 2 _{− (2.96)}

Dengan P0(x) = 1. Bilangan-bilangan xi adalah titik-titik nol dari polinomial ini dan koefisien-koefisien tersebut adalah

[

]

2 1 2 2 ) ( ) 1 ( 2 i n i i x P n x A − − = (2.97) Tabel-tabel yang memberikan xi dan Ai biasanya tersedia, yang akan disubstitusikan secara langsung ke dalam rumus Gauss-Legendre

∫

∑

= n i i i b a x y A dx x y 1 ) ( ~ ) ( (2.98) Berbagai sifat polinomial Legendre akan diperlukan di dalam pengembangan hasil-hasil ini termasuk yang berikut:

( ) 0 1 1 =

∫

− dx x P xk _{n untuk k = 0, 1, ..., n-1 (2.99)} )! 1 2 ( ) ! ( 2 ) ( 2 1 1 1 + = + −

∫

n n dx x P x n n n _(2.100)

[

]

1 2 2 ) ( 1 1 2 + =

∫

− n dx x P_n (2.101) ( ) ( ) 0 1 1 =

∫

− dx x P x P_{m n} untuk m≠n (2.102) Pn(x) mempunyai n titik nol riil di dalam (-1,1)

(n+1)Pn+₁(x)=(2n+1)xPn(x)−nPn−₁(x) (2.103)

∑

[

]

= + + − + = + − n i n n n n i i x P t n P t P x P t P x P i x t 0 1 1( ) ( ) ( ) ( ) ) 1 ( ) ( ) ( ) 1 2 ( ) ( (2.104)

∫

− + + − = − 1 1 ( 1) 1( ) 2 ) ( k n k n x P n dx x x x P (2.105) (1 2) ( ) ( ) ₁( ) x nP x nxP x P x n′ + n = n− − (2.106)

Perkiraan Lanczos mengenai besarnya kesalahan pemotongan untuk rumus Gauss-Legendre akan dinyatakan dalam bentuk

_⎥ ⎦ ⎤ ⎢ ⎣ ⎡ _{+ − − − ′} +

∑

= n i i i ix y x A I y y n E 1 ) ( ) 1 ( ) 1 ( 1 2 1 ~ (2.107)

Dimana I adalah integral aproksimasi yang didapatkan dengan menggunakan rumus n titik Gauss. Perhatikan bahwa suku

∑

melibatkan pemakaian rumus yang sama kepada fungsi xy’(x). Perkiraaan kesalahan ini kelihatannya cukup teliti untuk fungsi-fungsi yang licin.

2.6.4 Turunan dari Rumus Gauss Dua Titik

Rumus integrasi Gauss dua titik diberikan dari [Pers. (2.87) dengan n = 2] ( ) . ₁ ( ₁) ₂ ( ₂), 1 1 x f w x f w dx x f = +

∫

− (2.108) Dimana evaluasi dari keempat w1, w2, x1, dan x2 yang tidak diketahui membutuhkan

penggunaan empat kondisi. Karena n = 2, rumusnya harus memberikan nilai yang tepat bagi polinomial berorder tiga dan dibawahnya. Dengan memaksakan rumus agar tepat untuk polinomial tersebut, f(x) = 1, x, x2, dan x3, kita dapatkan persamaan-persamaan berikut: Ketika f(x) = 1, . ) ( ) ( 2 1 . ) ( 2 1 2 2 1 1 1 1 1 1 w w x f w x f w dx dx x f + = + = = =

∫

∫

− − (2.109) Ketika f(x) = x, . ) ( ) ( 0 2 . ) ( 2 2 1 1 2 2 1 1 1 1 1 1 2 1 1 x w x w x f w x f w x dx x dx x f + = + = = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = = − − −

∫

∫

(2.110)

Ketika f(x) = x2, . ) ( ) ( 3 2 3 . ) ( 2 2 2 2 1 1 2 2 1 1 1 1 3 1 1 2 1 1 x w x w x f w x f w x dx x dx x f + = + = = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = = − − −

∫

∫

(2.111) Ketika f(x) = x3_, . ) ( ) ( 0 4 . ) ( 3 2 2 3 1 1 2 2 1 1 1 1 4 1 1 3 1 1 x w x w x f w x f w x dx x dx x f + = + = = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = = − − −

∫

∫

(2.112)

Karena limit integrasi, -1 dan +1 simetris sekitar x = 0, kita harap x1, x2 juga

simetris sekitar x = 0. dengan menganggap x2 = -x1, kita dapatkan lanjutan dari Pers.

(2.109) dan (2.110):

w1 = w2 = 1.

Nilai ini secara otomatis memenuhi Pers. (2.111) dan Pers. (2.112) memberikan , 3 1 2 1 = x

Dari situ kita dapatkan

0.5773502691 89626 3 1 1 = = x Dan 0.5773502691 89626 3 1 1 2 =−x =− =− x 2.6.5 Prosedur Umum

Walaupun turunan dari rumus integrasi Gauss dua titik tidak rumit, turunan dari

Bagaimanapun juga, prosedur umum untuk menemukan widan xi melibatkan beberapa langkah berikut:

1. Titik-titik Gauss x1, x2, ..., xn adalah akar-akar dari polinomial Legendre dengan

derajat n, Pn(x). Polinomial-polinomial Legendre ortogonal pada interval [-1,1], sehingga

∫

− ≠ = 1 1 ; 0 ) ( ) (x P x dx n m P_{n m} Dan

{

( )

}

( ) 0 1 1 2 _{= ≠}

∫

− n c dx x P_n (2.113) Dimana c(n) adalah sebuah konstan yang nilainya tergantung dari n. Polinomial-polinomial Legendre dinyatakan dengan

P0(x) = 1, P1(x) = x, Dan ( ) 2 1 ₁( ) 1⎟ ₂( ); =2,3,4,... ⎠ ⎞ ⎜ ⎝ ⎛ − − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − = ₋ P₋ x n n n x P x n n x P_{n n n} (2.114)

Secara umum, polinomial acak manapun yang berderajat n, pn(x), dapat direpresentasikan dengan sebuah kombinasi linear dari polinomial Legendre sebagai

∑

= = n i i i n x P x p 0 ), ( ) ( α (2.115) Dimana αi adalah konstan.

2. Weight wi dapat dihitung sebagai

{

( )

}

. ) 1 ( 2 2 1 2 i n i i x nP x w − − = (2.116) Walaupun komputasi biasa dari xi dan wi agak rumit, nilai-nilai dari xi dan wi untuk berbagai nilai n telah dibuat dan diberikan dalam tabel 2.2.

Tabel 2.2 Tabel titik-titik Gauss, weight dan estimasi kesalahannya.

Nilai-nilai dalam tabel 2.2 didapat dari : Rumus Gauss- Legendre 1 titik

∫

− − = = 1 1 1 ..., , 1 , 0 , 0 ) (x xk dx k n π

{

( )

}

. ) 1 ( 2 2 1 2 k n k k x nP x w − − =

Untuk 1 titik, berarti n = 1.

Di sini polinomial π(x) tersebut adalah polinomial pangkat satu atau persamaan linear, katakanlah π(x) = a + x. Integrasi akan menghasilkan

0 2a=

Yang dengan cepat akan menghasilkan a = 0. Ini membuat x

x)= (

π

Maka argumen kolokasinya adalah 0 = k x Dan 2 = k w

Rumus Gauss- Legendre 2 titik

∫

− − = = 1 1 1 ..., , 1 , 0 , 0 ) (x xk dx k n π

{

( )

}

. ) 1 ( 2 2 1 2 k n k k x nP x w − − =

Untuk 2 titik, berarti n = 2.

Di sini polinomial π(x) tersebut adalah polinomial pangkat dua atau persamaan kuadratik, katakanlah π(x) = a + bx + x2 . Integrasi akan menghasilkan

, 0 3 2 2a+ = 0 3 2 ₌ b

Yang dengan cepat akan menghasilkan b = 0, a = -1/3. Ini membuat ) 3 / 1 )( 3 / 1 ( ) 3 / 1 ( ) ( ₌ 2 _{− = + −} x x x x x π

Maka argumen kolokasinya adalah

89626 5773502691 . 0 , 89626 5773502691 . 0 3 / 1 , 3 / 1 − = − = k x Dan

1 , 1 = k w

Rumus Gauss- Legendre 3 titik

∫

− − = = 1 1 1 ..., , 1 , 0 , 0 ) (x xk dx k n π

{

( )

}

. ) 1 ( 2 2 1 2 k n k k x nP x w − − =

Untuk 3 titik, berarti n = 3.

Di sini polinomial π(x) tersebut adalah polinomial pangkat tiga, katakanlah π(x) = a + bx + cx2 + x3. Integrasi akan menghasilkan

, 0 3 2 2a+ c= 0, 5 2 3 2 _{+ =} b 0 5 2 3 2 _{+ =} c a

Yang dengan cepat akan menghasilkan a = c = 0, b = -3/5. Ini membuat ) 5 / 3 ( ) 5 / 3 ( ) 5 / 3 ( ) ( ₌ 3 _{− = + −} x x x x x x π

Maka argumen kolokasinya adalah

41483 7745966692 . 0 , 0 , 41483 7745966692 . 0 5 / 3 , 0 , 5 / 3 − = − = k x Dan 55556 5555555555 . 0 , 88889 8888888888 . 0 , 55556 5555555555 . 0 = k w

Rumus Gauss- Legendre 4 titik

∫

− − = = 1 1 1 ..., , 1 , 0 , 0 ) (x xk dx k n π

{

( )

}

. ) 1 ( 2 2 1 2 k n k k x nP x w − − =

Untuk 4 titik, berarti n = 4.

Di sini polinomial π(x) tersebut adalah polinomial pangkat empat, katakanlah π(x) = a + bx + cx2 + dx3 + x4. Integrasi akan menghasilkan

, 0 5 2 3 2 2a+ c+ = 0, 5 2 3 2 = + d b 0, 7 2 5 2 3 2 = + + c a 0 7 2 5 2 = + d b

Yang akan menghasilkan b = d = 0, a = 3/35, c = -6/7. Ini membuat

3 30 35 ) 35 / 3 ( ) 7 / 6 ( ) ( 2 4 2 4 + − = + − = x x x x x π

Maka argumen kolokasinya adalah

94053 8611363115 . 0 , 848456 3399810435 . 0 , 84856 3399810435 . 0 , 94053 8611363115 . 0 35 30 2 15 , 35 30 2 15 , 35 30 2 15 , 35 30 2 15 − − = + − − − + − = k x Dan 47454 3478548451 . 0 , 62546 6521451548 . 0 , 62546 6521451548 . 0 , 47454 3478548451 . 0 = k w

Rumus Gauss- Legendre 5 titik

∫

− − = = 1 1 1 ..., , 1 , 0 , 0 ) (x xk dx k n π

{

( )

}

. ) 1 ( 2 2 1 2 k n k k x nP x w − − =

Di sini polinomial π(x) tersebut adalah polinomial pangkat lima, katakanlah π(x) = a + bx + cx2 + dx3 + ex4 + x5. Integrasi akan menghasilkan

, 0 5 2 3 2 2a+ c+ e= 0, 7 2 5 2 3 2 = + + d b 0, 7 2 5 2 3 2 = + + c e a 0, 9 2 7 2 5 2 = + + d b 0 9 2 7 2 5 2 _{+ + =} e c a

Yang akan menghasilkan a = c = e = 0, b = 5/21, d = -10/9. Ini membuat

x x x x x x x 15 70 63 ) 21 / 5 ( ) 9 / 10 ( ) ( 3 5 3 5 + − = + − = π

Maka argumen kolokasinya adalah

38664 9061798459 . 0 , 05683 5384693101 . 0 , 0 , 05683 5384693101 . 0 , 38664 9061798459 . 0 63 70 2 35 , 63 70 2 35 , 0 , 63 70 2 35 , 63 70 2 35 − − = + − − − + − = k x Dan 56189 2369268850 . 0 , 99366 4786286704 . 0 , 88889 5688888888 . 0 , 99366 4786286704 . 0 , 56189 2369268850 . 0 = k w

Rumus Gauss- Legendre 6 titik

∫

− − = = 1 1 1 ..., , 1 , 0 , 0 ) (x xk dx k n π

{

( )

}

. ) 1 ( 2 2 1 2 k n k k x nP x w − − =

Untuk 6 titik, berarti n = 6.

Di sini polinomial π(x) tersebut adalah polinomial pangkat lima, katakanlah π(x) = a + bx + cx2 + dx3 + ex4 + fx5 + x6. Integrasi akan menghasilkan

, 0 7 2 5 2 3 2 2a+ c+ e+ = 0, 7 2 5 2 3 2 _{+ + =} f d b 0, 9 2 7 2 5 2 3 2 _{+ + + =} e c a , 0 9 2 7 2 5 2 _{+ + =} f d b 0, 11 2 9 2 7 2 5 2 _{+ + + =} e c a 0 11 2 9 2 7 2 _{+ + =} f d b

Yang akan menghasilkan b = d = f = 0, a = -5/231, c = 5/11, e = -15/11. Ini membuat

5 105 315 231 ) 231 / 5 ( ) 11 / 5 ( ) 11 / 15 ( ) ( 2 4 6 2 4 6 − + − = − + − = x x x x x x x π

Maka argumen kolokasinya adalah

03152 9324695142 . 0 , 66265 6612093864 . 0 , 83197 2386191860 . 0 83197 2386191860 . 0 , 66265 6612093864 . 0 , 03152 9324695142 . 0 − − − = k x Dan 79170 1713244923 . 0 , 48139 3607615730 . 0 , 72691 4679139345 . 0 , 72691 4679139345 . 0 , 48139 3607615730 . 0 , 79170 1713244923 . 0 = k w 2.6.6 Estimasi Kesalahan

Kesalahan (E) dalam rumus Gauss n titik ( secara lebih akurat, rumus Gauss Legendre) adalah ( ); 1 1. } )! 2 ){( 1 2 ( } )! {( 2 (2 ) 3 4 1 2 < < − + ≈ + n ξ ξ n f n n n E (2.117)

Seperti yang ditetapkan sebelumnya, rumus n titik mengintegrasikan sebuah polinomial dengan derajat (2n – 1) secara tepat, karena turunan dari order (2n), f(2n), adalah nol dalam kasus ini. Asumsikan skala dari order yang lebih tinggi menurun (atau menaik secara lambat) dengan menaikkan nilai n, rumus Gauss secara signifikan lebih akurat daripada rumus Newton-Cotes.