Fisika Statistik untuk Mahasiswa MIPA

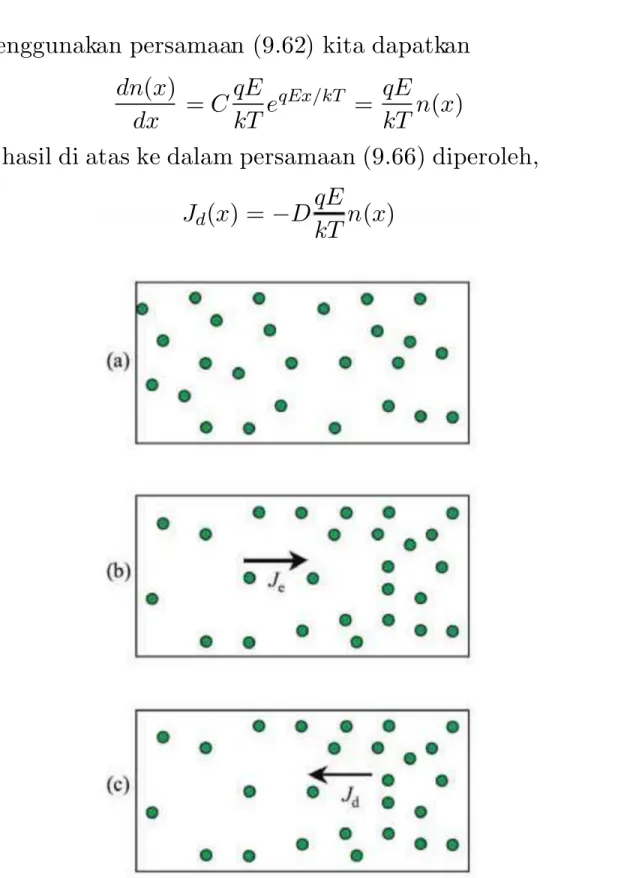
Fisika Statistik untuk Fisika Statistik untuk

Mahasiswa MIPA Mahasiswa MIPA

Mikrajuddin Abdullah, DR.Eng.

Mikrajuddin Abdullah, DR.Eng.

KK Fisika Material Elektronik - FMIPA, ITB 

KK Fisika Material Elektronik - FMIPA, ITB 

ii ii

Copyright

Copyright 2002009 9 by by MikrMikrajuddin ajuddin AbdullaAbdullahh

All rights reserved.

All rights reserved.

ISBN ...

ISBN ...

  

untuk Ayahanda 

untuk Ayahanda   H. Abdullah Hasan (  H. Abdullah Hasan (^alm alm ))  dan Ibunda   dan Ibunda  Hj.Hj.

St.Habibah St.Habibah

iv iv

Kata Pengantar Kata Pengantar

Buku ini disusun untuk membantu mahasiswa memahami Fisika Statistik Buku ini disusun untuk membantu mahasiswa memahami Fisika Statistik lebih mudah

lebih mudah. . Uraian diberikUraian diberikan serinci mungkian serinci mungkin, n, tahap demi tahap, sehinggatahap demi tahap, sehingga mahasiswa dapat mengikutinya dengan mudah. Mata kuliah Fisika Statistik mahasiswa dapat mengikutinya dengan mudah. Mata kuliah Fisika Statistik sampa

sampai i seksekarang menjadi momok bagi arang menjadi momok bagi sebagisebagian ban besar mahasiswesar mahasiswa. a. ketketidak-idak- tersediaan buku yang menjelaskan materi secara rinci tampaknya menjadi tersediaan buku yang menjelaskan materi secara rinci tampaknya menjadi salah

salah satu satu penypenyebab ebab terjaditerjadinynyaa   bottle neck   bottle neck  keterlambatan kelulusan maha- keterlambatan kelulusan maha- siswa akibat gagal dalam menyelesaikan mata kuliah tersebut.

siswa akibat gagal dalam menyelesaikan mata kuliah tersebut.

Buku ini hanya membahas dasar-dasar Fisika Statistik untuk memberi- Buku ini hanya membahas dasar-dasar Fisika Statistik untuk memberi- kan bekal yang memadai bagi mahasiswa untuk memahami Fisika Statistik kan bekal yang memadai bagi mahasiswa untuk memahami Fisika Statistik lanjut. Masih banyak kekurangan yang muncul disana-sini. oleh karena itu lanjut. Masih banyak kekurangan yang muncul disana-sini. oleh karena itu kritik dan saran yang membangun dari pembaca sangat diharapkan untuk kritik dan saran yang membangun dari pembaca sangat diharapkan untuk menyempurnakan isi buku ini.

menyempurnakan isi buku ini.

Penyelesaian buku ini tidak lepas dari tunjangan dana Hibah Penulisan Penyelesaian buku ini tidak lepas dari tunjangan dana Hibah Penulisan Buku T

Buku Teks 2009 eks 2009 dari Institut Tedari Institut Teknoloknologi gi Bandung yang penulis terima. Bandung yang penulis terima. OlehOleh karena itu penulis sampaikan terima kasih sebesar-besarnya kepada Wakil karena itu penulis sampaikan terima kasih sebesar-besarnya kepada Wakil Rektor Senior Bidang Akademik ITB dan Direktur Pendidikan ITB. Terima Rektor Senior Bidang Akademik ITB dan Direktur Pendidikan ITB. Terima k

kasasih ih jujuga ga penpenululis is sasampmpaiaikkan an kkepepadada a PrProfof. . IsIsmmununanandadar r dadan n DrDr. . DhDhiaiann Dam

Damajani ajani ataatas s supsupport port yayang ng sansangat gat berhaberharga rga daldalam am proproses ses penypenyeleselesaiaaiann buku ini.

buku ini.

Kepa

Kepada da penpenyunyuntinting, g, Dr. Dr. Siti Nurul KhatiSiti Nurul Khatimah dari mah dari ProdProdi i FisFisikika a ITBITB,, penulis sampaikan terima kasih sebesar-besaranya atas masukan dan saran penulis sampaikan terima kasih sebesar-besaranya atas masukan dan saran yang sangat berharga.

yang sangat berharga. Penulis juga ingin menyPenulis juga ingin menyampaikampaikan terima kasih kan terima kasih kepadaepada para rekan-rekan dosen di Program Studi Fisika-FMIPA ITB yang secara para rekan-rekan dosen di Program Studi Fisika-FMIPA ITB yang secara langs

langsung ung maupun maupun tidak tidak langslangsung ung memmembanbantu tu penulis menyelpenulis menyelesaikesaikan an bukubuku ini.

ini.

T

Terima kasih secara khusus ingin erima kasih secara khusus ingin penulis sampaikan pada keluarga penulis sampaikan pada keluarga penulispenulis (istri, Sri Rumiyati, dan anak-anakku, Shafira Khairunnisa, Fathan Akbar, (istri, Sri Rumiyati, dan anak-anakku, Shafira Khairunnisa, Fathan Akbar,

vi

dan Ardi Khalifah) yang tiada henti-hentinya memberikan support dalam setiap langkah pengabdian penulis dan ikut terlibat dalam pengecekan ke- salahan ketik dalam naskah buku ini.

Bandung, Desember 2009

Mikrajuddin Abdullah

Daftar Isi

1 Pendahuluan 1

2 Statistik Maxwell-Boltzmann 5

2.1 Konfigurasi Penyusunan Sistem Klasik . . . 5

2.2 Konfigurasi dengan Probabilitas Maksimum . . . 14

2.3 Harga Rata-Rata . . . 16

2.4 Nilai Peluang Konfigurasi Maksimum . . . 19

3 Ruang Fasa 23 3.1 Definisi Ruang Fasa . . . . . . . . . . . . . . . . . . . . . . . 23

3.2 Elemen volume Ruang Fasa . . . 25

3.3 Energi Kinetik . . . 26

3.4 N   Sistem dalam Ruang Fasa . . . 26

3.5 Menghitung Jumlah Keadaan . . . 28

3.6 Menentukan ns . . . . . . . . . . 31

3.7 Elemen Ruang Fasa dalam Momentum/Laju . . . 32

4 Parameter-Parameter Statistik 35 4.1 Menentukan Parameter β . . . . . . . . . . . . . . . . . . . . 35

4.2 Bagaimana Kebergantungan β pada Suhu? . . . 39

4.3 Menentukan β dari Energi Rata-Rata . . . 42

4.4 Menentukan Parameter α . . . . . . . . . . . . . . . . . . . . 44

4.5 Makna Parameter α . . . . . . . . . . 47

viii DAFTAR ISI

5 Statistik Bose-Einstein 51

5.1 Sifat Dasar Boson . . . 51

5.2 Konfigurasi Boson . . . 53

5.3 Konfigurasi Maksimum . . . 56

5.4 Parameter α untuk Photon dan Phonon . . . 59

6 Statistik Fermi-Dirac 63 6.1 Konfigurasi Fermion . . . 64

6.2 Konfigurasi Peluang Maksimum . . . 67

7 Rapat Keadaan Sistem Kuantum 71 7.1 Ketidakpastian Heisenberg . . . 71

7.2 Koordinat Spasial Satu Dimensi . . . 72

7.3 Koordinat Spasial Dua Dimensi . . . 73

7.4 Koordinat Spasial Tiga Dimensi . . . 76

8 Beberapa Besaran Gas 81 8.1 Laju dengan Peluang Maksimum . . . 81

8.2 Laju Rata-Rata . . . 84

8.3 Laju Root Mean Square  . . . . . . . . . . . . . . . . . . . . . 85

8.4 Distribusi Partikel dalam Besaran Lain . . . 87

9 Aplikasi Statistik Maxwell-Boltzmann 93 9.1 Efek Doppler . . . 93

9.2 Atom Magnetik dalam Medan Magnet . . . 97

9.3 Dipol Listrik . . . 102

9.4 Momen Magnetik Tiga Arah Orientasi . . . 104

9.5 Momen Magnetik Orientasi Sembarang . . . 106

9.6 Vibrasi Kisi dalam Kristal . . . 110

9.7 Hopping . . . 113

9.8 Persamaan Difusi Einstein . . . 117

9.9 Prinsip Ekipartisi Energi . . . 120

2.1 Konfigurasi Penyusunan Sistem Klasik 9

Jumlah sistem pada kelompok energi ketiga : n₃ ...

Jumlah sistem pada kelompok energi ke-s : ns

...

Jumlah sistem pada kelompok energi ke-M  : nM 

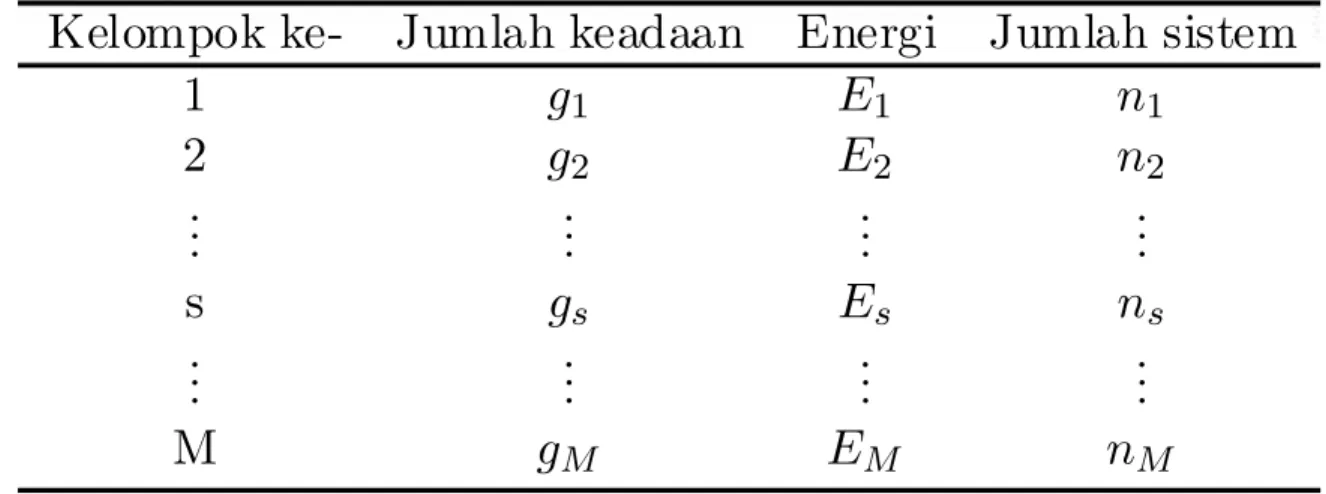
Deskripsi tentang jumlah sistem, jumlah keadaan dan energi pada kelompok- kelompok yang telah diuraikan di atas dapat diringkas dalam Table 2.1.

Tabel 2.1: Deskripsi jumlah sistem, jumlah keadaan, dan energi yang dimiliki tiap kelompok energi.

Kelompok ke- Jumlah keadaan Energi Jumlah sistem

1 g₁ E ₁ n₁

2 g2 E 2 n2

... ... ... ...

s gs E s ns

... ... ... ...

M g_M  E _M  n_M 

Jumlah total sistem dalam assembli adalah N . Karena N  sistem tersebut terdistribusi pada semua kelompok energi maka terpenuhi

N  =

M 



s=1

ns   (2.1)

Energi total assembli memenuhi

U =

M 



s=1

n_sE _s   (2.2)

Untuk menentukan nilai dari besaran-besaran yang dimiliki assembli ki- ta harus menentukan berapa probabilitas munculnya masing-masing kon- figurasi dalam assembli tersebut. Tiap penyusunan sistem dalam assembli

 

 

 

10 Statistik Maxwell-Boltzmann mempunyai peluang kemunculan yang persis sama. Dengan demikian, prob- abilitas kemunculan sebuah konfigurasi sebanding dengan jumlah penyusunan sistem yang dapat dilakukan untuk membangun konfigurasi tersebut.

Oleh karena itu, mencari probabilitas kemunculan konfigurasi dengan kondisi

Ada n1 sistem pada kelompok energi 1 Ada n₂ sistem pada kelompok energi 2 Ada n3 sistem pada kelompok energi 3

...

Ada n_s sistem pada kelompok energi s ...

Ada n_M  sistem pada kelompok energi M  ekivalen dengan mencari berapa cara penyusunan

n1 sistem pada g1 keadaan energi di kelompok energi 1 n₂ sistem pada g₂ keadaan energi di kelompok energi 2 n3 sistem pada g3 keadaan energi di kelompok energi 3

...

ns sistem pada gs keadaan energi di kelompok energi s ...

n_M  sistem pada g_M  keadaan energi di kelompok energi M 

 

 

 

 

 

 

 

 

 

 

2.1 Konfigurasi Penyusunan Sistem Klasik 11

Selanjutnya kita akan menentukan jumlah cara penyusunan sistem-sis- tem yang tersebar pada tingkat-tingkat energi di atas. Untuk maksud terse- but, mari kita mulai dengan menganggap semua keadaan energi kosong (tidak di tempati sistem) dan di luar ada sejumlah sistem yang akan diisi pada keadaan-keadaan tersebut. Di sini ada dua tahap proses yang terjadi.

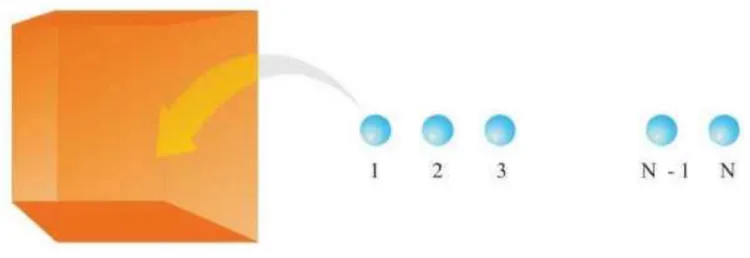
Proses I adalah membawa N  buah sistem dari luar ke dalam assembli dan proses II adalah menyusun sistem pada kempompok-kelompok energi yang ada di dalam assembli.

Gambar 2.3: Cara membawa sistem dari luar masuk ke dalam assembli.

Proses I: Membawa N  Buah Sistem ke Dalam Assembli. Mari kita hitung jumlah cara yang dapat ditempuh pada tiap proses pertama yaitu membawa N   buah sistem dari luar ke dalam assembli. Proses ini tidak bergantung pada konfigurasi assembli. Yang terpenting adalah bagaimana membawa masuk N   buah sistem ke dalam assembli. Untuk menentukan  jumlah cara tersebut, perhatikan tahap-tahap berikut ini.

i) Ambil satu sistem dari daftar N   buah sistem yang berada di luar assembli (Gbr. 2.3). Kita bebas memilih satu sistem ini dari N   buah sistem yang ada tersebut. Jadi jumlah cara pemilihan sistem yang pertama kali dibawa masuk ke dalam assembli adalah N   cara.

ii) Setelah sistem pertama dimasukkan ke dalam assembli maka tersisa N 

 −

1 sistem dalam daftar di luar. Ketika membawa masuk sistem kedua ke dalam assembli kita dapat memilih salah satu dari N 

 −

¹

buah sistem dalam daftar. Jumlah cara pemilihan sistem ini adalah N 

 −

^{1 cara.}

iii) Begitu seterusnya.

3

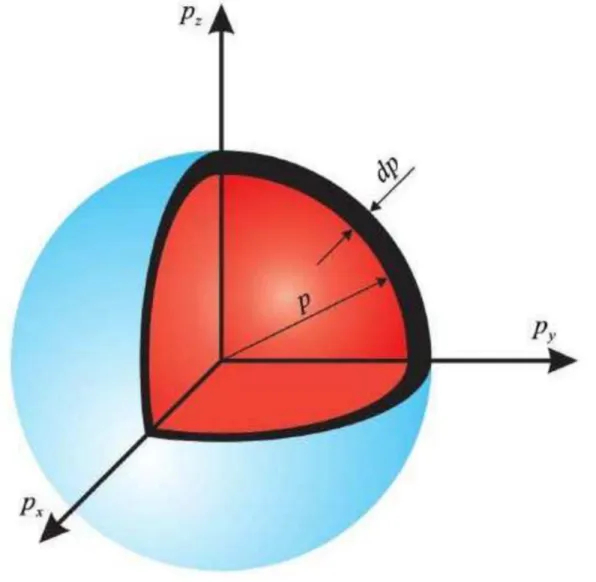
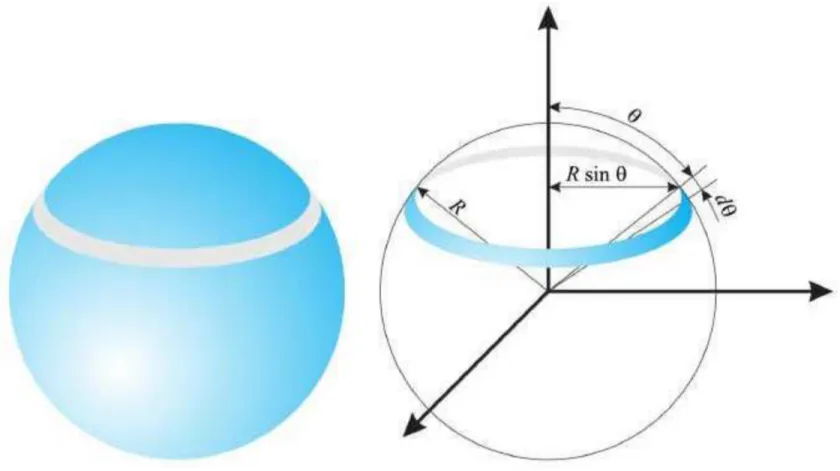
3..5 5 MMeenngghhiittuunng g JJuummllaah h KKeeaaddaaaan n 2299

Gambar 3.2:

Gambar 3.2: Bola pada ruang momentum. Jari-jari bola adalah Bola pada ruang momentum. Jari-jari bola adalah

√  √ 

_22mE mE ..

Jik

Jika a kita bagi kita bagi energi assemblenergi assembli i atas kelompok-atas kelompok-kelkelompok ompok energi maka tiapenergi maka tiap kel

kelompok akaompok akan n diwdiwakili oleh kulit akili oleh kulit bola bola dengan ketebdengan ketebalan tertentalan tertentu. u. Mari kitaMari kita ambil elemen volume pada kulit bola dengan jari-jari

ambil elemen volume pada kulit bola dengan jari-jari

√  √ 

_22mE mE  dan ketebalan dan ketebalan d

d((

√  √ 

_22mE mE ) (Gbr. 3.3). Luas kulit bola tersebut adalah) (Gbr. 3.3). Luas kulit bola tersebut adalah S 

S  p p = = 44ππ

 √  √ 22mE mE 22 = = 88πmE πmE     (3.7)(3.7)

Tebal kulit bola adalah Tebal kulit bola adalah d

d

 √  √ 22mE mE  = = √  √ 22mm dd √  √ E E 

=

=

√  √ 

_22mm

×

×

¹¹₂₂^E E 

− −

^11//22dE dE 

=

=

√ 

√ 

_22mm

22 E E 

− −

^11//22_dE dE 

(3.8) (3.8)

3

300 RRuuaanngg FFaassaa

Gambar 3.3:

Gambar 3.3: Elemen volume dalam ruang momentum berupa kulit bola. Elemen volume dalam ruang momentum berupa kulit bola.

Dengan demikian, volume kulit bola adalah Dengan demikian, volume kulit bola adalah

dV 

dV  _p p = = S  S  _p pdd

 √  √ 22mE mE 

=

= 88πmE πmE 

√ 

√ 

_22mm

22 E E 

− −

^11//22_dE dE 

=

= 22ππ(2(2mm))^33//22E E ^11//22dE dE 

(3.9) (3.9)

Volume ruang fasa yang ditempati oleh sistem yang berada pada kulit Volume ruang fasa yang ditempati oleh sistem yang berada pada kulit bola momentum serta dalam elemen volume spasial

bola momentum serta dalam elemen volume spasial dV dV ss = = dxdydz dxdydz adalah adalah d

dΓ Γ == dxdydz dxdydz22ππ(2(2mm))^33//22E E ^11//22dE dE     (3.10)(3.10) Volume ruang fasa yang ditempati oleh sistem pada semua ruang spasial, Volume ruang fasa yang ditempati oleh sistem pada semua ruang spasial, tetapi tetap berada dalam kulit bola momentum diperoleh dengan mengin- tetapi tetap berada dalam kulit bola momentum diperoleh dengan mengin-

3.6 Menentukan

3.6 Menentukan nn_ss 3131

tegralkan persamaan (3.10) pada elemen ruang spasial. Hasilnya adalah tegralkan persamaan (3.10) pada elemen ruang spasial. Hasilnya adalah

∆Γ

∆Γ p p ==

   

  _{dxdydz  dxdydz22ππ(2(2mm))}^33//22_E E ^11//22_dE dE 

=

= 22πV πV (2(2mm))^33//22E E ^11//22dE dE 

(3.11) (3.11)

dengan

dengan V V  ==

   

 ^{dxdydz dxdydz} adalah volume total ruang spasial yang tidak lain adalah volume total ruang spasial yang tidak lain merupakan volume assembli itu sendiri.

merupakan volume assembli itu sendiri.

Kita belum mengetahui berapa kerapatan keadaan dalam ruang fasa.

Kita belum mengetahui berapa kerapatan keadaan dalam ruang fasa.

Untuk sementara kita menganggap kerapatan keadaan tersebut adalah Untuk sementara kita menganggap kerapatan keadaan tersebut adalah BB..

Jumlah keadaan dalam elemen ruang fasa ∆Γ

Jumlah keadaan dalam elemen ruang fasa ∆Γ p p sama dengan volume ruang sama dengan volume ruang fasa dikali kerapatannya, yaitu

fasa dikali kerapatannya, yaitu B

B∆Γ∆Γ p p =  = 22πVπV BB(2(2mm))^33//22E E ^11//22dE dE     (3.12)(3.12) Persamaan (3.12) mirip dengan persamaan untuk mencari massa dengan Persamaan (3.12) mirip dengan persamaan untuk mencari massa dengan mengal

mengalikikan an rapat massa rapat massa dan dan volvolume. ume. JikJika a kelkelompok-kompok-kelompok energi elompok energi yayangng kita bangun di dalam assembli diwakili oleh kulit bola maka kita dapat kita bangun di dalam assembli diwakili oleh kulit bola maka kita dapat menyamakan dalam persamaan (2.11) dengan

menyamakan dalam persamaan (2.11) dengan B B∆Γ∆Γ p p pada persamaan (3.12). pada persamaan (3.12).

Akhirnya, kita dapatkan ungkapan untuk

Akhirnya, kita dapatkan ungkapan untuk ggss sebagai sebagai

ggss = = 22πVπV BB(2(2mm))^33//22E E ^11//22dE dE     (3.13)(3.13)

3.

3.6 6 Me Mene nen ntu tuk kan an n n

_ss

Setelah mengetahu

Setelah mengetahui i bentukbentuk gg_ss  dalam fungsi kontinu yaitu yang tertuang  dalam fungsi kontinu yaitu yang tertuang dalam persamaan (3.13), selanjutnya kita akan menentukan

dalam persamaan (3.13), selanjutnya kita akan menentukan nn_ss dalam ben- dalam ben- tuk kontinu juga. Dalam bentuk diskrit, hubungan antara

tuk kontinu juga. Dalam bentuk diskrit, hubungan antara n nss dandan g gss adalah adalah n

n_ss == gg_ss ex expp [[αα++E E _ss]. ]. PaPada huda hubungbungan ini,an ini, n n ss  menyatakan jumlah sistem.  menyatakan jumlah sistem.

Sekarang kita mendefisikan karapat sistem, yaitu jumlah sistem per satu- Sekarang kita mendefisikan karapat sistem, yaitu jumlah sistem per satu- an

an enerenergi. gi. UnUntuk keratuk kerapatpatan an sissistem kita tem kita gungunakakan an symsymbolbol nn((E E ). ). DeDengnganan demikian, jumlah sistem dalam kulit bola yang dibatasi oleh energi

demikian, jumlah sistem dalam kulit bola yang dibatasi oleh energi E E dandan E 

E  + +dE dE  adalah adalah n n((E E ))dE dE . Dengan mengganti. Dengan mengganti n n_ss dengan dengan n n((E E ))dE dE dandan g g_ss den- den- gan persamaan (3.13) kita dapatkan hubungan antara jumlah sistem dan gan persamaan (3.13) kita dapatkan hubungan antara jumlah sistem dan kerapatan keadaan dalam bentuk kontinu sebagai berikut

kerapatan keadaan dalam bentuk kontinu sebagai berikut n

n((E E ))dE dE = = 22πVπV BB(2(2mm))^33//22E E ^11//22dE dE 

 ×  ×

^{eeαα++βE βE} 

=

= 22πVπV BB(2(2mm))^33//22ee^{αα++βE βE} E E ^11//22dE dE  (3.14)(3.14)

3

322 RRuuaanngg FFaassaa

3.7

3.7 Ele Elemen men Rua Ruang F ng Fasa asa da dalam lam Mo Momen mentu tum/L m/Laju aju

Persamaan (3.11) menyatakan elemen volume ruang fasa dinyatakan dalam Persamaan (3.11) menyatakan elemen volume ruang fasa dinyatakan dalam v

variabel energi. ariabel energi. Kita juga Kita juga dapat menydapat menyatakatakan an elemen volumelemen volume e tersebutersebut t dalamdalam v

variariabel momenabel momentum atau latum atau laju. ju. KitKita a mumulai dari lai dari huhubungbunganan E E  == pp²²//22mm se-se- hingga

hingga

E 

E ^11//22 ==

 

¹¹

22mm





^11//22 _{p p    (3.15)(3.15)}

dE  dE == 11

m

m pdp pdp    (3.16)(3.16) Substitusi persamaan (3.15) dan (3.16) ke dalam persamaan (3.11) diperoleh Substitusi persamaan (3.15) dan (3.16) ke dalam persamaan (3.11) diperoleh ungkapan elemen ruang fasa dinyatakan dalam momentum sebagai berikut.

ungkapan elemen ruang fasa dinyatakan dalam momentum sebagai berikut.

∆Γ

∆Γ p p =  = 22πV πV (2(2mm))^33//22

× ×   11

22mm





^11//22 _p p

×

×

_mm^11 pdp pdp

=

= 44πVπV pp²²dpdp

(3.17) (3.17)

Mengingat hubungan antara momentum dan laju

Mengingat hubungan antara momentum dan laju pp == mvmv  maka  maka dpdp == mdv

mdv. Konsekuensinya, kita dapat menulis elemen ruang fasa dalam koordi-. Konsekuensinya, kita dapat menulis elemen ruang fasa dalam koordi- nat laju sebagai berikut,

nat laju sebagai berikut,

∆Γ

∆Γ_vv = = 44πV πV ((mvmv))²²((mdvmdv))

=

= 44πVπV mm³³vv²²dvdv (3.18)(3.18) Dengan menggunakan persamaan (3.18) maka kita dapatkan

Dengan menggunakan persamaan (3.18) maka kita dapatkan ggss == B B∆Γ∆Γ p p == 44πBVmπBVm³³vv²²dvdv dan kerapatan keadaan menjadi dan kerapatan keadaan menjadi

n

n((vv))dvdv = = gg_ssee^{αα++βE βE} 

=

= 44πBVmπBVm³³vv²²dvdv

× ×

^{eeαα++β β ((mvmv22//2)2)}

=

= (4(4πBVmπBVm³³ee^αα))vv²²ee^{βmvβmv22//22}dvdv

(3.19) (3.19)

Hasil yang kita peroleh di atas akan sering kita jumpai pada bab-bab berikut- Hasil yang kita peroleh di atas akan sering kita jumpai pada bab-bab berikut- ny

nya, a, khuskhususnusnya ya saat melakuksaat melakukan an transftransformasormasi i dari dari penjumlahpenjumlahan an diskrdiskrit it keke integral kontinu.

integral kontinu.

Soal Latihan Soal Latihan

1.

1. JelaskJelaskan apa yang dimakan apa yang dimaksud ruang fasa dan mengapa ruang fasa pen-sud ruang fasa dan mengapa ruang fasa pen- ting dalam fisika statistik.

ting dalam fisika statistik.

3

3..7 7 EElleemmeen n RRuuaanng g FFaassa a ddaallaam m MMoommeennttuumm//LLajaju u 3333 2.

2. Sebuah asseSebuah assemblmbli mengandungi mengandung N  N  sistem. Ada berapa koordinat ruang sistem. Ada berapa koordinat ruang fasa yang diperlukan untuk menggambar assembli tersebut?

fasa yang diperlukan untuk menggambar assembli tersebut?

3.

3. Berapa energi kinetBerapa energi kinetik suatu sistem yaik suatu sistem yang memilikng memiliki koordinat ruang fasai koordinat ruang fasa antara (

antara (x,y,z,px,y,z,p_xx,, pp_yy,, pp_zz) sampai () sampai (xx++dx,ydx,y + + dy,zdy,z + + dz,pdz,p_xx + + dpdp_xx,, pp_yy + + dp

dp_yy,, pp_zz + + dpdp_zz).).

4.

4. MisalMisalkkan kerapatan kerapatan keadaan dalam ruang fasa adalahan keadaan dalam ruang fasa adalah BB, berapa jum-, berapa jum- lah keadaan dalam elemen ruang fasa antara (

lah keadaan dalam elemen ruang fasa antara ( p p_xx,, pp_yy,, pp_zz) sampai () sampai ( p p_xx + + dp

dp_xx,, pp_yy + + dpdp_yy,, pp_zz + + dpdp_zz) pada seluruh ruang spasial.) pada seluruh ruang spasial.

5.

5. KeKemmbabali li kke e sosoal al nono. . 4, 4, berberapapa a jujumlmlah ah kkeaeadadaan an dadalalam m ruruanang g fafasasa dengan energi kinetik antara

dengan energi kinetik antara E E  sampai sampai E E  + + dE  dE  dalam seluruh ruang dalam seluruh ruang spasial?

spasial?

34 Ruang Fasa

Bab 4

Parameter-Parameter Statistik

Isi Bab ini.  Bab ini berisi penentuan parameter α dan β  yang terdapat dalam fungsi distribusi Maxwell-Boltzmann. Parameter-parameter terse- but telah diperkenalkan untuk mengakomodasi hukum kekekalan energi dan  jumlah partikel yang dimiliki assembli.

Tujuan Bab ini. Tujuan bab ini adalah mahasiswa memahami bagaimana menentukan parameter α dan β  dalam fungsi distribusi Maxwell-Boltzmann dan alasan-alasan yang digunakan dalam proses penentuan parameter-para- meter tersebut.

Apa yang Perlu Dikuasai Lebih Dahulu. Pemahaman tentang isi Bab 2 dan Bab 3 sangat penting untuk mengikuti penjelasan dalam bab ini.

Juga pemahaman tentang konsep entropi yang dipelajari di termodinami- ka serta dasar prinsip ekipartisi energi yang dipelajari pada gas ideal juga sangat membantu dalam memahami isi bab ini.

4.1 Menentukan Parameter β

Ketika mencari konfigurasi dengan probabilitas terbesar, kita memperke- nalkan dua pengali Lagrange, yaitu α dan β   untuk mengakomodasi syarat batas bahwa jumlah sistem dan energi assembli harus konstan. Pertanyaan berikutnya adalah adakah makna fisis parameter-parameter tersebut? Inilah yang kita bahas sekarang.

36 Parameter-Parameter Statistik

Sudah kita tunjukkan bahwa jumlah sistem yang menempati kelompok energi dengan energi rata-rata E s  dan mengandung keadaan sebanyak gs

memenuhi persamaan (2.11) yaitu n_s = g_se^α+βE s. Secara fisis kita meyakini bahwa tidak mungkin ada sistem yang memiliki energi tak berhingga. Oleh karena itu jika E _s

 → ∞

maka haruslah n_s

 →

0. Ini hanya mungkin terpenuhi  jika parameter β bernilai negatif . Lalu, bergantung pada besaran apakah 

parameter β ? 

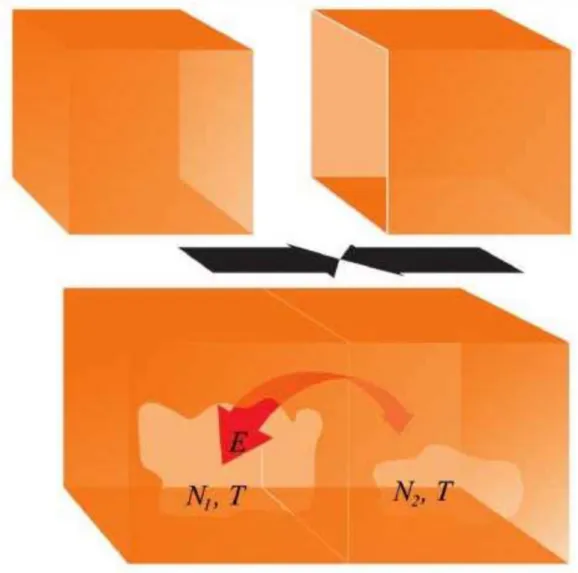
Gambar 4.1:   Dua buah assembli terisolasi digabung setelah membuka masing- masing satu sisinya. Pada batas dua assembli diijinkan pertukaran energi tetapi tidak diijinkan pertukaran partikel.

Setelah mengetahui bahwa nilai parameter β   harus negatif mari kita mencari bentuk ekspresi dari parameter tersebut. Untuk mempermudah mari kita tinjau dua assembli terisolasi dan berada pada suhu yang sama T . Kesamaan suhu bermakna bahwa kedua assembli berada dalam kesetim- bangan termal. Assembli pertama memiliki N 1 sistem dan assembli kedua mengandung N ₂  sistem. Kemudian salah satu sisi masing-masing assem- bli dilepas dan dua assembli dikontakkan pada sisi yang dilepas tersebut.

48 Parameter-Parameter Statistik

pati satu sistem adalah N/V . Jika dianggap satu sistem menempati ruang berbentuk kubus dengan panjang sisi l maka volume kubus adalah l³ dan memenuhi l³ = V /N . Jika sistem menempati pusat kubus, maka jarak rata- rata antar sistem sama dengan panjang sisi kubus, yaitu l.

Energi rata-rata sistem dalam ruang tiga dimensi adalah 3kT /2. Energi ini berasal dari energi kinetik sistem tersebut. Jadi

Energi kinetik rata-rata = ¯ p²/2m = 3kT /2 atau

¯

 p =

√ 

_{3mkT    (4.36)}

Panjang gelombang de Broglie rata-rata yang dimiliki sistem adalah λ =¯ h

¯  p

= h

√ 

_3mkT 

(4.37)

Dengan demikian, parameter α memenuhi

e^α = N/V 

Bh³(2π/3)3/2 (3mkT )^3/2 h³

= 1/³

Bh³(2π/3)^{3/2 1}_λ¯3

= 1

Bh³(2π/3)^3/2



^λ¯





³

(4.38)

Tampak dari persamaan (4.38) bahwa nilai α  bergantung pada rasio panjang gelombang de Broglie termal sistem dengan jarak rata-rata antar sistem. Pada suhu yang sangat rendah, momentum sistem sangat kecil se- hingga panjang gelombang de Broglie sangat besar. Akibatnya e^α jauh lebih besar dari satu. Sebaliknya, pada suhu sangat tinggi, momentum sistem san- gat besar sehingga panjang gelombang de Broglie sangat kecil. Akibatnya, nilai e^α jauh lebih kecil daripada satu.

Soal Latihan

1. Buktikan bahwa panjang gelombang termal de Broglie memenuhi λ = h/

√ 

_3mkT .

4.5 Makna Parameter α 49 2. Buktikan bahwa α

∝

ln(λ/) dengan λ  adalah panjang gelombang

termal de Broglie dan  adalah jarak rata-rata antar sistem.

50 Parameter-Parameter Statistik

5.4 Parameter α untuk Photon dan Phonon 61

2. Berapa batas jumlah sistem boson yang dapat menempati suatu keadaan?

3. Sebutkan contoh boson dan spin yang dimilikinya

4. Secara umum, fungsi distribusi untuk boson adalah n_s = g_s/

{

^exp[

−

^α

−

βE _s]

−

¹

}

. Tetapi, untuk foton, fungsi distribusi adalah n_s = g_s/

{

^exp[

−

^βE s]

−

1

}

. Jelaskan mengapa exp[

−

α] tidak muncul dalam fungsi distribusi foton?

62 Statistik Bose-Einstein

Bab 6

Statistik Fermi-Dirac

Isi Bab ini. Bab ini berisi perumusan statistik Fermi-Dirac untuk assembli fermion, yaitu partikel kuantum dengan spin merupakan kelipatan ganjil dari

 . Partikel ini memiliki satu sifat khas, yaitu memenuhi prinsip eksklusi Pauli. Bersadarkan prinsip ini maka  tidak ada fermion yang boleh memi- liki sekumpulan bilangan kuantum yang sama . Satu keadaan energi hanya boleh ditempati maksimum oleh dua fermion dengan syarat arah spin harus berlawanan. Contoh partikel fermion adalah elektron, proton, dan positron.

Tujuan Bab ini. Tujuan bab ini adalah mahasiswa memahami bagaimana proses membangun statistik Fermi-Dirac dengan menggunakan prinsip statis- tik murni yang digabungkan dengan prinsip kekekalan dalam fisika seperti kekekalan energi dan jumlah partikel.

Apa yang Perlu Dikuasai Lebih Dahulu. Untuk memahami penu- runan fungsi distribusi Fermi-Dirac mahasiswa perlu memahami prinsip per- mutasi untuk benda-benda yang tidak dapat dibedakan, sifat yang ditun-  jukkan oleh sebuah besaran yang nilainya kekal (konstan), serta bagaimana mencari nilai maksimum dari sebuah fungsi. Pemahaman tentang penu- runan distribusi Maxwell-Boltzmann serta Bose-Einstein juga merupakan modal berharga untuk memahami penurunan distribusi Fermi-Dirac secara lebih mudah.

6.2 Konfigurasi Peluang Maksimum 67 Selanjutnya kita perlu menentukan berapa cara membawa N  sistem dari luar untuk didistribusikan ke dalam keadaan-keadaan di dalam assembli.

Seperti yang kita bahas pada assembli boson, untuk partikel tidak terbe- dakan jumlah cara tersebut adalah N !/N ! = 1. Akhirnya, jumlah cara penyusunan fermion untuk konfigurasi di atas adalah

W =

M 



s=1

g_s!

(g_s

−

^ns)!ns!

atau dalam notasi logaritma

lnW =

M 



s=1

ln



^gs!

(g_s

−

^ns)!ns!



  _(6.4)

6.2 Konfigurasi Peluang Maksimum

Jumlah total sistem dalam assembli dan energi total assembli masing-masing adalah N  =



^M 

s=1

ns dan U  =



^M 

s=1

E sns. Untuk sistem terisolasi di mana tidak terjadi pertukaran partikel maupun energi antara assembli dan lingkungan maka jumlah partikel selalu konstan dan energi total juga konstan. Dengan demikian bentuk diferensial dari N  dan U   adalah

δN =

M 



s=1

δn_s = 0 (6.5)

δU  =

M 



s=1

E _sδn_s = 0 (6.6)

Konfigurasi dengan probabilitas maksimum diperoleh dengan memak- simalkan W   atau lnW  dengan memperhatikan konstrain pada persamaan (6.5) dan (6.6). Sebelum kearah itu kita coba sederhanakan pada persamaan (6.4).

lnW =

M 



s=1

lng_s!

−

^ln(gs

−

^ns)!

−

^lnns!

68 Statistik Fermi-Dirac Selanjutnya kita gunakan pendekatan Stirling untuk menyederhanakan fak- torial, yaitu

lng_s!

∼

^= gs lng_s

−

^gs

ln(g_s

−

^ns)!

∼

^= (gs

−

^ns)ln(gs

−

^ns)

−

^(gs

−

^ns)

lnns!

∼

^= ns lnns

−

^ns

Dengan demikian bentuk lnW  dapat diaproksimasi sebagai berikut lnW 

 ∼

⁼

M 



s=1

g_s lng_s

−

^gs

−

^(gs

−

^ns)ln(gs

−

^{ns) + (gs}

−

^ns)

−

^{ns lnns + ns}

=

M 



s=1

g_s lng_s

−

^(gs

−

^ns)ln(gs

−

^ns)

−

^ns lnns

(6.7) Selanjunya, ambil diferensial kedua ruas persamaan (6.7)

δ lnW =

M 



s=1

δ [g_s lngs]

−

^δ [(gs

−

^ns)ln(gs

−

^ns)]

−

^{δ [ns lnns] (6.8)}

Mari kita hitung satu per satu suku dalam persamaan (6.8) i)

δ [gs lngs] = ∂ 

∂ns [gs lngs]δns = 0 ii)

δ [(g_s

−

^ns)ln(gs

−

^{ns)] =} _∂n^∂ _s ^[(gs

−

^ns)ln(gs

−

^ns)]δns

=



−

^ln(gs

−

^{ns) + (gs}

−

^ns)

×

_(gs

−

^{1 ns)}

×

(

−

¹⁾



_δn

s

=

−

^[ln(gs

−

^{ns) + 1]δns}

iii)

δ [n_s lnn_s] = ∂ 

∂ns [n_s lnn_s]δn_s =



_lnn

s + n_s

×

_n¹_s

×

¹



_δn

s = [lnn_s + 1]δn_s

6.2 Konfigurasi Peluang Maksimum 69 Dari hasil di atas maka bentuk δ lnW   dapat ditulis dalam bentuk lebih sederhana sebagai berikut

δ lnW =

M 



s=1

0 + [ln(g_s

−

^{ns) + 1]δns}

−

^{[lnns + 1]δns}

=

M 



s=1

[ln(g_s

−

^ns)

−

^lnns]δns

=

M 



s=1

ln



^gs

−

^ns

n_s



_δn

s

(6.9)

Konfigurasi dengan probabilitas maksimum diperoleh dengan mencari solusi untuk persamaan δ lnW + αδN +βδU  = 0, atau

M 



s=1

ln



^gs

−

^ns

ns



_δn

s + α

M 



s=1

δn_s + β 

M 



s=1

E _sδn_s = 0

M 



s=1



_ln



^gs

−

^ns

n_s



_{+ α+βE} 

s



 _{= 0}

(6.10)

Agar persamaan (6.10) selalu nol untuk variasi δn_s  yang sembarang maka harus terpenuhi

ln



^gs

−

^ns

n_s



_{+ α+βE} 

s = 0 gs

−

^ns

n_s = exp (

−

^α

−

^βE s)

yang memberikan ungkapan untuk n_s sebagai n_s = gs

exp(

−

^α

−

^{βE s) + 1   (6.11)}

Berlaku juga pada fungsi distribusi fermion bahwa parameter β  memenuhi β  =

−

1/kT . Dengan parameter ini maka kita dapat menulis persamaan (6.11) secara lebih eksplisit sebagai

n_s = g_s

exp(

−

^{α+ E s/kT ) + 1   (6.12)}

Persamaan (6.12) merupakan bentuk umum fungsi distribusi Fermi-Dirac untuk fermion.

7

70 0 SSttaattiissttiik k FFeerrmmii--DDiirraacc

Soal Latihan Soal Latihan

1.

1. TTenentuktukan an semsemua ua kokonfignfiguraurasi si penypenyusuusunan nan yayang ng mumungkngkin in ununtuk tuk tigtigaa fermion pada empat tingkat energi

fermion pada empat tingkat energi E E ₁₁,, E E ₂₂,, E E ₃₃, dan, dan E E ₄₄, serta ener-, serta ener- gi yang berkaitan dengan masing-masing konfigurasi tersebut.

gi yang berkaitan dengan masing-masing konfigurasi tersebut.

2.

2. SebutkSebutkan contoh fermion dan an contoh fermion dan spin yang dimilikspin yang dimilikinyinyaa 3.

3. BuktikBuktikan an bahbahwa pada wa pada assemassembli fermion bli fermion jumlajumlah h keakeadaan lebih daan lebih banybanyakak daripada jumlah sistem.

daripada jumlah sistem.

4.

4. Suatu assemSuatu assembli fermion memilbli fermion memilikiiki M  M  keadaan dan keadaan dan N N   sistem. Sebutkan  sistem. Sebutkan bagaimana cara penyusunan sistem-sistem tersebut pada suhu

bagaimana cara penyusunan sistem-sistem tersebut pada suhu T T  = 00= K.

K.

5.

5. BerdasarkBerdasarkan fungsi an fungsi FFermi-Diracermi-Dirac n n_ss == g g_ss//

{{

^exp[exp[

− −

^αα

− −

^{βE βE ss]+]+11}

}}

^{, , buktikbuktikanan}

bahwa

bahwa nn_ss

 ≤  ≤

^ggss..

Bab 7 Bab 7

Rapat Keadaan Sistem Rapat Keadaan Sistem Kuantum

Kuantum

Isi Bab ini.

Isi Bab ini. Bab ini berisi diskusi tentang kerapatan keadaan sistem kuan- Bab ini berisi diskusi tentang kerapatan keadaan sistem kuan- tum, yang meliputi boson dan fermion. Salah satu perbedaan dengan sistem tum, yang meliputi boson dan fermion. Salah satu perbedaan dengan sistem klasik adalah terpenuhinya

klasik adalah terpenuhinya prinsip ketidakpastian Heisenberg prinsip ketidakpastian Heisenberg pada sis- pada sis- tem kaun

tem kauntum. tum. NamNamun un akakan an tampak bahwtampak bahwa, a, tidak ada tidak ada perbedaan perbedaan signifisignifikkanan an

antartara a kekeraprapataatan n kekeadaadaan an sissistem tem klaklasik dan sik dan sissistem tem kuakuantntum. um. PPerbedaerbedaanan hanya terletak pada keberadaan elemen ruang fasa minimal yang diijinkan hanya terletak pada keberadaan elemen ruang fasa minimal yang diijinkan bagi sistem kuantum.

bagi sistem kuantum.

Tujuan Bab ini.

Tujuan Bab ini. TTujuan bab ini ujuan bab ini adalah mahasiswa memahami bagaimanaadalah mahasiswa memahami bagaimana menurunkan kerapatan keadaan sistem kuantum dan bagaimana mendap- menurunkan kerapatan keadaan sistem kuantum dan bagaimana mendap- atkan kerapatan keadaan tersebut dari kerapatan keadaan sistem klasik.

atkan kerapatan keadaan tersebut dari kerapatan keadaan sistem klasik.

Apa yang Perlu Dikuasai Lebih Dahulu.

Apa yang Perlu Dikuasai Lebih Dahulu. Untuk memahami bab ini Untuk memahami bab ini lebih baik, mahasiswa diharapkan memahami terlebih dahulu isi Bab 3.

lebih baik, mahasiswa diharapkan memahami terlebih dahulu isi Bab 3.

7.1

7.1 Ket Ketida idakp kpast astian ian Hei Heisen senberg berg

Setelah membahas beberapa aplikasi statistik Maxwell-Boltzmann yang ber- Setelah membahas beberapa aplikasi statistik Maxwell-Boltzmann yang ber- laku untuk partikel klasik, kita akan membahas beberapa aplikasi assembli laku untuk partikel klasik, kita akan membahas beberapa aplikasi assembli kuantum yang diungkapkan oleh distribusi Bose-Einstein dan Fermi-Dirac.

kuantum yang diungkapkan oleh distribusi Bose-Einstein dan Fermi-Dirac.

Namun, sebelum melangkah lebih jauh membahas beberapa aplikasi assembli Namun, sebelum melangkah lebih jauh membahas beberapa aplikasi assembli kuan

kuantum tersebut, mari kita tum tersebut, mari kita tenttentukukan dahulu kerapaan dahulu kerapatan keadaatan keadaan. n. Kerap-Kerap- atan keadaan menjadi penting ketika kita akan menghitung besaran-besaran atan keadaan menjadi penting ketika kita akan menghitung besaran-besaran

7

72 2 RRaappaat t KKeeaaddaaaan n SSiisstteem m KKuuaannttuumm termodinamika assembli tersebut. Dan yang paling sering kita jumpai adalah termodinamika assembli tersebut. Dan yang paling sering kita jumpai adalah ketika kita berpindah dari penjumlahan yang bersifat diskrit ke integral yang ketika kita berpindah dari penjumlahan yang bersifat diskrit ke integral yang bersifat kontinu.

bersifat kontinu.

Karena merupakan partikel kuantum maka pada boson maupun fermion Karena merupakan partikel kuantum maka pada boson maupun fermion kita harus menerapkan prinsip-prinsip mekanika kuantum. Salah satu prin- kita harus menerapkan prinsip-prinsip mekanika kuantum. Salah satu prin- sip dasar mekanika kuantum adalah prinsip ketidak pastian Heisenberg yang sip dasar mekanika kuantum adalah prinsip ketidak pastian Heisenberg yang dapat ditulis sebagai

dapat ditulis sebagai

∆

∆ p p∆∆xx

≥ ≥

^{hh    (7.1)(7.1)}

Prinsip ini menyatakan bahwa perkalian antara ketidakpastian momentum Prinsip ini menyatakan bahwa perkalian antara ketidakpastian momentum dan posisi tidak boleh lebih kecil dari konstanta Planck. Implikasinya adalah dan posisi tidak boleh lebih kecil dari konstanta Planck. Implikasinya adalah kita tidak mungkin mendefinisikan sebuah keadaan kuantum jika keadaan kita tidak mungkin mendefinisikan sebuah keadaan kuantum jika keadaan tersebut memuat ukuran momentum dan ukuran posisi sedemikian sehing- tersebut memuat ukuran momentum dan ukuran posisi sedemikian sehing- ga perkaliannya kurang dari

ga perkaliannya kurang dari hh. . DenDengan perkgan perkataataan lain, nilai terkan lain, nilai terkeciecil l dardarii perkalian ∆

perkalian ∆ p p dan ∆x dan ∆x yang bisa mendefisinisikan sebuah keadaan adalah yang bisa mendefisinisikan sebuah keadaan adalah hh..

Dari hasil ini kita selanjunya bisa menentukan berapa jumlah kedaan kuan- Dari hasil ini kita selanjunya bisa menentukan berapa jumlah kedaan kuan- tum dalam ruang fase dengan volume tertentu. Kita akan membahas untuk tum dalam ruang fase dengan volume tertentu. Kita akan membahas untuk ruang fasa yang mengandung koordinat spasial satu, dua, dan tiga dimensi.

ruang fasa yang mengandung koordinat spasial satu, dua, dan tiga dimensi.

7.

7.2 2 Koo Koord rdin inat at Sp Spas asia ial Sa l Satu tu Di Dime mens nsii

Misalkan kita memiliki assembli yang hanya boleh bergerak bebas dalam satu Misalkan kita memiliki assembli yang hanya boleh bergerak bebas dalam satu arah. Posisi partikel dalam assembli tersebut dinyatakan dengan ko-ordinat arah. Posisi partikel dalam assembli tersebut dinyatakan dengan ko-ordinat x

x. . DenDengan gan demdemikiikian, an, mommomenentum partiktum partikel el hanhanya memilya memiliki iki satsatu u kkompoomponennen saja, yaitu

saja, yaitu p p_xx. Elemen kecil ruang fasa yang dimiliki sebuah partikel dalam. Elemen kecil ruang fasa yang dimiliki sebuah partikel dalam assembli tersebut adalah

assembli tersebut adalah d dΓ Γ == dxdp dxdp_xx. Volume ruang fasa untuk semua posisi. Volume ruang fasa untuk semua posisi yang mungkin diperoleh dengan melakukan integral

yang mungkin diperoleh dengan melakukan integral ddΓ pada semua ruangΓ pada semua ruang spasial,

spasial,

∆Γ

∆Γ _p p = =

   

  _{dxdp  dxdp}

x

x == Ldp Ldp_xx    (7.2)(7.2) Dalam satu dimensi, ukuran minimum ruang fasa yang diijinkan oleh Dalam satu dimensi, ukuran minimum ruang fasa yang diijinkan oleh prinsip ketidakpastian Heisenberg adalah ∆Γ

prinsip ketidakpastian Heisenberg adalah ∆Γ_minmin = = ∆∆xx∆∆ p p_xx

 ∼  ∼

^== h h. Oleh kare-. Oleh kare- na itu, jumlah keadaan yang terdapat dalam elemen ruang fase ∆Γ

na itu, jumlah keadaan yang terdapat dalam elemen ruang fase ∆Γ p p adalah adalah

dN 

dN == ∆Γ∆Γ _p p

∆Γ

∆Γminmin == LL h

hdpdp_xx    (7.3)(7.3)

7

7..3 3 KKoooorrddiinnaat t SSppaassiiaal l DDuua a DDiimmeennssi i 7733 Jumlah keadaan persatuan volume assembli menjadi

Jumlah keadaan persatuan volume assembli menjadi gg(( p pxx))dpdpxx == dN dN 

L L

=

= 11 h hdpdp_xx

(7.4) (7.4)

Kerapatan keadaan tersebut dapat juga diungkapkan dalam variable e- Kerapatan keadaan tersebut dapat juga diungkapkan dalam variable e- nergi partikel dengan menggunakan hubungan

nergi partikel dengan menggunakan hubungan E E == p p²²_xx//22mm. Dengan hubun-. Dengan hubun- gan ini kita dapatkan

gan ini kita dapatkan

 p

 p_xx = =

√  √ 

_22mm

√  √ 

_E E 

dan dan

dp

dp_xx = =

√  √ 

_22mm

 

¹¹

22 dE 

√ 

dE 

√ 

_E E 

 

 _= =

   

^mm

22 dE 

√ 

dE 

√ 

_E E  ^(7.5)(7.5)

Substitusi persamaan (7.5) ke dalam persamaan (7.4) diperoleh ungkapan Substitusi persamaan (7.5) ke dalam persamaan (7.4) diperoleh ungkapan kerapatan keadaan per satuan volume sebagai berikut

kerapatan keadaan per satuan volume sebagai berikut gg((E E ))dE dE == 11

h h

 

 

^mm

22 E  E 

− −

^11//22_{dE dE     (7.6)(7.6)}

Kera

Kerapatpatan an kekeadaadaan an terstersebut ebut dapadapat t jugjuga a diundiungkgkapkapkan an daladalam m vvariariabelabel pan

panjanjang g gelgelomombanbang g parpartiktikel. el. KitKita a beranberangkgkat at dardari i persapersamaamaan n de de BroBrogligliee  p

 p_xx == h/λh/λ. . DarDari persami persamaan ini kitaan ini kita dapata dapat dpdp_xx ==

 −  −

^{hdλ/λhdλ/λ22. . SubSubstistitustusii dpdpxx}

ke dalam persamaan (7.5) dan hilangkan tanda negatif maka kita dapatkan ke dalam persamaan (7.5) dan hilangkan tanda negatif maka kita dapatkan

gg((λλ))dλdλ = = 11 h h

h h λ λ²²dλdλ

=

= 11 λ λ²²dλdλ

(7.7) (7.7)

7.

7.3 3 Koo Koord rdin inat at Sp Spas asia ial D l Dua ua Di Dime mens nsii

Sekarang kita berlanjut ke assembli dalam kotak dua dimensi dengan ukuran Sekarang kita berlanjut ke assembli dalam kotak dua dimensi dengan ukuran panjang searah sumbu

panjang searah sumbu xx  dan sumbu  dan sumbu yy  masing-masing  masing-masing LL_xx dandan LL_yy. . PPososisisii partikel dalam assembli tersebut dinyatakan oleh koordinat

partikel dalam assembli tersebut dinyatakan oleh koordinat xx dandan yy  saja.  saja.

Akibatnya, momentum partikel hanya memiliki dua komponen saja, yaitu Akibatnya, momentum partikel hanya memiliki dua komponen saja, yaitu p pxx

dan

dan p p_yy. Elemen ruang fasa yang dibatasi koordinat. Elemen ruang fasa yang dibatasi koordinat x x sampai sampai x x++dxdx, sampai, sampai yy ++ dydy, , mommomenentumtum pp_xx  sampai  sampai pp_xx ++ dpdp_xx dandan pp_yy  sampai  sampai pp_yy ++ dpdp_yy  adalah  adalah

74 Rapat Keadaan Sistem Kuantum dΓ = dxdydp_xdp_y. Volume ruang fasa untuk semua posisi yang mungkin diperoleh dengan mengintegralkan dΓ pada semua variable spasial, yaitu

∆Γ _p =

  

  _{dxdy dp}

xdp_y = L_xL_ydp_xdp_y   (7.8) Dalam ruang dua dimensi, ukuran minimum ruang fasa yang diijinkan oleh prinsip ketidakpastian Heisenberg adalah ∆Γmin = ∆x∆ px∆y∆ py

∼

⁼

h

×

^h = h2. Dengan demikian, jumlah keadaan yang terdapat dalam elemen ruang fasa ∆Γ _p adalah

dN = ∆Γ _p

∆Γ_min = L_xL_y

h² dp_xdp_y   (7.9) Persaman (7.9) menyatakan jumlah keadaan dalam elemen momentum yang berada antara p_x sampai p_x+dp_x dan antara p_y sampai p_y+dp_y. Jadi ruang momentum berbentuk persegi panjang dengan sisi-sisi dp_x dan dp_y. Cara lain adalah membuat elemen ruang momentum yang dibatasi oleh momen- tum total antara p sampai p +dp di mana momentum total memenuhi

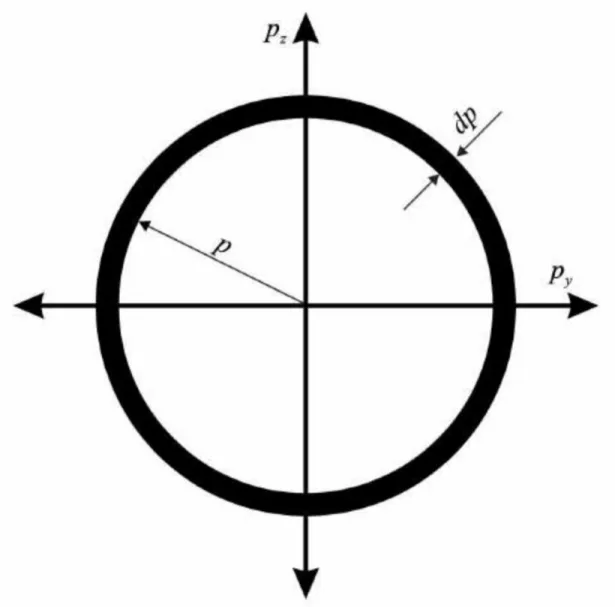
 p² = p²_x + p²_y   (7.10) Elemen ruang momentum tersebut akan berupa sebuah cincin dengan  jari-jari p dan ketebalan dp seperti pada Gbr. 7.1. Keliling cincin tersebut

adalah K  _p = 2πp sedangkan tebalnya adalah dp. Dengan demikian, luas cincin adalah

dS  _p = K  _pdp = 2πpdp   (7.11) Degan mengganti dp_xdp_y  pada persamaan (7.9) dengan dS  _p  pada per- samaan (7.11) diperoleh

dN = LxLy

h² 2πpdp   (7.12)

Kerapatan keadaan per satuan ”volume dua dimensi (luas)”adalah g( p)dp = dN 

LxLy

= 1

h²2πpdp

(7.13)

7.3 Koordinat Spasial Dua Dimensi 75

Gambar 7.1: Elemen ruang momentum berupa cincin dengan jari-jari p dan kete- balan dp.

Kembali kita ingin menyatakan kerapatan keadan dalam variabel energi.

Kita gunakan persamaan energi E = p²/2m sehingga

 p =

√ 

_2m

√ 

_{E    (7.14a)}

dp =

√ 

_2m



¹

2

√ 

dE _E 



 ₌

 

^m

2 E 

−

^1/2_{dE    (7.14b)}

Substitusi persamaan (7.14a) dan (7.14b) ke dalam persamaan (7.13) diper- oleh kerapatan keadaan sebagai berikut

g(E )dE = 1

h²2π

 √ 2m√ E   m

2 E 

−

^1/2_dE 



= 1

h²2πmdE 

(7.15)

Seperti sebelumya, jumlah keadaan tersebut dapat diungkapkan dalam vari- able panjang gelombang dengan menggunakan persamaan de Broglie p = h/λ.

76 Rapat Keadaan Sistem Kuantum Dari persamaan ini kita dapat dp =

−

^hdλ/λ2. Substitusi p dan dp ke dalam persamaan (7.13) dan hilangkan tanda negatif maka

g(λ)dλ = 1

h²2πh λ



^hdλ

λ²



= 2π λ³dλ

(7.16)

7.4 Koordinat Spasial Tiga Dimensi

Sekarang kita berlanjut ke assembli dalam kotak tiga dimensi dengan ukuran panjang sisi searah sumbu x, sumbu y, dan sumbu z masing-masing L_x, L_y, dan L_z. Posisi partikel dalam assembli tersebut dinyatakan oleh koordinat x, y, dan z. Dengan demikian, momentum partikel terdiri dari tiga komponen, yaitu p_x, p_y, dan p_z. Elemen kecil ruang fasa di dalam assembli tersebut adalah dΓ = dxdydzdp_xdp_ydp_z. volume ruang fasa untuk semua posisi yang mungkin adalah

∆Γ _p =

   

  dxdydz dp_xdp_ydp_z = L_xL_yL_zdp_xdp_ydp_z   (7.17) Dalam ruang tiga dimensi, ukuran minimum ruang fasa yang diijinkan oleh prinsip ketidakpastian Heisenberg adalah ∆Γmin = ∆x∆ px∆y∆ py∆z∆ pz

 ∼

⁼

h

×

^h

×

^{h = h3}. Akibatnya, jumlah keadaan yang terdapat dalam elemen ruang fase ∆Γ _p adalah

dN = ∆Γ _p

∆Γ_min = L_xL_yL_z

h³ dpxdpydpz   (7.18) Persamaan (7.18) menyatakan jumlah keadaan dalam elemen momentum yang berada antara p_x  sampai dp_x, antara p_y  sampai dp_y  dan antara p_z sampai dpz. Jadi ruang momentum berbentuk balok dengan ukuran dpx, dp_y, dan dp_z. Cara lain adalah membuat elemen ruang momentum yang dibatasi oleh momentum total antara p sampai p + dp di mana momentum total memenuhi

 p² = p²_x + p²_y + p²_z   (7.19) Elemen ruang momentum tersebut akan berupa sebuah kulit bola dengan  jari-jari p dan ketebalan p + dp seperti diilustrasikan pada Gbr. 7.2. Luas

7.4 Koordinat Spasial Tiga Dimensi 77

Gambar 7.2: Elemen ruang momentum berupa kulit bola dengan jari-jari p dan ketebalan dp.

kulit bola tersebut adalah S  _p = 4πp² dan ketebalannya adalah dp. Volume kulit bola menjadi

dV  p = S  pdp = 4πp²dp   (7.20) Dengan mengganti dpxdpydpz pada persamaan (7.18) dengan dV  p pada per- samaan (7.20) diperoleh ungkapan lain untuk jumlah keadaan

dN = L_xL_yL_z

h³ 4πp²dp   (7.21)

Kerapatan keadaan per satuan volume adalah g( p)dp = dN 

LxLyLz

= 1

h³4πp²dp

(7.22)

82 Beberapa Besaran Gas

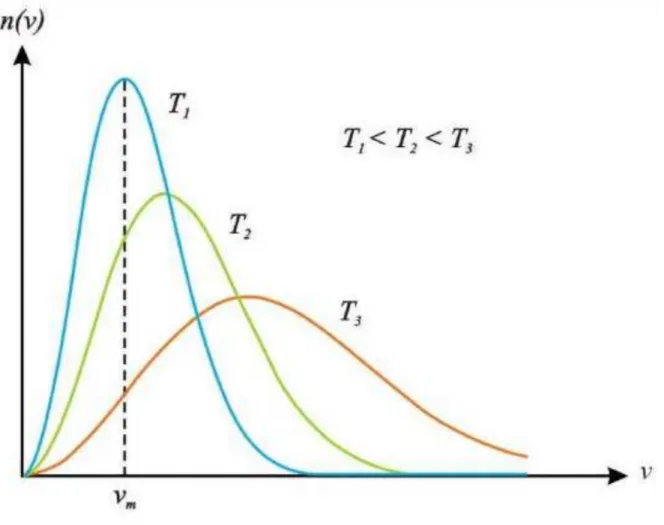
stan, berapa pun suhu assembli. Ini mengharuskan bahwa kurva yang lebih tinggi harus lebih sempit. Puncak kurva bergeser ke kiri ketika suhu ren- dah bermakna bahwa makin rendah suhu maka makin banyak sistem yang memiliki laju lebih kecil.

Gambar 8.1: Kerapatan partikel gas sebagai fungsi laju pada berbagai suhu.

Laju dengan peluang kemunculan paling besar tersebut ditentukan den- gan memecahkan persamaan

dn(v)

dv = 0 (8.1)

Dari persamaan (4.35) kita simpulkan

n(v) = 4πN m^3/2

(2πkT )^3/2v²e

−

^mv2/2kT  _(8.2)

8.1 Laju dengan Peluang Maksimum 83 sehingga persamaan (8.1) memberikan

dn(v)

dv = 4πN m^3/2 (2πkT )^3/2



_2ve

−

mv²/2kT +v² d

dve

−

^mv2/2kT 



= 4πN m^3/2 (2πkT )^3/2



_2ve

−

mv²/2kT +v²



−

^2mv_2kT 



_e

−

mv²/2kT 



= 4πN m^3/2

(2πkT )^3/2e

−

^mv2/2kT 



_2v

−

^mv

3

kT 



(8.3)

Jika v_m  adalah laju dengan peluang maksimum maka pada v_m  tersebut dn/dv = 0. Ini dipenuhi jika



_2v

m

−

^mv

m3

kT 



 _{= 0}

yang memberikan solusi untuk laju dengan peluang maksimum

v_m =

 

2kT 

m   (8.4)

Makin tinggi suhu maka makin banyak sistem yang memiliki laju be- sar sehingga kurva distribusi bergerak ke arah laju yang besar (ke kanan).

Sebaliknya, makin besar massa sistem maka makin sulit sistem tersebut un- tuk bergerak. Dengan demikian, pada suhu yang sama puncak distribusi bergeser ke laju rendah (ke kiri) jika massa sistem makin besar.

84 Beberapa Besaran Gas

8.2 Laju Rata-Rata

Selanjutnya kita akan menentukan laju rata-rata molekul gas. Laju rata-rata didefiniskan sebagai

v =

  ∞

0

vn(v)dv

  ∞

0

n(v)dv

=

4πN m^3/2/(2πkT )^3/2

∞

 

0

ve

−

^mv2/2kT _v²_dv

4πN m^3/2/(2πkT )^3/2

∞

 

0

ve

−

^mv2/2kT v²dv

=

  ∞

0

v³e

−

^mv2/2kT _dv

  ∞

0

v²e

−

^mv2/2kT dv

(8.5)

Untuk menyelesaikan persamaan (8.5) kita misalkan x = mv²/2kT . Dengan permisalan ini maka

v =

 

2kT  m x^1/2 v³ =



^2kT 

m



^3/2_x3/2

dv =

 

^2kT 

m

×

¹₂^x

−

^1/2d =