Introduction
The Baryon asymmetry and fundamental symmetry violation
However, the extent of CP violation in the Standard Model (generated by weak flavor-modifying interactions in the CKM matrix [3]) is too small to explain BAU [4, 5]. As discussed above, the Standard Model does not contain a sufficient CP violation (T violation) to explain BAU.
T-violating electromagnetic moments
In the context of the standard model, it arises through interaction of the electron with the quarks and the W boson. Measurements from the eEDM are only sensitive to T-violating physics that couple to the electron.
EDMs in molecules
The expected value of the internal electric field reaches its maximum value when the atom or molecule is fully polarized, increasing the sensitivity of eEDM. An atom or molecule is fully polarized when an external electric field completely mixes the opposite parity states.
YbOH for EDM measurements
Experiments using the laser cooling and molecule trapping [43] are expected to yield an additional order of magnitude improvement in EDM sensitivity (10−31 e cm) over the next ~5 years (2027). Fourth, YbOH has an electronic structure suitable for laser cooling [67] and similar to SrOH, which was laser cooled before the start of this work [53].
Overview
🝑 This nipple was mounted on top of the 300 K chamber (a drawing of the octagonal collar and custom nipple can be found in Appendix B).
Molecular Structure
Born–Oppenheimer approximation and separation of molecular wave-
In the BO approximation, the motions of the nuclei, both vibrations and rotations, are not coupled to the electrons so that the molecular wave function can be factored into two separate parts. 2.9) The electronic wave function, 𝜓𝑒 ( nuclei and depends only on the nuclear coordinates,𝑅.
Electronic structure
Yb and the F bond by filling a bonding orbital consisting of a linear combination of the Yb and F AOs. Here Σ denotes the projection of the total electron spin onto the internuclear axis (not to be confused with the term symbol of Σ for an electronic state with Λ = 1).

Vibrational structure
This bending angular momentum must take values of 𝑙 =𝜈, 𝜈−2, 𝜈−4, ..,−𝜈, where𝜈 is the quanta of the bending vibration. 𝑄±(𝜇2 is the reduced mass of the bending vibration), and 𝐺𝑙, 𝑧and𝐿𝑍 are the projections of the vibration and electron orbital angular momentum, 𝐺𝑙3and𝐿, along the internuclear axis.
Rotational structure
The energies and wavefunctions of the rotational states are found by solving the Schrödinger equation for a quantum rigid rotor [81]. 𝐽 (𝜃 , 𝜙) =|𝐽 , 𝑀⟩, (2.27) where 𝑙 is the angular momentum of the quantum state (𝐽 in the above equation) and 𝑚 is the projection of 𝐽 along the z axis (internuclear axis).
The effective Hamiltonian
We can now derive the form of the effective rotational Hamiltonian, which operates in the subspace of a single vibronic state |𝜂⟩, by setting ˆ𝐻1 = 𝐻ˆ𝑅 in Eq. The beauty of the effective Hamiltonian approach lies in the fact that the energy levels of a vibronic state can be calculated without diagonalizing the full Hamiltonian of the molecule.
Angular momentum coupling and Hund’s cases
Hund's case (a) is generally relevant for vibrational states with non-zero projections of Lon the internuclear axis (Λ≥ 0)8. Hund's case (b) provides a good description of molecular states with Λ = 0 or the rare case where the energy scale of the spin-orbit coupling is smaller than the rotation [89].
![Table 2.1: Relevant molecular angular momenta, in the absence of nuclear spins, and their projections on the internuclear axis ˆ 𝑛 [89, 91].](https://thumb-ap.123doks.com/thumbv2/123dok/10408338.0/39.918.165.707.158.650/relevant-molecular-angular-momenta-absence-nuclear-projections-internuclear.webp)
Fine structure and parity doublets
The spin spin interaction accounts for the interaction of the electron spin with the molecular spin, N. The first-order contribution, 𝛾(1), comes directly from the coupling of the electron spin with the magnetic moment of the rotating nuclei.
Hyperfine structure
In the equation above, 𝑙𝑧𝑖 is the z-component of the one-electron angular momentum operator of the 𝑖th electron. This will lead to different orientations of the quadrupole deformed core in an electric field gradient with different energies.
Molecular transitions
If the rotational, fine and hyperfine structure is resolved, the transition intensity will also depend on the details of the rotational/fine/hyperfine states involved. Here𝐹𝑖 does not refer to the angular momentum but indicates the spin orbital and spin rotation components of the ground and excited states.
Overview of laser cooling molecules
Therefore, if an atom or molecule of mass𝑚 is moving fast, then the atom or molecule can stop after 𝑁𝑠𝑡 𝑜 𝑝 =𝑚 𝑣/ℏ𝑘 photon is scattered. By closed, we mean that upon excitation, the atom or molecule will not decay into a state not addressed by the laser and stop emitting photons.
Overview of YbOH
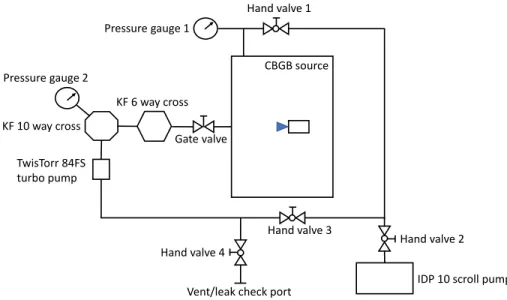
4 Kelvin Cryogenic Buffer Gas Beam Source
Cryogenic buffer gas beams
A three-dimensional CAD drawing of the full 4 K CBGB assembly (excluding the buffer gas cell) is shown in Fig. A temperature diode is attached to the bottom plate to monitor the temperature of the 50 K stage. Shown here is the mounting of the 50 K hexagonal extender to the 50 K stage of the pulse bath.

Diagnostics: Absorption and fluorescence
The number of molecules/atoms per unit area, 𝑛(𝑡), is time dependent due to the pulsating nature of the CBGB source. Measuring the frequency dependence of 𝑂 𝐷𝑖𝑛𝑡 results in a measurement of the absorption spectrum of the molecules/atoms. Therefore, a measurement of the integrated OD can also be used to determine the total number of molecules/atoms interacting with the laser beam.

YbOH production
On the other hand, stoichiometric Yb + Yb(OH) 3 targets produce large amounts of YbOH and the performance is very consistent from target to target. The stoichiometric Yb + Yb(OH) 3 targets have become our standard as we have not found any target that performs better. It is quite possible that a target composition and recipe exists that produces targets that outperform stoichiometric Yb + Yb(OH) 3 targets in performance.
Testing cell with mesh aperture
However, unlike 𝐴𝐹 𝑀(𝜔), the slope of the 𝐷𝐹 𝑀(𝜔) in 𝜔𝑟 𝑒 𝑠 increases with increasing 𝐴𝐹 𝑀(𝜔) and the 𝐷𝐹 𝑀(𝜔) lineshape in 𝜔𝑟 𝑒 𝑠 is plotted as a function of 𝜔𝑚/Γ. in Fig.

The Pure Rotational Spectrum of YbOH
Pump Probe Microwave Optical Double Resonance (PPMODR) spec-
Here, we used PPMODR spectroscopy to record the pure rotational spectrum of the ˜𝑋2Σ+(0,0,0) state of 174YbOH. By measuring LIF as a function of microwave frequency, rotational transitions ending in the 𝑁′rotational state are measured. The frequency of the microwave radiation was stepped in 6 kHz steps and the LIF from approximately 600 ablation images was summed at each frequency step.
After exhaustion of the rotational state, the molecular beam is exposed to tunable microwave radiation. The standard deviation of the fit was 23 kHz, which is proportional to the measurement error. This large discrepancy led to a reanalysis of the high temperature data by the original authors [106], where a reassignment of the 𝑄11and𝑅12 branches of the 174YbOH and 172YbOH high temperature data yielded a negative value of 𝛾, consistent with the value measured in this PPMODR study.

Negative spin rotation parameter and perturbing states
𝐺 = 𝑆+ 𝐼𝑌 𝑏 is the result of the coupling of the electron spin to the spin of the 173Yb nucleus. The rotational states were investigated via absorption spectroscopy of the 𝑄𝑄11(𝑁) transitions of the origin band [116]. The in-phase FM absorption spectrum of the [17.64] band of YbOH is shown in Fig.
Spectroscopy of Odd Isotopologues, 171 , 173 YbOH
Laser-enhanced chemical reactions: Enhancement of YbOH production 96
When the enhancement light is unblocked, the yield is increased to 3×1011 molecules in the cell and 8×1010 molecules in front of the cell. We note that the frequency dependence of the enhancement factor follows the dependence on the atomic resonance. The frequency of the enhancement laser is fixed to the 3𝑃1 ← 1𝑆0 transition of the desired Yb isotope.

Novel spectroscopic technique utilizing laser-enhanced chemical re-
The absolute frequency of the primary absorption laser is monitored by a digital wavemeter, and the relative frequency is tracked in a separate transmission cavity with respect to a stabilized HeNe laser (~7 MHz resolution). 5.4, this new technique using the chemical enhancement both isolates the spectrum of the desired isotopologue and increases the signal-to-noise ratio by a factor of (𝐸. Difference of the enhanced and non-enhanced spectrum (a-b ), this spectrum is pure of the 171YbOH isotopic.

Observation of the 171 , 173 YbOH spectra
The observed and predicted high-resolution absorption spectrum of the cryogenic buffer gas-cooled (CBGC) sample in the tape head region is shown in Fig. In contrast to the 173YbOH spectrum (shown in Fig. 5.6c), the 171YbOH spectrum has several unmixed features in the bandhead region. Although the strange isotopologue𝑅𝑅1𝐺branch features are relatively isolated (similar to the𝑂𝑃1𝐺features shown in Fig. 5.5), recording the chemically enhanced absorption spectrum was critical to disentangling and assigning the branch features in this region as well.

Analysis and discussion
The matrix elements used in the calculation of the effective Hamiltonians were taken from Ref. In addition to a view of the entire [17.64] spectrum (top panel), a closer view of the red part of the spectrum (panel second from top), the middle of the spectrum (panel second from bottom) and the blue part of the spectrum (bottom panel) is also shown.

Frequency Modulation Spectroscopy of YbOH
Frequency modulation absorption spectroscopy: Theory
𝑀 is the modulation depth which depends on the amplitude of the RF field driving the phase modulator. When the frequency modulated laser is passed through the sample, the electric field of the resulting emitted laser beam is the same. Experimentally, the phase angle 𝜃 that describes the mixing of the absorption and dispersion components in 𝐼𝐹 𝑀 is not easy to determine.
FM lineshapes and determining optimal modulation frequency
The x-axis is the relative normalized frequency, (𝜔 −𝜔𝑟 𝑒 𝑠)/Γ, where 𝜔𝑟 𝑒 𝑠 is the line center of the absorption line shape. The x-axis is the relative normalized frequency,(𝜔−𝜔𝑟 𝑒 𝑠)/Γ, where𝜔𝑟 𝑒 𝑠 is the line center of the absorption line shape. The absolute amplitude of the 𝐷𝐹 𝑀(𝜔) signals is arbitrary, while the relative amplitude between different line shapes is precise.

Modeling FM lineshapes
Therefore, given the absorption lineshape,𝛿(𝜔′), the dispersion lineshape is given by the negative Hilbert transform of the absorption lineshape. To include the effects of the second order sidebands we model the𝐴𝐹 𝑀(𝜔)en. An example of a fit of the model to FM data is shown later in this chapter in Fig.

Experimental implementation of FM absorption in buffer gas cell
The output of the I port is the in-phase demodulated DC signal resulting from mixing the photodiode signal (RF port) and the rf reference (LO port). The output of the Q gate is the in-quadrance demodulated DC signal resulting from mixing the photodiode signal (RF gate) and the rf reference (LO gate) with a 90◦ phase shift. Here, SNR is defined as the ratio of the DC or FM signal amplitude8 to the maximum positive amplitude of the noise.

A higher resolution view of the red half and blue half [17.68] of the spectrum is presented in Fig. Almost all of the differences in the combinations were matches between the spin-spin splittings in the ground state and the line splittings in [17.68]. The rotational level, 𝑁, ˜𝑋2Σ+(0,0,0) of the spin-rotation splitting is indicated, which matches the [17.68] line splitting.

Relevance of This Work to EDM Searches with YbOH
The calculated wavenumbers were obtained using the optimized parameters from fitting to the observed transition wavenumbers. Likewise, the differences between the observed (obs.) and calculated (calculated) transition wavenumbers are presented.

Cryogenic buffer gas cell
Miscellaneous