Slide Solusi Numerik Persamaan Differensial Biasa

Solusi Numerik Persamaan Differensial Biasa

(Dr. Ir. Bagus Adityawan)

KK TSA

Fakultas Teknik Sipil dan Lingkungan Insitut Teknologi Bandung

Bagus.adityawan@ftsl.itb.ac.id Mbagus_st@yahoo.com

Gedung CIBE

Lantai 5 - 504

1.1 Metode Euler

 Persamaan differensial orde satu dapat ditulis dalam bentuk eksplisit sebagai berikut

(2.1)

 Suatu permasalahan nilai awal terdiri dari persamaan differensial dan suatu kondisi solusi yang harus memenuhi. Kita dapat meninjau

permasalahan nilai awal dalam bentuk

, (2.2)

 Metode yang digunakan adalah metode iterasi. Kita mulai dari y₀ = y(x₀).

Pada tahap pertama kita hitung nilai perkiraan y₁ dari solusi y pada

persamaan (2.2) pada x = x₁ = x₀ + h . Pada tahap kedua kita hitung nilai perkiraan y₂ dengan solusi pada x = x₂ = x₀ + 2h, dan seterusnya. Disini h adalah sebuah bilangan tetap, sebagai contoh 0,2 atau 0,1 atau 0,01.

(3)

x₁ x₂ y

x

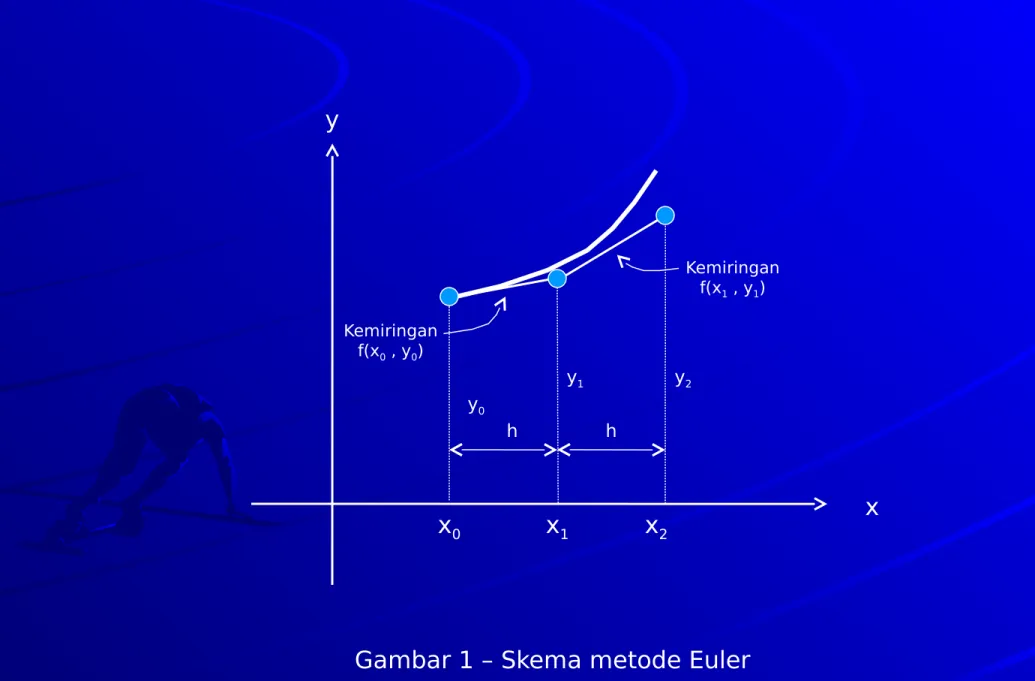
Gambar 1 – Skema metode Euler x₀

Kemiringan f(x₀ , y₀)

Kemiringan f(x₁ , y₁)

y₁ y₀

y₂

h h

 Dalam masing-masing tahap perhitungan dilakukan dengan formula yang sama. Formula seperti ini diberikan oleh deret Taylor dibawah

(2.3)

 Substitusi persamaan (2.2) ke dalam persamaan (2.3), sehingga persamaan menjadi

(2.4) atau

• Untuk nilai h yang kecil, pangkat lebih tinggi h² , h³ , …dalam persamaan (2.4) akan sangat kecil, sehingga persamaan (2.4) menjadi bentuk

pendekatan yang lebih singkat

(2.5)

 Dalam tahap pertama, untuk kita hitung

 Dalam tahap kedua, untuk kita hitung

 Dengan cara yang sama dilakukan untuk tahap berikutnya, sehingga bentuk persamaan iterasi secara umum

untuk i = 0, 1, … (2.6)

 Persamaan (2.6) dikenal dengan metode Euler atau Euler-Cauchy. Secara geometri, metode ini adalah pendekatan kurva y(x) dengan poligon yang mempunyai garis pertama adalah tangen terhadap kurva pada x₀ (Gambar 1).

• Metode ini disebut metode orde pertama, karena dalam persamaan (2.3) kita hanya mengambil suku konstan dan suku yang mengandung pangkat pertama dari h. Penghilangan suku berikutnya dalam persamaan (2.3) menyebabkan suatu error, yang disebut truncation error dari metode tersebut.

 Contoh 1

 Selesaikan persamaan differensial berikut untuk menggunakan h = 0,1

, Gunakan metode Euler.

 Solusi:

 Gunakan persamaan (2.5) untuk i = 0, kita dapatkan

 Nilai fungsi dievaluasi sebagai berikut

 Selanjutnya nilai fungsi pendekatan pada x₁ = h = 0,1 ditentukan sebagai

 Lebih jauh, untuk i = 1, didapat ,

dimana

• Sebagai konsekuennsi, nilai fungsi pendekatan dihitung pada x₂ = 2h = 0,2 menjadi

• Prosedur diatas diterapkan untuk i = 2, …, 9 untuk memberikan nilai pendekatan fungsi y₃ , …, y₁₀ . Selanjutnya bandingkan dengan solusi analitik yang diberikan dg persamaan y = e^x/2

• Untuk akurasi yang lebih baik dapat dilakukan dengan mengurangi interval h.

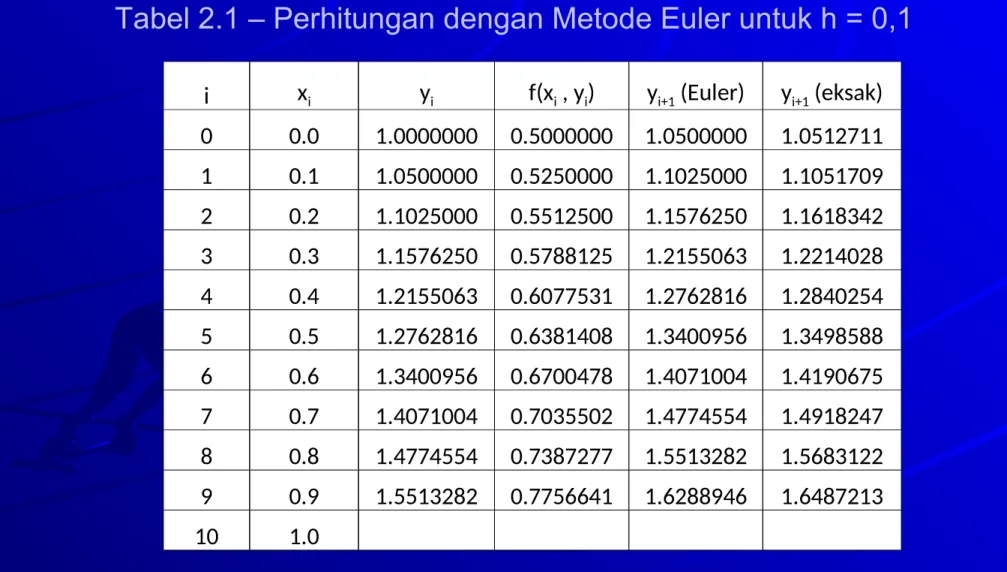
i x_i y_i f(x_i , y_i) y_i+1 (Euler) y_i+1 (eksak) 0 0.0 1.0000000 0.5000000 1.0500000 1.0512711 1 0.1 1.0500000 0.5250000 1.1025000 1.1051709 2 0.2 1.1025000 0.5512500 1.1576250 1.1618342 3 0.3 1.1576250 0.5788125 1.2155063 1.2214028 4 0.4 1.2155063 0.6077531 1.2762816 1.2840254 5 0.5 1.2762816 0.6381408 1.3400956 1.3498588 6 0.6 1.3400956 0.6700478 1.4071004 1.4190675 7 0.7 1.4071004 0.7035502 1.4774554 1.4918247 8 0.8 1.4774554 0.7387277 1.5513282 1.5683122 9 0.9 1.5513282 0.7756641 1.6288946 1.6487213

10 1.0

Tabel 2.1 – Perhitungan dengan Metode Euler untuk h = 0,1

1.2 Metode Euler Modifikasi (Metode Heun)

 Dengan menambah suku dalam persamaan (2.3) kedalam perhitungan kita menentukan metode numerik dengan orde dan akurasi yang lebih tinggi.

 Dalam metode Heun, suku turunan pertama dan kedua dalam deret Taylor dipertahankan, yang memberikan persamaan

(2.7)

 Suku kedua pada persamaan (2.7) dapat menggunakan pendekatan turunan maju berikut

(2.8)

• Subsitusi persamaan (2.8) ke persamaan (2.7), maka

atau diatur kembali menjadi

(2.9)

• Secara jelas, turunan pada x_i , dengan mudah dievaluasi.

sementara turunan pada x_i+1 , dapat dihitung dengan nilai pendekatan y_i+1 menggunakan metode Euler yang berikan pada

persamaan (2.6) . Nilai pendekatan selanjutnya digunakan untuk menghitung nilai yang diupdate pada persamaan (2.9).

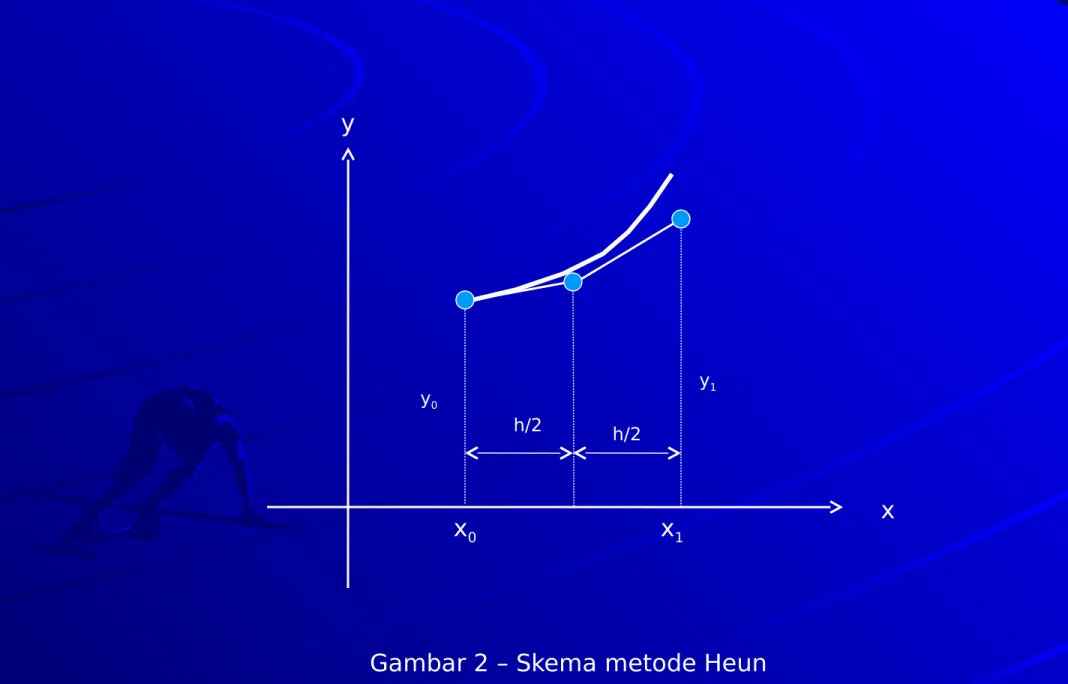
• Pada dasarnya, Metode Euler modifikasi adalah teknik sederhana predictor-corrector, karena di setiap langkah ditentukan nilai dengan menggunakan persamaan (2.6) dan selanjutnya mengoreksinya dengan persamaan (2.9) .Metode digambarkan pada Gambar 2.

• Metode Euler biasanya dinyatakan lebih mudah sebagai berikut dimana

• Metode Heun

dimana &

(2.10)

x₁ y

x

Gambar 2 – Skema metode Heun x₀

y₁ y₀

h/2 h/2

 Contoh 2

 Selesaikan persamaan differensial berikut untuk menggunakan h = 0,1

, Gunakan metode Heun.

 Solusi:

 Dimulai dengan menghitung faktor k₁ menggunakan persamaan (2.10) untuk i = 0

 Gunakan persamaan (2.5) untuk i = 0, kita dapatkan

 Gunakan persamaan (2.10), hitung k₂

 Pendekatan fungsi pada x₁ = 0,1 (i = 1) diberikan langsung dengan persamaan (2.10), yaitu

 Selanjutnya pada x₂ = 0,2, kita dapatkan ,

 Prosedur diatas diterapkan untuk i = 2, …, 9 untuk memberikan nilai pendekatan fungsi y₃ , …, y₁₀ . Selanjutnya bandingkan dengan solusi analitik.

 Untuk interval h yang sama metode Heun memberikan hasil yang lebih baik dibandingkan dengan Metode Euler.

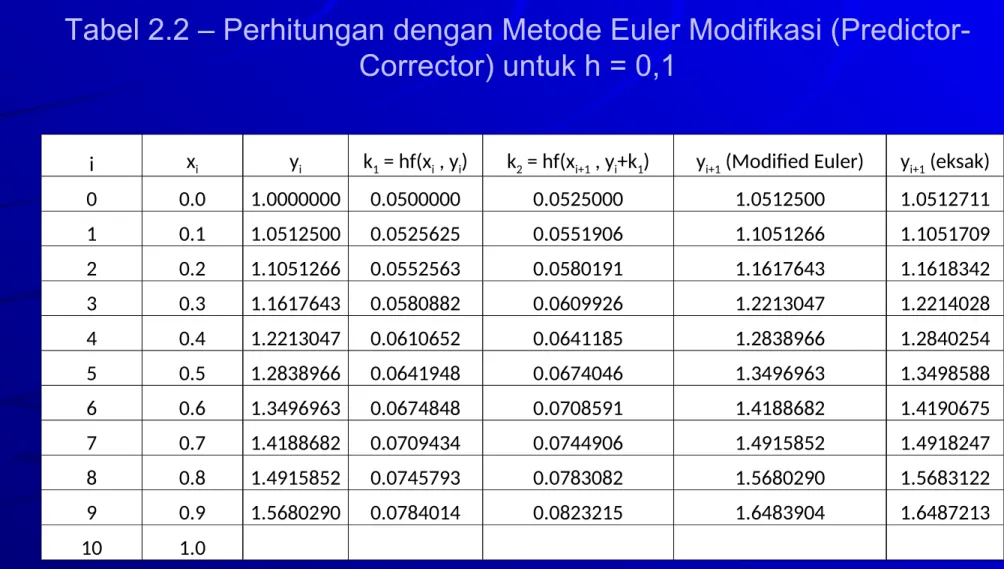
Tabel 2.2 – Perhitungan dengan Metode Euler Modifikasi (Predictor- Corrector) untuk h = 0,1

i x_i y_i k₁ = hf(x_i , y_i) k₂ = hf(x_i+1 , y_i+k₁) y_i+1 (Modified Euler) y_i+1 (eksak)

0 0.0 1.0000000 0.0500000 0.0525000 1.0512500 1.0512711

1 0.1 1.0512500 0.0525625 0.0551906 1.1051266 1.1051709

2 0.2 1.1051266 0.0552563 0.0580191 1.1617643 1.1618342

3 0.3 1.1617643 0.0580882 0.0609926 1.2213047 1.2214028

4 0.4 1.2213047 0.0610652 0.0641185 1.2838966 1.2840254

5 0.5 1.2838966 0.0641948 0.0674046 1.3496963 1.3498588

6 0.6 1.3496963 0.0674848 0.0708591 1.4188682 1.4190675

7 0.7 1.4188682 0.0709434 0.0744906 1.4915852 1.4918247

8 0.8 1.4915852 0.0745793 0.0783082 1.5680290 1.5683122

9 0.9 1.5680290 0.0784014 0.0823215 1.6483904 1.6487213

10 1.0

1.3 Metode Runge Kutta

 Prosedur Metode Rungke-Kutta dapat dengan mudah diilustrasikan dengan meninjau metode Euler Modifikasi. Gunakan kembali persamaan euler

modifikasi dalam menentukan turunanan kedua dalam suku-suku turunan pertama x_i dan x_i+1 . Kita perlu membuat evaluasi fungsi internal tambahan pada x_{i + h/2} . Sebagai konsekwensi dari jika suku turunan lebih tinggi

diikutsertakan.

 Untuk menggambarkan bagaimana metode Runge Kutta dikembangkan, penurunan metode orde kedua ditunjukkan. Gunakan kembali metode Euler modifikasi sbb

(2.11)

sebagai solusi untuk persamaan diferensial biasa orde satu dengan bentuk

• Metode Runge-Kutta mengasumsikan pendekatan yang sama dengan persamaan

(2.12a) dimana

(2.12b) (2.12c)

 Substitusi persamaan (2.12b) kedalam (2.12c) menghasilkan ekspresi berikut untuk k₂ :

(2.13)

• Persamaan (2.13) bisa diekspresikan dalam suku fungsional yang diberikan f(x_i , y_i) dan turunanannya dengan menggunakan deret Taylor dalam dua variabel untuk memberikan

(2.14a)

 Ekspresi diatas melibatkan hanya suku pertama dari deret. Jika kita adopsi f = f(x_i , y_i), f_x = ∂f/∂x , dan f_y = ∂f/∂y, selanjutnya persamaan (2.14a)

diberikan dengan lebih mudah sebagai:

(2.14b)

• Begitu juga dengan persamaan (2.12b) menjadi

(2.15)

• Substitusi persamaan (2.14) dan (2.15) ke dalam persamaan (2.12a) menghasilkan formula Runge-Kutta orde dua sbb:

(2.16)

• Terbukti bahwa persamaan (2.16) melibatkan empat koefisien tidak diketahui a, b, A, dan B. Sebagai konsekwensi, untuk menentukan

nilai2nya, persamaan (2.16) harus berkaitan dengan deret Taylor orde kedua, yaitu

(2.17a)

 atau

(2.17b)

• atau

(2.17c)

• Samakan persamaan (2.16) dan (2.17c) menjadi:

(2.18)

• sehingga

(2.19a) (2.19b) (2.19c)

• Jika dipilih faktor bobot a adalah ½ , maka dapat ditentukan b = ½ , A = 1 , dan B = 1. Situasi ini berkaitan dengan metode Euler modifikasi.

x_i+1 y

x

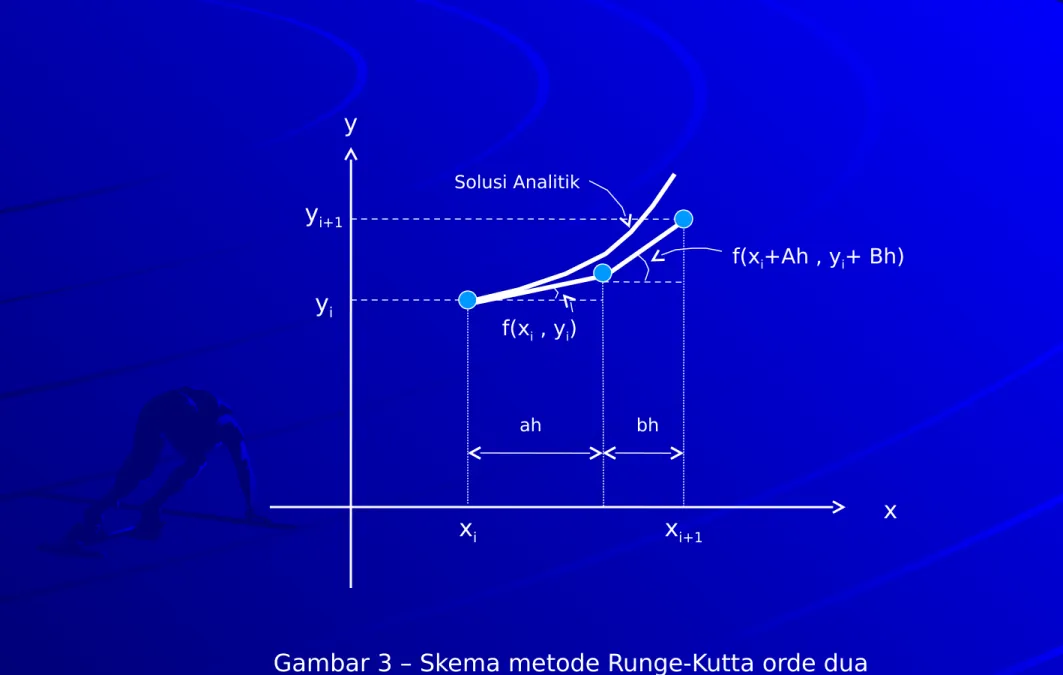
Gambar 3 – Skema metode Runge-Kutta orde dua x_i

ah bh

y_i y_i+1

f(x_i , y_i)

f(x_i+Ah , y_i+ Bh)

Solusi Analitik

 Salah satu metode yang banyak digunakan untuk menyelesaikan

persamaan diferensial ordinary secara numerik adalah metode Runge- Kutta orde 4. Metode ini melibatkan persamaan berikut:

(2.20a)

• dimana

(2.20b) (2.20c)

(2.20d)

(2.20e)

• Error global berkaitan dengan metode Runge-Kutta adalah orde (O)h⁴ . Ini berarti, tingkat akurasi metode Runge-Kutta orde 4 lebih tinggi (akurat) dan memerlukan langkah berhitungan lebih sedikit dibanding metode Runge-Kutta orde 2.

 Contoh 3

 Selesaikan persamaan diferensial berikut dengan menggunakan metode Runge-Kutta orde 4:

,

• Gunakan h = 1

 Solusi:

• Problem disini sama dengan yang diselesaikan sebelumnya dengan metode Euler. Jadi

 Substitusi nilai k diatas kedalam persamaan (20a) memberikan solusi:

 Bandingkan dengan solusi eksak

• Catatan: meskipun h = 1, nilai perhitungan metode Runge-Kutta orde 4 lebih baik dari yang ditentukan dengan menggunakan metode Euler dengan h = 0,1.

Tabel 2.3 – Perhitungan dengan Metode Runge Kutta orde 4 untuk h = 0,1

i x_i y_i k₁ = hf(x_i , y_i) k₂ = hf(x_i+1+h/2 , y_i+k₁/2) k₃ = hf(x_i+1+h/2 , y_i+k₂/2) k₄ = hf(x_i+1+h , y_i+k₃) y_i+1 (runge kutta) y_i+1 (eksak)

0 0.0 1.0000000 0.0500000 0.0512500 0.0512813 0.0525641 1.0512711 1.0512711

1 0.1 1.0512711 0.0525636 0.0538776 0.0539105 0.0552591 1.1051709 1.1051709

2 0.2 1.1051709 0.0552585 0.0566400 0.0566745 0.0580923 1.1618342 1.1618342

3 0.3 1.1618342 0.0580917 0.0595440 0.0595803 0.0610707 1.2214027 1.2214028

4 0.4 1.2214027 0.0610701 0.0625969 0.0626351 0.0642019 1.2840254 1.2840254

5 0.5 1.2840254 0.0642013 0.0658063 0.0658464 0.0674936 1.3498588 1.3498588

6 0.6 1.3498588 0.0674929 0.0691803 0.0692224 0.0709541 1.4190675 1.4190675

7 0.7 1.4190675 0.0709534 0.0727272 0.0727716 0.0745920 1.4918247 1.4918247

8 0.8 1.4918247 0.0745912 0.0764560 0.0765026 0.0784164 1.5683122 1.5683122

9 0.9 1.5683122 0.0784156 0.0803760 0.0804250 0.0824369 1.6487212 1.6487213

10 1.0

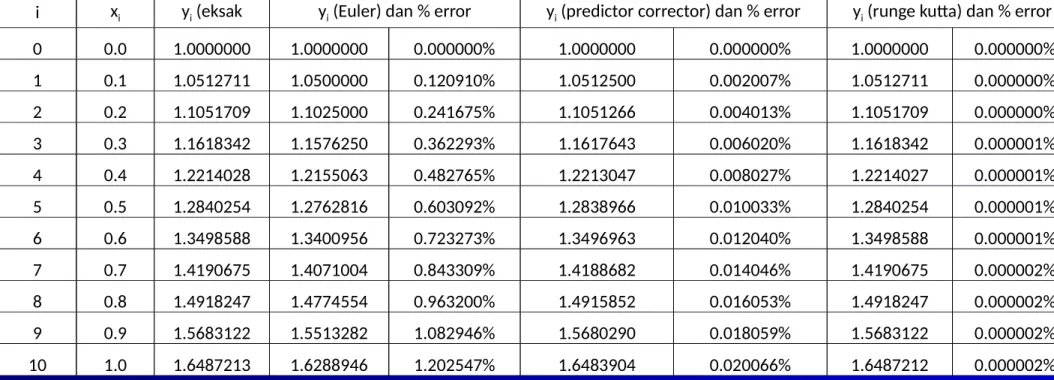
Tabel 2.4 – Perbandingan Persentase Error Metode Numerik Euler, Predictor Corrector, dan Runge Kutta terhadap Solusi Eksak

i x_i y_i (eksak y_i (Euler) dan % error y_i (predictor corrector) dan % error y_i (runge kutta) dan % error

0 0.0 1.0000000 1.0000000 0.000000% 1.0000000 0.000000% 1.0000000 0.000000%

1 0.1 1.0512711 1.0500000 0.120910% 1.0512500 0.002007% 1.0512711 0.000000%

2 0.2 1.1051709 1.1025000 0.241675% 1.1051266 0.004013% 1.1051709 0.000000%

3 0.3 1.1618342 1.1576250 0.362293% 1.1617643 0.006020% 1.1618342 0.000001%

4 0.4 1.2214028 1.2155063 0.482765% 1.2213047 0.008027% 1.2214027 0.000001%

5 0.5 1.2840254 1.2762816 0.603092% 1.2838966 0.010033% 1.2840254 0.000001%

6 0.6 1.3498588 1.3400956 0.723273% 1.3496963 0.012040% 1.3498588 0.000001%

7 0.7 1.4190675 1.4071004 0.843309% 1.4188682 0.014046% 1.4190675 0.000002%

8 0.8 1.4918247 1.4774554 0.963200% 1.4915852 0.016053% 1.4918247 0.000002%

9 0.9 1.5683122 1.5513282 1.082946% 1.5680290 0.018059% 1.5683122 0.000002%

10 1.0 1.6487213 1.6288946 1.202547% 1.6483904 0.020066% 1.6487212 0.000002%

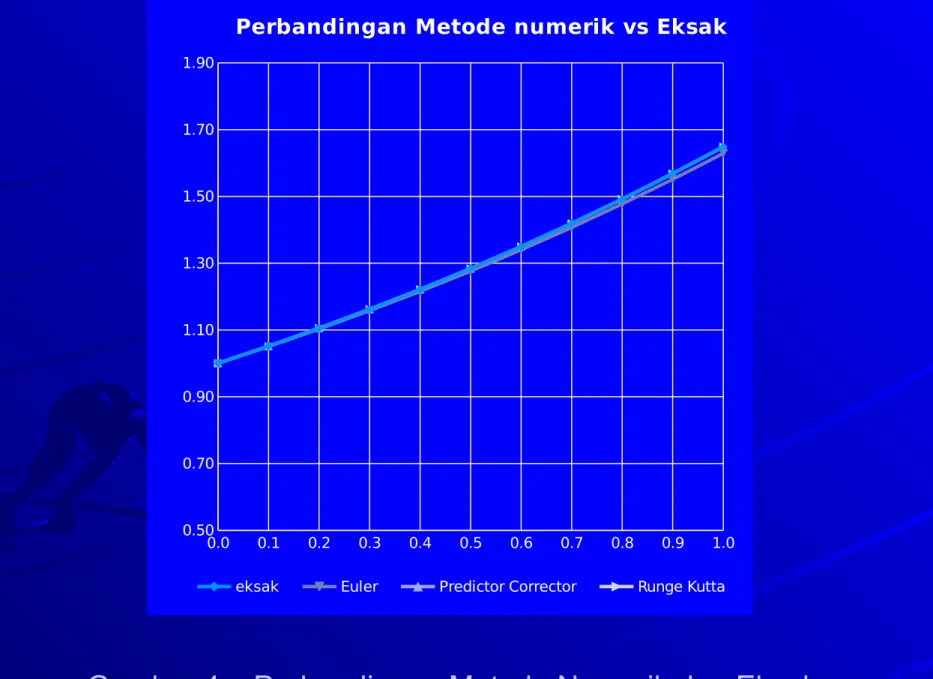
Gambar 4 – Perbandingan Metode Numerik dan Eksak

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 0.50

0.70 0.90 1.10 1.30 1.50 1.70 1.90

Perbandingan Metode numerik vs Eksak

eksak Euler Predictor Corrector Runge Kutta

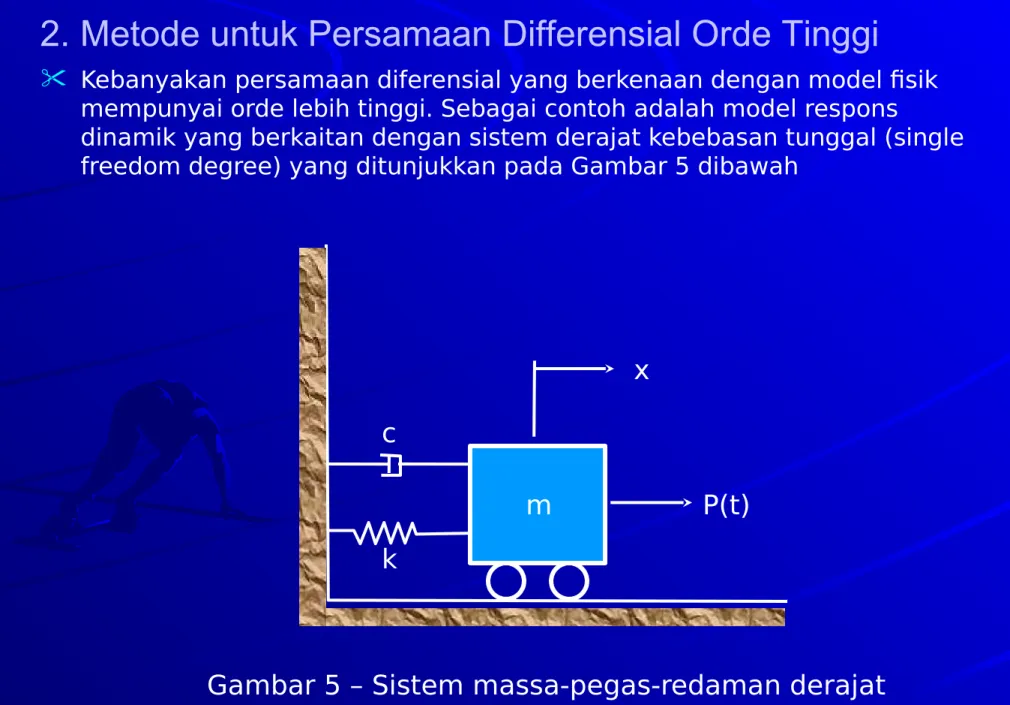
2. Metode untuk Persamaan Differensial Orde Tinggi

 Kebanyakan persamaan diferensial yang berkenaan dengan model fisik mempunyai orde lebih tinggi. Sebagai contoh adalah model respons

dinamik yang berkaitan dengan sistem derajat kebebasan tunggal (single freedom degree) yang ditunjukkan pada Gambar 5 dibawah

m P(t)

c

k

x

Gambar 5 – Sistem massa-pegas-redaman derajat

kebebasam tunggal

 Model diatas mewakili massa yang diberi pegas dan redaman

(mengisap/menyerap getaran) dimana massa dikenai gaya luar. Tujuannya adalah untuk mendapatkan fungsi perpindahan x(t) yang disebabkan oleh gaya luar P(t) dan kondisi awal. Kondisi awal mewakili kecepatan dan

perpindahan awal dari massa pada waktu t = 0. Sistem ini disebut sistem derajat kebebasan tunggal disebabkan massa m, kekakuan pegas k,

koefisien redaman (damping) c, dan gaya luar P(t) terkonsentrasi pada satu lokasi. Model matematik berkenaan dengan sistem seperti ini

diberikan sebagai berikut:

(3.1)

 Persamaan diatas dapat diselesaikan dengan mengurangi persamaan orde tinggi menjadi set persamaan orde pertama. Sebagai konsekwensi, jika kondisi awal ditetapkan untuk persamaan (3.1) pada t = t₀ menjadi

 Selanjutnya memungkinkan untuk mengurangi persamaan (3.1) menjadi set yang melibatkan dua persamaan orde satu dengan mengenalkan variabel baru y sebagai berikut

, (3.2a)

, (3.2b)

 Persamaan (3.2) adalah persamaan diferensial orde pertama yang dapat diselesaikan dengan metode yang dijelaskan sebelumnya. Konsep

mengurangi persamaan diferensial orde n menjadi set n persamaan orde pertama yang ekivalen dapat dikembangkan menjadi set orde yang lebih tinggi.

 Contoh 3.1

 Gunakan Deret Taylor untuk menyelesaikan persamaan ordinari orde dua berikut pada ∆t = 0,1:

dg kondisi awal ,

 Solusi:

 Karena gaya luar adalah nol, response yang disebabkan hanya oleh kondisi awal. Jadi asumsikan

, (3.3)

 Orde dua dinyatakan sebagai

, (3.4)

 Solusi saat ini dicapai dengan mengamati bahwa persamaan (3.3) dan (3.4) adalah dua persamaan diferensial ordinari orde pertama yang mana dapat dikembangkan sebagai deret Taylor sbb:

(3.5)

(3.6)

 Secara jelas, suku tambahan dapat disertakan dalam deret diatas jika

akurasi tinggi diinginkan. Dalam kasus tertentu, persamaan (3.5) dan (3.6) melibatkan turunan pada t = 0 yang mana dapat dievaluasi sebagai

berikut:

,

,

,

,

• Substitusi nilai-nilai diatas kedalam persamaan (3.5) dan (3.6)

menghasilkan solusi yang diinginkan untuk fungsi perpindahan dan kecepatan dalam suku waktu t

• Selanjutnya pada ∆t = 0,1 didapatkan

• Nilai diatas dibandingkan dengan nilai eksak x(0,1) = 1,0794013 dan y(0,1) = 0,5827277. Sebagai catatan bahwa perbandingan nilai

perpindahan cukup dekat sementara kecepatan tidak terlalu akurat. Hal ini disebabkan oleh pemotongan error, yang mana lebih kritikal ketika

mengevaluasi turunan y = dx/dt. Hasil perhitungan lihat Tabel dibawah.

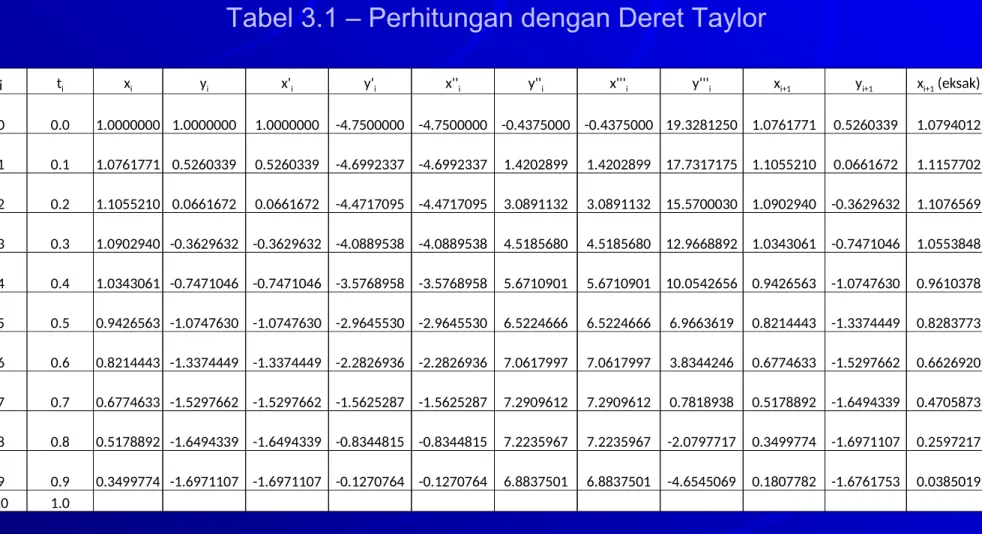
Tabel 3.1 – Perhitungan dengan Deret Taylor

i t_i x_i y_i x'_i y'_i x''_i y''_i x'''_i y'''_i x_i+1 y_i+1 x_i+1 (eksak)

0 0.0 1.0000000 1.0000000 1.0000000 -4.7500000 -4.7500000 -0.4375000 -0.4375000 19.3281250 1.0761771 0.5260339 1.0794012 1 0.1 1.0761771 0.5260339 0.5260339 -4.6992337 -4.6992337 1.4202899 1.4202899 17.7317175 1.1055210 0.0661672 1.1157702 2 0.2 1.1055210 0.0661672 0.0661672 -4.4717095 -4.4717095 3.0891132 3.0891132 15.5700030 1.0902940 -0.3629632 1.1076569 3 0.3 1.0902940 -0.3629632 -0.3629632 -4.0889538 -4.0889538 4.5185680 4.5185680 12.9668892 1.0343061 -0.7471046 1.0553848 4 0.4 1.0343061 -0.7471046 -0.7471046 -3.5768958 -3.5768958 5.6710901 5.6710901 10.0542656 0.9426563 -1.0747630 0.9610378 5 0.5 0.9426563 -1.0747630 -1.0747630 -2.9645530 -2.9645530 6.5224666 6.5224666 6.9663619 0.8214443 -1.3374449 0.8283773 6 0.6 0.8214443 -1.3374449 -1.3374449 -2.2826936 -2.2826936 7.0617997 7.0617997 3.8344246 0.6774633 -1.5297662 0.6626920 7 0.7 0.6774633 -1.5297662 -1.5297662 -1.5625287 -1.5625287 7.2909612 7.2909612 0.7818938 0.5178892 -1.6494339 0.4705873 8 0.8 0.5178892 -1.6494339 -1.6494339 -0.8344815 -0.8344815 7.2235967 7.2235967 -2.0797717 0.3499774 -1.6971107 0.2597217 9 0.9 0.3499774 -1.6971107 -1.6971107 -0.1270764 -0.1270764 6.8837501 6.8837501 -4.6545069 0.1807782 -1.6761753 0.0385019

10 1.0

Gambar 3.1 – Perbandingan Metode Deret Taylor dan Eksak

i t_i x_i (eksak x_i (Deret Taylor) dan % error

0 0.0 1.0000000 1.0000000 0.000000%

1 0.1 1.0794012 1.0761771 0.298699%

2 0.2 1.1157702 1.1055210 0.918572%

3 0.3 1.1076569 1.0902940 1.567526%

4 0.4 1.0553848 1.0343061 1.997253%

5 0.5 0.9610378 0.9426563 1.912672%

6 0.6 0.8283773 0.8214443 0.836936%

7 0.7 0.6626920 0.6774633 2.228987%

8 0.8 0.4705873 0.5178892 10.051684%

9 0.9 0.2597217 0.3499774 34.750901%

10 1.0 0.0385019 0.1807782 369.530860%

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 0.00

0.20 0.40 0.60 0.80 1.00 1.20

Perbandingan Metode numerik vs Eksak

eksak Deret Taylor

Tugas 3

• Soal 1

• Terapkan metode Euler, Predictor Corrector, dan Rungke Kutta untuk persamaan (0 ≤ x ≤ 1) dengan menggunakan program phyton. Bandingkan hasilnya dan beri analisis!

a) y’ =2xy , y(0) = 1 , h = 0,1

b) y’ = 2 – 2y , y(0) = 0 , h = 0,1

c) y’ = 1 + y

²

, y(0) = 0 , h = 0,1