In this study, the effects of variable nonlocal parameters on the free vibration of functionally graded sigmoid and variable nanoplates are investigated using a simple inverse hyperbolic shear deformation theory incorporating nonlocal elasticity theory. The novelty of this study is that the nonlocal parameter is assumed to vary smoothly through the thickness of functionally graded nanoplates. The results show that the change of the nonlocal parameter plays significant effects on the free vibration response of the functionally graded nanoplates.
The influence of nonlocal parameters on the free vibration of different types of functionally graded nanoplates is completely different, it depends on the change of material components along the thickness of the functionally graded nanoplates. Also, molecular dynamics simulations (MDS) are adopted to analyze and confirm the prediction of nonlocal plate theories. Therefore, this study focuses on modifying the classical Eringen theory of nonlocal elasticity to consider the variation of nonlocal parameters through the thickness of FG nanoplates.
The proposed formulations are applied to analyze the free vibration of the power law and sigmoid FG nanoplates to demonstrate the effects of the variation of the non-local parameters on the vibration of the FG nanoplates. The Cartesian coordinates xyz are on the middle surface of the FG nanoplate axis. In the case of power-law functionally graded (P-FG) nanosheets, the variation of the material properties through the thickness of the sheet is calculated by .
In this study, a simple shear deformation theory (SSDT) with a new inverse hyperbolic distribution shape function is used to investigate the free vibration of FGSW nanoplates.
The nonlocal elasticity theory
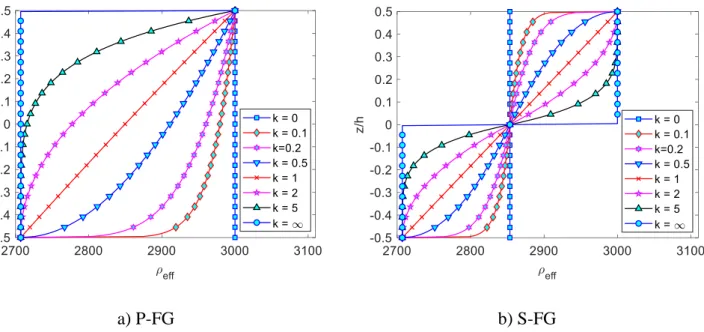
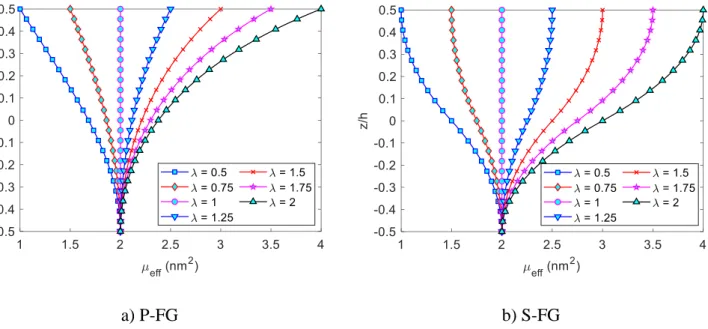
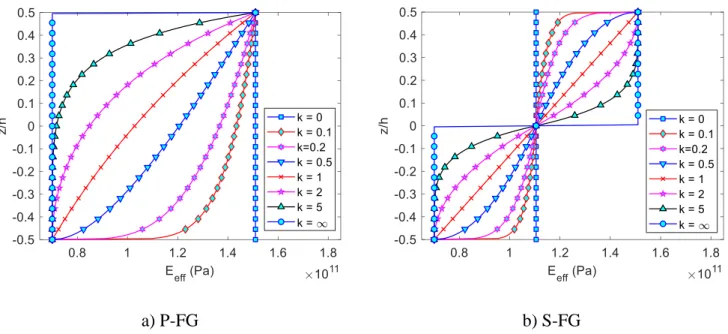
Therefore, the ratio between the nonlocal parameter of the ceramic phase and the metal phase. According to the present nonlocal constitutive relations, it can be seen that the small-scale effects not only vary through the in-plane directions, but also vary through the thickness direction of the nanoplates. Therefore, the current theory of nonlocal elasticity is completely different from the classical theory of nonlocal elasticity, where small-scale effects are similar through the thickness direction of nanoplates.
The proposed formulations can be used in a wide range of engineering calculations for micro/nanostructures.
Equations of motion
In the case of the conventional nonlocal elasticity theory, the nonlocal parameter is assumed to be constant through the thickness of the nanoplates. Consequently, the governing equations of motion Eq. 19) becomes the conventional governing equations of motion for the nanoplates with a constant non-local parameter, which is usually used by many researchers in the literature. In this study, the non-local parameter is assumed to vary through the thickness of the nanoplates as other material properties.
Navier’s solution
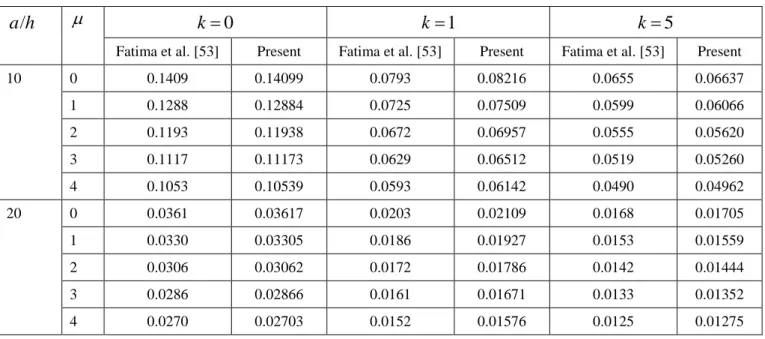
Numerical results 1. Verification study
Parameter study
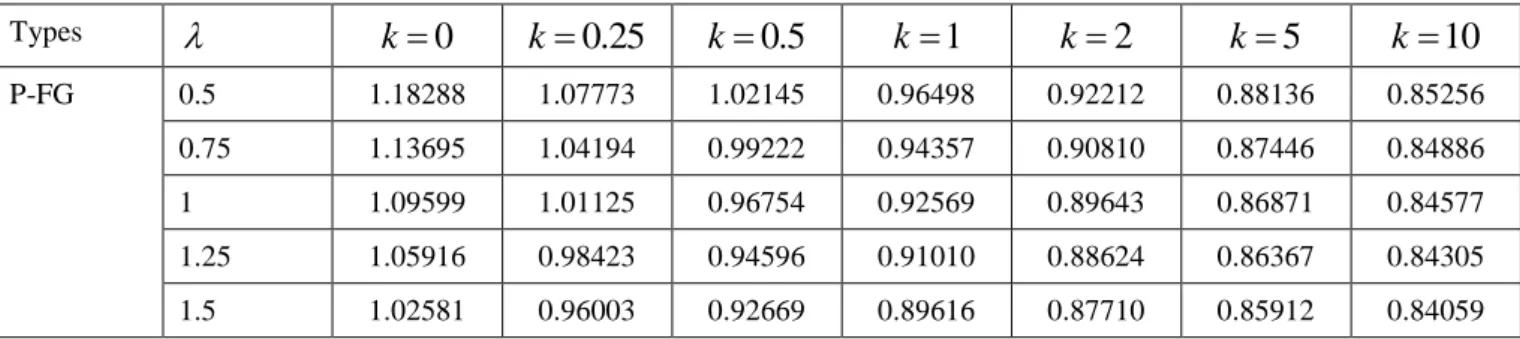
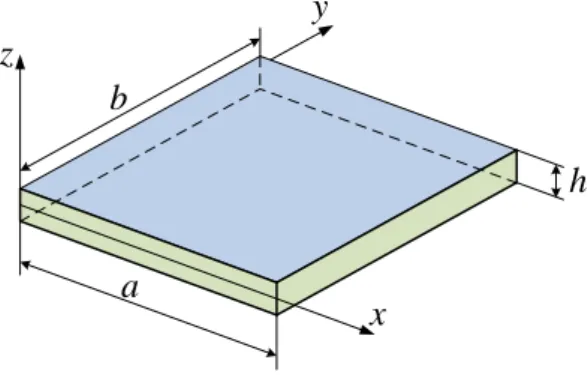
In general, when the power law index k increases, the fundamental frequencies of P-FG and S-FG nanoplates decrease. However, the frequency of P-FG nanoplates decreases faster than that of S-FG nanoplates. Then, the first eight non-dimensional frequencies of the P-FG and S-FG square nanoplates with.
The inclusion of the non-local parameter leads to a decrease in the frequencies of the nanoplates. As the ratio of the non-local parameter increases, the higher frequencies of the nanoplates decrease faster than the lower frequencies. When the power-law index is small, the frequencies of the P-FG nanoplates are higher than the S-FG nanoplates.
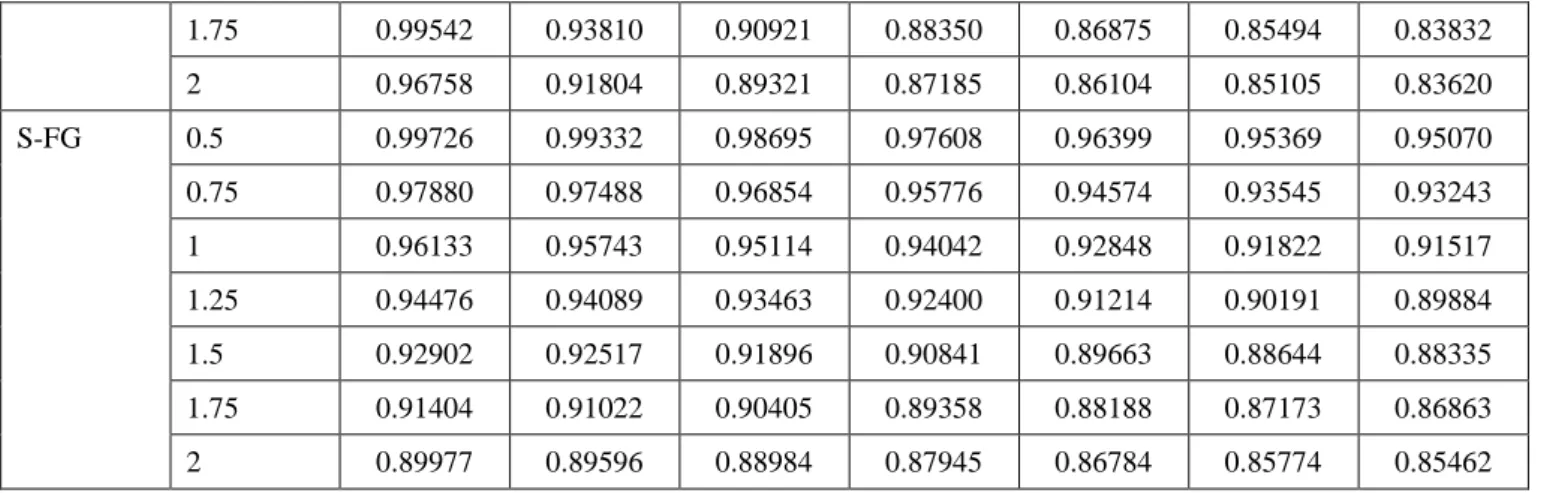
When the power-law index is higher, the frequencies of the P-FG nanosheets are smaller than those of the S-FG nanosheets, as shown in Table 4. Continuously, Figure 5 shows the effects of the non-local parameter variation at the non-dimensional fundamental frequencies of the square P-FG and S-FG nanoplates. The effects of the variation of the non-local parameter on the fundamental frequencies of the FG nanoplates.
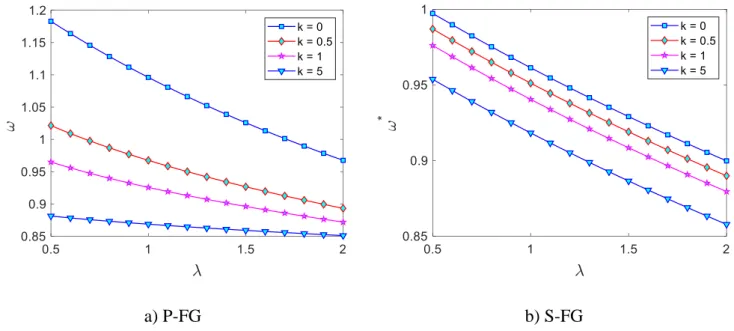
Then, the influence of the nonlocal parameter ratio on the higher frequencies of the P-FG and S-FG square nanoplates is investigated. Effects of changing the nonlocal parameter at high frequencies of FG nanoplates. The influence of the material parameter k on the behavior of free vibrations of P-FG and S-FG nanoplates is studied continuously.
It is clear that when the power law index increases, the non-dimensional frequencies of the nanoplates decrease for both cases of P-FG and S-FG nanoplates. It is pleasing that when the aspect ratio increases from 0.5 to 1, the non-dimensional frequencies of P-FG and S-FG nanoplates decrease. Finally, the influence of the side-thickness ratio a h/ on the non-dimensional frequencies of P-FG and S-FG nanoplates is considered.
The increase of the side-to-thickness ratio leads to a decrease of non-dimensional frequencies of the P-FG and S-FG nanoplates. The variation of the fundamental frequencies of the FG nanoplates as a function of side-to-thickness ratio.
Conclusions
Funding
Declaration of conflicting interests
Barati, A general nonlocal stress-strain gradient theory for forced vibration analysis of heterogeneous porous nanoplates, Eur. Al-Zahrani, Wave propagation analysis of ceramic-metal functionally graded sandwich panels with different porosity distributions. Mahmoud, Buckling analysis of functionally graded plates using a new refined quasi-3D theory of shear deformation and the concept of neutral surface position, Steel Compos.
Mahmoud, Buckling analysis of functionally graded plates using HSDT in conjunction with the stress function method, Comput. Mahmoud, Four unknown refined plate theory for dynamic analysis of FG-sandwich plates under different boundary conditions, Steel Compos. Tounsi, Theory of Four Variable Trigonometric Integral Plates for Hygro-Thermo-Mechanical Bending Analysis of AFG.
Vinh, Analysis of bidirectional functionally graded sandwich plates via higher order shear deformation theory and finite element method, J. Hoa, Modified single variable shear deformation plate theory for free vibration analysis of rectangular FGM plates, Structs. Vinh, Deflections, stresses and free vibration analysis of bi-functionally graded sandwich plates resting on Pasternak elastic foundations via a hybrid quasi-3D theory, Mech.
Huy, Finite element analysis of functionally graded sandwich plates with porosity via a new hyperbolic shear deformation theory, Def. Yu, Buckling analysis of graphene sheets embedded in an elastic medium based on the kp-Ritz method and nonlocal elasticity theory, Eng. Tahani, Vibrational analysis of orthotropic circular and elliptical nanoplates embedded in elastic medium based on nonlocal Mindlin plate theory and using the Galerkin method, J.
Abdelouahed, Zero-order nonlocal shear deformation theory for free vibrations of functionally graded nanometer-scale plates resting on an elastic foundation, Steel Compos. Radwan, Buckling analysis of functionally graded nanometer slabs using a nonlocal mixed variational formula, Math. Hadi, Size-dependent analysis of free vibrations of nanoplates from functionally graded materials based on nonlocal elasticity theory with high-order theories, Int.
Narendar, Buckling analysis of micro/nanoscale plates based on two-variable refined plate theory incorporating non-local scale effects, Compos. Gopalakrishnan, Scale effects on buckling analysis of orthotropic nanoplates based on nonlocal two-variable refined plate theory, Acta Mech.