The purpose of this study is to assess the performance of the spectral-based numerical methods in solving systems of differential equations. The performance of the methods is measured in terms of computational efficiency (in terms of time taken to generate solutions), accuracy and convergence rate.
Taylor series expansion
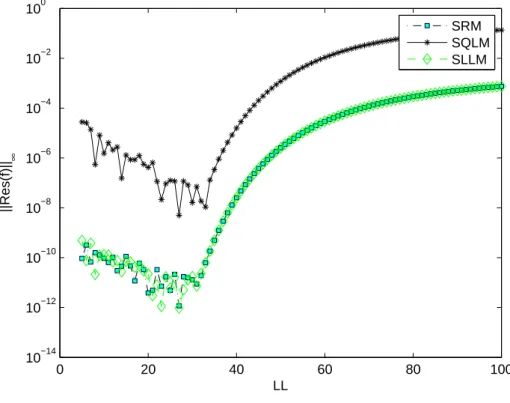
As the number of collocation points became very large, the accuracy of SQLM decreased. In this subsection, the application of SRM to the system of equations is presented. In this subsection, the application of SLLM to the system of equations is shown.
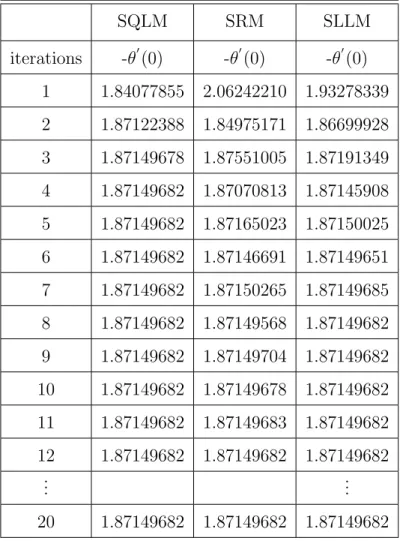
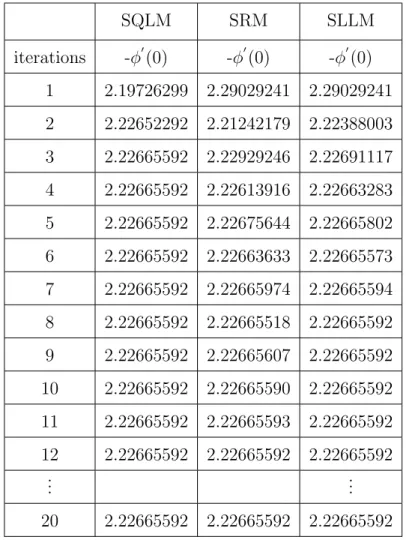
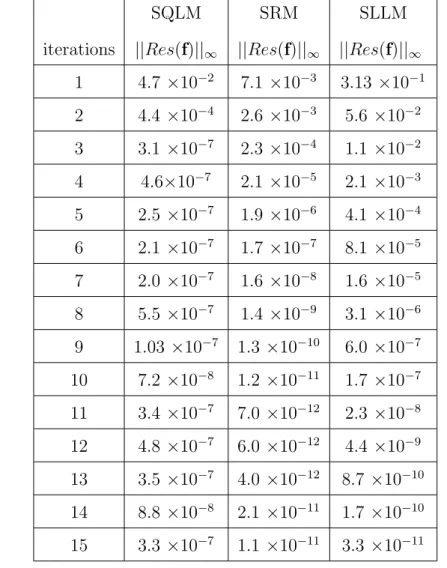
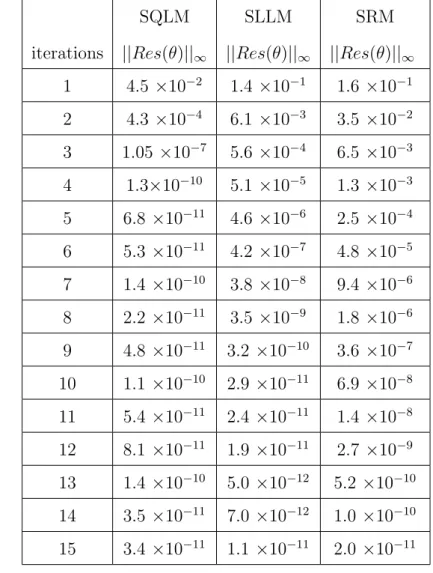
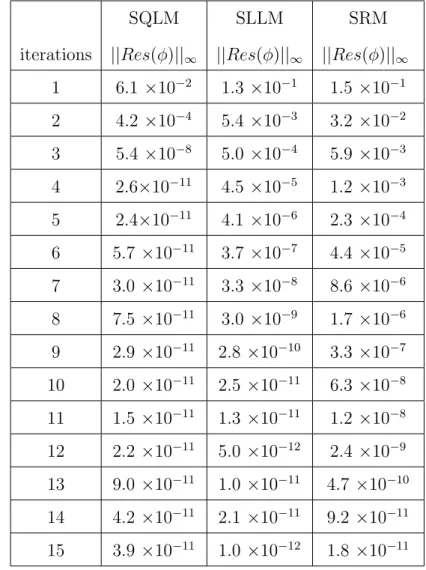
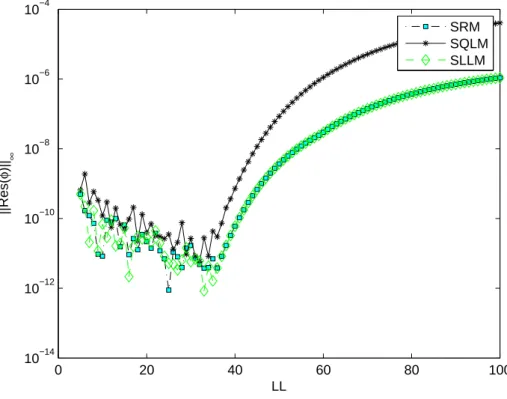
The slope of SQLM is observed to be steepest, further indicating that SQLM converges faster than SLLM and SRM. Tables 3.3 and 3.4 show the residual error norm of the solutions of the system of partial differential equations (3.4) obtained using SRM, SLLM and SQLM. Figures 4.1 - 4.6 show the effect of iterations and time ξ on the accuracy of the obtained solutions using SRM, SLLM and SQLM.
Tables 4.5, 4.6 and 4.7 show the residual error norm of the solutions to the system of partial differential equations (4.1) obtained with the SRM, SLLM and the SQLM. Figures 4.4 - 4.6 show the effect of the time functionξ on the system of partial differential equations 4.48 using the SRM, SLLM and SQLM.
Linearization of a univariate function
Linearization of a multivariate function
Condition for convergence
Gauss-Seidel Method
The Gauss-Seidel method decouples the system (1.7) so that the solution obtained for x1 in (1.7) is immediately substituted into (1.8) to solve for x2 and so on.
Finite Difference methods
The explicit finite difference method, which is forward in time tn and central in space xj, is expressed as (Trefethen (2000)). The implicit method, which is backward in time tn and central in space xj, expressed as.
Crank-Nicolson finite difference method
Finite differences represent partial derivatives with finite difference approximations which are solved instead of the differential equations. 1999) performed a comparative study by applying the linearized Crank-Nicolson finite difference method and 7 other numerical methods to three problems in the nonlinear generalized schr¨odinger equation, and it was observed that the Crank-Nicolson finite difference- the method was very competent. 2008) obtained numerical solutions to the Rosenau–Burgers equation when it proposed the Crank–Nicolson finite difference method as an efficient method.
Spectral Methods
Residual Error
Quasilinearization Method (QLM)
It has been widely applied to many research areas. 1967) extended the QLM to multipoint nonlinear boundary value problems for systems of nonlinear ordinary differential equations. The QLM has been applied in physics by Mandelzweig and Tabakin (2001) to the equations of Lane-Emden, Thomas-Fermi, Duffing and Blasius, and in quantum physics by Krivec and Mandelzweig (2001).
Method Introduction
Spectral Relaxation Method (SRM)
2001) applied QLM to a second-order nonlinear differential equation with Neumann boundary conditions while Nieto (1997) solved second-order nonlinear ODEs with dirichlet boundary conditions with QLM and Ahmad et al. 2002) extended the QLM to solve the same problem with mixed boundary conditions. To obtain numerical solutions from (1.22), the Chebyshev spectral collocation method is applied to the system to integrate it.
Spectral Local Linearization Method (SLLM)
System (1.27) is a decoupled linear system of equations where terms containing r-subscripts are previous approximations and (r+ 1)-subscripts are current approximations. The Chebyshev spectral collocation method is applied to system (1.27) to obtain approximate solutions using the differentiation matrixD= 2D/(b−a).
Spectral Quasilinearization Method (SQLM)
The system (1.34) is a coupled linear system of equations where the r−terms are initial (previous) approximations and (r+ 1)−terms are next (current) approximations. The main idea behind the spectral collocation method is the use of the differentiation matrix D = 2D/(b−a) to approximate derivatives of unknown variables (terms at (r+ 1)).
Structure of Dissertation
Introduction
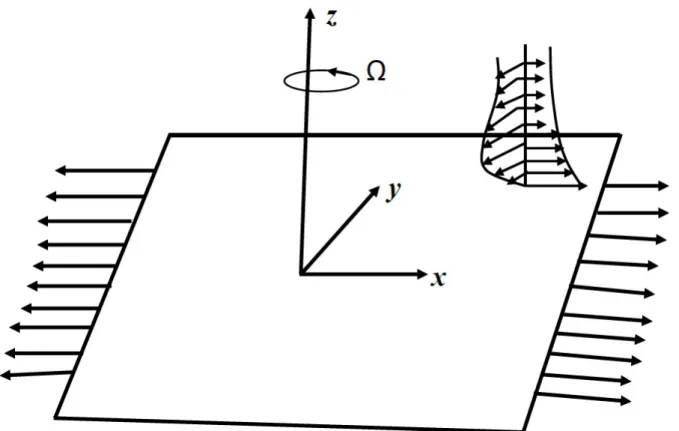
Motsa (2013a) examined the same problem using the spectral local linearization method (SLLM) and the spectral quasilinearization method (SQLM) and concluded that the accuracy of SQLM decreased as the number of collocation points used increased. This chapter begins with a formulation of the mathematical equations that model the unsteady convective transfer of heat and mass across a stretching surface in a porous suction/injection medium.
Mathematical formulation
1−ct, (2.6) while tire care constants with <1, and both and chave dimension time−1, Υw is the suction/injection parameter. By introducing the relations (2.7) into equations, the following dimensionless ordinary differential equations and dimensionless boundary conditions are obtained:. 2.11) where a prime number indicates differentiation with respect to η, fw is the suction parameter when fw >0 and the injection parameter when fw <0,γ is the chemical reaction constant, P r= υα is the Prandtl number, Sc= Dυ is the Schmidt number, A= ac is a parameter that measures flow instability, K = kυx.
Problem Solution Techniques
Spectral Relaxation Method (SRM)
As described by Trefethen (2000), the basic idea of the spectral method is to approximate unknown functions in system (2.19) (the functions at r+ 1) in the full domain by interpolating a higher order Lagrange polynomial at the given collocation points used. Chebyshev differentiation matrix: Let rows and columns of the Chebyshev differentiation matrix be indexed from 0 to Nx for each Nx ≥ 1.
Spectral Local Linearization Method
2.44) and the nonlinear system is decoupled using the concept of the Gauss-Seidel relaxation method to obtain: 2.50) where terms in r denote known terms from the previous iteration while terms in r + 1 denote unknown terms in the current iteration. Boundary conditions are applied to the system in the same procedure as shown in the previous subsection.
Spectral Quasi-linearization Method
Apart from the observation that SQLM solves a system as coupled while SLLM solves as decoupled, SLLM linearizes only nonlinear terms containing the dominant function and its derivative in a particular equation (e.g. g2), while SQLM linearizes both univariate and multivariate non-linear expressions.
Results and Discussion
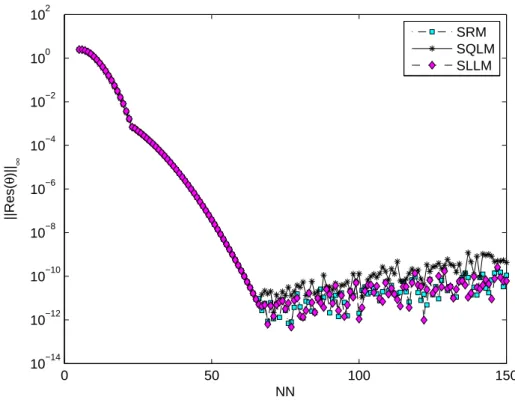
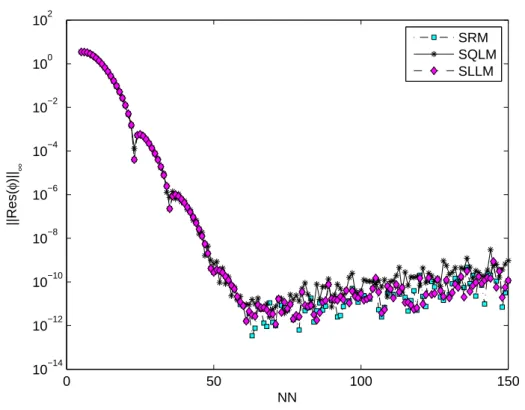
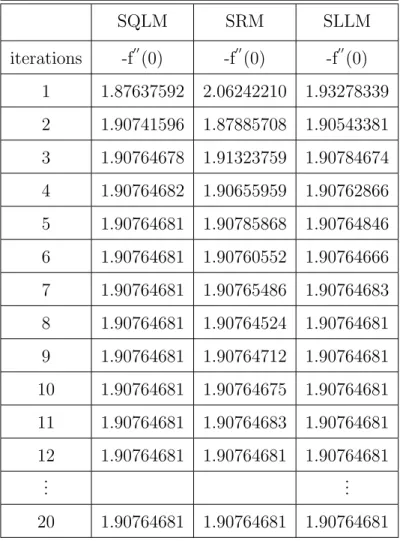
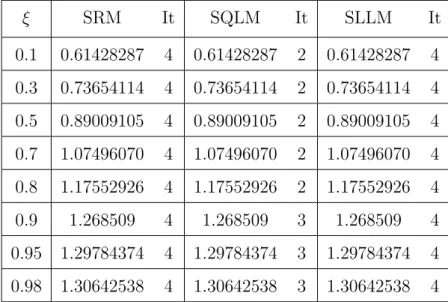
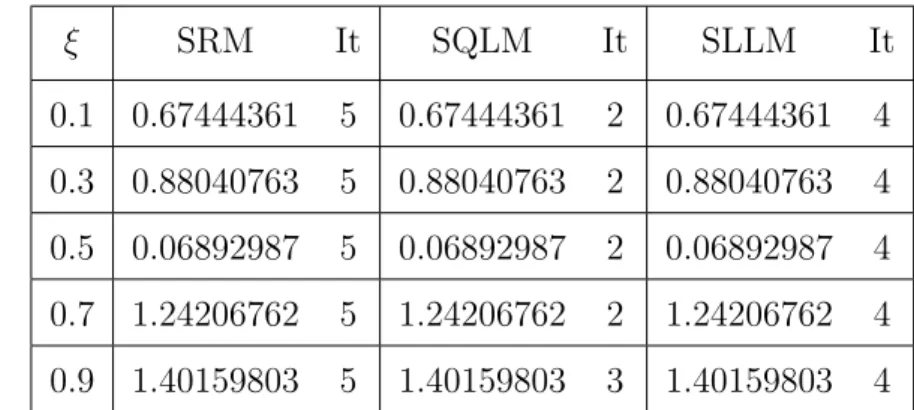
It can be observed that the optimal residual of SQLM is around 10−9, while the optimal residuals of SRM and SLLM are around 10−12. At the maximum residual error (which is when 20 It turns out that the residual error of the SQLM is smaller than that of the other methods at the 5th iteration at 10−10. The slope of SQLM is seen to be steeper than the other two slopes implying faster convergence than SLLM and SRM. The computational efficiency of the methods was also investigated using the time taken to obtain solutions. The third main finding was that increasing the number of iterations improved the accuracy of the solutions. The steps used in the development of SRM, SLLM and SQLM algorithms for a system of partial differential equations will be shown in full. The application of the methods to the system of PDEs is as described in Chapter 1, but with an additional use of the Crank-Nicolson finite difference method to solve in the direction of time. The number of iterations used to obtain converged solutions is also examined to compare the speed of the methods. Finally, the effect of the dimensionless time ξ on the accuracy of the obtained solutions is also investigated. Initial unstable solution is obtained by setting ξ = 0 (τ = 0) for the system of equations (3.4), and the new system is of the form. In this subsection, SRM is applied to the system of equations (3.4) and the corresponding boundary conditions (3.5) by applying the idea of the Gauss-Seidel relaxation method to decouple the system and applying spectral collocation technique to the decoupled system. After applying the concept of the Gauss-Seidel relaxation technique to decouple the system (3.14), the decoupled system becomes . The compact form (3.17) has no significant significance other than making coding much easier or organized on the M AT LAB package. The pseudo-spectral collocation technique (recorded in Hussaini and Zang (1987), Trefethen (2000) and described in the previous chapter) uses a differentiation matrix applied in approximating derivatives of unknown functions and denoted as D, which performs the approximation on the collocation points (grid points) as the matrix vector product. Spectral Local Linearization Method(SLLM) Spectral Quasi-Linearization Method(SQLM) Figure 3.2 - 3.5 gives the graphical representation of the number of iterations and time on the residual error norm for the solutions obtained. As the number of iterations increases, the norm of the residual error for the three methods can be seen to decrease until a point where convergence of the norm is achieved. From Figure 3.3, it can be observed that the residual error norm of SQLM converges at 10−13, which is the same point where SRM and SLLM also achieve convergence. The slope of SQLM can be seen to be steeper than the slopes of SRM and SLLM, indicating that SQLM converges faster than the other methods. The problem of unsteady three-dimensional MHD boundary layer flow and heat transfer over an impulsively stretching plate has been solved using other methods by several researchers. The ease of implementation of the SRM, SLLM and SQLM algorithms in the system of partial differential equations is shown. The residual error rate of the obtained approximate solutions is used to perform the appropriate comparative study of the three methods. Finally, the effect of the dimensionless time ξ on the accuracy of the solutions obtained was also observed. In this subsection, the SLLM is applied to the system (4.1) and the corresponding boundary conditions (4.2). This is done by identifying the nonlinear terms of the same function and its derivative in each of the system's equations (4.1), applying single-term Taylor series expansion to the nonlinear terms to linearize the system of equations, which is decoupled and spectral. collocation technique is used to integrate the system. The system (4.26) is a coupled non-linear system of equations which must be decoupled in order for the system to be solved. Taylor series expansion to nonlinear terms in order to obtain a linear coupled system of equations and the spectral collocation method is applied to a linearized coupled system. System (4.36) is a coupled nonlinear system of equations that must be linearized to solve the system. The slope of the SQLM can also be observed to be steeper than the slopes of the SRM and the SLLM showing that the SQLM converges faster than the other methods. The convergence rate of the SQLM is 0.29 (superlinear convergence) which is lower than the SLLM and SRM which are. It can be seen that the SQLM maintains a residual error norm close to 10−8, while the norm of the residual of the SRM and the SLLM oscillates between 10−10 and 10−12. It is noted that the SRM and the SLLM are quite comparable in terms of accuracy. In Chapter 3, an unsteady boundary layer flow due to a flat surface in a rotating fluid was investigated. In Chapter 4, an unsteady three-dimensional MHD boundary layer flow and heat transfer over an impulsively stretching plate was investigated using SRM, SLLM and SQLM. Analytical solution of three-dimensional unsteady MHD boundary layer flow and heat transfer due to impulsively stretched plane surface. Corresponding solutions for the unsteady boundary layer flow and heat transfer due to a stretching plate. Effect of collocation points on ||Res(f )|| ∞ Effect of collocation points on ||Res(θ)|| ∞ Effect of collocation points on ||Res(φ)|| ∞ Effect of domain truncation on ||Res(f)|| ∞ Effect of domain truncation on ||Res(θ)|| ∞ Effect of domain truncation on ||Res(φ)|| ∞ Effect of iterations on ||Res(f )|| ∞ Effect of iterations on ||Res(θ)|| ∞ Effect of iterations on ||Res(φ)|| ∞ Physical model and coordinate systemSummary
Method formulation
Solution Techniques
Spectral Relaxation Method (SRM)
Results and Discussion
Summary
Problem formulation
Spectral Local Linearization Method (SLLM)
Spectral Quasi-Linearization Method (SQLM)
Results and Discussion
Summary