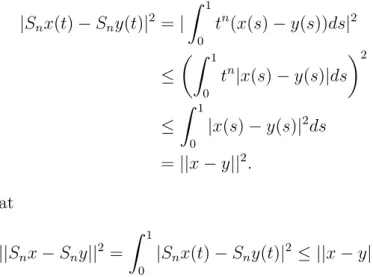In this thesis we study the fixed point approach for solving optimization problems in real Hilbert, Banach and Hadamard spaces. These optimization problems can be converted into a fixed point problem (FPP) of a suitable nonlinear map.
Research problems and motivation
Research problems
In this study, we propose a new inertial iterative algorithm with self-adaptive step size to approximate the joint solution of the finite family SMVqIP (1.2.13) and FPP (1.1.1) of the non-expansive mapping between Banach and Hilbert spaces. Furthermore, we propose a generalized implicit viscosity rule to find a joint solution of a finite family of MP and FPP for a finite family of quasi-pseudocontractive mappings in Hadamard space.
Motivation
The problem of finding a common solution to split equations EP, VIP and FPP of non-expansive semigroups has applications to many nonlinear problems. 70] proposed an iterative algorithm for approximating the joint solution of a finite family of MP and FPP for two demicontractive mappings in Hadamard spaces.
Objectives
This motivates the need to extend the results for optimization and FPP from Hilbert and Banach spaces to Hadamard spaces. Inspired by the viscosity technique, we propose a generalized viscosity implicit rule for approximating the joint solution of a finite family of MPs and FPP for a finite family of quasi-pseudocontractive mapping in Hadamard space.
Organization of the thesis
Some inequalities that characterize Hilbert spaces
Some nonlinear single-valued mappings in Hilbert spaces
Furthermore, both η-strongly monotone and η-inverse strongly monotone mappings are monotone while monotone mappings are pseudo-monotone. A is averaged if and only if the complement I−A is strongly inverse monotonic for someη >.
Geometric properties of Banach spaces
Some inequalities that characterize Banach spaces
Some nonlinear single-valued mappings in Banach spaces
Geometric properties of geodesic metric spaces
- Metric midpoints
- Geodesic triangles
- Geometric properties of Hadamard spaces
- Examples of Hadamard spaces
- Quasilinearization mapping and dual space
- Some inequalities that characterize Hadamard spaces
- Some nonlinear single-valued mappings in Hadamard spaces
- Monotone operators and its resolvents in Hadamard spaces
A geodesic metric space X is called a CAT(0) space if all geodesic triangles satisfy the CAT(0) inequality. The dual of closed and convex subsets of a Hilbert space H with nonempty interior is a Hadamard space and t(b−a) Some inequalities characterizing Hadamard spaces.
Metric and generalized projections
Convex functions
Let X be a uniformly convex and smooth Banach space with a Gˆateaux differential norm and let B :X →2X∗ be a maximal one-tone operator. The solvent plays an important role in the approximation theory for zero points of maximal one-tone operators in Banach spaces.
Review on some optimization problems
Variational inequality and fixed point problems
In this study we focus on the approximation of the solution of VIP (1.2.1) using the projection method. Recently, Yang and Liu [266] proposed and studied an extragradient Tseng method combined with the Moudafi viscosity scheme, which does not require prior knowledge of the Lipschitz constant of the monotone operator.
Split variational inequality problem
Note that Algorithm (2.5.9) does not require the formation of the product space, so it takes full advantage of the attractive distributional structure of the SVIP. Therefore, it is necessary to develop efficient SVIP solving algorithms that do not require a product space formulation and converge to a minimum SVIP norm solution.
Split equalities of equilibrium, variational inequality and fixed point
115] investigated and proposed a method to estimate the step size which does not require prior knowledge of the operator norms for solving the SFP. Zhao [271] also proposed new step size choices that do not require prior knowledge of the operator norm for solving the SECFPP.
Variational inclusion and split equilibrium problems
Under certain conditions they obtained a weak convergence of Algorithm 2.5.23 with one element in the solution set (1.2.12). Furthermore, the operator B in Algorithm 2.5.23 and other algorithms above is required to be co-constraining (strongly monotone inverse) which is a very strict condition.
Split monotone variational inclusion and fixed point problems
They proved that the sequence {xn} defined by (2.5.28) strongly converges to a solution of the SVqIP under certain conditions. Therefore, there is a need to develop efficient iterative algorithms (where the step size does not depend on the operator norm) to approximate the common solution of the SVqIP and FPP.
Minimization and fixed point problems
For example, the PPA in Hadamard spaces (non-linear version of Hilbert spaces) is known to have applications in computational phylogenetics, consensus algorithms, modeling airway systems in human lungs and blood vessels, computation of medians and means, among others (see and the references in there). They proved that under suitable conditions the generated sequence strongly converges to a fixed point of the non-expansive map, which also solves the variation inequality.
Some important lemmas
9] Let {an} be a sequence of nonnegative real numbers, {γn} a sequence of real numbers in (0,1) with conditions. In this chapter, we present our results on VIP and monotone FPP of an infinite family of strict pseudo-contracting mappings in real Hilbert space and apply these results to solve other nonlinear problems. Also, we present our result for quasimonotone VIP and FPP of a quasi-pseudocontracting map in real Hilbert space.
Preliminaries
Let C be a nonempty closed convex subset of a strictly convex Banach space X. Let {Si′} be an infinite family of nonexpansive mappings of C itself such that T∞. Then we have the following: 69] Let C be a nonempty closed convex subset of a strictly convex Banach space X. Let {Si′} be an infinite family of nonexpansive mappings of C into itself such that T∞. 276] If S is a k-string pseudo-contraction on closed convex subset C of a real Hilbert space H, then I−S is demiclosed at every vertex ∈ H.
Common solution of the variational inequality and the fixed point problems 59
Convergence analysis
Then the sequence {xn} strongly converges to a point x∗ ∈ Γ, where x∗ = PΓ(I−D+γ1f)x∗ is a solution of the variation inequality. Then the sequence {xn} strongly converges to a point x∗ ∈ Γ, where x∗ =PΓ(f)x∗ is a solution of the variation inequality. Then the sequence {xn} strongly converges to a point x∗ ∈Γ, where x∗ = PΓ(f)x∗ is a solution of the variation inequality.
Applications
Then the sequence {xn} strongly converges to the point x∗ ∈Γ, where x∗ = PΓ(f)x∗ is a solution of the variational inequality. 3) A monotone operator B on H is said to be maximal if its graph is not properly contained in the graph of any other monotone operator on H;. Let Bi : H → 2H be an infinite family of maximal monotone mappings with D(Bi)̸=∅ and JrBii the resolvent of Bi for every ri >0. Let Bi : H → 2H be an infinite family of maximal monotone mappings with D(Bi) ̸= ∅, JrBii be the resolvent of Bi for every ri ∈ (0,2δi) and Fi : H → H an infinite family of δi− inverse strongly monotone mappings.
Numerical experiments
Let {ζn} be a sequence of nonnegative real numbers defined by ζn ={n+1n } for all n ∈ N and Wn be a map generated by {Sn} and {ζn}.
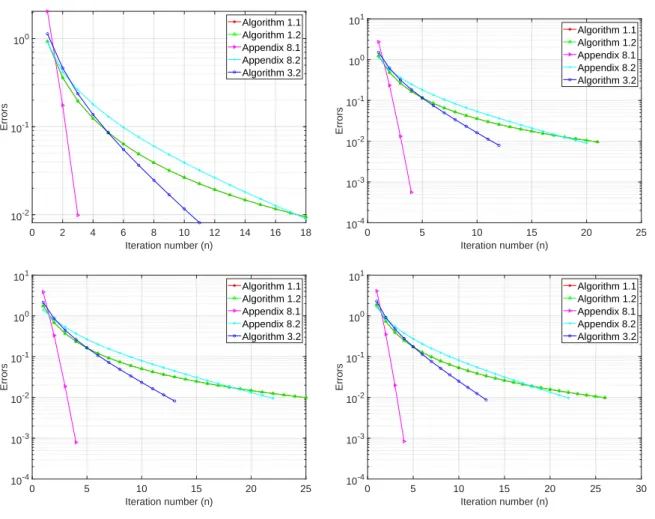
On quasimonotone variational inequality problems
Proposed methods
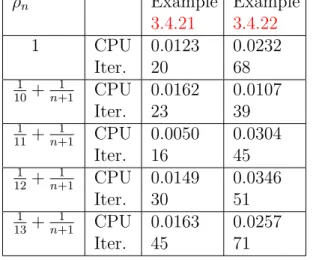
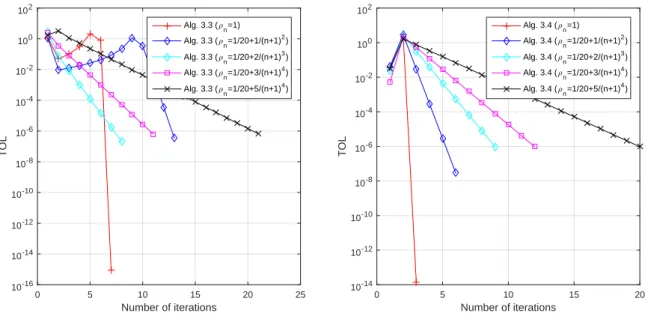
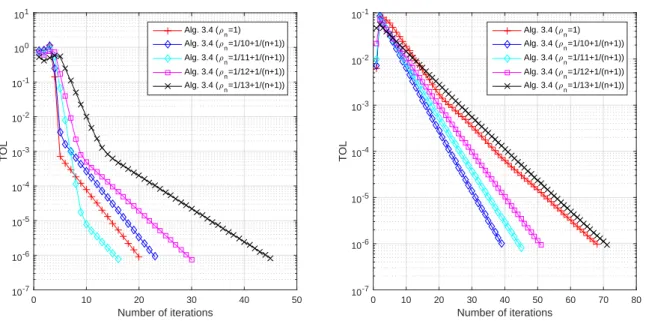
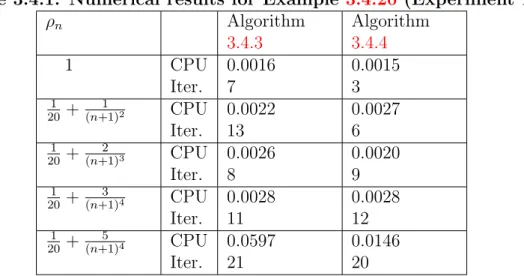
In such a case, we have the following simple criteria that guarantee assumption 3.4.1, as well as assumption (2.5.37). When ρn ̸= 1, then we have the following statement which provides some criteria to ensure assumption 3.4.1, as well as assumption (2.5.37). Thus, assumption 3.4.1, as well as assumption (2.5.37) are much weaker than the assumptions in those works in the literature.
Convergence analysis
In light of the above remark, we analyze the convergence of Algorithm 3.4.4 in what follows. In the study of inertial methods for solving GDPs (even for monotone mapping), the inertia parameter is usually limited to [0,13) and/or required to be non-decreasing. One of the novelties of this work is that we derived a general condition (Assumption3.4.1) that is weaker than the above conditions used in the literature to ensure the convergence of inertial methods for GDPs.
Numerical experiments
Moreover, we used the condition (Assumption 3.4.1) where joint adjustments of the inertial and relaxation parameters play a crucial role (for example, see Experiment 1). We do this to control the effects of the relaxation parameter in our methods. Our result improves, extends and generalizes some of the recently announced results in this direction.
Proposed method
Our result improves, expands and generalizes some of the recently announced results in this direction. g) Let {ϵn} be a positive sequence such that lim. h) Let {ρn} be a non-negative sequence such that. The algorithm involves only one projection on the feasible set C per iteration, which makes the algorithm implementation computationally cheaper. This allows the implementation of algorithm 3.5.2 without prior knowledge of the Lipschitz constant.
Convergence analysis
Since yn =PC(wn−λnwn) andp∈ΓD ⊂C, we obtain from the characteristic property of PC that. Next, by the boundedness of {xnk}, it follows that there exists a subsequence {xnkj} of {xnk} that converges weakly to some ˆx∈ H, and so that.
Numerical experiments
Therefore, we can only compare our algorithm 3.5.2 in infinite dimensional Hilbert spaces with Appendix 3.5.4 in Example 3.5.12. Our goal is to restore the original image x, given the blurry image data v. In this case, the operator A is known to be monotonic and ∥DTD∥-Lipschitz continuous (so A is quasimonotonic and uniformly continuous).
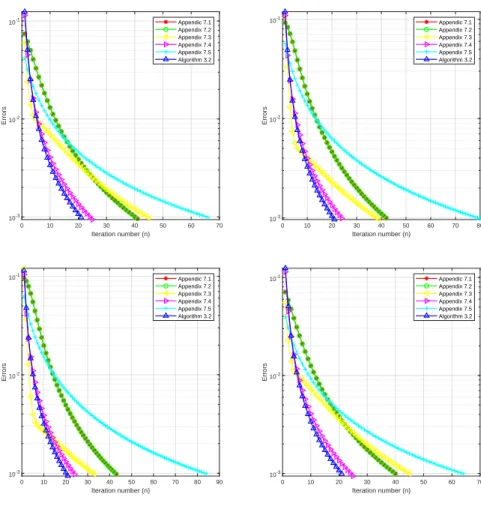
On split variational inequality problems without product space formulation 128
Convergence analysis
Since yn =PQn(T wn−λF Twn) and T p∈ Qn, we get from the characteristic property of PQn that. Following the same arguments as in Lemma 4.2.5 and Theorem 4.2.6, we obtain the rest of the proof. Similar to Remark 4.2.7, we obtain a relaxed inertia Tseng's forward-backward-forward with adaptive step sizes involving only one projection on the half-space Cn per iteration to solve the classical VIP (1.2.4) when Ais monotone and Lipschitz continuous as a consequence.
Numerical experiments
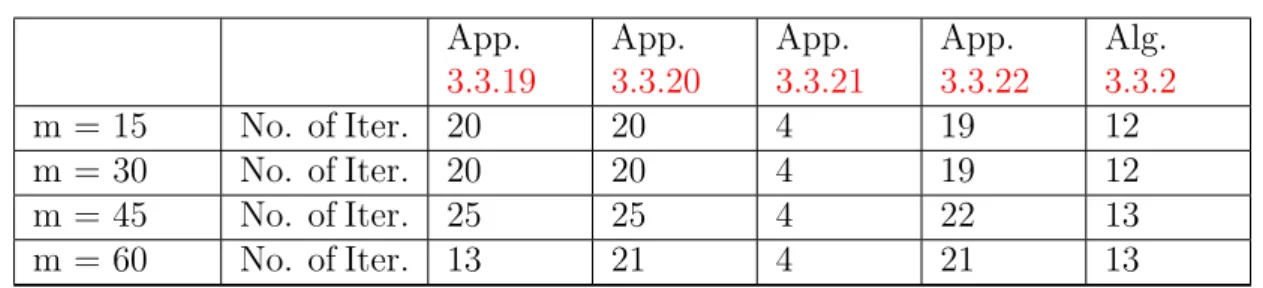
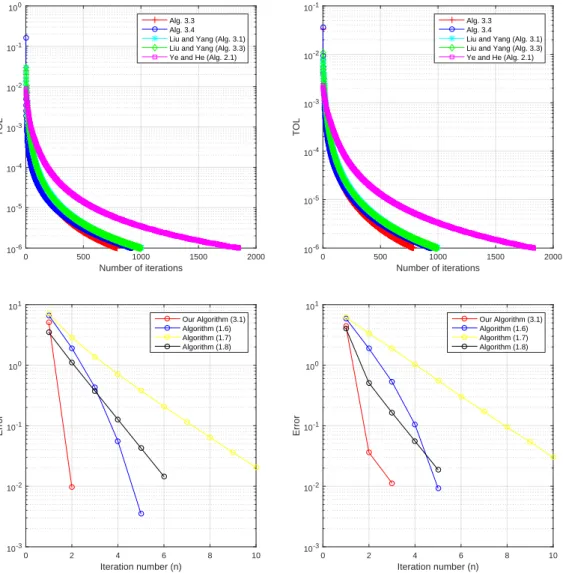
We also take ε= 10−6 as the stopping criterion and obtain the numerical results listed in Table 4.2.1 and Figure 4.1. By considering the following examples for numerical experiments, we obtain the numerical results shown in Table 4.2.2 and Figure 4.2. From table 4.2.1 and figure 4.1 we can also see that when solving problem (4.2.71) the effectiveness of algorithm 4.2.2 is slightly affected by the dimensionality of the problem.
On split variational inequality problem beyond monotonicity
Proposed methods
The step sizes {λn} and {µn} given by (4.3.3) and (4.3.4) respectively are generated at each iteration by some simple calculations. Unlike , we can see that Algorithm 4.3.2 and Algorithm 4.3.3 do not require any formulation of the product space, thereby avoiding potential problems that the product space might cause. The choice of the step size ηn in step 3 of algorithms 4.3.2 and 4.3.3 does not require prior knowledge of the norm of the operator ∥T∥.
Convergence analysis
Thus, from the weak sequential continuity of F onQ, we get that {F ynk} converges weakly to F T z. Thus, by the following weak continuity of A in C, we get that {Aunk} converges weakly to Az. Note that by setting H1 =H2 =H, F = 0 and T =IH (the identification operator on H) in Theorem 4.3.6, we obtain as a consequence an inertial projection and contraction method that requires only one projection into the potential setC for iteration, with fixed step size for solving the classical VIP (1.2.1) when A is pseudomonotone and Lipschitz continuous.
Numerical experiments
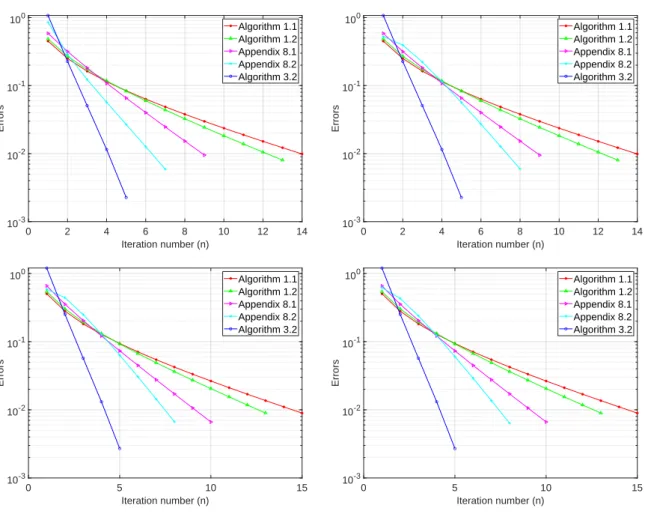
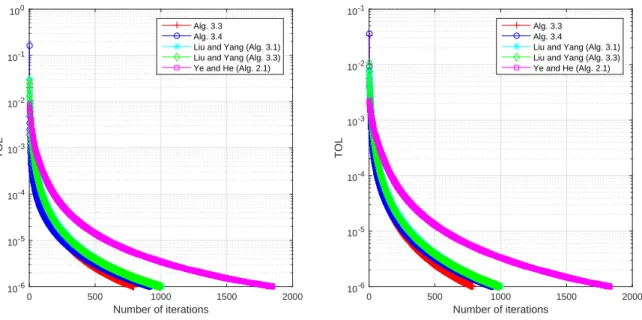
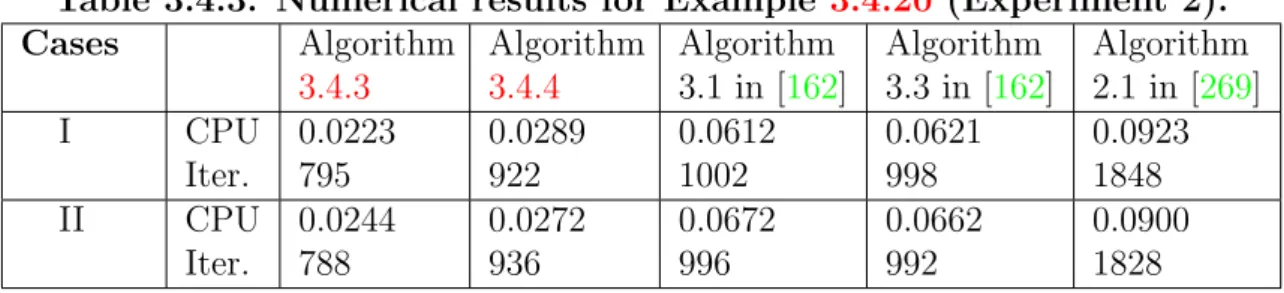
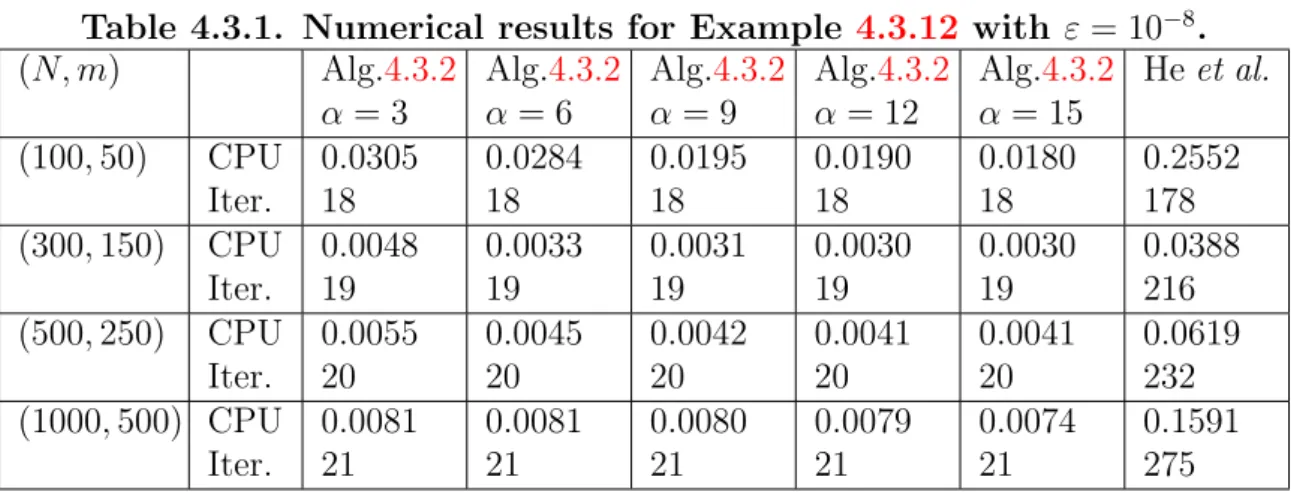
In these cases, we perform comparisons with the methods of Pham et al. From Table 4.3.1, we can also conclude that in Example 4.3.12, the number of iterations for our proposed Algorithm 4.3.2 is almost the same for all starting points, while the method of He et al. From the tables and figures, we can clearly see that both in terms of CPU time and number of iterations, our proposed algorithm 4.3.2 outperforms the method of He et al.
Projection and contraction methods for split variational inequality problem 185
Convergence analysis
Numerical experiments
On a class of generalized variational inequality problem
Main results
Numerical experiments
On split equalities of some nonlinear optimization problems
Proposed method
Convergence analysis
Numerical experiments
On minimum-norm solutions of inclusion and split equilibrium problems
Proposed method
Convergence analysis
Applications
Numerical experiments
On pseudomonotone variational inequalities with non-Lipschitz operators . 274
Convergence analysis
Numerical experiments
On finite family of split monotone variational inclusion and fixed point
Proposed method
Convergence analysis
Application
Numerical experiments
Preliminaries
Modified proximal point methods
Main results
Extension to monotone inclusion problems
Numerical experiments
On generalized viscosity implicit rule for quasi- pseudocontractive mappings 330
Contributions to Knowledge
Future research