The membership logic is the ideal of the canon whose theories are the relative congruence classes on the free algebra. For example, we have many uses of the symbol ``·', the · indicates where the parameter goes.
Relationships, Relations, Operations and Matrices
- Basic Specifications
- Binary Relationships and their Images
- Binary Relations and Quotients
- Unary Matrices
- Families, Vectors and Tuples
- Products
- Reduced Products
- Realms, Matrices and Relations
- Operations
Our notion of a binary relationship from one collection to another strongly 'types' the domain and codomain, as is typical of functions. Recall the idea that an equivalence relation α is compatible with a subset B of its universe (see Definition 1.65 on page 24).

Order
- Quasi-Orders and Directions
- Orders
- Semilattice and Lattice Orders
- Compactness and Algebraic Lattice Orders
- Ideals and Filters
- Order Preserving and Reflecting Functions
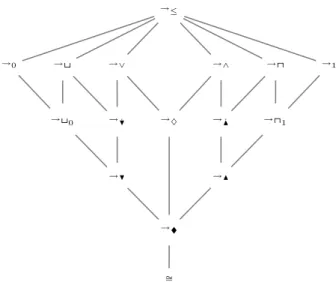
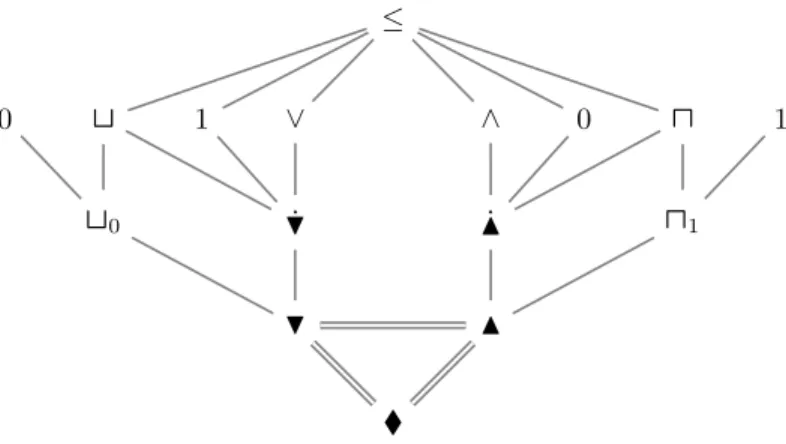
An order with one smaller (greater) element is called bounded (ie upper bound) or an order with 0 (with 1). The transitivity i≤ ensures that the upper setP(X) (P(P(X))) of all upper (respectively lower) bounds is an inversion (respectively lower).
Systems
The systems we will deal with in this text are either >-systems or ⊥-systems (or both), and therefore are not empty by definition. We prefer the alternative term "final", which we tend to use later in the text to avoid possible confusion with other uses of the term "algebraic".
Constructs and Categories
Constructs
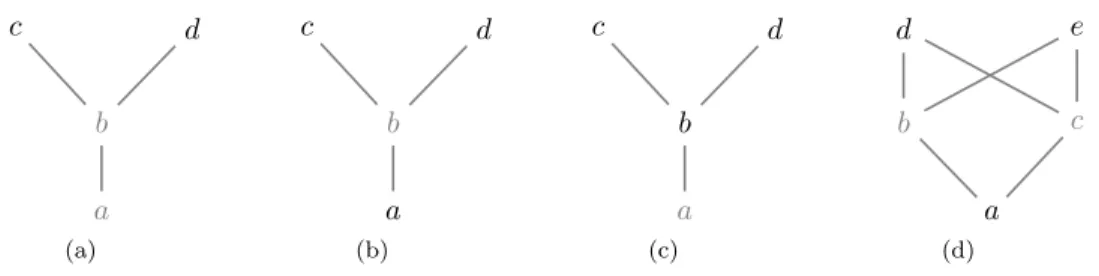
We say that a subobject B of A is generated by M (in A), if B is the smallest subobject of A with M ⊆uni(B). This explains the fact that algebraists see injective homomorphisms as embeddings, while order theorists do not (see Definition 1.173 on page 39 and Definition 1.289 on page 58).
Categories
Algebras and Structures
Types of Algebras and Structures
A type e is called an algebra type or algebraic type (relation type or relational type) if it has no relation symbols (or operation symbols). While it is possible to liberate the specification of the underlying type of a particular symbology, as is the typical approach in model theory texts, such an approach is unnecessarily technical and cumbersome for the reader and user of the language. The type of unary matrices over a is a base type that extends a type with a single unary relational symbol, usually denoted by the symbol D.
Algebras and Structures
Anunarya-matrix, is a type structure of unary matrices over a, in which case we call DM thedesignator. The A-reduction of a unarya-M matrix is denoted by alg(M) and is called the matrix algebra. For an arbitrary matrix-algebra M, we denote the "algebra" subtype of type (M) by types (M), which we call the matrix algebra subtype.
Class Operators
Structure Homomorphisms
We denote the set of all epimorphisms (resp. monomorphisms and isomorphisms) from A to B by AB (resp. We denote the set of all algebra homomorphisms (resp. algebra embeddings, algebra epimorphisms and algebra isomorphisms). H(K) (C(K), E(K)) denotes the class of all e-structures which are the homomorphic image (resp. contraction, expansion) of some member of K.
Substructures and Subuniverses
Some universal algebraic texts define subuniverses of algebras in the manner of definition 1.223 (i.e. subuniverses are the universes of subalgebras), while still positing a notion of subuniverse generation (e.g. [vA95] and [Bar95] by this author). A useful characterization of the generation of subuniverses, via closure under term functions, is given in Theorem 1.344 on page 65. See in particular Example 5.44 on page 188, which follows from the previous theorem, and which is crucial for the origin. from the subuniverse logic of example 6.80 on page 242.
Products
Terms, Term Algebras, Term Functions and Polynomials
When a finite symbol sequence is analyzed, it is a term over V if either, (i) it is an element of V, or (ii) it is an e-constant symbol, or (iii) the sequence starts with a symbol ?, where ?is a one-operation symbol for arytyn >0, and is followed by a sequence of symbols of the form (p1, . . . , pn), where for each i= 1,. The key to interpreting such notation is to recognize which 'symbols' in the production rule are 'variable' after the intervals for the other 'symbols' have been specified. A set of terms P must be called invariant (resp.p-invariant, where pis is a term) if σ[P] ⊆P for every substitutionσ(resp. every substitution σ that fixessp, i.e. that has σ(p) =p) .
Quotients and Congruences
Correspondence theorem]Letα∈Con(A). The filter sublattice [α)Con(A) of the algebraic lattice Con(A) is isomorphic to the algebraic lattice Con(A/α) under the mapping spanning β 7→β/α. When studying classes of algebras that are not closed with respect to homomorphic images, especially quasivarieties of algebras (see Section 1.5.14), not all congruences on the class algebra of the core of 'valid' homomorphisms, i.e. of homomorphisms that give homomorphic images lying in the class. In Section 1.5.14, we introduce the notion of an aquavariety, and for classes of algebras that form quasivarieties, a relative congruence forms an algebraic closed system, in which case a relative congruence generation is defined, albeit more.
Reduced Products and Ultraproducts
We deliberately present the definition of reduced products of algebras and structures separately, because, as we will see, the former is a real quotient, while the latter is generally not a quotient. The reader is invited to note how in the following definition, although the algebraic reduction is a standard quotient (it is simply the reduced product as in the previous definition), the relational components are not defined as they would be for a quotient (i.e. say: as in Definition 1.365 on page 69). Consequently, reduced products and ultraproducts of structures are not really quotients, since according to Note 1.348 on page 66 the quotient mapping on a quotient structure must be strict.
Free Structures
Let PR(K) denote the class of all e-structures that are reduced products of some members of K, and let PS(K) denote the class of all structures that are ultraproducts of some members of K. The term algebra, although free for any class of algebras, it will never be a member of any interesting class of algebras, mainly because of its absolute freedom. The following construction gives a more interesting free algebra for the class of algebras and is often a member of that class (see Theorem 1.385 on page 73).
The Model Theory of Structures
Important groupoid formulas with equality are 1.74) With 'universal groups', existential identity and existential inverse are 'expressible' by group formulas (with equality). 1.76) Definition 1.407 (Identities and Quasi-identities). Recall that sets of small structures must be classes, and if Kis are classified structures, then every structure in Kisssmall (see Definition 1.7 on page 15 and the following remark). In the next example, notice how "simple" the characteristic formulas are, compared to the previous example.
Characterizing the Leibniz Relation
A ring with unity is an algebra of type ring with unity, with a ring reduction (the natural one) and a monoidh·,1i reduction. The former, on the other hand, are essentially defined by sets of universally quantified equations. The former classes of algebras, defined by such equations, are known as equation classes or varieties, and yield a relatively simple model theory (see H.
The Equational Theory of Algebras and Varieties
A characterization of a variety of varieties (or more precisely, a class of varieties) by the presence of certain terms and the satisfaction of certain identities involving these terms will be referred to as a Mal'cev characterization of said formula. For a more formally precise definition, see [Tay73].) For example, it is well known [Mal54] that a variety V is congruently permutable if and only if. The above characterization of congruence-permutability (or more precisely of the class of congruence-permutable varieties) is thus a Mal'cev characterization. Congruence regularity and congruence point regularity, when satisfied by all algebras of a variety, also have Mal'cev characterizations.
The Quasi-Equational Theory of Algebras and Quasivarieties
Aquasi-Mal'cev condition is a characterization of a property satisfied by a class of algebras in terms of the satisfaction by the class of certain quasi-identities and identities. The Mal'cev characterization of congruence regularity, given in Theorem 1.444, can be given a much simpler (and much more intuitive) quasi-Mal'cev characterization. The next quasi-Mal'cev characterization was discovered by Cs´ak´any [Cs´a70] over a decade before the first Mal'cev characterization was discovered by Duda [Dud83].
Further Examples
Thea-reduct of ana-matrixMis denoted byalg(M), and is called the scalar algebra of the matrix. Recall that, according to Theorem 1.360 and Definition 1.361, the Leibniz relation ΩA is the largest congruence on structure A. 2.5, where the concept of equivalence concerns theorem provers of the same algebraic type, but with possibly different dimensions.
Languages of Sentential Calculi
Sentential Calculus
Axioms, Rules and Derivations
Sentential Calculi
Some texts take the consequence relation as the starting point for the definition of a logic, in which case there is no need for the concept of equivalence. The consequence relations of theorems can be characterized as exactly the binary relations from P(Fm(p)) to Fm(p) satisfactorily. It is not immediately clear what this formal system is, because of the role that substitution plays in the definition of derivation.
The Matrix Model Theory of Sentential Calculi
- Suggesting Matrix Models
- Matrix Models
- Constituting Models and Semantics
- Leibniz Analysis
A set F ⊆uni−→(M) is called anS-filterofMifDM⊆F and. 2.6) The set of allS filters on M, called FiS(M), forms an algebraically closed system on uni−→(M). We highlight the examples of the previous results that will be most important in the future. Recall the definition of the Leibniz relation ΩA, associated with a structure A, given in Definition 1.361 on page 69.
Examples
As mentioned in the previous paragraph, the logic of S(K, τ) correlates with generalizations of the notion of point regularity in universal algebra; more formally, S(K, τ) is algebraic if K hK, τi-regular (see Definition 2.124 of Case 2.124 as well as Theorem 2.125 of the same case). While hK,τi-regularity captures the well-known pointwise regularity condition in universal algebra (see Definition 1.375 on page 71), neither hK,τi-regularity nor (more general) hK,Ni-regularity captures perfect regularity (see Definition 1.375). A special case of the logic S(K, τ) is obtained when τ={hx,0i}, where x is a variable and 0 is a K-constant (see definition 1.460 on page 88); these logics are called propositional logics in [BR99].
Equivalent Sentential Calculi
Examples
The following example shows that if the relative congruence logics of two quasivarieties are formally equivalent, then these logics are equal to the quasivarieties.
Algebraization
Examples
We briefly consider this algebraization of assertion logic and its relation to the well-known universal algebraic condition of point regularity (see Definition 1.375 on page 71). In Counterexample 3.1 on page 124, we shall demonstrate that the well-known variation of quasigroups, although fully congruence regular (see Definition 1.359 on page 68), is the equivalent algebraic semantics without theorem-determining 1-calculus, and furthermore, contains a non -trivial (complete congruence regular) submanifold that is not even the algebraic semantics of a non-trivial theorem-1 calculus. The primary purpose of this text is to remedy this problem by associating with each quasivariety K a propositional 1 calculus called its membership logic, and two to develop a theory of parameterized algebraization such that K is the (appropriately parameterized) parameterized equivalent algebraic semantics of its membership logic, exactly when K is relatively congruence regular (see Definition 1.375 on page 71).
Protoalgebraicity
Examples
The following characterization of the proto-algebraicity of S(K, τ) follows directly from Corollary 2.138 together with Theorem 2.89 of Example 2.85. For the sake of the following discussion, we call a quasivariety algebraic if it is equivalent to the algebraic semantics of some sentence 1-calculus. In [BJ06], the theory of transformers between closure operators was published as part of a generalization of algebraic logic theory.
Elementary Closure
- Elementary Closure Operators
- Elementary Closed Systems
- Elementary Consequence Relations
- Elementary Closed Equivalence Relations
- Elementary Proto-Leibniz Relations
- Granularity
An elementary closure operator is a type(eco)-structurec=hunie(c);≤c;k·kci, whose ≤-reduction is an order, denoted Pc and called the fundamental order, and such that c satisfies the axioms (Further). For an orderPand a unaryclone(P), when we say that it defines a (elementary) closed system in P, or we say that hP;cli is a (elementary) closed system, we mean that huni(P);≤P;cli is an elementary closure operator. For a Pand order a triple connection mc(·) on uni(P), when we say that mc(·) defines a (elementary) proto-Leibniz relation on P, or we say that hP;mc(·)i is an (elementary ) proto-Leibniz relation, we mean see(P);≤P;mc(·)i is an elementary proto-Leibniz relation.
Concrete Closure
- The Closed System of all Closed Systems
- Bases
- Filtrations
- The Point Proto-Leibniz Relations
- Unary Matrices as Closed Systems
Further, our conflation convention unites these three objects, i.e., the closure operator associated with the closed system of closed sets of a topological closed system is the closure operator of that closed system, etc. universeuni(X) and defined byclCCC(X,base)={uni(X)} ∪ {T. We then define the notion of closed filtering system, which is the closed system obtained from the closed system C by selecting only those closed sets that contain a certain subset of the universe.
Algebraic Closure and Formal Systems
Algebraic Closure
Since the closed system of congruences for this term algebra is never trivial, this sential calculus has no theory;. We denote the final closed system Cos∅(Con(A)) of all sets of congruences in an algebraA, by Cos(A). In the case where Kis is trivial, for every algebraA, the closed system of relative congruences overAistrivial.
Formal Systems
In the following example we give a formal axiomatization of F(Con(A),cos) based on inference 1.356 on page 68. Γ`S1 φimplies τ[Γ]`S2 τ[[φ]] (5.3) (we will use this condition in H.17.3 of Part VI, characterizing precisely those formal translations that commute with substitutions, the latter condition playing a central role in algebraic logic; see especially Corollary 17.27 on page 475). In H5.4 we characterize continuous translations, strictly continuous translations and iseomorphisms in terms of H-conservative functions, H-embeddings and isomorphisms respectively (see Definition 1.180 on page 40) between the closed set of lattices, thus obtaining opposite results from the elementary results to acquire. obtained in the previous part.
Translations
Similar results obtained for, what we called, the reduced example. briefly introduced) of formal translations in the context of a formal equivalent semantics [BP89a]. In the definition of the reduced image, we insist that b∈rg(r), to avoid allowing points b with ←−r[[b]] =∅ ⊆A. In the case of functions, seen as binary relations, the reduced example and the functional inverse image coincide.