MondalNishatRahmanAlam2011.15.2. 320KB Jun 04 2011 12:09:14 AM
Teks penuh
Gambar
Dokumen terkait
The asymptotic convergence of paths given by the asip (log) then allows these results to pass over from the self-similar processes to the coordinate-changed random walk, by Lemma 6.1
Our aim in in this section is to show that in the case of metabelian groups the lower estimate (11) can be complemented with a similar upper bound. We keep the notation of §2.. §2)
As we mentioned just after Theorem 2.8, it is possible to adapt the change-of-measure argument to prove non-coincidence of quenched and annealed critical points in dimension d ≥ 4
We will see in Section 4.1 that, assuming the Lifshitz tail effect in [ 12 ] , our result indeed derives the correct upper bound of the quenched asymptotics for the Brownian
Still in the Gaussian case, [13] derived upper bounds of large deviations type for the spectral measure of band matrices, including certain sample covariance matrices.. Her
It remains to find an upper bound for the second term. Thus, we can rewrite the r.h.s. and have the same law as the number of vertices visited by the walk before the time D of its
The class of graphs we consider includes hyperbolic graphs with sufficiently high degree, where the best upper bound on the mixing time of the free boundary dynamics is polynomial in
This Gaussian concentration is derived from a Gaussian upper bound of the density of the scheme and a modification of the so-called “Herbst argument” used to prove Logarithmic
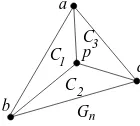
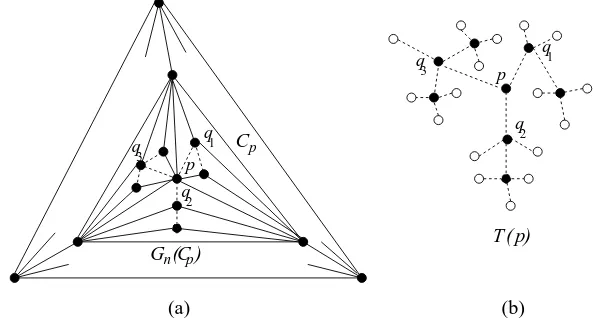
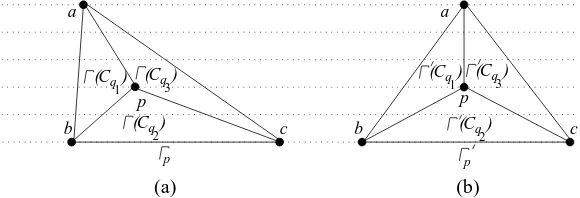
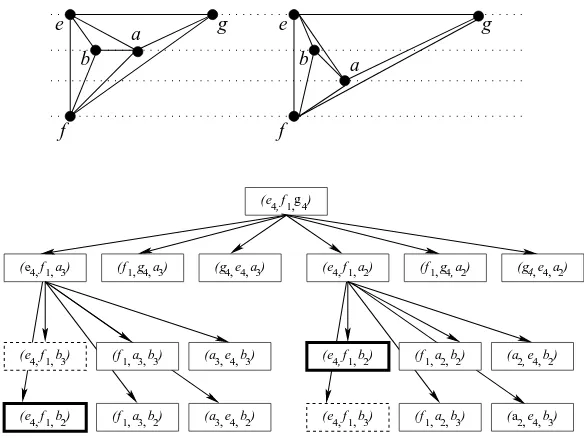
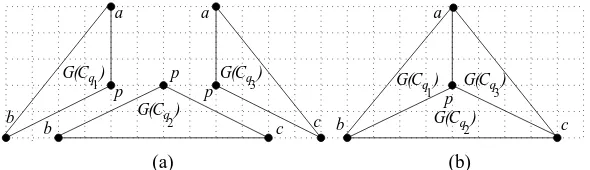
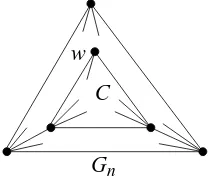
![Figure 6 illustrates the representative tree Tn−3 of the plane 3-tree Gn. Notethat the “4-block trees” [21] and the tree of the “tree decomposition” [5] arequite similar to the representative trees for the plane 3-trees.](https://thumb-ap.123doks.com/thumbv2/123dok/936949.905651/8.612.196.419.172.247/figure-illustrates-representative-notethat-decomposition-arequite-similar-representative.webp)