PEMBELAJARAN MATEMATIKA DENGAN MODEL CORE UNTUK MENINGKATKAN KEMAMPUAN PENALARAN DAN KONEKSI MATEMATIS SISWA DI SEKOLAH MENENGAH KEJURUAN.

(1)

Lala Isum, 2012

Pembelajaran Matematika dengan Model CORE untuk Meningkatkan Kemampuan Penalaran dan Koneksi Matematis Siswa Di Sekolah Menengah Kejuruan

Universitas Pendidikan Indonesia|repository.upi.edu DAFTAR ISI

halaman

LEMBAR PENGESAHAN ... i

LEMBAR PERNYATAAN ... ii

ABSTRAK ... iii

KATA PENGANTAR ... iv

UCAPAN TERIMA KASIH ... vi

LEMBAR PERSEMBAHAN ... viii

DAFTAR ISI ... ix

DAFTAR TABEL ... xii

DAFTAR GAMBAR ... xv

DAFTAR LAMPIRAN ... xvi

BAB I PENDAHULUAN ... 1

A.Latar Belakang...1

B.Rumusan Masalah...11

C.Tujuan Penelitian...12

D.Manfaat Penelitian...13

E.Definisi Operasional...14

BAB II L ANDASAN TEORI ... 17

A.Kemampuan Dasar Matematis ... 17

B.Penalaran matematis... 19

C.Koneksi Matematis... 24

D.Pembelajaran Metode Ekspositori ... 27

E.Pembelajaran Model CORE...29

F.Teori Belajar yang mendukung ... 36

G.Penelitian yang Relevan...39

H.Hipotesis Penelitian...43

BAB III METODE PENELITIAN... 44

A.Desain Penelitian...44

B.Populasi dan Sampel Penelitian...45

(2)

Lala Isum, 2012

Universitas Pendidikan Indonesia|repository.upi.edu

D.Instrumen Penelitian... 46

D.1. Tes Matematik ... 46

D.2. Lembar Observasi ... 48

D.3. Skala Sikap ... 48

E.Analisis Tes Kemampuan Penalaran dan Koneksi Matematis...49

E.1. Analisis validitas tes ... 49

E.2. Analisis Reliabilitas ... 52

E.3. Analisis Daya Pembeda ... 54

E.4. Analisis Indeks Kesukaran ... 56

E.5. Rekapitulasi Analisis Hasil Uji Coba Soal Tes Matematika ... 58

F.Teknik Analisis Data...59

F.1. Data Hasil Tes Penalaran dan Koneksi Matematis ... 60

F.2. Data Hasil Observasi ... 66

G.Prosedur penelitian...67

H.Jadwal Penelitian...70

BAB IV HASIL PENELITIAN DAN PEMBAHASAN ... 71

A.Hasil Penelitian...71

A.1. Deskriptif Hasil Pengolahan Data ... 72

A.2. Analisis Hasil Pretes ... 74

A.3. Analisis Peningkatan Kemampuan Penalaran Matematis ... 78

A.4.Analisis Peningkatan Kemampuan Koneksi Matematis...85

A.5.Hasil Penelitian tentang Skala Sikap Siswa...95

A.6. Aktivitas Guru dan Siswa selama Proses Pembelajaran ... 104

B.Pembahasan...11

1 B.1. Peningkatan Kemampuan Penalaran dan Koneksi Matematis .. 111

B.2. Sikap Siswa terhadap Pembelajaran Model CORE ... 115

B.3. Aktivitas Guru dan Siswa... 115

B.4. Keterbatasan Penelitian ... 116

BAB V KESIMPULAN DAN SARAN ... 118

A. Kesimpulan...118

B Saran...119

(3)

Lala Isum, 2012

LAMPIRAN-LAMPIRAN ... 125 LAMPIRAN A: INSTRUMEN PENELITIAN………... 163 LAMPIRAN B: ANALISIS HASIL UJI COBA TES

MATEMATIKA...180

LAMPIRAN C: ANALISIS DATA HASIL PENELITIAN...197

LAMPIRAN D: ANALISIS DATA SKALA SIKAP DAN OBSERVASI...219

(4)

Lala Isum, 2012

DAFTAR TABEL

Tabel 3.1 Pedoman Pemberian Skor Kemampuan Penalaran matematis ... 47

Tabel 3.2 Pedoman Pemberian Skor Kemampuan koneksi matematis ... 47

Tabel 3.3 Klasifikasi Koefisien Validitas ... 50

Tabel 3.4 Uji Validitas Tes Penalaran Matematis ... 51

Tabel 3.5 Uji Validitas Tes Koneksi Matematis ... 52

Tabel 3.6 Klasifikasi Tingkat Reliabilitas ... 53

Tabel 3.7 Uji Reliabilitas Tes Penalaran dan koneksi Matematis………53

Tabel 3. 8 Klasifikasi Daya Pembeda ... 55

Tabel 3.9 Daya Pembeda Tes Penalaran Matematis ... 55

Tabel 3.10 Daya Pembeda Tes Koneksi Matematis ... 55

Tabel 3.11 Kriteria Tingkat Kesukaran ... 57

Tabel 3.12 Tingkat Kesukaran Butir Soal Penalaran Matematis ... 57

Tabel 3.13 Tingkat Kesukaran Butir Soal koneksi Matematis ... 57

Tabel 3.14 Rekapitulasi Analisis Hasil Uji Coba Tes Penalaran Matematis...58

Tabel 3.15 Rekapitulasi Analisis Hasil Uji Coba Tes koneksi………...59

Tabel 3.16 Klasifikasi Gain Ternormalisasi………..61

Tabel 3.17 Jadwal Kegiatan Penelitian……….70

Tabel 4.1 Statistik Deskriptif Skor Kemampuan Penalaran Matematis ... 73

Tabel 4.2 Statistik Deskriptif Skor Kemampuan koneksi Matematis ... 74

Tabel 4.3 Hasil Uji Normalitas Pretes Penalaran dan koneksi Matematis ... 75

(5)

Lala Isum, 2012

koneksi Matematis Siswa………...…78

Tabel 4.6 Uji Normalitas Gain Ternormalisasi Penalaran………..80

Tabel 4.7 Uji Homogenitas Varians Gain Ternormalisasi Penalaran…... 81

Tabel 4.8 Uji Perbedaan Rata-rata Gain Ternormalisasi Penalaran…... .. 82

Tabel 4.9 Klasifikasi Gain Ternormalisasi Penalaran Matematis ... 83

Tabel 4.10 Analisis Varians Gain Kemampuan Penalaran Matematis Menurut Pendekatan Pembelajaran dan Kategori Siswa... 85

Tabel 4.11 Uji Perbedaan Rata-rata Gain Kemampuan Penalaran Matematis Berdasarkan Kategori Kemampuan Siswa ... 85

Tabel 4.12 Uji Normalitas Gain Ternormalisasi koneksi ... 88

Tabel 4.13 Uji Homogenitas Varians Gain Ternormalisasi koneksi... 89

Tabel 4.14 Uji Perbedaan Rata-rata Gain Ternormalisasi koneksi …... ... 90

Tabel 4.15 Klasifikasi Gain Ternormalisasi koneksi Matematis...91

Tabel 4.16 Analisis Varians Gain Kemampuan koneksi Matematis Menurut Pendekatan Pembelajaran dan Kategori Siswa... 93

Tabel 4.17 Uji Perbedaan Rata-rata Gain Kemampuan koneksi Matematis Berdasarkan Kategori Kemampuan Siswa ... 94

Tabel 4.18 Sikap Siswa Kelas Eksperimen terhadap Pelajaran Matematika .. 96

Tabel 4.19 Sikap Siswa terhadap Pembelajaran dengan CORE ... 99

Tabel 4.20 Sikap Siswa terhadap Soal Penalaran dan koneksi Matematis ... 102

Tabel 4.21 Kesimpulan Skala Sikap Siswa ... 103

Tabel 4.22 Hasil Pengamatan Aktivitas Guru selama Pembelajaran dengan CORE ... 105

Tabel 4.23 Hasil Pengamatan Aktivitas Siswa selama Pembelajaran dengan CORE ... 109

(6)

Lala Isum, 2012

DAFTAR GAMBAR

Gambar 3.1 Diagram Alur Statistik Penelitian ... ..65 Gambar 3.2 Diagram Alur Penelitian... ..69 Gambar 4.1 Diagram Batang Perkembangan Aktifitas Guru pada

Pembelajaran model CORE ... 108 Gambar 4. 2 Diagram Batang Perkembangan Aktivitas Siswa pada

(7)

Lala Isum, 2012

DAFTAR LAMPIRAN

LAMPIRAN A: INSTRUMEN PENELITIAN ... 125

A.1 Silabus Bahan Ajar ... 126

A.2 Rencana Pelaksanaan Pembelajaran (RPP) ... 127

A.3 Lembar Kegitan Siswa (LKS) ... 149

A.4 Kisi-kisi Soal dan Tes Kemampuan Penalaran dan koneksi Matematis ... 163

A.5 Kisi-kisi dan Angket Sikap Siswa ... 177

A.7 Lembar Observasi Aktivitas Guru dan Siswa ... 180

LAMPIRAN B: ANALISIS HASIL UJI COBA TES MATEMATIKA B.1 Tabel Skor Uji Coba Tes Penalaran Matematis ... 186

B.2 Tabel Skor Uji Coba Tes koneksi Matematis ... 187

B.3 Perhitungan Hasil Uji Coba Tes Matematika dengan Microsoft Excell 2007 ... 188

LAMPIRAN C: ANALISIS DATA HASIL PENELITIAN C.1 Kategori Kemampuan Siswa Kelas Eksperimen ... 195

C.2 Data Hasil Pretes ... 197

C.3 Data Hasil Postes ... 201

C.4 Data Gain Ternormalisasi ... 204

C.5 Perhitungan Data dan Uji Statistik untuk Data Pretes, Postes dan Gain Ternormalisasi ... 211

LAMPIRAN D: ANALISIS DATA SKALA SIKAP DAN OBSERVASI D.1 Data Skala Sikap Kelas Eksperimen ... 218

(8)

Lala Isum, 2012

(9)

Lala Isum, 2012

Universitas Pendidikan Indonesia|repository.upi.edu BAB I

PENDAHULUAN A. Latar Belakang

Pendidikan merupakan faktor yang berperan mencerdaskan kehidupan

bangsa. Bangsa yang cerdas adalah bangsa yang dihasilkan dari sistem pendidikan

yang baik dan tepat. Hal tersebut diperjelas dalam Undang - Undang No 2 Tahun

2003 Sisdiknas, yang menyatakan bahwa pendidikan nasional berfungsi

mengembangkan kemampuan dan membentuk watak serta peradaban bangsa yang

bermartabat dalam rangka mencerdaskan kehidupan bangsa, bertujuan untuk

berkembangnya potensi peserta didik agar menjadi manusia yang beriman

bertakwa kepada Tuhan Yang Maha Esa, berakhlak mulia, sehat, berilmu, cakap,

kreatif, mandiri dan menjadi warga negara yang demokratis serta bertanggung

jawab

Matematika merupakan salah satu mata pelajaran yang terdapat di

kurikulum pendidikan nasional dan dinilai cukup berperan dalam meningkatkan

kualitas pendidikan. Hal itu dapat ditunjukkan, pada pelaksanaan Uji Nasional,

mulai dari tingkat sekolah dasar hingga tingkat menengah mata pelajaran

matematika selalu menjadi bagian dalam pelaksanaan Ujian Nasional.

Sumarmo (2010a: 1) menyatakan bahwa pendidikan matematika

(10)

Lala Isum, 2012

(doing math) dapat memberikan sumbangan yang penting kepada siswa dalam

pengembangan nalar, berfikir logis, sistematis, kritis, cermat dan bersikap terbuka

dalam menghadapi berbagai permasalahan. Hal ini berarti pendidikan matematika

diyakini mampu mendorong dan memaksimalkan potensi seseorang sebagai calon

sumber daya manusia yang handal, untuk dapat bersikap kritis, logis dan inovatif

dalam menyelesaikan setiap permasalahan yang dihadapinya.

Depdiknas (2006) menyatakan pada Standar Isi (SI) mata pelajaran

matematika ditujukan untuk semua jenjang pendidikan dasar dan menengah,

tujuan mata pelajaran matematika di sekolah adalah agar siswa mampu:

1. Memahami konsep matematika, menjelaskan keterkaitan antarkonsep, dan

mengaplikasikan konsep atau algoritma secara luwes, akurat, efisien, dan tepat

dalam koneksi;

2. Menggunakan penalaran pada pola dan sifat, melakukan manipulasi

matematika dalam membuat generalisasi, menyusun bukti, atau menjelaskan

gagasan dan pernyataan matematika;

3. Memecahkan masalah yang meliputi kemampuan memahami masalah,

merancang model matematika, menyelesaikan model, dan menafsirkan solusi

yang diperoleh;

4. Mengomunikasikan gagasan dengan simbol, tabel, diagram, atau media lain

(11)

Lala Isum, 2012

5. Memiliki sikap menghargai kegunaan matematika dalam kehidupan, yaitu rasa

ingin tahu, perhatian, dan minat dalam mempelajari matematika, serta sikap

ulet dan percaya diri dalam koneksi.

Hal ini sesuai dengan tujuan umum pembelajaran matematika yang

dirumuskan dalam National Council of Teacher of Mathematics(2000) yaitu:

(1) komunikasi matematis (Mathematical Communication); (2) Penalaran

matematis (Mathematical Reasoning); (3) Pemecahan masalah matematis

(Mathematical Problem Solving); (4) koneksi matematis (Mathematical

Connections); (5) represntasi matematis (Mathematical Power). Senada dengan

pernyataan di atas, Soemarmo (2002) menyatakan kemampuan-kemampuan di atas

disebut daya matematis (mathematical power) atau keterampilan matematis (doing

math). Keterampilan matematis berkaitan dengan karakteristik matematis yang

dapat digolongkan dalam berfikir tingkat rendah dan berfikir tingkat tinggi.

Aktivitas berfikir yang menyangkut tingkat rendah termasuk kegiatan melakukan

operasi hitung sederhana, menerapkan rumus matematika secara langsung,

mengikuti prosedur (algoritma) yang baku, sedangkan aktivitas berfikir yang

menyangkut tingkat tinggi termasuk kemampuan memahami matematika secara

lebih mendalam, mengamati data dan menggali ide yang tersirat, menyusun

konjektur, analogi dan generalisasi menalar secara logis, menyelesaikan masalah

(problem solving), berkomunikasi secara matematis dan mengaitkan ide matematis

(12)

Lala Isum, 2012

keterampilan yang baik dalam pembelajaran matematika, tentunya minimal satu

dari lima kemampuan dasar matematika tersebut wajib dimiliki siswa bahkan akan

lebih baik jika dua atau lebih kemampuan dasar matematika dimiliki siswa.

Telah kita ketahui, soal-soal dan buku pelajaran yang diberikan kepada

siswa hampir semua materi dan soal-soal yang disajikan memenuhi kelima aspek

kemampuan matematis di atas, namun tetap saja pada kenyataannya untuk siswa

tingkat menengah kemampuan penalaran dan koneksi yang dimilki siswa masih

kurang memuaskan.

Secara empirik ditemukan bahwa siswa-siswa sekolah menengah (high

school) dan perguruan tinggi (college) mengalami kesukaran menggunakan

strategi dan kekonsistenan penalaran logika (logical reasoning), Numedal

(Kurniawan, 2007). Senada dengan pernyataan di atas, Sumarmo (1987)

menemukan bahwa keadaan skor kemampuan siswa dalam penalaran matematika

sangat rendah.

Pada penelitian lainnya, Rusgianto (2002) menunjukkan kemampuan siswa

mengaplikasikan pengetahuan matematika yang dimilikinya dalam kehidupan

yang nyata masih belum memuaskan. Senada dengan penelitian di atas Ruspiani

(Kurniawan, 2007: 8) mengungkapkan bahwa rerata kemampuan mengoneksi

matematis siswa tingkat menengah masih rendah, nilai reratanya 60 pada skor total

(13)

Lala Isum, 2012

Pengembangan kemampuan berpikir, perlu mendapat perhatian yang serius,

karena sejumlah hasil studi yang diungkapkan oleh (Suryadi, 2005) menunjukkan

pembelajaran matematika pada umumnya masih berfokus pada pengembangan

kemampuan berpikir tahap rendah yang bersifat prosedural. Studi Trends in

International Mathematics and Science Study (TIMSS) (1999) yang dilakukan di

38 negara, antara lain menjelaskan bahwa sebagian besar pembelajaran

matematika belum berfokus pada pengembangan penalaran matematik siswa.

Siswa masih mengalami kesulitan ketika dihadapkan pada persoalan yang

menuntut kemampuan penalaran maupun kemampuan koneksi (Suherman dkk,

2003).

Pada beberapa hasil penelitian yang telah dipaparkan di atas dapat dimaknai

bahwa cukup jelas untuk kemampuan berfikir tahap tinggi yang di dalamnya

terdapat kemampuan penalaran dan koneksi matematis, siswa masih mengalami

kesulitan.

Hasil temuan rendahnya kemampuan siswa Indonesia tidak hanya

diungkapkan dari para peneliti nasional. Akan tetapi hasil penelitian internasional

seperti Program for International Students Assessment (PISA) tahun 2006 dan The

Trends in International Mathematics and Science Study (TIMSS) tahun 2007 juga

menunjukkan hal yang sama. Menurut Kesumawati (Anriani, 2011: 2-3) siswa

Indonesia berturut-turut berada pada peringkat ke-52 dari 57, serta ke-36 dari 48

(14)

Lala Isum, 2012

mengenai kemampuan koneksi, penalaran, komunikasi, pengetahuan tentang fakta,

prosedur, penerapan pengetahuan dan pemahaman konsep.

Peneliti menyimpulkan dari beberapa hasil penelitian sebelumnya,

kurangnya kemampuan penalaran dan koneksi matematis siswa disebabkan oleh

beberapa faktor seperti kurangnya pemahaman awal pada mata pelajaran tersebut

dan kurangnya persiapan siswa terhadap materi tersebut.

Hal tersebut diperkuat dengan pendapat (Wahyudin, 1999) menemukan

empat kelemahan yang ada pada siswa, yaitu

(1) Kurang memiliki pengetahuan prasyarat yang baik

(2) Kurang memiliki kemampuan untuk memahami dan menggali konsep-konsep

dasar matematika (aksioma, definisi, kaidah teorema) yang berkaitan dengan

pokok bahasan yang dibicarakan.

(3) Kurang memiliki kemampuan dan ketelitian dalam menyimak atau menggali

sebuah persoalan atau soal-soal matematika yang berkaitan dengan pokok

bahasan tertentu.

(4) Kurang memiliki kemampuan menyimak kembali sebuah jawaban yang

diperoleh (apakah jawaban itu mungkin atau tidak) dan kurang memiliki

kemampuan nalar logis dalam persolan atau soal-soal matematika.

Penalaran matematis yang dimaksud adalah kemampuan siswa untuk

membuat sebuah kesimpulan setelah siswa mengalami proses belajar matematika.

(15)

Lala Isum, 2012

menghubungkan fakta-fakta yang diketahui menuju kepada suatu kesimpulan.

Sedangkan, koneksi yang dimaksud adalah kemampuan mengaitkan pengetahuan

matematis yang dimiliki siswa dengan konsep matematis lain, dengan mata

pelajaran lain dan dengan kehidupan nyata. Menurut Wahyudin (2008) pendekatan

koneksi meminta para siswa bertanggung jawab untuk apa yang sudah mereka

pelajari dan untuk menggunakan pengetahuan itu untuk memahami dan memaknai

gagasan.

Salah satu contoh permasalahan terhadap kurangnya kemampuan penalaran

dan koneksi yang terjadi pada mata pelajaran matematika di tingkat Sekolah

Menengah Kejuruan, misalnya pada materi keliling dan luas bangun datar yang

terkait pada bidang keahlian pada mata pelajaran (produktif) Tata Hidang, ketika

siswa diberi permasalahan sebagai berikut :

“Berapa panjang skirting cloth untuk menutup meja ukuran 3 m × 1 m

dengan ketinggian 75 cm”. Berdasarkan pengalaman, siswa sering mengalami

kesulitan untuk menetapkan konsep yang harus diterapkan untuk menyelesaikan

masalah tersebut.

Berdasarkan pemaparan di atas dapat dijelaskan, ketika siswa berhadapan

dengan suatu permasalahan, mereka menyadari bahwa hal tersebut dapat dilihat

dari berbagai sudut pandang, artinya mereka menyadari bahwa untuk dapat

menyelesaikan masalah tersebut siswa harus dapat mengonstruksikan pengetahuan

(16)

Lala Isum, 2012

informasi, ide-ide serta konsep pengetahuan dari berbagai disiplin ilmu yang telah

ia miliki sehingga dapat ditemukan solusi dari permasalahan tersebut.

Pada penelitian ini dipilih materi Geometri Dimensi Dua. Dipilihnya

materi tersebut karena peneliti mencoba untuk membuat instrumen penelitian yang

berhubungan dengan mata pelajaran bidang produktif (Tata Hidang) yang siswa

dapat pada semester sebelumnya. Ternyata setelah dilihat materi dimensi dua yang

bersesuaian dengan mata pelajaran produktif (Tata Hidang) siswa dibandingkan

dengan materi lain. Hal ini dimaksud agar siswa lebih mudah memahami soal-soal

dan dapat memaknai kegunaan ilmu matematika pada mata pelajaran utama

mereka yaitu produktif. Selain itu materi geometri dipilih karena pada penyelesain

soal-soal geometri dimensi dua banyak terdapat hal-hal yang mengukur

kemampuan penalaran dan koneksi. Hal ini senada dengan pendapat Abdussakir

(Siregar, 2011: 6) geometri menempati posisi khusus dalam kurikulum matematika

menengah, karena banyaknya konsep-konsep yang termuat di dalamnya. Dari

sudut pandang psikologi, geometri merupakan penyajian abstraksi dari

pengalaman visual dan spasial, misalnya bidang, pola, pengukuran dan pemetaan.

Agar permasalahan tersebut dapat diatasi, sehingga kemampuan penalaran

dan koneksi dapat ditingkatkan maka diperlukan sebuah model pembelajaran

matematika sesuai dengan bahar ajar yang dapat memaknai sebuah proses

pembelajaran, karena pembelajaran matematika merupakan suatu arena bagi

(17)

Lala Isum, 2012

Sejalan dengan pendapat Wahyudin (1999) di atas tentang 4 kelemahan yang

dialami siswa pada proses pembelajaran, maka dipilih model pembelajaran

Connecting, Organizing, Reflecting dan Extending (CORE) yang ingin diterapkan

dalam pembelajaran matematika pada penelitian ini, untuk menghubungkan,

mengorganisasikan, menggambarkan dan menyampaikan pengetahuan yang ada

dalam pikiran siswa serta memperluas pengetahuan mereka. Pada tahap

connecting, siswa diajak untuk dapat mengaitkan pengetahuan baru yang akan

dipelajari dengan pengetahuan lain. Organizing membawa siswa untuk dapat

mengoranisasikan pengetahuannya. Kemudian dengan reflecting siswa dilatih

untuk dapat menjelaskan kembali pengetahuan yang telah mereka peroleh dan

extending siswa dapat memperluas pengetahuan mereka sehingga mereka dapat

menggunakan pengetahuan tersebut pada mata pelajaran produktif.

Model pembelajaran CORE merupakan model pembelajaran yang

menekankan kemampuan berpikir siswa untuk menghubungkan,

mengorganisasikan, mendalami, mengelola dan mengembangkan informasi yang

didapat. Pada model pembelajaran ini kegiatan aktivitas belajar sangat ditekankan

kepada siswa, guru hanya berperan sebagai fasilitator, motivator dan mediator.

Siswa dituntut untuk dapat berpikir lebih luas terhadap informasi yang

didapatnya. Kegiatan mengoneksikan konsep lama-baru, siswa dilatih untuk

mengingat informasi lama dan menggunakan informasi/konsep lama tersebut

(18)

ide-Lala Isum, 2012

ide, dapat melatih kemampuan siswa untuk mengorganisasikan, mengelola

informasi yang telah dimilikinya. Kegiatan refleksi, merupakan kegiatan

memperdalam, menggali informasi untuk memperkuat konsep yang telah

dimilikinya. Kegiatan extending (memperluas), dengan kegiatan ini siswa dilatih

untuk, memperluas informasi yang sudah didapatnya, menggunakan informasi dan

dapat menemukan konsep dan informasi baru yang bermanfaat. Hal tersebut

menimbulkan motivasi dan pengetahuan yang mampu menghasilkan pemaknaan

dan pemahaman dalam belajar. Pembelajaran dengan model CORE diduga dapat

bermanfaat bagi usaha-usaha perbaikan proses pembelajaran matematika dalam

upaya meningkatkan kemampuan penalaran dan koneksi matematis siswa.

Hasil penelitian yang dilakukan, Tamalene (2010), di dalam tesisnya dengan judul “Pembelajaran Matematika dengan Model CORE melalui

Pendekatan Keterampilan Metakognitif Untuk Meningkatkan Kemampuan Penalaran Matematis Siswa SMP”, menjelaskan bahwa kemampuan penalaran

matematis siswa yang menggunakan pembelajaran model CORE lebih baik

dibandingkan siswa yang menggunakan model pembelajaran konvensional.

Berdasarkan hasil temuan pada penelitian sebelumnya, peneliti mencoba

untuk melakukakan penelitian dengan model pembelajaran yang sama dan satu

kemampuan yang sama yaitu penalaran dipadukan dengan kemampuan koneksi

namun sampel yang diambil berbeda yaitu berasal dari Sekolah Menengah

(19)

Lala Isum, 2012

Sikap siswa terhadap pembelajaran model CORE dapat dipandang sebagai

cerminan proses pembelajaran yang terjadi di kelas. Proses pembelajaran yang

memberikan kesempatan kepada siswa untuk aktif mengajukan masalah dan

menyelesaikan masalah tersebut serta diberi kesempatan untuk berinteraksi serta

berdiskusi baik dengan sesama siswa maupun dengan guru, memungkinkan siswa

merasa senang dan termotivasi untuk belajar. Bila hal ini benar-benar terjadi

dalam proses pembelajaran, bukan mustahil sikap positif siswa terhadap

pembelajaran yang diikuti tumbuh. Oleh karena itu, peneliti merasa perlu untuk

mengkaji sikap siswa terhadap matematika, pembelajaran dengan model CORE

dan soal-soal penalaran dan koneksi matematis

Sebagai bentuk kepedulian insan pendidikan yang bertanggung jawab,

peneliti ingin membuat sebuah penelitian yang membahas hal-hal yang berkenaan

dengan permasalahan di atas, dengan singkat penulis mengangkat tema “Pembelajaran Matematika dengan Model CORE untuk Meningkatkan

Kemampuan Penalaran dan Koneksi Matematis Siswa di Sekolah Menengah Kejuruan”

B. Rumusan Masalah

Berdasarkan latar belakang yang telah diuraikan, maka masalah yang

(20)

Lala Isum, 2012

1. Apakah peningkatan kemampuan penalaran matematis siswa yang

mendapatkan pembelajaran model CORE lebih baik daripada siswa yang

mendapat pembelajaran model ekpositori?

2. Apakah peningkatan kemampuan koneksi matematis siswa yang mendapatkan

pembelajaran model CORE lebih baik daripada siswa yang mendapat

pembelajaran model ekpositori?

3. Apakah terdapat perbedaan peningkatan kemampuan penalaran matematis

siswa yang mendapatkan pembelajaran model CORE ditinjau dari tingkat

Kemampuan Awal Siswa (tinggi, sedang, rendah)?

4. Apakah terdapat perbedaan peningkatan kemampuan koneksi matematis siswa

yang mendapatkan pembelajaran model CORE ditinjau dari tingkat

Kemampuan Awal Siswa (tinggi, sedang, rendah)?

5. Bagaimanakah respon siswa SMK terhadap pembelajaran model CORE?

C. Tujuan Penelitian

Berpedoman pada rumusan masalah, penelitian ini bertujuan untuk:

1. Menelaah dan mendeskripsikan peningkatan kemampuan penalaran

matematis siswa yang mendapatkan pembelajaran model CORE

dibandingkan dengan siswa yang mendapat pembelajaran model

ekpositori.

2. Menelaah dan mendeskripsikan peningkatan kemampuan koneksi

(21)

Lala Isum, 2012

dibandingkan dengan siswa yang mendapat pembelajaran model

ekpositori.

3. Menelaah dan mendeskripsikan peningkatan kemampuan penalaran

matematis siswa yang mendapatkan pembelajaran model CORE ditinjau

dari tingkat Kemampuan Awal Siswa (tinggi, sedang, rendah).

4. Menelaah dan mendeskripsikan peningkatan kemampuan koneksi

matematis siswa yang mendapatkan pembelajaran model CORE ditinjau

dari tingkat Kemampuan Awal Siswa (tinggi, sedang, rendah).

5. Mengetahui respon siswa SMK terhadap pembelajaran model CORE.

D. Manfaat Penelitian

Penelitian ini bermanfaat untuk:

1. Untuk Peneliti

Memberikan gambaran atau informasi tentang peningkatan yang terjadi

pada kemampuan penalaran serta koneksi matematis yang mendapat

pembelajaran model CORE baik berdasarkan keseluruhan maupun

berdasarkan kemampuan siswa.

2. Untuk Guru

Memberikan sumbangan pemikiran yang signifikan terhadap upaya

perencanaan pembelajaran pada pokok bahasan matematika serta kerangka

(22)

Lala Isum, 2012

meningkatkan kemampuan penalaran dan koneksi matematis siswa, serta

dapat dijadikan sebagai sebuah rujukan dalam meningkatkan kemampuan

kompetensi dasar matematika siswa pada umumnya.

3. Bagi sekolah

Tindakan yang dilakukan dengan menerapkan pembelajaran model CORE

dapat menjadi salah satu cara yang dapat diterapkan untuk meningkatkan

kemampuan penalaran dan koneksi matematis siswa. Pembelajaran model

CORE diharapkan pihak sekolah lebih memperhatikan model pembelajaran

siswa yang dibuat guru dalam perangkat pembelajaran (RPP) agar tidak

monoton dan menggunakan model pembelajaran yang lebih bervariasi agar

siswa lebih tertantang lagi pada pembelajaran.

E. Definisi Operasional

Untuk memberikan arahan dan batasaan yang jelas mengenai aspek-aspek

yang akan diungkapkan dalam penelitian ini perlu dijelaskan beberapa batasan

sebagai berikut :

1. Penalaran Matematis

Penalaran matematis (mathematical reasoning) adalah pemikiran logis

matematika yang menggunakan logika induktif dan deduktif untuk

menghasilkan kesimpulan. Kemampuan penalaran matematis mencakup

(23)

Lala Isum, 2012

solusi serta memberikan penjelasan terhadap model, fakta, sifat, hubungan

atau pola yang ada.

2. Koneksi Matematis

Kemampuan koneksi matematis adalah kemampuan mengaitkan konsep

matematika dengan matematika (antar topik matematika), matematika

dengan bidang ilmu lain, dan matematika dengan kehidupan nyata. Pada

penelitian ini indikator kemampuan koneksi yang dilihat adalah

kemampuan matematika dengan bidang ilmu lain dan kemampuan

matematika kehidupan nyata.

3. Model CORE

Model pembelajaran yang mengharapkan siswa untuk dapat

mengkonstruksi pengetahuannya sendiri dengan cara menghubungkan dan

mengorganisasikan pengetahuan baru dengan pengetahuan lama kemudian

memikirkan kembali konsep yang sedang dipelajari serta diharapkan siswa

dapat memperluas pengetahuan mereka selama proses belajar mengajar

berlangsung.

4. Pembelajaran Model Ekspositori

Pembelajaran ekspositori adalah pembelajaran yang biasa digunakan

(24)

Lala Isum, 2012

pada guru. Pembelajarannya bersifat informatif di mana guru memberi dan

menjelaskan materi pelajaran dengan cara ceramah, siswa

mendengarkan dan mencatat penjelasan yang disampaikan guru, siswa

mengerjakan latihan secara mandiri dan siswa dipersilahkan untuk

bertanya apabila tidak mengerti selama pembelajaran berlangsung.

5. Sikap siswa dalam penelitian ini adalah sikap siswa terhadap

matematika dan pembelajaran matematika dengan pembelajaran model

CORE yaitu sikap yang menunjukkan rasa sukanya terhadap

matematika dan pembelajaran matematika, kesungguhannya dalam

pembelajaran matematika dan apresiasinya terhadap soal-soal penalaran

dan koneksi matematis.

6. Peningkatan

Peningkatan yang dimaksud adalah peningkatan kemampuan penalaran dan

koneksi matematis siswa, yang ditinjau berdasarkan gain ternormalisasi

(25)

44

Lala Isum, 2012

Universitas Pendidikan Indonesia|repository.upi.edu BAB III

METODE PENELITIAN A. Desain Penelitian

Penelitian ini merupakan kuasi eksperimen. Pada kuasi eksperimen ini

subyek tidak dikelompokkan secara acak. Menurut Ruseffendi (2005) penelitian

eksperimen pada umumnya dilakukan untuk membandingkan dua kelompok atau

lebih dan menggunakan ukuran-ukuran statistik tertentu.

Desain penelitian yang digunakan adalah non equivalent groups

pretest-posttest design (McMillan & Schumacher, 2001). Desain ini dipilih karena peneliti

beranggapan bahwa subjek tidak dikelompokkan secara acak, tetapi peneliti

menerima keadaan subjek seadanya. Penelitian dilakukan pada siswa dari dua

kelas yang sudah terbentuk, dengan model pembelajaran yang berbeda. Kelompok

pertama diberikan pembelajaran model CORE dan merupakan kelompok

eksperimen, sedangkan kelompok kedua merupakan kelompok kontrol yang

memperoleh pembelajaran ekspositori. Desain pada penelitian ini berbentuk:

Kelompok eksperimen : O X O

Kelompok kontrol : O - O

Keterangan :

X : Pembelajaran Model CORE

(26)

45

Lala Isum, 2012

Untuk melihat secara lebih mendalam pengaruh penggunaan pembelajaran

model CORE terhadap kemampuan penalaran dan koneksi matematis siswa,

dalam penelitian ini dilibatkan kategori Kemampuan Awal Siswa (tinggi, sedang

dan rendah) hanya untuk kelas eksperimen. Pembagian level kemampuan tinggi,

sedang dan rendah berdasarkan (Afgani, 2004) 30% untuk kelas tinggi, 40%

untuk kelas sedang, 30% rendah.

Pembelajaran yang dilakukan baik pada kelompok eksperimen maupun

kontrol dilakukan sendiri oleh peneliti. Hal ini dilakukan agar tindakan

pembelajaran yang direncanakan oleh peneliti dapat terlaksana dengan maksimal.

B. Populasi dan Sampel Penelitian

Populasi penelitian ini adalah seluruh siswa kelas XI SMK Pariwisata

tahun ajaran 2011/2012.

Pemilihan tingkat kelas dalam hal ini kelas XI, dikarenakan peneliti

menelaah bahwa materi bahan ajar yang ingin disampaikan pada penelitian ini

terdapat di kelas XI. Penentuan sampel dilakukan dengan menggunakan teknik

Purposive Sampling, yaitu teknik pengambilan sampel dengan pertimbangan

tertentu (Sugiyono, 2010). Pertimbangan pengambilan sampel dikarenakan kelas

yang dijadikan sampel memiliki kemampuan awal yang setara. Hal tersebut dilihat

(27)

46

Lala Isum, 2012

sampel penelitian, yaitu kelas XI boga 1 sebagai kelas kontrol dan XI boga 2

sebagai kelas ekspeimen.

C. Variabel Penelitian

Variabel dalam penelitian ini adalah pembelajaran dimensi dua melalui

model CORE sebagai variabel bebas, sedangkan variabel terikatnya adalah

kemampuan penalaran dan koneksi matematis siswa.

D. Instrumen Penelitian

Data dalam penelitian ini diperoleh dengan menggunakan instrumen

yang disusun dalam bentuk tes yang dijawab oleh responden secara tertulis.

Instrumen yang digunakan berupa:

D.1. Tes Matematika

Tes matematika yang digunakan berupa tes kemampuan penalaran dan

koneksi. Agar kemampuan matematis tersebut dapat terlihat dengan jelas maka tes

akan dibuat dalam bentuk uraian. Tes tertulis ini terdiri dari tes awal (pretes) dan

tes akhir (postes). Tes diberikan pada setiap siswa. Soal-soal pretes dan postes

dibuat ekuivalen/sama. Tes awal dilakukan untuk mengetahui Kemampuan Awal

Siswa setiap kelompok dan digunakan sebagai tolak ukur peningkatan prestasi

belajar sebelum mendapatkan pembelajaran dengan model pembelajaran yang

akan diterapkan, sedangkan tes akhir dilakukan untuk mengetahui perolehan hasil

belajar dan ada tidaknya perubahan yang signifikan setelah mendapatkan

(28)

47

Lala Isum, 2012

Berikut ini adalah pedoman pemberian skor untuk tes kemampuan

penalaran dan koneksi matematis.

Tabel 3.1

Pedoman Pemberian Skor Kemampuan Penalaran Matematis

Skor Indikator

0 Tidak ada jawaban

1 Menjawab tidak sesuai dengan aspek pertanyaan tentang penalaran atau

menarik kesimpulan salah

2 Dapat menjawab hanya sebagian aaspek pertanyaan tentang penalaran dan

dijawab dengan benar

3 Dapat menjawab hampir semua aspek pertanyaan tentang penalaran dan

dijawab dengan benar

4 Dapat menjawab semua aspek pertanyaan tentang penalaran dan dijawab

dengan benar dan jelas atau lengkap

(Menggunakan Holistic Scoring Rubrics dikemukakan ole Cai, Lanen dan Jakabesin (1996))

Tabel 3.2

Pedoman Pemberian Skor Kemampuan Koneksi Matematis

Skor Indikator

0 Tidak ada jawaban, kalaupun ada hanya memperlihatkan ketidakpahaman

tentang konsep sehingga informasi yang diberikan tidak berarti apa-apa

1 Hanya sedikit dari penjelasan yang benar

2 Penjelasan secara matematis masuk akal namun hanya sebagian lengkap dan

benar

3 Penjelasan secara matematis masuk akal namun hanya sebagian lengkap dan

benar, walaupun tidak tersusun secara logis atau terdapat sedikit kesalahan bahasa

4 Penjelasan secara matematis masuk akal dan jelas serta tersusun secara logis

dan sistematis

(Menggunakan Holistic Scoring Rubrics dikemukakan ole Cai, Lanen dan Jakabesin (Izzati, 2010))

Pedoman pemberian skor dimaksudkan agar hasil penilaian yang diberikan

(29)

48

Lala Isum, 2012

jawaban siswa selalu berpedoman pada patokan yang jelas sehingga mengurangi

kesalahan pada penilaian.

D.2. Lembar Observasi

Lembar observasi digunakan untuk mengamati penampilan dan

perkembangan siswa terkait dengan konsep diri yang dimiliki siswa.

sedangkan aktivitas guru yang diamati kemampuan guru dalam menerapkan

pembelajaran model CORE. Tujuannya adalah untuk dapat memberikan refleksi

pada proses pembelajaran, agar pembelajaran berikutnya dapat menjadi lebih baik.

Observasi tersebut dilakukan oleh peneliti dan satu orang guru matematika.

D.3. Skala Sikap

Skala sikap siswa bertujuan untuk mengetahui sikap siswa selama

pembelajaran melalui model CORE. Sikap siswa tersebut berkenaan dengan sikap

siswa terhadap pembelajaran model CORE. Skala sikap yang dibuat mempunyai

indikator: 1) Sikap siswa terhadap mata pelajaran matematika; 2) Sikap siswa

terhadap pembelajara model CORE; 3) Sikap siswa terhadap soal kemampuan

penalaran dan koneksi matematis. Skala sikap ini terdiri dari pernyataan positif

dan negatif. Pembuatan skala sikap berpedoman pada bentuk skala Likert dengan

empat option. Menurut Suherman (Siregar, 2009) pemberian skor untuk setiap

pernyataan adalah 1 (STS), 2 (TS), 3 (S), 4 (SS), untuk pernyataan favorable

(30)

49

Lala Isum, 2012

untuk pernyataan unfavorable (pernyataan negatif). Empat option tersebut berguna

untuk menghindari sikap ragu-ragu atau rasa aman dan tidak memihak pada suatu

pernyataan yang diajukan pada siswa.

E. Analisis Tes Kemampuan Penalaran dan Koneksi Matematis

Sebelum penyusunan tes kemampuan representasi matematis siswa dibuat

kisi-kisi soal terlebih dahulu. Kemudian tes tersebut diukur face validity dan

content validity oleh ahli (expert) dalam hal ini dosen pembimbing dan rekan

sesama mahasiswa pascasarjana. Langkah selanjutnya adalah tes diujicobakan

untuk memeriksa keterbacaan, validitas item, reliabilitas, daya pembeda, dan

tingkat kesukarannya. Uji coba dilakukan pada siswa kelas XII SMK Pariwisata

pada jurusan yang sama, yang sebelumnya telah mendapatkan materi yang akan

diteskan pada penelitian.

Analisis instrumen menggunakan Software Microsoft Excell 2007

kemudian masing-masing hasil yang diperoleh dikonsultasikan.

Alat pengumpul data yang baik dan dapat dipercaya adalah yang memiliki

tingkat validitas dan reliabilitas yang tinggi atau sedang. Oleh karena itu, sebelum

instrumen tes digunakan terlebih dahulu dilakukan uji coba pada siswa yang telah

mendapatkan materi yang akan disampaikan. Setelah uji coba, dilakukan analisis

untuk mengetahui tingkat validitas, reliabilitas, tingkat kesukaran dan daya

(31)

50

Lala Isum, 2012

Universitas Pendidikan Indonesia|repository.upi.edu E.1. Analisis validitas tes

Validitas butir soal digunakan untuk mengetahui dukungan suatu butir soal

terhadap skor total. Hasil perhitungan validitas ini dapat digunakan untuk

menyelidiki lebih lanjut butir-butir soal yang mendukung dan yang tidak

mendukung. Dukungan setiap butir soal dinyatakan dalam bentuk korelasi. Karena

tes yang akan digunakan berupa uraian, maka untuk mendapatkan validitas butir

soal digunakan rumus korelasi Product Moment Pearson, yaitu:

= =1 − =1 =1

2

=1 − =1 2 =1 2 − =1 2

(Suherman dan Kusumah, 1990: 14)

dengan:

: koefisien validitas,

: skor butir soal data ke - i,

: skor total data ke - i,

n: jumlah siswa.

Hasil perhitungan koefisien korelasi diinterpretasikan dengan

[image:31.612.125.514.260.563.2]

menggunakan klasifikasi koefisien validitas yang dapat dilihat pada tabel berikut

Tabel 3.3.

Klasifikasi Koefisien Validitas tes menurut J.P Guilford yaitu:

(32)

51

Lala Isum, 2012

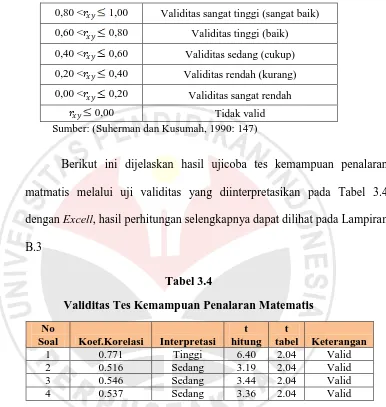
0,80 < 1,00 Validitas sangat tinggi (sangat baik)

0,60 < 0,80 Validitas tinggi (baik)

0,40 < 0,60 Validitas sedang (cukup)

0,20 < 0,40 Validitas rendah (kurang)

0,00 < 0,20 Validitas sangat rendah

0,00 Tidak valid

Sumber: (Suherman dan Kusumah, 1990: 147)

Berikut ini dijelaskan hasil ujicoba tes kemampuan penalaran

matmatis melalui uji validitas yang diinterpretasikan pada Tabel 3.4

dengan Excell, hasil perhitungan selengkapnya dapat dilihat pada Lampiran

B.3

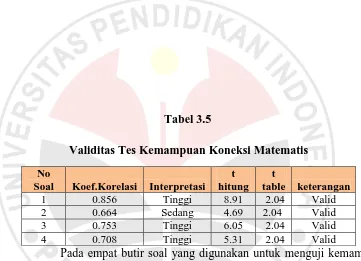
[image:32.612.139.525.111.518.2]

Tabel 3.4

Validitas Tes Kemampuan Penalaran Matematis

No

Soal Koef.Korelasi Interpretasi

t hitung

t

tabel Keterangan

1 0.771 Tinggi 6.40 2.04 Valid

2 0.516 Sedang 3.19 2.04 Valid

3 0.546 Sedang 3.44 2.04 Valid

4 0.537 Sedang 3.36 2.04 Valid

Pada empat butir soal yang digunakan untuk menguji kemampuan

penalaran matematis tersebut berdasarkan kriteria validitas tes, diperoleh

tiga soal (soal nomor 2,3 dan 4) yang mempunyai validitas sedang, dan

satu soal sisanya mempunyai validitas tinggi. Pada Tabel 3.4 ditunjukkan

(33)

52

Lala Isum, 2012

Selanjutnya akan dijelaskan hasil ujicoba tes kemampuan koneksi

matematis melalui uji validitas yang diinterpretasikan pada Tabel 3.5

dengan Excell, yang hasil perhitungan selengkapnya dapat dilihat pada

[image:33.612.140.501.219.480.2]

Lampiran B.3.

Tabel 3.5

Pada empat butir soal yang digunakan untuk menguji kemampuan

koneksi matematis tersebut berdasarkan kriteria validitas tes, diperoleh tiga

soal (soal nomor 1,3 dan 4) yang mempunyai validitas tinggi, dan satu soal

sisanya mempunyai validitas sedang. Pada Tabel 3.5 ditunjukkan bahwa

nilai t tabel lebih kecil dari t hitung jadi dinyatakan keempat soal valid.

E.2. Analisis Reliabilitas

Suatu alat evaluasi dikatakan reliabel jika hasil evaluasi tersebut

relatif tetap jika digunakan untuk subjek yang sama pada waktu yang Validitas Tes Kemampuan Koneksi Matematis

No

Soal Koef.Korelasi Interpretasi

t hitung

t

table keterangan

1 0.856 Tinggi 8.91 2.04 Valid

2 0.664 Sedang 4.69 2.04 Valid

3 0.753 Tinggi 6.05 2.04 Valid

(34)

53

Lala Isum, 2012

berbeda (Suherman dan Kusumah, 1990). Untuk tes berbentuk uraian

perhitungan reliabilitas tes dapat digunakan rumus Cronbach’s Alpha,

yaitu: ₁₁ =

−1 1−

2 =1

2 ,

(Suherman dan Kusumah, 1990: 194),

dengan:

r11 : derajat reliabilitas,

n : jumlah butir soal,

s_i2 : variansi skor butir soal data ke-i

s_t2 : variansi skor total data ke-i

Peneliti menggunakan program Excell untuk menghitung

reliabilitas. Hasil derajat reliabilitas soal kemudian diinterpretasikan

[image:34.612.136.537.170.629.2]

dengan menggunakan klasifikasi derajat reliabilitas pada tabel berikut

Tabel 3.6

Klasifikasi Koefisien Reliabilitas tes menurut J.P Guilford yaitu:

Besarnya 11 Interpretasi

11 0,20 Derajat reliabilitas sangat rendah

0,20 < ₁₁ 0,40 Derajat reliabilitas rendah

0,40 < 11 0,70 Derajat reliabilitas sedang

0,70 < 11 0,90 Derajat reliabilitas tinggi

0,90 < 11 1,00 Derajat reliabilitas sangat tinggi

Rumus yang digunakan untuk mencari koefisien reliabilitas bentuk

(35)

54

Lala Isum, 2012

peneliti menggunakan program Excell pada Tabel 3.7. Hasil perhitungan

reliabilitas tes untuk kemampuan penalaran dan koneksi matematis siswa

[image:35.612.137.528.218.564.2]

dapat dilihat pada tabel di bawah ini.

Tabel 3.7

Reliabilitas Tes Kemampuan Penalaran dan Koneksi Matematis

No. ₁₁ Interpretasi Keterangan

1 0,64 Sedang Penalaran

2 0,66 Sedang Koneksi

E.3. Analisis Daya Pembeda

Daya pembeda suatu butir soal menyatakan seberapa jauh

kemampuan butir soal tersebut mampu membedakan antara siswa yang

dapat menjawab soal dan siswa yang tidak dapat menjawab soal

(Suherman dan Kusumah, 1990: 199). Daya pembeda dihitung dengan

membagi subjek menjadi dua kelompok setelah diurutkan menurut

peringkat perolehan skor hasil tes. Kelompk tersebut adalah 50%

kelompok atas (kelas unggul) dan 50% kelompok bawah (kelas assor).

��= −

� atau ��=

− �

(Suherman dan Kusumah, 1990: 201),

dengan:

DP: Daya Pembeda,

JB_A: jumlah siswa kelompok atas yang menjawab soal dengan benar,

(36)

55

Lala Isum, 2012

Universitas Pendidikan Indonesia|repository.upi.edu JS_A: jumlah siswa kelompok atas,

JS_B: jumlah siswa kelompok bawah

Proses penentuan kelompok unggul dan asor ini dengan cara terlebih

dahulu mengurutkan skor total setiap siswa mulai dari skor tertinggi

sampai dengan yang terendah, untuk perhitungan lengkapnya

menggunakan Excell.

Hasil perhitungan daya pembeda diinterpretasikan dengan

menggunakan tabel berikut:

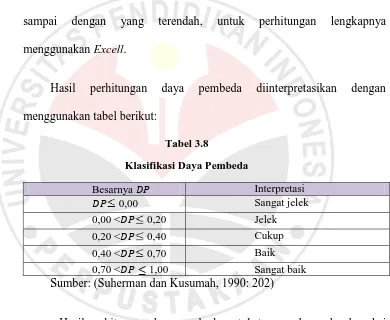
[image:36.612.141.531.223.543.2]

Tabel 3.8

Klasifikasi Daya Pembeda

Besarnya �� Interpretasi

�� 0,00 Sangat jelek

0,00 <�� 0,20 Jelek

0,20 <�� 0,40 Cukup

0,40 <�� 0,70 Baik

0,70 <�� ≤ 1,00 Sangat baik

Hasil perhitungan daya pembeda untuk tes penalaran dan koneksi

matematis disajikan masing-masing dalam Tabel 3.9 dengan Excell dan

Tabel 3.10 dengan Excell berikut ini:

Tabel 3.9

Daya Pembeda Tes Penalaran Matematis

(37)

56

Lala Isum, 2012

1 0.64 Baik

2 0.36 Cukup

3 0.30 Cukup

[image:37.612.138.530.109.518.2]

4 0.69 Baik

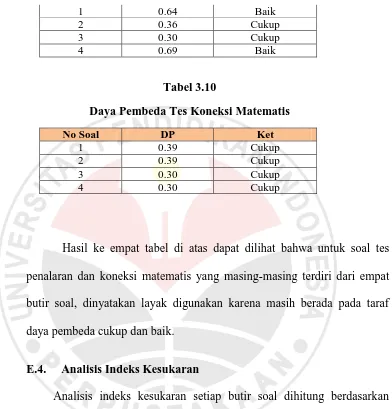
Tabel 3.10

Daya Pembeda Tes Koneksi Matematis

No Soal DP Ket

1 0.39 Cukup

2 0.39 Cukup

3 0.30 Cukup

4 0.30 Cukup

Hasil ke empat tabel di atas dapat dilihat bahwa untuk soal tes

penalaran dan koneksi matematis yang masing-masing terdiri dari empat

butir soal, dinyatakan layak digunakan karena masih berada pada taraf

daya pembeda cukup dan baik.

E.4. Analisis Indeks Kesukaran

Analisis indeks kesukaran setiap butir soal dihitung berdasarkan

jawaban seluruh siswa yang mengikuti tes. Skor hasil tes yang diperoleh

siswa diklasifikasikan benar dan salah seperti pada analisis daya pembeda.

Rumus yang digunakan untuk menghitung indeks kesukaran adalah:

= +

� + � ,

(38)

57

Lala Isum, 2012

Universitas Pendidikan Indonesia|repository.upi.edu dengan,

IK: Indeks Kesukaran,

JB_A: jumlah siswa kelompok atas yang menjawab soal dengan benar,

JB_B: jumlah siswa kelompok bawah yang menjawab soal dengan benar,

JS_A: jumlah siswa kelompok atas,

JS_B: jumlah siswa kelompok bawah.

Hasil perhitungan daya pembeda diinterpretasikan dengan

[image:38.612.137.532.219.533.2]

menggunakan tabel berikut.

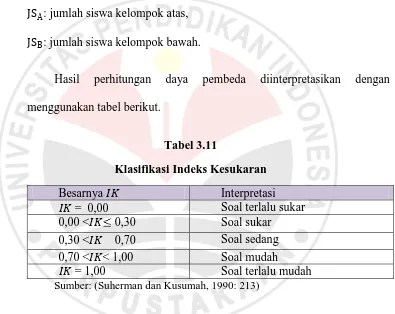
Tabel 3.11

Klasifikasi Indeks Kesukaran

Besarnya Interpretasi

= 0,00 Soal terlalu sukar

0,00 < 0,30 Soal sukar

0,30 < 0,70 Soal sedang

0,70 < < 1,00 Soal mudah

= 1,00 Soal terlalu mudah

Hasil perhitungan diperoleh tingkat kesukaran tiap butir soal tes penalaran

dan koneksi matematis yang terangkum dalam Tabel 3.12 dengan Excell

dan Tabel 3.13 dengan Excell berikut ini:

Tabel 3.12

Tingkat Kesukaran Butir Soal Penalaran Matematis

(39)

58

Lala Isum, 2012

1 _0.35 _Sukar

2 _0.46 _Mudah

3 _0.40 _Sedang

[image:39.612.134.511.113.526.2]

4 _0.46 _Mudah

Tabel 3.13

Tingkat Kesukaran Butir Soal Koneksi Matematis

Nomor Soal Tingkat Kesukaran Interpretasi

1 0.47 Sukar

2 0.22 Mudah

3 0.26 Sedang

4 0.32 Mudah

Hasip pada kedua tabel di atas dapat dilihat bahwa untuk soal tes penalaran

dan koneksi matematis yang masing-masing terdiri dari empat butir soal,

dinyatakan layak digunakan karena masih berada pada taraf kesukaran yang

bervariasi. Pada soal dengan taraf kesukaran sukar soal dikonsultasikan lagi ke

dosen pembimbing untuk direvisi ulang agar masih dapat digunakan.

E.5. Rekapitulasi Analisis Hasil Uji Coba Soal Tes Matematika

Rekapitulasi dari semua perhitungan analisis hasil uji coba tes kemampuan

[image:39.612.154.504.114.190.2]

penalaran dan koneksi matematis disajikan secara lengkap dalam Tabel 3.14 dan

Tabel 3.15 di bawah ini:

(40)

59

Lala Isum, 2012

Rekapitulasi Analisis Hasil Uji Coba Soal Tes Penalaran Matematis

Nomor Soal Interpretasi Validitas Interpretasi Tingkat Kesukaran Interpretasi Daya Pembeda Interpretasi Reliabilitas

1 Tinggi Baik Sukar

Sedang

2 Sedang Cukup Mudah

3 Sedang Cukup Sedang

[image:40.612.127.510.133.604.2]

4 Sedang Baik Mudah

Tabel 3.15

Rekapitulasi Analisis Hasil Uji Coba Soal Tes Koneksi Matematis

Nomor Soal Interpretasi Validitas Interpretasi Tingkat Kesukaran Interpretasi Daya Pembeda Interpretasi Reliabilitas

1 Tinggi Cukup Sukar

Sedang

2 Sedang Cukup Mudah

3 Tinggi Cukup Sedang

4 Tinggi Cukup Mudah

Berdasarkan hasil analisis keseluruhan terhadap hasil ujicoba tes

kemampuan penalaran dan koneksi matematis yang dilaksanakan di SMKN kelas

(41)

60

Lala Isum, 2012

pembeda dan tingkat kesukaran soal, maka dapat disimpulkan bahwa soal tes

tersebut layak dipakai sebagai acuan untuk mengukur kemampuan penalaran dan

koneksi matematis siswa di SMKN kelas XI Jasa Boga yang merupakan

responden dalam penelitian ini.

F. Teknik analisis data

Data-data yang diperoleh dari hasil pretes dan postes dianalisis secara

statistik, sedangkan data dari hasil pengamatan observasi pembelajaran dianalisis

secara deskriptif.

Pengolahan data penulis menggunakan bantuan program software SPSS

17, dan Microsoft Excell 2007.

F.1. Data Hasil Tes Penalaran dan Koneksi Matematis

Penelitian ini ingin melihat peningkatan kemampuan penalaran dan

koneksi matematis siswa Sekolah Menengah Kejuruan (SMK) yang belajar

melalui pembelajaran dengan model CORE dan siswa yang mendapat

pembelajaran model ekspositori, serta perbedaan kemampuan penalaran dan

koneksi matematis siswa ditinjau dari tingkat Kemampuan Awal Siswa. Oleh

karena itu, uji statistik yang digunakan adalah uji t dan Analisis Varians

(ANAVA) .

Data yang diperoleh dari hasil tes diolah melalui tahap-tahap sebagai

(42)

61

Lala Isum, 2012

1. Memberikan skor jawaban siswa sesuai dengan kunci jawaban dan sistem

penskoran yang digunakan.

2. Membuat tabel skor pretes dan postes siswa kelas eksperimen dan kelas

kontrol.

3. Peningkatan kompetensi yang terjadi sebelum dan sesudah pembelajaran

dihitung dengan rumus gain ternormalisasi, yaitu:

Gain ternormalisasi (g) = −

� −

Hasil perhitungan gain kemudian diinterpretasikan dengan menggunakan

[image:42.612.138.529.237.548.2]

klasifikasi sebagai berikut:

Tabel 3.16 Klasifikasi Gain (g)

Besarnya Gain (g) Interpretasi

g  0,7 Tinggi

0,3  g < 0,7 Sedang

g <0,3 Rendah

(Hake, 1999)

Melakukan uji normalitas untuk mengetahui kenormalan data skor

pretes dan gain kemampuan penalaran dan koneksi matematis

menggunakan uji statistik Kolmogorof-Smirnov (Jika data ≤ 30 data)

atau Shapiro-Wilk (Jika data > 30 data). Perhitungan melalui Uji

(43)

62

Lala Isum, 2012

sebagai pengganti uji kai kuadrat untuk ukuran sampel yang lebih

kecil. Kriteria pengujian adalah

tolak H0 apabila Asymp.Sig ≤ taraf signifikansi (�= 0,05)

terima H0 apabila Asymp.Sig > taraf signifikansi (�= 0,05).

Adapun rumusan hipotesisnya adalah:

H0 : Data berdistribusi normal

H1 : Data tidak berdistribusi normal

Jika datanya tidak berdistribusi normal, maka uji yang dilakukan adalah uji

statistik non-parametrik seperti uji Mann-Whitney.

4. Menguji homogenitas varians data skor pretes, postes dan gain kemampuan

penalaran matematis dan koneksi matematis menggunakan uji Homogeneity

of Variance (Levene Statistic).

Adapun hipotesis yang akan diuji adalah:

H0 : �12 =�22 varians gain ternormalisasi kemampuan penalaran atau

koneksi matematis kedua kelompok homogen

H1 : �12 ≠ �22 varians gain ternormalisasi kemampuan penalaran atau

koneksi matematis kedua kelompok tidak homogen

Keterangan:

�12: varians skor gain ternormalisasi kelompok eksperimen

�22_{: varians skor gain ternormalisasi kelompok kontrol}

(44)

63

Lala Isum, 2012

tolak H0 apabila Asymp.Sig ≤ taraf signifikansi (� = 0,05)

terima H0 apabila Asymp.Sig > taraf signifikansi (�= 0,05)

Kemudian dilanjutkan dengan uji kesamaan rerata untuk data pretes untuk

mengetahui bahwa kedua kelmpok berasal dari kelas yang tingkat

kemampuannya sama dan uji perbedaan untuk data gain ternormalisasi untuk

mengetahui peningkatan kemampuan yang terdapat di dua kelas. Jika data

berdistribusi normal dan homogen, maka uji yang dilakukan adalah uji

statistik t, sedangkan jika datanya berdistribusi normal tetapi tidak homogen, maka uji yang dilakukan adalah uji statistik t’.

5. Melakukan uji kesamaan dua rerata pada data skor pretes kedua kelompok

eksperimen dan kontrol untuk masing-masing kemampuan, penalaran dan

koneksi, dengan menggunakan independent samples t-test. Hipotesis yang

diajukan adalah:

H₀∶ � =�

H₁∶ � ≠ �

Keterangan:

� : rerata pretest penalaran atau koneksi kelompok eksperimen

� : rerata pretest penalaran atau koneksi kelompok kontrol

Selanjutnya melakukan uji perbedaan dua rerata untuk data skor gain

ternormalisasi pada kedua kelompok tersebut. Berikut ini adalah rumusan

(45)

64

Lala Isum, 2012

H₀∶ �_� =�_�

H₁∶ �_� >�_�

Keterangan:

�_� : rerata gain ternormalisasi penalaran atau koneksi kelompok

eksperimen

�_� : rerata gain ternormalisasi penalaran atau koneksi kelompok

kontrol

Kriteria pengujian adalah

terima H0 apabila Asymp.Sig > taraf signifikansi (�= 0,05)

kemudian untuk mengetahui perbedaan peningkatan yang terdapat di kelas

yang diberikan pembelajaran model CORE saja, dilihat berdasarkan Kemampuan

Awal Siswa (KAS) tinggi, sedang dan rendah diujikan dengan uji statistik Analisis

Varians (ANAVA) satu jalur.

6. Uji statistik yang digunakan adalah analisis varian ANAVA satu jalur

menggunakan Compare means One Way ANOVA, Jika data normal dan homogen

maka menggunakan uji Compare means One Way ANOVA scheffe tetapi jika data

normal dan tidak homogen maka menngunakan One Way ANOVA Games Howell.

Sedangkan jika datanya tidak berdistribusi normal dan tidak homogen, maka uji

yang dilakukan adalah uji statistik non-parametrik Kruskal Wallis H.

(46)

65

Lala Isum, 2012

H₀ ∶ �_� =�_� = �_�

H₁ ∶ � ≠ � , untuk minimal terdapat dua (i,j)

dimana : i≠ j, i = get, ges, ger

(paling sedikit ada satu tanda = yang tidak terpenuhi)

Kriteria pengujian adalah

terima H0 apabila Asymp.Sig > taraf signifikansi (� = 0,05)

μget = rata−rata gain ternormalisasi kelas eksperimen berkemampuan tinggi

μges = rata−rata gain ternormalisasi kelas eksperimen berkemampuan sedang

μger = rata−rata gain ternormalisasi kelas eksperimen berkemampuan rendah

H0 : Tidak terdapat perbedaan kemampuan penalaran atau koneksi matematis

siswa yang mendapatkan pembelajaran model CORE ditinjau dari tingkat

Kemampuan Awal Siswa (tinggi, sedang, rendah).

H1 : Terdapat perbedaan kemampuan penalaran atau koneksi matematis siswa

yang mendapatkan pembelajaran model CORE ditinjau dari tingkat

Kemampuan Awal Siswa (tinggi, sedang, rendah).

Normal Tidak Normal

N-Gain

(47)

66

Lala Isum, 2012

[image:47.612.107.497.104.427.2]

Homogen Tidak homogen

Gambar 3.1 Diagram Alur Statistik Penelitian

F.2. Data Hasil Observasi

Data hasil observasi yang dianalisis adalah aktivitas siswa selama proses

pembelajaran berlangsung yang dirangkum dalam lembar observasi. Tujuannya

adalah untuk membuat refleksi terhadap proses pembelajaran, agar pembelajaran

berikutnya dapat menjadi lebih baik dari pembelajaran sebelumnya dan sesuai

dengan skenario yang telah dibuat. Selain itu, lembar observasi ini digunakan

untuk mendapatkan informasi lebih jauh tentang temuan yang diperoleh secara

kuantitatif dan kualitatif.

a. Data Hasil skala sikap

Sebelum digunakan, skala sikap yang telah dibuat terlebih dahulu diuji

face validitynya dengan meminta pertimbangan dosen pembimbing agar

Uji Non Parametrik (Uji Mann-Whitney) Uji Homogenitas

Uji Parametrik (Uji –t) / Uji ANAVA

(48)

67

Lala Isum, 2012

memenuhi persyaratan, sehingga diperoleh 25 butir pernyataan yang digunakan

sebagai instrumen penelitian. Instrumen skala sikap dalam penelitian ini diberikan

kepada siswa kelompok eksperimen setelah semua kegiatan pembelajaran berakhir

atau setelah posttest. Untuk menganalisa respon siswa pada skala sikap yang

diberikan, digunakan dengan mengkomulatif semua jawaban siswa pada setiap

option soal, kemudian diubah kedalam bentuk persen. Selain diubah ke dalam

persen data hasil skala sikap di intervalkan dengan menggunakan program MSI.

G. Prosedur penelitian 1. Tahap Persiapan

a. Merancang instrumen penelitian (seperti: silabus, RPP, soal tes penalaran

dan koneksi matematis, LKS, set kartu pertanyaan, lembar jawaban kartu

pertanyaan, papan nama kelompok, pembagian kelompok, lembar

observasi, dan angket skala sikap) dan meminta penilaian ahli.

b. Melakukan uji coba instrumen penelitian dan dianalisis daya pembeda,

tingkat kesukaran, validitas, dan reliabilitas instrumen tersebut.

2. Tahap Pelaksanaan

Kegiatan yang dilakukan pada tahap pelaksanaan ini adalah:

a. Melaksanakan pretes untuk mengukur kemampuan penalaran dan

(49)

68

Lala Isum, 2012

b. Melaksana