34;Compression Schemes for High Dimensional Data based on Extendible Multidimensional Arrays" was approved by the examination committee for partial fulfillment of the conditions for the Master's degree in Computer Science and Engineering at the Department of Computer Science and Engineering, no. Khulna University of Engineering Furthermore, we found that the recovery time of the proposed compression schemes is independent of different dimensions.

Problem Statement
Many of the TMA-based compression schemes, such as compressed row/column storage (CRS/CCS) [114,23] or chunk-offset compression [22,24] already exist. Thus, efficient compression schemes are needed to store such sparse data for multi-dimensional datasets without any reorganization and movement.
Objectives
In this thesis, we will propose and evaluate new and efficient compression schemes based on scalable multidimensional array (EMA to handle the scalability problem without data reorganization and apply a suitable compression scheme to EMA to have a good compression ratio. To analyze the increment operation (which is known as expansion operation) along with basic operations on the proposed compression schemes with respect to the existing traditional compression schemes.
Scope of the Thesis
Developing compression schemes for high-dimensional data based on EMA, which will impose less space and the maximum range of usable data density, will be advanced for practical applications.
Thesis Organization
The forward and backward mapping techniques of the proposed schemes are explained with examples in this chapter. This chapter also describes the theoretical analysis along with cost models for existing schemes and proposed schemes.
Literature Review
Introduction
The Multidimensional Array Systems
- Extendible Multidimensional Array (EMA)
- Extendible Karnaugh Array (EKA)
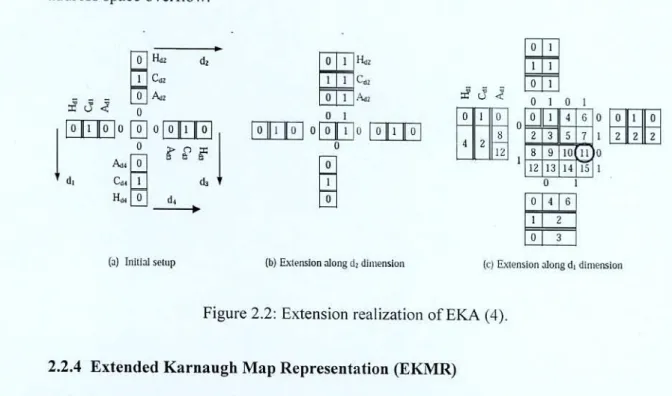
This capability is due to the fact that the size of each dimension of a multidimensional array is fixed, so that a simple addressing function can be used to address any element of the array. The history table stores the expansion history and the address table stores the first address of the expanded subarray.
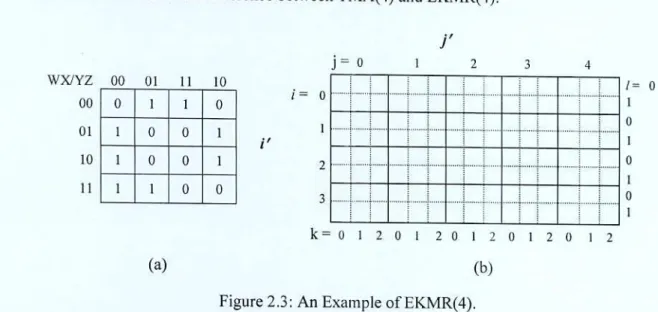
- Extended Karnaugh Map Representation (EKMR)
As it is already expanded to dimension d3 and d4, the history value reaches 3, now for expansion to d1 the value becomes 4 which is stored in 1-I1. EKA has the property of dynamic expansion during runtime and significantly delays the appearance of address space overflow.
Compression schemes for multidimensional arrays
- Offset Compression for TMA
- Chunk-offset compression for TMA
- CRSI CCS scheme for Multidimensional Arrays
The backward mapping algorithm R-F is used to determine the coordinates of the corresponding multidimensional array. The inverse array linearization function (see equation 2.2) is used for backward mapping to obtain the original coordinates of the array.
1 flEiflhiflilul
EKA Based Compression (SCEKA)
The segment number within the subarray is also unique and can also be uniquely determined. The offset value within the segment is also unique and can be determined by the addressing function.
EKMR Based Compression (ECRS or ECCS)
Therefore, the tuple (history value, segment number, offset) can uniquely map an array cell of the EKA. Moreover, the offset value (i.e., logical location) of the element in the subarray can be calculated using the addressing function and it is also unique in the subarray.
Compression Schemes for High Dimensional Data based on Extendible Multidimensional Array
Introduction
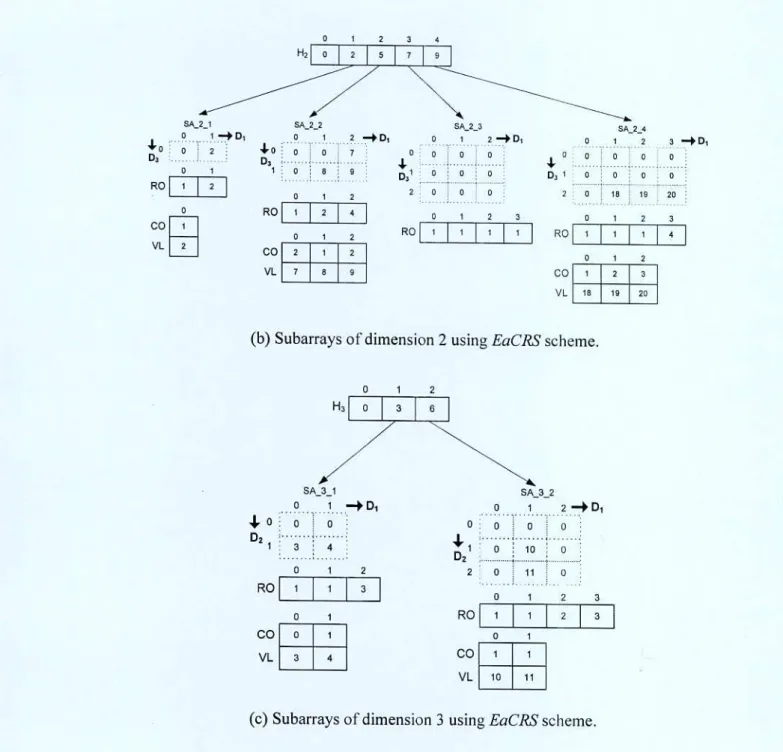
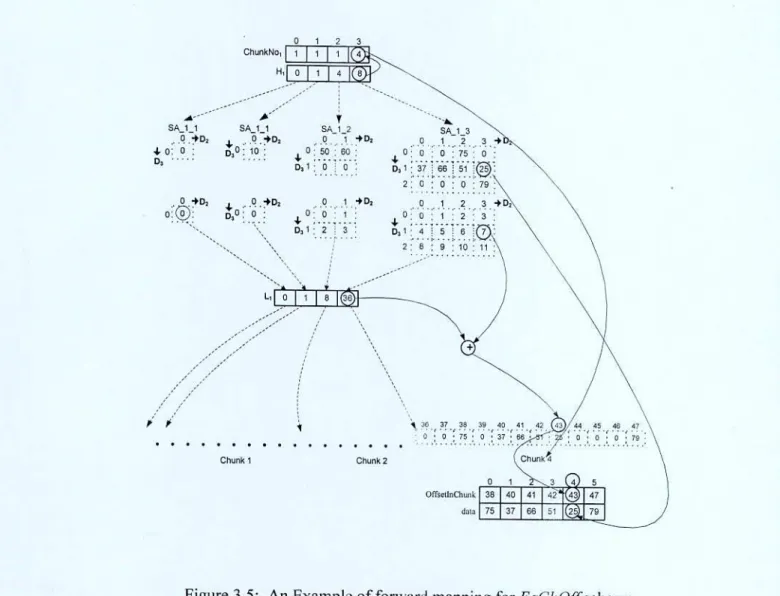
In the EaCRS scheme, for an n dimensional EMA, among the three kinds of auxiliary tables (history table, address table, coefficient table), only the history table H1 is needed to store for each dimension. History tables are used to calculate the extension dimension of the subarray and the length of other dimension to calculate the row dimension and number of rows of that subarray. An example of the EaCRS scheme for a three-dimensional EMA of Figure 2.3 is shown in Figure 3.1.
For convenience here, we refer to each subarray as SAiJ, where i denotes the extended dimension to which the subarray belongs and j denotes the length of that dimension.
Forward Mapping for EaC'RS scheme
Since H113J > H2[3] and H1[3] > I-I3 f1J, extended dimension is 1 and the element involved in the subarray SA_1 — The dimension with the minimum length at the time of subarray SA13's expansion is considered to be the row dimension for the subarray SA_1_3. Since subarrays are two-dimensional, in this case dimension 2 is the only column of the subarray SA_1_3. Consider the physical position <9,4,3> of the physical database; where <9> is the history value, <4> is the value that RO stores and <3> is the column index of a non-null array element, i.e.
We perform the binary search on the history tables to find the given history value <9>. Therefore, the second coordinate value for the desired logical position is <4> in the logical database, and the other two dimensions (dimensions 1 and 3) are considered the row dimension and the column dimension. As we have described above, the dimension with the smallest length at the time of subarray (SA_2 4) 's expansion is considered the row dimension of subarray SA_2_4.
Since the subloads are two-dimensional, in this case dimension I is the only dimension of the subload column SA_2_4 and the first coordinate value of the desired logical position is <3> in the logical database. Therefore, the physical position <9,4,3> of the physical database is mapped to a logical position <3,4,2> in the logical database.
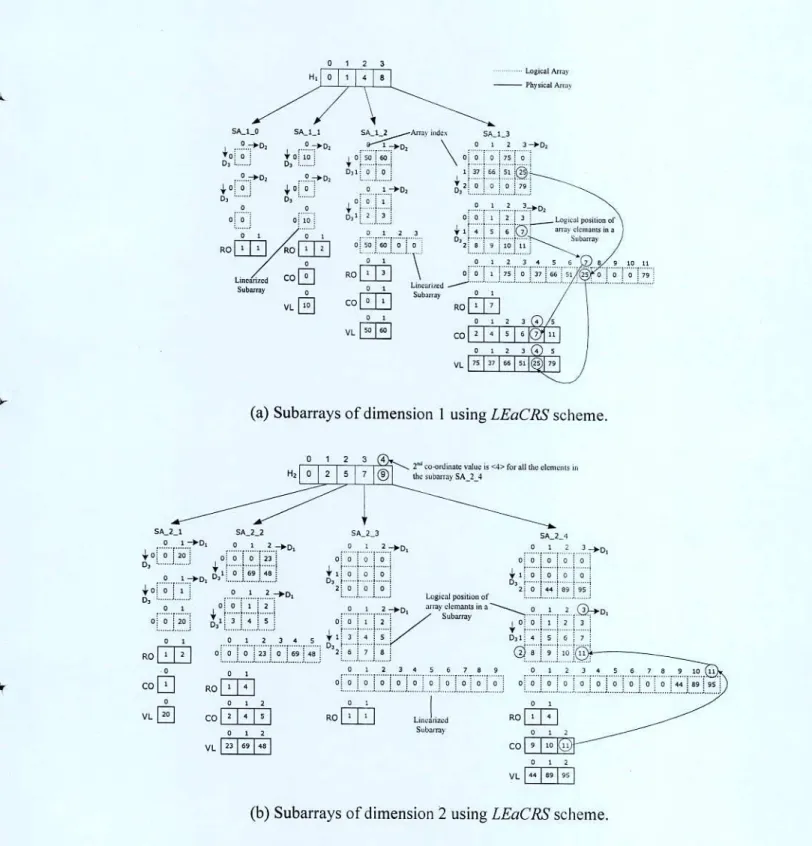
Linearized Extendible Array Based Compressed Row Storage Scheme (LEaC'RS) Given a 3-dimensional EMA. The Linearized Extendible Array Based Compressed Row
Consider the physical position <9,]]> of the physical database; where <9> is the history value and <11> is the column index of a non-zero array element in the linearized subarray, i.e. Therefore, the second coordinate value of the desired logical array indices is <4> in the logical database and the other two dimensions (dimension I and 3) are considered as the row dimension and column dimension. Since subarrays are two-dimensional, in this case dimension 1 is the only column dimension of the subarray SA_2_4.
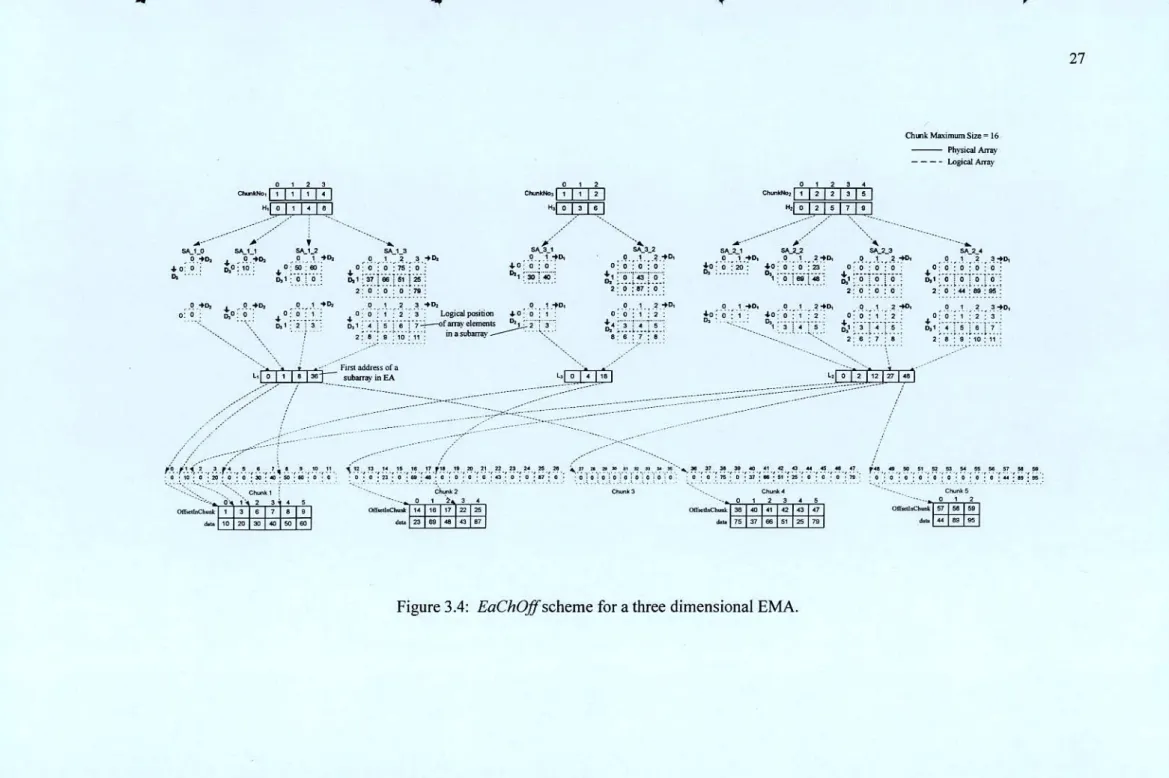
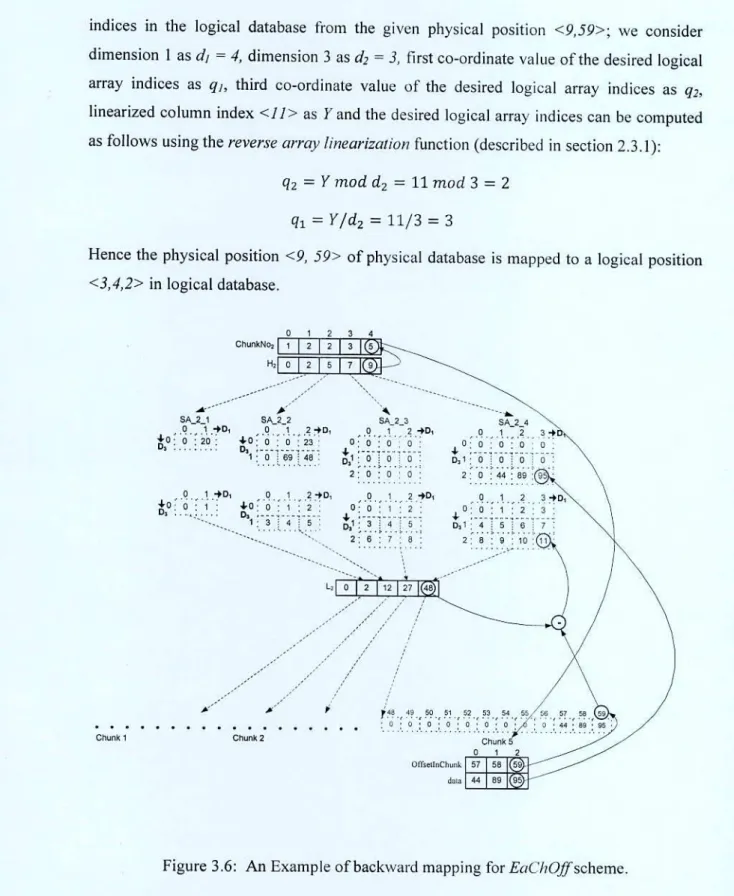
An example of the EaChOff plot for a three-dimensional EMA of Figure 2.1 is shown in Figure 3.4. To calculate the logical position of the string element <3,3,1>; we consider dimension 2 as d1= 4, dimension 3 as. Consider the physical position <9,59> of the physical database; where <9> is the history value and <59> is the logical index of a non-zero array element in a chunk ie.
Therefore, the second coordinate value for the desired logical array indexes is <4> in the logical database. 4 To calculate the first coordinate and the third coordinate value for the desired logical array.
Theoretical Analysis
- Assumptions
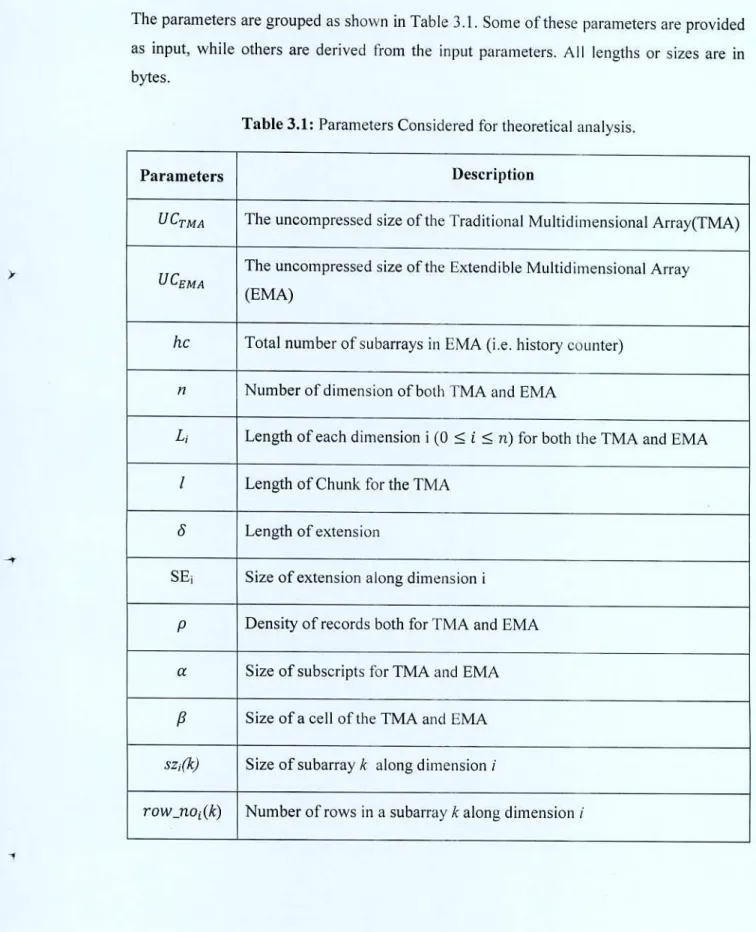
- Parameters
- Cost Model for Compression Ratio
- Range of usability Analysis
- Extension Cost Analysis
Since the dimension length is the same for all schemes, the uncompressed size of the matrix A' will be equal to the uncompressed size of A, i.e. the total number of non-zero elements of the matrix oiA' can be obtained by summing all non-zero elements of the sub-matrices. One of the goals of using a data compression scheme is to reduce the memory space required for a sparse field.
For the derivation of the range of usefulness for the CRS scheme we consider T1CRS = land n=3 in equation (3.2) and we get,. For the derivation of the range of usefulness for the EaCRS scheme we consider 71EaCRS = 1 in equation (3.9) and we get,. For the derivation of the range of usefulness for the LEaCRS scheme we consider 7/LEaCRS = 1 in equation (3.11) and we get,.
For the derivation of the range of usefulness for the EaChOff scheme we consider 17EaChOff = 1 in equation (3.14) and we get,. Range of usefulness of the Ch0Jf LEaCRS and EaChO/j' schemes is the same for any dimensional EMA, while the range of usefulness of the CRS and EaCRS schemes decreases with the increase of dimensionality.
- Conclusion
- Experimental Setup
- Experimental parameters
- Experimental Results
- Comparison of Compression Ratio
- Extension Cost
- Retrieval Cost
- Discussion
Thus, EG8CRS is equal to double the initial volume of CRS and the expansion cost for a single CO array of EaCRS (since the EaCRS scheme requires one less CO auxiliary array for each subarray than the CRS scheme). Thus, EGaCRS is equal to twice the initial volume of CRS and the expansion cost for 'n - 2 nrs. The analytical analysis of the proposed compression schemes, including the theoretical analysis of the traditional CRS and Chunk-Ojftet schemes, are also presented in this chapter presented.
Analytical analysis shows that the expansion gain of the proposed EaCRS and LEaCRS scheme compared to the CRS scheme is more than twice the initial volume of CRS and the expansion gain of the EaChoff scheme compared to the ChOff scheme is exactly twice the initial volume of Chunk 0/je1 for which any value ofS with a fixed initial volume. This is an important metric for determining the range of applicability (see Definition 3.1) of compression schemes. The cost of the expansion and the acquisition of the expansion depends on the initial volume of the set, ie.
We compare the space requirements and scope of applicability of the EacRS, LEaCRS and EaChOff schemes with the CRS and C/iOff schemes on the TMA. The recovery times of the CRS, ChOff, EaC'hOff, EaC'RS and LEaCRS schemes are examined and compared to the recovery time of the EMA.

Conclusion
Concluding Remarks
Future Recommendations
Therefore, it will be very efficient to apply these schemes in a parallel and multiprocessor environment. The schemes can be applied to implement the compressed form of MOLAP server and data warehouses. EaCRS, LEaCRS and EaChQ/f schemes can be efficiently applied for incremental aggregation, i.e. a form of speed for big data analysis.
The scheme can be applied to multidimensional database implementations using a conventional RDBMS for multidimensional data analysis. Jen Efficient data-parallel algorithms for multidimensional matrix operations based on the EKMR scheme for multicomputers with distributed memory," IEEE Parallel and Distributed Systems. Masudul Ahsan, "An efficient implementation scheme for multidimensional index matrix operations and its evaluation," Thesis.
Azharul Hasan, 2013 "An Efficient Encoding Scheme to 1-Landle the Address Space Overflow for Large Multidimensional Arrays", Journal of Computers, Vol.8, No. 5, p. Chun-Yuan Lin, Yeh-Ching Chung, Jen-Shiuh Liu, December 2003, 'Efficient data compression methods for multidimensional sparse matrix operations based on the EKMR scheme,' IEEE Transactions on Computers.