TUGAS AKHIR
ANALISA PERBANDINGAN PENGARUH NILAI KAPASITOR EKSITASI
TERHADAP REGULASI DAN EFISIENSI PADA MOTOR INDUKSI SEBAGAI
GENERATOR ( MISG ) PENGUATAN SENDIRI
( Aplikasi pada Laboratorium Konversi Energi Listrik FT-USU )
Diajukan untuk memenuhi salah satu persyaratan dalam menyelesaikan pendidikan sarjana (S-1) pada
Departemen Teknik Elektro
O l e h
ANDI HALIM
NIM. 060402051
DEPARTEMEN TEKNIK ELEKTRO
FAKULTAS TEKNIK
UNIVERSITAS SUMATERA UTARA
MEDAN
ABSTRAK
Motor induksi merupakan salah satu penggerak yang paling sering digunakan dalam
aplikasi industri. Disamping fungsinya sebagai penggerak, motor induksi juga dapat dijadikan sebagai generator atau sering juga disebut dengan Motor Induksi Sebagai Generator (MISG).
Secara umum konstruksi motor induksi adalah sama dengan konstruksi generator induksi, hanya saja dalam pengoperasiannya generator induksi memerlukan prime over untuk menggerakkan rotor motor induksi tersebut. Rotor tersebut dikopelkan ke prime over lalu
diputar sedemikian sehingga menghasilkan slip negatif (1>s ). Artinya kecepatan putaran rotor harus di atas kecepatan medan putar stator (ns<nr). Tidak hanya itu saja, motor induksi
tersebut juga memerlukan kapasitor untuk menyediakan daya reaktif. Kapasitor ini dipasangkan secara paralel ke statornya yang disebut sebagai “kapasitor eksitasi”.
Besar nilai kapasitor daya reaktif yang dihasilkan tergantung besar nilai kapasitor
yang digunakan. Daya reaktif mempengaruhi regulasi dan efisiendi generator induksi tersebut. Oleh karena itu penulis akan menganalisis perbandingan regulasi dan efisiensi
generator induksi dengan nilai kapasitor yang berbeda.
Puji syukur penulis panjatkan kehadirat Tuhan Yang Maha Esa atas berkah dan rahmat-Nya kepada penulis, sehingga penulis dapat menyelesaikan dengan baik Tugas Akhir yang berjudul:
“ANALISA PERBANDINGAN PENGARUH NILAI KAPASITOR EKSITASI
TERHADAP REGULASI DAN EFISIENSI PADA MOTOR INDUKSI SEBAGAI
GENERATOR ( MISG ) PENGUATAN SENDIRI”
Penulisan Tugas Akhir ini merupakan salah satu persyaratan yang wajib dipenuhi sebagai salah satu syarat untuk memperoleh gelar Sarjana Teknik pada Departemen Teknik Elektro FT USU.
Tugas Akhir ini penulis persembahkan untuk kedua orangtua yang telah membesarkan penulis dengan kasih sayang yang tidak terhingga yaitu: Mak Bun Meng dan Nursia Hartono; kakak penulis, yaitu: Fenni Puspita Dewi; paman penulis, yaitu: Hermanto; bibi penulis yaitu: Nuraini Hartono.
Selama masa kuliah sampai masa penyelesaian Tugas Akhir ini, penulis mendapat dukungan, bimbingan, dan pertolongan dari berbagai pihak. Untuk itu, dengan setulus hati penulis hendak menyampaikan ucapan terima kasih yang sebesar-besarnya kepada:
1. Bapak Ir. Surya Tarmizi Kasim, M.Si selaku dosen pembimbing Tugas Akhir saya, yang telah bersedia meluangkan waktu di sela-sela kesibukan beliau untuk membimbing penulis mulai dari awal sampai selesainya Tugas Akhir ini;
2. Bapak Ir., M.Natsir Amin, M.M selaku dosen wali penulis yang banyak memberikan masukan dan pengarahan selama penulis menempuh perkuliahan;
3. Bapak Ir. Surya Tarmizi Kasim, M.Si dan Bapak Rahmat Fauzi, ST, MT selaku Ketua dan Sekretaris Departemen Teknik Elektro, Fakultas Teknik Universitas Sumatera Utara;
4. Seluruh staf pengajar dan administrasi Departemen Teknik Elektro, Fakultas Teknik Universitas Sumatera Utara,
5. Rekan-rekan kerja penulis di CORPUS English Tutorial Centre, Franky Pandana, Mery, Valentina Wijaya, Harry Hidayat, Yolven, Elizabeth Rimba, Jansen Lee dan Steveni Winata yang telah memberikan dorongan dan semangat kepada penulis di dalam menyelesaikan tugas akhir ini;
7. Sahabat penulis, Sally Nathania yang telah memotivasi dan meluangkan banyak waktu untuk menemani penulis baik dalam keadaan suka maupun duka;
8. Teman-teman terbaik semasa SMP sampai sekarang, yaitu: Davin Arden , Dannish Kurniago dan Johanna Aveline atas segala motivasi dan dukungannya selama ini;
9. Teman-teman semasa SMA sampai sekarang, yaitu: Andy Thomas, Biondi, Malvin, Renalto Wijaya, Jenny Yeonardy, Vera dan seluruh keluarga besar “FANTASY” lainnya yang memberikan semangat dan inspirasi dalam hidup ini;
10. Teman-teman sesama mahasiswa stambuk 2006, Thomas William, Sugianto, Hendrik, Fredy Angga, Budiman Chandra, Firmanto, Desmanto, Sanita SFN, Sukesih, Iqbal, Taufik, Nasir Andi Hakim Nasution, Supenson, Fransiscus, Folda, Jaitun, dan yang lainnya;
11. Teman-teman junior, yaitu: Joni, Angel, Denny Tanaya, Yuyanto, Yudi, Antonius, Teguh, Wilfian, dan yang lainnya;
12. Semua orang yang tidak dapat penulis sebutkan satu per satu, yang telah memberikan kontribusinya kepada penulis, baik secara langsung maupun tidak langsung, jasa kalian akan senantiasa penulis kenang dan sebagai acuan untuk menempuh hari-hari ke depan dengan penuh semangat dan lebih baik lagi.
Penulis menyadari bahwa Tugas Akhir ini masih jauh dari sempurna. Oleh karena itu penulis sangat mengharapkan saran dan kritik yang membangun demi penyempurnaan Tugas Akhir ini. Akhirnya penulis berharap Tugas Akhir ini dapat bermanfaat bagi para pembaca, khususnya mahasiswa yang ingin lebih mengetahui dan mendalami masalah sistem kendali berbasis diagram tangga untuk keperluan otomatisasi industri.
Medan, Agustus 2011 Penulis
DAFTAR ISI
Hal
KATA PENGANTAR ………... i
ABSTRAK ………... ii
DAFTAR ISI ………. iv
DAFTAR GAMBAR ... vii
DAFTAR TABEL ... ix
BAB I PENDAHULUAN ……….... 1
1.1 Latar Belakang ………... 1
1.2 Tujuan & Manfaat Penulisan ... 2
1.3 Batasan Masalah ………... 2
1.4 Metode Penulisan ……….………. 3
1.5 Sistematika Penulisan ... 4
BAB II MOTOR INDUKSI TIGA PHASA ... 6
II.1 Umum ... 6
II.2 Konstruksi Motor Induksi Tiga Phasa ... 6
II.3 Prinsip Kerja Motor Induksi Tiga Phasa ... 9
II.4 Medan Putar ... 13
II.4.1 Analisis secara Vektor ... 14
II.5 Rangkaian Ekivalen Motor Induksi ... 16
II.5.1 Rangkaian Ekivalen Stator ... 16
II.5.2 Rangkaian Ekivalen Rotor ... 18
II.6 Aliran Daya Motor Induksi ... 22
II.7 Torsi Motor Induksi Tiga Phasa ... 25
II.8 Efisiensi Motor Induksi Tiga Phasa ... 28
II.9 Disain Motor Induksi Tiga Phasa ... 29
II.10 Penentuan Parameter Motor Induksi ... 30
II.10.1 Percobaan DC ... 30
II.10.3 Percobaan Rotor Tertahan ... 36
BAB III MOTOR INDUKSI SEBAGAI GENERATOR ... 38
III.1 Umum ………... 38
III.2 Syarat – syarat Motor Induksi Sebagai Generator... 39
III.3 Slip ... 40
III.4 Frekuensi Rotor ... 40
III.5 Prinsip Kerja Generator Induksi Penguatan Sendiri ………. 41
III.6 Kapasitor Eksitasi ... 43
III.7 Pemasangan Kapasitor... 44
III.7.1 Kapasitor Hubungan Delta ( ∆ ) ... 44
III.7.2 Kapasitor Hubungan Wye ( Y ) ... 44
III.8 Proses Pembangkitan Tegangan dan Rangkaian Ekivalen Generator Induksi ... 45
III.9 Pengaruh Pembebanan Terhadap Arus Eksitasi ... 48
III.10 Aliran Daya Nyata Generator Induksi Penguatan Sendiri ... 49
III.11 Efisiensi ... 50
III.12 Generator Induksi Penguatan Sendiri Hubungan Short Shunt ... 50
III.13 Persamaan Tegangan, Arus dan Daya Pada Generator Induksi Pengu- atan Sendiri ... 51
BAB IV ANALISA PERBANDINGAN PENGARUH BESAR KAPASITOR EKSITASI TERHADAP REGULASI DAN EFISIENSI MOTOR INDUKSI SEBAGAI GENERATOR ( MISG ) PENGUATAN SENDIRI ... 52
IV.1 Umum ... 52
IV.2 Peralatan Yang Digunakan ... 52
IV.3 Penentuan Besar Nilai Kapasitor ... 53
IV.4 Pengujian Analisa Perbandingan Pengaruh Besar Kapasitor Eksitasi Terhadap Regulasi Dan Efisiensi Motor Induksi Sebagai Generator Induksi (MISG) Penguatan Sendiri ... 55
IV.4.1 Pengujian Pengukuran Tahanan Stator ... 55
IV.4.1.1 Rangkaian Pengujian ... 56
IV.4.1.2 Prosedur Pengujian ... 56
IV.4.1.3 Data Hasil Pengujian ... 56
IV.4.1.4 Analisa Data Pengujian ... 57
Dalam Keadaan Berbeban ... 58
IV.4.2.1 Rangkaian Pengujian ... 58
IV.4.2.2 Prosedur Pengujian ... 58
IV.4.2.3 Data Hasil Pengujian ... 59
IV.4.3 Analisa Data Perbandingan Pengaruh Besar Kapasitor Eksitasi Terhadap Regulasi Dan Efisiensi Pada Motor Induksi Sebagai Generator (MISG)Penguatan Sendiri ... 61
IV.4.3.1 Regulasi Tegangan ... 61
IV.4.3.2 Efisiensi ... 63
IV.4.4 Tabel Analisa Data Percobaan ... 68
IV.4.5 Kurva Perbandingan Pengaruh Besar Kapasitor Eksitasi Terhadap Regulasi dan Efisiensi pada Motor Induksi sebagai Generator Pe- nguatan Sendiri ... 70
BAB V PENUTUP ... 72
V.1 Kesimpulan ... 72
V.2 Saran ... 73
DAFTAR GAMBAR
Hal.
Gambar 2.1 Penampang rotor dan stator motor induksi ………. 7
Gambar 2.2 Komponen stator motor induksi tiga phasa ……….... 8
Gambar 2.3 Rotor sangkar dan bagian-bagiannya ... 8
Gambar 2.4 Rotor belitan dan motor induksi rotor belitan ... 9
Gambar 2.5 Diagram phasor fluksi 3 phasa & Arus 3 phasa seimbang ... 13
Gambar 2.6 Medan putar pada motor induksi tiga phasa ... 13
Gambar 2.7 Arah fluks yang ditimbulkan oleh arus yang mengalir dalam suatu lingkar …... 14
Gambar 2.8 Diagram vektor untuk fluks total pada keadaan t1, t2, t3, t4…….. 14
Gambar 2.9 Rangkaian ekivalen stator motor induksi …….………... 15
Gambar 2.10 Rangkaian ekivalen motor induksi tiga phasa ………..……... 17
Gambar 2.11 Rangkaian ekivalen pada rotor motor induksi ………... 18
Gambar 2.12 Rangkaian ekivalen dilihat dari sisi stator motor induksi ... 19
Gambar 2.13 Rangkaian ekivalen lain dilihat dari sisi stator motor induksi .... 19
Gambar 2.14 Rangkaian ekivalen lain dari motor induksi ... 20
Gambar 2.15 Diagram aliran daya motor induksi ………. 23
Gambar 2.16 Rangkaian ekivalen motor induksi ……….. 24
Gambar 2.17 Rangkaian ekivalen motor induksi dengan terminal a-b dilepas ... 24
Gambar 2.18 Rangkaian ekivalen motor induksi yang lain ……….. 25
Gambar 2.19 Karakteristik motor induksi ……….……….... 26
Gambar 2.20 Efisiensi pada motor induksi ………... 27
Gambar 2.21 Karakteristik torsi-kecepatan motor induksi pada berbagai disain ... 29
Gambar 2.22 Rangkaian phasa stator saat pengukuran DC hubungan Y ... 29
Gambar 2.23 Rangkaian phasa stator saat pengukuran DC hubungan delta ...... 30
Gambar 2.24 Rangkaian ekivalen pada saat berbeban ... 32
Gambar 2.25 Rangkaian ekivalen pada saat beban nol ... 32
Gambar 2.26 Rangkaian ekivalen pada saat rotor tertahan (s = 1) ... 34
Gambar 3.2 Karakteristik torsi – kecepatan mesin induksi ... 42
Gambar 3.3 Kapasitor terhubung delta ... 44
Gambar 3.4 Kapasitor terhubung bintang ... 44
Gambar 3.5 Rangkaian proses pembangkitan tegangan ………. 46
Gambar 3.6 Rangkaian ekivalen perfasa generator induksi ... 46
Gambar 3.7 Proses pembangkitan tegangan ……... 47
Gambar 3.8 Diagram vektor tegangan generator induksi ... 48
Gambar 3.9 Diagram aliran daya nyata ... 49
Gambar 3.10 Rangkaian generator induksi penguatan sendiri hubungan short shunt ... 50
Gambar 3.11 Rangkaian ekivalen per phasa generator induksi keadaan berbeban ... 51
Gambar 4.1 Rangkaian percobaan dengan suplai DC ... 56
Gambar 4.2 Rangkaian pengujian berbeban pada generator penguatan sendiri ... 58
Gambar 4.3 Kurva pengaruh kapasitor eksitasi terhadap regulasi tegangan motor induksi sebagai generator penguatan sendiri ... 70
DAFTAR TABEL
Hal.
Tabel 2.1 Distribusi empiris dari Xbr ... 37
Tabel 4.1 Data hasil pengujian tahanan stator DC ... 56
Tabel 4.2 Data hasil pengujian berbeban generator induksi penguatan
sendiri dengan menggunakan kapasitor eksitasi ... 59
Tabel 4.3 Data hasil pengujian beban nol generator induksi penguatan
sendiri dengan menggunakan kapasitor eksitasi ... 60
ABSTRAK
Motor induksi merupakan salah satu penggerak yang paling sering digunakan dalam
aplikasi industri. Disamping fungsinya sebagai penggerak, motor induksi juga dapat dijadikan sebagai generator atau sering juga disebut dengan Motor Induksi Sebagai Generator (MISG).
Secara umum konstruksi motor induksi adalah sama dengan konstruksi generator induksi, hanya saja dalam pengoperasiannya generator induksi memerlukan prime over untuk menggerakkan rotor motor induksi tersebut. Rotor tersebut dikopelkan ke prime over lalu
diputar sedemikian sehingga menghasilkan slip negatif (1>s ). Artinya kecepatan putaran rotor harus di atas kecepatan medan putar stator (ns<nr). Tidak hanya itu saja, motor induksi
tersebut juga memerlukan kapasitor untuk menyediakan daya reaktif. Kapasitor ini dipasangkan secara paralel ke statornya yang disebut sebagai “kapasitor eksitasi”.
Besar nilai kapasitor daya reaktif yang dihasilkan tergantung besar nilai kapasitor
yang digunakan. Daya reaktif mempengaruhi regulasi dan efisiendi generator induksi tersebut. Oleh karena itu penulis akan menganalisis perbandingan regulasi dan efisiensi
generator induksi dengan nilai kapasitor yang berbeda.
BAB I
PENDAHULUAN
1.1 Latar Belakang
Mesin induksi dapat dioperasikan sebagai motor maupun sebagai generator. Namun, sedikit sekali masalah generator induksi ditulis sebagai subjek. Alasannya adalah karena
generator induksi tidak mampu mengendalikan tegangan dan frekuensi pada kondisi berbeban dan kecepatan perputaran yang berubah. Sehingga dari salah satu penyebabnya tersebut, generator sinkron selalu digunakan dalam unit – unit pembangkit tenaga listrik.
Namun, akhir – akhir ini karena cadangan sumber energi yang tidak terbarukan seperti minyak, gas bumi, batubara dan lain – lain dirasakan semakin menipis,maka
pengembangan generator induksi penguatan sendiri yang digerakkan oleh energi angin, pembangkit mikrohidro, biogas dan lain – lain mulai menjadi semakin mendapat perhatian yang nyata. Selain itu, keuntungan lain dari mesin ini adalah kontruksinya yang kokoh, biaya
pemeliharaan yang rendah dan tidak membutuhkan penguatan DC.
Eksitasi generator induksi penguatan sendiri diperoleh dari kapasitor yang
dihubungkan dengan terminal stator generator. Kapasitor ini berfungsi sebagai pembangkit daya reaktif untuk menghasilkan fluksi magnetisasi di celah udara. Jadi tanpa adanya daya reaktif untuk kebutuhan arus eksitasi, kerja mesin induksi sebagai generator tidak mungkin
terlaksana.
Besar daya reaktif yang dihasilkan tergantung besar nilai kapasitor eksitasi yang
dipakai. Besarnya daya reaktif akan mempengaruhi regulasi dan efisiensi generator induksi tersebut. Oleh karena itu penulis akan menganalisa perbandingan pengaruh besar nilai kapasitor eksitasi terhadap regulasi dan efisiensi motor induksi sebagai generator (MISG)
1.2 Tujuan dan Manfaat Penulisan
Tugas Akhir ini bertujuan untuk menganalisa pengaruh besar kapasitor eksitasi terhadap karakteristik beban nol dan berbeban pada motor induksi sebagai generator (MISG) penguatan sendiri.
Adapun manfaat dari penelitian ini adalah :
1. Menambah wawasan mengenai generator induksi penguatan sendiri.
2. Mengetahui besar nilai kapasitor yang akan disuplai pada generator induksi untuk
membangkitkan arus eksitasi yang diperlukan.
3. Mengetahui cara memperoleh nilai kapasitor eksitasi untuk mendapatkan regulasi dan
efisiensi yang lebih baik pada generator induksi.
4. Menambah aplikasi-aplikasi pada laboratorium konversi energi listrik
1.3 Batasan Masalah
Untuk menjaga agar pembahasan materi dalam Tugas Akhir ini lebih terarah,
maka penulis menetapkan beberapa batasan masalah sebagai berikut :
1. Motor induksi yang penulis ambil sebagai aplikasi adalah Motor Induksi Tiga Phasa Rotor Sangkar Tupai pada Laboratorium Konversi Energi Listrik FT.USU.
2. Analisa dilakukan dalam kondisi steady state.
3. Hanya menganalisa hubungan short shunt untuk generator induksi penguatan
sendiri dengan berbagai nilai kapasitor yang telah ditentukan.. 4. Tidak membahas tentang pengaturan.
5. Tidak membahas gangguan yang terjadi pada generator induksi.
6. Data yang diambil adalah tegangan terminal generator, arus kapasitor, arus beban, putaran, dan daya, sesuai dengan perubahan beban.
8. Rugi-rugi inti, rugi gesek+angin, dan rugi-rugi di rotor diabaikan, hanya rugi-rugi tembaga stator yang diperhitungkan.
9. Kapasitor eksitasi yang digunakan adalah hubungan Delta ( ∆ ).
10.Kondisi beban yang menjadi objek penelitian adalah beban yang bersifat resistif berupa lampu pijar.
11.Analisa data berdasarkan peralatan yang tersedia di Laboratorium Konversi
Energi Listrik.
1.4 Metode Penulisan
Untuk dapat menyelesaikan tugas akhir ini maka penulis menerapkan beberapa metode studi diantaranya :
1. Studi literatur yaitu dengan membaca teori-teori yang berkaitan dengan topik tugas akhir ini, dari buku-buku referensi baik yang dimiliki oleh penulis atau di
perpustakaan dan juga dari artikel-artikel, jurnal, internet dan lain-lain.
2. Studi lapangan yaitu dengan melaksanakan percobaan di Laboratorium Konversi Energi Listrik FT USU.
3. Studi bimbingan yaitu dengan melakukan diskusi tentang topik tugas akhir ini dengan dosen pembimbing yang telah ditunjuk oleh pihak departemen Teknik
1.5 Sistematika Penulisan
Tugas akhir ini disusun berdasarkan sistematika penulisan sebagai berikut :
BAB I. PENDAHULUAN
Bab ini merupakan pendahuluan yang berisi tentang latar belakang
masalah, tujuan dan manfaat penulisan, batasan masalah, metode penulisan, dan sistematika penulisan.
BAB II. MOTOR INDUKSI TIGA PHASA
Bab ini membahas mengenai motor induksi tiga phasa secara umum, konstruksi motor induksi tiga phasa, prinsip kerja motor induksi tiga
phasa, medan putar, rangkaian ekivalen motor induksi, aliran daya pada motor induksi, torsi motor induksi tiga phasa, efisiensi motor induksi tiga phasa, disain motor induksi, dan penentuan parameter motor induksi.
BAB III. MOTOR INDUKSI SEBAGAI GENERATOR ( MISG )
PENGUATAN SENDIRI
Bab ini membahas mengenai motor induksi sebagai generator secara umum, syarat – syarat motor induksi sebagai generator, prinsip kerja generator induksi penguatan sendiri, proses pembangkitan tegangan dan
rangkaian ekivalen, aliran daya nyata generator induksi penguatan sendiri, pengaruh pembebanan terhadap arus eksitasi, pembebanan dengan faktor
kerja satu, generator induksi penguatan sendiri hubungan short shunt, persamaan tegangan, arus dan daya pada generator induksi penguatan sendiri hubungan short shunt. keuntungan dan kelemahan motor induksi
BAB IV. PENGUJIAN PEMBEBANAN TERHADAP REGULASI DAN
EFISIENSI GENERATOR INDUKSI DENGAN NILAI
KAPASITOR YANG BERBEDA
Bab ini membahas tentang pengujian pengaruh pembebanan terhadap
regulasi tegangan dan efisiensi. Pengambilan data dilakukan dengan melakukan percobaan di laboratorium. Hasil yang diinginkan adalah parameter generator induksi penguatan sendiri untuk mendapatkan nilai
regulasi tegangan dan efisiensi generator induksi tersebut.
BAB V. KESIMPULAN DAN SARAN
Bab ini merupakan bagian penutup berupa kesimpulan dan saran yang berkaitan dengan pembahasan mengenai analisa perbandingan pengaruh besar nilai kapasitor eksitasi terhadap regulasi dan efisiensi generator
BAB II
MOTOR INDUKSI TIGA PHASA
2.1 Umum
Motor induksi merupakan motor arus bolak – balik ( AC ) yang paling luas digunakan
dan dapat dijumpai dalam setiap aplikasi industri maupun rumah tangga. Penamaannya berasal dari kenyataan bahwa arus rotor motor ini bukan diperoleh dari sumber tertentu, tetapi merupakan arus yang terinduksi sebagai akibat adanya perbedaan relatif antara putaran rotor
dengan medan putar (rotating magnetic field) yang dihasilkan arus stator.
Motor ini memiliki konstruksi yang kuat, sederhana, handal, serta berbiaya murah. Di
samping itu motor ini juga memiliki efisiensi yang tinggi saat berbeban penuh dan tidak membutuhkan perawatan yang banyak. Akan tetapi jika dibandingkan dengan motor DC, motor induksi masih memiliki kelemahan dalam hal pengaturan kecepatan. Dimana pada
motor induksi pengaturan kecepatan sangat sukar untuk dilakukan, sementara pada motor DC hal yang sama tidak dijumpai.
2.2 Konstruksi Motor Induksi Tiga Phasa
Secara umum motor induksi terdiri dari rotor dan stator. Rotor merupakan bagian
Rotor
Stator
Gambar 2.1. Penampang rotor dan stator motor induksi
Komponen stator adalah bagian terluar dari motor yang merupakan bagian yang diam
dan mengalirkan arus phasa. Stator terdiri atas tumpukan laminasi inti yang memiliki alur yang menjadi tempat kumparan dililitkan yang berbentuk silindris. Alur pada tumpukan
laminasi inti diisolasi dengan kertas (Gambar 2.2.(b)). Tiap elemen laminasi inti dibentuk dari lembaran besi (Gambar 2.2 (a)). Tiap lembaran besi tersebut memiliki beberapa alur dan beberapa lubang pengikat untuk menyatukan inti. Tiap kumparan tersebar dalam alur yang
disebut belitan phasa dimana untuk motor tiga phasa, belitan tersebut terpisah secara listrik sebesar 120o. Kawat kumparan yang digunakan terbuat dari tembaga yang dilapis dengan
isolasi tipis. Kemudian tumpukan inti dan belitan stator diletakkan dalam cangkang silindris (Gambar 2.2.(c)). Berikut ini contoh lempengan laminasi inti, lempengan inti yang telah disatukan, belitan stator yang telah dilekatkan pada cangkang luar untuk motor induksi tiga
phasa.
(c)
Gambar 2.2. Komponen stator motor induksi tiga phasa,
(a) Lempengan inti,
(b) Tumpukan inti dengan kertas isolasi pada beberapa alurnya. (c) Tumpukan inti dan kumparan dalam cangkang stator.
Rotor motor induksi tiga phasa dapat dibedakan menjadi dua jenis yaitu rotor sangkar (squirrel cage rotor) dan rotor belitan (wound rotor). Rotor sangkar terdiri dari susunan
batang konduktor yang dibentangkan ke dalam slot – slot yang terdapat pada permukaan rotor dan tiap – tiap ujungnya dihubung singkat dengan menggunakan shorting rings.
(a) (b)
Gambar 2.3. Rotor sangkar, (a) Tipikal rotor sangkar
(b) Bagian – bagian rotor sangkar
Sementara itu pada rotor belitan, rotornya dibentuk dari satu set belitan tiga phasa
yang merupakan bayangan dari belitan statornya. Biasanya belitan tiga phasa dari rotor ini terhubung Y dan kemudian tiap - tiap ujung dari tiga kawat rotor tersebut diikatkan pada slip
dirancang untuk dapat disisipkan dengan tahanan eksternal, yang mana hal ini akan memberikan keuntungan dalam memodifikasi karakteristik torsi – kecepatan dari motor.
(a)
(b)
Gambar 2.4. (a) Rotor belitan
(b) Motor induksi rotor belitan
2.3 Prinsip Kerja Motor Induksi Tiga Phasa
Motor induksi adalah peralatan pengubah energi listrik ke bentuk energi mekanik.
Pengubahan energi ini bergantung pada keberadaan phenomena alami magnetik, medan listrik, gaya mekanis dan gerak.
Dalam motor induksi, tidak ada hubungan listrik ke rotor, arus rotor merupakan arus
induksi. Tetapi ada kondisi yang sama seperti motor dc, dimana pada rotor mengalir arus. Arus ini berada dalam medan magnetik sehingga akan terjadi gaya (F) pada rotor yang akan
menggerakkan rotor dalam arah tegak lurus medan.
Jika pada belitan stator diberi tegangan tiga fasa, maka pada stator akan dihasilkan arus tiga fasa, arus ini menghasilkan medan magnetik yang berputar dengan kecepatan
sinkron. Ketika medan melewati konduktor rotor, dalam konduktor ini diinduksikan ggl yang sama seperti ggl yang diinduksikan dalam lilitan sekunder transformator oleh fluksi arus
mengalir pada konduktor rotor dalam medan magnet yang dihasilkan stator akan menghasilkan gaya (F) yang bekerja pada rotor.
Gambar 2.5 di bawah ini menggambarkan penampang stator dan rotor motor induksi, dengan medan magnet diumpamakan berputar searah jarum jam dan dengan statornya diam
seperti pada saat start.
Gambar 2.5. Penampang stator dan rotor motor induksi
Untuk arah fluksi dan gerak yang ditunjukkan gambar di atas, penggunaan aturan tangan kanan Fleming bahwa arah arus induksi dalam konduktor rotor menuju pembaca. Pada
kondisi seperti itu, dengan konduktor yang mengalirkan arus berada dalam medan magnet seperti yang ditunjukkan, gaya pada konduktor mengarah ke atas karena medan magnet di
bawah konduktor lebih kuat dari pada medan di atasnya. Agar sederhana, hanya satu konduktor rotor yang diperlihatkan. Tetapi, konduktor – konduktor rotor yang berdekatan lainnya dalam medan stator juga mengalirkan arus dalam arah seperti pada konduktor yang
ditunjukkan, dan juga mempunyai suatu gaya ke arah atas yang dikerahkan pada mereka. Pada setengah siklus berikutnya, arah medan stator akan dibalik, tetapi arus rotor juga akan
kutup – kutup medan stator lain akan mempunyai gaya yang semuanya cenderung memutarkan rotor searah jarum jam. Jika kopel yang dihasilkan cukup besar untuk mengatasi
kopel beban yang menahan, motor akan melakukan percepatan searah jarum jam atau dalam arah yang sama dengan perputaran medan magnet stator.
Untuk memperjelas prinsip kerja motor induksi tiga fasa, maka dapat dijabarkan dalam langkah – langkah berikut:
1. Pada keadaan beban nol Ketiga phasa stator yang dihubungkan dengan sumber tegangan
tiga phasa yang setimbang menghasilkan arus pada tiap belitan phasa. 2. Arus pada tiap phasa menghasilkan fluksi bolak-balik yang berubah-ubah
3. Amplitudo fluksi yang dihasilkan berubah secara sinusoidal dan arahnya tegak lurus terhadap belitan phasa
4. Akibat fluksi yang berputar timbul ggl pada stator motor yang besarnya adalah
e1 =
dt d
N Φ
− 1 ( Volt ) ...(2.1)
atau E1 =4,44fN1Φ( Volt ) ...(2.2)
5. Penjumlahan ketiga fluksi bolak-balik tersebut disebut medan putar yang berputar dengan kecepatan sinkron ns, besarnya nilai ns ditentukan oleh jumlah kutub p dan frekuensi
stator f yang dirumuskan dengan
p f
ns =120× ( rpm ) ...(2.3)
6. Fluksi yang berputar tersebut akan memotong batang konduktor pada rotor. Akibatnya pada kumparan rotor timbul tegangan induksi (ggl) sebesar E2 yang besarnya
E2 = Tegangan induksi pada rotor saat rotor dalam keadaan diam (Volt)
N2 = Jumlah lilitan kumparan rotor
Фm = Fluksi maksimum(Wb)
7. Karena kumparan rotor merupakan rangkaian tertutup, maka ggl tersebut akan
menghasilkan arus pada rotor sebesar I2
8. Adanya arus pada rotor sebesar I2 di dalam medan magnet akan menimbulkan gaya pada rotor
9. Bila kopel mula yang dihasilkan oleh gaya cukup besar untuk memikul kopel beban, rotor akan berputar searah medan putar stator
10.Perputaran rotor akan semakin meningkat hingga mendekati kecepatan sinkron. Perbedaan kecepatan medan stator (ns) dan kecepatan rotor (nr) disebut slip (s) dan dinyatakan dengan
100% s
r
s − ×
=
n n n
s ...(2.5)
11.Pada saat rotor dalam keadaan berputar, besarnya tegangan yang terinduksi pada kumparan rotor akan bervariasi tergantung besarnya slip. Tegangan induksi ini
dinyatakan dengan E2s yang besarnya
E2s =4,44sfN2Φm( Volt )...(2.6)
dimana
E2s = tegangan induksi pada rotor dalam keadaan berputar (Volt)
f2 = s.f = frekuensi rotor (frekuensi tegangan induksi pada rotor dalam keadaan berputar)
12.Bila ns = nr, tegangan tidak akan terinduksi dan arus tidak akan mengalir pada kumparan
rotor, karenanya tidak dihasilkan kopel. Kopel ditimbulkan jika nr < ns
Perputaran motor pada mesin arus bolak – balik ditimbulkan oleh adanya medan putar ( fluks yang berputar ) yang dihasilkan dalam kumparan statornya. Medan putar ini terjadi
apabila kumparan stator dihubungkan dalam fasa banyak, umumnya fasa 3. Hubungan dapat berupa hubungan bintang atau delta.
Misalkan kumparan a – a; b – b; c – c dihubungkan 3 fasa, dengan beda fasa masing – masing 1200 ( gambar 2.6a ) dan dialiri arus sinusoid. Distribusi arus ia, ib, ic sebagai fungsi waktu adalah seperti gambar 26b. Pada keadaan t1, t2, t3, dan t4, fluks resultan yang
ditimbulkan oleh kumparan tersebut masing – masing adalah seperti gambar 2.7c, d, e, dan f. Pada t1 fluks resultan mempunyai arah sama dengan arah fluks yang dihasilkan oleh
kumparan a – a; sedangkan pada t2, fluks resultannya mempunyai arah sama dengan arah fluks yang dihasilakan oleh kumparan c – c; dan untuk t3 fluks resultan mempunyai arah sama dengan fluks yang dihasilkan oleh kumparan b – b. Untuk t4, fluks resultannya berlawanan
arah dengan fluks resultan yang dihasilkan pada saat t1 keterangan ini akan lebih jelas pada analisa vektor.
Gambar 2.6. (a) Diagram phasor fluksi tiga phasa
(b) Arus tiga phasa setimbang
(b)Arus tiga phasa setimbang
Dari gambar c, d ,e, dan f tersebut terlihat fluks resultan ini akan berputar satu kali. Oleh karena itu untuk mesin dengan jumlah kutub lebih dari dua, kecepatan sinkron dapat
diturunkan sebagai berikut :
ns =
p f
. 120
( rpm )
f = frekuensi ( Hz )
p = jumlah kutub
2.4.1 Analisis Secara Vektor
Analisis secara vektor didapatkan atas dasar:
1. Arah fluks yang ditimbulkan oleh arus yang mengalir dalam suatu lingkar sesuai dengan perputaran sekrup ( gambar 2.8 ).
Gambar 2.8. Arah fluks yang ditimbulkan oleh arus yang mengalir dalam suatu
lingkar
2. Kebesaran fluks yang ditimbulkan ini sebanding dengan arus yang mengalir. Notasi yang dipakai untuk menyatakan positif atau negatifnya arus yang mengalir pada kumparan a – a, b – b, dan c – c pada gambar 2.6a yaitu: harga positif, apabila tanda
silang (x) terletak pada pangkal konduktor tersebut ( titik a, b, c ), sedangkan negatif apabila tanda titik ( . ) terletak pada pangkal konduktor tersebut (gambar 2.7 ). Maka diagram vektor
Gambar 2.9. Diagram vektor untuk fluks total pada keadaan t1, t2, t3, t4
Dari semua diagram vektor di atas dapat pula dilihat bahwa fluks resultan berjalan (berputar).
2.5 Rangkaian Ekivalen Motor Induksi
2.5.1 Rangkaian Ekivalen Stator
Untuk mempermudah analisis motor induksi, digunakan metoda rangkaian ekivalen per – fasa. Motor induksi dapat dianggap sebagai transformator dengan rangkaian sekunder
berputar. Rangkaian ekivalen statornya dapat digambarkan sebagai berikut :
1 V
1 R
1 X
1 I
c
R Xm
0
I
c
I Im
2 I
1 E
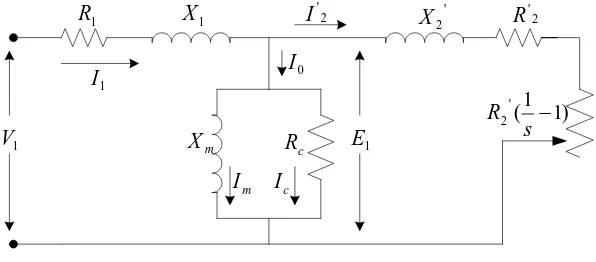
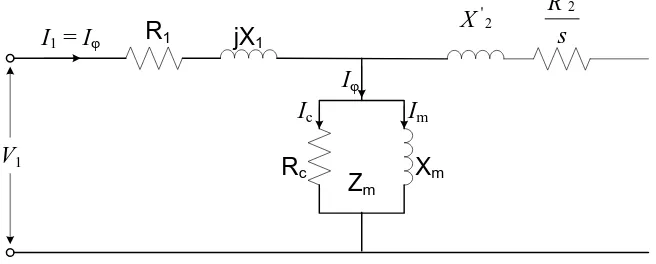
Gambar 2.10. Rangkaian ekivalen stator motor induksi
dimana :
V1 = tegangan terminal stator ( Volt )
R1 = tahanan efektif stator ( Ohm ) X1 = reaktansi bocor stator ( Ohm )
Arah positif dapat dilihat pada rangkaian Gambar 2.10.
Arus stator terbagi atas 2 komponen, yaitu komponen arus beban dan komponen arus penguat
I0. Komponen arus penguat I0 merupakan arus stator tambahan yang diperlukan untuk menghasilkan fluksi celah udara resultan, dan merupakan fungsi ggm E1.
Komponen arus penguat I0 terbagi atas komponen rugi – rugi inti IC yang sefasa
dengan E1 dan komponen magnetisasi Im yang tertinggal 900 dari E1.
Hubungan antara tegangan yang diinduksikan pada rotor sebenarnya ( Erotor )
dan tegangan yang diinduksikan pada rotor ekivalen ( E2s ) adalah :
dimana a adalah jumlah lilitan efektif tiap fasa pada lilitan stator yang banyaknya a kali
jumlah lilitan rotor.
Hubungan antara arus rotor sebenarnya Irotor dan arus I2s pada rotor ekivalen adalah :
I2s =
a Irotor
………...………. ( 2.8 )
sehingga hubungan antara impedansi bocor dari rotor ekivalen Z2s dan impedansi bocor dari
rotor sebenarnya Zrotor adalah :
Z2s = =
Nilai tegangan, arus dan impedansi tersebut diatas didefinisikan sebagai nilai yang referensinya ke stator.
=
Z2s = impedansi bocor rotor frekuensi slip tiap fasa dengan referensi ke stator ( Ohm ).
R2 = tahanan efektif referensi ( Ohm )
sX2 = reaktansi bocor referensi pada frekuensi slip X2 didefinisikan sebagai harga reaktansi bocor rotor dengan referensi frekuensi stator ( Ohm ).
Untuk mempermudah penjelasan dari rumus-rumus di atas, maka dapat dilihat pada gambar rangkaian ekicalen di bawah ini.
1
2.11. Rangkaian ekivalen motor induksi tiga phasa
2.5.2 Rangkaian Ekivalen Rotor
Reaktansi yang didapat pada persamaan (2.10) dinyatakan dalam cara yang demikian
karena sebanding dengan frekuensi rotor dan slip. Jadi X didefinisikan sebagai harga yang 2
akan dimiliki oleh reaktansi bocor pada rotor dengan patokan pada frekuensi stator.
Pada stator ada gelombang fluks yang berputar pada kecepatan sinkron. Gelombang
fluks ini akan mengimbaskan tegangan pada rotor dengan frekuensi slip sebesar E2s dan ggl
lawan stator E . Bila bukan karena efek kecepatan, tegangan rotor akan sama dengan 1
tegangan stator, karena lilitan rotor identik dengan lilitan stator. Karena kecepatan relatif gelombang fluks terhadap rotor adalah s kali kecepatan terhadap stator, hubungan antara ggl
E2s = sE ………...……...…….(2.11) 1
Gelombang fluks magnetik pada rotor dilawan oleh fluks magnetik yang dihasilkan
komponen beban I dari arus stator, dan karenanya, untuk harga efektif 2
I2s= I ...(2.12) 2
Dengan membagi persamaan (2.11) dengan persamaan (2.12) didapatkan:
=
Didapat hubungan antara persamaan (2.12) dengan persamaan (2.13), yaitu
=
Dengan membagi persamaan (2.14) dengan s, maka didapat
Dari persamaan (2.15) dapat dibuat rangkaian ekivalen untuk rotor.
Dari persamaan (2.10) , (2.11) dan (2.15) maka dapat digambarkan rangkaian ekivalen pada rotor sebagai berikut :
s
Gambar 2.12. Rangkaian ekivalen pada rotor motor induksi.
Dari penjelasan mengenai rangkaian ekivalen pada stator dan rotor di atas, maka dapat dibuat rangkaian ekivalen motor induksi tiga fasa pada masing – masing fasanya.
Perhatikan gambar di bawah ini.
Untuk mempernudah perhitungan maka rangkaian ekivalen pada gambar 2.12 diatas
dapat dilihat dari sisi stator, rangkaian ekivalen motor induksi tiga fasa akan dapat digambarkan sebagai berikut.
1
Gambar 2.13. Rangkaian ekivalen dilihat dari sisi stator motor induksi
Atau seperti gambar berikut :
1
Gambar 2.14. Rangkaian ekivalen dilihat dari sisi stator motor induksi
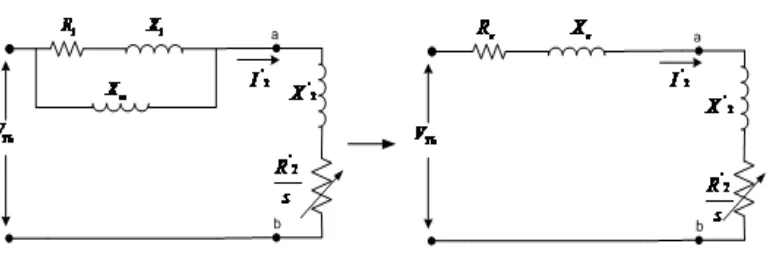
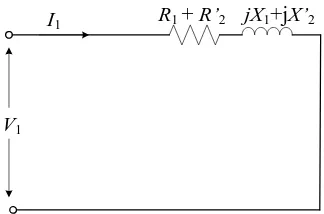
Dalam teori transformator-statika, analisis rangkaian ekivalen sering disederhanakan dengan mengabaikan seluruh cabang penalaran atau melakukan pendekatan dengan
memindahkan langsung ke terminal primer. Pendekatan demikian tidak dibenarkan dalam motor induksi yang bekerja dalam keadaan normal, karena adanya celah udara yang
menjadikan perlunya suatu arus peneralan yang sangat besar (30% sampai 40% dari arus beban penuh) dan karena reaktansi bocor juga perlu lebih tinggi. Untuk itu dalam rangkaian
ekivalen R dapat dihilangkan (diabaikan) dan dapat disederhanakan menjadi gambar seperti c
berikut.
Gambar 2.15. Rangkaian ekivalen lain dari motor induksi
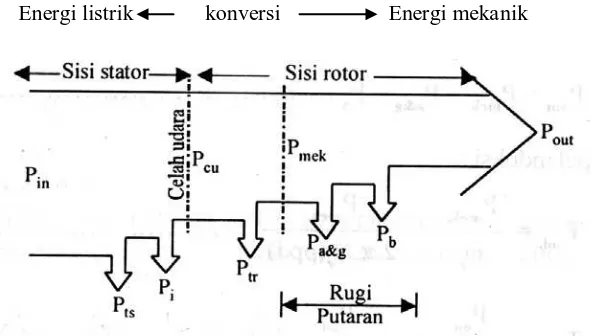
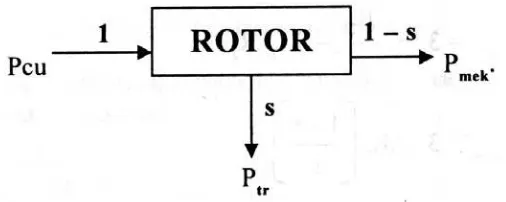
2.6 Aliran Daya Motor Induksi
Pada motor induksi, tidak ada sumber listrik yang langsung terhubung ke rotor,
sehingga daya yang melewati celah udara sama dengan daya yang diinputkan ke rotor. Daya total yang dimasukkan pada kumparan stator (Pin) dirumuskan dengan
θ
θ = perbedaan sudut phasa antara arus masukan dengan tegangan sumber.
Daya listrik disuplai ke stator motor induksi diubah menjadi daya mekanik
pada poros motor. Berbagai rugi – rugi yang timbul selama proses konversi energi listrik antara lain :
1. rugi – rugi tetap ( fixed losses ), terdiri dari :
rugi – rugi inti stator ( Pi )
Pi =
C
R E12 . 3
( Watt ) ………...( 2.18 )
rugi – rugi gesek dan angin
2.rugi – rugi variabel, terdiri dari :
rugi – rugi tembaga stator ( Pts )
Pts = 3. I12. R1 ( Watt ) ………....( 2.19 )
rugi – rugi tembaga rotor ( Ptr )
Ptr = 3. I22. R2 ( Watt ) ………...( 2.20 ) Daya pada celah udara ( Pcu ) dapat dirumuskan dengan :
Pcu = Pin – Pts – Pi ( Watt ) ……….…( 2.21 )
Jika dilihat pada rangkaian rotor, satu – satunya elemen pada rangkaian ekivalen yang
mengkonsumsi daya pada celah udara adalah resistor R2 / s. Oleh karena itu daya pada celah udara dapat juga ditulis dengan :
Pcu = 3. I22.
S R2
( Watt ) ………...( 2.22 )
Apabila rugi – rugi tembaga dan rugi – rugi inti dikurangi dengan daya input motor,
maka akan diperoleh besarnya daya listrik yang diubah menjadi daya mekanik. Besarnya daya mekanik yang dibangkitkan motor adalah :
Pmek = 3. I22.
S R2
- 3. I22. R2
Pmek = 3. I22. R2. ( s
s − 1
)
Pmek = Ptr x ( s
s − 1
) ( Watt ) …………...…( 2.24 )
Dari persamaan ( 2.20 ) dan ( 2.22 ) dapat dinyatakan hubungan rugi – rugi tembaga
dengan daya pada celah udara :
Ptr = s. Pcu ( Watt ) ………...………( 2.25 )
Karena daya mekanik yang dibangkitkan pada motor merupakan selisih dari daya
pada celah udara dikurangi dengan rugi – rugi tembaga rotor, maka daya mekanik dapat juga ditulis dengan :
Pmek = Pcu x ( 1 – s ) ( Watt ) ……….…( 2.26 )
Daya output akan diperoleh apabila daya yang dikonversikan dalam bentuk daya mekanik dikurangi dengan rugi – rugi gesek dan angin, sehingga daya keluarannya :
Pout = Pmek – Pa&g – Pb ( Watt ) ………..…( 2.27 )
Secara umum, perbandingan komponen daya pada motor induksi dapat dijabarkan dalam bentuk slip yaitu :
Pcu : Ptr : Pmek = 1 : s : 1 – s.
Gambar 2.16 menunjukkan aliran daya pada motor induksi tiga phasa :
Gambar 2.16. Diagram aliran daya motor induksi
2.7 Torsi Motor Induksi Tiga Fasa
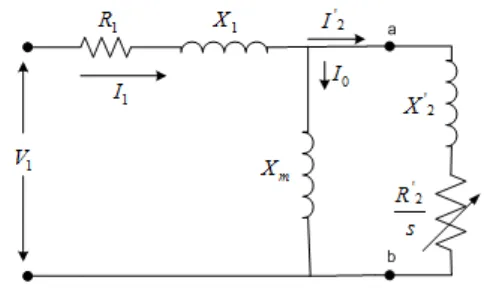
Suatu persamaan torsi pada motor induksi dapat dihasilkan dengan bantuan teori rangakaian thevenin. Dalam bentuk umumnya, teorema thevenin mengijinkan penggantian sembarang jaringan yang terdiri atas unsur – unsur rangkaian linier dan sumber tegangan
fasor tetap. Rangkaian rotor direfrensikan terhadap stator. Misalkan V tegangan input motor, 1
dengan melihat dari sisi terminal a-b, dapat dicari tegangan theveninnya. Perhatikan gambar
berikut ini.
Gambar 2.17. Rangkaian ekivalen motor induksi
Untuk mempermudah perhitungan maka pada gambar 2.17, terminal a-b dibuka. Perhatikan
Gambar 2.18. Rangkaian ekivalen motor induksi dengan terminal a-b dilepas
Dari gambar 2.18 dapat dihitung tegangan thevenin ( V ) Th
Th
Rangkaian ekivalen pada gambar 2.18 berubah menjadi seperti pada gambar 2.19 berikut.
Gambar 2.19. Rangkaian ekivalen motor induksi yang lain
Dengan demikian I dapat dihitung dengan persamaan 2
2
Torsi ( τd) dapat juga dihitung dengan persamaan
τd=
τd=
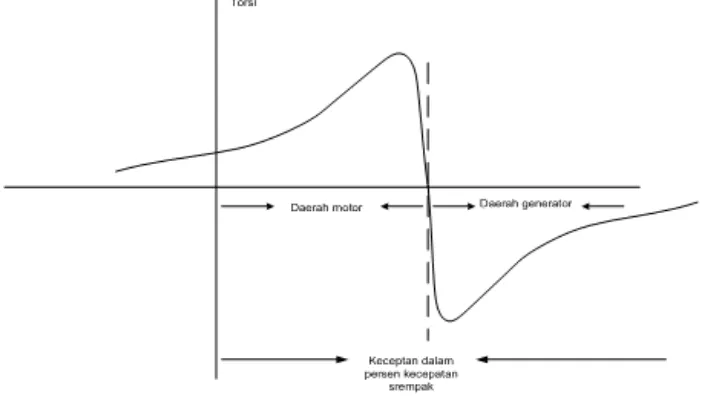
pada keadaan motor bekerja normal, rotor berputar pada arah putaran medan magnetik yang dihasilkan oleh arus stator, kecepatannya diantara nol sampai kecepatan serempak, dan slipnya diantara nol dengan satu. Lihat gambar – 2.20 berikut.
Gambar 2.20. Karakteristik motor induksi
Untuk mendapatkan mesin induksi yang bekerja sebagai generator, maka terminal stator dihubungkan pada suatu sumber tegangan dengan frekuensi tetap dan rotornya digerakkan diatas kecepatan serempak dengan suatu penggerak mula, seperti pada gambar
diatas. Sumber tersebut menjaga supaya kecepatan serempak tetap dan mencatu masukan daya reaktif yang diperlukan untuk meneral medan magnetis celah udara. Karenanya slip
berharga negatif.
Efisiensi dari suatu motor induksi didefenisikan sebagai ukuran keefektifan motor induksi untuk mengubah energi listrik menjadi energi mekanik yang dinyatakan sebagai
perbandingan / rasio daya output ( keluaran ) dengan daya input ( masukan ), atau dapat juga dirumuskan dengan :
Loss
Dari persamaan di atas dapat dilihat bahwa efisiensi motor tergantung pada besarnya rugi – rugi. Pada dasarnya metode yang digunakan untuk menentukan efisiensi motor induksi bergantung pada dua hal apakah motor itu dapat dibebani secara penuh atau pembebanan
simulasi yang harus digunakan.
Gambar 2.21. Efisiensi pada motor induksi
dimana :
Pcu = daya yang diinputkan ke rotor ( Watt )
Ptr = rugi – rugi tembaga rotor ( Watt )
Pmek = daya mekanik dalam bentuk putaran ( Watt )
Efisiensi dari motor induksi dapat diperoleh dengan melakukan pengujian beban nol dan pengujian hubung singkat. Dari pengujian beban nol akan diperoleh rugi – rugi mekanik dan rugi – rugi inti. Rugi – rugi tembaga stator tidak dapat diabaikan sekalipun motor
2.9 Disain Motor Induksi Tiga Phasa
Standard NEMA pada dasarnya mengkategorikan motor induksi ke dalam empat kelas yakni disain A,B,C, dan D.
1. Kelas A : disain ini memiliki torsi start normal (150 – 170%) dari nilai ratingnya) dan arus start relatif tinggi. Torsi break down nya merupakan yang paling tinggi dari semua disain NEMA. Motor ini mampu menangani beban lebih dalam jumlah besar
selama waktu yang singkat. Slip < = 5%
2. Kelas B : merupakan disain yang paling sering dijumpai di pasaran. Motor ini
memiliki torsi start yang normal seperti halnya disain kelas A, akan tetapi motor ini memberikan arus start yang rendah. Torsi locked rotor cukup baik untuk menstart berbagai beban yang dijumpai dalam aplikasi industri. Slip motor ini < =5 %.
Effisiensi dan faktor dayanya pada saat berbeban penuh tinggi sehingga disain ini merupakan yang paling populer. Aplikasinya dapat dijumpai pada pompa, kipas
angin/ fan, dan peralatan – peralatan mesin.
3. Kelas C : memiliki torsi start lebih tinggi (200 % dari nilai ratingnya) dari dua disain yang sebelumnya. Aplikasinya dijumpai pada beban – beban seperti konveyor, mesin
penghancur (crusher ), komperessor,dll. Operasi dari motor ini mendekati kecepatan penuh tanpa overload dalam jumlah besar. Arus startnya rendah, slipnya < = 5 %
4. Kelas D : memiliki torsi start yang paling tinggi. Arus start dan kecepatan beban penuhnya rendah. Memiliki nilai slip yang tinggi ( 5 -13 % ), sehingga motor ini cocok untuk aplikasi dengan perubahan beban dan perubahan kecepatan secara
Gambar 2.22. Karakteristik torsi-kecepatan motor induksi pada berbagai disain
2.10 Penentuan Parameter Motor Induksi
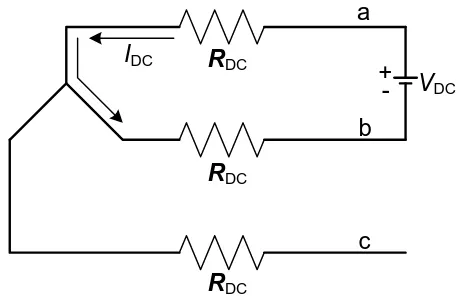
2.10.1 Percobaan DC
Untuk memperoleh harga R dilakukan dengan pengukuran DC yaitu dengan 1
menghubungkan sumber tegangan DC (VDC) pada dua terminal input dan arus DC-nya (IDC) lalu diukur. Di sini tidak mengalir arus rotor karena tidak ada tegangan yang terinduksi.
1. Kumparan hubungan Wye (Y)
Gambar rangkaian ketika kumparan motor induksi tiga phasa terhubung Y, dan diberi suplai DC dapat dilihat pada Gambar 2.23 di bawah ini.
a
b
c
RDC
RDC
RDC
VDC +
-IDC
Gambar 2.23 Rangkaian phasa stator saat pengukuran DC hubungan Y
Harga R1DC dapat dihitung, untuk kumparan dengan hubungan Y, adalah sebagai
2. Kumparan Hubungan Delta (∆)
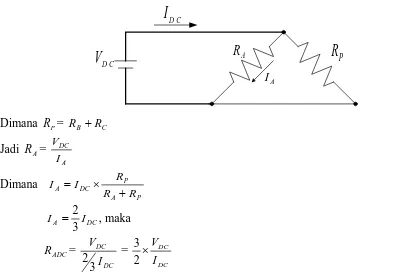
Gambar rangkaian ketika kumparan motor induksi tiga phasa terhubung delta dan diberi suplai DC, dapat dilihat pada Gambar 2.24 di bawah ini.
Gambar 2.24 Rangkaian phasa stator saat pengukuran DC hubungan delta
Diketahui bahwa tahanan pada kumparan pada masing – masing phasa adalah sama, maka
R R R
RA = B = C = . Jadi gambar diatas dapat disederhanakan menjadi gambar berikut.
A
Harga R1 ini dinaikkan dengan faktor pengali 1,1-1,5 untuk operasi arus bolak-balik, karena pada operasi arus bolak-balik resistansi konduktor meningkat karena distribusi arus yang
DC
ac k R
R1 = × 1 ( Ohm )...(2.37)
Dimana k =faktor pengali, besarnya 1,1 – 1,5
Karena besar tahanan konduktor stator dipengaruhi oleh suhu, dan biasanya bila rugi-rugi motor ditentukan dengan pengukuran langsung pada motor, maka untuk mengetahui nilai tahanan yang paling mendekati, biasanya dilakukan dengan beberapa kali pengukuran dan
mengambil besar rata-rata dari semua pengukuran yang dilakukan.
2.10.2 Percobaan Beban Nol
Motor induksi dalam keadaan beban nol dibuat dalam keadaan berputar tanpa
memikul beban pada rating tegangan dan frekuensinya. Besar tegangan yang digunakan ke
belitan stator perphasanya adalah V ( tegangan nominal), arus masukan sebesar1 I dan 0
dayanya P . Nilai ini semua didapat dengan melihat alat ukur pada saat percobaan beban nol. 0
Dalam percobaan beban nol, kecepatan motor induksi mendekati kecepatan
sinkronnya. Dimana besar s 0, sehingga
s R'
2
~ sehingga besar impedansi total bernilai
tak berhingga yang menyebabkan arus I'2 pada Gambar 2.24 bernilai nol sehingga rangkaian ekivalen motor induksi pada pengukuran beban nol ditunjukkan pada Gambar 2.25.
Namun karena pada umumnya nilai kecepatan motor pada pengukuran ini n yang diperoleh r0
tidak sama dengan ns maka slip tidak sama dengan nol sehingga ada arus I2’ yang sangat kecil
mengalir pada rangkaian rotor, arus I'2 tidak diabaikan tetapi digunakan untuk menghitung
rugi – rugi gesek + angin dan rugi – rugi inti pada percobaan beban nol. Pada pengukuran ini
didapat data-data antara lain : arus input (I1=I ), tegangan input (V0 1 = V ), daya input 0
perphasa (P0) dan kecepatan poros motor (n ). Frekuensi yang digunakan untuk eksitasi r0
Gambar 2.25 Rangkaian ekivalen pada saat berbeban
Gambar 2.26 Rangkaian ekivalen pada saat beban nol
Dengan tidak adanya beban mekanis yang terhubung ke rotor dan tegangan normal
diberikan ke terminal, dari Gambar 2.25 didapat besar sudut phasa antara arus antara I dan 0
0
E1 =V1∠0o −(Iϕ∠θ0)(R1+ jX1) (Volt )...(2.39)
ro
n adalah kecepatan rotor pada saat beban nol. Daya yang didissipasikan oleh Rc
dinyatakan dengan :
2 1
R didapat pada saat percobaan dengan tegangan DC.
Harga Rc dapat ditentukan dengan
jauh lebih besar dari X , sehingga impedansi yang didapat dari percobaan beban nol m
dianggap jX dan 1 jX yang diserikan. m
2.10.3 Percobaan Rotor Tertahan
Pada pengukuran ini rotor dipaksa tidak berputar (n = 0, sehingga s = 1) dan r
kumparan stator dihubungkan dengan tegangan seimbang. Karena slip s = 1, maka pada
Gambar 3.2, harga '2
R dapat diabaikan. Sehingga rangkaian ekivalen motor induksi dalam keadaan rotor
jX1+jX’2
R1 + R’2
V1
I1
Gambar 2.27 Rangkaian ekivalen pada saat rotor tertahan (s = 1)
Impedansi perphasa pada saat rotor tertahan (ZBR) dapat dirumuskan sebagai berikut:
ZBR =R1 +R2' + j(X1+X2')=RBR + jXBR( Ohm )...(2.44)
Pengukuran ini dilakukan pada arus mendekati arus rating motor. Data hasil pengukuran ini
meliputi : arus input (I1 =IBR), tegangan input (V1 = V ) dan daya input perphasa ( BR P = PBR in
). Karena adanya distribusi arus yang tidak merata pada batang rotor akibat efek kulit, harga
'
2
R menjadi tergantung frekuensi. Maka umumnya dalam praktek, pengukuran rotor tertahan
dilakukan dengan mengurangi frekuensi eksitasi menjadi fBR untuk mendapatkan harga R 2'
yang sesuai dengan frekuensi rotor pada saat slip rating. Dari data-data tersebut, harga RBR
dan XBR dapat dihitung :
2 1 BR BR
I P
R = (Ohm )...(2.45)
RBR =R1 +R2'(Ohm )...(2.46)
BR BR BR
I V
Z = (Ohm )...(2.47)
XBR = ZBR2 −RBR2 (Ohm )...(2.48)
Untuk menentukan harga X1 dan X2 digunakan metode empiris berdasarkan IEEE standar 112. hubungan X1 dan X2 terhadap Xbr dapat dilihat pada Tabel 2.1
Disain Kelas Motor
X1 X 2'
A 0,5 Xbr 0,5 Xbr
B 0,4 Xbr 0,6 Xbr
C 0,3 Xbr 0,7 Xbr
D 0,5 Xbr 0,5 Xbr
Rotor Belitan 0,5 Xbr 0,5 Xbr
di sini besar XBR harus disesuaikan dahulu dengan frekuensi rating f.
'BR XBR f
f X
BR
= (Ohm )...(2.49)
BAB III
MOTOR INDUKSI SEBAGAI GENERATOR
III.1 Umum
Mesin induksi dapat dioperasikan sebagai motor maupun sebagai generator. Bila dioperasikan sebagai motor, mesin induksi harus dihubungkan dengan sumber tegangan (
jala – jala ) yang akan memberikan energi mekanis pada mesin tersebut dengan mengambil arus eksitasi dari jala – jala dan mesin bekerja dengan slip lebih besar dari nol sampai satu ( 0 ≤ s ≤ 1 ).
Jika mesin dioperasikan sebagai generator, maka diperlukan daya mekanis untuk memutar rotornya searah dengan arah medan putar melebihi kecepatan sinkronnya dan
sumber daya reaktif untuk memenuhi kebutuhan arus eksitasinya. Kebutuhan daya reaktif dapat diperoleh dari jala – jala atau dari suatu kapasitor. Tanpa adanya daya reaktif, mesin induksi yang dioperasikan sebagai generator tidak menghasilkan tegangan. Jika generator
induksi terhubung dengan jala – jala, maka kebutuhan daya reaktif diambil dari jala – jala. Namun, bila generator induksi tidak tehubung dengan jala – jala, maka kebutuhan daya
reaktif dapat disediakan dari suatu unit kapasitor. Kapasitor tersebut dihubungkan paralel dengan terminal keluaran generator. Kapasitor yang terpasang harus mampu memberikan daya reaktif yang dibutuhkan untuk menghasilkan fluksi di celah udara. Karena generator
dapat melakukan eksitasi sendiri maka generator tersebut dinamakan generator induksi penguatan sendiri. Mesin induksi yang beroperasi sebagai generator ini bekerja dengan slip
III.2 Syarat – Syarat Motor Induksi Sebagai Generator
Motor induksi tiga phasa dapat dioperasikan sebagai generator dengan cara memutar
rotor pada kecepatan di atas kecepatan medan putar ( nr > ns ) dan atau mesin bekerja pada slip negatip ( s < 0 ).
ns =
p f
120
………...………...( 3.1 )
dengan :
ns : Kecepatan medan putar, rpm
f : Frekuensi sumber daya, Hz p : Jumlah kutub motor induksi. Sehingga ;
s =
s r s
n n n −
. 100 % , nr > ns………...……...………..( 3.2 )
dengan : s : slip
ns : Kecepatan medan putar, rpm nr : Kecepatan putar rotor, rpm
Karena Motor Induksi Sebagai Generator ( MISG ) ini bekerja stand alone maka mesin ini memerlukan kapasitor untuk membangkitkan arus eksitasi. Fungsi pemasangan
III.3 Slip
Selisih antara kecepatan rotor dengan kecepatan sinkron disebut slip ( s ). Slip dapat
dinyatakan dalam putaran setiap menit, tetapi lebih umum dinyatakan sebagai persen dari kecepatan sinkron.
Slip ( s ) =
s r s
n n n −
x 100 %...( 3.3 )
dimana:
nr = kecepatan rotor ( rpm )
ns = kecepatan sinkron ( rpm )
Apabila nr < ns, ( 0 < s < 1 ), kecepatan dibawah sinkron akan menghasilkan kopel, rotor dijalankan dengan mempercepat rotasi medan magnet, tenaga listrik diubah ke tenaga
gerak ( daerah motor ).
Bila nr = ns, ( s = 0 ), tegangan tidak akan terinduksi dan arus tidak akan mengalir pada
belitan rotor, sehingga tidak akan dihasilkan kopel.
Bila nr > ns, ( s < 0 ), kecepatan di atas sinkron, rotor dipaksa berputar lebih cepat daripada medan magnet. Tenaga gerak diubah ke tenaga listrik ( daerah generator ).
s = 1, rotor ditahan, tidak ada transfer tenaga.
s > 1, kecepatan terbalik, rotor dipaksa bekerja melawan medan magnet ( daerah
pengereman ).
III.4 Frekuensi Rotor
Kecepatan dan jumlah kutub derajat ac menentukan frekuensi tegangan yang dibangkitkan. Jika generator mempunyai dua kutub ( utara dan selatan ) dan kumparan
f =
120 pn
………...………( 3.4 )
dimana :
f = Frekuensi tegangan yang diinduksikan ( Hz )
p = jumlah kutub pada rotor
n = kecepatan rotor per menit ( r / menit )
Besarnya tegangan yang di bangkitkan tergantung pada kecepatan pada garis medan magnet yang dipotong atau dalam hal generator ac, besarnya tegangan tergantung pada kuat medan dan kecepatan rotor. Karena sebagian besar dioperasikan pada kecepatan konstan,
jumlah GGL yang dibangkitkan menjadi tergantung pada penguatan medan.
III.5 Prinsip Kerja Generator Induksi Penguatan Sendiri
Gambar 3.1. Prinsip kerja generator induksi penguatan sendiri
Pada mesin induksi tidak terdapat hubungan listrik antara stator dengan rotor, karena arus pada rotor merupakan arus induksi. Jika belitan stator diberi tegangan tiga phasa, maka
pada stator akan dihasilkan arus tiga phasa, arus ini kemudian akan menghasilkan medan magnet yang berputar dengan kecepatan sinkron ( ns ) dan kemudian akan melakukan
untuk mensuplai tegangan ke stator nanti untuk mempertahankan kecepatan sinkron ( ns ) motor induksi pada saat dilakukan pelepasan sumber tegangan tiga phasa pada stator.
Mesin dc sebagai prime mover yang dikopel dengan mesin induksi diputar secara perlahan memutar rotor mesin induksi hingga mencapai putaran sinkronnya ( nr = ns ). Saklar
sumber tegangan tiga phasa untuk stator dilepas, dan kapasitor yang sudah discharge akan bekerja dan akan mempertahankan besar ns. Motor dc diputar hingga melewati kecepatan putaran sinkronnya mesin induksi ( nr > ns ), sehingga slip yang timbul antara putaran rotor
dan putaran medan magnet menghasilkan slip negatif ( s < 0 ) dan akan menghasilkan tegangan sehingga motor induksi akan berubah fungsi menjadi generator induksi.
Gambar 3.2. Karakteristik torsi – kecepatan mesin induksi
Dari kurva karakteristik antara kecepatan dan kopel motor induksi dapat dilihat, jika sebuah motor induksi dikendalikan agar kecepatannya lebih besar daripada kecepatan sinkron oleh penggerak mula, maka arah kopel yang terinduksi akan terbalik dan akan beroperasi
tegangan pada saat putaran rotor ( nr ) sedikit lebih cepat dari putaran sinkron (ns) mesin induksi tersebut.
Pada motor induksi yang dioperasikan sebagai generator tidak terdapat pengatur tegangan seperti governor pada generator sinkron. Oleh karena itu tegangan keluaran sangat
dipengaruhi oleh beban dan nilai kapasitor.
III.6 Kapasitor Eksitasi
Kapasitor adalah suatu peralatan listrik untuk menyimpan muatan listrik. Konstruksi kapasitor pada umumnya terdiri dari dua buah konduktor yang berdekatan namun dipisahkan
oleh bahan elektrik.
Kapasitor eksitasi adalah kapasitor yang digunakan sebagai penghasil daya reaktif pada generator induksi. Besar kapasitor eksitasi dapat diperoleh dengan cara perhitungan.
Penentuan besar nilai kapasitor eksitasi dapat diperoleh dengan persamaan di bawah ini. ∆Q = V.I ………...………….( 3.5 )
= V.
c
X V
=
Xc V2
………, Xc =
fC
π
2 1
∆Q = V2.2π. f. C ………...……( 3.6 )
C = f V
Q π
2
2
∆ …………...……….( 3.7 )
Dimana :
∆Q : jumlah daya reaktif yang diperlukan (VAR)
C : kapasitansi kapasitor adalah suatu kemampuan kapasitor untuk
III.7 Pemasangan Kapasitor
Untuk sistem 3 phasa, kapasitor dapat dihubungkan dalam dua bagian yaitu:
1. Hubungan delta (∆) 2. Hubungan wye (Y)
III.7.1 Kapasitor Hubungan Delta ( ∆ )
•
•
•
•
∆
c
V
∆
C
I
Gambar 3.3. Kapasitor terhubung delta
Apabila dihubungkan dengan hubungan delta ( ∆ ) maka besar kapasitansi kapasitor adalah:
C∆ perphasa =
f V
Q π
2 3 2
∆ ( Farad )….……..………...……....( 3.8)
III.7.2 Kapasitor Hubungan Wye ( Y )
•
•
•
•
•
•
•
•
CY
V
I
CYApabila dihubungkan dengan hubungan bintang ( Υ ) maka besar kapasitansi
Dari kedua hubungan kapasitor diatas, maka diperoleh persamaan untuk kapasitor terhubung bintang dan delta sebagai berikut :
Untuk kapasitor yang terhubung bintang, kapasitor yang dibutuhkan tiga kali
kapasitor yang terhubung delta.
III.8 Proses Pembangkitan Tegangan dan Rangkaian Ekivalen Generator Induksi
Syarat utama terbangkitnya tegangan generator induksi adalah adanya remanensi di rotor atau kapasitor eksitasi yang digunakan harus mempunyai muatan listrik terlebih dahulu.
Remanensi atau muatan kapasitor merupakan tegangan awal yang diperlukan untuk proses pembangkitan tegangan selanjutnya. Proses pembangkitan tegangan akan terjadi bila salah satu syarat di atas dipenuhi. Gambar 3.5 memperlihatkan rangkaian proses pembangkitan
E2 E1
C eksitasi beban
rotor stator
Gambar 3.5 Rangkaian proses pembangkitan tegangan
Dari gambar 3.5 dapat dibuat rangkaian ekivalen per phasa generator induksi seperti gambar 3.6.
Xm s
R
X
R X
I
Xc
Ic E1
b
e
b
a
n
V 2
2
1 1
1
IL
Gambar 3.6. Rangkaian ekivalen perfasa generator induksi
Dimana :
R1 = tahanan stator IL = arus beban
R2 = tahanan rotor s = slip
X1 = reaktansi stator v = tegangan keluaran (phasa-netral) X2 = reaktansi rotor
Xm = reaktansi magnetisasi XC = reaktansi kapasitansi
Dengan menghubungkan kapasitor di terminal stator, akan terbentuk suatu rangkaian tertutup. Dengan adanya tegangan awal tadi, di rangkaian akan mengalir arus. Arus tersebut
akan menghasilkan fluksi di celah udara, sehingga di stator akan terbangkit tegangan induksi sebesar E1. Tegangan E1 ini akan mengakibatkan arus mengalir ke kapasitor sebesar I1.
Dengan adanya arus sebesar I1, akan menambah jumlah fluksi di celah udara, sehingga tegangan di stator menjadi E2. Tegangan E2 akan mengalirkan arus di kapasitor sebesar I2 yang akan menyebabkan fluksi bertambah dan tegangan yang dibangkitkan juga akan
meningkat. Proses ini terjadi sampai mencapai titik keseimbangan E = VC seperti ditunjukkan dalam gambar 3.7. Dalam kondisi ini tidak terjadi lagi penambahan fluksi ataupun tegangan
yang dibangkitkan.
Gambar 3.7. Proses pembangkitan tegangan.
Nilai kapasitor yang dipasang sangat menentukan terbangkitnya tegangan atau tidak. Untuk terbangkitnya tegangan generator induksi, nilai kapasitor yang dipasang harus lebih
III.9 Pengaruh Pembebanan Terhadap Arus Eksitasi
Dari gambar rangkaian ekivalen gambar 3.6, hubungan antara tegangan keluaran
dengan arus stator diperlihatkan pada persamaan berikut :
V = E1 – I1 ( R1 + jX1 ) ………...……( 3.12 )
I1 = IC + IL …...…………..………...………..( 3.13 ) dimana,
V = tegangan keluaran generator ( Volt )
E1 = ggl induksi yang dibangkitkan pada stator ( Volt ) I1 = arus stator ( Ampere )
IL = arus beban ( Ampere )
Dari persamaan ( 3.12 ) diatas dapat digambarkan diagram vektor tegangan generator induksi, seperti gambar 3.8.
Gambar 3.8. Diagram vektor tegangan generator induksi
Tegangan keluaran generator tergantung kepada antara lain komponen magnetisasi
arus stator I1. Tanpa adanya beban yang mampu memberikan arus maknetisasi ini, tegangan keluaran generator ini akan hilang. Dalam generator induksi penguatan sendiri, beban yang
dimaksudkan dipenuhi dengan pemasangan kapasitor eksitasi pada terminal generator.
III.10 Aliran Daya Nyata Generator Induksi Penguatan Sendiri I 2
I 1
I' 2
E' 2 = E1
I m I o
IRC
I2 R2
E2S jI2X2S
-I 1 R
1
-jI1 X1 V
Diagram aliran daya nyata dan rugi-rugi daya generator induksi penguatan sendiri ditunjukkan dengan gambar 3.9.
Gambar 3.9. Diagram aliran daya nyata
Rugi-rugi gesekan dan angin Pg+a, rugi-rugi inti stator Pi biasanya dianggap konstan
dan disebut rugi-rugi beban nol. Sedangkan rugi-rugi tembaga stator dan rotor tidak tetap dan besarnya sangat tergantung kepada arus beban. Diagram aliran daya dan rugi-rugi daya nyata generator induksi dapat dinyatakan dengan persamaan-persamaan sebagai berikut :
P1 = Pmek - Pg+a………...…………...(3.14) Pc = P1 - Pcu2………..…...……….(3.15)
P2 = Pc – Pcu1 – Pi………..………...…….(3.16) dengan :
P1 = daya masukan rotor (Watt)
P2 = daya keluaran stator (Watt) Pmek = daya mekanis dari prime mover (Watt)
Pg+a = rugi-rugi gesek dan angin (Watt) Pi = rugi-rugi inti stator (Watt) Pc = daya pada celah udara (Watt)
III.11 Efisiensi
Sama halnya dengan mesin – mesin listrik yang lain, pada motor induksi sebagai
generator rugi – rugi terdiri dari rugi – rugi tetap dan rugi – rugi variabel. Pada kondisi beban nol daya outputnya sama dengan nol, sehingga efisiensi bernilai nol. Apabila motor induksi
berbeban ringan, maka rugi – rugi tetap akan lebih besar jika dibandingkan terhadap outputnya, sehingga efisiensi rendah. Jika beban meningkat, maka efisiensinya juga akan meningkat dan akan menjadi maksimum sewaktu rugi – rugi variabel sama dengan rugi – rugi
inti. Efisiensi maksimum terjadi saat 80 hingga 95 persen dari rated output. Jika beban ditingkatkan secara terus – menerus hingga melampaui efisiensi maksimumnya rugi – rugi
beban akan meningkat dengan sangat cepat daripada outputnya, sehingga efisiensi menurun.
III.12 Persamaan Tegangan, Arus dan Daya Pada Generator Induksi Penguatan
Sendiri
Berdasarkan rangkaian ekivalen perfasa generator induksi maka dapat dibentuk
persamaan – persamaan sebagai berikut.
arus stator (I1)
……...( 3.17 )
arus beban (IL)
………...( 3.18 )
tegangan Beban (VL) = IL ( RL + j XL ) ………..……...( 3.19 ) Daya Output Perfasa ( Pout ) = IL2 RL ………...( 3.20 )
VR ( % ) =
FL L F NL
V V
V −
BAB IV
ANALISA PERBANDINGAN PENGARUH
BESAR KAPASITOR EKSITASI TERHADAP
REGULASI DAN EFISIENSI PADA MOTOR INDUKSI
SEBAGAI GENERATOR PENGUATAN SENDIRI
IV.1 Umum
Untuk dapat melihat bagaimana pengaruh besar nilai kapasitor eksitasi terhadap regulasi dan efisiensi pada motor induksi sebagai generator penguatan sendiri, maka diperlukan beberapa pengujian. Pengujian tersebut adalah:
1. Pengujian tahanan stator DC
2. Pengujian motor induksi sebagai generator dalam keadaan berbeban dan tidak berbeban
Parameter mesin yang diperlukan adalah Tahanan stator R1. Parameter tersebut digunakan untuk menghitung nilai rugi-rugi tembaga stator. Parameter tersebut diperoleh melalui pengukuran langsung dengan pengujian tegangan DC. Penelitian ini dimaksudkan untuk melihat pengaruh pembebanan terhadap regulasi tegangan dan efisiensi pada generator induksi penguatan sendiri. Dalam percobaan ini digunakan beban jenis lampu pijar yang dirangkai sedemikian rupa dan dengan menggunakan saklar sehingga besar beban dapat diubah-ubah sesuai dengan tujuan penelitian.
IV.2 Peralatan Yang Digunakan
Peralatan yang digunakan dalam penelitian motor induksi sebagai generator induksi penguatan sendiri di laboratorium adalah sebagai berikut :
1. Motor induksi 3 fasa (berfungsi sebagai generator) Tipe : Rotor sangkar tupai (squirrel cage)
Spesifikasi :
- AEG Typ B AL 90 LA - 4 - ∆ / Y 220/ 380 V ; 6,3/ 3,6 A - 1,5 kW, cos ϕ 0,82