Perbandingan Hasil Akurasi Prediksi Model Regresi Logistik Spasial untuk Berbagai Model Variogram

(1)

ABSTRAK

Status kemiskinan desa dipengaruhi oleh faktor-faktor potensi desa yang bersangkutan dan diduga terdapat potensi spasial antar desa. Pengaruh spasial tersebut perlu diakomodir dalam model. Hubungan antara status kemiskinan desa dengan faktor-faktor potensi desa dapat dimodelkan dengan regresi logistik. Keragaman spasial status kemiskinan desa dimodelkan dengan empat model variogram (exponential, power, spherical, dan gaussian). Melalui model variogram maka informasi spasial dimasukkan ke dalam regresi logistik untuk memperbaiki keakuratan hasil prediksi.

(2)

PERBANDINGAN HASIL AKURASI PREDIKSI MODEL REGRESI

LOGISTIK SPASIAL UNTUK BERBAGAI MODEL VARIOGRAM

Vinda Pratama

G14104042

DEPARTEMEN STATISTIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(3)

This thesis is especially dedicated to my beloved father, Agus Dadang S.

I hope with this thesis you would be proud to me as you’re daughter

I am really proud to be you’re daughter

(4)

ABSTRAK

Status kemiskinan desa dipengaruhi oleh faktor-faktor potensi desa yang bersangkutan dan diduga terdapat potensi spasial antar desa. Pengaruh spasial tersebut perlu diakomodir dalam model. Hubungan antara status kemiskinan desa dengan faktor-faktor potensi desa dapat dimodelkan dengan regresi logistik. Keragaman spasial status kemiskinan desa dimodelkan dengan empat model variogram (exponential, power, spherical, dan gaussian). Melalui model variogram maka informasi spasial dimasukkan ke dalam regresi logistik untuk memperbaiki keakuratan hasil prediksi.

(5)

PERBANDINGAN HASIL AKURASI PREDIKSI MODEL REGRESI

Oleh :

Vinda Pratama

G14104042

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

DEPARTEMEN STATISTIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

(6)

Judul Skripsi : Perbandingan Hasil Akurasi Prediksi Model Regresi Logistik

Spasial untuk Berbagai Model Variogram

Nama

: Vinda Pratama

NRP

: G14104042

Menyetujui :

Pembimbing I, Pembimbing II,

Utami Dyah Syafitri, M.Si Bagus Sartono, M.Si

NIP. 132311922 NIP. 132311923

Mengetahui :

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Dr. Drh. Hasim, DEA

NIP. 131578806

(7)

RIWAYAT HIDUP

Penulis dilahirkan di Bogor, pada tanggal 3 September 1987 dari pasangan Agus Dadang S. dan Yulfitrawasih. Penulis dikaruniai seorang adik laki-laki yang bernamakan Taufik Hidayat.

Pendidikan penulis berawal dari TK. Kemuning Bogor dan lulus pada tahun 1993, kemudian dilanjutkan pendidikan formal di SD. Bina Insani Tanah Sareal Bogor pada tahun 1993 sampai tahun 1999. Penulis menyelesaikan pendidikan di SLTP Negeri 6 Bogor pada tahun 2002 dan syukur Alhamdulillah pada tahun 2002 penulis diterima sebagai salah satu siswi di SMA Negeri 3 Bogor program akselerasi angkatan pertama di Kota Bogor yang lulus pada tahun 2004. Pada tahun yang sama penulis di terima sebagai mahasiswa di Departemen Statistika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor melalui jalur Undangan Seleksi Masuk IPB (USMI).

(8)

KATA PENGANTAR

Alhamdulillahirabbil’alamin, segala puji dan rasa syukur penulis panjatkan kehadirat Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini dapat terselesaikan. Shalawat serta salam semoga senantiasa tercurahkan kepada suri tauladan manusia Rasulullah Muhammad SAW beserta keluarga, sahabat, dan umatnya. Karya ilmiah ini memiliki tema perbaikan terhadap model regresi logistik dan berjudulkan “Perbandingan Hasil Akurasi Prediksi Model Regresi Logistik Spasial untuk Berbagai Model Variogram”.

Pada kesempatan ini, penulis ingin menyampaikan ucapan terima kasih kepada semua pihak yang telah berperan serta dalam penyusunan karya ilmiah ini, terutama kepada :

1. Ibu Utami Dyah Syafitri, M.Si dan Bapak Bagus Sartono, M.Si selaku pembimbing yang senantiasa memberikan bimbingan dan saran yang sangat membangun.

2. Mama dan Papa yang sangat penulis idolakan, terima kasih atas doa, cinta, dan kasih sayang yang telah diberikan. My lovely brother Taufik Hidayat, makasih untuk kenakalan dan keceriaannya. Randy Ramadhan Jeanero, terima kasih untuk semangat, dukungan and for cheerful days.

3. Sahabat-sahabat, teman-teman statistika 41 dan adik-adik statistika 42 for the unforgettable moments we spent since first term.

4. Seluruh staf pengajar Departemen Statistika FMIPA IPB, Bu Markonah, Bu Sulis, Bu Dedeh, Bu Aat, Mang Dur, dan Mang Herman yang selalu setia mendampingi dan membantu segala keperluan yang menyangkut penyelesaian karya ilmiah ini. 5. Terima kasih kepada Departemen Statistika IPB yang telah membiayai karya ilmiah

ini dalam rangka program hibah PHK A2 Departemen Statistika FMIPA IPB tahun 2007.

Semoga semua amal baik dan bantuan yang diberikan kepada penulis mendapatkan balasan dari Allah SWT, dan semoga karya ilmiah ini dapat bermanfaat bagi semua pihak yang membutuhkan.

Bogor, Agustus 2008

(9)

DAFTAR ISI

Halaman

DAFTAR TABEL... i

DAFTAR GAMBAR ... ii

DAFTAR LAMPIRAN ... iii

PENDAHULUAN Latar Belakang ... 1

Tujuan... 1

Kerangka Pikir... 1

TINJAUAN PUSTAKA Regresi Logistik Spasial ... 2

Variogram... 2

Generalized Inverse Matrices...4

BAHAN DAN METODE Bahan... 4

Metode... 5

PEMBAHASAN Deskripsi Data ... 5

Pemodelan Regresi Logistik Klasik ... 6

Model Variogram Status Kemiskinan Desa ... 7

Pembuatan Matriks Pembobot Spasial ... 7

Dugaan Model Regresi Logistik Spasial ... 8

KESIMPULAN ... 10

DAFTAR PUSTAKA ... 10

(10)

DAFTAR TABEL

1.

Daftar nama kota dan kabupaten yang digunakan... 4

2.

Peubah penjelas yang digunakan ... 4

3.

Distribusi jumlah keluarga miskin berdasarkan kabupaten / kota ... 5

4.

Distribusi jumlah desa berdasarkan kabupaten / kota ... 6

5.

Nilai dugaan koefisien untuk model regresi logistik klasik ... 6

6.

Karakteristik desa miskin dan desa tidak miskin ... 6

7.

Nilai dugaan parameter model variogram ... 7

8.

Nilai dugaan koefisien regresi logistik dari model klasik dan model spasial menggunakan matriks pembobot spasial dari 1/Vij... 8

9.

Nilai dugaan koefisien regresi logistik dari model klasik dan model spasial menggunakan matriks pembobot spasial (V)-... 9

DAFTAR GAMBAR

1.

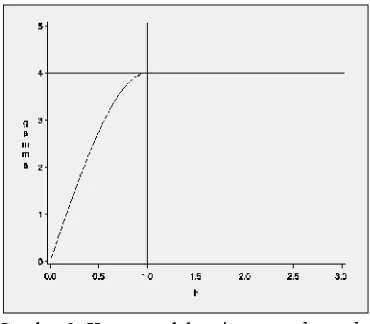
Kurva model variogram exponensial dengan a = 1 dan c = 4 ... 3

2.

Kurva model variogram power dengan  = 0.4 dan dan p=4... 3

3.

Kurva model variogram spherical dengan a = 1 dan c = 4 ... 3

4.

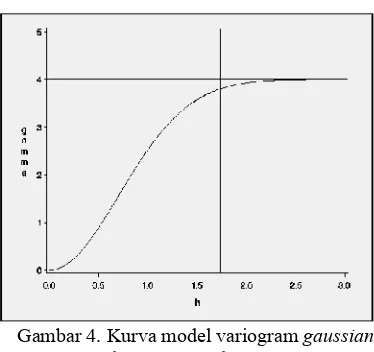
Kurva model variogram gaussian dengan a = 1 dan c= 4 ... 3

5.

Bagan Alur Penelitian ... 5

6.

Plot antar jarak (h) dengan nilai variogramnya ... 7

7.

Plot dugaan dari masing-masing model variogram ... 7

8.

Perbandingan nilai c-statistic model regresi logistik klasik dengan model regresi logistik spasial untuk berbagai model variogram... 9

9.

Perbandingan hasil correct classification rate model regresi logistik klasik dengan model regresi logistik spasial untuk berbagai model variogram ... 10

(11)

1

PENDAHULUAN Latar Belakang

Penggunaan model regresi logistik telah berkembang pesat seiring dengan kemajuan ilmu pengetahuan. Dalam beberapa kasus, nilai peubah respon yang digunakan tidak bebas terhadap nilai-nilai di sekitarnya. Menurut Frei (2005) pola seperti ini dinyatakan sebagai autokorelasi spasial. Adanya hubungan spasial dalam peubah respon model regresi logistik akan menyebabkan pendugaan menjadi tidak tepat karena asumsi kebebasan galat dilanggar.

Berdasarkan permasalahan di atas diperlukan modifikasi terhadap model regresi logistik yang telah ada, yaitu dengan memasukkan hubungan spasial ke dalam model. Terdapatnya hubungan spasial antar daerah maka perlu mengakomodir keragaman spasial tersebut yang mengarah kepada regresi logistik spasial.

Keragaman spasial salah satunya dapat dimodelkan dengan variogram. Cressie (1993) dan Bohling (2005) menyebutkan bahwa terdapat empat model variogram, yaitu: exponential, power, spherical, dan gaussian. Sehingga dalam penelitian ini dicobakan beberapa model variogram tersebut untuk mengakomodir keragaman spasial yang kemudian akan digunakan untuk perbaikan pendugaan dalam regresi logistik.

Penelitian ini menggunakan studi kasus pendugaan status kemiskinan pada sebagian desa di Jawa Barat. Status kemiskinan di suatu desa tidak berdiri sendiri, tetapi dipengaruhi oleh kondisi desa lainnya (terdapat pengaruh spasial).

Tujuan

Tujuan dari penelitian ini adalah :

1. Mengetahui faktor-faktor yang berperan terhadap status kemiskinan sebagian desa di Jawa Barat dengan menggunakan regresi logistik.

2. Pemodelan regresi logistik spasial dengan menggunakan matriks pembobot yang berasal dari beberapa model variogram (studi kasus pendugaan status kemiskinan pada sebagian desa di Jawa Barat). Model variogram yang digunakan yaitu: exponential, power, spherical, dan gaussian.

3. Membandingkan tingkat akurasi hasil prediksi keempat model regresi logistik spasial.

Kerangka Pikir

Penelitian ini memfokuskan pada pengembangan analisis regresi logistik spasial yang kerangka berpikirnya akan disampaikan pada bagian ini. Andaikan sebuah bidang S tersekat-sekat n buah sub bidang (lokasi) yang saling lepas, yaitu s1, s2, ..., sn dengan s1 s2

 …  sn = S dan si sj = . Setiap sub-bidang si memiliki sentroid pada titik ci. Nilai pengukuran Y, X1, X2, … Xp di masing-masing sub-bidang adalahyi, x1i, x2i, … xpi.

Jika Y memiliki hubungan spasial, dan dipengaruhi oleh X1, X2, … Xp maka model yang bisa dibentuk adalah :

y

i

=

x

i

’

β

+

z

i’

y

β

* +

ε

i

...

(1)

dengan xi = (1x1i, 1x2i, …, 1xpi)’ adalah vektor

p x 1 yang berisi nilai-nilai pengamatan peubah X1, X2, … Xp pada sub-bidang si dan y’= (y1, y2 … yn) adalah nilai-nilai pengamatan peubah Y dari seluruh lokasi. Vektor z berukuran n x 1 menyatakan bobot spasial antar sub-bidang terhadap nilai di sub-bidang lainnya.

Menggunakan notasi matriks, model (1) dapat dituliskan sebagai

y

=

X

β

+

Zy

β

*+

ε

...(2)

pada model (2) terdapat Z yang merupakan sebuah matriks bobot spasial. Dalam pencariannya, matriks pembobot spasial ini memerlukan informasi variogram yang merupakan ukuran keragaman spasial.

Penelitian awal dalam pencarian matriks pembobot spasial telah dilakukan oleh Syafitri, dkk (2007). Dimana hasil pemodelan regresi logistik spasial dengan matriks pembobot yang berasal dari tiga model variogram (model exponential, model power, dan model spherical) relatif tidak berbeda jauh dengan regresi logistik biner. Oleh karena itu, perlu dilakukannya perubahan metode terhadap pencarian matriks pembobot spasialnya.

Matriks pembobot spasial diharapkan dapat menggambarkan pengaruh antar desa, dimana desa yang berdekatan memberikan pengaruh yang lebih besar dibandingkan dengan desa yang berjauhan. Variogram yang akan digunakan untuk menghitung matriks pembobot spasial ini menggambarkan keragaman antar daerah berdasarkan jaraknya. Semakin jauh jarak antar daerah maka keragaman yang terbentuk akan semakin besar menuju kekonvergenan. Sehingga perlu dilakukan proses pembalikan matriks variogram terlebih dahulu, yang kemudian hasil pembalikan matriks variogram yang dijadikan sebagai matriks pembobot spasial.

(12)

2

selanjutnya akan dianggap sebagai sebuah peubah penjelas baru (w) dan akan digunakan dalam analisis regresi logistik .

TINJAUAN PUSTAKA Regresi Logistik Spasial

Hosmer dan Lemeshow (1989) menjelaskan bahwa yang membedakan model regresi logistik dan model regresi linear adalah peubah hasil pada regresi logistik berskala biner atau dikhotom, sedangkan pada regresi linear peubah hasilnya berskala numerik. Model regresi logistik dengan E(Y=1|x) sebagai  (x) adalah :

) ( ) (

1

)

(

_g _x

x g

e

x







dalam regresi logistik diperlukan fungsi penghubung logit, transformasi logit sebagai fungsi dari  (x) adalah :

p p

X

x

g

























...

)

(

1

)

(

ln

)

(

₀ ₁ ₁

Terdapat dua pendekatan dasar untuk mempertimbangkan ketergantungan spasial yaitu: membangun model yang lebih kompleks dengan memasukkan struktur autoregresi dan mendesain skema sampling spasial untuk memperluas selang jarak antara tempat-tempat sampel (Xie et al, 2005).

Preisler et al. (1995) dalam Fernandez (2003) menyebutkan bahwa pendekatan dengan memasukkan hubungan spasial ke dalam model terdapat dua pendekatan yaitu memasukkan lokasi ke dalam model dan memasukkan suku autologistik.

Augustin et al. (1996) dalam Fernadez (2003) menggunakan model dalam bentuk :

   _         ) ( 1 ) ( log x x

y dengan



   k j ij k j i ij i w y w 1 1 ˆ 

model dari



merupakan bentuk dari autokovarian dan merupakan rataan terboboti dari jumlah kejadian dalam suatu lokasi ke-i yang terdiri dari k tetangganya. Pembobot dari lokasi ke-j adalah wij = 1/hij dimana hijadalah jarak euclidean antara lokasi ke-i dan ke-j. Serta yˆ adalah dugaan dari ada/tidaknya suatu kejadian.

Variogram

Analisis variogram melakukan penghitungan pada sejumlah lokasi dan melihat hubungan antar observasi pada berbagai lokasi. Variogram menghitung hubungan antara perbedaan pengukuran berpasangan dan jarak dari poin-poin yang bersesuaian satu sama lain. Variogram merupakan keragaman spasial antar lokasi dengan saling ketergantungan satu sama lain dalam ruang berdimensi m. Variogram merupakan fungsi spasial terbaik yang diketahui (Ashraf et al., 1997).

Persamaan umum untuk contoh variogram adalah (Matheron 1962, dalam Cressie 1993):









) ( 2

)

(

,

;

))

(

)

(

)

(

1

)

(

2

h N j

i

z

x

i

j

N

h

x

z

h

N

h



dengan N(h) adalah banyaknya pasangan lokasi (contoh) yang berjarak h. Variogram akan memenuhi beberapa asumsi. Misalkan terdapat gugusan nilai z(xi) pada lokasi xi, i=1,2,3, ..., n dalam ruang berdimensi m, maka asumsi yang harus terpenuhi adalah (Cressie, 1993):

1.

E

(

Z

(

x



h

)



Z

(

x

))



0

2.

Var

(

Z

(

x



h

)



Z

(

x

))



2



(

h

)

dengan h adalah jarak antara dua lokasi yang terpisah. Sifat dari variogram, adalah:

1. Monoton tidak turun 2. Bernilai positif

Variogram memiliki beberapa model yaitu (Cressie 1993 dan Bohling 2005):

1. Model exponential

Model ini menggambarkan hubungan antara variogram dengan jarak dalam bentuk persamaan :                 a h c c

h) 1 exp 3

( ₀



dengan :

c0 = intersep

(13)

3

Gambar 1. Kurva model variogram exponentialdengan a = 1 dan c = 4

2. Model Power

Hubungan antara variogram dengan jarak untuk model power dibentuk dalam persamaan sebagai berikut :



(

h

)



c

_o



ph

, dengan 0 < α < 2 dengan :

c0 = intersep

p = kemiringan kurva h = jarak antar pengamatan Jika diketahui  = 0.4 dan dan p=4 untuk persamaan tersebut maka kurva yang terbentuk dapat dilihat pada Gambar 2.

Gambar 2. Kurva model variogram power dengan = 0.4 dan dan p=4 3. Model spherical

Bentuk persamaan untuk model spherical dalam menggambarkan hubungan antara variogram dengan jarak adalah sebagai berikut:

a

h

a

h

a

h

c

h













































,

2

3

)

(

3 3 0



a

h

c

h

)





,



(

₀



dengan :

c0 = intersep

c = ambang semi variogram (sill) a = batas pengaruh contoh h = jarak antar pengamatan Kurva model variogram spherical ketika diketahui c0= 0, a = 1 dan c = 4 secara visual dapat terlihat pada Gambar 3.

Gambar 3. Kurva model variogram spherical dengan a = 1 dan c= 4

4. Model Gaussian

Berikut ini adalah persamaan yang dibentuk oleh model Gaussian dalam menggambarkan hubungan antara variogram dengan jarak :

 























 





1

exp

3

₂2

a

h

c

h



dengan :

c = ambang semi variogram (sill) a = parameter model gaussian h = jarak antar pengamatan Gambar 4 merupakan kurva yang terbentuk dari model variogram gaussian ketika a = 1 dan c = 4.

(14)

4

Generalized Inverse Matrices

(Matriks Kebalikan Umum)

Searle (1971) menyebutkan bahwa generalized inverse dari matriks A adalah sembarang matriks G yang memenuhi persamaan:

A

AGA



Searle (1971) juga menekankan bahwa generalized inverse penting karena ini merupakan aplikasi umum untuk matriks non-square dan square, singular. Matriks A memiliki generalized inverse ketika matriksnya singular atau rectangular dalam menyelesaikan permasalahan persamaan

y

Ax



untuk x.

Ketika sebuah model dapat ditulis sebagai

e

Xb

y





, prosedur kuadrat terkecil untuk penduagaan b dapat ditunjukan dengan persamaan

X

'

X

b

ˆ



X

'

y

dimana matriks

X

' adalah singular. Oleh karena itu, solusinya tidak dapat ditulis

 

X'X 1X'y,

tetapi solusinya adalah dengan menggunakan generalized inverse dari

X

'

X

.

BAHAN DAN METODE Bahan

Bahan yang digunakan merupakan hasil survei oleh Badan Pusat Statistik tentang Potensi Desa (PODES) tahun 2006 meliputi kota dan kabupaten yang terlihat pada Tabel 1.

Tabel 1. Daftar nama kota dan kabupaten yang digunakan

Kode

Kabupaten Nama Kabupaten

Jumlah Desa

3201000000 KAB BOGOR 415

3202000000 KAB SUKABUMI 340

3203000000 KAB CIANJUR 344

3204000000 KAB BANDUNG 436

3213000000 KAB SUBANG 248

3214000000 KAB

PURWAKARTA 190

3215000000 KAB KARAWANG 304

3216000000 KAB BEKASI 179

3271000000 KOTA BOGOR 63

3272000000 KOTA SUKABUMI 33

3273000000 KOTA BANDUNG 139

3275000000 KOTA BEKASI 43

3277000000 KOTA CIMAHI 15

TOTAL 2749

Peubah-peubah yang digunakan merupakan hasil dari regresi logistik dengan menggunakan operasi bertatar dalam pemilihan peubah penjelasnya, dimana peubah respon yang digunakan adalah status kemiskinan desa (0 = tidak miskin, 1 = miskin) dan peubah penjelas yang digunakan disajikan pada Tabel 2.

Tabel 2. Peubah penjelas yang digunakan

Peubah Jenis Keterangan

Ada/tidak penduduk desa yang bekerja sebagai TKI (X1)

Kategorik 1 = ada

0 = tidak ada

Jarak dari desa ke ibukota kabupaten / kota (X2)

Numerik Satuan kilometer

(km)

Persentase keluarga yang menerima kartu sehat (X3)

Numerik Jumlah penerima

Jumlah keluarga

Persentase luas sawah (X4)

Numerik Luas lahan sawah

Luas desa / kelurahan Persentase

rumah tangga yang menggunakan listrik (X5)

Numerik

Jumlah pemakai Jumlah keluarga

Ada/tidak puskesmas di desa tersebut (X6)

Kategorik 1 = ada

0 = tidak ada

Status kemiskinan suatu desa ditentukan dari persentase keluarga miskin di masing-masing desa, dimana persentase keluarga miskin suatu desa diperoleh dari jumlah keluarga miskin suatu desa dibagi dengan jumlah keluarga secara keseluruhan di desa tersebut. Jika persentase keluarga miskin suatu desa lebih besar dari persentase keluarga miskin secara keseluruhan maka desa tersebut dikategorikan sebagai desa miskin.

(15)

5

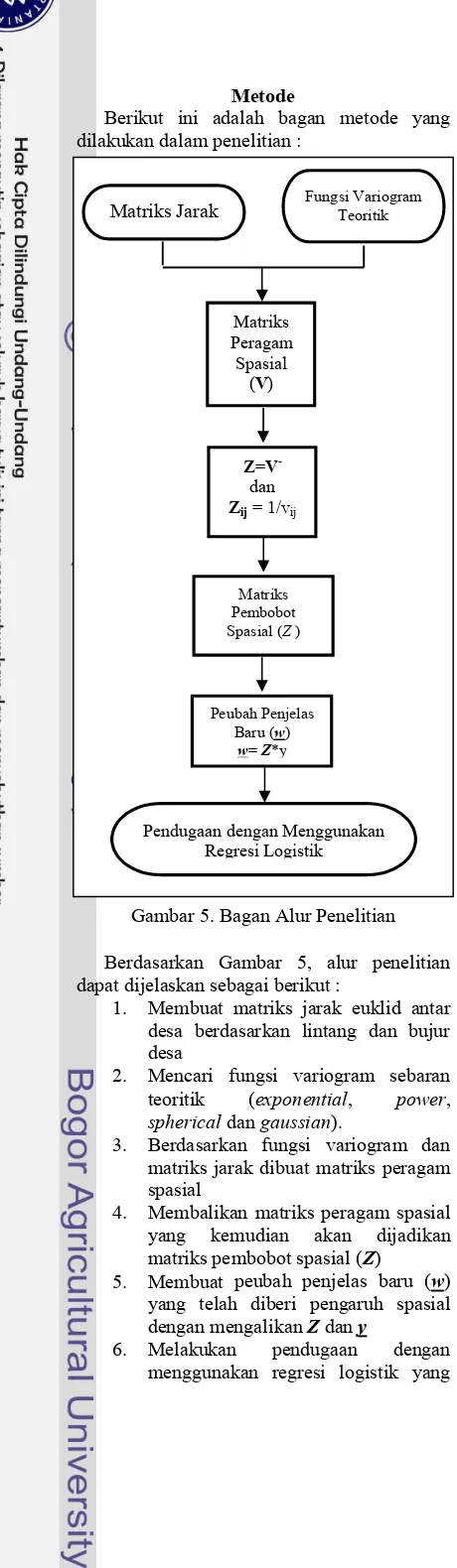
Metode

Berikut ini adalah bagan metode yang dilakukan dalam penelitian :

Gambar 5. Bagan Alur Penelitian

Berdasarkan Gambar 5, alur penelitian dapat dijelaskan sebagai berikut :

1. Membuat matriks jarak euklid antar desa berdasarkan lintang dan bujur desa

2. Mencari fungsi variogram sebaran teoritik (exponential, power, spherical dangaussian).

3. Berdasarkan fungsi variogram dan matriks jarak dibuat matriks peragam spasial

4. Membalikan matriks peragam spasial yang kemudian akan dijadikan matriks pembobot spasial (Z)

5. Membuat peubah penjelas baru (w) yang telah diberi pengaruh spasial dengan mengalikan Z dan y

6. Melakukan pendugaan dengan menggunakan regresi logistik yang

telah ditambahkan peubah penjelasnya.

7. Membandingkan hasil pendugaan regresi logistik menggunakan matriks pembobot dari model variogram exponential, power, spherical dan gaussian.

Pembandingan model dilihat dari nilai correct classification rate dan c-statistic. Perangkat lunak yang digunakan dalam penelitian ini adalah SAS ver 9.1 dan Microsoft Office Excel 2003.

PEMBAHASAN Deskripsi Data

Berdasarkan Tabel 3 dapat diketahui distribusi jumlah keluarga miskin untuk setiap kabupaten/kota. Persentase keluarga miskin untuk setiap kabupaten relatif lebih tinggi dibandingkan dengan persentase keluarga miskin di kota. Hal ini sebanding dengan jumlah keluarga di setiap kabupaten lebih banyak dibandingkan dengan jumlah keluarga di setiap kota.

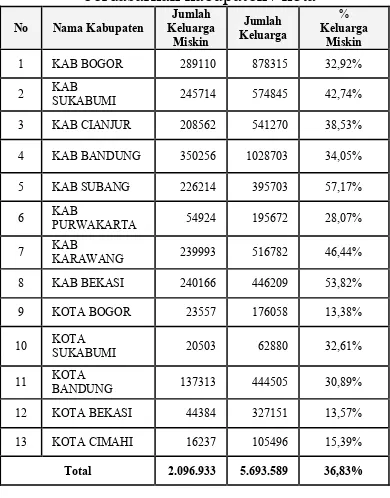
Tabel 3. Distribusi jumlah keluarga miskin berdasarkan kabupaten / kota

No Nama Kabupaten

Jumlah Keluarga Miskin

Jumlah Keluarga

%

Keluarga Miskin

1 KAB BOGOR 289110 878315 32,92%

2 KAB

SUKABUMI 245714 574845 42,74% 3 KAB CIANJUR 208562 541270 38,53%

4 KAB BANDUNG 350256 1028703 34,05%

5 KAB SUBANG 226214 395703 57,17%

6 KAB

PURWAKARTA 54924 195672 28,07% 7 KAB

KARAWANG 239993 516782 46,44% 8 KAB BEKASI 240166 446209 53,82%

9 KOTA BOGOR 23557 176058 13,38%

10 KOTA

SUKABUMI 20503 62880 32,61%

11 KOTA

BANDUNG 137313 444505 30,89% 12 KOTA BEKASI 44384 327151 13,57%

13 KOTA CIMAHI 16237 105496 15,39%

Total 2.096.933 5.693.589 36,83%

Total keluarga miskin dari 13 kabupetan/kota tersebut adalah 2.096.933 dari total 5.693.589 keluarga atau sekitar 36% keluarga termasuk keluarga miskin (Tabel 3). Berdasarkan batasan ini maka jika suatu desa mempunyai persentase keluarga miskin lebih dari 36% maka dikategorikan ke dalam desa miskin sedangkan jika kurang dari sama

Matriks Peragam

Spasial (V)

Matriks Pembobot Spasial (Z)

Peubah Penjelas Baru (w)

w= Z*y

Fungsi Variogram Teoritik

Matriks Jarak

Z=V -dan

Zij = 1/vij

(16)

6

dengan 36% dikategorikan sebagai desa tidak miskin. Berdasarkan kriteria tersebut terdapat 1550 desa (56,38%) tergolong ke dalam desa miskin. Sedangkan sisanya sebesar 1199 (43,62%) tergolong ke dalam desa tidak miskin (Tabel 4).

Tabel 4. Distribusi jumlah desa berdasarkan kabupaten / kota

No Nama

Kabupaten

Jumlah Desa Miskin

Jumlah Desa Tidak Miskin

Total Desa

1 KAB BOGOR 201 214 415

2 KAB

SUKABUMI 210 130 340

3 KAB CIANJUR 179 165 344

4 KAB

BANDUNG 227 209 436

5 KAB SUBANG 205 43 248

6 KAB

PURWAKARTA 77 113 190

7 KAB

KARAWANG 229 75 304

8 KAB BEKASI 155 24 179

9 KOTA BOGOR 1 62 63

10 KOTA

SUKABUMI 15 18 33

11 KOTA

BANDUNG 49 90 139

12 KOTA BEKASI 1 42 43

13 KOTA CIMAHI 1 14 15

Total 1550 1199 2749

Distribusi jumlah desa berdasarkan kabupetan/kota terlihat pada Tabel 4. Kabupaten relatif memiliki desa lebih banyak dibandingkan dengan kota. Hal ini berkaitan dengan luas wilayah dari kabupaten yang umumnya lebih besar dibanding luas wilayah dari kota.

Pemodelan Regresi Logistik Klasik Pemodelan regresi logistik tanpa memperhatikan pengaruh spasial dari data dinamakan dengan pemodelan regresi logistik klasik. Tujuan dari pemodelan regresi logistik klasik ini adalah sebagai batasan untuk melihat perbaikan pendugaan parameter setelah dimasukkan pengaruh spasial ke dalam model. Hasil dugaan koefisien model dengan enam peubah penjelas dapat dilihat pada Tabel 5.

Hasil dugaan koefisien yang terdapat pada Tabel 5 merupakan hasil dugaan koefisien ketika dimodelkan dalam peluang Y=0 (status desa tidak miskin).

Tabel 5. Nilai dugaan koefisien untuk model regresi logistik klasik

Parameter Coef

Wald Chi-Square

P

Intercept 0,9429 23,2457 <0,0001

Ada/tidak penduduk yang bekerja sebagai TKI

-0,2839 7,1612 0,0074

Jarak dari desa ke ibukota kabupaten/kota

-0,0172 4,234 0,0396

Persentase keluarga yang menerima kartu sehat

-3,4685 135,2959 <0,0001

Persentase luas

sawah -1,6589 96,3885 <0,0001

Pesentase keluarga yang memakai listrik

0,441 5,9096 0,0151

ada/tidak puskesmas di desa tersebut

0,2169 6,6489 0,0099

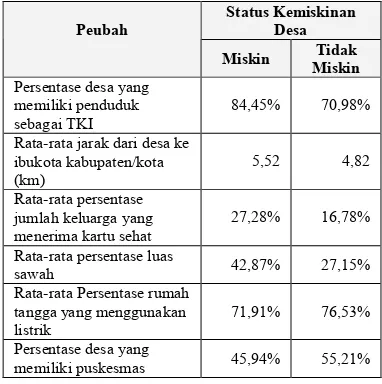
Setelah diperoleh peubah penjelas yang akan digunakan maka ingin diketahui karakteristik desa miskin dan desa tidak miskin untuk setiap peubah penjelas. Berdasarkan Tabel 6 dapat diketahui bahwa desa yang berstatuskan desa miskin dicirikan dengan desa-desa yang memiliki penduduk sebagai TKI lebih banyak, jarak dari desa ke ibukota kabupaten/kota yang lebih jauh, jumlah keluarga penerima kartu sehat yang lebih banyak, sawah yang lebih luas, rumah tangga yang menggunakan listrik lebih sedikit, dan desa yang memiliki puskesmas lebih sedikit dibandigkan dengan desa yang berstatuskan desa tidak miskin.

Tabel 6. Karakteristik desa miskin dan desa tidak miskin

Status Kemiskinan Desa Peubah

Miskin _MiskinTidak

Persentase desa yang memiliki penduduk sebagai TKI

84,45% 70,98%

Rata-rata jarak dari desa ke ibukota kabupaten/kota (km)

5,52 4,82

Rata-rata persentase jumlah keluarga yang menerima kartu sehat

27,28% 16,78%

Rata-rata persentase luas

sawah 42,87% 27,15%

Rata-rata Persentase rumah tangga yang menggunakan listrik

71,91% 76,53%

Persentase desa yang

(17)

7

Model Variogram Status Kemiskinan Desa Variogram dari status kemiskinan sebagian desa di Jawa Barat terlihat pada Gambar 6. Dari Gambar 6 terlihat bahwa semakin jauh jarak antrar desa maka nilai variogram akan semakin besar, menuju konvergen pada jarak tertentu. Hal ini mengindikasikan adanya unsur spasial dari status kemiskinan suatu desa.

Gambar 6. Plot antar jarak (h) dengan nilai variogramnya

Berdasarkan hasil dugaan variogram dari status kemiskinan desa tersebut dilakukan pemodelan variogram secara teoritik yaitu model exponential, power, spherical, gaussian. Adapun nilai dugaan parameter dari masing-masing model terdapat pada Tabel 7.

Tabel 7. Nilai dugaan parameter model variogram

Model Dugaan Model

Expo-nential 1823 , 0 3 , 0 3 exp 1 0670 , 0 ) ( ^                 h h 

R2 _=92,82%

Power ( ) 0,1753h0,3 0,0802

^

 

h



R2 _=73,21%

Spheri-cal 0,1877, 0,25

25 , 0 * 2 25 , 0 3 0,0605 ) ( ₃ 3 ^                       h h h h  25 , 0 , 2482 , 0 ^   h 

R2 _=94,26%

Gaussian ₀_,₂₆ 0,1994

3 exp 1 0,0498 ) ( ₂ 2 ^                 h h 

R2 _=95,22%

Model gaussian merupakan model terbaik untuk menggambarkan hubungan antara jarak antar desa dengan nilai variogramnya. Hal ini ditunjukkan oleh nilai R2 tertinggi (95,22%). Sedangkan model power tidak terlalu baik untuk menggambarkan hubungan jarak antar desa dengan nilai variogramnya, hal ini ditunjukkan oleh nilai R2 terendah (73,21%). Sedangkan model power tidak terlalu baik

dalam menggambarkan hubungan antara jarak antar desa dengan nilai variogramnya, hal ini ditunjukkan oleh R2 terendah (73,21%) dan didukung oleh Gambar 7.

Gambar 7. Plot dugaan dari masing-masing model variogram

Terlihat dari plot hasil dugaan masing-masing model dengan nilai variogram bahwa hanya model power yang tidak mampu menggambarkan kondisi variogram yang sebenarnya (Gambar 7).

Pembuatan Matriks Pembobot Spasial Setelah dilakukan pemodelan variogram secara teoritik untuk beberapa model variogram, langkah selanjutnya adalah memanfaatkan hasil dugaan parameter model variogram yang terdapat pada Tabel 6 untuk pembuatan matriks pembobot spasial (Z). Dalam pembuatan matriks pembobot spasial ini juga memanfaatkan matriks jarak yang akan digunakan untuk membuat matriks peragam spasial (V). Matriks ragam spasial adalah sebuah matriks yang merupakan fungsi dari matriks jarak dengan model variogram teoritik.

Setelah diperoleh matriks V, maka dilakukan proses pembalikan matriks terhadap matriks V untuk memperoleh matriks Z. Pembalikan matriks V antara lain dapat dilakukan dengan metode :

1. Membuat matriks yang berisikan nilai-nilai dari satu per matriks V (1/Vij). Hal ini dimaksudkan untuk mempercepat komputasi.

2. Membuat matriks yang merupakan hasil dari generalized inverse matriks V. Data pembobot spasial yang digunakan untuk pemodelan regresi logistik spasial dibatasi sampai jarak 27,5 km, sedangkan untuk jarak yang lebih dari 27,5 km nilai pembobot spasialnya sama dengan nol.

(18)

8

yang diharapkan adalah plot pencaran yang monoton menurun dari kiri atas ke kanan bawah. Pembalikan matriks V menggunakan 1/Vij menghasilkan plot pencaran yang tidak sesuai dengan harapan. Lain halnya dengan pembalikan matriks V menggunakan generalized inverse matriks V untuk model variogram exponential dan power menghasilkan plot pencaran sesuai dengan monoton menurun dari kiri atas ke kanan bawah.

Dugaan Model Regresi Logistik Spasial Matriks pembobot spasial yang menggambarkan pengaruh spasial antar desa yang berasal dari beberapa model variogram, dikalikan dengan peubah responnya dan kemudian dimasukan ke dalam model regresi logistik sebagai sebuah peubah penjelas baru yang dinamakan dengan x-spasial. Pemodelan regresi logistik dengan melibatkan pengaruh spasial ke dalam model dinamakan dengan model regresi logistik spasial, yang hasil dugaan parameternya terlihat pada Tabel 8 dan Tabel 9. Penelitian ini fokus dalam pencarian arah koefisien dari dugaan parameter, belum memperhatikan segi interpretasi dari dugaan parameter.

Nilai dugaan parameter untuk peubah penjelas x-spasial pada seluruh model regresi logistik spasial berkoefisien negatif, yang dapat diartikan jika suatu desa berdekatan erat dengan desa yang miskin maka peluang desa tersebut berstatus tidak miskin adalah kecil, dan dengan kata lain desa tersebut berpeluang besar sebagai desa miskin. Dugaan terhadap

koefisiean x-spasial ini telah sesuai dengan perkiraan awal penelitian yang menyatakan bahwa status kemiskinan suatu desa diperkirakan dipengaruhi oleh kondisi desa lainnya.

Hasil dugaan parameter untuk setiap metode pembalikan matriks V, menghasilkan arah koefisien yang seragam untuk masing-masing peubah penjelasnya. Keseragaman koefisien yang dihasilkan yaitu koefisien negatif untuk peubah penjelas ada/tidak penduduk yang bekerja sebagai TKI, jarak dari desa ke ibukota kabupaten/kota, persentase keluarga yang menerima kartu sehat, dan persentase luas sawah. Sedangkan koefisien positif untuk peubah penjelas persentase keluarga yang memakai listrik, dan ada/tidak puskesmas di desa tersebut.

Keseragamaan arah koefisien untuk masing-masing peubah penjelas ini akan

memberikan kemudahaan dalam

menginterpretasikan hubungan antar peubah penjelas dengan peubah responnya. Misalkan untuk peubah penjelas persentase luas sawah, yang berkoefisienkan negatif. Interpretasinya adalah ketika persentase luas tanah suatu desa bertambah, maka peluang desa tersebut berstatus desa tidak miskin akan semakin kecil. Sedangkan interpretasi untuk peubah penjelas yang berkoefisien positif, misalkan untuk peubah penjelas persentase keluarga yang memakai listrik maka interpretasinya adalah ketika persentase keluarga yang memakai listrik bertambah, maka peluang desa tersebut berstatuskan desa tidak miskin akan semakin besar.

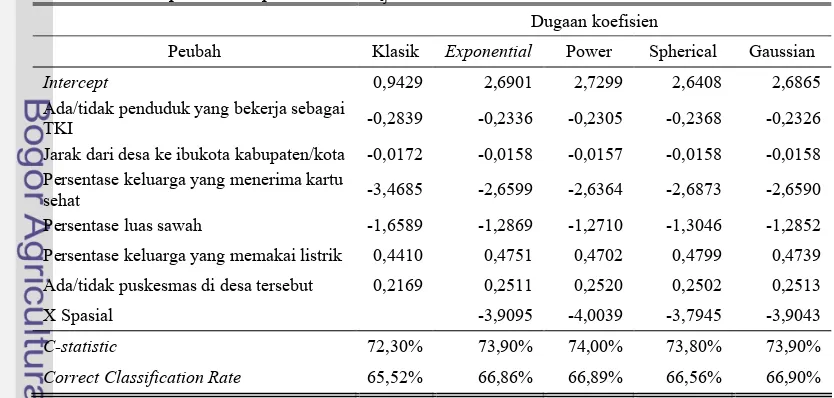
Tabel 8. Nilai dugaan koefisien regresi logistik dari model klasik dan model spasial menggunakan matriks pembobot spasial dari 1/Vij

Dugaan koefisien

Peubah Klasik Exponential Power Spherical Gaussian

Intercept 0,9429 2,6901 2,7299 2,6408 2,6865

Ada/tidak penduduk yang bekerja sebagai

TKI -0,2839 -0,2336 -0,2305 -0,2368 -0,2326

Jarak dari desa ke ibukota kabupaten/kota -0,0172 -0,0158 -0,0157 -0,0158 -0,0158

Persentase keluarga yang menerima kartu

sehat -3,4685 -2,6599 -2,6364 -2,6873 -2,6590

Persentase luas sawah -1,6589 -1,2869 -1,2710 -1,3046 -1,2852

Persentase keluarga yang memakai listrik 0,4410 0,4751 0,4702 0,4799 0,4739

Ada/tidak puskesmas di desa tersebut 0,2169 0,2511 0,2520 0,2502 0,2513

X Spasial -3,9095 -4,0039 -3,7945 -3,9043

C-statistic 72,30% 73,90% 74,00% 73,80% 73,90%

Correct Classification Rate 65,52% 66,86% 66,89% 66,56% 66,90%

Catatan :

(19)

9

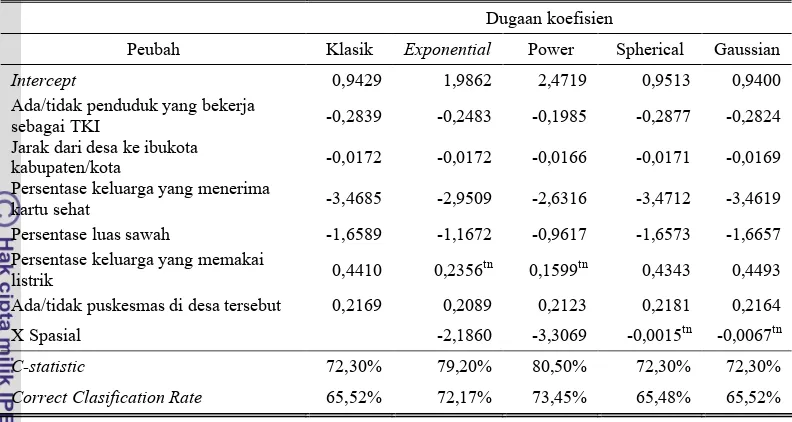
Tabel 9. Nilai dugaan koefisien regresi logistik dari model klasik dan model spasial menggunakan matriks pembobot spasial dari (V)

-Dugaan koefisien

Peubah Klasik Exponential Power Spherical Gaussian

Intercept 0,9429 1,9862 2,4719 0,9513 0,9400

Ada/tidak penduduk yang bekerja

sebagai TKI -0,2839 -0,2483 -0,1985 -0,2877 -0,2824

Jarak dari desa ke ibukota

kabupaten/kota -0,0172 -0,0172 -0,0166 -0,0171 -0,0169

Persentase keluarga yang menerima

kartu sehat -3,4685 -2,9509 -2,6316 -3,4712 -3,4619

Persentase luas sawah -1,6589 -1,1672 -0,9617 -1,6573 -1,6657

Persentase keluarga yang memakai

listrik 0,4410 0,2356

tn

0,1599tn 0,4343 0,4493

Ada/tidak puskesmas di desa tersebut 0,2169 0,2089 0,2123 0,2181 0,2164

X Spasial -2,1860 -3,3069 -0,0015tn -0,0067tn

C-statistic 72,30% 79,20% 80,50% 72,30% 72,30%

Correct Clasification Rate 65,52% 72,17% 73,45% 65,48% 65,52%

Catatan :

tn= peubah yang tidak nyata pada taraf α=10%

Yang dimodelkan P(Y=0)

Berdasarkan nilai c-statistic yang terdapat pada Tabel 8 dan Tabel 9 terlihat bahwa secara umum model regresi logistik spasial memiliki nilai c-statistic yang lebih besar dibandingkan dengan nilai c-statistic dari model regresi logistik klasik. Kecuali untuk model spherical dan gaussian ketika menggunakan metode pembalikan matriks V dengan generalized inverse matriks V nilai c-statistic yang diperoleh sama dengan model klasik (72,3%). Hal ini dapat dinyatakan bahwa terdapat perbaikan pendugaan parameter model regresi logistik setelah diberikan pengaruh spasial terhadap data. Perbaikan pendugaan parameter juga didukung dengan correct classification rate model regresi logistik spasial lebih tinggi dibandingkan dengan model regresi logistik klasik.

Nilai c-statistic untuk masing-masing model regresi logistik spasial dapat terlihat secara deskriptif pada Gambar 8. Berdasarkan Gambar 8, terlihat bahwa model power menghasilkan nilai c-statistic tertinggi pertama yaitu sebesar 80,50% untuk pembalikan matriks V menggunakan generalized inverse variogram. Sedangkan nilai c-statistic tertinggi kedua dihasilkan oleh model exponential yaitu sebesar 79,20% dengan metode pembalikan matriks V yang sama. Metode pembalikan matriks V menggunakan 1/Vij menghasilkan nilai c-statistic yang relatif sama untuk setiap model regresi logistik spasial yaitu sekitar 74,00%. Nilai c-statistic terkecil dihasilkan oleh model spherical dan gaussian yaitu

sebesar 72,3% ketika menggunakan pembalikan matriks V dengan generalized inverse variogram, hal ini dikarenakan oleh x-spasial yang tidak nyata dalam pemodelan regresi logistik spasial.

0 10 20 30 40 50 60 70 80 90 100

Klasik Exponential Power Spherical Gaussian

Model Variogram

C

-S

ta

ti

s

ti

c

(

%

)

C-statistic (1/Vij) C-statistic (ginv(V))

Gambar 8. Perbandingan nilai c-statistic model regresi logistik klasik dengan model regresi logistik spasial untuk berbagai model variogram

(20)

10

untuk metode pembalikan matriks V yang sama yaitu menggunakan generalized inverse variogram. Correct classification rate terendah dihasilkan dari model spherical yaitu sebesar 65,48% ketika menggunakan metode pembalikan matriks V dengan generalized inverse variogram. Metode pembalikan matriks V menggunakan 1/Vij menghasilkan correct classification rate yang sama untuk model power, eksponenesial, dan Gaussian yaitu sebesar 66,9%, sedangkan untuk model spherical menghasilkan correct classification rate terendah yaitu sebesar 66,56%.

0,0 10,0 20,0 30,0 40,0 50,0 60,0 70,0 80,0 90,0 100,0

Klasik Exponential Power Spherical Gaussian

Model Variogram

C

o

rr

e

c

t

C

la

s

if

ic

a

ti

o

n

R

a

te

(

%

)

Correct Classification rate (1/Vij) Correct Classification Rate (ginv(V))

Gambar 9. Perbandingan hasil correct classification rate model regresi logistik klasik dengan model regresi logistik spasial untuk berbagai model variogram

Pembalikan matriks V dengan menggunakan generalized inverse variogram dan 1/Vijmenghasilkan nilai dugaan parameter yang berbeda dan dapat dilihat pada Tabel 8 dan Tabel 9. Pada Tabel 8 terlihat bahwa seluruh nilai dugaan untuk x-spasial nyata

pada taraf α=10%, sedangkan pada Tabel 9 nilai dugaan untuk x-spasial model spherical dan Gaussian tidak nyata pada taraf α=10%. Oleh karena itu, pembalikan matriks dengan menggunakan 1/Vij lebih baik dalam menggambarkan matriks pembobot spasial yang diharapkan.

KESIMPULAN

Terdapat enam peubah penjelas yang dapat mempengaruhi status kemiskinan sebagian desa di Jawa Barat, yaitu :

 Ada/tidak penduduk yang bekerja sebagai TKI

 Jarak dari desa ke ibukota kabupaten/kota

 Persentase keluarga yang menerima kartu sehat

 Persentase luas sawah

 Persentase rumah tangga yang menggunakan listrik

 Ada/tidak puskesmas di desa tersebut Peubah-peubah tersebut dipilih dari hasil analisis regresi logistik setelah melalui proses bertatar dalam pemilihan peubah penjelasnya.

Data status kemiskinan sebagian desa di Jawa Barat memiliki pola spaisal dan dapat dimodelkan dengan model variogram teoritik (model exponential, model power, model spherical, dan model gaussian). Hasil terbaik pemodelan regresi logistik spasial untuk berbagai model variogram, secara umum dihasilkan dari model power dengan nilai c-statistic sebesar 80,50% untuk pembalikan matriks V menggunakan generalized inverse variogram dan 74,00% untuk membalikan matriks V menggunakan 1/Vij. Secara umum nilai c-statistic dancorrect classification rate yang dihasilkan dari model regresi logistik spasial lebih tinggi dibandingkan dengan regresi logistik klasik yang memiliki nilai c-statistic sebesar 72,3% dan correct classification rate sebesar 65,52%. Hal ini dapat dinyatakan bahwa terjadi perbaikan pendugaan dalam pemodelan regresi logistik setelah dimasukkan pengaruh spasial ke dalam model.

SARAN

Untuk penelitian selanjutnya disarankan agar dalam penyusunan matriks pembobot spasial dilakukan simulasi dengan mencoba berbagai variasi radius jarak desa yang diakomodir dalam model, sehingga dihasilkan pemodelan yang lebih tepat dalam memprediksi status kemiskinan desa.

DAFTAR PUSTAKA

Ashraf, M., Jim C. L., K. G. Hubbard. 1997. Application of Geostatistics to Evaluate Partial Weather Station Network. J. Agricultural and Forest Meteorology. 84:255-271.

Bohling, Geoff. 2005. Introduction to Geostatistics and Variogram Analysis. Kansas Geological Survey 864-2093.

http://people.ku.edu/~gbohling/cpe940

(21)

11

Fernández. Bernal Herrera. 2003. Classification and modeling of trees outside forest in Central American landscapes by combining remotely sensed data and GIS. Dissertation. Forstwissenschaftlichen Fakultät. Albert-Ludwigs-Universität.

http://www.freidok.uni-freiburg.de/volltex

te/752/[8 Mei 2008]

Frei, Allan. 2005. Notes On Spatial Autoccorelation and Regrresion. Hunter College.

http://www.geography.hunter.cuny.edu/~a frei/gtech702_fall03_webpages/notes_spa

tial_autocorrelation.htm[25 April 2008]

Hosmer DW, Lemeshow S. 1989. Applied Logistic Regression. New York: J. Wiley. Searle, S. R. 1971. Linear Models. John Wiley

& Sons, Inc: New York, hal 1-7.

Syafitri, U. D., Bagus S., Vinda P. 2007. Pembandingan Hasil Akurasi Prediksi Model Regresi Logistik Spasial untuk Berbagai Model Variogram. Makalah Seminar ITS 3 November 2007.

Xie, Chenglin, Bo Huang, Christophe Claramunt and Magesh Chandramouli. 2005. Spatial Logistic Regression and GIS to Model Rural-Urban Land Conversion.

http://www.civ.utoronto.ca/sect/traeng/ilut e/processus2005/PaperSession/Paper10_X ie-etal_SpatialLogisticRegression_CD.pdf

(22)

(23)

12

Lampiran 1. Plot pencaran antara bobot spasial data dengan jarak untuk berbagai model variogram

Model Eksponensial (1/Vij) Model Power (1/Vij)

Model Spherical (1/Vij) Model Gaussian (1/Vij)

Model Eksponensial (ginv( variogram)) Model Power (ginv( variogram))

(24)

PERBANDINGAN HASIL AKURASI PREDIKSI MODEL REGRESI

Vinda Pratama

G14104042

DEPARTEMEN STATISTIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

(25)

1

PENDAHULUAN Latar Belakang

Penggunaan model regresi logistik telah berkembang pesat seiring dengan kemajuan ilmu pengetahuan. Dalam beberapa kasus, nilai peubah respon yang digunakan tidak bebas terhadap nilai-nilai di sekitarnya. Menurut Frei (2005) pola seperti ini dinyatakan sebagai autokorelasi spasial. Adanya hubungan spasial dalam peubah respon model regresi logistik akan menyebabkan pendugaan menjadi tidak tepat karena asumsi kebebasan galat dilanggar.

Berdasarkan permasalahan di atas diperlukan modifikasi terhadap model regresi logistik yang telah ada, yaitu dengan memasukkan hubungan spasial ke dalam model. Terdapatnya hubungan spasial antar daerah maka perlu mengakomodir keragaman spasial tersebut yang mengarah kepada regresi logistik spasial.

Keragaman spasial salah satunya dapat dimodelkan dengan variogram. Cressie (1993) dan Bohling (2005) menyebutkan bahwa terdapat empat model variogram, yaitu: exponential, power, spherical, dan gaussian. Sehingga dalam penelitian ini dicobakan beberapa model variogram tersebut untuk mengakomodir keragaman spasial yang kemudian akan digunakan untuk perbaikan pendugaan dalam regresi logistik.

Penelitian ini menggunakan studi kasus pendugaan status kemiskinan pada sebagian desa di Jawa Barat. Status kemiskinan di suatu desa tidak berdiri sendiri, tetapi dipengaruhi oleh kondisi desa lainnya (terdapat pengaruh spasial).

Tujuan

Tujuan dari penelitian ini adalah :

1. Mengetahui faktor-faktor yang berperan terhadap status kemiskinan sebagian desa di Jawa Barat dengan menggunakan regresi logistik.

2. Pemodelan regresi logistik spasial dengan menggunakan matriks pembobot yang berasal dari beberapa model variogram (studi kasus pendugaan status kemiskinan pada sebagian desa di Jawa Barat). Model variogram yang digunakan yaitu: exponential, power, spherical, dan gaussian.

3. Membandingkan tingkat akurasi hasil prediksi keempat model regresi logistik spasial.

Kerangka Pikir

Penelitian ini memfokuskan pada pengembangan analisis regresi logistik spasial yang kerangka berpikirnya akan disampaikan pada bagian ini. Andaikan sebuah bidang S tersekat-sekat n buah sub bidang (lokasi) yang saling lepas, yaitu s1, s2, ..., sn dengan s1 s2

 …  sn = S dan si sj = . Setiap sub-bidang si memiliki sentroid pada titik ci. Nilai pengukuran Y, X1, X2, … Xp di masing-masing sub-bidang adalahyi, x1i, x2i, … xpi.

Jika Y memiliki hubungan spasial, dan dipengaruhi oleh X1, X2, … Xp maka model yang bisa dibentuk adalah :

y

i

=

x

i

’

β

+

z

i’

y

β

* +

ε

i

...

(1)

dengan xi = (1x1i, 1x2i, …, 1xpi)’ adalah vektor

p x 1 yang berisi nilai-nilai pengamatan peubah X1, X2, … Xp pada sub-bidang si dan y’= (y1, y2 … yn) adalah nilai-nilai pengamatan peubah Y dari seluruh lokasi. Vektor z berukuran n x 1 menyatakan bobot spasial antar sub-bidang terhadap nilai di sub-bidang lainnya.

Menggunakan notasi matriks, model (1) dapat dituliskan sebagai

y

=

X

β

+

Zy

β

*+

ε

...(2)

pada model (2) terdapat Z yang merupakan sebuah matriks bobot spasial. Dalam pencariannya, matriks pembobot spasial ini memerlukan informasi variogram yang merupakan ukuran keragaman spasial.

Penelitian awal dalam pencarian matriks pembobot spasial telah dilakukan oleh Syafitri, dkk (2007). Dimana hasil pemodelan regresi logistik spasial dengan matriks pembobot yang berasal dari tiga model variogram (model exponential, model power, dan model spherical) relatif tidak berbeda jauh dengan regresi logistik biner. Oleh karena itu, perlu dilakukannya perubahan metode terhadap pencarian matriks pembobot spasialnya.

Matriks pembobot spasial diharapkan dapat menggambarkan pengaruh antar desa, dimana desa yang berdekatan memberikan pengaruh yang lebih besar dibandingkan dengan desa yang berjauhan. Variogram yang akan digunakan untuk menghitung matriks pembobot spasial ini menggambarkan keragaman antar daerah berdasarkan jaraknya. Semakin jauh jarak antar daerah maka keragaman yang terbentuk akan semakin besar menuju kekonvergenan. Sehingga perlu dilakukan proses pembalikan matriks variogram terlebih dahulu, yang kemudian hasil pembalikan matriks variogram yang dijadikan sebagai matriks pembobot spasial.

(26)

2

TINJAUAN PUSTAKA Regresi Logistik Spasial

) ( ) (

1

)

(

_g _x

x g

e

x







p p

X

x

g

























...

)

(

1

)

(

ln

)

(

₀ ₁ ₁

   _         ) ( 1 ) ( log x x

y dengan



   k j ij k j i ij i w y w 1 1 ˆ 

model dari



Variogram









) ( 2

)

(

,

;

))

(

)

(

)

(

1

)

(

2

h N j

i

z

x

i

j

N

h

x

z

h

N

h



1.

E

(

Z

(

x



h

)



Z

(

x

))



0

2.

Var

(

Z

(

x



h

)



Z

(

x

))



2



(

h

)

h) 1 exp 3

( ₀



dengan :

c0 = intersep

(27)

2

TINJAUAN PUSTAKA Regresi Logistik Spasial

) ( ) (

1

)

(

_g _x

x g

e

x







p p

X

x

g

























...

)

(

1

)

(

ln

)

(

₀ ₁ ₁

   _         ) ( 1 ) ( log x x

y dengan



   k j ij k j i ij i w y w 1 1 ˆ 

model dari



Variogram









) ( 2

)

(

,

;

))

(

)

(

)

(

1

)

(

2

h N j

i

z

x

i

j

N

h

x

z

h

N

h



1.

E

(

Z

(

x



h

)



Z

(

x

))



0

2.

Var

(

Z

(

x



h

)



Z

(

x

))



2



(

h

)

h) 1 exp 3

( ₀



dengan :

c0 = intersep

(28)

3

Gambar 1. Kurva model variogram exponentialdengan a = 1 dan c = 4

2. Model Power

Hubungan antara variogram dengan jarak untuk model power dibentuk dalam persamaan sebagai berikut :



(

h

)



c

_o



ph

, dengan 0 < α < 2 dengan :

c0 = intersep

p = kemiringan kurva h = jarak antar pengamatan Jika diketahui  = 0.4 dan dan p=4 untuk persamaan tersebut maka kurva yang terbentuk dapat dilihat pada Gambar 2.

Gambar 2. Kurva model variogram power dengan = 0.4 dan dan p=4 3. Model spherical

Bentuk persamaan untuk model spherical dalam menggambarkan hubungan antara variogram dengan jarak adalah sebagai berikut:

a

h

a

h

a

h

c

h













































,

2

3

)

(

3 3 0



a

h

c

h

)





,



(

₀



dengan :

c0 = intersep

c = ambang semi variogram (sill) a = batas pengaruh contoh h = jarak antar pengamatan Kurva model variogram spherical ketika diketahui c0= 0, a = 1 dan c = 4 secara visual dapat terlihat pada Gambar 3.

Gambar 3. Kurva model variogram spherical dengan a = 1 dan c= 4

4. Model Gaussian

Berikut ini adalah persamaan yang dibentuk oleh model Gaussian dalam menggambarkan hubungan antara variogram dengan jarak :

 























 





1

exp

3

₂2

a

h

c

h



dengan :

c = ambang semi variogram (sill) a = parameter model gaussian h = jarak antar pengamatan Gambar 4 merupakan kurva yang terbentuk dari model variogram gaussian ketika a = 1 dan c = 4.

(29)

4

A

AGA



y

Ax



untuk x.

e

Xb

y





X

'

X

b

ˆ



X

'

y

dimana matriks

X

 

X'X 1X'y,

X

'

X

.

BAHAN DAN METODE Bahan

Kode

Jumlah Desa

3201000000 KAB BOGOR 415

3203000000 KAB CIANJUR 344

3204000000 KAB BANDUNG 436

3213000000 KAB SUBANG 248

3214000000 KAB

PURWAKARTA 190

3216000000 KAB BEKASI 179

3271000000 KOTA BOGOR 63

TOTAL 2749

Peubah Jenis Keterangan

Kategorik 1 = ada

0 = tidak ada

(km)

Jumlah keluarga

Numerik

Kategorik 1 = ada

0 = tidak ada

(30)

4

A

AGA



y

Ax



untuk x.

e

Xb

y





X

'

X

b

ˆ



X

'

y

dimana matriks

X

 

X'X 1X'y,

X

'

X

.

BAHAN DAN METODE Bahan

Kode

Jumlah Desa

3201000000 KAB BOGOR 415

3203000000 KAB CIANJUR 344

3204000000 KAB BANDUNG 436

3213000000 KAB SUBANG 248

3214000000 KAB

PURWAKARTA 190

3216000000 KAB BEKASI 179

3271000000 KOTA BOGOR 63

TOTAL 2749

[image:30.595.320.511.198.437.2]

Peubah Jenis Keterangan

Kategorik 1 = ada

0 = tidak ada

(km)

Jumlah keluarga

Numerik

Kategorik 1 = ada

0 = tidak ada

(31)

5

Metode

[image:31.595.75.305.43.833.2]

Berikut in