KAJIAN CADANGAN ASURANSI DENGAN METODE ZILLMER DAN METODE KANADA

KAJIAN CADANGAN ASURANSI

DENGAN METODE ZILLMER DAN METODE KANADA

(Skripsi)

Oleh

ROZA ZELVIA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

i

ABSTRACT

RESERVE INSURANCE STUDY WITH THE ZILLMER AND

CANADA METHOD

By

Roza Zelvia

Reserve insurance is amount of money that must be provided by the insurance company in time account and used to pay compensation in compliance with agreement at the beginning of the contract. Reserve will be adjusted based on the premi into several methods. Methods which is used in this thesis is Zillmer and Canada methods. This research aimed at determinig formulations of reserve for life-insurance products theoretically with assessing Zillmer and Canada methods and doing simulation to the cencepts of reserves individual ordinary life insurance (ordinary insurance) which include periodically insurance, Pure Endowment Insurance, Dwiguna Insurance, and Lifetime Insurance. The measures used to assess the value of these reserves are : (1) determine the value of APV (Actual Present Value), (2) Determine the value of the annuity, (3). Determine the value of premi, (4) determine the value of net reserves, (5) determine the value of reserves using Zilmer and Canada Method as a result of the cost factor of premi. Based on the results of the study, the authors conclude Canada methods suitable for Pure Endowment Insurance and Dwiguna Insurance while the Zillmer method almost can be used in all types of insurance.

KAJIAN CADANGAN ASURANSI

DENGAN METODE ZILLMER DAN METODE KANADA

Oleh ROZA ZELVIA

Skripsi

Sebagai Salah Satu Syarat untuk Memperoleh Gelar SARJANA SAINS

pada

Jurusan Matematika

Fakultas Matematika dan Ilmu Pengetahuan Alam

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS LAMPUNG

ii

Judul Skripsi : KAJIAN CADANGAN ASURANSI DENGAN METODE ZILLMER DAN METODE KANADA Nama Mahasiswa : Roza Zelvia

Nomor Pokok Mahasiswa : 0717031060

Jurusan : Matematika

Fakultas : Matematika dan Ilmu Pengetahuan Alam

MENYETUJUI

1. Komisi Pembimbing

Drs. Rudi Ruswandi, M.Si. Widiarti, S.Si., M.Si. NIP. 19560208 198902 1 001 NIP. 19800502 200501 2 003

2. Mengetahui

Ketua Jurusan Matematika FMIPA Universitas Lampung

iv

PERNYATAAN

Saya yang bertanda tangan di bawah ini, menyatakan bahwa skripsi saya yang berjudul “KAJIAN CADANGAN ASURANSI DENGAN METODE ZILLMER DAN METODE KANADA“ merupakan hasil karya saya sendiri dan bukan hasil karya orang lain. Semua hasil tulisan yang tertuang dalam skripsi ini telah mengikuti kaidah penulisan karya ilmiah Universitas Lampung. Apabila dikemudian hari terbukti bahwa skripsi ini merupakan hasil salinan atau dibuat oleh orang lain, maka saya bersedia menerima sanksi sesuai dengan ketentuan akademik yang berlaku.

Bandar Lampung, 1 Desember 2012

Penulis

RIWAYAT HIDUP

Penulis dilahirkan di Kalianda, Lampung Selatan pada tanggal 31 Juli 1989. Penulis merupakan anak keempat dari empat bersaudara, dari pasangan Bapak Afrizal dan Ibu Rosni.

Pendidikan Taman Kanak-kanak Aisyiyah Kalianda diselesaikan pada tahun 1995. Sekolah Dasar diselesaikan di SD N 1 Way Urang, Kalianda pada tahun 2001. Sekolah Menengah Pertama diselesaikan di SMP N 1 Kalianda pada tahun 2004. Kemudian Sekolah Menengah Atas diselesaikan di SMA N 1 Kalianda pada tahun 2007.

iii

MENGESAHKAN

1. Tim Penguji

Ketua : Drs. Rudi Ruswandi, M.Si. ………

Sekretaris : Widiarti, S.Si., M.Si. ………

Penguji

Bukan Pembimbing : Mustofa Usman, M.A., Ph.D. ………

2. Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Prof. Suharso, Ph.D. NIP. 19690530 199512 1 001

RIWAYAT HIDUP

Penulis dilahirkan di Kalianda, Lampung Selatan pada tanggal 31 Juli 1989. Penulis merupakan anak keempat dari empat bersaudara, dari pasangan Bapak Afrizal dan Ibu Rosni.

Pendidikan Taman Kanak-kanak Aisyiyah Kalianda diselesaikan pada tahun 1995. Sekolah Dasar diselesaikan di SD N 1 Way Urang, Kalianda pada tahun 2001. Sekolah Menengah Pertama diselesaikan di SMP N 1 Kalianda pada tahun 2004. Kemudian Sekolah Menengah Atas diselesaikan di SMA N 1 Kalianda pada tahun 2007.

MOTTO

"Man Shabara Zhafira",

Siapa yang bersabar akan beruntung.

(Pepatah Arab)

“Maka sesungguhnya bersama kesulitan ada kemudahan.”

PERSEMBAHAN

Aku persembahkan karya sederhana ini dengan rasa syukur kepada Allah SWT atas segala ridho dan berkatNya serta dengan

kerendahan hati kupersembahkan karya sederhana ini kepada orang-orang terkasih.

Mama dan Papa yang sangat aku sayangi dan cintai dengan tulus serta keikhlasannya membesarkan dan mendidikku dengan limpahan cinta dan kasih sayang. Terima kasih atas doa yang tak

pernah putus, nasehat, pengorbanan, dukungan, dan kesabaran dalam membimbing setiap langkah demi keberhasilanku.

Abang-abang ku Anto, Deni dan Yowan, serta Kakak ku Dina yang sangat aku sayangi. Terima kasih atas do’a dan segala

dukungannya

Sahabat dan teman – teman yang memberikan dukungan dan doanya dalam penyelesaian tugas ini, terima kasih atas semuanya.

Almamaterku tercinta...“ Universitas Lampung”.

SANWANCANA

Puji syukur kehadirat Allah SWT yang telah melimpahkan segala berkah, nikmat dan rahmat-Nya sehingga penulis diberikan kesehatan dan kekuatan untuk dapat menyelesaikan skripsi ini. Penulisan skripsi ini dibuat sebagai salah satu syarat untuk memperoleh gelar sarjana Ilmu Sains.

Adapun judul dari skripsi ini adalah “KAJIAN CADANGAN ASURANSI DENGAN METODE ZILLMER DAN METODE KANADA”.

Penulisan skripsi ini juga tidak terlepas dari dukungan dan bantuan berbagai pihak, maka pada kesempatan ini penulis mengucapkan terima kasih kepada:

1. Bapak Drs. Rudi Ruswandi, M.Si., selaku pembimbing utama yang telah memberikan bimbingan dan dukungan semangat.

2. Ibu Widiarti, S.Si., M.Si., selaku pembimbing kedua yang telah membimbing dan memberikan saran.

3. Bapak Mustofa Usman, M.A., Ph.D., selaku pembahas yang telah memberikan kritik dan saran dalam perbaikan skripsi ini.

4. Ibu Fitriani, M.Sc, selaku pembimbing akademik penulis.

5. Bapak Drs. Tiryono Ruby, M.Sc.,Ph.D., selaku Ketua Jurusan Matematika Universitas Lampung.

dukungan semangat, pengorbanan secara moril dan materiil serta

mendoakan dengan setulus hati. Terimakasih atas semua yang telah mama berikan.

9. Abang-abang tersayang, Bang Anto, Bang Deni, dan Bang Yowan yang telah mendoakan dan selalu mendukung. Kakak ipar penulis tercinta, Kak Dina yang selalu mendukung dan mendoakan. Terimakasih sudah menjadi kakak pertama yang baik sekali.

10.Teman-teman Matematika angkatan 2007 (Sundy, Ana, Eva, Rohman, Mahfudz, dll), kostan (Erwi, Ade, Yuni, Dewi, Siti, Ratih, Ina dll) yang membangkitkan gairah jiwa penulis untuk terus maju. Yadi, Uda Jani, Uni, Mb’Eka, Mb’Ami, Mb’Dian, Mb’Tya yang selalu memberi

dukungan dan mendoakan penulis.

11.Semua pihak yang telah mendukung dan mendoakan penulis.

Semoga kebaikan mereka dapat bermanfaat dan mendapat balasan pahala dari Allah SWT.

Akhir kata harapan penulis semoga skripsi ini dapat berguna bagi para pembaca dan juga dapat menambah khasanah ilmu pengetahuan bidang Matematika khususnya Matematika Asuransi (Aktuaria) , Aamiin Allohumma Aamiin.

Bandar Lampung, Desember 2012 Penulis

I.

PENDAHULUAN

1.1 Latar Belakang

Asuransi dalam hukum dan ekonomi adalah bentuk manajemen risiko yang dipakai untuk proteksi terhadap kerugian. Asuransi didefinisikan sebagai transfer sepadan dari risiko potensi kerugian dengan suatu premi. Menurut Undang-Undang Hukum Dagang pasal 246 “Asuransi adalah suatu perjanjian dengan nama seseorang penanggung mengikatkan diri kepada seseorang tertanggung, dengan menerima suatu premi untuk memberikan penggantian karena suatu kerugian, kerusakan, atau kehilangan keuntungan yang diharapkan, yang mungkin terjadi karena suatu peristiwa tak tentu” (KUHD, 2000 : 205). Untuk mengantisipasi kemungkinan adanya kerugian keuangan yang mungkin timbul akibat kejadian-kejadian yang tidak diharapkan, maka seseorang biasanya mengikuti program asuransi, dengan begitu kerugian yang diderita oleh orang tersebut akan berkurang dengan adanya jaminan dari perusahaan asuransi.

2

atau dibayar lunas yang disebut premi asuransi dan perusahaan asuransi memberikan jaminan terhadap risiko yang terjadi sesuai kesepakatan berupa sejumlah uang yang disebut klaim asuransi. Berdasarkan konsep dasar asuransi jiwa, dengan memperhitungkan premi dan pertanggungan timbul suatu cadangan yaitu sejumlah dana yang harus disediakan oleh pihak perusahaan asuransi dalam waktu pertanggungan dan digunakan untuk membayar santunan sesuai dengan kesepakatan pada awal kontrak. Dalam kenyataan, suatu ketidakpastian mungkin terjadi bahkan dapat melahirkan suatu kerugian, ini merupakan risiko bagi perusahaan. Penyebab dari risiko tersebut adalah jumlah dari klaim diluar perkiraan, penghentian pembayaran premi oleh pemegang polis karena suatu hal, dan atau pengeluaran dana tidak terduga perusahaan. Maka sangatlah penting bagi perusahaan untuk mempersiapkan segala sesuatunya untuk menghadapi hal tersebut. Salah satu cara adalah dengan menganalisa cadangan yaitu untuk mengalokasikan risiko sehingga perusahaan dapat menentukan kebijakan-kebijakan baru yang ada hubungannya dengan pengaruh risiko tersebut untuk kemajuan perusahaan.

dibayarkan pada tahun kedua dan berikutnya. Sehingga pada skripsi ini akan dikaji nilai cadangan dengan menggunakan metode Zillmer dan metode Kanada.

1.2 Perumusan Masalah

Dari latar belakang di atas, maka permasalahan yang akan dibahas dalam skripsi ini adalah mengkaji cadangan dari suatu produk asuransi. Jenis asuransi yang akan dikaji adalah Asuransi Berjangka, Asuransi Endowment Murni, Asuransi Dwiguna, dan Asuransi Seumur Hidup. Kemudian kajian akan difokuskan pada nilai cadangan secara umum dan metode Kanada.

1.3 Tujuan

4

II. LANDASAN TEORI

Kajian tentang perhitungan nilai aktuaria yang akan dibayarkan n-kali pertahun untuk berbagai produk asuransi jiwa, dapat dilakukan dengan terlebih dahulu mengetahui beberapa teori-teori dasar terkait asuransi.

2.1 Fungsi Kelangsungan Hidup (Survival Function)

Misalkan X adalah usia seseorang dan x adalah usia seseorang yang hidup pada saat menutup polis asuransi, sehingga X merupakan peubah acak waktu meninggal (Bowers, 1997).

Fungsi distribusi X dinyatakan dengan

� � = � � , �

Untuk selanjutnya fungsi kelangsungan hidup (Survival Function) akan disingkat dengan istilah fungsi hidup dinyatakan dengan :

� = − � � = � > � , �

� adalah peluang orang yang berusia 0 tahun yang akan hidup mencapai usia x

2.2 Peluang Waktu Sisa Hidup

Satu notasi yang digunakan untuk menyatakan seseorang masih hidup pada usia tertentu adalah (x). Jika meninggal pada usia X (X>x) maka T(x)=X– x

menyatakan waktu hidup yang tersisa dari (x). T(x) merupakan fungsi peubah acak kontinu X, oleh sebab itu T(x) merupakan suatu peubah acak kontinu, dengan fungsi distribusinya didefinisikan sebagai berikut :

= Pr � Pr � =� � �

� � (t) = Pr ( T (x) | > x) = Pr (X−x | > � ) = Pr � < � + | > �

= �� �+� −�� �

−�� �

= ( − �+� )− − �

�

=

� − �+�

�

=

�

�

−

�+� �

= 1

−

�+�

�

= � � (2.2.1)

Dalam ilmu aktuaria simbol tqx menyatakan peluang seseorang berusia x akan meninggal t tahun lagi atau akan meninggal sebelum usia (x+t) tahun. Sedangkan fungsi hidupnya :

Pr � > = − Pr �

= 1− _{� �}

= − [ − �+� � ]

6

Simbol _��_� menyatakan sebagai peluang seseorang yang berusia x akan hidup sampai dengan usia t tahun lagi atau akan hidup sampai usia (x+t) tahun, sehingga

untuk seseorang yang baru lahir (new born) _�� merupakan survival function dan dituliskan dengan

�

� = s(x)

Kondisi lainnya adalah bahwa x akan berlangsung hidup sampai t tahun dan meninggal dalam u tahun, dengan demikian x akan meninggal antara x+t dan x+t+u. Kondisi ini disebut sebagai peluang meninggal yang ditangguhkan dan didefinisikan sebagai berikut :

�

� = � < � +

= � � + − � � < = _{�+ �}− _{� �}

=

�_� − �_� +

=

�+� �

−

�+�+ �

=

�+� �

.

�+� �+�

−

�+� �+�

.

�+�+ �

=

�+� �

−

�+�+ �+�

=

�_� − − �_�+

=

�_� ∙ _�+

Jika u=1, maka peluang meninggal yang ditangguhkan dapat dinyatakan dengan

�

� , sehingga:

�

Dalam kasus diskrit sering disebut dengan Curtate-Future-Lifetime, dengan simbol K(x). K(x) adalah bilangan integer terbesar dari T(X). Fungsi distribusinya adalah:

Pr[ � = ] = Pr[ � < + ]

= Pr[ < � + ]

=

�_� − ₊ �_�

= �� � ∙ �+�

=

_�

 , k= 0,1,2,3,…..

Diketahui sebelumnya _{� �} adalah fungsi distribusi dari T(x), sehingga fungsi

densitas T(x) adalah:

f(t)

=

� tqx

=

_� − �_{� �}

=

�

[ −

�+�

�

]

=

�

[−

�+�

�

]

=

− ′ �+�

�

=

�+�

�

.

− ′ �+�

�+�

(2.2.3)

2.3 Life Table

8

Tabel 2.1 Tabel Mortalita

� � �� �� � � 0 1 2 . . 50 51 . . 105 106 … … … … � � � … … � � … … � � � � … … � � … … � … … … … … … … … Keterangan :

� : usia �_� : peluang hidup � : jumlah yang hidup � : peluang meninggal

�� : jumlah yang meninggal � : nilai harapan hidup

Pada anggota kelompok yang diamati di atas dimisalkan dilahirkan pada saat yang sama dan jumlahnya , selama satu tahun berikutnya jumlah yang meninggal adalah � sehingga yang bisa mencapai umur satu tahun sebanyak . Satu tahun berikutnya jumlah yang meninggal adalah � sehingga yang mencapai umur dua

tahun sebanyak . Untuk usia 50 tahun terdapat sebanyak . Satu tahun kemudian jumlah yang meninggal sebanyak � sehingga yang mencapai usia 51 sebanyak . Proses tersebut terus berlangsung, sampai terdapat keadaan _� =

Dari keterangan tersebut didapatkan hubungan sebagai berikut :

�+ = �− �� dan juga hubungan di bawah ini n ≥1, maka

� = �+ + ��

Perhitungan nilai peluang hidup �_� dan peluang meninggal _� ditentukan dengan

�� = �+

� . .

� =�� � =

�− �+

� . .

Berdasarkan persamaan (2.3.1) dan (2.3.2) diperoleh hubungan-hubungan sebagai berikut :

�+ = �∙ ��

�� = �∙ �

��+ � =

�� = − �

2.4 Laju Kematian (the force of mortality)

Laju kematian dari seseorang yang baru lahir dan akan meninggal antara usia x

dan x + ∆x dengan syarat hidup pada usia x dapat dinyatakan dengan :

� � < < � + ∆x| > � = � + ∆� − �_{− �}

10

lim

Δx→

F x + Δx – F x – F x =

lim

Δx→ F x + Δx – F x ΔxΔx

lim

Δx→ – F x

= ∆x→lim � + ∆� − �_lim ∆� . ∆�

∆x→ − �

= _{− �}′ � ∆�

≅ _{− �}� �

Untuk setiap usia x, laju tingkat kematian dari seseorang yang berusia x tahun dapat dinyatakan dengan :

� � = lim_∆x→ � � < < � + ∆x| > �_∆x

= lim ∆x→ ∆�.

�′ � ∆� −� �

� � = �_{−� �}′ �

� � = _{−� �}� � (2.4.1)

atau

� � + = _{−� �+�}� �+�

dengan � � + adalah probabilitas (peluang) sisa umur hidup seseorang yang

berusia x tahun antara t dan t + ∆ tahun dengan syarat ia masih hidup pada usia x

sampai x + t tahun.

karena s(x) = 1- F(x) atau F(x) = 1 – s(x), maka :

F’(x) = f(x) = -s’(x)

� � = − ′_{� =}� −_{� .}�( � )_{� �}

=−� ln �_{� �} .�( � )_{� �}

=−� ln �_{� �}

� � �� = −� ln �

Dengan mengganti x menjadi y, maka diperoleh :

� � = −� ln

dan dengan menggunakan intergral tertentu pada batas x sampai x+t maka diperoleh :

∫ � �

�+�

�

= − ∫ � ln

�+�

�

= −ln |��+�

= −{ln � + − ln � }

= − ln � +_�

= − ln ( � +_{� )}

= − ln �� �

�� � = − ∫ �

�+� �

Jika nilai laju kematiannya konstan (� � = � untuk semua x ≥ 0, artinya besarnya nilai dari force of mortality (laju kematian) adalah sama untuk semua usia nasabah yang hidup, maka diperoleh :

� = � =� − ∫ �

�

12

Diketahui sebelumya bahwa _{� �} adalah fungsi distribusi dari T(x), sehingga fungsi densitas dari T(x) adalah :

� =_�� � �

= _{� ( −}� _{� �}� � �)

= _{� ( −}� � +_{� )}

= _{� (−}� � +_{� )}

= − ′ � +_�

= � +_{� . −} ′ � +_{� +}

� = �� � . � � +

2.5 Distribusi Gompertz

Terdapat beberapa hukum yang dapat digunakan untuk menghitung mortalita dan fungsi survival yaitu Hukum De Moivre, Gompertz, Makeham, dan Weibull. Dalam tulisan ini hanya digunakan Hukum Gompertz sebagai perhitungan simulasi data. Menurut Wai Sum Chan dan Yui Kuen Tse, dengan SDF (Survival Distribution Function) atau fungsi distribusi tahan hidupnya dari distribusi Gompertz

� � = �� [ − �� ] , > , > , � > .

� � = − �� [�_� − �� ]

Sehingga dari fungsi tersebut didapatkan juga pdf sebagai berikut :

�� � =_{�� ( − �� [}� − �� ])

= − �� [ − �� _] �

�� [ − �� ]

= − �� [ − �� _{] −} ��

= �� _{�� [ −} �� _]

Sehingga diperoleh Force Mortality-nya sebagai berikut

��= �� � � � =

�� _{�� [ −} �� _]

�� [ − �� _] =

��_{, > � � >}

R merupakan tingkat kematian umum dan adalah laju pertumbuhan umur yang spesifik dari force mortality.

Benyamin Gompertz (1825) mengumumkan bahwa force mortality akan semakin meningkat secara eksponensial. Menurut Jordan, C.W fungsi Force Mortality-nya didapatkan sebagai berikut

��= � (2.5.1)

dan pdf adalah

� �, , = � − (

�− ₎

l g _{, � , > ,}

di mana B dan c adalah parameter.

sehingga diperoleh survival function bagi (x) sebagai

14

= exp (−_l� �_{− ) = exp −} �_{− (2.5.2)}

= −_l� (2.5.3)

Berdasarkan persamaan ( 2.2.2) dan (2.2.3) diperoleh :

� � = �� �∙ � �+�

= � +_� � � +

Dengan mensubstitusikan persamaan (2.5.1) dan (2.5.2) diperoleh :

� � =exp[−_exp[− �+�_{�− ] .}− ] �+�

� � = exp[− �+�₋ � _{] .} �+� _(2.5.4)

2.6 Bunga (Interest)

Bunga atau bunga bank merupakan pembayaran yang dilakukan oleh peminjam sebagai balas jasa atas pemakaian uang yang dipinjam (Sudarto, 1976). Secara umum cara perhitungan bunga dibagi menjadi dua yaitu :

2.6.1. Bunga Sederhana

1 1+i 1+2i 1+3i 1+4i 1+t.i

[image:30.595.114.514.124.183.2]

0 1 2 3 4 t

Gambar 2.1 Sistem Bunga Sederhana

Gambar 2.1 menggambarkan modal (pokok investasi) dengan bunga sebesar I

pertahun dan waktu t= 0,1,2,…,n.

2.6.2 Bunga Majemuk

Bunga majemuk adalah suatu perhitungan bunga dimana besar pokok jangka investasi selanjutnya adalah besar pokok sebelumnya ditambah dengan besar bunga yang diperoleh (Takasi, 1993). Misal P besar pokok , i tingkat bunga, t

jangka tahun investasi (dalam tahun), maka total pokok beserta bunga (S) adalah : S = P (1 + i)t.

1 (1+i) (1+i (1+i (1+i (1+i �

[image:30.595.116.515.498.563.2]

0 1 2 3 4 t Gambar 2.2 Sistem Bunga Majemuk

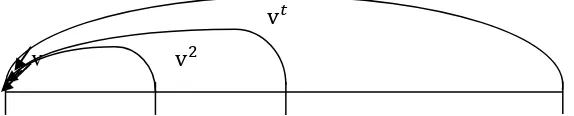
Fungsi v dalam bunga majemuk didefinisikan sebagai faktor diskonto :

16

[image:31.595.173.460.105.163.2]

v� v v

Gambar 2.3 Nilai sekarang dalam bunga majemuk

v adalah nilai sekarang (Present Value) dari pembayaran sebesar 1 yang dilakukan 1 tahun kemudian. Sedangkan untuk tingkat diskonto didefinisikan d, sebagai berikut :

d = _+ii = iv = − v maka − d = v

Karena v adalah Present Value untuk pembayaran sebesar 1 yang akan dibayarkan 1 tahun kemudian, apabila pembayarannya dilakukan 1 tahun lebih cepat maka besarnya bunga yang hilang adalah d = 1 - v. Dalam perhitungan asuransi, terdapat dua jenis suku bunga majemuk yaitu suku bunga nominal dan suku bunga efektif. Perbedaan kedua suku bunga tersebut terletak pada periode pembayaran (perhitungan) bunga yang biasa disebut periode konversi. Apabila periode pembayaran bunganya adalah tahunan, maka suku bunganya disebut suku bunga efektif. Selain dari itu, suku bunganya disebut suku bunga nominal. Suku bunga nominal dan suku bunga efektif dinyatakan dalam bentuk persen per tahun serta dinotasikan dalam i untuk suku bunga efektif dan untuk suku bunga nominal, dimana j menyatakan frekuensi bunga yang dibayarkan dalam setahun.

Sehingga secara akumulasi terdapat hubungan antara tingkat suku bunga nominal dengan tingkat suku bunga efektif sebagai berikut :

1+i=[ + � ]

Sehingga diperoleh : + � = + /

= [ + �_{− + ]}

= + −_/ + .6.

Sedangkan hubungannya dengan tingkat diskon

1- d= [ + �]

Sehingga diperoleh : � = [ − − � �_{] = [ − �}�_]

dan terdapat hubungan antara tingkat suku bunga nominal dengan tingkat diskon :

� = − � = − ₊ = ₊ = _{+ /}

Jika frekuensi perhitungan bunga nominal semakin besar dalam satu satuan waktu bunga efektif, maka akan terjadi perhitungan bunga secara kontinu :

lim_→⋈ = �

konvergen pada suatu nilai yang dikatakan sebagai percepatan pembungaan (force of interest) dan ekivalen dengan tingkat suku bunga efektif, i.

perhatikan persamaan (2.6.1) :

= + −_/ +

maka dapat dilihat bahwa � merupakan derivative dari fungsi + � pada titik x=0.

Misal = + �

�_{�� =��}� + �

�

18

′ = ln +

′ _{= ∙ ln +}

′ _{= +} �_{∙ ln +}

Untul x=0, maka

′ _{= ln +}

Karena = � � → = + � = � � → � � + ∆� = + �+∆�

�

�� = � � �

�� = lim∆�→

� � + ∆� − � � ∆�

�

�� = lim∆�→

+ �+∆�_{− +} �

∆� �

�� |�= = lim∆�→

+ ∆�_{− +}

∆�

Ambil ∆� =

lim_{/ →} + − + =�_{�� |}�= = ln +

lim_→⋈ = ln +

Sehingga diperoleh

2.7 Asuransi

Asuransi berasal dari kata assurance atau insurance yang artinya jaminan atau pertanggungan. Sedangkan asuransi jiwa adalah asuransi yang bertujuan menanggung orang terhadap kerugian finansial tak terduga yang disebabkan karena meninggalnya terlalu cepat atau hidupnya terlalu lama (Salim, 1993). Risiko yang timbul pada asuransi jiwa terutama terletak pada “unsur waktu (time)”, oleh karena itu sulit untuk menentukan kapan seseorang meninggal dunia. Sehingga untuk memperkecil risiko tersebut maka sebaiknya diadakan pertanggungan jiwa. Dalam dunia yang makin maju, bidang asuransi terlibat dalam banyak segi kehidupan manusia. Perusahaan asuransi telah tumbuh menjadi perusahaan besar di dunia dan bersamaan dengan itu permintaan akan tenaga ahli asuransi seperti aktuaris makin meningkat pula. Menurut keputusan

Menteri Keuangan No. 1250/KMK. 013/1998, “Aktuaris adalah seseorang yang

berdasarkan latar belakang pendidikannya memiliki keahlian untuk melakukan

perhitungan matematis asuransi jiwa”. Oleh karena itu perusahaan asuransi

mempekerjakan aktuaris adalah untuk menyusun perhitungan secara matematis produk-produk asuransi.

Jumlah dan waktu pembayaran benefit pada asuransi jiwa tergantung pada panjang interval dari dikeluarkannya polis sampai tertanggung (nasabah meninggal), sehingga untuk menghitung nilai APV (Actuarial Present Value) dari suatu produk asuransi jiwa dipengaruhi oleh vt _{= faktor diskon (fungsi dari t) dan}

bt = benefit (manfaat) yang akan diterima. Dan keduanya membentuk suatu

20

sebagai Zt = vt . bt. Diketahui T(x) adalah random variabel dari waktu sisa hidup nasabah atau waktu dari dikeluarkannya polis sampai waktu meninggalnya nasabah, maka Zt adalah fungsi peubah acak atau Present Value pembayaran benefit pada saat polis asuransi dikeluarkan.

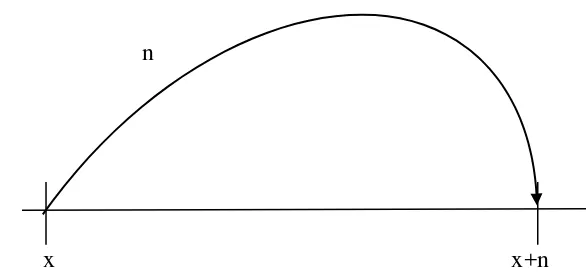
2.7.1 Asuransi Seumur Hidup (Whole Life Insurance)

Asuransi jiwa seumur hidup adalah asuransi yang menjamin seumur hidup tertanggung dan akan mendapatkan uang pertanggungan bila tertanggung tersebut meninggal.

n

[image:35.595.146.439.390.530.2]

x x+n Gambar 2.4 Sistem Pembayaran pada Asuransi seumur Hidup

Diilustrasikan bahwa besarnya manfaat (bt) sebesar 1 satuan dibayarkan segera pada saat meninggal, maka :

Untuk bt = 1, t ≥ 0, dan vt = vt diperoleh nilai Zt = vt, t ≥ 0. Sehingga untuk menentukan nilai dari Net Single Premium (Premi Tunggal) atau disebut juga nilai sekarang {Actuarial Present Value (APV)} dengan simbol �̅_�adalah :

= ∫ �∞ �∙ �_{� �}∙ �_��

Dengan mensubtitusikan persamaan (2.5.4) dan (2.6.2) diperoleh nilai APV dengan distribusi Gompertz :

�̅� = ∫ exp −� ∙ exp[−∞ �+�− � ] ∙ �+��

= ∫ exp −� + [ − �+�− � ] ∙ �+��

∞

. .

Persamaan 2.7.1 adalah nilai APV untuk Asuransi Seumur Hidup.

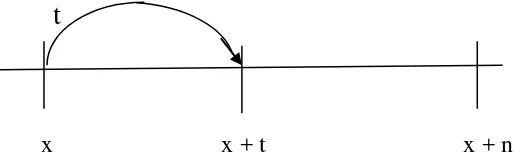
2.7.2 Asuransi Berjangka (Term Insurance)

Asuransi berjangka adalah suatu asuransi yang apabila tertanggung sampai dengan jangka waktu tertentu meninggal, maka akan mendapatkan uang pertanggungan (manfaat).

t

[image:36.595.171.428.489.568.2]

x x + t x + n Gambar 2.5 Sistem Pembayaran Benefit pada Asuransi Berjangka

Besarnya manfaat (bt) sebesar satu satuan diberikan segera setelah meninggal, maka :

bt = 1 t n bt = 0 t > n

22

E[Z_t]=E[Vt]= �̅′_�:�̅|= ∫ �� �. � � + ∫ . � �_�∞

�̅′�:�̅|= ∫ ��.�px μx+t �

�

Dengan mensubtitusikan persamaan (2.5.4) dan (2.6.2) diperoleh nilai APV dengan distribusi Gompertz :

�̅′�:�̅|= ∫ exp −� ∙ exp[−� �+�− � ] ∙ �+��

= ∫ exp −� + [ −� �+�₋ � _{] ∙} �+�_�

= ∫ exp −� −� �+�₋ � _∙ �+�_{� (2.7.2)}

Persamaan 2.7.2 adalah nilai APV untuk Asuransi Berjangka.

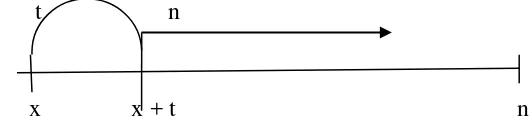
2.7.3 Asuransi Endowment Murni (Pure Endowment Insurance)

Asuransi endowment murni adalah suatu asuransi yang apabila tertanggung sampai dengan jangka waktu tertentu masih hidup, maka akan mendapatkan sejumlah uang pertanggungan. Untuk endowment murni, t dapat lebih besar atau sama dengan interval waktu dari diterbitkannya polis sampai pembayaran benefit / manfaat.

t x n

Gambar 2.6 Sistem Pembayaran Manfaat pada Asuransi Endowment Murni

Besarnya manfaat (bt) sebesar 1 satuan diberikan sesaat setelah meninggal, maka : bt= 1 t > n vt = vn t > n

Dengan Zt = vt t > n dan Zt = 0 t �

Maka nilai APV dari asuransi ini adalah :

E[Z_t]=E[Vt]= �̅_�:′�̅̅̅_= ∫ �_�∞ �. � � = �� ∫ � �_�∞

Catatan _{� �} = p(t(x) = ∫ � �

_��_�= p(t(x) > t) = ∫ � �∞

Dari persamaan (2.5.4) dan persamaan (2.6.2) diperoleh nilai APV dengan distribusi Gompertz :

�̅�:′�̅̅̅̅= ��∙ �� �

= exp −�� ∙ exp [− �+�₋ � _]

= exp −�� − �+�₋ � _(2.7.3)

Persamaan (2.7.3) adalah nilai APV untuk Asuransi Endowment Murni.

2.7.4 Asuransi Dwiguna

Asuransi dwiguna adalah suatu asuransi yang apabila tertanggung meninggal dunia atau masih hidup dalam jangka waktu asuransi maka tetap akan mendapatkan sejumlah uang pertanggungan.

t n

[image:38.595.210.475.624.688.2]

24

Besarnya manfaat (bt) sebesar 1 satuan diberikan sesaaat setelah meninggal atau diberikan sesaat setelah masa kontrak habis dan tertanggung masih hidup, maka : bt= 1 t < n vt = vt t < n

bt= 1 t > n vt = vt t > �

Dengan Zt = Vt t <n dan Zt = Vn t � Maka besarnya APV untuk asuransi ini adalah :

E[Z_t]=E[Vt]= �̅_�:�̅|= ∫ �� �. � � + ∫ �_�∞ �. � �

Dari persamaan (2.5.4) dan (2.6.2) diperoleh nilai APV dengan distribusi Gompertz :

�̅�:�̅̅̅̅̅| = ∫ ��.�px μx �

� +��_. ��_�

= ∫ �� −� −� �+�+ � ∙ �+�� + exp −�� − �+�− �

(2.7.4)

Persamaan (2.7.4) adalah nilai APV untuk Asuransi Dwiguna.

2.8 Anuitas (Annuity)

Anuitas didefinisikan sebagai suatu rangkaian pembayaran dengan jumlah tertentu dalam selang dan periode waktu tertentu (Sembiring, 1986).

2.8.1 Anuitas Tentu

tidak perlu sama. Anuitas tentu dibagi menjadi dua yaitu anuitas yang dibayarkan di awal jangka waktu pembayaran disebut anuitas awal (due-annuity) dan anuitas yang dibayarkan di akhir jangka waktu pembayaran disebut anuitas akhir (immediate annuity). Total nilai sekarang dari anuitas akhir yang dinotasikan dengan _�|̅̅̅ adalah :

PV = _�|̅̅̅= v + v 2 + v3+… + vn-1 +vn

Dengan menggunakan rumus deret geometri, maka :

�|

̅̅̅= v(1+v + v 2 _{+ v}3+… + vn-2 _+vn-1₎ = v −��

−�

= v −�� �

�|

̅̅̅= − � �

Sedangkan anuitas awal dinotasikan sebagai ̈_�|̅̅̅ adalah :

̈_�|̅̅̅=1+v + v 2 + v3+… + vn-2 +vn-1

= − �_{− �}�

= − �_� �

Nilai akumulasi dari anuitas tentu akhir dengan n pembayaran diberi notasi _�|̅̅̅ .

Nilai akumulasi dari anuitas ini adalah jumlah nilai akumulasi dari tiap pembayaran sehingga :

�|

̅̅̅= + �− + + �− + ⋯ + + +

26 �| ̅̅̅= + �− − + −� − + − ∙ + + �| ̅̅̅= + � ₋ + − �| ̅̅̅= + � ₋

Untuk anuitas tertentu awal dengan n pembayaran, nilai akumulasinya diberi

notasi _�|̅̅̅, maka :

�|

̅̅̅ = + �− + + �− + ⋯ + +

� ∙ �|̅̅̅= + �− + + �− + ⋯ +

� ∙ �|̅̅̅= �

2.8.2 Anuitas Tentu (Pembayaran j-kali Setahun)

Suatu anuitas tentu yang pembayarannya dilakukan m-kali dalam setahun dengan selang pembayaran setiap 1/m tahun dan total pembayaran dalam setahun sebesar

1. Maka total nilai sekarang dari anuitas akhir yang dinotasikan _�|̅̅̅ adalah :

�|̅̅̅ = v1/j + v 2/j + v3/j+… + vn-1/j +vn)

= v /j −��− /� −� .� =

−��

[ + .�_{− ]}

= −�_��

Sedangkan untuk anuitas awal

̈_�|̅̅̅ = + v1/j + v 2/j + v3/j+… + vn-1/j +vn-1/j)

= −�� −� .� =

−�� [ − − .�_]

2.8.3 Anuitas Tentu (Untuk Pembayaran Kontinu)

Suatu anuitas tentu yang pembayarannya dilakukan sebanyak j kali dalam setahun dengan j→∞, dengan pembayaran yang dapat dilakukan setiap saat. Anuitas ini dinotasikan dengan :

�|

̅̅̅= ∫ ��� �

�|

̅̅̅= − � �

�

2.8.4 Anuitas Hidup (Life Annuity)

Anuitas hidup deretan pembayaran yang sifatnya periodik di mana masih hidup pada saat pembayaran jatuh tempo. Seperti halnya anuitas tentu, anuitas hidup juga dibagi menjadi dua, yaitu : anuitas hidup awal dan anuitas hidup akhir. Perbedaan antara anuitas hidup awal dan anuitas hidup akhir adalah terletak pada pembayaran pertama sedangkan pembayaran berikutnya bersamaan waktunya. Karena dianggap bahwa akhir tahun berimpit dengan awal tahun berikutnya, sehingga didapat hubungan : ̈_�|̅̅̅= + _�|̅̅̅ (Sudarto, 1976).

Sedangkan anuitas hidup sebesar satu per akhir tahun yang pembayarannya dilakukan secara kontinu atau setiap saat disebut anuitas hidup kontinu. Dengan nilai sekarang (Present Value) dari pembayarannya anuitas tersebut dinotasikan dengan variabel acak Y adalah = ̅_�dengan T ≥0.

28

Actuarial Present Value (APV) dari anuitasnya adalah :

̅�= [ ] = [̅�] = ∫ ̅� ∞ ∙ � � = ∫ −�� � ∙ � � ∞

Dengan menggunakan integral parsial tertentu diperoleh

∫ �� = [ �] − ∫ � � � � Misalkan, = ̅� →�_{� =�}� − � � � = � � − �� � = − � ∙ ��� � = − � ∙ ��

∙ ln � = − � ∙ ��_{∙ � +} −

= � ∙ ��_{∙ �}

= �� _{→ � = �}�_�

�� = � �

diketahui dari persamaan (2.2.3), maka

�� = �� �∙ ��+� → � =− �� � Sehingga, ̅�= ∫ ̅� ∞ ∙ � � = ̅_�∙ (− �_{� �})∞ − ∫ − �∞ _{� �}∙ ���

Jika, = ∞ → �_{� �}= � � ̅_� = −�� � =�

= → �_{� �} = � � ̅_� = −� � = Maka,

Dengan mensubtitusikan persamaan (2.5.4) dan persamaan (2.6.2) diperoleh nilai anuitas dengan distribusi Gompertz :

̅�= [̅�] = ∫ exp −� ∞

∙ exp [− �+�₋ � _]�

= ∫ exp −�∞ − �+�₊ � _{� (2.8.1)}

Persamaan (2.8.1) adalah nilai dari anuitas kontinu dari asuransi seumur hidup.

Selain anuitas untuk asuransi seumur hidup terdapat juga anuitas untuk asuransi berjangka yaitu pada asuransi berjangka n tahun, asuransi pure endowment dan asuransi dwiguna. Perbedaannya adalah pada jangka waktu asuransinya karena besarnya pembayaran akan dipengaruhi oleh tingkat bunga, peluang hidup dan lamanya pembayaran. Dengan menggunakan cara yang sama pada anuitas seumur hidup, didapatkan :

̅′�:�̅= [̅�] = ∫ exp −� �

∙ exp [− �+�₋ � _]�

= ∫ exp −�� − �+�₊ � _{� (2.8.2)}

Persamaan (2.8.2) adalah nilai dari anuitas kontinu untuk asuransi berjangka.

2.9 Premi

30

memperhatikan peluang meninggal dan tingkat bunga. Di dalam premi bersih belum diperhitungkan biaya-biaya yang dikeluarkan untuk pengelolaan, antara lain : biaya administrasi, biaya penutupan, komisi dan lain-lain. Biaya-biaya yang dikeluarkan oleh perusahaan asuransi sebenarnya dibebankan kepada pemegang polis. Biaya-biaya tersebut sudah termasuk di dalam premi yang dibayar dan umumnya disebut sebagai premi bruto atau gross premium. Sehingga untuk memperoleh premi bruto harus ditambah biaya pada premi netto atau dapat ditulis sebagai berikut :

Premi Bruto (gross premium) = Premi netto + Biaya

Salah satu prinsip yang digunakan untuk menentukan nilai premi adalah prinsip ekivalensi yaitu nilai tunai premi yang dibayarkan oleh pihak nasabah harus sama dengan nilai tunai asuransi atau santunan yang akan dibayarkan oleh pihak perusahaan asuransi. Nilai tunai adalah sejumlah uang yang dijamin oleh perusahaan asuransi untuk dibayarkan kepada pemegang polis membatalkan pertanggungan asuransi dan menyerahkan polis kepada perusahaan. Berikut akan dibahas mengenai beberapa hal yang mendasari perhitungan nilai premi.

2.9.1 Fungsi Kerugian

Terdapat dua jenis kewajiban di dalam asuransi yaitu :

2. Kewajiban pihak nasabah adalah membayar premi langsung sekaligus diawal kontrak atau secara berkala pada setiap periode yang telah ditentukan.

Kedua jenis kewajiban di atas membentuk suatu fungsi total kerugian untuk menghitung seberapa besar kerugian yang akan ditanggung oleh pihak perusahaan asuransi dan dihitung dengan

= − � ∙

Dimana, L : nilai dari fungsi kerugian Z : nilai tunai asuransi jiwa P : premi Y: nilai tunai anuitas hidup

= − � ∙ ̅�

Apabila diberikan santunan sebesar Rp. 1,- untuk asuransi jiwa berjangka yang dibayarkan pada akhir tahun kematian, maka fungsi kerugian yang diperoleh sebagai berikut :

= �� � + _{− � ∙ ̈} � � + | ̅̅̅̅̅̅̅̅̅̅̅

Resiko kerugian perusahaan terjadi ketika nilai kerugiannya memberikan nilai positif, dimana nilai santunan yang dibayarkan kepada pihak nasabah lebih besar dari premi yang diterima oleh pihak perusahaan asuransi. Secara teoritis nilai kerugian yang positif terjadi ketika pihak nasabah meninggal dunia pada awal kontrak asuransi.

2.9.2 Prinsip Ekivalensi

32

[ ] =

[ − � ∙ ] = [ ] − � ∙ [ ] = � ∙ [ ] = [ ]

� = [ ]_{[ ] .9.}

2.9.3 Penentuan Nilai Premi

Berikut ini akan dikemukakan beberapa persamaan untuk menentukan besarnya nilai premi, khusus untuk produk asuransi jiwa berjangka n tahun untuk usia tertanggung x tahun dimana santunan dibayarkan seketika pada saat nasabah meninggal dunia dan pembayaran premi dilakukan secara kontinu selama masih hidup.

Berdasarkan persamaan (2.9.1) maka diperoleh persamaan baru yang akan digunakan untuk menghitung nilai premi kontinu sebagai berikut :

� = [ ]_{[ ]}

� =�̅′_̅′�:�̅

�:�̅ =

∫� −��∙ �� �∙ ��+��

∫� −��_{∙ ��}

� �

Dengan �̅′_�:�̅ adalah premi tunggal netto asuransi berjangka dan ̅′_�:�̅merupakan

Dengan demikian berdasarkan (2.9.1) didapatkan rumus nilai premi untuk beberapa jenis asuransi yang lain :

1. Asuransi seumur hidup

� =�̅_̅�

� .9. 2. Asuransi berjangka

� =�̅′�:�̅

̅′�:�̅ .9.

3. Asuransi Endowment murni

� =�̅_̅�:′�̅̅̅

�:′�̅̅̅ .9. 4. Asuransi dwiguna

� =�̅_̅�:�̅̅̅̅̅

�:�

̅̅̅̅̅ .9.

2.10 Cadangan

34

asuransi harus mencadangkan sejumlah dana untuk menutupi kerugian yang terjadi.

2.10.1 Fungsi Kerugian dan Equal Principle

Berkenaan dengan cadangan untuk sebuah pembayaran dalam batas waktu kelangsungan hidup t tahun maka cadangan didefinisikan sebagai sebuah nilai harapan dari kerugian masa mendatang pada waktu t oleh perusahaan asuransi, diberikan pada (x) yang sudah bertahan hidup sampai t tahun. Nilai kerugian yang dilambangkan dengan L merupakan variabel acak dari nilai sekarang santunan yang dibayarkan oleh penanggung lebih kecil dari premi anuitas yang dibayarkan oleh tertanggung. Prinsip ini dikenal dengan prinsip ekuivalen (Equivalent Principle) dan mempunyai syarat bahwa E[L] = 0, maka

E[nilai sekarang santunan – nilai sekarang premi] = 0 E[nilai sekarang santunan] = E[nilai sekarang premi]

Sehingga untuk variabel acak kerugiannya didefinisikan :

= = ��_{− � ̅} �

Secara umum untuk T(x) > t, didapat :

� = �� � −�− � �̅� ̅� � −�

Dari persamaan (2.7.2) dengan cadangan asuransi berjangka n tahun yang

dinotasikan _��̅ �̅′_�:�̅ maka diperoleh :

�̅

= (�� � −�_{ � > ) − � �̅′}

�:�̅ ̅� � −� � >

= �̅�+�:�̅− � �̅′�:�̅ ∙ ̅�+�:�̅ (2.10.1)

Persamaan (2.10.1) merupakan cadangan untuk asuransi berjangka n tahun. Dengan mengunakan prinsip ekuivalen tersebut maka akan diperoleh persamaan untuk cadangan netto untuk asuransi yang lainnya.

2.10.2 Cadangan Netto

Cadangan adalah sejumlah uang yang harus disediakan oleh pihak perusahaan asuransi dalam waktu pertanggungan dan digunakan untuk membayar santunan sesuai dengan kesepakatan pada awal kontrak. Jadi, cadangan bukanlah milik perusahaan tetapi milik pemegang polis. Cadangan diperlukan semata-mata agar perusahaan asuransi dapat berjalan sesuai dengan dasar-dasar yang sudah ditentukan. Cadangan didefinisikan sebagai selisih antara nilai sekarang (Present Value) dari manfaat yang akan diterima dengan nilai sekarang (Present Value) dari premi bersih yang akan datang sesuai dengan anuitas yang telah ditentukan. Besarnya cadangan tergantung kepada perkembangan premi, artinya semakin banyak jumlah pemegang polis semakin besar jumlah cadangan yang dibutuhkan.

36

1. Cadangan Retrospektif

Cadangan retrospektif adalah perhitungan cadangan dengan berdasarkan jumlah total pendapatan di waktu yang lalu sampai saat dilakukan perhitungan cadangan dikurangi dengan jumlah pengeluaran di waktu yang lampau, untuk tiap pemegang polis (Takasi, 1993).

Past

Outflow �_�∙ …….. �_�+�− ∙ �_�+�− ∙

[image:51.595.115.508.244.378.2]

x x+1 ……… x+t-1 x+t Inflow _�∙ �_{� �+} ∙ �_{� �+�−} ∙ �_�

Gambar 2.8. Cadangan Retrospektif

Dengan Benefit Rp.1,-, dari Gambar 2.8 akan diperoleh cadangan retrospektif akhir tahun t sebagai berikut:

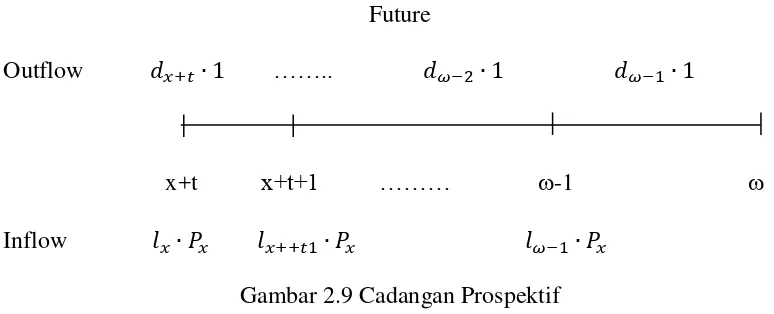
2. Cadangan Prospektif

Cadangan prospektif adalah besar cadangan yang berorientasi pada pengeluaran diwaktu yang akan atau dengan pengertian lain yaitu perhitungan cadangan dengan berdasarkan nilai sekarang dari semua pengeluaran diwaktu yang akan datang dikurangi dengan nilai sekarang total pendapatan di waktu yang akan datang untuk tiap pemegang polis (Takasi, 1993).

Future

Outflow �_�+�∙ …….. �_�− ∙ �_�− ∙

x+t x+t+1 ……… -1 

[image:52.595.112.499.285.442.2]

Inflow _�∙ �_{� �++�} ∙ �_{� �−} ∙ �_� Gambar 2.9 Cadangan Prospektif

Dengan Benefit Rp.1,-, dari Gambar 2.9 akan diperoleh cadangan prospektif akhir tahun t sebagai berikut:

� = ��+�∙ ∙ � + ⋯ + ��− ∙ ∙ ��− �+� � − �+�∙ ��+ �+�+ ∙ ��� + ⋯ + �− ∙ ����− �+� − = ∙ (��+�∙ � + ⋯ + ��− ∙ ��− �+� ) − �� �+�∙ � + �+�+ ∙ � + ⋯ + �− ∙ ��− �+� − = ∙ �+� � ∙ � + ⋯ + �− � ∙ � �− �+� _{− �} � �+� � ∙ � + �+�+ � ∙ � + ⋯ + �− � ∙ ��− �+� − = � �∙ � + ⋯ +�−  �∙ ��− �+� − �� ���∙ � +�+ ��∙ � + ⋯ +�− ��∙ ��− �+� − � = ∙ ��+�− ��∙ ̈�+�

38

Cadangan prospektif juga merupakan cadangan netto, dan pada tulisan kali ini cadangan yang dipakai adalah cadangan prospektif.

Berdasarkan persamaan (2.10.3) maka akan didapatkan formula untuk cadangan dengan berbagai jenis asuransi :

1. Asuransi Seumur Hidup

� = ∙ �̅�− � ∙ ̅�

� (2.10.4)

2. Asuransi Berjangka

� = ∙ �̅′�:�̅− � ∙ ̅′�:�̅

� (2.10.5)

3. Asuransi Endowment murni

� = ∙�̅_�:′�̅̅̅− � ∙ ̅�:′�̅̅̅

� (2.10.6)

4. Asuransi Dwiguna

� = ∙ �̅�:�̅̅̅̅̅− � ∙ ̅�:�̅̅̅̅̅

III. METODE PENELITIAN

3.1 Waktu dan Metode Penelitian

Pada bab sebelumnya telah dibahas bahwa cadangan adalah sejumlah uang yang harus disediakan oleh pihak perusahaan asuransi dalam waktu pertanggungan dan digunakan untuk membayar santunan sesuai dengan kesepakatan pada awal kontrak. Jadi, cadangan bukanlah milik perusahaan tetapi milik pemegang polis. Seiring berjalannya waktu cadangan akan disesuaikan berdasarkan premi yang dibayarkan. Jika pada cadangan netto menggunakan premi bersih maka pada cadangan yang disesuaikan akan terdapat biaya yang harus ditanggung pemegang polis sehingga disebut premi kotor. Pada bab ini membahas penelitian yang dilakukan dengan mengkaji teori-teori yang berhubungan dengan cadangan pada produk asuransi jiwa yang pembayaran preminya dilakukan satu kali pertahun yang diteliti pada tahun Ajaran 2011/2012. Langkah-langkahnya secara garis besar dapat diuraikan sebagai berikut :

1. Menentukan nilai APV (Actuarial Present Value). 2. Menentukan nilai anuitas.

40

4. Menentukan nilai cadangan netto.

5. Menentukan nilai cadangan metode Zillmer dan cadangan metode Kanada sebagai akibat adanya faktor biaya pada premi.

Untuk mengerjakan langkah-langkah tersebut, maka akan diuraikan terlebih dahulu mengenai cadangan lebih khusus.

3.2 Cadangan Disesuaikan

Cadangan disesuaikan yaitu cara menghitung atau menilai cadangan yang disesuaikan dengan kemampuan perusahaan (Sembiring, 1986). Perusahaan asuransi memerlukan biaya dalam melaksanakan tugasnya, maka premi yang disajikan oleh perusahaan asuransi jiwa kepada masyarakat adalah gross premium yang terdiri dari premi netto dan biaya. Beberapa biaya yang terpenting adalah biaya pemeriksaan kesehatan bagi orang yang diasuransikan, biaya pemeriksaan kesehatan, komisi dan pembuatan polis asuransi sehingga biaya pada tahun kedua dan seterusnya jauh lebih kecil dari biaya tahun pertama. Biaya dari premi tidak akan cukup pada tahun-tahun permulaan polis tetapi kekurangan tersebut akan tertutup oleh premi tahun terakhir.

Misalkan P menyatakan premi bersih datar untuk suatu jenis asuransi. Premi tersebut

akan diganti dengan α pada tahun pertama dan diikuti oleh β pada tahun-tahun

berikutnya. α dan β adalah premi yang disesuaikan. Sebenarnya pemegang polis

hanya membayar premi kotor yang sama besarnya tiap tahun, yaitu P+ biaya. α dan β

hanya ada dalam perhitungan para aktuaris dan tidak ada sangkut pautnya dengan pemegang polis. P di satu pihak dan α dan β dipihak lain dihubungkan oleh ;

Nilai tunai seluruh P = nilai tunai α + nilsi tunai seluruh β

Persamaan ini berlaku pada waktu polis dikeluarkan. Bila n menyatakan jangka waktu penyesuaian cadangan, maka hubungan di atas dapat dinyatakan secara matematika sebagai

+ �:�−̅̅̅̅̅̅ = � ∙ ̈�:�̅

α < P, karena sebagian dari P dipakai untuk biaya tahun pertama yaitu sebesar P-α.

Jadi dari premi bersih tahun pertama sebesar P, hanya α yang disediakan untuk

membayar santunan di tahun tersebut, sisanya P-α “dipinjam” perusahaan dan pinjaman tersebut akan dibayar kelak dari premi tahun-tahun berikutnya. Karena itu β>P, jadi α<P<β.

3.3 Cadangan Metode Zillmer

42

masih muda sehingga masih tumbuh. Dalam metode Zillmer melibatkan premi kotor, premi bersih dan beberapa macam biaya. Di dalam premi kotor mengandung beberapa macam biaya yang diperlukan oleh perusahaan asuransi. Secara umum biaya-biaya itu dapat dibagi menjadi :

1. Biaya permulaan (tahun pertama), yaitu biaya yang harus dikeluarkan waktu polis dikeluarkan (komisi, pemeriksaan kesehatan, alat-alat tulis dan sebagainya). 2. Biaya lanjutan, yaitu biaya tahun-tahun selanjutnya (komisi lanjutan, biaya

mengadministrasikan polis, biaya penyelesaian tagihan dan sebagainya)

Dari segi lain biaya-biaya dapat dibagi menjadi :

1. Biaya yang sebanding dengan premi, misalnya komisi pada agen atau tenaga lapangan, utama sekali pada tahun kedua dan seterusnya.

2. Biaya yang sebanding dengan besar santunan, misalnya komisi pertama pada agen.

3. Biaya yang tidak tergantung pada premi maupun santunan, misalnya biaya pemeriksaan kesehatan, prangko, alat-alat tulis dan sebagainya.

Misalkan premi bersih datar dinyatakan dengan P dan premi kotor dinyatakan dengan P”. Misalkan juga banyak k% dari premi kotor sehingga diperoleh hubungan :

P” = P + k.P” , k dalam %

Sehingga �" =

−�∙ �

�" _{= � + �}"

+ = − ∙ � +

Misalkan f menyatakan selisih antara biaya permulaan dengan biaya lanjutan per 1 rupiah santunan. Jika premi dibayarkan secara tahunan maka :

�" ∙ � = � + �"+ �+ �

�" = � + �"_{+ +} � �

�" = � + � +₋ + + �

�

�" =� − + � +₋ + − + �

�

�" =� +_{− +} �

�

� + �

�= �" − −

�� + � = �"-k∙P" − �, nilai tunai dari f adalah f sendiri

= �" �- kP" + � (3.2.1)

Diketahui sebelumnya bahwa cadangan didefinisikan sebagai berikut :

� = ∙ ��+�− ��∙

� �+�

Sehingga untuk cadangan yang disesuaikan dengan metode Zillmer diperoleh :

�� _{= �}

�+�− �" ∙ �+�

� − ∙ �" + �+�

�� _{= �}

�+�− �" ∙ �+�

� − ∙ �" + �+�

�� _{= �}

�+�− �"

44

�� _{= �}

�+�− �

� + �

� �+�

�� _{= �}

�+�− � ∙ �+�

� − � �+�

� . . Berdasarkan persamaan (3.2.2), bila �

�� kita nyatakan dengan p dan P+p kita nyatakan

dengan Pz disebut premi Zillmer maka persamaan (3.2.2) menjadi :

��

� = ��+�− � ∙ �+�− � ∙ �+�

��

� = ��+�− � + � ∙ �+�

��

� = ��+�− ��∙ �+� (3.2.3)

Persamaan (3.2.3) adalah cadangan Zillmer dalam bentuk prospektif untuk asuransi seumur hidup. Untuk jenis asuransi yang lain bentuk ini, perlu mendapat penyesuaian seperti biasa. Sering pula biaya permulaan f dinyatakan dalam persentasi dari santunan, dan disebut kuota Zillmer (Zillmer’s quato). Misalnya f=1,5% dari besar santunan, jadi bila santunan sebesar 1 juta rupiah maka f=Rp.15.000.

3.4 Cadangan Metode Kanada

Untuk membedakan dengan metode yang lain, pada metode Kanada ini akan diberi simbol K pada bagian atas dari lambang yang digunakan jadi untuk cadangan adalah

��

Aturan ini membagi polis atas dua kelompok sebagai berikut :

a. Polis yang mempunyai premi bersih datar lebih besar dari premi bersih datar asuransi seumur hidup dengan besar santunan dan usia waktu dikeluarkan yang sama.

b. Polis lainnya.

Aturan Kanada menentukan bahwa semua polis yang termasuk kelompok (a) menggunakan metode Kanada sedangkan polis yang dalam kelompok (b) tetap menggunakan metode berjangka permulaan penuh.

Penyesuaian mencakup seluruh jangka waktu pembayaran premi dan didasarkan pada selisih antara premi bersih datar P dengan �, penyesuaian premi bersih tahun

pertama. Bila �_� menyatakan asuransi seumur hidup dengan santunan yang sama besarnya maka metode ini menentukan bahwa :

� − � _{= �}

�− �_� (3.2.4)

Untuk � > �_�(artinya, polis masuk kelompok (a)). Jadi,

� _{= � − �}

�− �_� (3.2.5)

46

� ₊ �_∙

�:�−̅̅̅̅̅̅= � ∙ �:�̅ atau

� ₌ � ∙ �:�̅− �

�:�−̅̅̅̅̅̅ . .6

Dengan �

� adalah sebagai berikut :

� � =

�

��_{∙ �}

=_{� �+ − �+}� _∙

�

= ��+ � � �+ _{∙ �}

Kemudian penyebut dan pembilang sama-sama dikaliiakan dengan ��

=_� � ∙_�+ �_∙

�

= � ∙

�

��+ �

= � ∙��

�

= �̅′�:̅| (3.2.7)

Dengan mensubstitusikan persamaan (3.2.7) ke dalam persamaan (3.2.5) maka dapat diperoleh :

� _{= � − �} �− �

�

Berdasarkan persamaan (2.10.3) maka akan didapatkan formula untuk cadangan Kanada dengan berbagai jenis asuransi untuk tahun pertama dan berikutnya :

1. Asuransi seumur hidup

�� _{= ∙ �̅}

�− �∙ ̅�

�� _{= ∙ �̅}

�− �∙ ̅�

� (3.2.8)

2. Asuransi berjangka

� = ∙ �̅′�:�̅− �∙ ̅′�:�̅

� = ∙ �̅′�:�̅− �∙ ̅′�:�̅

� (3.2.9)

3. Asuransi Endowment murni

� = ∙�̅_�:′�̅̅̅− �∙ ̅�:′�̅̅̅

� = ∙�̅_�:′�̅̅̅− �∙ ̅�:′�̅̅̅

� (3.2.10)

4. Asuransi Dwiguna

� = ∙ �̅�:�̅̅̅̅̅− � ∙ ̅�:�̅̅̅̅̅

� = ∙ �̅�:�̅̅̅̅̅− �∙ ̅�:�̅̅̅̅̅

� (3.2.11)

58

V.

KESIMPULAN DAN SARAN

5.1 Kesimpulan

Dari hasil penelitian dan pembahasan yang telah dilakukan maka dapat diambil beberapa kesimpulan dari tulisan ini yaitu :

1. Terbukti benar bahwa pada akhir tahun polis, perusahaan menyediakan cadangan yang nilainya mendekati dengan uang pertanggungan atau benefit untuk Asuransi Endowment Murni, Asuransi Dwiguna sedangkan pada Asuransi Berjangka dan Asuransi Seumur Hidup cadangannya bernilai nol. 2. Cadangan Kanada cocok untuk jenis Asuransi Endowment Murni dan

Dwiguna, sedangkan Cadangan dengan metode Zillmer cocok untuk semua jenis polis asuransi.

5.2 Saran

1. Untuk peminat kajian cadangan pada Asuransi Jiwa maka dapat diteruskan dengan menggunakan beberapa metode yang lain yaitu Full Preliminary Term dan Commissioners.