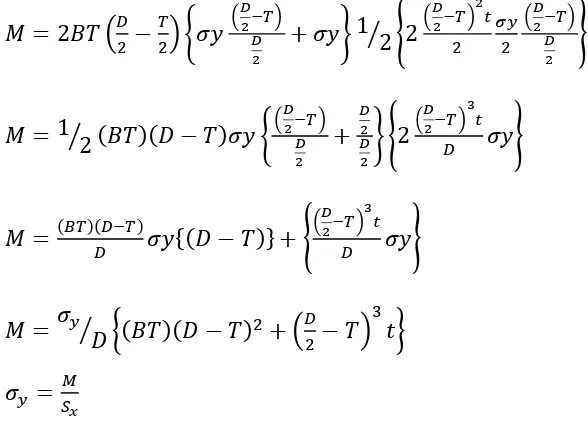ANALISA P
Collapse
PADA GABLE FRAME DENGAN
INERSIA YANG BERBEDA MENGGUNAKAN PLASTISITAS
PENGEMBANGAN DARI FINITE ELEMENT METHOD
Tugas Akhir
Diajukan untuk melengkapi tugas-tugas dan memenuhi Syarat untuk menempuh ujian sarjana Teknik Sipil
Disusun oleh:
AUGUSLIN SABTIAN HALAWA 050404136
SUB JURUSAN STRUKTUR DEPARTEMEN TEKNIK SIPIL
FAKULTAS TEKNIK
UNIVERSITAS SUMATERA UTARA MEDAN
LEMBAR PENGESAHAN
ANALISA P Collapse PADA GABLE FRAME DENGAN INERSIA YANG BERBEDA MENGGUNAKAN PLASTISITAS PENGEMBANGAN DARI
FINITE ELEMENT METHOD
Tugas Akhir
Diajukan untuk melengkapi tugas-tugas dan memenuhi Syarat untuk menempuh ujian sarjana Teknik Sipil
Disusun oleh:
AUGUSLIN SABTIAN HALAWA 05 0404 136
Disetujui oleh:
Dosen Pembimbing
NIP. 195612241981031002 Prof.Dr.Ing.Johannes Tarigan
SUB JURUSAN STRUKTUR DEPARTEMEN TEKNIK SIPIL
FAKULTAS TEKNIK
UNIVERSITAS SUMATERA UTARA MEDAN
Pada perencanaan struktur, telah diketahui bahwa analisa desain
berdasarkan teori linear elastis belum mencerminkan faktor kekuatan struktur
yang sebenarnya. Penyebabnya adalah bahwa dalam merencanakan struktur
tersebut, mengabaikan kemampuan beberapa material tertentu seperti baja, untuk
mengalami deformasi setelah titik lelehnya terlampaui.
ABSTRAK
Dalam tugas akhir ini, penulis mencoba menganalisa perilaku gable frame
yang dibebani dengan beban terpusat dengan inersia yang berbeda dalam tahapan
pembentukan sendi –sendi plastis berdasarkan teori plastis. Analisis struktur
diselesaikan dengan finite element method (metode elemen hingga) untuk struktur
plane frame. Analisis yang dilakukan berdasarkan mekanisme keruntuhan suatu
struktur dalam mencapai beban runtuhnya.
Dari hasil perhitungan, terlihat bahwa analisa secara plastis pada strutur
gable frame menghasilkan faktor beban runtuh (P Collapse) akibat pertambahan beban. Akibat pertambahan beban struktur akan mengalami mekanisme
keruntuhan dengan jumlah sendi plastis yang terbentuk sebelum mengalami
`
Abstrak ... i
DAFTAR ISI
Kata pengantar ... iiDaftar Isi ... iv
Daftar Notasi ... vii
Daftar Tabel ... ix
Daftar Gambar ... x
BAB I Pendahuluan ... 1
1.1 Latar Belakang Masalah ... 1
1.2 Ruang Lingkup Pembahasan ... 3
1.3 Tujuan Penulisan ... 6
1.4 Pembatasan Masalah ... 7
1.5 Metodologi ... 8
BAB II Tinjauan Pustaka ... 9
2.1 Dasar-Dasar Teori ... 9
2.1.1 Hubungan Tegangan Regangan ... 9
2.1.2 Distribusi Tegangan Regangan ... 14
2.1.3 Menentukan Garis Netral Profil ... 16
2.1.4 Hubungan Momen Kelengkungan ... 17
2.1.5 Analisa Penampang ... 22
2.2 Sendi Plastis ... 23
2.2.1 Umum ... 23
2.2.2 Bentuk Sendi Plastis ... 24
2.3.1 Pendahuluan ... 27
2.3.2 Perhitungan Struktur ... 29
2.3.3 Metode Kerja Virtual ... 31
2.3.4 Metode Element Aingga Untuk Plane Frame... 31
BAB III Metode Analisa ... 38
3.1 Umum ... 38
3.1.1 Analisa Elastis ... 38
3.1.2 Analisa Plastis ... 39
3.2 Faktor Bentuk (Shape Faktor) ... 41
3.2.1 Modulus Elastis (sumbu x ) ... 41
3.2.2 modulus Plastis ... 42
3.3 Analisa Plastis Struktur Sederhana ... 44
3.3.1 Analisa Tahap Demi Tahap ... 44
3.3.2 Metode statis ... 49
3.4 Gable Frame ... 49
3.5 Metode Kerja Virtual ... 55
3.6 Pusat rotasi ... 58
3.7 Analisa plastis dengan metode elemen hingga (FEM) ... 61
3.7.1 Penyiapan data dan menentukan model ... 62
3.7.2 Tahap analisa elastis dengan menggunakan FEM ... 62
3.7.3 Memodifikasi kekakuan batang akibat terbentuknya sendi plastis ... 64
3.7.4 Prosedur langkah demi langkah... 65
BAB IV Aplikasi Analisa P Kritis Pada Gable frame ... 68
4.1 Aplikasi perhitungan ... 68
4.3 Memodifikasi kekakuan batang akibat terbentuknya sendi plastis ... 79
BAB V Kesimpulan ... 88
A = Luas potongan penampang
DAFTAR NOTASI
E = Modulus elastisitas
� = Regangan
My = Momen leleh
Mp = momen plastis
� = faktor bentuk, Mp/My
P = Gaya Luar Total
�� = faktor beban (load faktor) l0 = panjang mula –mula l = Gaya Luar Total
��� ,��� = Jarak titik berat luas tekanan dan tarikan ke garis netral dalam kondisi
plastis penuh
fy = Kuat leleh yang disyaratkan untuk tulangan non-prategang u = komponen perpindahan elemen dalam arah x
v = komponen perpindahan elemen dalam arah y
w = komponen perpindahan elemen dalam arah z
σ = Tegangan normal
�� = tegangan leleh
�� = regangan leleh
�� = regangan plastis
ε
s = regangan strain hardening� = jari- jari kelengkungan ( radius of curvature )
K = kelengkungan pada kondisi plastis sebagian (partially plastic state) Ky = kelengkungan pada saat kondisi leleh
f = faktor bentuk
Wi = beban luar ( beban terpusat atau terbagi rata)
∆� = deformasi struktur
∆� = ��2tan� , untuk sudut yang kecil
Mj = momen pada tampang kritis
�� = sudut rotasi sendi plastis
{f} = Matriks gaya-gaya batang
[k] = Matriks kekakuan struktur
Tabel.2.1 : Hubungan persentase karbon ( C ) terhadap tegangan ... 12
DAFTAR TABEL
Tabel.3.1 : Nilai faktor bentuk pada profil IWF ... 43Tabel.4.1 : gaya –gaya dalam masing –masing element ... 78
Tabel.4.2 : momen ujung pada tahap 1... 79
Tabel.4.3 : momen ujung pada tahap 2... 81
Tabel.4.4 : momen ujung pada tahap 3... 83
Gambar.1.1 : Distribusi tegangan pada penampang lintang simetris ... 2
DAFTAR GAMBAR
Gambar.1.2 : Sistem koordinat untuk batang tipikal. ... 4Gambar.1.3 : Pola pembebanan pada gable frame ... 6
Gambar.2.1 : Hubungan tegangan dan regangan ... 10
Gambar. 2.2 : Efek bauschinger ... 13
Gambar. 2.3 : Hubungan plastic ideal ... 13
Gambar.2.4 : Perletakan sederhana ... 14
Gambar.2.5 : Distribusi tegangan – regangan ... 16
Gambar.2.6 : Penentuan garis netral ... 16
Gambar.2.7 : Kelengkungan balok ... 18
Gambar.2.8 : Distribusi tegangan pada penampang ... 20
Gambar. 2.9 : Hubungan momen kelengkungan ... 21
Gambar. 2.10 : Distribusi tegangan pada keadaan leleh dan keadaan plastis pada tampang persegi ... 22
Gambar. 2.11 : Balok dengan pembebanan terpusat ... 24
Gambar. 2.12 : Lengkung sendi plastis beban terpusat ... 25
Gambar. 2.13 : Balok dengan pembebanan terbagi rata ... 25
Gambar. 2.14 : Gambar dengan sendi plastis terbagi rata ... 26
Gambar. 2.15 : Balok dengan pembebanan terbgi rata segitiga... 26
Gambar. 2.16 : Gambar sendi plastis beban segitiga ... 27
Gambar 2.18 : Struktur pembebanan dan mekanisme runtuh perletakan
sendi – jepit ... 28
Gambar. 2.19 : Struktur pembebanan dan mekanisme runtuh perletakan jepit – jepit ... 29
Gambar. 2.20 : sistem koordinat untuk batang tipikal ... 33
Gambar. 2.21 : derajat kebebasan untuk elemen plane frame... 34
Gambar. 3.1 : kondisi struktur pada analisis plastis dan analisis elastis ... 40
Gambar. 3.2 : perbedaan perancangan plastis dengan perancangan elastis ... 40
Gambar. 3.3 : Distribusi tegangan pada keadaan leleh dan keadaan plastis pada profil IWF ... 41
Gambar. 3.4 : balok kedua ujungnya terjepit ... 45
Gambar. 3.5 : kondisi pertama peningkatan momen dalam ... 46
Gambar. 3.6 : kondisi kedua peningkatan momen dalam ... 46
Gambar. 3.7 : diagram momen kondisi ketiga ... 47
Gambar. 3.8 : bentuk lendutan dan mekanisme runtuhnya ... 48
Gambar. 3.9 : hubungan beban – lendutan ... 48
Gambar. 3.10 : pembebanan gable frame ... 50
Gambar. 3.11 : momen resultan ... 51
Gambar. 3.12 : mekanisme keruntuhan ... 54
Gambar. 3.13 : mekanisme runtuh pada struktur tak seragam ... 55
Gambar. 3.14 : mekanisme pada gable frame ... 57
Gambar. 3.15 : struktur pembebanan dan mekanisme yang terjadi ... 58
Gambar. 3.16 : mekanisme kombinasi ... 61
Gambar. 4.2 : gambar bidang momen ... 78
Gambar. 4.3 : gambar bidang momen pada tahap 1 ... 80
Gambar. 4.4 : gambar bidang momen pada tahap 2 ... 82
Gambar. 4.5 : gambar bidang momen pada tahap 3 ... 84
KATA PENGANTAR
Puji syukur penulis ucapkan atas kehadirat Tuhan Yang Maha Pengasih
yang telah memberikan berkat dan kasih-Nya sehingga penulis dapat
menyelesaikan tugas akhir ini yang merupakan syarat utama yang harus dipenuhi
untuk memperoleh gelar sarjana teknik dari Universitas Sumatera Utara. Tugas
akhir ini dengan judul “Analisa P Collapse Pada Gable Frame Dengan Inersia
Yang Berbeda Menggunakan Plastisitas Pengembangan Dari Finite Element
Method”.
Tugas akhir ini disusun untuk diajukan sebagai syarat dalam ujian sarjana
teknik sipil bidang studi struktur pada fakultas teknik Universitas Sumatera Utara
Medan. Penulis menyadari bahwa isi dari tugas akhir ini masih banyak
kekurangannya. Hal ini disebabkan keterbatasan pengetahuan dan kurangnya
pemahaman penulis. Untuk penyempurnaannya, saran dan kritik dari bapak dan
ibu dosen serta rekan mahasiswa sangatlah penulis harapkan.
Penulis juga menyadari bahwa tanpa bimbingan, bantuan dan dorongan
dari berbagai pihak, tugas akhir ini tidak mungkin dapat diselesaikan dengan baik.
Oleh karena itu pada kesempatan ini penulis menyampaikan rasa terima kasih
yang sebesar-besarnya kepada kedua orang tua yang senantiasa penulis cintai
yang dalam keadaan sulit telah memperjuangkan hingga penulis dapat
menyelesaikan perkuliahan ini.
Ucapan terima kasih juga penulis ucapkan kepada :
1. Bapak Prof.Dr.Ing.Johannes Tarigan. Selaku dosen pembimbing dan juga
banyak meluangkan waktu, tenaga dan pikiran untuk memberikan bimbingan
dalam menyelesaikan tugas akhir ini
2. Bapak Ir.Sharizal,MT. Selaku Sekretaris Departemen Teknik Sipil
Universitas Sumatera Utara
3. Bapak/Ibu staf pengajar jurusan teknik sipil Universitas Sumatera Utara.
4. Seluruh pegawai administrasi yang telah memberikan bantuan dan
kemudahan dalam penyelesaian administrasi
5. Kedua Orang Tuaku tercinta ( Y Halawa dan A Zai ) yang selalu memberi
dukungan dan kasih sayangnya dan juga doa yang selalu menyertai penulis.
Buat keempat adikku ( Elman, Hening, Ifan dan Fiktor ) yang kusayangi,
terima kasih kuucapkan kepada kalian atas dorongan dan doanya.
6. Seluruh rekan-rekan mahasiswa-mahasiswi jurusan teknik sipil.
7. Semua pihak yang tidak dapat disebutkan satu-persatu yang telah membantu
penulis baik secara langsung maupun tidak langsung dalam menyelesaikan
tugas akhir ini.
Akhir kata penulis mengharapkan tugas akhir ini dapat bermanfaat bagi
kita semua.
Medan, Agustus 2012
Pada perencanaan struktur, telah diketahui bahwa analisa desain
berdasarkan teori linear elastis belum mencerminkan faktor kekuatan struktur
yang sebenarnya. Penyebabnya adalah bahwa dalam merencanakan struktur
tersebut, mengabaikan kemampuan beberapa material tertentu seperti baja, untuk
mengalami deformasi setelah titik lelehnya terlampaui.
ABSTRAK
Dalam tugas akhir ini, penulis mencoba menganalisa perilaku gable frame
yang dibebani dengan beban terpusat dengan inersia yang berbeda dalam tahapan
pembentukan sendi –sendi plastis berdasarkan teori plastis. Analisis struktur
diselesaikan dengan finite element method (metode elemen hingga) untuk struktur
plane frame. Analisis yang dilakukan berdasarkan mekanisme keruntuhan suatu
struktur dalam mencapai beban runtuhnya.
Dari hasil perhitungan, terlihat bahwa analisa secara plastis pada strutur
gable frame menghasilkan faktor beban runtuh (P Collapse) akibat pertambahan beban. Akibat pertambahan beban struktur akan mengalami mekanisme
keruntuhan dengan jumlah sendi plastis yang terbentuk sebelum mengalami
BAB I
PENDAHULUAN
1.1. Latar Belakang Masalah
Dalam perencanaan struktur dapat dilakukan dengan dua cara yaitu
analisa elastis dan plastis. Pada analisa elastis, diasumsikan bahwa ketika struktur
dibebani maka tegangan yang terjadi lebih kecil dari tegangan leleh (yield stress) dimana tegangan serat terluar tepi atas dan serat terluar tepi bawah adalah linear.
apabila gaya luar mengakibatkan perubahan bentuk (deformation) tidak melebihi batas tertentu, maka perubahan bentuk akan hilang setelah gaya dilepas. Hampir
semua bahan teknik memiliki sifat elastisitas ini. Deformasi yang terjadi akibat
beban yang bekerja akan dapat kembali ke bentuk semula ketika gaya tidak lagi
diberikan. Deformasi elastis mengacu pada hukum hooke yang menyatakan bahwa:
�= ��
Dimana � adalah tegangan yang bekerja, E adalah suatu konstanta pembanding
yang dikenal sebagai modulus elastistisitas atau seringkali disebut sebagai
modulus young ( young’s modulus ) dan ℰ adalah regangan yang dihasilkan. Hubungan ini hanya dapat diterapkan pada keadaan elastis dan mengindikasikan
suatu kemiringan antara tegangan dan regangan yang dapat digunakan untuk
menentukan besarnya modulus young.
Sedangkan pada analisa plastis tegangan yang terjadi adalah tegangan
sehingga struktur akan mengalami deformasi elastis plastis akibat penambahan
beban. Pada daerah plastis Hukum hooke (Hooke’s law) tidak berlaku lagi. Apabila beban terus diperbesar, keadaan plastis penuh akan tercapai, hingga pada
suatu beban plastis, maka seluruh serat akan mengalami tegangan leleh.
Akibatnya pada bagian itu akan mengalami perputaran sudut (rotasi) dengan momen yang tetap (momen plastis) besarnya pada penampang tersebut walaupun tanpa diberikan penambahan beban, keadaan ini yang disebut sebagai sendi
plastis, dalam keadaan ini sejumlah sendi plastis terbentuk. Apabila telah tercapai
sejumlah sendi plastis tertentu, maka struktur tersebut akan runtuh (collapse).
Gambar 1.1. Distribusi tegangan pada penampang lintang simetris.
Distribusi tegangan pada gambar 1.1 menunjukkan tahap – tahap struktur
akan runtuh dimulai dengan momen lentur yang bertambah besar (gambar 1.1a),
penampang balok elastis (gambar 1.1b), plastis diserat atas (gambar 1.1c), plastis
penuh (gambar 1.1d) disini struktur struktur telah runtuh (collapse).
Titik berat My
l y
sy sy
sy distribusi tegangan
(a) (b) (c) (d)
a /2
a /2 Garis netral dalam kondisi plastis penuh
yc yc
sy
sy
Perencanaan struktur berdasarkan pendekatan plastis (perencanaan batas/limit design) semakin banyak dipakai dan diterima dibandingkan dengan design konvensional elastis terutama untuk konstruksi baja misalnya portal baja,
portal beratap lancip (pitched roof portal) ataupun balok menerus karena baja merupakan material yang memiliki daktalitas yang tinggi. Daktalitas merupakan
suatu sifat yang menggambarkan kemampuan suatu material untuk mengalami
deformasi secara plastis (tidak dapat kembali pada bentuk semula).
1.2. Ruang Lingkup Pembahasan
Dalam analisa P collapse pada gable frame diperlukan perencanaan yang matang. Hal ini menjadi poin penting yang akan menentukan apakah struktur
tersebut sudah sesuai atau belum dengan standar perencanaan.
Pada tugas akhir ini akan dibahas perhitungan factor beban runtuhnya
(collapse load factor,��) akibat struktur mengalami mekanisme keruntuhan. Beban runtuh diperoleh dengan melacak keadaan pembebanan portal, dan dengan
melakukan analisa elastis (metode finite element untuk plane frame element) pada
portal yang dimodifikasi akibat terbentuknya sendi plastis baru yang disebabkan
pertambahan beban.
Jika sendi plastis terbentuk di salah satu atau kedua ujung batang, maka
matriks kekakuan batang perlu diubah agar sesuai dengan kenyataaan bahwa
Gambar 1.2. sistem koordinat untuk batang tipikal.
Tiga kombinasi di ujung adalah:
(i) Sendi di ujung kiri (gambar 1.2), gaya dan perpindahan dihubungkan
oleh: {�} = [�]{�} ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧���1
�1
��1 ��2 ��2 ��2⎭⎪⎪
⎬ ⎪ ⎪ ⎫ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢
⎡ ��� 0 0
0 12�� �3
6�� �2
0 6�� �2
4�� �
−��� 0 0
0 −12�� �3
6�� �2
0 −6�� �2
2�� �
−��� 0 0
0 −12��
�3 −6���2
0 6��
�2 2���
��
� 0 0
0 12��
�3 −6���2
0 −6��
�2 4��� ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎩ ⎪ ⎨ ⎪ ⎧��11
�1
�2
�2
�2⎭⎪
⎬ ⎪ ⎫
Karena momen lentur di sendi (akibat pertambahan beban) sama
dengan nol ( Mz1=0 ) maka
�1=�− 3 2��1+
3 2��2−
1 2�2�
Menghasilkan matriks kekakuan yang telah dimodifikasi {�∗��} = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢
⎡��� 0 0 0 3���3 0 0 0 0
−��� 0 0
0 −3���3 3���2
0 0 0
−��� 0 0 0 −3��
�3 0 0 3���2 0
��
� 0 0 0 3��
�3 −
3�� �2 0 −3���2 3��� ⎦⎥
⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
(ii) sendi di ujung kanan. Prosedur yang sama menghasilkan :
{�∗��} = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢
⎡��� 0 0 0 3��
�3 3��
�2 0 3���2 3���
−��� 0 0 0 −3��
�3 0 0 −3���2 0 −��� 0 0
0 −3���3 −3���2
0 0 0
��
� 0 0 0 3���3 0
0 0 0⎦
⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
(iii) sendi di kedua ujung. Disini matriks kekakuan direduksi ke kakuan
batang yang dibebani secara aksial, karena lenturan tidak mungkin
lagi. {�∗��} = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢
⎡ ��� 0 0
0 0 0
0 0 0
−��� 0 0
0 0 0
0 0 0
−��� 0 0
0 0 0
0 0 0
��
� 0 0
0 0 0
0 0 0 ⎦
⎥ ⎥ ⎥ ⎥ ⎥ ⎤
Pada prinsipnya teori dan cara perhitungan pendekatan yang akan
dibahas berlaku hanya untuk konstruksi gable frame yang prismatis dengan inersia
Pada contoh perhitungan, kasus yang ditinjau adalah gable frame Pola
pembebanannya adalah seperti pada gambar 1.2
Gambar 1.3. pola pembebanan pada gable frame
1.3. Tujuan Penulisan
Adapun maksud dan tujuan utama penulisan tugas akhir ini adalah untuk
mendapatkan factor beban runtuhnya (collapse load factor,��) akibat struktur mengalami mekanisme keruntuhan pada gable frame akibat adanya beban yang
disebabkan oleh beban terpusat asimetris dengan jumlah sendi plastis yang
terbentuk sebelum megalami keruntuhan.
Tugas akhir ini juga bertujuan untuk memberikan gambaran akan
pentingnya analisa plastis pada suatu bangunan khususnya pada pada bangunan
yang berubah fungsi.
Tujuan lain adalah membuka wawasan kepada masyarakat, khususnya
kaum intelektual seperti mahasiswa, perencana, ilmuwan mengenai mekanisme
keruntuhan pada gable frame.
4Pc
Pc
3Pc
a
b
c
d
h1
h2
h3
h4
h5
h6
1.4. Pembatasan masalah
Dalam tugas akhir ini akan dibahas mengenai analisa P collapse pada gable frame yang mengalami mekanisme keruntuhan dengan jumlah sendi plastis
yang terbentuk.
Adapun pembatasan masalah yang diambil untuk mempermudah
penyelesaian adalah :
1. Material dianggap isotropis dan homogen.
2. Hubungan tegangan-regangan dalam batas elastis linier (berlaku
hukum Hooke)
3. Pengaruh temperatur, kecepatan regang dan residual stress tidak
ditinjau
4. Analisis struktur dilakukan dengan Finite Element Methode untuk
element plane frame
5. Hanya ditinjau untuk kondisi beban runtuh (Pkritis) dan load faktor ��.
6. Berat sendiri atau beban terdistribusi merata tidak diperhitungkan.
7. beban terpusat asimetris dan dengan inersia tampang yang berbeda-
beda.
1.5. Metodologi
Metode yang digunakan dalam penulisan tugas akhir ini adalah literature
berhubungan dengan pembahasan pada tugas akhir ini serta masukan-masukan
dari dosen pembimbing. Untuk perhitungan tabel-tabel dilakukan dengan bantuan
program Microsoft Excel 2007. Sedangkan untuk perhitungan gaya-gaya dalam
BAB II
TINJAUAN PUSTAKA
2.1. Dasar –Dasar Teori
2.1.1. Hubungan tegangan dan regangan
Hubungan teganan dan regangan pertama kali dikemukakan oleh Robert Hooke pada tahun 1678. Dalam hokum hooke dijelaskan bahwa baja lunak ditarik oleh gaya aksial tertentu pada kondisi temperatur ruang maka material tersebut
akan mengalami regangan yang nilainya berbanding lurus dengan tegangan
ataupun dengan beban aksial yang diberikan kondisi tersebut kemudian disebut
sebagai kondisi elastis. Hubungan antara tegangan dan regangan dapat
diinterpretasikan sebagai berikut:
• � =�
� (2.1)
• ε =(�−�� 0)
0 (2.2)
• � =�� (2.3)
Dimana: P = Beban Aksial
A = Luas Profil
lo = Panjang Mula-mula
Tegangan didefinisikan sebagai intensitas gaya yang bekerja pada tiap
satuan luas bahan sedangkan regangan didefinisikan sebagai suatu perbandingan
antara perubahan dimensi suatu bahan dengan dimensi awalnya. Karena regangan
merupakan rasio antara dua panjang, maka regangan ini merupakan besaran tak
berdimensi, artinya regangan tidak mempunyai satuan. Dengan demikian,
regangan dinyatakan hanya dengan suatu bilangan, tidak bergantung pada sistem
satuan apapun. Harga numerik dari regangan biasanya sangat kecil karena batang
yang terbuat dari bahan struktural hanya mengalami perubahan panjang yang kecil
apabila dibebani. Hubungan antara regangan dan tegangan untuk lebih jelasnya
dapat digambarkan pada gambar 2.1
Gambar 2.1. Hubungan tegangan dan regangan
Daerah pertama yaitu OA, merupakan garis lurus dan menyatakan daerah
linear elastis. Kemiringan garis ini menyatakan besarnya modulus elastis atau
disebut juga Modulus young, E. diagram tegangan- regangan untuk baja lunak
�
���
M
C ��
A’ B
�y ��
0
�
umumnya memiliki titik leleh atas ( Upper Yield Point ),
σ
yu dan daerah lelehdatar. Secara praktis, letak titik leleh atas ini, A’ tidaklah terlalu berarti sehingga
pengaruhnya sering diabaiakan. Lebih lanjut, tegangan pada titik A disebut
sebagai tegangan leleh, dimana regangan pada kondisi ini berkisar 0.00012. Dari
grafik tersebut dapat dilihat bahwa bila regangan terus bertambah hingga
melampaui harga ini, ternyata tegangannya dapat dikatakan tidak mengalami
pertambahan. Sifat dalam daerah AB ini kemudian kemudian disebut sebagai
daerah plastis. Lokasi titik B, yaitu titik akhir sebelum tegangan mengalami sedikit kenaikan, tidaklah dapat ditentukan. Tetapi, sebagai perkiraan dapat
ditentukan terletak pada regangan 0,014 atau secara praktis dapat ditetapkan
sebesar sepuluh kali besarnya regangan leleh.
Daerah BC merupakan daerah strain- hardening, dimana pertambahan regangan akan diikuti oleh pertambahan sedikit tegangan. Disamping itu
hubungan tegangan- regangannya tidak bersifat linear. Kemiringan garis setelah
titik B ini didefinisikan sebagai Es. Di titik M, tegangan mencapai titik maksimum
yang disebut sebagai tegangan tarik ultimit ( ultimate tensile strength ). Pada akhirnya material akan putus ketika mencapai titik C.
Besaran- besaran pada gambar 2.1 akan tergantung pada komposisi baja,
proses pembuatan pengerjaan baja dan temperature baja pada saat percobaan.
Tetapi factor- faktor tersebut tidak terlalu mempengaruhi besarnya modulus elastisitas ( E ). Roderick dan Heyman (1951), melakukan percobaan terhadap empat jenis baja dengan kadar karbon yang berbeda, data yang dihasilkan
Table 2.1 Hubungan persentase karbon ( C ) terhadap tegangan
% C
σ
(N/mm2)σ
ya/σ
yε
s /ε
y Es / Ey0.28 340 1.33 9.2 0.037
0.49 386 1.28 3.7 0.058
0.74 448 1.19 1.9 0.070
0.89 525 1.04 1.5 0.098
Dari table 2.1 dapat dilihat bahwa semakin besar tegangan lelehnya maka
semakin besar kadar karbon yang dibutuhkan. Tegangan bahan akan berpengaruh
pada daktalitas bahan. Semakin tinggi tegangan leleh maka semakin rendah
daktalitas dari material tersebut. Daktalitas adalah perbandingan antara
ε
s danε
ydimana
ε
s adalah regangan strain hardening danε
y adalah regangan leleh.Selanjutnya, apabila suatu material logam mengalami keadaan tekan dan
tarik secara berulang, diagram tegangan regangannya dapat berbentuk seperti
gambar 2.2. lintasan dan tekan akan sama. Hal ini menunjukkan suatu keadaan
Gambar 2.2. Efek bauschinger
Hubungan regangan-tegangan untuk keperluan analisis ini diidealisasikan
dengan mengabaikan pengaruh tegangan leleh atas (strain hardening ) dan efek bauschinger, sehingga hubungan antara tegangan dan regangan menjadi seperti gambar 2.3. keadaan semacam ini sering disebut sebagai keadaan hubungan
plastis ideal (ideal plastic relation).
�
��
�
��
�
−�
��
�Gambar 2.3. Hubungan plastic ideal
2.1.2. Distribusi Tegangan Regangan
Sebuah balok diatas dua tumpuan sendi dan menahan beban terpusat W
seperti gambar 2.4. dari persamaan keseimbangan, kita dapat memperoleh reaksi
tumpuan sebesar W/2. Diagram momen lenturnya terdapat pada 2.4b, dengan
momen maksimumnya sebesar Wl/4 yang terletak dibawah titik beban.
Gambar 2.4. Perletakan sederhana
Jika besarnya tegangan maksimum belum mencapai tegangan leleh,
distribusi tegangan dan regangan dari semua penampangnya akan berupa garis
lurus. Hal ini sesuai dengan hukum Bernoulli dan Navier, yaitu bersifat linear dan
nol pada garis netral. Dengan demikian, tegangan dan regangan disuatu serat yang
ditinjau adalah berbanding lurus terhadap jarak dari garis netral penampang.
Teganan tarik maksimum pada serat bawah dan tegangan tekan pada serat atas
adalah :
���� =�� (2.4)
Dengan M = momen lentur
W
a
A C B
W/2 W/2
Wl/4
S = modulus penampang (section modulus).
Jika beban terpusat semakin besar, tegangan di setiap serat penampang
turut bertambah pula. Keadaan ini dapat kita lihat pada gambar 2.5, gambar 2.5b
menunjukkan tegangan dan regangan pada serat terluar yang telah mencapai
kondisi leleh. Keadaan ini terletak ditik A pada gambar 2.1, dan besarnya momen
padatitik ini disebut sebagai momen leleh (yield stress), My.
Apabila beban w diperbesar lagi, tengangan lelehnya mulai menjalar keserat sebelah dalam, gambar 2.5c-d. bahwa tidak ada tegangan yang lebih besar
daripada tegangan leleh, tetapi momen dalam dapat terus bertambah karena resultan gaya dalamnya bertambah besar. Dengan pemberian sedikit penambahan
beban lagi, akan tercapailah keadaan dimana seluruh serat penampang mengalami
tegangan leleh, gambar 2.5e. momen dalam menjadi maksimum dan merupakan
momen plastis. Pada kondisi ini, penampang tadi akan mengalami rotasi yang cukup besar tanpa terjadi perubahan momen. Dengan kata lain dititik tersebut
telah terjadi sendi plastis. Titik c pada gambar 2.4 memiliki harga momen yang
terbesar, sehingga titk ini akan lebih cepat untuk berubah menjadi sendi plastis
Gambar 2.5. Distribusi tegangan - regangan
2.1.3. Menentukan garis netral profil
Garis netral untuk tampak yang sama pada kondisi elastis tidak akan
sama dengan kondisi garis netral pada saat plastis. Pada kondisi elastis, garis
netral merupakan garis yang membagi penampang menjadi dua bagian yang sama
luasnya. Pada kondisi plastis, garis netral ditinjau sebagai berikut :
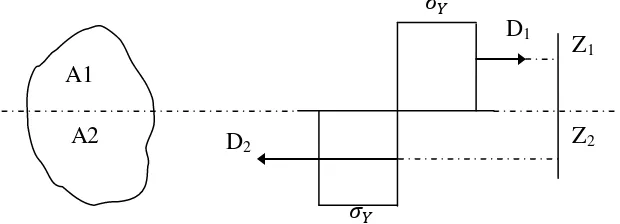
gambar 2.6. penentuan garis netral
• D1 = A1. σy (2.5)
regangan
�� 2��
�� −2��
10��
−10��
(a) (b) (c) (d) (e)
tegangan
�< �� �� �� �� ��
A1
A2
Z1
D2
��
��
• D2 = A2. σy (2.6)
Agar terjadi keseimbangan maka D1 = D2
• Sehingga A1 = A2 = 1/2 A
• Selanjutnya Z1 = S1/A1
Z2 = S2/A2
Dimana : S1 = statis momen pada bidang A1 terhadap garis netral plastis
S2 = statis momen pada bidang A2 terhadap garis netral plastis
D1 = resultan gaya tekan diatas garis netral plastis
D2 = resultan gaya tarik diatas garis netral plastis
Z1 = section modulus luasan 1
Z2 = section modulus luasan 2
Untuk menentunkan momen plastis batas digunakan :
• Mp = D1 (Z1 + Z2)
• Mp = σy ½ A ( Z1 + Z2 )
2.1.4. Hubungan momen kelengkungan
Pada saat terjadi sendi plastis pada suatu struktur dengan perletakan
sederhana, suatu struktur akan berotasi secara tidak terbatas. Sebelun gaya luar
Gambar 2.7. Kelengkungan balok
Setelah gaya luar bekerja, balok akan mengalami pelenturan.
Diasumsikan bahwa material penyusun balok adalah homogen dan diasumsikan
bahwa balok hanya mengalami lentur murni tanpa gaya aksial.
Perubahan kelengkungan akibat lentur murni ditunjukkan oleh gambar
2.5. titik A, B dan C akan tertekan sedangkan titik A1, B1, C1, akan meregang.
Perpanjangan titik A1-A, B1-B, C1-C akan mengalami perpotongan pada titik O.
sudut yang terbentuk akibat trjadinya perubahan kelengkungan ditik A dan B atau
B dan C, dinyatakan dengan �. Kalau � ini sangat kecil maka :
• �� = (� − �)�
• �1�1 = ��
dengan � adalah jari- jari kelengkungan ( radius of curvature )
A B C
A1 B1 C1
O
� �
�
M M
C B
A
y a
b a1
b1
c1
A1
sehingga, regangan pada arah memanjang disuatu serat sejauh y dari sumbu netral
dapat dinyatakan sebagai:
• �= ��−�1�1�1�1
�= −�� (2.7)
Dimana 1/� menunjukkan kelengkungan ( K ). Tanda negatif menunjukkan bahwa
bagian diatas garis netral, berada pada kondisi tekan, sedangkan pada kondisi
dibawah garis netral berada pada kondisi tarik. Dengan
• �
� = � � 1 R=
σ
Ey (2.8)
Tegangan tarik pada serat bawah dan tegangan tekan pada sera atas adalah :
• �= ��
Dimana : S adalah modulus penampang
• �=�
2
Akhirnya didapat 1 �=
M
ESD/2 dimana S.D/2 = I (momen inersia)
• 1
�= M EI=
d2y
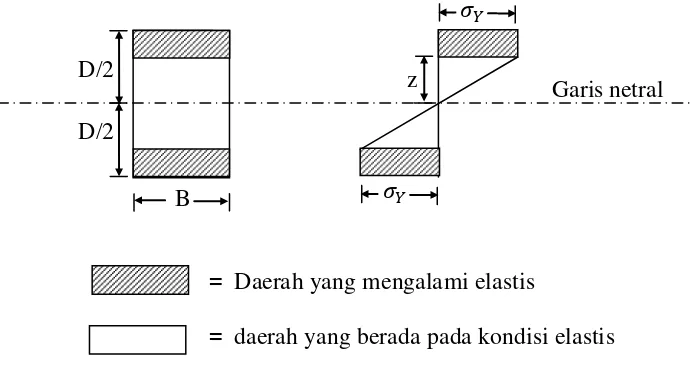
= Daerah yang mengalami elastis
[image:35.595.108.453.99.282.2]= daerahyang berada pada kondisi elastis
gambar 2.8. Distribusi tegangan pada penampang
Pada gambar 2.8. dapat dilihat bahwa regangan pada serat terluar telah
mencapai tegangan leleh. Sedangkan serat terjauh Z dari garis netral belum
mengalami tegangan leleh. Dengan demikian daerah sejauh 2Z materialnya masih
berada pada kondisi elastis dan besarnya momen dalam dapat dicari dari resultan
bagian elastis dan plastis.
Jika Z=D/2, hanya serat terluar saja yang mencapai kondisi leleh dan
besar momen dalam yang ditahan disebut sebagai momen leleh (My).
• My = S .�� (2.10)
Dimana S adalah modulus penampang (section modulus)
Dari persamaan (2.6) dengan harga �= �� , �=�, dapat diperoleh :
• � =��/� (2.11)
Selanjutnya untuk Z = ½ D diperoleh :
• �� = 2 ��/� (2.12)
Dimana K = kelengkungan pada kondisi plastis sebagian (partially plastic state)
Garis netral
B ��
��
z D/2
Ky = kelengkungan pada saat kondisi leleh
Perbandingan antara momen plastis (Mp) dengan momen leleh (My)
menyatakan peningkatan kekuatan penampang akibat ditinjau dari kondisi plastis.
[image:36.595.138.481.223.407.2]Perbandingan ini tergantung dari bentuk penampang (shape factor) yang dinotasikan sebagai f.
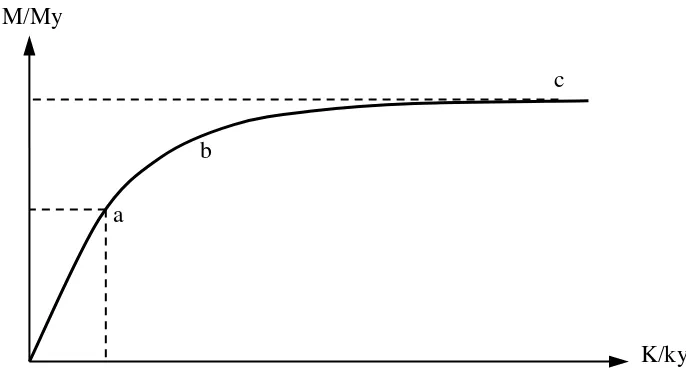
Gambar 2.9. Hubungan momen kelengkungan
dari gambar 2.9 dapat dilihat bahwa suatu kurva hubungan momen terhadap
kelengkungan (M-K), dimana dari kurva tersebut dapat dilihat bahwa nilai momen
( M ) akan semakin mendekati f. My apabila harga K semakin besar. Bila nilai
menjadi factor bentuk ( f ) maka harga K akan mencapai harga tidak berhingga,
dimana ini menandakan bahwa nilai z dalam persaamaan 2.11 sama dengan nol,
dimana y = z, maka seluruh penampang serat mencapai kondisi plastis penuh dan
momen plastisnya adalah Mp = f. My. Dimana f adalah factor bentuk yang
merupakan perbandingan antara momen plastis dan momen leleh menyatakan b
c M/My
peningkatan kekuatan penampang akibat ditinjau dari kondisi plastis.
Perbandingan ini tergantung dari bentuk penampang.
2.1.5. Analisa penampang
Pada bagian ini akan diberikan paparan yang lebih mendetail tentang
distribusi tegaganan pada keadaan leleh menuju kondisi plastis penuh yang
digambarkan pada gambar 2.10.
Gambar 2.10. Distribusi tegangan pada keadaan leleh dan keadaan plastis pada
tampang persegi
Modulus elastis
My = 2M1+2M2
= 2��
2− �� �.�� 1 2�
�
2+��+ 2. 1
2�.�.��� 2 3��
= ��
2− �� � �
2+�� �.�� +�.�� 2 3�2
= �.������ 2�
2
− �2�+2 3�2�
= �.����2 4 −
1 3�2�
= �.����2 4 −
1 3�
� 2�
2
�
= �.���3�212−�2� D/2
D/2
B
1 2
2
1
2 1 1
2
Momen elastis Momen plastis ��
��
��
= 1
6�.�2.�� (2.13a)
Modulus plastis
Momen plastis yaitu luasan tampang kali lengan momen
Mp = 2.���1
2�.�� � 1 4��
= 1
4�.�2.�� (2.13b)
Jika menggunakan factor bentuk (shape factor) yang dinotasikan dengan f, maka hubungan antara kapasitas momen pada saat keadaan leleh (My) dan kapasitas
momen pada keadaan plastis (Mp) akan menghasilkan :
• � = ����
• � =
1 4�.�2.�� 1 6�.�2.�� • � = 1,5
2.2. SENDI PLASTIS
2.2.1. Umum
Sendi plastis merupakan suatu kondisi dimana terjadi perputaran (rotasi)
pada suatu struktur yang berlangsung secara terus menerus sebelum pada akhirnya
mencapai keruntuhan yang diakibatkan oleh pembebanan eksternal.
Dengan timbulnya sendi plastis pada suatu sturktur maka sifat dari
konstruksi tersebut akan berubah, sebagai contoh:
1. Bila konstruksi semula merupakan statis tertentu, maka dengan
timbulnya satu sendi plastis akan membuat konstruksi menjadi labil dan
2. Pada suatu konstruksi yang hiperstatis berderajat n, bila timbul satu sendi
plastis maka konstruksi akan berubah derajat kehiperstatis dari suatu
konstruksi.
Dengan timbulnya sendi plastis pada suatu konstruksi maka momen yang
yang semula dihitung dengan cara elastis harus dihitung kembali sesuai dengan
perubahan sifat konstruksi yang ditimbulkan oleh sendi plastis tersebut.
2.2.2. Bentuk sendi plastis
Sendi plastis akan membentuk satu persamaan garis tertentu sebelum
terjadi keruntuhan.
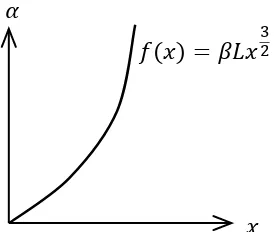
Kita tinjau proses terjadinya sendi plastis dan panjang plastis ( lp ) pada
balok sepanjang L dengan pembebanan terpusat asimetris
Gambar 2.11. Balok dengan pembebanan terpusat
�� =��(1−��)
�� =��(1− ��2)
(1−�
�) = (1− ��2)
O P
lP x gn
� = ���2
�= ��√�
�(�) =��√�
Gambar 2.12. Lengkung sendi plastis beban terpusat
Kita tinjau proses terjadinya sendi plastis dan panjang plastis ( lp ) pada
balok sepanjang L dengan pembebanan terbagi rata
Gambar 2.13. Balok dengan pembebanan terbagi rata
�� =��(1−� 2
�2)
�� =��(1− ��2)
(1−� 2
�2) = (1− ��2)
� = ��2�2
�= ���
�(�) =���
�
� �(�) =��√�
O
lP x gn
Gambar 2.14.Gambar dengan sendi plastis terbagi rata
Kita tinjau proses terjadinya sendi plastis dan panjang plastis ( lp )
pada balok sepanjang L dengan pembebanan terbagi rata segitiga
Gambar 2.15. Balok dengan pembebanan terbagi rata segitiga
�� =��(1−� 3
�3)
�� =��(1− ��2)
(1−� 3
�3) = (1− ��2)
�=��3�2
�=���32
�(�) =���32
�
� �(�) =���
O
lP x gn
[image:41.595.172.455.350.498.2]Gambar 2.16. Gambar sendi plastis beban segitiga
2.3. ANALISA STRUKTUR SECARA PLASTIS
2.3.1. Pendahuluan
Analisa struktur secara plastis bertujuan untuk menentukan beban batas
yang dapat dipikul oleh suatu struktur ketika mengalami keruntuhan. Kruntuhan
struktur dimulai dengan terjadinya sendi plastis. Keruntuhan dapat bersifat
menyeluruh ataupun parsial.
Suatu struktur hiperstatis berderajat n akan mengalami mengalami
keruntuhan total jika kondisinya labil, di sini telah terbentuk lebih dari n buah
sendi plastis. Keruntuhan parsial terjadi apabila sendi plastis yang terjadi pada
mekanisme keruntuhan tidak menyebabkan struktur hiperstatis dengan derajat
yang lebih rendah dari yang semula.
Suatu struktur statis tak tentu mempunyai sejumlah mekanisme
keruntuhan yang berbeda. Setiap mekanisme keruntuhan itu menghasilkan beban
runtuh yang berbeda. Sehingga pada akhirnya dipilih mekanisme yang
menghasilkan beban runtuh yang terkecil. �
Jumlah sendi plastis yang dibutuhkan untuk mengubah suatu struktur
kedalam kondisi mekanisme runtuhnya sangat berkaitan dengan derajat statis tak
tentu yang ada dalam struktur tersebut. Dalam hal ini dapat dibuat runusan
sebagai berikut : �= �+ 1
Dimana n = jumlah sendi plastis untuk runtuh r = derajat statis tak tentu
1. untuk struktur balok dua perletakan sendi- sendi (struktur statis tertentu )
dengan � = 0 ���� = 1
Gambar 2.17. struktur pembebanan dan mekanisme runtuh perletakan sendi- sendi
Struktur diatas hanya memerlukan sebuah sendi platis untuk mencapai
mekanisme runtuhnya yaitu sendi plastis pad momen maksimum (dibawah
beban titik).
2. Suatu balok dua perletakan sendi- jepit ( struktur statis tak tentu berderajat
1) dengan � = 1 ����= 2
Gambar 2.18. struktur pembebanan dan mekanisme runtuh perletakan sendi- jepit P
Struktur perletakan ini memerlukan dua buah sendi plastis untuk mencapai
mekanisme keruntuhannya . sendi plastis pada system perletakan tersebut
akan terjadi pada titik dimana terjadinya momen maksimum dan pada
perletakan jepit.
3. Untuk balok struktur dua perletakan jepit- jepit (struktur statis tak tentu
berderajat dua) dengan � = 2 ���� = 3
Gambar 2.19. struktur pembebanan dan mekanisme runtuh perletakan jepit –jepit
Pada struktur perletakan ini diperlukan tiga buah sendi platis untuk mencapai
mekanisme keruntuhannya. Sendi pada system perletakan tersebut akan terjadi
pada titik dimana terjadinya momen maksimum dan pada perletakan jepit.
2.3.2. Perhitungan struktur
Pada prinsipnya, jika suatu struktur mencapai kondisi keruntuhan maka
akan dipenuhi ketiga kondisi berikut:
1. Kondisi leleh (Yield Condition)
Momen lentur dalam struktur tidak ada yang melampaui momen batas
(Mp)
2. Kondisi keseimbangan (Equilibrium Condition) 3. Kondisi mekanisme (mechanism condition)
Ketiga kondisi diatas menjadi syarat dari teorema berikut:
1. Teorema batas bawah ( lower bound theorem)
Teorema batas bawah menetapkan atau menghitung distribusi momen
dalam struktur berdasarkan kondisi keseimbangan dan leleh. Beban yang
dianalisa memiliki factor beban (� ) yang memiliki nilai yang lebih kecil
dari harga yang sebenarnya (��), dirumuskan � ≤ �� sehingga hasil yang
dihasilkan mungkin aman mungkin tidak.
2. Teorema batas atas (upper bound theorem)
Jika distribusi momen yang diperoleh dihitung berdasrkan syarat yang
memenuhi kondisi keseimbangan dan mekanisme, dapat dipastikan bahwa
harga factor bebannya akan lebih besar atau sama dengan harga
sebenarnya, (��), � ≥ ��
Sehingga hasil yang dihasilkan mungkin benar atau mungkin tidak.
3. Teorema unik (unique theorem)
Distribusi momen untuk teorema ini akan memenuhi ketiga kondisi
tersebut di atas sehingga akan diperoleh nilai factor beban dari mekanisme
struktur yang ditinjau :�= ��. Pada teorema ini terdapat 4 metode yang
dapat digunakan :
a. Metode statis
b. Metode kerja virtual (virtual work method) c. Metode distribusi momen
2.3.3. Metode kerja virtual
Metode kerja virtual adalah metode yang meninjau keseimbangan energi
dari struktur tersebut ketika mengalami mekanisme runtuhnya.
Persamaan kerja virtual ini dapat ditulis sebagagai berikut :
∑��.∆� =∑��.�� (2.14)
Dimana : Wi = beban luar ( beban terpusat atau terbagi rata)
∆� = deformasi struktur
∆� = ��2tan� , untuk sudut yang kecil tan� =�
tan� = �
Mj = momen pada tampang kritis
�� = sudut rotasi sendi plastis
2.3.4. Metode Elemen Hingga Untuk Elemen Plane frame
Metode elemen hingga merupakan salah satu metode yang digunakan
untuk menghitung gaya-gaya dalam yang terjadi dalam suatu komponen struktur.
Metode elemen hingga juga dikenal sebagai metode kekakuan ataupun
displacement methode karena yang didapat terlebih dahulu dari perhitungan adalah perpindahan baru kemudian gaya batang dicari.
Dalam hubungannya dengan tugas akhir ini, metode elemen hingga ini
digunakan untuk perhitungan gaya-gaya dalam yang terjadi pada komponen
struktur. Untuk itu, metode elemen hingga yang digunakan adalah metode elemen
hingga untuk Elemen Plane frame dimana gaya yang bekerja pada struktur yang
diperhitungkan hanya terbatas pada gaya normal, gaya lintang, dan momen pada
Persamaan umum untuk metode elemen hingga ini adalah :
{�} = [�]{�} (2.15)
dimana : {f} = Matriks gaya-gaya batang ( kg )
[k] = Matriks kekakuan struktur ( N/m2 ) {d} = Matriks perpindahan ( m dan rad )
Kemudian rumus untuk menentukan kekakuan global dapat diturunkan sebagai
berikut :
��̅�= [�]{�}
��̅�= [�]{�}
{�} = [�]{�}
[�]−1��̅�= [�][�]−1��̅�
��̅�= [�][�][�]−1��̅�
Maka ditentukan matriks kekakuan global adalah :
����= [�][�][�]−1
Dengan [�] adalah suatu faktor konversi gaya-gaya ke arah sumbu global yang
berbeda-beda untuk tiap jenis struktur dan akan dijabarkan kemudian. Setelah
diperoleh matriks kekakuan global, maka dapat disusun suatu matriks kekakuan
struktur yang memasukkan semua komponen-komponen elemen yang ada.
��1̅
�̅2�= ��
�1 0 0 ��2� ��
̅
1
Langkah berikutnya yaitu menentukan syarat-syarat batas yang ada dan kemudian
nilai perpindahan dapat diperoleh. Dengan nilai perpindahan global yang
diperoleh, gaya-gaya batang untuk tiap element dapat ditentukan dengan :
{�} = [�]{�}
dimana :
{�} = [�]−1��̅�
Dalam menggunakan metode elemen hingga, perlu diperhatikan, bahwa
pada tiap elemen / batang akan terdapat dua buah titik simpul yaitu simpul awal
yang diberi tanda (1) dan simpul akhir yang diberi tanda (2) dan sebuah elemen
yang diberi tanda (a) seperti tampak pada Gambar.2.14
Derajat kebebasan adalah jumlah komponen perpindahan yang dapat
terjadi pada kedua simpul yang ada pada suatu elemen. Jumlah derajat kebebasan
berbeda-beda untuk tiap jenis struktur. Misalnya, untuk elemen rangka, jumlah
derajat kebebasannya adalah dua yaitu masing-masing satu perpindahan dalam
arah sumbu batang ( biasanya disebut sebagai sumbu 1 ) pada titik simpul (1) dan
(2).
Dari jumlah derajat kebebasan yang ada, suatu matriks kekakuan untuk
suatu jenis struktur dapat ditentukan. Masing-masing jenis struktur memiliki suatu
matriks kekakuan tersendiri dimana matriks kekakuan untuk elemen rangka
Gambar.II.11.Titik Simpul dan Elemen
2
1
berbeda dengan matriks kekakuan untuk elemen frame dan lain-lainnya. Begitu
pula halnya dengan matriks kekakuan untuk elemen grid. Matriks kekakuan dari
elemen plane frame dapat diperoleh dengan menggabungkan Matriks kekakuan
truss element dengan beam element. Memiliki 6 buah DOF dimana
element-elementnya mengalami gaya normal, gaya lintang, dan momen pada arah z.
Kekakuan dalam suatu struktur terbagi dalam dua jenis yaitu kekakuan
lokal dan kekakuan global. Kekakuan lokal adalah kekakuan elemen yang
mengacu arah sumbu masing-masing elemen sedangkan kekakuan global adalah
kekakuan elemen yang mengacu pada sistem koordinat global yaitu sistem
koordinat kartesian (XYZ). Jika dalam suatu struktur terdapat lebih dari satu
batang dengan arah sumbu lokal yang berbeda, maka kekakuan lokal dari tiap
elemen harus diubah menjadi kekakuan global agar matriks kekakuan dari semua
elemen yang ada dapat digabungkan.
Untuk elemen plane frame, seperti yang telah disebutkan di atas,
kekakuan lokalnya merupakan gabungan dari kekakuan lokal untuk truss element
dengan beam element.
ΕΙz
ΕΑ
Sy1
Μz1
Sx1
Sy2
Μz2
Sx2
L
•
Syarat keseimbangan :
��1 =−��2 ; ��1 = −��2 ; ��1= −��2+��2.� Menentukan Matriks Kekakuan Untuk Flane-Frame Element
dimana :
��1 =��
� (�1− �2) ; ��2 = ��
� (�2− �1)
��1 =12 ��
�3 (�1− �2) + 6 ��
�2 (�1+�2) ; ��2 =12 ��
�3 (�2− �1)− 6 ��
�2 (�1+�2)
��1 =6 ��
�2 (�1− �2 ) + 2 ��
� (2�1+�2) ; ��2 = 6 ��
�2 (�1− �2 ) + 2 ��
� (�1+ 2�2)
Maka diperoleh :
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧���1
�1
��1 ��2 ��2 ��2⎭⎪
⎪ ⎬ ⎪ ⎪ ⎫ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢
⎡ ��� 0 0
0 12�� �3
6�� �2 0 6��
�2
4�� �
−��� 0 0
0 −12�� �3
6�� �2
0 −6��
�2
2�� �
−��� 0 0
0 −12�� �3 −
6�� �2 0 6���2 2���
��
� 0 0
0 12��
�3 −
6�� �2 0 −6���2 4��� ⎦⎥
⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎩ ⎪ ⎨ ⎪ ⎧��11
�1
�2
�2
�2⎭
⎪ ⎬ ⎪ ⎫
Jadi matriks kekakuan lokal untuk plane-frame element :
[�] = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢
⎡ ��� 0 0
0 12�� �3
6�� �2 0 6���2 4���
−��� 0 0
0 −12�� �3
6�� �2 0 −6���2 2���
−��� 0 0
0 −12�3�� −6���2
0 6��
�2
2�� �
��
� 0 0
0 12�3�� −6���2 0 −6��
• Menentukan Matriks Kekakuan Global Untuk Plane-Frame Element
perhatikan gambar 1.2. pada sistem koordidat batang tipikal, Untuk simpul 1 pada
gambar tersebut, dapat dituliskan :
�̅1= �
�̅�1 �̅�1 ���1
�=�
cos� −sin� 0
sin� cos� 0
0 0 1
� � ��1 ��1 ��1�
= [�]{�1}
Untuk satu element / batang berlaku :
��̅��= [��]{��}
��1̅ �̅2�=��
0 0 �� �
�1
�2�
dimana :
[��] =�� 0
0 ��
Maka matriks kekakuan global untuk truss element adalah :
�����= [��][��][��]−1
Karena matriks [��] merupakan matriks ortogonal maka dapat ditulisakan sebagai :
����� = [��][��][��]� ����� = ⎣ ⎢ ⎢ ⎢ ⎢
⎡cossin�� −cossin�� 00
0 0 1
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0
cos� −sin� 0 sin� cos� 0 0 0 1⎦
⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢
⎡ ��� 0 0
0 12 �� �3
6 �� �2
0 6 �� �2
4 �� �
−��� 0 0
0 −12 �� �3
6 �� �2
0 −6 �� �2
2 �� �
−��� 0 0
0 −12 ��
�3 −
6 �� �2
0 6 �� �2
2 �� �
��
� 0 0
0 12 ��
�3 −
6 �� �2
0 −6 �� �2
4 ��
� ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢
⎡−cossin�� cossin�� 00
0 0 1
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0
cos� sin� 0 −sin� cos� 0 0 0 1⎦
⎥ ⎥ ⎥ ⎥ ⎤
Jika dimisalkan cos α = c dan sin α = s, maka matriks kekekakuan global untuk
�����= ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡
��2+12�
�2 �2 �� −
12�
�2� �� −
6�
� �
�� −12�2�� �� ��2+12�
�2 �2
6�
��
−6��� 6�
�� 4�
− ���2+12�
�2 �2� − �� −
12�
�2� �� −
6�
� �
− �� −12�2�� �� − ���2+12�
�2 �2�
6�
� �
6�
�� −
6�
� � 2�
− ���2+12�
�2 �2� − �� −
12�
�2� ��
6�
� �
− �� −12�2�� �� − ���2+12�
�2�2� −
6�
��
−6��� 6��� 2�
��2+12�
�2 �2 �� −
12�
�2� �� −
6�
��
�� −12�2�� �� ��2+12�
�2 �2 −
6�
� �
−6��� −6�
�� 4� ⎦⎥
⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
Setelah matriks kekakuan diperoleh maka gaya-gaya batang untuk
elemen plane frame dapat dihitung dengan terlebih dahulu menghitung besarnya
perpindahan yang terjadi pada titik-titik simpul dengan menggunakan persamaan
(2.15). ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧���1
�1
��1 ��2 ��2 ��2⎭⎪
⎪ ⎬ ⎪ ⎪ ⎫ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢
⎡ ��� 0 0
0 12�� �3
6�� �2 0 6���2 4���
−��� 0 0
0 −12�� �3
6�� �2 0 −6���2 2���
−��� 0 0
0 −12�3�� −6���2
0 6��
�2
2�� �
��
� 0 0
0 12�3�� −6���2 0 −6��
�2 4�� � ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎩ ⎪ ⎨ ⎪ ⎧��11
�1
�2
�2
�2⎭
⎪ ⎬ ⎪ ⎫
(2.16)
Setelah nilai-nilai perpindahan diperoleh dari persamaan (2.16), maka
gaya-gaya dalam untuk tiap elemen dapat dicari dengan menggunakan persamaan
BAB III
METODE ANALISA
3.1 Umum
3.1.1. Analisa elastis
Analisa struktur secara elastis memakai asumsi bahwa tegangan yang
terjadi pada struktur masih terletak dalam batas elastis dan defleksinya kecil.
Dengan analisa elastis sebagian besar dari struktur tersebut bertegangan rendah
dan dapat menimbulkan pemborosan.
Analisa elastis dapat dilakukan dengan menghitung gaya - gaya pada
struktur (seperti gaya aksial, gaya geser,momen serta puntir) akibat gaya luar yang
bekerja. Gaya - gaya dalam yang terjadi masih dalam batas elastis. Beberapa
contoh penyelesaian elastis : metode cross, takabeya, kani, matriks kekakuan,
termasuk metode elemen hingga.
Analisa elastis dapat dilakukan dengan mudah pada semua jenis struktur,
struktur rangka maupun struktur plat cangkang, karena gaya – gaya dalam yang
terjadi masih dalam batas – batas elastis, maka analisis elastis dapat dipakai pada
struktur dari semua jenis bahan (bahan bersifat getas dan daktail).
Hasil perhitungan analisis elastis, yang berupa gaya – gaya dalam yang
terjadi umumnya digunakan untuk memeriksa keamanan struktur atau untuk
3.1.2. Analisis plastis
Analisis secara plastis memanfaakan kemampuan struktur secara penuh
hingga beban batas akhir (ultimate load) sehingga timbul dengan kekuatan struktur sampai tegangan lelehnya.
Analisis plastis pada umumnya digunakan untuk menentukan besar
beban runtuh (ultimate load) pada suatu struktur serta perilaku keruntuhannya (mechanism). Gaya – gaya dalam yang telah terjadi telah melebihi batas elastis dan defleksi yang terjdi cukup besar. Dengan demikian analisis plastis hanya
dapat diterapkan pada struktur yang bersifat daktail, seperti baja dan beton
bertulang dengan pendaktailan yang baik.
Dalam analisis plastis digunakan persamaan matematik yang relatif
sederhana dan lebih mudah dibanding persamaan pada analisis elastis, analisis
plastis cocok untuk perhitungan struktur statis tak tentu berderajat banyak, seperti
portal (dapat bertingkat maksimum 2), portal beratap lancip dan balok menerus.
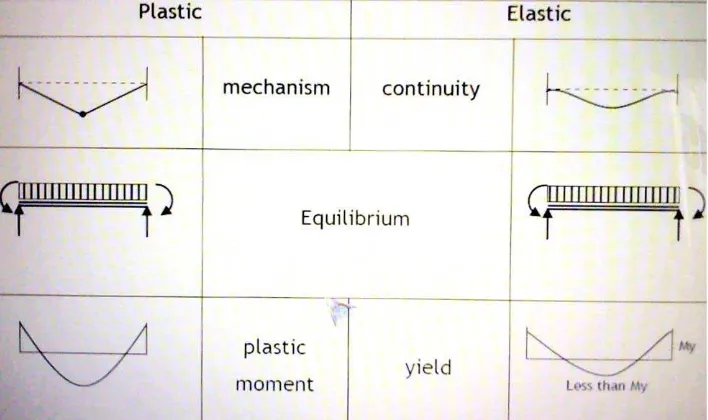
Gambar 3.1 kondisi struktur pada analisis plastis dan analisis elastis
Di bawah ini gambaran perbedaan perancangan plastis dengan
perancangan elastis.
[image:55.595.134.501.409.632.2]3.2.FAKTOR BENTUK ( Shape Factor )
Faktor bentuk ( f ) merupakan indeks yang menyatakan perbandingan
antara momen plastis dan elastis seperti yang telah dijelaskan dalam Bab II
sebelumnya. Pada bagian ini akan diberikan paparan yang lebih mendetail tentang
distribusi tegangan pada keadaan leleh menuju kondisi plastis penuh pada profil
[image:56.595.111.405.541.753.2]IWF yang digambarkan pada gambar III.2 berikut.
gambar 3.3. Distribusi tegangan pada keadaan leleh dan keadaan plastis pada
profil IWF
3.2.1. Modulus elastis ( sumbu X )
� = 2�1 + 2�2
� = 2�� �� 2−
� 2� ���
��2−�� � 2
+���1� �2 2� � 2−��
2 � 2
�� 2
��2−�� � 2
�
� = 1 2� (��)(� − �)�� �� � 2−��
� 2
+ � 2 � 2� �
2� � 2−��
3 �
� ���
� = (��)(�−�)
� ��{(� − �)} +�
��2−��3�
� ���
� = ��� �� (��)(� − �)2+�� 2− ��
3
��
��= �� �=
��/��(��)�� 2−��
3 �� ��
��= 1��(��)(� − �)2+��2− �� 3
�� (3.1)
3.2.2. Modulus plastis
�� = 2�1 + 2�2
�� = 2��� ��2−�2� ���+ 2��2− ��2 �2��
�� = ���(� − �)���+��2− ��2 �2��
�� = ���(� − �) +��2− �� 2
����
�� = �� �
�� =�� � =
���(� − �) +��2 − ��2���� ��
�� = ���(� − �) +��2− �� 2
�� (3.2)
Jika menggunakan faktor bentuk (shape faktor) yang dinotaskan dengan
f, dimana f = Zx/Sx ( untuk sumbu x) maka hubungan antara kapasitas momen
pada saat keadaan leleh ( My ) dan kapasitas momen pada keadaan plastis ( Mp )
akan menghasilkan persamaan berikut :
��
�� =
����
���� =
��
�� = �
Mp = f. My (3.3)
dari persamaan (3.3) diperoleh :
� = ���
(�−�)+�� 2−��
2 �� 1
��(��)(�−�)2+��2−�� 3
�� (3.4)
Tabel 3.1 Nilai faktor bentuk pada profil IWF
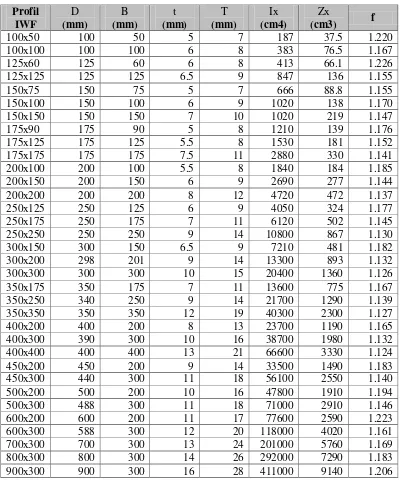
Profil IWF
D
(mm)
B
(mm)
t
(mm)
T
(mm)
Ix
(cm4)
Zx
(cm3) f
100x50 100 50 5 7 187 37.5 1.220
100x100 100 100 6 8 383 76.5 1.167
125x60 125 60 6 8 413 66.1 1.226
125x125 125 125 6.5 9 847 136 1.155
150x75 150 75 5 7 666 88.8 1.155
150x100 150 100 6 9 1020 138 1.170 150x150 150 150 7 10 1020 219 1.147
175x90 175 90 5 8 1210 139 1.176
175x125 175 125 5.5 8 1530 181 1.152 175x175 175 175 7.5 11 2880 330 1.141 200x100 200 100 5.5 8 1840 184 1.185 200x150 200 150 6 9 2690 277 1.144 200x200 200 200 8 12 4720 472 1.137 250x125 250 125 6 9 4050 324 1.177 250x175 250 175 7 11 6120 502 1.145 250x250 250 250 9 14 10800 867 1.130 300x150 300 150 6.5 9 7210 481 1.182 300x200 298 201 9 14 13300 893 1.132 300x300 300 300 10 15 20400 1360 1.126 350x175 350 175 7 11 13600 775 1.167 350x250 340 250 9 14 21700 1290 1.139 350x350 350 350 12 19 40300 2300 1.127 400x200 400 200 8 13 23700 1190 1.165 400x300 390 300 10 16 38700 1980 1.132 400x400 400 400 13 21 66600 3330 1.124 450x200 450 200 9 14 33500 1490 1.183 450x300 440 300 11 18 56100 2550 1.140 500x200 500 200 10 16 47800 1910 1.194 500x300 488 300 11 18 71000 2910 1.146 600x200 600 200 11 17 77600 2590 1.223 600x300 588 300 12 20 118000 4020 1.161 700x300 700 300 13 24 201000 5760 1.169 800x300 800 300 14 26 292000 7290 1.183 900x300 900 300 16 28 411000 9140 1.206
Rata – rata sampel ( x ) = 3934.591= 1.164
[image:58.595.112.513.178.663.2]= 0.01
faktor bentuk rata-rata =1.164 – (1.164 x 0.01)
=1.147
maka faktor bentuk (f ) = 1.147
3.3.Analisa plastis struktur sederhana
Jika kita perhatikan tingkah laku struktur dengan beban yang bekerja
pada struktur tersebut relatif kecil dan terus bertambah besar secara linear maka
momen –momen yang ada pada setiap penampangnya masih terletak dalam
daerah elastis, atau momen tersebut belum melampaui momen lelehnya.
Peningkatan beban selanjutnya masih dapat dilakukan; namun akan
mengakibatkan besar momen pada salah satu penampangnya menjadi sama
dengan momen plastisnya, sehingga terbentuklah sendi plastis yang pertama.
Apabila struktur merupakan struktur statis tak tentu, maka keruntuhan belum
terjadi dengan satu buah sendi plastis. Dengan peningkatan beban berikutnya akan
terbentuklah sendi yang kedua, ketiga dan seterusnya, hingga terbentuk jumlah
sendi plastis yang cukup untuk menyebabkan struktur ini runtuh.
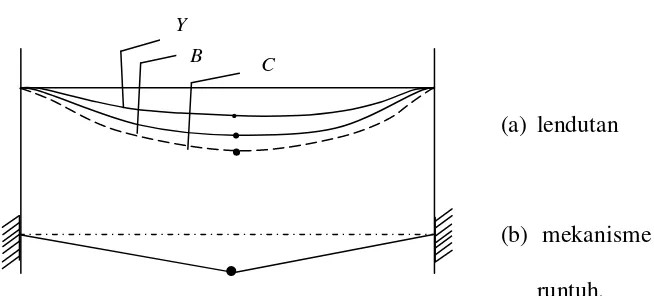
3.3.1 Analisis tahap demi tahap
Sebuah balok dengan kedua ujung terjepit, yaitu panjang dinyatakan
dengan L, momen plastis penampang Mp, dan beban meratanya ditetapkan
gambar 3.4. balok kedua ujungnya terjepit
dengan menerapkan analisa elastis, maka momen tumpuan MA = MB = wL2/12. sedangkan momen ditengah bentang Mc = wL2/24. Dengan menggunakan momen –momen ini, kita dapat menggambarkan diagram momen seperti gambar 3.4. Bila
momen terbesar yang terdapat pada tumpuan A dan B telah mencapai kapasitas
momen plastisnya, akan kita peroleh beban w sebesar 12 Mp/L2, yang mengakibatkan terjadinya sendi plastis pada kedua tumpuan.
Dengan pertambahan beban berikutnya, nilai momen pada kedua
tumpuan tersebut tidak berubah, tetapi di titik ini akan terjadi rotasi yang
menunjukkan bahwa struktur tersebut bertingkah laku seperti balok statis tertentu
(gambar 3.4). Tampak bahwa momen dikedua tumpuan sama dengan nol dan
momen ditengah bentang adalah w’L2/8. sedangkan w’ merupakan factor beban yang baru, maka momen maksimum ditengah bentang (titik c ) adalah :
Mc = Mp/2 + w’L2/8 (3.5)
dimana momen ini sama dengan kapasitas momen plastis Mp, bila mencapai 4 Mp/L2 atau w sebesar 16 Mp/L2. Dengan terbentuknya tiga buah sendi plastis, dapat kita pastikan bahwa struktur mengalami keruntuhan.
C L
B A
w/satuan panjang
wL2/8
wL2/12
MP
MP/2
w/satuan panjang
C
L w’L
2
/8
MP
MP gambar 3.5. kondisi pertama peningkatan momen dalam
gambar 3.6 kondisi kedua peningkatan momen dalam
Uraian diatas dapat pula menggunakan metode moment – area untuk menggambarkan analisi tersebut.
��= �� 3 24��−
��� 3�� −
���
6�� (3.6)
��= �� 3 24��−
��� 6�� −
���
3�� (3.7)
∆�= 5�� 4 384��−
���2 16�� −
���2
16�� (3.8)
dengan ��,��,∆� berturut –turut menyatakan besarnya rotasi di titik A, B, dan
lendutan (defleksi ) di titik C. Syarat kompatibilitas pada kondisi elastis menghendaki bahwa titik A,dan B tidak terjadi rotasi, sehingga ��,�� bernilai nol.
dengan memasukkan harga –harga kedalam persamaan diatas, kita peroleh:
MA = MB = wL2/12 (3.9)
dengan meninjau keseimbangan momen ditengah bentang (gambar 3.5) akan kita
peroleh:
MC = wL2/8 – (MA + MB)/2 = wL2/24 (3.9) dengan mencubtitusikan harga kedua momen tersebut menghasilkan :
∆�=�L4/348EI (3.10)
wL2/8
C
MB
MB
MC
merupakan lendutan dalam kondisi elastis.
Dengan memperhatikan diagram momennya, dipastikan secara serentak
akan terjadi sendi plastis pada tumpuan A dan B, dimana bebannya mencapai
12Mp/L2. Dengan berarti bahwa momen di kedua tumpuan tersebut sama dengan kapasitas momen plastis dari penampanggnya, MP (gambar 3.4). Selanjutnya, dari persamaan (3.8) dapat kita tentukan besarnya lendutan di tengah bentang, yakni:
∆�=3845 �12��2�� �4 ��−
���2 8�� =
���2
32�� (3.11)
gambar 3.7. diagram momen kondisi ketiga
Adanya penambahan beban berikutnya dapat menyebabkan terbentuknya
sendi plastis yang ketiga, dan dari gambar ini dapat kita pastikan letak sendi
tersebut terletak ditengah bentangan. dengan demikian momen di titik ini sama
dengan Mp dan kita hasilkan (lihat gambar 3.5): �� =��2� − �8 �