Studi Menentukan Distribusi Tegangan Pada Isolator Rantai Di Sistem Transmisi Tenaga Listrik Menggunakan Matlab

(1)

Sukra Zainuddin : Studi Menentukan Distribusi Tegangan Pada Isolator Rantai Di Sistem Transmisi Tenaga Listrik Menggunakan Matlab, 2008.

STUDI MENENTUKAN DISTRIBUSI TEGANGAN PADA ISOLATOR

RANTAI DI SISTEM TRANSMISI TENAGA LISTRIK MENGGUNAKAN

MATLAB

OLEH :

SUKRA ZAINUDDIN

040422008

JURUSAN TEKNIK ELEKTRO

FAKULTAS TEKNIK

PROGRAM PENDIDIKAN SARJANA EKSTENSI

UNIVERSITAS SUMATERA UTARA

(2)

LEMBAR PENGESAHAN

STUDI MENENTUKAN DISTRIBUSI TEGANGAN PADA ISOLATOR

RANTAI DI SISTEM TRANSMISI TENAGA LISTRIK MENGGUNAKAN

MATLAB

Disusun Oleh:

Nama : Sukra Zainuddin

NIM : 040422008

DISETUJUI OLEH:

Pembimbing,

Ir. Zulkarnaen Pane

NIP : 131 288 519

Ketua Departemen Teknik Elektro,

Ir. Nasrul Abdi, MT

NIP : 131 459 554

JURUSAN TEKNIK ELEKTRO

FAKULTAS TEKNIK

PROGRAM PENDIDIKAN SARJANA EKSTENSI

UNIVERSITAS SUMATERA UTARA

(3)

ABSTRAK

Perkembangan sistem tenaga listrik yang pesat membutuhkan saluran

transmisi tegangan tinggi, karena itu komponen – komponen pendukung saluran

transmisi tersebut seperti isolator rantai menjadi sangat perlu diperhatikan

dikarenakan fungsi dan kemampuannya dalam mengisolasi antara konduktor saluran

bertegangan tinggi dengan kawat tanah.

Isolator transmisi yang paling banyak digunakan adalah isolator jenis piring

atau jenis clevis. Isolator jenis ini biasanya dipasang dalam jumlah rentengan.

Didalam penentuan jumlah piring isolator biasanya tingkat kesulitannya terdapat

pada perhitungan distribusi tegangan pada masing – masing piring isolator.

Oleh karena itu, perhitungan distribusi tegangan pada isolator rantai menjadi

(4)

KATA PENGANTAR

Segala puji dan syukur hanya milik Rabb sekalian alam Allah Subhanahu wa

Ta’ala yang mana atas Rahmat dan Hidayah-Nya penulis dapat menyelesaikan tugas

akhir ini, dengan judul “Studi Menentukan Distribusi Tegangan Pada Isolator Rantai

Di sistem Transmisi Tenaga Listrik Dengan Menggunakan Matlab”.

Penulisan tugas akhir ini merupakan salah satu syarat untuk memperoleh

gelar sarjana Teknik di Departemen Teknik Elektro, Fakultas Teknik, Universitas

Sumatera Utara.

Selama masa kuliah sampai penyelesaian tugas akhir ini, penulis banyak

menerima bimbingan dan bantuan dari berbagai pihak.Untuk itu dengan penuh

ketulusan hati, penulis mengathurkan terima kasih kepada :

a. Ayahanda Drs.Abdul Kadir dan Ibunda Astuti Ningshi, yang tidak terhitung

cinta dan kasih sayangnya, yang tidak pernah bosan-bosannya mengasuh,

mendidik dan membimbing penulis semenjak kecil hingga sekarang ini.

b. Kakanda Ariyah, Andinda Ismail Hafid dan keponakan (dicky, habib,

fadiyah) yang selalu menjadi tempat berbagi dan bercanda dalam suka

maupun duka.

c. Bapak Ir.Zulkarnaen Pane, selaku dosen pembimbing penulis yang telah

banyak meluangkan waktu dan memberikan ide-ide cemerlangnya dalam

(5)

d. Bapak Ir.Nasrul Abdi, MT dan Bapak Ir.Rahmat Fauzi, MT, selaku ketua

dan sekretaris Departemen Teknik Elektro, Fakultas Teknik, Universitas

Sumatera Utara.

e. Bapak Ir. Soeharwinto, MT. selaku dosen wali penulis, yang senantiasa

memberikan bimbingannya selama perkuliahan.

f. Teman-teman satu stambuk 2004 Ekstansi. M. Idris Rusli, ST, Nova A. Trg,

ST, Purwanto simamora, ST, Veronika, ST, Aditia O.Sitepu, Rahmat

Zulfahri, Pranto Panjaitan, ST dan teman-teman yang belum disebut

namanya, yang selama ini menjadi teman diskusi, belajar, memberikan

semangat dalam penulisan Tugas Akhir ini.

g. Temen-temanku di kost setia budi (Jemingan, Amd, Tambi Loto dan Bang

Muliadi Sembiring, ST) yang telah memberikan tumpangan tempat, terima

kasih atas tumpangan anda.

h. Seluruh stap pengajar dan pengawai Departemen Teknik Elektro yang telah

mendidik dan membantu penulis selama perkuliahan sampai dengan selesai.

Penulis menyadari bahwa Tugas Akhir ini belum sempurna, karena masih

terdapat kekurangan baik dari segi isi maupun susunan bahasanya.Saran dan kritik

dari pembaca dengan tujuan menyempurnakan dan mengembangkan kajian dalam

bidang ini sangat penulis harapkan.

Akhir kata kesempuranan hanya milik Allah Subahanahu wa Ta’ala dan

kesalahan semata-mata dari penulis.Semoga Tugas Akhir ini berguna dan

memberikan ilmu pengetahuan bagi kita semua.

(6)

Sukra Zainuddin Nim:04042200

DAFTAR ISI

ABSTRAK...………... i

KATA PENGANTAR...………. ii

DAFTAR ISI………... iv

DAFTAR GAMBAR……… vi

BAB I PENDAHULUAN I.1 Latar Belakang Masalah………. 1

I.2 Tujuan Penulisan……… 2

I.3 Batasan Masalah………. 3

I.4 Metodologi Penulisan………. 3

I.5 Sistematika Penulisan………. 4

BAB II ISOLATOR SALURAN TRANSMISI II.1 Umum………... 6

II.2 Kapasitansi Isolator……….. 6

II.3 Kurva Distribusi Tegangan Pada Isolator Rantai……… 8

II.4 Menghitung Distribusi Tegangan……… 9

II.4.1 Distribusi Tegangan Tanpa Menghitungkan Kapasitansi C2 Dan C3……….10

II.4.2 Distribusi Tegangan Memperhitungkan C2………....11

(7)

III.2 Lingkungan Kerja Matlab……….. 20

III.3 Cara Bekerja Dengan Matlab………. 24

III.3.1 Langsung Di Command Window………. 24

III.3.2 Menggunakan File M……… 26

III.4 Manajeman File Dan Direktori……….. 28

BAB IV PERHITUNGAN DISTRIBUSI TEGANGAN PADA ISOLATOR RANTAI DENGAN METODE MATLAB IV.1 Umum……….. 31

IV.2 Perhitungan Secara Manual………. 31

IV.2.1 Perhitungan Distribusi Tegangan Tanpa Kapasitansi C2 Dan C3……… 31

IV.2.2 Memperhitungan Kapasitansi C1 Dan C2………... 32

BAB V KESIMPULAN DAN SARAN V.1 Kesimpulan……… 48

V.2 Saran……….. 48

DAFTAR PUSTAKA………...vii

LAMPIRAN A Lampiran Tabel hasil perhitungan dari jumlah lima sampai dua

belas isolator piring.

LAMPIRAN B Lampiran Kurva hubungan jumlah isolator dengan besar

tegangan yang dipikul setiap isolator dan Kurva hubungan

factor kerataan dengan jumlah isolator.

(8)

DAFTAR GAMBAR

Gambar 2.1. Ekivalensi suatu isolator piring….……….... 7

Gambar 2.2. Susunan “ konduktor – dielektrik – konduktor “ pada isolator rantai... 8

Gambar 2.3. Distribusi tegangan pada isolator rantai……….... 8

Gambar 2.4. Rangkaian pengganti isolator rantai dengan mengabaikan C2 dan C3. 10 Gambar 2.5. Rangkaian pengganti isolator rantai dengan kapasitansi C2……….... 11

Gambar 3.1. Ikon Matlab pada dekstop window……….. 21

Gambar 3.2. Window utama Matlab………. 21

Gambar 3.3. Launch pad window………. 22

Gambar 3.4. Workspace window……….. 22

Gambar 3.5. Current directory window……… 23

Gambar 3.6. Command history window………... 23

Gambar 3.7. Commang window………... 23

Gambar 3.8. Matlab editor window……….. 24

Gambar 3.9. Menu file……….. 30

(9)

BAB I

PENDAHULUAN

I.I. LATAR BELAKANG MASALAH

Perkembangan ilmu pengetahuan dan teknologi turut mempengaruhi sistem

kelistrikan suatu daerah dan kualitas pelayananya, sehingga keberadaan energi listrik

dapat dijadikan sebagai tolak ukur kemajuan suatu daerah.

Listrik merupakan bentuk energi yang paling cocok dan nyaman bagi

manusia modern.Tanpa listrik infra-struktur masyarakat sekarang tidak akan

menyenangkan.Makin bertambahnya konsumsi listrik per kapita diseluruh dunia

menunjukan kenaikan standar kehidupan manusia.Pemanfaatan secara optimum

bentuk energi ini oleh masyarakat dapat dibantu dengan sistem distribusi yang

efektif.

Pusat pembangkit tenaga listrik umumnya jauh dari pusat beban, karena itu

tenaga listrik yang dibangkitkan harus disalurkan melalui kawat – kawat atau saluran

transmisi. Ada dua kategori saluran transmisi yaitu saluran transmisi hantaran udara

(overhead transmission line ) dan saluran kabel bawah tanah ( underground cable

transmission line ).Pada saluran transmisi hantaran udara, menyalurkan tenaga listrik

melalui kawat – kawat yang digantung pada tiang – tiang transmisi dengan

(10)

Isolator rantai dijumpai pada jaringan transmisi, jaringan distribusi hantaran

udara, gardu induk, panel pembagi daya, terminal ujung kabel dan peralatan

tegangan tinggi.Komponen suatu isolator terdiri dari dielektrik, bahan isolasi, jepitan

logam dan bahan perekat yang mengikat jepitan dengan dielektrik.Dengan demikian

suatu islolator merupakan gabungan dari “konduktor – dielekrik – konduktor” yang

analog dengan komposisi suatu kapasitor.Untuk transmisi tegangan tinggi, isolator

piring didisain berbentuk rantai, dimana setiap unitnya dianggap sebagai suatu

kapasitor.Sehingga suatu isolator rantai dapat dianggap sebagai susunan dari

beberapa unit kapasitor yang terhubung seri ataupun paralel.Akibatnya jika isolator

diberi tegangan AC, maka distribusi tegangan pada setiap unit tidak sama.Hal ini

terjadi karena pada isolator rantai terdapat tiga kelompok kapasitansi yaitu :

1) Kapasitansi sendiri (C1) : yang dibentuk oleh jepitan logam isolator –

dielektrik – jepitan logam dibawahnya.

2) Kapasitansi tegangan rendah (C2) : jepitan logam isolator – udara –

menara.

3) Kapasitansi tegangan tinggi (C3) : jepitan logam isolator – udara –

kawat transmisi.

Banyaknya unit ( piring ) isolator yang digunakan dan kapasitansi C1, C2 dan

C3 akan mempengaruhi distribusi tegangan yang dipikul setiap unit isolator. Semakin

banyak isolator yang digunakan maka distribusi tegangan yang dipikul setiap isolator

akan semakin kecil.

Idealnya kurva distribusi tegangan pada isolator rantai adalah berbentuk garis

lurus, akan tetapi karena pengaruh ketiga kapasitansi tersebut diatas kurva itu sulit

(11)

membahayakan satuan – satuan piring isolator yang terutama yang terdekat dengan

kawat fasa, karena tegangan yang dipukul dapat melebih tegangan nominal isolator

itu.Dalam penulisan ini, penulis melakukan studi tentang : ”Menentukan distribusi

tegangan pada isolator rantai di sistem transmisi tenaga listrik dengan Matlab”.

I.2. TUJUAN PENULISAN

Adapun tujuan penulisan ini untuk :

1. Untuk mengetahui distribusi tegangan pada isolator rantai di sistem

transmisi tenaga listrik.

2. Untuk mengetahui bagaimana cara dan langkah – langkah dalam

perhitungan distribusi tegangan pada isolator rantai di sistem transmisi

tenaga listrik dengan menggunakan metode Matlab.

I.3. BATASAN MASALAH

Untuk mengarahkan dan membatasi pembahasan maka penulis membuat

suatu batasan masalah yakni :

1. Tidak membahas perataan tegangan masing – masing isolator rantai.

2. Membahas menentukan distribusi tegangan pada isolator rantai di

sistem transmisi tenaga listrik yang diasumsikan dalam penulisan ini

berjumlah dua belas piring isolator rantai.

3. Dalam pembahasan ini hanya memperhitungkan distribusi tegangan

pada isolator rantai dengan mengabaikan C2 dan C3 dan distribusi

tegangan pada isolator rantai dengan memperhitungkan C2.

(12)

Metode yang digunakan dalam penulisan tugas akhir ini adalah sebagai

berikut:

1. Studi literature : penulis membaca buku – buku, manual, artikel,

bahan kuliah dan buku teks yang mendukung dan berkaitan dengan

topik tugas akhir ini.

2. Studi bimbingan : penulis melakukan diskusi/konsultasi dengan dosen

pembimbing yang telah ditunjuk oleh pihak Departemen Teknik

Elektro USU dan juga sumber – sumber lain yang berkompeten.

I.5. SISTEMATIKA PENULISAN

Tugas akhir ini disusun berdasarkan sistematika pembahasan sebagai berikut :

BAB I : PENDAHULUAN

Bab ini berisikan latar belakang, tujuan penulisan, batasan masalah, metode

penulisan dan sistematika penulisan sebagai gambaran umum dari pembahasan

secara keseluruhan.

BAB II : ISOLATOR SALURAN TRANSMISI

Bab ini berisikan tentang isolator, karakteristik, kapasitansi isolator, kurva distirbusi

tegangan pada isolator rantai dan menghitung distribusi tegangan.

BAB III : PEMOGRAMAN MATLAB

Bab ini berisikan tentang sekilas Matlab, lingkungan kerja Matlab, cara bekerja

dengan Matlab, manajeman file dan direktori,

BAB IV : PERHITUNGAN DISTRIBUSI TEGANGAN PADA ISOLATOR

(13)

Bab ini berisikan tentang umum perhitungan distribusi tegangan, prosedur

perhitungan dengan Matlab, dan aplikasi Matlab untuk dua belas piring isolator

rantai.

BAB V : KESIMPULAN DAN SARAN

Bab ini berisikan penutup berupa kesimpulan yang diambil dari pembahasan bab –

(14)

BAB II

ISOLATOR SALURAN TRANSMISI

II.1. UMUM

Isolator berfungsi untuk mengisolir kawat jaringan yang bertegangan dengan

tiang atau menara penyangga kawat jaringan agar arus listrik tidak mengalir dari

kawat jaringan tersebut ketanah.Isolator dipasang atau digantung pada travers

(crossarm) struktur pendukung, sedangkan konduktor daya dipasang pada jepit

isolator.Isolator perlu memiliki kekuatan mekanik dan elektrik yang baik.

Isolator terdiri dari bahan isolasi yang diapit oleh elektroda –

elektroda.Dengan demikian isolator terdiri dari sejumlah kapasitansi.Karena

kapasitansi ini, maka distribusi tegangan pada suatu deretan isolator menjadi tidak

seragam.Potensial pada ujung yang terkena langsung dengan kawat konduktor adalah

yang terbesar.Menurut penggunaan dan konstruksinya, isolator pasang luar (outdoor

insulator) atau isolator saluran udara (overhead insulator) diklasifikasikan menjadi

isolator pasak (pin type insulator), isolator piring (suspension insulator), isolator

batang panjang (long rod insulator), isolator pos saluran (line pos insulator).

II.2. KAPASITANSI ISOLATOR

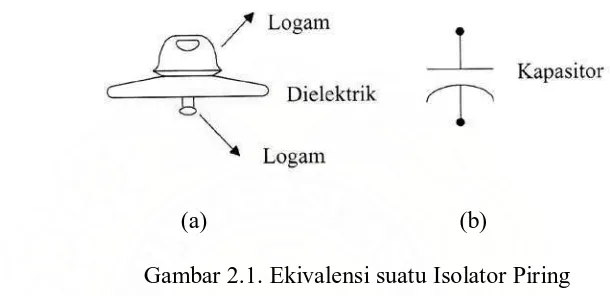
Isolator piring dipakai pada isolator rantai, konstruksi dari isolator piring

dapat dilihat pada Gambar 2.1.a.Isolator piring berupa dua konduktor yang

(15)

merupakan suatu susunan kapasitor, ekivalensi dari isolator piring ini dapat dilihat

pada Gambar 2.1.b. Semua isolator merupakan dua konduktor yang diantarai oleh

suatu dielektrik. Pada Gambar 2.1 ditunjukkan contoh suatu isolator, yaitu satu unit

isolator piring. Isolator tersebut membentuk suatu susunan “konduktor – dielektrik –

konduktor “, oleh karena itu isolator tersebut dapat dianggap sebagai suatu kapasitor.

(a) (b)

Gambar 2.1. Ekivalensi suatu Isolator Piring

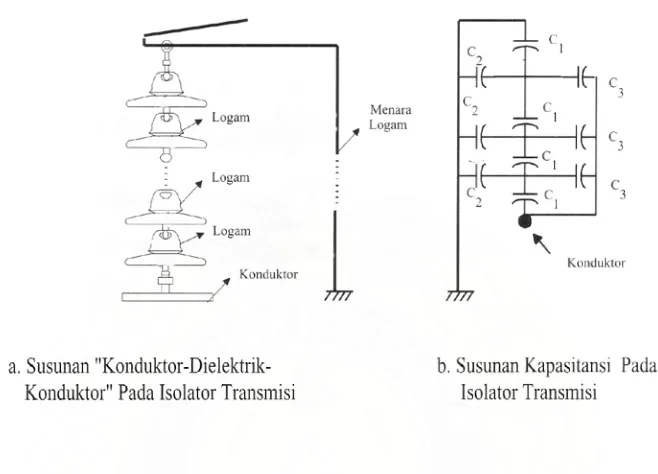
Jika beberapa isolator piring dirangkai menjadi isolator rantai seperti pada

Gambar 2.2.a. , maka akan dijumpai tiga kelompok susunan “

konduktor-dielektrik-konduktor “ , masing – masing dibentuk oleh :

a. Jepitan logam isolator-dielektrik isolator-jepitan logam dibawahnya.

Susunan ini membentuk kapasitansi sendiri isolator ( C1 ).

b. Jepitan logam isolator-udara-menara. Susunan ini membentuk kapasitansi

jepitan logam isolator dengan menara yang dibumikan (C2). Kapasitansi ini

disebut kapasitansi tegangan rendah.

c. Jepitan logam isolator-udara-konduktor transmisi. Susunan ini dibentuk oleh

(16)

memperhitung-kan C3

memperhitung-kan C2 dan C3

memperhitung-kan C2

100 % n/N

Vn/V

G

C2 dan C3 tdk diperhitungkan

1 3

2 4

Oleh karena itu, isolator rantai dapat dianggap sebagai susunan dari beberapa

unit kapasitor yang terhubung seperti pada Gambar 2.2.b

Gambar 2.2. Susunan “Konduktor – Dielektrik – Konduktor “ pada isolator rantai

II.3. KURVA DISTRIBUSI TEGANGAN PADA ISOLATOR RANTAI

Idealnya kurva distribusi tegangan pada isolator rantai adalah linear, akan

tetapi hal ini sulit dicapai disebabkan adanya pengaruh kapasitansi sendiri isolator

(C1), kapasitansi tegangan rendah (C2) dan kapasitansi tegangan tinggi (C3). Dan

pada Gambar 2.3 diperlihatkan kurva distribusi tegangan pada isolator rantai akibat

(17)

Gambar 2.3. Distribusi Tegangan pada Isolator Rantai

Kurva distribusi tegangan yang ideal adalah linier (Kurva 1), yaitu jika

kapasitansi ke menara (C2) dan kapasitansi tegangan tinggi (C3) tidak ada. Jika

kapasitansi ke menara (C2) diperhitungkan sedangkan kapasitansi tegangan tinggi

(C3) diabaikan, maka kurva distribusi tegangan adalah seperti kurva 2 dan jika ada

kapasitansi tegangan tinggi sedangkan kapasitansi tegangan rendah (C2) diabaikan,

maka kurva distribusi tegangan menjadi seperti kurva 3. Jika semua kapasitansi (C1,

C2 dan C3 ) diperhitungkan, maka kurva distribusi tegangan merupakan resultan

kurva 2 dan kurva 3.Dengan superposisi kedua kurva tersebut diperoleh distribusi

tegangan seperti kurva 4.

II.4. MENGHITUNG DISTRIBUSI TEGANGAN

Untuk menghitung distribusi tegangan disepanjang isolator rantai perlu kita

pahamkan bahwa sebagaimana yang diperlihatkan pada Gambar 2.2.Setiap pengaruh

kapasitansi yang terdapat disepanjang isolator rantai tersebut dianggap sebagai

elemen kapasitansi, dan kapasitansi ini sangat mempengaruhi distribusi tegangan

pada isolator rantai.Perhitungan distribusi tegangan pada isolator rantai dapat

dilakukan dengan beberapa cara :

a. Distribusi tegangan pada isolator rantai dengan mengabaikan kapasitansi

jepitan logam isolator dengan menara (C2) dan kapasitansi tegangan tinggi

(C3).

(18)

c. Distribusi tegangan dengan memperhitungkan kapasitansi C2 dan C3.

d. Distribusi tegangan pada isolator rantai dengan memperhitungkan semua

kapasitansi.

Agar perhitungan distribusi tegangan pada isolator rantai lebih mudah, maka

kita membutuhkan beberapa asumsi, yaitu :

a. Semua piring isolator memiliki karakteristik yang sama.

b. Jarak menara ke isolator sama.

c. Isolator adalah ideal, artinya tiap konduktor dapat dianggap sebagai

kapasitansi murni.

II.4.1. Distribusi tegangan tanpa menghitungkan kapasitansi C2 dan C3

Jika kapasitansi antara penghubung isolator rantai dengan menara (C2) dan

kapasitansi antara penghubung isolator rantai dengan konduktor tegangan tinggi (C3)

diabaikan, maka rangkaian ekivalen kapasitansi isolator rantai ini terlihat seperti

pada Gambar 2.4. Jika diberi tegangan sebesar V yaitu tegangan antara konduktor

phasa dengan menara maka tegangan pada setiap unit isolator adalah :

V1

V₂

V3

I

I C

C

C I

C

Vn

Konduktor phasa

1

2

3

n

(19)

Gambar 2.4. Rangkaian pengganti isolator rantai dengan mengabaikan C2 dan C3

V1 = I1Z1 ; V2 = I2 Z2 ; Vn = In Zn

Karena kapasitansi-kapasitansi unit isolator sama, maka

Z1 = Z2 = Zn………...(2.1)

Dengan demikian

V1 = V2 = ………. = Vn ………....(2.2)

atau

N V

V_n = ………....(2.3)

Dimana : Vn = Tegangan pada unit ke-n dari isolator rantai yang ditinjau

V = Tegangan konduktor ke menara

N = Jumlah unit pada suatu isolator rantai.

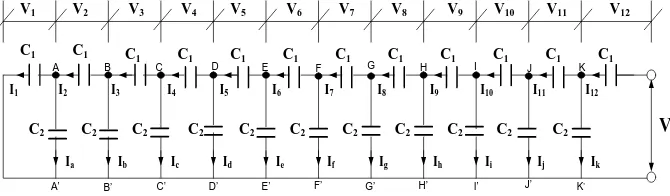
II.4.2. Distribusi Tegangan memperhitungkan C2

Jika kapasitansi antara penghubung isolator rantai dengan konduktor

tegangan tinggi (C3) diabaikan, maka hanya kapasitansi sendiri (C1) dan kapasitansi

antara penghubung isolator dengan menara (C2) yang mempengaruhi distribusi

tegangan. Rangkaian ekivalen isolator menjadi seperti Gambar 2.5. Jika diberi

tegangan sebesar V yaitu tegangan antara konduktor phasa dengan tanah maka

tegangan pada setiap unit isolator tidak terdistribusi secara merata, karena adanya

(20)

Gambar 2.5. Rangkaian pengganti isolator rantai dengan kapasitansi C2

Dan misalkan :

Besarnya arus listrik yang mengalir pada tiap unit isolator dapat ditentukan.

Pada titik A, persamaan arusnya adalah:

I2 = I1 +Ia …………...………...(2.5)

Persamaan 2.25 dapat dituliskan menjadi

j C1V2 = j C1V1+ j mC1V1

(21)

Pada titik B, persamaan arus adalah:

I3 = I2 + Ib...(2.7)

I3 = adalah arus yang mengalir pada isolator 3.

I3 = j C1V3

I2 = j C1V2

Ib = j C2 (V1 + V2) = j mC1 (V1 + V2)

Maka: Persamaan 2.7 menjadi :

j C1V3 = j C1V2 + j mC1 (V1 + V2)

V3=V2 + m (V1 + V2) ...(2.8)

Maka dengan mensubtitusikan Persamaan 2.6 ke dalam Persamaan 2.8 :

V3 = V1 (1 + m) + m{V1 + V1 (1 + m)}

= V1 + mV1 + m(V1 + mV1 + V1)

= V1 + mV1 + mV1 + m2V1 + mV1

= V1 + 3 mV1 + m2V1

V3= V1(1 + 3m + m2) ...(2.9)

Pada titik C, persamaan arusnya adalah :

I4=I3 + Ic ...(2.10)

I4 = adalah arus yang mengalir pada isolator 4

I4= j C1V4

I3= j C1V3

Ic= j C2(V1 + V2 + V3) = j mC1(V1 + V2 + V3)

Maka dengan demikian Persamaan 2.10 menjadi,

j C1V4= j C1V3+ j mC1(V1 + V2 + V3)

(22)

Dan dengan mensubstitusikan Persamaan 2.6 dan 2.9 ke Persamaan 2.11 :

V4 = V1(1 + 3m + m2) + m { V1 + (V1 (1 + m)) + V1(1 + 3m + m2)}

= V1 + 3mV1 + m2 V1 + m { V1 + 3mV1 + m2 V1 + V1 + mV1 + V1)

= V1 + 3mV1 + m2 V1 + 3m2V1 + m3V1 + mV1 + m2 V1 + mV1

= V1 + 6 mV1 + 5m2V1 + m3V1

V4 = V1 (1 + 6m + 5m2+ m3) ...(2.12)

Pada titik D, akan kita lihat persamaan arusnya,

I5 =I4 +Id ...(2.13)

I5 = merupakan arus yang mengalir pada isolator 5.

I5= j C1V5

I4= j C1V4

Id= j C2 (V1 + V2 + V3 + V4) = j mC1(V1 + V2 + V3 + V4)

Maka: Persamaan 2.13 menjadi,

j C1V5= j C1V4+ j mC1(V1 + V2 + V3 + V4)

V5 = V1 (1 + 6m + 5m2 + m3) + m{V1 + V1 (1 + m) + V1(1 + 3m + m2) +

V1(1 + 6m + 5m2 + m3)}

V5 = V1 + 6mV1 + 5m2V1 + m3V1 + m(V1 + V1 + mV1 + V1 + 3mV1 +

m2V1 + V1 + 6mV1 + 5m2V1 + m3V1)

= V1 + 6mV1 + 5m2V1 + m3V1 + mV1 + mV1 + m2V1 + mV1 + 3m2V1

+ m3V1 + mV1 + 6 m2V1 + 5 m3V1 + m4V1

V5 = V1 (1+10m + 15m2 + 7m3 + m4) ...(2.14)

Pada titik E, akan kita lihat persamaan arusnya,

I6 = I5 + Ie ...(2.15)

(23)

I6= j C1V6

I5= j C1V5

Ie= j C2 (V1 + V2 + V3 + V4 + V5) = j mC1(V1 + V2 + V3 + V4 +V5)

j C1V6 = j C1V5+ j mC1(V1 + V2 + V3 + V4+V5)

V6 = V5 + m (V1+V2+V3+V4+V5)

V6 =V1 (1 + 15m +35m2 + 28m3 + 9m4 + m5 )...(2.16)

Pada titik F, akan kita lihat persamaan arusnya,

I7 = I6 +If ...(2.17)

I7 = j C1V7

I6 = j C1V6

If = j C2 (V1 + V2 + V3 + V4 + V5 +V6) = j mC1(V1 + V2 + V3 + V4 +V5+V6)

j C1V7 = j C1V6+ j mC1(V1 + V2 + V3 + V4+V5 +V6)

V7 = V6 + m (V1+V2+V3+V4+V5+V6)

V7= V1 (1+2m+70m2+84m3+45m4+11m5+m6)...(2.18)

Pada titik G, akan kita lihat persamaan arusnya,

I8= I7 +Ig ...(2.19)

I8= j C1V8

I7= j C1V7

Ig= j C2 (V1+ V2 + V3 + V4 + V5 +V6+V7) = j mC1(V1 + V2 + V3 + V4 +V5

(24)

j C1V8= j C1V7+ j mC1(V1 + V2 + V3 + V4+V5 +V6+V7)

V8 = V7 + m (V1+V2+V3+V4+V5+V6+V7)

V8= V1 (1+28m+116m2+220m3+175m4+66m5+13m6+m7)...(2.20)

Pada titik H, akan kita lihat persamaan arusnya,

I9= I8 + Ih...(2.21)

I9= j C1V9

I8= j C1V8

Ih=j C2(V1+V2+V3+V4+V5+V6+V7+V8) = j mC1(V1+V2+V3+V4+V5+V6+V7

+V8)

j C1V9= j C1V8+ j mC1(V1 + V2 + V3 + V4+V5 +V6+V7+V8)

V9 = V8 + m (V1+V2+V3+V4+V5+V6+V7+V8)

V9=V1 (1+36m+200m2+462m3+515m4+290m5+91m6+14m7+m8)...(2.22)

Pada titik I, akan kita lihat persamaan arusnya,

I10= I9 + Ii...(2.23)

I10= j C1V10

I9 = j C1V9

Ii = j C2(V1+V2+V3+V4+V5+V6+V7+V8+V9)=j C1(V1+V2+V3+V4+V5+V6+

V7+V8+V9)

(25)

V10 = V9 + m (V1+V2+V3+V4+V5+V6+V7+V8+V9)

V10 =V1(1+45m+320m2+904m3+1317m4+1035m5+459m6+119m7+16m8+m9)

...(2.24)

Pada titik J, akan kita lihat persamaan arusnya,

I11= I10 + Ij...(2.25)

I11= j C1V11

I10 = j C1V10

Ij= j C2(V1+V2+V3+V4+V5+V6+V7+V8+V9+V10)=j C1(V1+V2+V3+V4+V5+

V6+ V7+V8+V9+V10)

j C1V11= j C1V10+ j mC1(V1 + V2 + V3 + V4+V5 +V6+V7+V8+V9+V10)

V11 = V10 + m (V1+V2+V3+V4+V5+V6+V7+V8+V9+V10)

V11=V1(1+55m+485m2+1666m3+3023m4+3096m5+1862m6+683m7+150m8+

18m9+m10)...(2.26)

Pada titik K, akan kita lihat persamaan arusnya,

I12 = I11 + Ik...(2.27)

I12= j C1V12

I11 = j C1V11

Ik=j C2(V1+V2+V3+V4+V5+V6+V7+V8+V9)=j C1(V1+V2+V3+V4+V5+V6+

V7+V8+V9+V10+V11)

(26)

V12 = V11 + m (V1+V2+V3+V4+V5+V6+V7+V8+V9+V10+V11)

V12=V1(1+66m+705m2+2913m3+6395m4+8181m5+6361m6+3109m7+967m8

+185m9+20m10+m11)...(2.28)

Sesuai Persamaan 2.1, maka untuk isolator gantung berjumlah 12 unit berlaku

Persamaan,

V=V1+V2+V3+V4+V5+V6+V7+V8+V9+V10+V11+V12...(2.29)

Maka dengan memasukan Persamaan (2.6) (2.9) (2.12) (2.14) (2.16) (2.18) (2.20)

(2.22) (2.24) (2.26) dan (2.28) kedalam Persamaan (2.29), maka :

V=V1+V1(1+m)+V1(1+3m+m2)+V1(1+6m+5m2+m3)+V1(1+10m+15m2+7m3

V=V1(12+286m+1942m2+6285m3+6980m4+11748m5+8679m6+3926m7+1134m8+2

(27)

BAB III

PEMOGRAMAN MATLAB

III.1. SEKILAS MATLAB

Bahasa pemrograman sebagai media untuk berinteraksi antara manusia

dengan computer dewasa ini dibuat agar semakin mudah dan cepat.Matlab muncul

didunia bahasa pemrograman yang cenderung di kuasai oleh bahasa yang telah

mapan.Logikanya, sebagai pemain baru tentu saja Matlab akan sukar mendapat hati

dari pemakai (programmer).Namun Matlab hadir tidak dengan fungsi dan

karakteristik yang ditawarkan bahasa pemrograman lain (yang biasanya hampir

seragam).Matlab dikembangkan sebagai bahasa pemrograman sekaligus alat

visualisasi, yang menawarkan banyak kemampuan untuk menyelesaikan berbagai

kasus yang berhubungan langsung dengan disiplin keilmuan matematika, seperti

bidang rekayasa teknik, fisika, statistika, komputasi dan modeling.Matlab dibangun

dari bahasa induknya yaitu bahasa C, namun tidak dapat dikatakan sebagai varian

dari C, karena dalam sintak maupun cara kerjanya sama sekali berbeda dengan

(28)

kelebihan-kelebihan bahasa C bahkan mampu berjalan pada semua platform system

operasi tanpa mengalami perubahan sintal sama sekali.

Matlab adalah bahasa pemrograman level tinggi (ingat dalam dunia

pemrograman semakin tinggi level bahasa semakin mudah cara menggunakannya)

yang dikhususkan untuk komputasi teknis.Bahasa ini mengintegrasikan kemampuan

komputasi, visualisasi dan pemrograman dalam sebuah lingkungan yang tunggal dan

mudah digunakan.Matlab memberikan sistem interaktif yang menggunakan konsep

array/matrik sebagai standar variabel elemennya tanpa membutuhkan pendeklarasian

array seperti pada bahasa lainnya.Matlab dikembangkan oleh MathWorks, yang pada

awalnya dibuat untuk memberikan kemudahan mengakses data matrik pada proyek

LINPACK dan EISPACK.Selanjutnya menjadi sebuah aplikasi untuk komputasi

matrik.Dari sejak awal dipergunakan, matlab memperoleh masukan ribuan

pemakai.Dalam lingkungan pendidikan ilmiah menjadi alat pemrograman standar

bidang matematika, rekayasa dan keilmuan terkait.Dan dalam lingkungan industri

dapat menjadi pilihan paling produktif untuk riset, pengembangan dan analisa.

III.2. LINGKUNGAN KERJA MATLAB

Sebagaimana bahasa pemrograman lainnya, matlab juga menyediakan

lingkungan kerja terpadu yang sangat mendukung dalam pembangunan aplikasi.Pada

setiap versi MATLAB yang terbaru, lingkungan terpadunya akan semakin

dilengkapi.Lingkungan terpadu ini terdiri atas beberapa from/window yang memiliki

kegunaan masing-masing.Untuk memulai aplikasi Matlab, anda hanya perlu

mengklik ikon Matlab pada Dekstop Window, atau bisa juga dengan menu start

(29)

Setiap pertama kali mulai membuka aplikasi Matlab, anda akan memperoleh

beberapa from/window, yang sebenarnya menurut penulis hanya membuat Dekstop

anda kelihatan penuh, anda dapat menutup semua Window tersebut kecuali

Command Window yang menjadi Window utama Matlab.Matlab akan menyimpan

mode/setting terakhir lingkungan kerja yang anda gunakan sebagai mode/setting

lingkungan kerja pada saat anda membuka aplikasi Matlab diwaktu berikutnya.

Gambar.3.1.Ikon Matlab pada dekstop window

Window ini adalah window induk yang melingkupi seluruh lingkungan kerja

Matlab.Pada versi-versi pendahulu, window ini secara khusus belum ada namun

terintegrasi dengan Command Window.Tidak ada fungsi utama yang ditawarkan oleh

window ini selain sebagai tempat dock-ing bagi from yang lain.

(30)

Window ini mulai diperkenalkan pada versi 6, berfungsi sebagai penuntun

bagi pemakai dalam memilih opsi dari fungsi dan toolbox yang ditawarkan oleh

Matlab.

Gambar.3.3.launch pad window

Window ini juga baru diperkenalkan pada versi 6, berfungsi sebagai navigator

bagi pemakai dalam penyediaan informasi mengenai variabel yang sedang aktif

dalam Workspace adalah suatu lingkungan abstrak yang menyimpan seluruh variabel

dan perintah yang pernah digunakan selama penggunaan Matlab berlangsung.

Gambar.3.4.Workspace window

Window ini juga fasilitas yang diperkenalkan pada versi 6.Berfungsi sebagai

(31)

Gambar.3.5.Current directory window

Window ini berfungsi sebagai penyimpan perintah-perintah yang pernah

dikerjakan pada suatu Workspace.Juga baru ada pada Matlab versi 6 keatas.

Gambar.3.6.Command history window

Window ini berfungsi sebagai penerima perintah dari pemakai untuk

menjalakan seluruh fungsi-fungsi yang disediakan oleh Matlab.Pada dasarnya

Window inilah inti dari pemrograman Matlab yang menjadi media utama

satu-satunya bagi kita untuk berinteraksi dengan Matlab.

(32)

Window ini berfungsi untuk membuat skrip program Matlab.Walaupun skrip

program dapat dibuat dengan menggunakan berbagai program editor seperti

Notepad, Wordpad, Word dan lain-lain.Namun sangat dianjurkan untuk

menggunakan Matlab Editor ini karena kemampuannya dalam mendeteksi kesalahan

pengetikan sintak oleh Programmer. Ketika Window utama Matlab muncul, window

Matlab Editor tidak akan muncul dengan sendirinya, anda harus memanggilnya

dengan cara mengetikan edit pada Prompt Matlab, Atau dengan cara mengklik pada

ikon Create New.

Gambar.3.8.Matlab editor window

III.3. CARA BEKERJA DENGAN MATLAB

Dalam melakukan pekerjaan pemrograman menggunakan bahasa Matlab,

anda dapat menggunakan salah satu cara yaitu :

III.3.1. LANGSUNG DI COMMAND WINDOW

Cara ini adalah yang paling sering dilakukan oleh pemula, namun akan sulit

bagi anda untuk mengevaluasi perintah secara keseluruhan karena biasanya perintah

hanya dilakukan baris perbaris.Untuk membuat program, anda hanya perlu

(33)

>> pjg = 5 ;

Tekan tombol enter, lalu ketikan :

>> lbr = 10 ;

Tekan enter, lalu ketikan :

>> luas = pjg * lbr

Untuk skrip terakhir sengaja tidak diberikan tanda (;) tititk koma, sehingga anda bisa

langsung melihat hasil akhir dilayar Command Window.

Hasil akhirnya yaitu :

>> luas =

50

Program anda telah selesai.

Dan untuk mengganti nilai salah satu atau lebih variabel, misalnya anda ingin

mengganti nilai pjg dengan 10, maka anda tinggal mengetikkan sebagai berikut:

>> pjg = 10 ;

Tekan enter, lalu tekan tanda panah () atau ( ) sehingga pada Prompt Matlab

muncul:

>> luas = pjg * lbr

Tekan enter lagi, sehingga anda akan melihat hasil akhir berubah sebagai berikut :

>> luas =

(34)

Artinya Matlab secara otomatis akan menggunakan nilai terakhir yang digunakan

oleh variabel.Namun cara ini memilki kelemahan, terutama untuk membuat

perhitungan dengan rumus yang cukup panjang.Dapat anda bayangkan jika dalam

satu tahap perhitungan anda harus melakukan perubahan nilai pada beberapa variabel

sekaligus.

III.3.2. MENGGUNAKAN FILE M

Cara ini biasanya akan dipilih untuk digunakan oleh Programmer yang lebih

mahir (jangan khawatir dalam beberapa menit kedepan, andapun akan menjadi salah

satu dari kelompok ini).Kelebihan cara ini adalah kemudahan untuk mengevaluasi

perintah secara keseluruhan.Terutama untuk program yang membutuhkan waktu

pengerjaan yang cukup lama serta skrip yang cukup panjang.Untuk contoh dapat kita

gunakan program yang sebelumnya anda kerjakan dengan cara pertama, dengan

tahapan sebagai berikut :

1. Pada Command Window, ketikan :

>> edit

2. Tekan enter, selanjutnya muncul Matlab Editor dan anda ketiklah program

dibawah berikut :

% - - - - - - - -

% Program latihan 1

% Matlab Programing

% oleh : gunay

% - - -

(35)

Clc;

disp ( - - - ) ;

disp ( Program Latihan 1 ) ;

disp ( - - - ) ;

pjg = 10 ;

lbr = 10 ;

luas = pjg * Lbr ;

disp ( [ Luas  ‘num2str (Luas) ] );

3. Setelah selesai mengetik program diatas, anda simpan didirektori c:/Latihanku,

dengan nama latihan 01.m.

4. Anda kembali ke Command Window.Agar Matlab dapat mengenali lokasi tempat

file anda tersimpan, pada Prompt Matlab ketiklah direktori c:?latihanku pada Prompt

Matlab :

>>cd c : \ Latihanku

5. Tekan enter, lalu ketiklah nama file latihan 01 tanpa ekstensi :

>>Latihan 01

6. Tekan enter, selanjutnya program akan dijalankan dan menghasilkan sebagai

berikut :

- - -

Program Latihan 1

- - -

Luas - > 100

(36)

Jika tahap enam telah anda capai, maka program pertama telah sukses anda

kerjakan.Selamat datang dan bergabung sebagai Programmer Matlab.Untuk

penulisan skrip yang digunakan ini anda akan menemukan kedua cara pemrograman

yang dijelaskan diatas.Agar tidak bingung, perhatikan jika ditulis :

>> pjg = 10 ;

>> lbr = 10 ;

>> luas = pjg * lbr ;

>> disp ( [‘luas - > ‘ num2str (luas) ] ) ;

Maka artinya anda harus menuliskan skrip tersebut pada Command Prompt

Matlab.Dan jika ditulis :

pjg = 10 ;

lbr = 10 ;

luas = pjg * lbr ;

disp ( [‘luas -> ‘ num2str (luas) ] );

Tanpa tanda >>, maka anda menuliskannya pada Editor Matlab dan menyimpannya

sebagai file M.

III.4. MANAJEMAN FILE DAN DIREKTORI

Matlab menggunakan metode Path Searching (pencarian direktori) untuk

menemukan File dengan ekstensi M yang mengandung skrip dan fungsi.File M

Matlab terorganisir dengan rapi pada beberapa Folder/direktori.Urutan pencarian

Matlab dalam menjalankan perintah pada Command Window secara bertahap adalah

(37)

• Matlab mencoba untuk mengenali apakah ‘kubus’ adalah variabel, jika ya,

selesai.Jika tidak, maka Matlab berasumsi bahwa ‘kubus’ adalah sebuah nama

File dengan ekstensi M, lanjut ketahap berikutnya.

• Matlab mencoba untuk mengenali apakah ‘kubus’ merupakan fungsi bawaan

standar, jika ya, eksekusi.Jika tidak , lanjut ketahap berikutnya.

• Matlab akan mencari File M yang bernama kubus.m pada direktori aktif

(Curent Directory), jika ditemukan , ekskusi.Jika tidak, lanjut ketahap

berikutnya.

• Matlab akan mencari File M yang bernama kubus.m diseluruh direktori yang

terdaftar pada daftar pencariannya, jika ditemukan, eksekusi.Jika tidak, matlab

akan menyampaikan pesan sebagai berikut :

>> kubus

??? Undefined function or variabel ‘kubus’

Jika pesan diatas muncul kehadapan anda, maka kesimpulannya hanya ada dua,

yaitu :

1. Anda salah menulis nama File, atau

2. File anda tidak berada dalam direktori yand diketahui oleh Matlab.

Jika anda yakin nama File yang anda ketikan benar, maka yang harus anda lakuka n

juga ada dua pilihan, yaitu :

1. Memindahkan dierktori aktif ke direktori tempat File anda berada.

Misalkan direktori tempat anda menyimpan File adalah c;/latihanku.Maka

caranya adalah dengan perintah berikut :

>>cd c: / latihanku

(38)

2. Menambahkan direktori anda kedalam daftar pencarian direktori Matlab.

Untuk membuka Tool yang mengatur pencarian path ini dapat dilakukan

dengan cara mengklik Set Path pada menu File sebagai berikut :

Gambar.3.9.Menu file

Selanjutnya akan muncul dialog Set Path sebagai berikut :

Gambar.3.10.Dialog set path

Setelah melakukan pemilihan Folder yang diinginkan dengan cara mengklik

tombol Add Folder, lalu dilanjutkan dengan mengklik tombol Save dan diakhiri

dengan tombol Close.Maka direktori anda telah tersimpan didaftar pencarian

direktori Matlab.Jika anda memilih menggunakan cara pertama, maka setiap anda

membuka aplikasi Matlab anda harus melakukannya lagi.Tetapi jika anda memilih

cara kedua, maka anda tidak perlu melakukannya lagi pada kesempatan lainnya,

(39)

BAB IV

PERHITUNGAN DISTRIBUSI TEGANGAN PADA ISOLATOR

RANTAI DENGAN METODE MATLAB

IV.1. UMUM

Dalam perhitungan distribusi tegangan pada isolator rantai ini, mengacu pada

beberapa hal, yaitu :

1) Perhitungan distribusi tegangan pada isolator rantai yang berjumlah 12 unit

berdasarkan rumus di bab 2.

2) Langkah – langkah aplikasi Matlab seperti di bab 3.

3) Rumus – rumus penentuan perhitungan untuk pemrograman dalam Matlab.

Untuk membuktikan kebenaran hasil perhitungan ini, maka kita akan

membandingkan hasil perhitungan dengan cara manual dan dengan metode

Matlab.Bila hasil perhitungannya sama, maka kita dapat menentukan distribusi

tegangan pada isolator rantai di sistem transmisi tenaga listrik dengan menggunakan

metode Matlab.

IV.2. PERHITUNGAN SECARA MANUAL (KALKULATOR)

IV.2.1. Perhitungan Distribusi Tegangan tanpa Kapasitansi C2 dan C3

Dalam perhitungan ini menggunakan isolator rantai yang terdiri dari atas dua

(40)

dengan kapasitansi sendiri (C1) adalah 0,1.Dan tegangan transmisi ke konduktor

yang digunakan adalah 150 kV/50 Hz.

Rangkaian ekivalennya adalah seperti ditunjukan pada Gambar 2.4

Menurut Rumus 2.1, maka tegangan pada setiap unit isolator piring adalah

kV N

V

V_n L N 12,5 12 150

= =

= −

V1 = V2 = V3 = V4 = V5 = V6 = V7 = V8 = V9 = V10 = V11 = V12 = 12,5 kV

Dari hasil perhitungan diperoleh tegangan pada setiap unit isolator

sama.Berdasarkan persamaan 2.1, faktor kerataannya adalah (AF) = 12,5 – 12,5 =

0.Dalam hal ini tegangan pada setiap unit isolator piring terdistribusi merata.

IV.2.2. Memperhitungkan Kapasitansi C1 dan C2

Rangkaian ekivalen isolator rantai dengan memperhitungkan kapasitansi C2,

adalah seperti yang terlihat pada Gambar 2.5.Untuk distribusi tegangan dengan

memperhitungkan C2, sedang kapasitansi (C3) diabaikan, yang ada hanya kapasitansi

sendiri (C1) dan kapasitansi tegangan rendah (C2).

Kasus : jika tegangan yang ditentukan pada pengujian sebesar 150 kV, faktor

pengali m = 0,1 , maka :

 Untuk 5 (lima) piring isolator rantai :

Vt = V1+V2+V3+V4+V5

=V1+V1+mV1+V1+3mV1+m2V1+V1+6mV1+5m2V1+m3V1+V1+10mV1+15m2V1+

7m3V1+m4V1

= 5V1+20mV1+21m2V1+8m3V1+m4V1

(41)

V1 =

Tegangan pada V3, berdasarkan Persamaan 2.9, maka V3 adalah :

V3 = V1(1+3m+m2)

= 20,781 (1+3(0,1)+(0,1)2)

= 27,223 kV

V4 = V1(1+6m+5m2+m3)

= 20,781(1+6(0,1)+5(0,1)2+(0,1)3)

= 34,309 kV

V5 = V1(1+10m+15m2+7m3+m4)

= 20,781(1+10(0,1)+15(0,1)2+7(0,1)3+(0,1)4)

= 44,826 kV

Dari hasil perhitungan, faktor kerataannya adalah :

AF = 44,826 kV – 20,781 kV = 24,045 kV

 Untuk 6 (enam) piring isolator rantai :

(42)

=5V1+20mV1+21m2V1+8m3V1+m4V1+V1+15mV1+35m2V1+28m3V1+9m4V1+m5

V3 = V1(1+3m+m2)

V3 = 15,004(1+3(0,1)+(0,1)2)

V3 = 19,655 kV

V4 = V1(1+6m+5m2+m3)

V4 = 15,004(1+6(0,1)+5(0,1)2+(0,1)3)

V4 = 24,772 kV

V5 = V1(1+10m+15m2+7m3+m4)

V5 = 15,004(1+10(0,1)+15(0,1)2+7(0,1)3+(0,1)4)

(43)

V6 = V1(1+12m+35m2+28m3+9m4+m5)

V6 = 15,004(1+12(0,1)+35(0,1)2+28(0,1)3+9(0,1)4+(0,1)5)

V6 = 43,196 kV

AF = 43,196 kV – 15,004 kV = 28,192 kV

 Untuk 7 (tujuh) piring isolator rantai :

Vt = V1+V2+V3+V4+V5+V6+V7

V3 = V1(1+3m+m2)

V3 = 10,803(1+3(0,1)+(0,1)2)

(44)

V4 = V1(1+6m+5m2+m3)

V4 = 10,803(1+6(0,1)+5(0,1)2+(0,1)3)

V4 = 17,836 kV

V5 = V1(1+10m+15m2+7m3+m4)

V5 = 10,803(1+10(0,1)+15(0,1)2+7(0,1)3+(0,1)4)

V5 = 23,303 kV

V6 = V1(1+12m+35m2+28m3+9m4+m5)

V6 = 10,803(1+12(0,1)+35(0,1)2+28(0,1)3+9(0,1)4+(0,1)5)

V6 = 31,101 kV

V7 = V1(1+21m+70m2+84m3+45m4+11m5+m6)

V7 = 10,803(1+21(0,1)+70(0,1)2+84(0,1)3+45(0,1)4+11(0,1)5+(0,1)6

V7 = 42,009 kV

AF = 42,009 kV – 10,803 kV = 31,206 kV

 Untuk 8 (delapan) piring isolator rantai :

Vt = V1+V2+V3+V4+V5+V6+V7+V8

=6V1+35mV1+46m2V1+36m3V1+10m4V1+m5V1+V1+21mV1+70m2V1+84m3V1+

45m4V1+11m5V1+m6V1+V1+28mV1+116m2V1+220m3V1+175m4V1+66m5V1+

13m6V1+m7V1.

(45)

Vt = V1(8+84m+232m2+340m3+230m4+78m5+14m6+m7)

V3 = V1(1+3m+m2)

V5 = V1(1+10m+15m2+7m3+m4)

V5 = 7,860(1+10(0,1)+15(0,1)2+7(0,1)3+(0,1)4)

V5 = 16,954 kV

V6 = V1(1+12m+35m2+28m3+9m4+m5)

(46)

V6 = 22,628 kV

V7 = V1(7+56m+116m2+119m3+55m4+12m5+m6)

V7 = 7,860(7+56(0,1)+116(0,1)2+119(0,1)3+55(0,1)4+12(0,1)5+(0,1)6

V7 = 30,564 kV

V8 = V1(1+28m+116m2+220m3+175m4+66m5+13m6+m7)

V8 = 7,860(1+28(0,1)+116(0,1)2+220(0,1)3+175(0,1)4+66(0,1)5+13(0,1)6+(0,1)7)

V8 = 40,858 kV

AF = 40,858 kV – 7,860 kV = 32,997 kV

 Untuk 9 (sembilan) piring isolator rantai :

Vt = V1+V2+V3+V4+V5+V6+V7+V8+V9

Tegangan pada V2 , berdasarkan Persamaan 2.6, maka V2 adalah :

(47)

V2 = 5,725(1+0,1)

V2 = 6,297 kV

Tegangan pada V3, berdasarkan Persamaan 2.9, maka V3 adalah

V3 = V1(1+3m+m2)

V3 = 5,725(1+3(0,1)+(0,1)2)

V3 = 7,499 kV

V4 = V1(1+6m+5m2+m3)

V4 = 5,725(1+6(0,1)+5(0,1)2+(0,1)3)

V4 = 9,452 kV

V5 = V1(1+10m+15m2+7m3+m4)

V5 = 5,725(1+10(0,1)+15(0,1)2+7(0,1)3+(0,1)4)

V5 = 12,349 kV

V6 = V1(1+12m+35m2+28m3+9m4+m5)

V6 = 5,725(1+12(0,1)+35(0,1)2+28(0,1)3+9(0,1)4+(0,1)5)

V6 = 16,482 kV

V7 = V1(7+56m+116m2+119m3+55m4+12m5+m6)

V7 = 5,725(7+56(0,1)+116(0,1)2+119(0,1)3+55(0,1)4+12(0,1)5+(0,1)6

V7 = 22,262 kV

(48)

V8 = 5,725(1+28(0,1)+116(0,1)2+220(0,1)3+175(0,1)4+66(0,1)5+13(0,1)6+(0,1)7)

V8 = 29,760 kV

V9 = V1(1+36m+200m2+462m3+515m4+290m5+91m6+14m7+m8)

V9= 5,725(1+36(0,1)+200(0,1)2+462(0,1)3+515(0,1)4+290(0,1)5+91(0,1)6+14(0,1)7+

(0,1)8

V9 = 40,742 kV

AF = 40,742 kV – 5,725 kV = 35,017 kV

 Untuk 10 (sepuluh) piring isolator rantai :

(49)

V2 = 4,591 kV

V3 = V1(1+3m+m2)

V3 = 4,173(1+3(0,1)+(0,1)2)

V3 = 5,467 kV

V4 = V1(1+6m+5m2+m3)

V4 = 4,173(1+6(0,1)+5(0,1)2+(0,1)3)

V4 = 6,891 kV

V5 = V1(1+10m+15m2+7m3+m4)

V5 = 4,173(1+10(0,1)+15(0,1)2+7(0,1)3+(0,1)4)

V5 = 9,003 kV

V6 = V1(1+12m+35m2+28m3+9m4+m5)

V6 = 4,173(1+12(0,1)+35(0,1)2+28(0,1)3+9(0,1)4+(0,1)5)

V6 = 12,016 kV

V7 = V1(7+56m+116m2+119m3+55m4+12m5+m6)

V7 = 4,173(7+56(0,1)+116(0,1)2+119(0,1)3+55(0,1)4+12(0,1)5+(0,1)6

V7 = 16,230 kV

V8 = V1(1+28m+116m2+220m3+175m4+66m5+13m6+m7)

(50)

V8 = 21,696 kV

V9 = V1(1+36m+200m2+462m3+515m4+290m5+91m6+14m7+m8)

V9= 4,173(1+36(0,1)+200(0,1)2+462(0,1)3+515(0,1)4+290(0,1)5+91(0,1)6+14(0,1)7+

(0,1)8

V9 = 29,703 kV

V10 = V1(1+45m+320m2+904m3+1317m4+1035m5+459m6+119m7+15m8+m9)

V10 = 4,173(1+45(0,1)+320(0,1)2+904(0,1)3+1317(0,1)4+1035(0,1)5+459(0,1)6+119

(0,1)7+15(0,1)8+(0,1)9)

V10 = 40,681 kV

AF = 40,681 kV – 4,173 kV = 36,507 kV.

 Untuk 11 (sebelas) piring isolator rantai :

Vt = V1+V2+V3+V4+V5+V6+V7+V8+V9+V10+V11

Vt = V1(10+165m+752m2+1706m3+2026m4+471m5+564m6+134m7+17m8+m9)+V1

(1+55m+485m2+1666m3+3023m4+3096m5+1862m6+683m7+150m8+18m9+m10)

Vt=10V1+165mV1+752m2V1+1706m3V1+2026m4V1+471m5V1+564m6V1+134m7V1

+17m8V1+m9V1+V1+55mV1+485m2V1+1666m3V1+3023m4V1+3096m5V1+

1862m6V1+683m7V1+150m8V1+18m9V1+m10V1.

Vt = 11V1+220mV1+1237m2V1+3372m3V1+5085m4V1+3567m5V1+2318m6V1+817

m7V1+167m8V1+19m9V1+m10V1.

Vt = V1(11+220m+1237m2+3372m3+5085m4+3567m5+2318m6+817m7+167m8+

(51)

V3 = V1(1+3m+m2)

V5 = V1(1+10m+15m2+7m3+m4)

V5 = 3,043(1+10(0,1)+15(0,1)2+7(0,1)3+(0,1)4)

V5 = 6,564 kV

V6 = V1(1+12m+35m2+28m3+9m4+m5)

V6 = 3,043(1+12(0,1)+35(0,1)2+28(0,1)3+9(0,1)4+(0,1)5)

(52)

V7 = V1(7+56m+116m2+119m3+55m4+12m5+m6)

V7 = 3,043(7+56(0,1)+116(0,1)2+119(0,1)3+55(0,1)4+12(0,1)5+(0,1)6

V7 = 11,834 kV

V8 = V1(1+28m+116m2+220m3+175m4+66m5+13m6+m7)

V8 = 3,043(1+28(0,1)+116(0,1)2+220(0,1)3+175(0,1)4+66(0,1)5+13(0,1)6+(0,1)7)

V8 = 15,819 kV

V9 = V1(1+36m+200m2+462m3+515m4+290m5+91m6+14m7+m8)

V9= 3,043(1+36(0,1)+200(0,1)2+462(0,1)3+515(0,1)4+290(0,1)5+91(0,1)6+14(0,1)7+

(0,1)8

V9 = 21,657 kV

V10 = V1(1+45m+320m2+904m3+1317m4+1035m5+459m6+119m7+15m8+m9)

V10 = 3,043(1+45(0,1)+320(0,1)2+904(0,1)3+1317(0,1)4+1035(0,1)5+459(0,1)6+119

(0,1)7+15(0,1)8+(0,1)9)

V10 = 29,661 kV

V11= V1( 1+55m+485m2+1666m3+3023m4+3096m5+1862m6+683m7+150m8+18m9

+m10).

V11= 3,043(1+55(0,1)+485(0,1)2+1666(0,1)3+3023(0,1)4+3096(0,1)5+1862(0,1)6+

(53)

V11 = 40,631 kV

AF = 40,631kV – 3,043 kV = 37,588 kV.

 Untuk 12 (dua belas) piring isolator rantai :

Vt = V1+V2+V3+V4+V5+V6+V7+V8+V9+V10+V11+V12

(54)

V3 = ( 1 + 3m + m2 ) V1

V3 = ( 1 + 3(0,1) + (0,1)2) 2,234 kV

V3 = 2,927 kV

V4 = (1 + 6m + 5m2 + m3) V1

V4 = (1 + 6(0,1) +5(0,1)2+ (0,1)3 )2,234 kV

V4 = 3,689 kV

V5 = (1 + 10 m + 15 m2 + 7 m3 + m4) V1

V5 = (1 +10(0,1) +15(0,1)2+ 7(0,1)3 + (0,1)4)2,234 kV

V5 = 4,820 kV

V6 = (1+15m+35m2+28m3+9m4+m5)V1

V6 = (1+15(0,1)+35(0,1)2+28(0,1)3+9(0,1)4+(0,1)5)2,234 kV

V6 = 6,432 kV

V7 = (1+21m+70m2+84m3+45m4+11m5+m6)V1

V7 = (1+21(0,1)+70(0,1)2+84(0,1)3+45(0,1)4+11(0,1)5+(0,1)6)2,234 kV

V7 =8,689 kV

V8 = (1+28m+116m2+220m3+175m4+66m5+13m6+m7)V1

V8 = (1+28(0,1)+116(0,1)2+220(0,1)3+175(0,1)4+66(0,1)5+13(0,16)+(0,1)7)2,234 kV

V8 =11,615 kV

(55)

V9 = (1+36m+200m2+462m3+515m4+290m5+91m6+14m7+m8)V1

V9 = (1+36(0,1)+200(0,1)2+462(0,1)3+515(0,1)4+29(0,1)5+91(0,1)6+14(0,1)7+(0,1)8)

2,234 kV

V9 = 15,901 kV

V10 = (1+45m+320m2+904m3+1317m4+1035m5+459m6+119m7+15m8+m9)V1

V10= (1+45(0,1)+320(0,1)2+904(0,1)3+1317(0,1)4+1035(0,1)5+459(0,1)6+119(0,17)+

15(0,1)8+(0,1)9) 2,234 kV

V10 = 21,778 kV

V11 = (1+55m+485m2+1666m3+3023m4+3096m5+1862m6+683m7+150m8+18m9+

m10) V1

V11 = (1+55(0,1)+(485(0,1)2+1666(0,1)3+3023(0,1)4+3096(0,1)5+1862(0,1)6+683

(0,1)7+150(0,1)8+18(0,1)9+(0,1)10) 2,234 kV

V11 = 29,833 kV

V12 = (1+66m+705m2+2913m3+6395m4+8181m5+6361m6+3109m7+967m8+185m9

+20m10+m11) V1

V12 = (1+66(0,1)+705(0,1)2+2913(0,1)3+6395(0,1)4+8181(0,1)5+6361(0,1)6+3109

(0,1)7 +967(0,1)8+185(0,1)9+20(0,1)10+(0,1)11) 2,234 kV

V12 = 40,870 kV

Dari hasil perhitungan, faktor kerataanya adalah :

(56)

Dari hasil perhitungan semua (dari jumlah lima sampai dua belas

piring isolator rantai), dapat dibuat tabel-tabel hasil perhitungan yang terdapat

dilampiran a.Dan perhitungan secara metode Matlab (Matrrix Laboratory) terdapat

dilampiran c.

BAB V

KESIMPULAN DAN SARAN

V.1. KESIMPULAN

Kesimpulan yang diperoleh dari perhitungan distribusi tegangan pada isolator

rantai dengan menggunakan Matlab, penulis menyimpulkan antara lain :

1. Hasil perhitungan secara manual sama dengan metode Matlab.

2. Dengan menggunakan metode perhitungan Matlab akan mempermudah

dalam perhitungan distribusi tegangan pada isolator rantai karena lebih

cepat memperoleh hasilnya.

3. Dapat dilihat dari jumlah lima sampai dua belas isolator, nilai faktor

kerataanya semakin menaik.

4. Dari perhitungan terlihat bahwa tegangan terbesar isolator rantai

terdapat di isolator yang paling dekat dengan konduktor tegangan

tinggi.

V.2. SARAN

Adapun saran yang ingin disampaikan penulis antara lain:

1. Pada Tugas Akhir ini tidak membahas perhitungan distribusi tegangan

dengan memperhitungakan C1 dan C3 dan distribusi tegangan pada

isolator rantai dengan memperhitungan semua kapasitansi.Diharapkan

(57)

2. Pada program yang disajikan kali ini terbatas untuk perhitungan, yaitu

distribusi tegangan tanpa kapasitansi C2 dan C3, dan distribusi tegangan

memperhitungkan kapasitansi C1 dan C2.Diharapkan dikemudian hari

program ini dapat dikembangkan untuk semua kapasitansi.

3. Program yang digunakan dalam perhitungan distribusi tegangan pada

isolator rantai disini adalah menggunakan metode Matlab.Diharapkan

dikemudian hari dapat digunakan dengan program - program yang lain,

dengan tampilan disain yang lebih menarik dan mempunyai ketelitian

(58)

(59)

DAFTAR PUSTAKA

1. Arismunandar, Artono. 1968. Teknik Tegangan Tinggi, PT. Pradya Paramita:

Jakarta.

2. Kadir, Abdul. 1998. Transmisi Tenaga Listrik, Universitas Indonesia : Jakarta

3. Tobing, Bonggas L. 2003. Dasar Teknik Pengujian Tegangan Tinggi,

PT Gramedia Pustaka Utama: Jakarta.

4. Tobing, Bonggas L. 2003. Peralatan Tegangan Tinggi, PT Gramedia Pustaka

Utama: Jakarta

5. Uppal. 1989. Electric Power, Khana Publishers : Delhi-6..

6. Gunaidi Abdia Away.2006.The Shortcut Of Matlab Programming.Informatika:

Bandung.

7. Cekmas Cekdin, “Sistem Tenaga Listrik” : “Contoh Soal Dan Penyelesaiannya

(60)

LAMPIRAN A

Lampiran

:

Tabel hasil perhitungan dari jumlah lima sampai dua belas isolator deng an memperhitungkan kapasitansi C1 dan C2.

Lampiran 1

NOMOR ISOLATOR

BESAR TEGANGAN (KV)

1 20,781

2 22,859

3 27,223

4 34,309

5 44,826

Tabel. Hasil perhitungan untuk 5 (lima) piring isolator

1 15,004

2 16,504

3 19,655

4 24,772

5 32,366

6 43,196

(61)

Lampiran 2

1 10,803

2 11,883

3 14,152

4 17,836

5 23,303

6 31,101

7 42,009

Tabel. Hasil perhitungan untuk 7 (tujuh) piring isolator

1 7,860

2 8,646

3 10,296

4 12,976

5 16,954

6 22,628

7 30,564

(62)

Tabel. Hasil perhitungan untuk 8 (delapan) piring isolator

Lampiran 3

1 5,725

2 6,297

3 7,499

4 9,452

5 12,349

6 16,482

7 22,262

8 29,760

9 40,742

Tabel. Hasil perhitungan untuk 9 (sembilan) piring isolator

1 4,173

2 4,591

3 5,467

4 6,891

5 9,003

6 12,016

7 16,230

8 21,696

9 29,703

(63)

Tabel. Hasil perhitungan untuk 10 (sepuluh) piring isolator

Lampiran 4

BESAR TEGANGAN (KV)

1 3,043

2 3,347

3 3,986

4 5,024

5 6,564

6 8,761

7 11,834

8 15,819

9 21,657

10 29,661

11 40,631

Tabel. Hasil perhitungan untuk 11 (sebelas) piring isolator

BESAR TEGANGAN (KV)

1 2,234

2 2,457

3 2,927

4 3,689

5 4,820

6 6,432

7 8,689

8 11,615