PENGARUH PENDEKATAN PROBLEM POSING TERHADAP KEMAMPUAN PEMAHANAN KONSEP
MATEMATIS SISWA
( Studi pada Siswa Kelas VII SMP Negeri 8 Bandar Lampung Semester Genap Tahun Pelajaran 2014/2015)
Oleh HESTI LESTARI
Skripsi
Sebagai Salah Satu Syarat untuk Mencapai Gelar SARJANA PENDIDIKAN
pada
Program Studi Pendidikan Matematika
Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS LAMPUNG
ABSTRAK
PENGARUH PENDEKATAN PROBLEM POSING TERHADAP KEMAMPUAN PEMAHAMAN KONSEP
MATEMATIS SISWA
(Studi pada Siswa Kelas VII SMP Negeri 8 Bandar Lampung Semester Genap Tahun Pelajaran 2014/2015)
Oleh HESTI LESTARI
Penelitian eksperimen semu ini bertujuan untuk mengetahui pengaruh pendekatan Problem Posing terhadap kemampuan pemahaman konsep matematis siswa. Desain penelitian ini menggunakan posttest only control design. Populasi penelitian adalah seluruh siswa kelas VII SMP Negeri 8 Bandar Lampung tahun
pelajaran 2014/2015 sebanyak 322 siswa yang terdistribusi dalam empat belas
kelas. Sampel penelitian adalah siswa kelas VII L dan VII I yang diambil
menggunakan teknik purposive random sampling. Berdasarkan pengujian hipotesis, diperoleh bahwa rata-rata nilai posttest siswa yang mengikuti pembelajaran dengan pendekatan Problem Posing lebih tinggi daripada rata-rata nilai posttest siswa yang mengikuti pembelajaran konvensional. Dengan demikian, disimpulkan bahwa pembelajaran matematika dengan pendekatan Problem Posing berpengaruh terhadap pemahaman konsep matematis siswa
PENGARUH PENDEKATAN PROBLEM POSING TERHADAP KEMAMPUAN PEMAHANAN KONSEP
MATEMATIS SISWA
( Studi pada Siswa Kelas VII SMP Negeri 8 Bandar Lampung Semester Genap Tahun Pelajaran 2014/2015)
(Skripsi)
Oleh
HESTI LESTARI
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS LAMPUNG
ix DAFTAR LAMPIRAN
Lampiran Halaman
A. Perangkat Pembelajaran
A.1 Rencana Pelaksanaan Pembelajaran (RPP) Kelas Pembelajaran
Problem posing ... 40
A.2 Rencana Pelaksanaan Pembelajaran (RPP) Kelas Pembelajaran Konvensional... 68
A.3 Lembar Kerja Kelompok (LKK) ... 89
B. Perangkat Tes B.1 Kisi-Kisi Tes Pemahaman Konsep Matematis ...145
B.2 SoalPosttestPemahaman Konsep Matematis...146
B.3 Pedoman Penskoran Tes Pemahaman Konsep ...148
B.4 Kunci JawabanPostestPemahaman Konsep Matematis...149
B.4 Form Validasi Instrumen Tes Pemahaman Konsep Matematis...152
C. Analisis Data C.1 Analisis Uji Reliabilitas Postte ...154
C.2 Analisis Daya Pembeda dan Taraf Kesukaran Posttest ...155
C.3 Hasil Nilai Posttest Kelas Eksperimen ...156
C.4 Hasil Nilai Posttest Kelas Kontrol...157
x C.6 Uji Normalitas Postest Kemampuan Pemahaman Konsep Matematis
Siswa Kelas Eksperimen ...159 C.7 Uji Normalitas Postest Kemampuan Pemahaman Konsep Matematis
Siswa Kelas Kontrol...160 C.8 Uji Non Parametri Kemampuan Pemahaman Konsep Matematis
Antara Kelas Eksperimen dan Kelas Kontrol ...161 C.9 Pencapaian Indikator dan Rekapitulasi Pencapaian Pemahaman
Konsep Matematis...163 C.10 Pencapaian Indikator dan Rekapitulasi Pencapaian Pemahaman
Konsep Matematis...166
D. Lain-lain
viii DAFTAR TABEL
Halaman
Tabel 3.1 Desain Penelitian ... 18
Tabel 3.2 Pedoman Penskoran Tes Pemahaman Konsep Matematis... 21
Tabel 3.3 Interpretasi Nilai Daya Pembeda ... 24
Tabel 3.4 Interpretasi Nilai Tingkat Kesukaran ... 25
Tabel 3.5 Rekapitulasi Hasil Tes Uji Coba ... 26
Tabel 3.6 Rekapitulasi Uji Normalitas Data Penelitian ... 27
Tabel 4.1 Rekapitulasi Data Pemahaman Konsep Matematis ... 30
Tabel 4.2 Rekapitulasi Uji Mann Whitney Data Pemahaman Konsep Matematis Siswa ... 31
vi DAFTAR ISI
Halaman
DAFTAR TABEL . ... viii
DAFTAR LAMPIRAN ... ix
I. PENDAHULUAN A. Latar Belakang ... 1
B. Rumusan Masalah ... 5
C. Tujuan Penelitian ... 5
D. Manfaat Penelitian ... 6
E. Ruang Lingkup Penelitian ... 6
II. TINJAUAN PUSTAKA A. Kemampuan Pemahaman Konsep ... 8
B. Pendekatan Problem Posing ... 10
C. Penelitian Relevan ... 12
D. Kerangka Pikir ... 13
E. Anggapan Dasar ... 15
F. Hipotesis ... 16
III. METODE PENELITIAN A. Populasi dan Sampel ... 17
vii
C. Prosedur Penelitian ... 18
D. Data Penelitian ... 19
E. Teknik Pengumpulan Data ... 20
F. Instrumen Penelitian. ... 20
1. Instrumen Tes ... 20
a. Validitas Isi ... 22
b. Riliabilitas ... 22
c. Daya Pembeda ... 23
d. Tingkat Kesukaran ... 24
G. Teknik Analisis Data ... 26
1. Uji Normalitas ... 26
2. Uji Hipotesis ... 28
IV. HASIL PENELITIAN DAN PEMBAHASAN A. Hasil Penelitian ... 30
1. Uji Hipotesis ... 31
B. Pembahasan ... 34
V. SIMPULAN DAN SARAN A. Simpulan ... 38
B. Saran ... 38
MOTO
Tidak ada harapan yang hanya
sebatas mimpi ketika kita mau
berusaha mewujudkannya, dan
yakinlah tidak pernah ada usaha yang
sia-sia
PERSEMBAHAN
Dengan mengucap syukur kehadirat ALLAH SWT, kupersembahkan
karya ini dengan kesungguhan hati sebagai tanda bakti dan cinta
kasihku kepada:
Ayah ku tersayang Baherman dan Umi ku tercinta Sofiah (Almh)
yang telah memberikan doa, kasih sayang, motivasi, dan bekal
kehidupan yang tak henti-hentinya, yang selalu ada disampingku
serta selalu memberikanku yang terbaik untuk menjadikanku sesuatu
yang terbaik dalam kehidupan ini.
seluruh keluarga besarku baik dari ayah maupun umi,
yang telah memberikan do a dan dukungan padaku.
Para pendidik yang telah mendidikku, yang menjadikanku semakin
berwawasan.
RIWAYAT HIDUP
Penulis dilahirkan di Desa Pasar Sukadana Kecamatan Sukadana Kabupaten Lampung Timur, 11 Agustus 1992. Penulis adalah anak tunggal dari pasangan Bapak Baherman dan Ibu Sofiah.
Penulis menyelesaikan pendidikan Taman Kanak-Kanak di TK PGRI 2 Sukadana pada tahun 1998, kemudian menyelesaikan pendidikan dasar di SD Negeri 2 Sukadana pada tahun 2004, pendidikan menengah pertama di SMP Negeri 1 Sukadana pada tahun 2007, dan pendidikan menengah atas di SMA Negeri 1 Sukadana pada tahun 2010. Penulis melanjutkan pendidikan di Universitas Lampung pada tahun 2010 melalui jalur Penelusuran Kemampuan Akademik dan Bakat (PKAB) dengan mengambil program studi Pendidikan Matematika.
ii
SANWACANA
Puji syukur kehadirat Allah SWT Yang Maha Pengasih dan Maha Penyayang yang telah melimpahkan rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan penyusunan skripsi yang berjudul “Pengaruh Pendekatan Problem Posing Terhadap Kemampuan Pemahaman Konsep Matematis Siswa (Studi Pada Siswa Kelas VII SMP Negeri 8 Bandar Lampung Tahun Pelajaran 2014/2015)”.
Penulis menyadari sepenuhnya bahwa selesainya skripsi ini tidak terlepas dari bantuan berbagai pihak. Untuk itu, penulis mengucapkan terimakasih kepada: 1. Ayahku tersayang Baherman yang tak pernah henti mendoakan dan
menyemagatiku dalam bentuk apapun dan yang selalu ada disaat apapun, yang tidak pernah lelah menasehatiku, dan yang selalu menjadi motivasi dalam hidupku, Umiku tercinta Sofiah (Almh) yang aku yakin hingga detik ini selalu memperhatikan dan mendoakanku, dan yang selalu aku yakini bahwa beliau selalu ada didekatku.
iii
3. Ibu Dr. Sri Hastuti Noer, M.Pd., selaku dosen pembimbing II yang telah ber-sedia meluangkan waktu untuk membimbing, memberikan perhatian, motivasi, kritik, saran, dan semangat kepada penulis demi terselesaikannya skripsi ini.
4. Bapak Drs. Pentatito Gunowibowo, M.Pd., selaku dosen pembahas yang telah memberikan masukan, kritik, dan saran kepada penulis.
5. Bapak Dr. Caswita, M.Si., selaku Ketua Jurusan Pendidikan MIPA yang telah memberikan kemudahan kepada penulis dalam menyelesaikan skripsi ini. 6. Bapak Dr. Bujang Rahman, M.Si., selaku Dekan FKIP Universitas Lampung,
beserta staf dan jajarannya yang telah memberikan bantuan kepada penulis dalam menyelesaikan skripsi ini.
7. Bapak dan Ibu dosen pendidikan matematika di Fakultas Keguruan dan Ilmu Pendidikan yang telah memberikan bekal ilmu pengetahuan kepada penulis. 8. Orang-orang terdekatku adik sepupuku Mira, none Aas, kakak sepupuku kiyai
Ridwan, aing Lia, gusti Salbiah, om Prapto, tante Mery, bunda May, cicik Ina yunda Tika, Ana Safitri, Rizki abed, 2 ponakan centil dan tampan gusti Echa dan dede Rafif juga seluruh keluarga besarku yang selalu menyayangi, mendoakan dan selalu menjadi penyemangat dalam hidupku.
9. Ibu Ratnasari, S.Pd. MM., selaku kepala SMP Negeri 8 Bandar Lampung beserta Wakil, staff, dan karyawan yang telah memberikan kemudahan selama penelitian.
iv
11. Sahabat-sahabat seperjuanganku angkatan 2010 A, Suqor, Asih, Sulis, Ute, Ria Artha, Beni, Fertil, Ma’e (Endang), Tri H, Imas, Dhea, Rini, Novi, Sueb, Nurul H, Yulisa, Dian, Intan, Aan, Trifau, Novrian, Rusdi, Arif atas persahabatan, kebersamaan, nasehat, dan semangat yang diberikan selama ini. Jangan pernah letih menggapai cita-cita yang diinginkan.
12. Sahabat-sahabat tersayang Andri makasih buat semua saran, nasehat, juga motivasi yang selalu ada yang gak pernah lelah buat selalu kasih semangat, Sulia pembimbing 3 yang gak pernah lelah kasih semangat buat revisian juga kasih saran plus ide-ide kalau udah mentok, Citut dan Ria terima kasih atas semangat, tawa, canda dan kebersamaanya selama ini. Semoga setelah saling mendapatkan gelar sarjana, persahabatan, dan kebersamaan kita tetap bisa terjalin dengan baik.
13. Teman-teman seperjuangan KKN PPL di Desa Gedung Ratu, Pujo, Lusi, ely, Emak Ayu, Mitha, Teteh Oja, Irfan, Jodi dan Imam terima kasih atas kebersamaan selama 75 hari yang sangat luar biasa.
14. Teman-teman angkatan 2010 B khususnya Selvi Utami yang selalu setia bimbingan bareng, kakak-kakak angkatan 2008 dan 2009 kak Kiki, Kak Umpu, Mba Ve, Kak Yose, Mba Amel, adik-adik angkatan 2011 Ria Oktavia, Yulisa, Fuji, Enggar, Hani, Laili, Dewi, Nourma, Ipeh, Aliza, Bayu, Ige, Yusuf, Venti, Ismi, Yola, Winda, Ista, Dian, Rizka, Selvy, Ayu, Titi, ule dan angkatan 2012 serta 2013 terima kasih atas kebersamaannya.
v
Qibtiyah, Nur, Jefri, Neas, Sibu, Bang Tom, Riko terima kasih atas semangat, tawa dan canda kalian selama ini.
16.Siswa kelas VII I, dan VII L SMP Negeri 8 Bandar Lampung tahun pelajaran 2014/2015, terimakasih atas perhatian dan kerjasama yang telah terjalin. 17. Almamaterku.
18. Semua pihak yang telah membantu dalam penyusunan skripsi ini.
Semoga dengan bantuan dan dukungan yang diberikan mendapat balasan pahala di sisi Allah SWT dan semoga skripsi ini bermanfaat.
Bandar Lampung, Juni 2015 Penulis,
1
I. PENDAHULUAN
A. Latar Belakang Masalah
Pendidikan merupakan hal penting dalam kehidupan guna membangun sumber daya manusia yang berkualitas. Sumber daya manusia yang berkualitas adalah mereka yang mampu berpikir secara cerdas, aktif, kreatif, terampil, produktif, serta bertanggung jawab. Salah satu cara memperoleh sumber daya manusia yang berkualitas adalah dengan menyelenggarakan suatu pendidikan. Hal ini tercantum dalam Undang-Undang Sistem Pendidikan Nasional Nomor 20 tahun 2003 bahwa tujuan pendidikan nasional adalah mencerdaskan kehidupan bangsa dan mengembangkan manusia Indonesia seutuhnya yaitu manusia yang bertakwa kepada Tuhan Yang Maha Esa dan berbudi pekerti luhur, memiliki pengetahuan dan keterampilan, kesehatan jasmani dan rohani, kepribadian yang mantap dan mandiri serta tanggung jawab kemasyarakatan dan kebangsaan.
2
rupa sehingga tingkah laku siswa berubah ke arah yang lebih baik. Apabila suatu pembelajaran berjalan dengan baik maka pembelajaran tersebut akan membawa hasil yang baik, demikian pula untuk pembelajaran dalam matematika.
Matematika memiliki banyak peranan untuk menyelesaikan permasalahan dalam kehidupan sehari-hari. Daryanto dan Rahardjo (2012:240) mengungkapkan bahwa matematika tidak hanya sebatas menguasai perhitungan matematika tetapi juga untuk melatih kemampuan berpikir logis, analitis, sistematis, kritis dan kreatif serta kemampuan bekerja sama. Oleh sebab itu, mempelajari matematika memerlukan ketekunan walaupun banyak terdapat kesulitan dalam proses belajarnya.
Permendiknas nomor 22 tahun 2006 tentang Standar Isi dinyatakan bahwa pembelajaran matematika bertujuan agar siswa memiliki kemampuan:
1. Memahami konsep matematika, menjelaskan keterkaitan antar konsep dan mengaplikasikan konsep atau algoritma, secara luas, akurat, efisien, dan tepat dalam memecahkan masalah.
2. Menggunakan penalaran pada pola dan sifat, melakukan manipulasi matematika, dalam membuat generaalisasi, menyusun bukti, atau menjelaskan gagasan dan pertanyaan matematika.
3. Memecahkan masalah yang meliputi kemampuan memahami masalah, merancang model matematika, menyelesaikan model dan menafsirkan solusi yang diperoleh.
4. Mengkomunikasikan gagasan dengan simbol, tabel, diagram, media lain untuk memperjelas keadaan atau masalah.
3
konsep materi maka siswa akan mudah untuk memahami konsep selanjutnya dan mengembangkan kemampuan berpikir.
Pada kenyataannya, sebagian besar siswa Indonesia mengalami kesulitan dalam memahami konsep-konsep matematika, yang menyebabkan rendahnya kemampuan matematis siswa. Hal ini dapat dilihat dari hasil survei Trends in International Mathematics and Science Study (TIMSS) tahun 2011 (Mullis et al., 2012), bahwa Indonesia berada pada urutan ke-38 dari 42 negara dengan skor rata-rata 386 dari skor ideal 1000. Skor Indonesia pada tahun 2011 turun 11 poin dari tahun 2007. Hal ini karena siswa di Indonesia kurang terbiasa menyelesaikan soal-soal dengan karakteristik seperti soal-soal pada TIMSS, yang subtansinya kontekstual, menuntut penalaran, argumentasi dan kreativitas dalam penyelesaian.
Kondisi ini juga terjadi pada siswa di SMP Negeri 8 Bandar Lampung. Berdasarkan wawancara terhadap guru bidang studi matematika di SMP Negeri 8 Bandarlampung memberikan sebuah gambaran bahwa kemampuan pemahaman konsep siswa dinilai masih kurang baik. Kurangnya kemampuan pemahaman konsep siswa ini salah satunya akibat penerapan pola pembelajaran yang kurang tepat. Pembelajaran matematika yang terjadi kebanyakan didominasi oleh pembelajaran satu arah, siswa hanya pasif menerima informasi dari guru. Model pembelajaran yang seperti ini tentu saja mengakibatkan kurang optimalnya kemampuan pemahaman konsep matematis siswa.
4
matematis siswa dapat ditingkatkan. Salah satu upaya yang dapat dilakukan adalah menerapkan pendekatan pembelajaran yang menuntut siswa untuk aktif dalam memahami pokok bahasan yang diajarkan. Pendekatan pembelajaran tersebut antara lain adalah pendekatanProblem Posing.
5
berpengaruh positif terhadap kemampuan pemahaman konsep matematis siswa. Pengaruh dalam penelitian ini dilihat apabila terdapat perbedaan antara kemampuan pemahaman konsep matematis siswa yang menggunakan pembelajaran dengan pendekatan Problem Posing dan pembelajaran konvensional.
Berdasarkan uraian di atas, penulis tertarik untuk mengadakan penelitian tentang pengaruh pendekatan Problem Posing terhadap kemampuan pemahaman konsep matematis siwa.
B. Rumusan Masalah
Berdasarkan latar belakang masalah yang telah diuraikan sebelumnya, maka rumusan masalah dalam penelitian ini adalah sebagai berikut: “Apakah pendekatanProblem Posing berpengaruh terhadap pemahaman konsep matematis siswa di SMP Negeri 8 Bandar lampung?”
Dari rumusan masalah di atas dapat dibuat pertanyaan penelitian yatu: “Apakah
kemampuan pemahaman konsep matematis siswa melalui pendekatan Problem Posing lebih tinggi dari kemampuan pemahaman konsep matematis siswa melalui pembelajaran konvensional?”
C. Tujuan penelitian
6
D. Manfaat Penelitian
Manfaat yang diharapkan dari hasil penelitian ini adalah: 1. Manfaat Teoritis
Hasil penelitian ini diharapkan dapat memberikan sumbangan informasi dalam pendidikan matematika berkaitan dengan pendekatan pembelajaran Problem Posingserta hubungannya dengan pemahaman konsep matematis siswa.
2. Manfaat Praktis
PendekatanProblem Posingdiharapkan dapat dijadikan pendekatan pembelajaran alternatif yang dapat meningkatkan kemampuan pemahaman konsep matematis siswa serta dapat digunakan sebagai bahan pertimbangan bagi peneliti lain yang ingin meneliti lebih lanjut mengenai pendekatan pembelajaran tersebut.
E. Ruang Lingkup
Adapun ruang lingkup dalam penelitian ini adalah sebagai berikut:
7
2. Pendekatan Problem Posing dimulai dari merumuskan soal atau pengajuan soal yang melibatkan siswa secara langsung dalam pembuatan soal dan menyelesaikannya sesuai dengan konsep atau materi yang di pelajari. Ada tiga aktivitas kognitif problem posing dalam pembelajaran matematika. Pertama, pre solution posing yaitu membuat soal atau masalah dari situasi atau per-nyataan yang diadakan sesuai materi yang dijelaskan. Kedua, within solution posing yaitu merumuskan ulang pertanyaan soal tersebut menjadi sub-sub pertanyaan baru yang akan menuntun mereka dalam penyelesaian soal ter-sebut. Sedangkan yang ketiga, post solution posing yaitu merumuskan ulang tujuan atau kondisi soal yang sudah diselesaikan untuk membuat soal yang baru yang sejenis berdasarkan pada tahap sebelumnya.
II. TINJAUAN PUSTAKA
A. Kemampuan Pemahaman Konsep
Pemahaman konsep terdiri dua kata pemahaman dan konsep. Dalam kamus Besar Bahasa Indonesia, paham berarti mengerti dengan tepat. Hal tersebut sejalan dengan pendapat Sadiman (2008: 42) yang menyatakan bahwa Pemahaman atau comprehensiondapat diartikan menguasai sesuatu dengan pikiran. Oleh sebab itu, belajar harus mengerti secara makna dan filosofinya, maksud dan implikasi serta aplikasi-aplikasinya, sehingga menyebabkan siswa memahami suatu situasi. Mulyasa (2005: 78) menyatakan bahwa pemahaman adalah kedalaman kognitif dan afektif yang dimiliki oleh individu. Sejalan dengan pendapat di atas, Rusman (2010: 139) menyatakan bahwa pemahaman merupakan proses individu yang menerima dan memahami informasi yang diperoleh dari pembelajaran yang didapat melalui perhatian.
9 menghitung luas permukaan kubus. Pemahaman terhadap konsep materi pra-syarat sangat penting karena apabila siswa menguasai konsep materi prapra-syarat maka siswa lebih mudah untuk memahami konsep materi selanjutnya.
Menurut Soedjadi (2000: 14) konsep adalah ide abstrak yang dapat digunakan untuk menggolongkan atau mengklasifikasikan sekumpulan obyek. Sebagai con-toh, segitiga adalah nama dari suatu konsep abstrak dan bilangan asli adalah nama suatu konsep yang lebih kompleks karena terdiri dari beberapa konsep yang sederhana, yaitu bilangan satu, bilangan dua, dan seterusnya. Konsep berhubung-an erat dengberhubung-an definisi. Definisi adalah ungkapberhubung-an yberhubung-ang membatasi konsep. Dengan adanya definisi, orang dapat membuat ilustrasi atau gambaran atau lambang dari konsep yang didefinisikan, sehingga menjadi jelas apa yang dimaksud konsep tertentu.
Menurut Nasution (2005: 164) siswa yang menguasai konsep dapat meng-identifikasi dan mengerjakan soal baru yang lebih bervariasi. Selain itu, apabila anak memahami suatu konsep maka ia akan dapat menggeneralisasikan suatu obyek dalam berbagai situasi lain yang tidak digunakan dalam situasi belajar.
Selanjutnya, penilaian perkembangan siswa terhadap pemahaman konsep matematis dicantumkan dalam beberapa indikator sebagai hasil belajar matematika. Depdiknas (Wardhani, 2006: 4) menyatakan bahwa ada beberapa indikator yang menunjukkan suatu pemahaman konsep adalah:
1. Menyatakan ulang sebuah konsep.
2. Mengklasifikasi obyek-obyek menurut sifat-sifat tertentu (sesuai dengan konsepnya).
10 4. Menyajikan konsep dalam berbagai bentuk representasi matematis.
5. Mengembangkan syarat perlu atau syarat cukup suatu konsep.
6. Menggunakan, memanfaatkan, dan memilih prosedur atau operasi tertentu. 7. Mengaplikasikan konsep atau algoritma pemecahan masalah.
Berdasarkan beberapa pendapat di atas dapat disimpulkan bahwa pemahaman konsep matematis adalah proses individu menguasai dengan cara menerima dan memahami informasi yang diperoleh dari pembelajaran yang dilihat melalui kemampuan bersikap, berpikir dan bertindak yang ditunjukkan oleh siswa dalam memahami definisi, pengertian, ciri khusus, hakikat dan inti /isi dari materi matematika dan kemampuan dalam memilih serta menggunakan prosedur secara efisien dan tepat. Indikator pemahaman konsep yang akan digunakan dalam penelitian ini yaitu: menyatakan ulang suatu konsep, mengklasifikasi obyek-obyek menurut sifat-sifat tertentu (sesuai dengan konsepnya), memberi contoh dan non contoh, menyajikan konsep dalam berbagai bentuk representasi matematika, menggunakan syarat perlu atau syarat cukup suatu konsep, menggunakan, memanfaatkan, dan memilih prosedur atau operasi tertentu, dan mengaplikasikan konsep atau algoritma pemecahan masalah.
B. PendekatanProblem Posing
11 matematika untuk mencari alternatif pemecahan masalah yang relevan, dan yang ketiga Problem Posing ialah merumuskan atau mengajukan pertanyaan matematika.
Merumuskan soal pada Problem Posing diharapkan mampu memancing siswa untuk menemukan pengetahuan yang bukan diakibatkan dari ketidaksengajaan melainkan melalui upaya mereka untuk mencari hubungan-hubungan dalam informasi yang dipelajarinya. Semakin luas informasi yang dimiliki akan semakin mudah pula menemukan hubungan-hubungan tersebut. Oleh sebab itu, penemuan pertanyaan serta jawaban yang dihasilkan siswa dapat menyebabkan perubahan dan ketergantungan pada penguatan luar pada rasa puas akibat keberhasilan menemukan sendiri, baik berupa pertanyaan atau masalah maupun jawaban atas permasalahan yang diajukan (Suryosubroto, 2009: 203).
Menurut Mulyatiningsih (2012: 238) langkah-langkah pembelajaran dengan problem posingdapat dirancang sebagai berikut :
1) Guru menjelaskan materi pelajaran, kemudian memberi soal-soal latihan secukupnya
2) Siswa mengerjakan soal latihan dikelas kemudian membahas hasilnya secara bersama-sama supaya siswa tahu cara mengerjakan soal yang benar.
3) Siswa diberi tugas mengajukan 1 atau 2 buah soal yang menantang dan siswa yang bersangkutan harus mampu menyelesaikannya.
12 Silver dan Cai (Herdian, 2009: 1) menjelaskan bahwa pengajuan soal mandiri dapat diaplikasikan dalam 3 bentuk aktivitas kognitif matematika yakni sebagai berikut:
a. Pre solution posing
Pre solution posing yaitu jika seorang siswa membuat soal dari situasi yang diadakan. Jadi guru diharapkan mampu membuat pertanyaan yang berkaitan dengan pernyataan yang dibuat sebelumnya.
b. Within solution posing
Within solution posing yaitu jika seorang siswa mampu merumuskan ulang pertanyaan soal tersebut menjadi sub-sub pertanyaan baru yang urutan penyelesaiannya seperti yang telah diselesaikan sebelumnya.jadi, diharapkan siswa mampu membuat sub-sub pertanyaaan baru dari sebuah pertanyaan yang ada pada soal yang bersangkutan.
c. Post solution posing
Post solution posing yaitu jika seorang siswa memodifikasi tujuan atau kondisi soal yang sudah diselesaikan untuk membuat soal yang baru yang sejenis.
Berdasarkan beberapa pendapat di atas mengenai tahapan pelaksanaan pem-belajaran dengan pendekatan Problem Posing, maka dapat diketahui bahwa pembelajaran dengan Problem Posing diawali dengan pemberian masalah (soal) oleh guru, kemudian dilanjutkan dengan siswa membuat soal berdasarkan masalah tersebut, lalu membuat sub-sub pertanyaan/soal berdasarkan soal yang mereka buat, tahap yang selanjutnya yaitu menentukan jawaban yang tepat dari soal yang mereka buat.
C. Penelitian Relevan
13 pemahaman konsep antara siswa yang memperoleh pembelajaran problem posing dengan siswa yang memperoleh pembelajaran konvensional, atau dengan kata lain pendekatan problem posing berpengaruh terhadap kemampuan pemahaman konsep matematika siswa. Penelitian lainnya yang dilakukan oleh Masyitoh (2013: 1) yang berjudul pendekatan problem posing terhadap kemampuan pemahaman konsep matematis siswa. Hasil yang diperoleh bahwa pendekatan problem posingberpengaruh terhadap kemampuan pemahaman konsep matematis siswa.
D. Kerangka Pikir
Tingkat keberhasilan kegiatan belajar matematika bergantung dari bagaimana proses belajar yang terjadi dan dapat dilihat dari hasil belajar dan tingkat kemampuan matematis siswa. Salah satu kemampuan yang harus dimiliki siswa adalah kemampuan pemahaman konsep matematis. Hal ini karena kemampuan pemahaman konsep matematis sangat diperlukan siswa ketika siswa ingin menyajikan dan memperjelas ide dan argumen matematika mereka. Menyadari akan peran penting kemampuan pemahaman konsep matematis dalam pembelajaran matematika, maka kemampuan pemahaman konsep matematis harus ditingkatkan. Salah satu cara untuk meningkatkan pemahaman konsep matematis adalah dengan memilih pendekatan pembelajaran yang efektif dan efisien.
14 tujuan pembelajaran. Pendekatan yang dipilih hendaknya dapat menciptakan suasana pembelajaran siswa yang aktif, kreatif, dan menyenangkan, sehingga dapat mempelajari matematika dengan mudah. Salah satu alternatif pendekatan yang dapat diterapkan yaitu pendekatanProblem Posing.
PendekatanProblem Posingmerupakan salah satu pendekatan pembelajaran yang dapat membuat siswa lebih aktif di dalam pembelajaran. Dengan pendekatan ini siswa dilatih untuk bertanya dengan pertanyaan yang mereka rancang sendiri sesuai dengan pemahaman siswa tersebut. Kegiatan pengajuan soal (problem posing) ini juga dapat meningkatkan kreativitas siswa dan mengajak siswa untuk berpikir kritis.
15 matematika. Ketiga, post solution posing yaitu siswa merumuskan ulang tujuan atau kondisi soal yang sudah diselesaikan untuk membuat soal yang baru yang sejenis. Dalam tahap ini, siswa dituntut untuk mengembangkan konsep yang ada menjadi sebuah konsep yang baru sehingga kegiatan ini dapat melatih siswa untuk memahami keterkaitan antar konsep, dan pada tahap ketiga aktivitas kognitif ini memuat indikator pemahaman konsep berupa mengembangkan syarat perlu atau syarat cukup suatu konsep dan menggunakan, memanfaatkan, dan memilih prosedur atau operasi tertentu.
Dari ketiga aktivitas kognitif yang terdapat dalam pembelajaran Problem Posing, siswa dibimbing untuk merancang pertanyaan-pertanyaan dari pernyataan yang diberikan oleh guru, dan siswa belajar untuk membuat penyelesaian sendiri berkenaan dengan pertanyaan yang mereka rancang. Hal tersebut dapat menggali pemahaman konsep siswa sehingga siswa yang mengikuti pembelajaran dengan pendekatan Problem Posing dapat mengembangkan kemampuan pemahaman konsep matematis dengan memperoleh hasil yang baik.
E. Anggapan Dasar
Penelitian ini mempunyai anggapan dasar sebagai berikut:
16 2. Faktor lain yang mempengaruhi kemampuan pemahaman konsep matematis siswa selain pendekatan Problem Posing dikontrol sehingga memberikan pengaruh yang sangat kecil.
F. Hipotesis
17
III. METODE PENELITIAN
A. Populasi dan sampel
Penelitian ini telah dilaksanakan di SMP Negeri 8 Bandar Lampung yang terletak di Jl. Untung Suropati Gg. Bumimanti II No.16 Kampung Baru, kota Bandar Lampung. Populasi dalam penelitian ini adalah seluruh siswa kelas VII SMP Negeri 8 Bandar Lampung semester genap tahun pelajaran 2014-2015 dengan jumlah siswa sebanyak 322 siswa yang terdistribusi dalam empat belas kelas (VII A-VII N).
Pengambilan Sampel dari penelitian ini diambil melalui teknik purposive random sampling. Pengambilan sampel secara purposive dengan pertimbangan bahwa kelas yang dipilih diajar oleh guru yang sama sehingga memiliki pengalaman belajar yang sama. Setelah berdiskusi dengan guru mitra, terpilihlah kelas VII L dengan jumlah 24 siswa sebagai kelas eksperimen dan kelas VII I dengan jumlah 22 siswa sebagai kelas kontrol.
B. Desain Penelitian
18 posttest only control designyang merupakan bentuk desain penelitian eksperimen semu. Sesuai dengan yang dikemukakan oleh Setiyadi (2006: 142) desain pelaksanaan penelitian digambarkan sebagai berikut.
Tabel 3.1. Desain Penelitian
X = Pembelajaran dengan pendekatanProblem Posing O = Pembelajaran konvensional
T1 = Skorposttestpada kelas eksperimen T2 = Skorposttestpada kelas kontrol
Pada kelas eksperimen diterapkan pembelajaran dengan pendekatan Problem Posing sedangkan pada kelas kontrol diterapkan pembelajaran konvensional. Setelah pokok bahasan selesai, dilakukan tes akhir. Tes akhir (posttest) adalah tes kemampuan pemahaman konsep matematis siswa yang dilakukan pada kedua kelas sampel dengan soal tes yang sama.
C. Prosedur Penelitian
Langkah–langkah dalam penelitian yang dilakukan memiliki beberapa tahapan yang dilakukan, yaitu sebagai berikut:
1) Tahap Persiapan Penelitian
Tahap-tahap persiapan penelitian ini adalah :
19 Negeri 8 Bandar Lampung.
b. Menyusun Rencana Pelaksanaan Pembelajaran (RPP) penelitian dan instrumen penelitian. RPP dibuat sesuai dengan model akan digunakan selama penelitian, yaitu RPP dengan pendekatanProblem Posing.
c. Melakukan validasi instrumen dan uji coba soal tes 2) Tahap Pelaksanaan Penelitian
Tahap-tahap pelaksanaan penelitian ini adalah :
a. Memberikan perlakuan pada kelas sampel dengan menggunakan pendekatanProblem Posing
b. Mengadakanposttestpada kelas sampel. 3) Tahap Pengolahan Data
Tahap-tahap pengolahan data penelitian ini adalah : a. Mengolah dan menganilisis data hasil penelitian. b. Mengambil kesimpulan
4) Tahap Laporan
Tahap-tahap penyusunan laporan penelitian ini adalah : a. Melaporkan hasil penelitian pada dosen pembimbing b. Menyusun laporan akhir
D. Data Penelitian
20 E. Teknik Pengumpulan Data
Teknik pengumpulan data pada penelitian ini adalah tes. Tes diberikan kepada kedua kelas sesudah diberikan perlakuan. Tes ini digunakan untuk memperoleh pengaruh kemampuan pemahaman konsep matematis siswa pada kelas yang menerapkan pendekatan Problem Posing dan kelas yang menerapkan pembelajaran konvensional sesudah pembelajaran.
F. Instrumen Penelitian
Instrumen yang digunakan dalam penelitian ini berupa soal yang mengukur pemahaman konsep matematis. Instrumen tes berupa tes tertulis berbentuk uraian. Setiap soal memiliki satu atau lebih indikator pemahaman konsep matematis.
1. Instrumen Tes
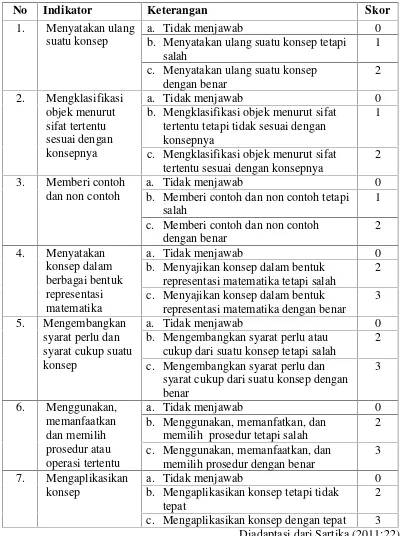
21 Tabel 3.2. Pedoman Penskoran Tes Pemahaman Konsep Matematis
No Indikator Keterangan Skor
1. Menyatakan ulang suatu konsep
a. Tidak menjawab 0
b. Menyatakan ulang suatu konsep tetapi salah
1 c. Menyatakan ulang suatu konsep
dengan benar
b. Mengklasifikasi objek menurut sifat tertentu tetapi tidak sesuai dengan konsepnya
1
c. Mengklasifikasi objek menurut sifat tertentu sesuai dengan konsepnya
2 3. Memberi contoh
dan non contoh
a. Tidak menjawab 0
b. Memberi contoh dan non contoh tetapi salah
1 c. Memberi contoh dan non contoh
dengan benar
b. Menyajikan konsep dalam bentuk representasi matematika tetapi salah
2 c. Menyajikan konsep dalam bentuk
representasi matematika dengan benar
b. Mengembangkan syarat perlu atau cukup dari suatu konsep tetapi salah
2 c. Mengembangkan syarat perlu dan
syarat cukup dari suatu konsep dengan benar memilih prosedur tetapi salah
2
b. Mengaplikasikan konsep tetapi tidak tepat
2 c. Mengaplikasikan konsep dengan tepat 3
Diadaptasi dari Sartika (2011:22)
22 a) Validitas Isi
Dalam penelitian ini, validitas didasarkan pada validitas isi. Validitas isi dari tes
pemahaman konsep matematis ini dapat diketahui dengan cara membandingkan isi yang terkandung dalam instrumen tes pemahaman konsep matematis dengan indikator pembelajaran yang telah ditentukan. Penilaian terhadap kesesuaian butir tes dengan indikator pembelajaran dilakukan oleh guru mata pelajaran matematika. Penilaian terhadap kesesuaian isi instrumen tes dengan kisi-kisi instrumen tes yang diukur dan kesesuaian bahasa yang digunakan dalam instrumen tes dengan bahasa siswa, yang dilakukan dengan menggunakan daftar check list ( ) oleh guru mata pelajaran matematika. Setelah dikonsultasikan, diperoleh bahwa seluruh instrumen tes telah sesuai dengan kisi-kisi tes yang akan diukur serta bahasa yang digunakan telah sesuai dengan kemampuan bahasa siswa.
b) Reliabilitas
23
= koefisien reliabilitas instrumen (tes)
n
= banyaknya butir soal (item)= jumlah varians dari tiap-tiap item tes = varians data total
N = banyaknya data = jumlah data total
= jumlah kuadrat data total
Menurut Arikunto, suatu tes dikatakan baik apabila koefisien reliabilitasnya sama dengan atau lebih besar dari 0,70 ( 0,70), sehingga dalam penelitian ini kriteria reliabilitas tes yang akan digunakan adalah lebih besar atau sama dengan 0,70 ( 0,70)
Berdasarkan hasil perhitungan uji coba instrumen tes, diperoleh bahwa koefisien reliabilitas tes adalah 0,88 (Lampiran C.1 halaman 154). Hal ini menunjukkan bahwa instrumen tes memiliki reliabilitas yang tinggi
c) Daya Pembeda
24 DP =
Keterangan :
DP: indeks daya pembeda satu butir soal tertentu
JA : jumlah skor kelompok atas pada butir soal yang diolah JB : jumlah skor kelompok bawah pada butir soal yang diolah IA : jumlah skor ideal kelompok (atas/bawah).
Hasil perhitungan daya pembeda diinterpretasikan berdasarkan klasifikasi yang tertera dalam Tabel 3.3 berikut :
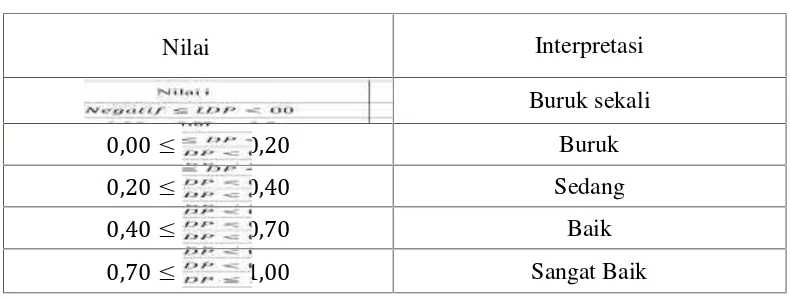
Tabel 3.3 Interpretasi Nilai Daya Pembeda
Kriteria soal tes yang akan digunakan dalam penelitian ini adalah yang memiliki interpretasi sedang dan baik. Setelah dilakukan perhitungan diperoleh daya pembeda butir item soal yang telah diuji cobakan disajikan pada Tabel 3.5. Hasil perhitungan daya pembeda butir item soal selengkapnya dapat dilihat pada Lampiran C.2 halaman 155.
d) Tingkat Kesukaran
Sudijono (2008: 372) menyatakan bahwa untuk menghitung tingkat kesukaran suatu butir soal digunakan rumus berikut:
TK =
Nilai Interpretasi
< 0,00 Buruk sekali
0,00 < 0,20 Buruk
0,20 < 0,40 Sedang
0,40 < 0,70 Baik
25 Keterangan:
TK : tingkat kesukaran suatu butir soal
: jumlah skor yang diperoleh siswa pada butir soal yang diperoleh
: jumlah skor maksimum yang dapat diperoleh siswa pada suatu butir soal.
Untuk menginterpretasi tingkat kesukaran suatu butir soal digunakan kriteria indeks kesukaran menurut Sudijono (2008: 372) sebagai berikut:
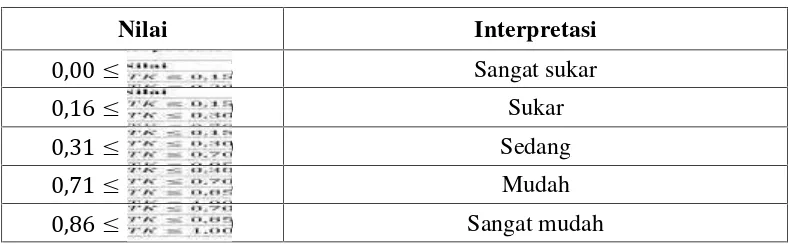
Tabel 3.4. Interpretasi Nilai Tingkat Kesukaran
Nilai Interpretasi
0,00 0,15 Sangat sukar
0,16 0,30 Sukar
0,31 0,70 Sedang
0,71 0,85 Mudah
0,86 1,00 Sangat mudah
Kriteria soal tes yang akan digunakan dalam penelitian ini adalah yang memiliki interpretasi mudah sedang sukar dan sangat sukar.kriteria soal yang mempunyai Interprestasi sangat mudah tidak dipakai dalam penelitian ini. Setelah dilakukan perhitungan diperoleh tingkat kesukaran butir soal yang disajikan pada Tabel 3.5. Hasil perhitungan selengkapnya dapat dilihat di Lampiran C.2 halaman 155.
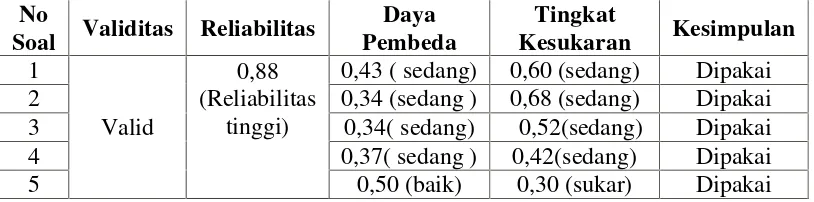
26 Tabel 3.5 Rekapitulasi Hasil Tes Uji Coba
No
0,43 ( sedang) 0,60 (sedang) Dipakai
2 0,34 (sedang ) 0,68 (sedang) Dipakai
3 0,34( sedang) 0,52(sedang) Dipakai
4 0,37( sedang ) 0,42(sedang) Dipakai
5 0,50 (baik) 0,30 (sukar) Dipakai
G. Teknik Analisis Data
Data yang diperoleh dari hasil postest dianalisis untuk mengetahui besarnya pengaruh kemampuan pemahaman konsep matematis siswa kelas eksperimen dan kelas control yang dilakukan dengan prosedur sebagai berikut.
1. Uji Normalitas
Uji normalitas data dilakukan untuk melihat apakah kedua sampel berdistribusi normal atau tidak. Dalam penelitian ini, uji normalitas yang digunakan adalah uji Kolmogorov-Smirnov Z. Rumusan hipotesis untuk uji ini adalah sebagai berikut. H0: data berasal dari populasi yang berdistribusi normal
H1: data berasal dari populasi yang tidak berdistribusi normal
Dalam Russefendi (1998: 405), untuk menghitung nilai Uji Kolmogorov-Smirnov Z, rumus yang digunakan sebagai berikut.
=
Keterangan:
27 Kemudian dilanjutkan dengan menggunakan persamaan Kolmogorov-Smirnov Z sebagai berikut:
= | ( ) ( )|
Keterangan:
Dn : Nilai hitung Kolmogorov-Smirnov Z Fn(xi) : Peluang harapan data ke i
F(xi) : Luas kurva z data ke i
Dalam penelitian ini, uji Kolmogorov-Smirnov Z menggunakan software SPSS Statistic 17.0 dengan kriteria pengujian adalah terima H0 jika nilai probabilitas (sig) > 0,05 (Trihendradi, 2005: 113). Hasil uji normalitas data penelitian disajikan dalam Tabel 3.7 dan data selengkapnya pada Lampiran C.6 dan C.7 halaman 159 dan 160.
Tabel 3.6 Rekapitulasi Uji Normalitas Data Penelitian
Sumber Data Kelompok
Eksperimen 22 0,213 0,011 Ditolak
Kontrol 24 0,124 0,200 Diterima
28 2. Pengujian Hipotesis
Setelah dilakukan uji normalitas, diketahui bahwa salah satu data berasal dari populasi yang tidak berdistribusi normal. Oleh sebab itu, langkah selanjut-nya adalah melakukan uji hipotesis, yaitu uji Mann-Whitney U skor posttest (skor kemampuan pemahaman konsep) sebagai berikut:
a) Hipotesis Uji
H0 : µ1= µ2 (tidak ada perbedaan rata-rata peringkat antara kemampuan pemahaman konsep matematis siswa yang mengikuti pembelajaran dengan pendekatan Problem Posing dengan kemampuan pemahaman konsep matematis siswa yang mengikuti pembelajaran konvensional)
H1 : µ1> µ2 (ada perbedaan rata-rata peringkat antara kemampuan pemahaman konsep matematis siswa yang mengikuti pembelajaran dengan pendekatan Problem Posing dengan kemampuan pemahaman konsep matematis siswa yang mengikuti pembelajaran konvensional)
Untuk menguji data posttest kemampuan pemahaman konsep matematis dapat digunakan rumus sebagai berikut.
Min(U1,U2) dengan = + ( )
Keterangan:
Ui = Nilai uji Mann-Whitney
n1 = banyaknya sampel pada kelas eksperimen n2 = banyaknya sampel pada kelas kontrol Ri = Ranking ukuran sampel ke i
38
V. SIMPULAN DAN SARAN
A. Simpulan
Berdasarkan hasil penelitian dan pembahasan diperoleh kesimpulan bahwa pendekatan Problem Posing berpengaruh terhadap kemampuan pemahaman konsep matematis siswa di kelas VII SMPN 8 Bandar Lampung semester genap tahun pelajaran 2014/2015.
B. Saran
Berdasarkan dari hasil kesimpulan dan penelitian, dikemukakan saran-saran sebagai berikut:
1. Pembelajaran dengan pendekatan Problem Posing dapat diterapkan sebagai pembelajaran matematika untuk membantu siswa dalam memahami konsep matematika, namun dalam penerapannya harus diimbangi dengan perencanaan yang matang, pengelolaan kelas yang baik, dan pengelolaan waktu yang tepat agar suasana belajar semakin kondusif sehingga memperoleh hasil yang optimal.
40
DAFTAR PUSTAKA
Daryanto, Mulyo Rahardjo. 2012. Model Pembelajaran Inovatif. Yogyakarta: Gava Media.
Daryanto. 2013.Inovasi Pembelajaran Efektif. Bandung: Yrama Widya.
Herdian. 2009. Model Pembelajaran Problem Posing. [Online]. Tersedia: http://herdy07.wordpress.com/2009/04/19/model-pembelajaran-problem-posing/ [10 september 2014].
Irwan. 2011. Pengaruh Pendekatan Problem Posing Model Search, Solve, Create and Share (Sscs) dalam Upaya Meningkatkan Kemampuan Penalaran Matematis Mahasiswa Matematika.Jurnal UPI.Vol.1 No.12. [Online]. Tersedia: http://jurnal.upi.edu/file/irwan.pdf. [03 Desember 2014] Masyitoh, Fitria, Dkk. 2013. Pengaruh Pendekatan Problem Posing terhadap
Kemampuan Pemahaman Konsep Matematis Siswa.Jurnal UNILA.Vol.1 No 6. [Online]. Tersedia : http://jurnal.fkip.unila.ac.id.
Merry, Ratnu. 2013. Pengaruh Pendekatan Problem Posing terhadap Kemampuan Komunikasi Matematis Siswa. Skripsi. Bandar Lampung: Universitas Lampung.
Mullis, I. V. S., Martin, M. O., Foy, Pierre, and Arora, Alka. 2012. Trends in International Mathematics and Science Study (TIMSS) 2011 Inter-national Result in Mathe-matics. Boston: TIMSS and PIRLS International Study Center.
Mulyasa, E. 2005.Menjadi Guru Profesional. Bandung: Remaja Rosdakarya. Mulyatiningsih, Endang. 2012.Metode Penelitian Terapan Bidang Pendidikan.
Bandung: Alfabeta.
Nasution. 2005. Berbagai Pendekatan Dalam Proses Belajar Mengajar. Jakarta: Bumi Aksara.
39
Sadiman, A.M. 2008. Interaksi dan Motivasi Belajar Mengajar. Jakarta: PT Grafindo Persada.
Sartika, Dewi. 2011. Efektivitas Model Pembelajaran Kooperatif Tipe TGT Untuk Meningkatkan Kemampuan Pemahaman Konsep Matematis Siswa.(Studi pada Siswa Kelas VIII Semester Ganjil SMP Negeri 29 Bandar Lampung Tahun Pelajaran 2010/2011). (Skripsi). Universitas Lampung. Bandar Lampung
Setiyadi, Bambang. 2006. Metode penelitian Untuk Pengajaran Bahasa Asing Pendekatan Kuantitatif dan Kualitatif. Yogyakarta: Graha Ilmu.
Siroj, Rusdi, Dkk. 2010. Pengaruh Pembelajaran Problem Posing terhadap Kemampuan Pemahaman Konsep Matematika Siswa Kelas XI IPA SMAN 6 Palembang. Sumatra Selatan: Jurnal UNSRI. [Online]. Tersedia : http://ejurnal.unsri.ac.id. [04 Juli 2015]
Soedjadi. 2000. Kiat Pendidikan Matematika di Indonesia. Jakarta: Direktorat Jenderal Pendidikan Tinggi Departemen Pendidikan Nasional.
Sudjana. 2005.Metode Statistika. Bandung: PT Tasito Edisi keenam.
Sukesi, Wahyu. 2014. Peningkatan kemampuan berpikir kreatif matematis siswa melalui penerapan model pembelajaran Problem posing. Jurnal UNILA. Vol. 2 No.3. [Online]. Tersedia : http://jurnal.fkip.unila.ac.id. [04 Juli 2015] Suryosubroto. 2009.Proses Belajar Mengajar di Sekolah.Jakarta: Rineka Cipta Trihendradi, Cornelius. 2005. Step By Step SPSS 13.0 Analisis Data Statistik.
Yogyakarta: Andi Offset.
Uno, Hamzah. B. 2003.Perencanaan Pembelajaran. Jakarta: Bumi Aksara
Wardhani, Sri. 2006. Pembelajaran dan Penilaian Kecakapan Matematika di SMP. Disampaikan pada Diklat Instruktur/Pengembang Matematika SMP Tingkat Nasional di PPPG Matematika Yogyakarta, tanggal 22 Maret sampai dengan 4 April 2006