Model Matematika Sis-Si Dalam Penyebaran Penyakit Malaria Dengan Vaksinasi Taksempurna.

MODEL MATEMATIKA SIS-SI DALAM PENYEBARAN

PENYAKIT MALARIA DENGAN VAKSINASI

TAKSEMPURNA

NUR FAJRI

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa tesis berjudul Model Matematika SIS-SI dalam Penyebaran Penyakit Malaria dengan Vaksinasi Taksempurna adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Oktober 2015

RINGKASAN

NUR FAJRI. Model Matematika SIS-SI dalam Penyebaran Penyakit Malaria dengan Vaksinasi Taksempurna. Dibimbing oleh PAIAN SIANTURI dan TONI BAKHTIAR.

Malaria merupakan penyakit menular yang disebabkan oleh parasit yang dikenal dengan Plasmodium. Pembawa parasit Plasmodium ialah nyamuk Anopheles betina yang mengakibatkan rusaknya sel-sel darah merah pada manusia dan hewan melalui gigitannya. Malaria juga dapat ditularkan melalui transfusi darah. Malaria adalah penyakit yang mematikan. Untuk itu, diperlukan pencegahan untuk mengendalikan baik tingkat infeksi maupun tingkat penyebaran penyakit ini. Dalam penelitian ini, dibahas sebuah model penyebaran penyakit malaria tipe SIS (Susceptible-Infected-Susceptible)-SI (Susceptible-Infected). Dalam model ini, populasi manusia dibagi menjadi tiga kelas, yaitu kelas rentan, kelas terinfeksi dan kelas tervaksinasi. Sementara itu, populasi nyamuk dibagi menjadi dua kelas, yaitu kelas rentan dan kelas terinfeksi. Manusia pada kelas rentan dapat berpindah ke kelas terinfeksi karena gigitan nyamuk terinfeksi ataupun penularan dari manusia terinfeksi melalui transfusi darah. Manusia di kelas rentan dapat berpindah ke manusia tervaksinasi karena vaksinasi. Manusia di kelas terinfeksi dapat berpindah ke kelas rentan karena pemberian obat-obatan. Manusia di kelas tervaksinasi dapat berpindah ke kelas terinfeksi karena kegagalan vaksin dan berpindah ke kelas rentan karena kehilangan kekebalan tubuh. Nyamuk pada kelas rentan dapat berpindah ke kelas terinfeksi akibat menggigit manusia terinfeksi. Modifikasi model dilakukan dengan menambahkan asumsi bahwa manusia yang sembuh masih dapat tertularkan penyakit, laju kelahiran manusia dan nyamuk dianggap sama dengan laju kematian dan manusia yang vaksinasinya efektif akan berpindah ke kelas rentan apabila kekebalan tubuhnya menghilang. Selain itu, modifikasi model juga dilakukan dengan pemberian vaksin pada manusia.

Tujuan dari penelitian ini ialah memodifikasi model matematika penyebaran penyakit malaria, melakukan analisis kestabilan lokal dan global pada model modifikasi, melakukan analisis bifurkasi pada model modifikasi, menganalisis pengaruh faktor vaksinasi taksempurna terhadap penularan penyakit malaria melalui simulasi komputer.

Dalam penelitian ini diperoleh dua titik tetap pada model, yaitu titik tetap tanpa penyakit dan titik tetap endemik. Dengan menggunakan bilangan reproduksi dasar

 

R0 , maka diperoleh bahwa titik tetap tanpa penyakit bersifat stabil global, jika R01 dan titik tetap endemik bersifat stabil global, jika R01. Selain itu, digunakan juga analisis bifurkasi yang bertujuan untuk mengetahui eksistensi dan jumlah titik tetap endemik pada model untuk setiap parameter yang diberikan. Parameter yang dianalisis hanya untuk parameter  1, 2 dan 3. Hal ini dikarenakan parameter-parameter tersebut merupakan laju interaksi antarpopulasi. Hasil analisis bifurkasi menunjukkan bahwa jika terjadi bifurkasi maju, maka titik tetap endemik bersifat stabil dan jika terjadi bifurkasi mundur, maka titik tetap endemik bersifat takstabil.

populasi manusia dan nyamuk yang ditunjukkan dengan bilangan reproduksi dasar

 

R0 . Secara umum, jika efektivitas vaksin ditingkatkan, maka menyebabkan menurunnya bilangan reproduksi dasar. Jika diperoleh R01, maka jumlah individu yang terinfeksi semakin berkurang, sehingga penyakit tidak akan menyebar dan dalam jangka waktu tertentu penyakit akan menghilang dari populasi. Kata kunci: malaria, vaksinasi taksempurna, bifurkasi, kestabilan global, model

SUMMARY

NUR FAJRI. Mathematical SIS-SI Model in Spread Malaria with Imperfect Vaccination. Supervised by PAIAN SIANTURI and TONI BAKHTIAR.

Malaria is an infectious disease caused by a parasite known as Plasmodium. The Plasmodium parasite carrier is a female Anopheles mosquito that causes the destruction of red blood cells in humans and animals through mosquito bites. Malaria can also be transmitted through blood transfusion. Malaria is a deadly disease. For that, we need prevention for controlling both the rate of infection and the spread of the disease.

In this study, we discuss a model of the spread of malaria type of SIS (Susceptible-Infected-Susceptible)-SI (Susceptible-Infected). In this model, the human population is divided into three classes, namely Susceptible, Infected and Vaccinated. Meanwhile, the mosquito population is divided into two classes namely Susceptible and Infected. Humans on susceptible class may move to the infected class. Susceptible humans can be transferred to vaccinated humans. Infected humans can be transferred to the susceptible class because of the provision of drugs. Vaccinated humans can move to class infections due to vaccine failure and switch to the susceptible class because of loss of immunity. Mosquitoes on susceptible class can move to class of mosquitoes infected from biting an infected human. Modification of the model is done by adding the assumption that people who recover can still be transmitted disease, human birth rate and mosquitoes are considered equal to the rate of death and human vaccination will effectively move to susceptible class if their immune has disappeared. Moreover, modification of the model is also done with the vaccination in humans.

The aim of this study is to modify a mathematical model of the spread of malaria, to analyze the local and global stability on the modified model, to analyze the bifurcation on the modified model and to show the influence imperfect vaccination against malaria disease transmission through computer simulation.

Through this study, we found that there are two equilibrium points on the model, which is disease free equilibrium point and endemic equilibrium point. By using basic reproduction number, we get if R0 1. then the model will be globally stable in the disease free equilibrium and if R01, the model will be globally stable in the endemic equilibrium point. Moreover, it is used also bifurcation analysis that aims to determine the existence of the endemic equilibrium point in the model for each of the given parameters. The parameters that were analyzed only for  1, 2 and 3. This is because these parameters are rate among population interactions. The result of analysis show that the endemic equilibrium point is stable if forward bifurcation and unstable if backward bifurcation.

individuals decreased, so that the smaller the spread of disease and illness in a certain time will disappear from the population.

© Hak Cipta Milik IPB, Tahun 2015

Hak Cipta Dilindungi Undang-Undang

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains

pada

Program Studi Matematika Terapan

MODEL MATEMATIKA SIS-SI DALAM PENYEBARAN

PENYAKIT MALARIA DENGAN VAKSINASI

TAKSEMPURNA

NUR FAJRI

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala anugerah-Nya sehingga penulis dapat menyelesaikan tesis ini. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan September 2014 ini ialah pemodelan matematika dengan judul Model Matematika SIS-SI dalam Penyebaran Penyakit Malaria dengan Vaksinasi Taksempurna.

Penulisan tesis ini merupakan salah satu syarat memperoleh gelar Magister Sains pada program studi Matematika Terapan Sekolah Pascasarjana Institut Pertanian Bogor. Terima kasih penulis ucapkan kepada:

1 Bapak H Ramli dan Ibu Hj Suwarni selaku orang tua dan kakak, adik serta seluruh keluarga yang selalu memberikan dorongan dan mendoakan untuk keberhasilan studi bagi penulis.

2 Bapak Dr Paian Sianturi selaku ketua komisi pembimbing.

3 Bapak Dr Toni Bakhtiar, MSc selaku anggota komisi pembimbing sekaligus Ketua Departemen Matematika Institut Pertanian Bogor.

4 Bapak Dr Jaharuddin, MS selaku Penguji Luar Komisi dan Ketua Program Studi Matematika Terapan Institut Pertanian Bogor.

5 Seluruh dosen dan tenaga kependidikan Departemen Matematika Institut Pertanian Bogor.

6 Kak Sonna yang selalu menemani dan membantu penulis dalam menyelesaikan studi di Institut Pertanian Bogor.

7 Sahabat-sahabat yang tidak dapat disebutkan satu persatu yang telah banyak membantu penulis dalam menyelesaikan studi.

8 Direktorat Pendidik dan Tenaga Kependidikan (Diktendik)-DIKTI sebagai sponsor Beasiswa Pendidikan Pascasarjana Dalam Negeri (BPP-DN).

Akhirnya, semoga penulisan tesis ini dapat bermanfaat dan memperkaya pengalaman belajar dan wawasan kita semua.

Bogor, Oktober 2015

DAFTAR ISI

DAFTAR TABEL vii

DAFTAR GAMBAR vii

DAFTAR LAMPIRAN viii

1 PENDAHULUAN 1

Latar Belakang 1

Tujuan Penelitian 2

2 TINJAUAN PUSTAKA 3

Sistem Persamaan Diferensial 3

Persamaan Diferensial Biasa Orde-1 3

Persamaan Diferensial Biasa Mandiri dan Takmandiri 3

Sistem Persamaan Diferensial Biasa 3

Nilai Eigen dan Vektor Eigen 3

Titik Tetap 4

Pelinearan 4

Analisis Kestabilan Titik Tetap 5

Titik Tetap Stabil 5

Titik Tetap Takstabil 5

Kestabilan Titik Tetap 5

Kestabilan Global 5

Pengertian Orbit Periodik 5

Kriteria Bendixson di _n ₆

Bilangan Reproduksi Dasar 6

Bifurkasi 7

Definisi Bifurkasi 7

Kurva Bifurkasi 7

Teorema 1: Akar-akar persamaan polinomial orde-3 7

3 MODEL MATEMATIKA 9

Penelitian Sebelumnya 9

Penelitian Abdullahi et al. (2013) 10

Penelitian Safan et al. (2014) 12

Model Modifikasi 13

4 ANALISIS DAN SIMULASI 17

Analisis Kestabilan Titik Tetap Tanpa Penyakit

 

xdfe 17

Kestabilan Global 18

Penentuan Bilangan Reproduksi Dasar 19

Analisis Bifurkasi 20

Arah Bifurkasi 22

Simulasi 22

Simulasi kurva bifurkasi untuk parameter 1 22 Simulasi kurva bifurkasi untuk parameter 2 25 Simulasi kurva bifurkasi untuk parameter 3 27

Simulasi Efektivitas Vaksin pada Manusia 29

5 SIMPULAN 31

DAFTAR PUSTAKA 32

LAMPIRAN 34

DAFTAR TABEL

3.1 Nilai parameter pada model SIS-SI dan satuannya 15 4.1 Efektivitas vaksin pada manusia terhadap R0 30

DAFTAR GAMBAR

3.1 Skema penyebaran penyakit malaria model SIR-SI 11

3.2 Skema penyebaran penyakit model SIS 13

3.3 Skema penyebaran penyakit malaria model modifikasi 14 4.1 Kurva bifurkasi untuk parameter 1 terhadap dua akar F





1, Ih**



0

yang terbesar 23

4.2 Kurva bifurkasi untuk parameter 1 terhadap akar yang lain dari persamaan



**



1, h 0

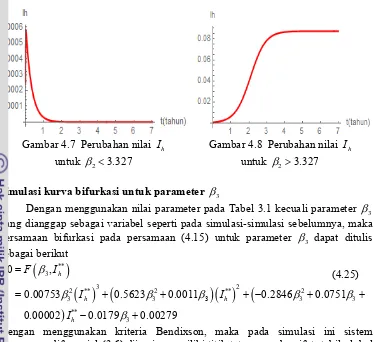
F



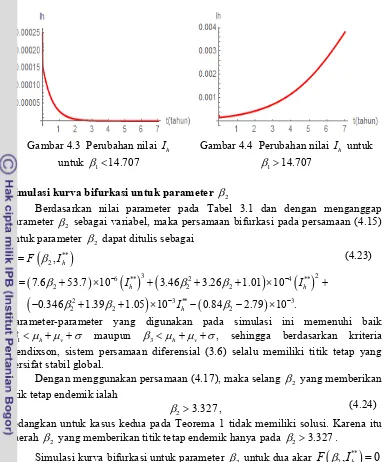
I  24

4.3 Perubahan nilai I_h untuk 114.707 25

4.4 Perubahan nilai I_h untuk 114.707 25

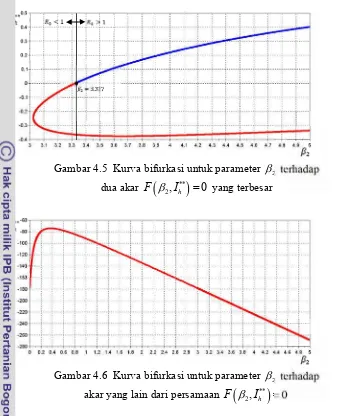
4.5 Kurva bifurkasi untuk parameter 2 terhadap dua akar F





2, Ih**



0

yang terbesar 26

4.6 Kurva bifurkasi untuk parameter 2 terhadap akar yang lain dari persamaan



**



2, h 0

F



I  26

4.7 Perubahan nilai Ih untuk 2 3.327 27

4.8 Perubahan nilai Ih untuk 2 3.327 27

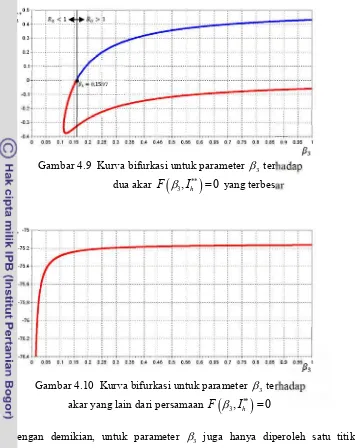
4.9 Kurva bifurkasi untuk parameter 3 terhadap dua akar F





3, Ih**



0

yang terbesar 28

4.10 Kurva bifurkasi untuk parameter 3 terhadap akar yang lain dari persamaan



**



3, h 0

F



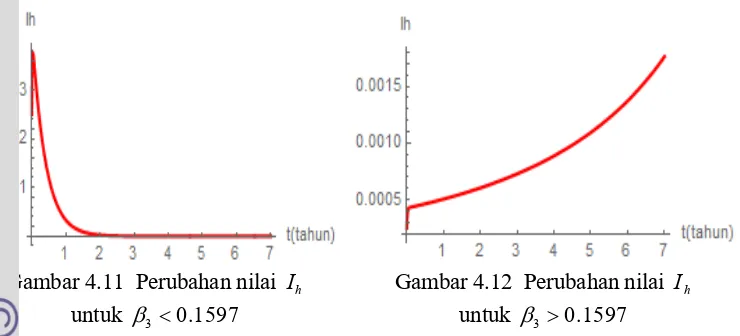
I  28

4.11 Perubahan nilai Ih untuk 30.1597 29

4.12 Perubahan nilai Ih untuk 3 0.1597 29

DAFTAR LAMPIRAN

1 Penyederhanaan sistem persamaan diferensial model Abdullahi et al. 34 2 Penyederhanaan sistem persamaan diferensial model Safan et al. 36 3 Penyederhanaan sistem persamaan diferensial model modifikasi 37

4 Penentuan titik tetap 39

5 Penentuan matriks Jacobi 40

6 Kriteria Bendixson untuk kestabilan global 41

7 Penentuan bilangan reproduksi dasar 43

8 Penentuan persamaan bifurkasi 45

9 Perhitungan analisis bifurkasi terhadap parameter 1 48 10 Perhitungan analisis bifurkasi terhadap parameter 2 51 11 Perhitungan analisis bifurkasi terhadap parameter 3 54

12 Simulasi efektivitas vaksinasi pada manusia 57

13 Simulasi kestabilan titik tetap tanpa penyakit 59

1

PENDAHULUAN

Latar Belakang

Malaria merupakan penyakit menular yang disebabkan oleh parasit yang dikenal dengan Plasmodium. Ada empat jenis Plasmodium yang dapat menyebabkan penyakit malaria yaitu Plasmodium falciparum, Plasmodium vivax, Plasmodium ovale dan Plasmodium malariae. Pembawa parasit Plasmodium ini ialah nyamuk Anopheles betina yang menyebabkan rusaknya sel-sel darah merah. Malaria dapat ditularkan melalui transfusi darah maupun bawaan. Di Indonesia, kelompok yang berisiko tinggi terkena malaria ialah bayi, anak balita dan ibu hamil. Berdasarkan API (Annual Parasite Incidence), Indonesia bagian timur termasuk dalam wilayah risiko malaria tinggi; Kalimantan, Sulawesi dan Sumatera termasuk dalam wilayah risiko malaria sedang; sedangkan Jawa dan Bali termasuk dalam wilayah risiko malaria rendah (Ditjen PP 2011).

Metode yang paling sering digunakan dalam penanggulangan penyakit malaria ialah obat-obatan, penyemprotan dan pencegahan gigitan. Sampai saat ini, belum ada vaksin malaria yang benar-benar ampuh. Pada tahun 2011, GlaxoSmithKline menemukan vaksin malaria pertama yang diizinkan untuk digunakan di Afrika. Berdasarkan percobaan paling akhir, vaksin tersebut mampu memberi kekebalan hingga empat tahun pada anak-anak (The RTS,S Clinical Trials Partnership 2011) dan berdasarkan uji coba yang dilakukan terhadap laki-laki di Kenya oleh Universitas Oxford Inggris diperoleh bahwa vaksin tersebut menunjukkan efektivitas hingga 67% (Hill et al. 2015).

Beberapa penelitian tentang model matematika telah dilakukan untuk mempelajari transmisi penyakit malaria. Abdullahi et al. (2013) mengembangkan model penyebaran penyakit malaria SIR-SI dengan mempertimbangkan adanya penularan dari manusia ke manusia melalui transfusi darah dan melalui ibu hamil yang terinfeksi malaria. Selain itu, Laarabi et al. (2012) memformulasikan model matematika untuk penyakit dengan tingkat infeksi yang bentuknya taklinear dan melihat akibat dari vaksinasi terhadap populasi manusia. Safan et al. (2014) memformulasikan model matematika untuk sebarang penyakit epidemik pada satu populasi dengan melihat adanya pengaruh vaksinasi taksempurna untuk penyakit

2

Tujuan Penelitian

Penelitian ini bertujuan untuk

1. Memodifikasi model matematika penyakit malaria. 2. Melakukan analisis kestabilan pada model modifikasi. 3. Melakukan analisis bifurkasi pada model modifikasi.

3

2

TINJAUAN PUSTAKA

Sistem Persamaan Diferensial Persamaan Diferensial Biasa Orde-1

Persamaan diferensial biasa orde-1 dapat dinyatakan sebagai ( , )

x f t x

dengan f t x

 

, adalah fungsi kontinu. Untuk f fungsi taklinear, maka persamaan (2.1) disebut persamaan diferensial biasa (PDB) taklinear, sedangkan untuk f fungsi linear maka disebut PDB linear.

Persamaan Diferensial Biasa Mandiri dan Takmandiri

Misalkan diberikan PDB seperti pada persamaan (2.1). Untuk PDB yang memuat peubah waktu t secara explisit, PDB tersebut disebut PDB takmandiri (nonautonomous). Sementara itu, persamaan (2.1) disebut persamaan diferensial biasa mandiri (autonomous) apabila tidak memuat t secara eksplisit di dalamnya sehingga dapat ditulis sebagai

 

x f x_ .

Sistem Persamaan Diferensial Biasa

Misalkan diberikan



1, ,...,2



T n

x x x



x dan



1, ,...,2



T n

f f f



f dengan fi

adalah fungsi dalam x, di mana _xn_{, maka persamaan (2.2) dapat ditulis sebagai} ( )



x f x

1 1 1 2

1 2 ( ) ( , , , )

( ) ( , , , ) n

n n n

x t f x x x

x t f x x x

      _                    .

Persamaan (2.3) disebut Sistem Persamaan Diferensial Biasa orde-1 mandiri. Untuk sistem persamaan diferensial biasa, linear dan mandiri, persamaan (2.3) dapat ditulis dalam notasi matriks sebagai



x Ax

dengan A disebut matriks koefisien berukuran n n .

Nilai Eigen dan Vektor Eigen

Diberikan matriks koefisien konstan A berukuran n n dan sistem persamaan diferensial biasa homogen

 

.

0

, 0 , n.

  

x Ax x x x  Suatu vektor

taknol x di dalam _n _{disebut vektor eigen dariA jika untuk semua skalar}



berlaku

.





Ax x

Nilai skalar



dinamakan nilai eigen dariA.

Untuk mencari nilai



dari A, maka sistem persamaan (2.4) dapat ditulis sebagai

(2.1)

(2.3)

4



A



I x



0,

dengan I adalah matriks identitas. Sistem persamaan (2.5) memiliki penyelesaian taknol jika dan hanya jika





det A



I 0.

Persamaan (2.6) merupakan persamaan karakteristik dari matriksA (Leon 1998).

Titik Tetap

Misalkan diberikan sistem persamaan diferensial biasa sebagaimana pada sistem (2.3). Titik x disebut titik tetap, jika f x 0

 

 . Titik tetap disebut juga titik kritis atau titik kesetimbangan atau titik ekuilibrium. Untuk selanjutnya digunakan titik tetap (Tu 1994).

Pelinearan

Analisis kestabilan sistem persamaan diferensial taklinear dapat dilakukan melalui pelinieran. Misalkan diberikan sistem persamaan diferensial biasa mandiri taklinear

 

( ), _t n.

 

x f x x 

dengan x

 

t adalah satu fungsi bernilai vektor dalam t dan f adalah suatu fungsi mulus yang terdefinisi pada _{U }n_.

Misalkan diberikan sistem persamaan diferensial biasa sebagaimana pada sistem (2.3), maka dengan menggunakan ekspansi Taylor di sekitar titik tetap ,x

maka sistem persamaan diferensial (2.7) dapat ditulis sebagai ( ),

  

x η J η φ η 

dengan J adalah matriks Jacobi yang didefinisikan sebagai berikut

1 1 1

1 2

2 2 2

1 2 1 2 ... ... ( ) ... k k

k k k

k

f f f

x x x

f f f

x x x

f f f

x x x _

     _{  }         _{  }   _{  }  _{ } _{  }    _{  } 

 x x

f

J x

x

   

dan ( )φ η adalah suku berorde tinggi yang bersifat lim ( )

 

η 0φ η 0, dengan η = x x .

Bentuk η = Jη pada sistem persamaan diferensial (2.8) disebut pelinearan sistem persamaan diferensial (2.7) (Tu 1994).

(2.5)

(2.6)

(2.7)

(2.8)

5

Analisis Kestabilan Titik Tetap Titik Tetap Stabil

Misalkan x adalah titik tetap dari sistem persamaan diferensial (2.3) dan

 

t

x adalah solusi dengan kondisi awal x

 

0 x0. Titik x dikatakan titik tetap stabil, jika untuk setiap  0, terdapat r0, sedemikian sehingga x x₀ r , maka x( )t x  untuk t0 _{(Vershult 1990).}

Titik Tetap Takstabil

Misalkan x adalah titik tetap dari sistem persamaan diferensial (2.3) dan

 

t

x adalah sebuah solusi sistem persamaan diferensial yang memenuhi kondisi awal x

 

0 x0 dengan x0 x. Titik x dikatakan titik tetap takstabil jika terdapat radius



0, _{sedemikian hingga posisi awal x0 memenuhi} x x₀ r, untuk setiap r0 dan solusi x

 

t memenuhi x

 

t  x



, untuk suatu t0 (Verhulst 1990).

Kestabilan Titik Tetap

Misalkan diberikan sistem persamaan diferensial (2.3) dengan x sebagai titik tetap. Kestabilan titik tetap x dapat ditentukan dengan memperhatikan nilai-nilai eigen dari matriks Jacobian J, yaitu , 1,2,...,i i n , yang diperoleh dari persamaan karakteristik. Secara umum, kestabilan titik tetap mempunyai perilaku sebagai berikut

1. Stabil, jika

a. Re

 



i  0, i, atau

b. j sedemikian sehingga Re( ) 0j  dan Re( ) 0,i   i j. 2. Takstabil, jika i sedemikian sehingga Re( ) 0i  .

(Tu 1994).

Kestabilan Global

Diberikan sistem persamaan diferensial taklinear (2.3). Titik tetap _xn dikatakan stabil global jika dan hanya jika untuk sembarang nilai awal x0 yang diberikan, setiap solusi sistem tersebut yaitu x

 

t berlaku lim

 

t x t x (Boyd 2008).

Pengertian Orbit Periodik

Misalkan x



 

t merupakan solusi untuk persamaan x f x

 

, _{x }n _dan misalkan terdapat bilangan positif terkecil T sedemikian sehingga





t T







 

t untuk setiap t_, maka



 

t disebut solusi periodik dari persamaan x = f x

 

6

Kriteria Bendixson di _n

Sistem persamaan diferensial (2.3) dikatakan tidak memiliki solusi periodik pada daerah Σ ⊆ ℝ , jika memenuhi salah satu kondisi di bawah ini

(i)

,

sup r s q q :1 0

q r s

r s r s

f f f

f _{r s n}

x x  x x

        _{     } _   _{     }      



 (ii) ,

sup r s r s :1 0

q r s

r s q q

f f

f f _{r s n}

x x  x x

_{ }  _{ }    _{       } _ _{     }      



 (iii) ,

inf r s q q :1 0

q r s

r s r s

f f f

f _{r s n}

x x  x x

        _{     } _   _{     }      



 (iv) ,

inf r s r s :1 0

q r s

r s q q

f f

f f _{r s n}

x x  x x

_{ }  _{ }  

 _{       } _

_{     } 

   







(Li & Muldowney 1993).

Bilangan Reproduksi Dasar

Bilangan reproduksi dasar, dinotasikan dengan R0 merupakan suatu ukuran potensi penyebaran penyakit dalam suatu populasi. Bilangan reproduksi dasar didefinisikan sebagai nilai harapan banyaknya populasi rentan yang menjadi terinfeksi selama masa infeksi berlangsung (Van den Driessche dan Watmough 2008). Kondisi yang timbul ialah

1. Jika R01, maka jumlah manusia terinfeksi akan menurun pada masa infeksi berikutnya, sehingga penyakit tidak akan menyebar.

2. Jika R0 1, maka jumlah manusia terinfeksi akan meningkat pada masa infeksi berikutnya, sehingga penyakit akan menyebar.

Nilai R0 dalam penelitian ini ditentukan dari nilai eigen taknegatif dengan modulus terbesar The Next Generation Matrix. Matriks ini merupakan suatu matriks yang dikonstruksi dari subpopulasi yang menyebabkan infeksi saja. Untuk model umum dengan p kompartemen penyakit dan q kompartemen tanpa penyakit, nilai

0

R dapat dihitung untuk setiap kompartemen.

Misalkan diberikan sistem persamaan diferensial taklinear _{x = f x x}

 

, _n dan misalkan _ap _{dan b}q _{adalah sub-subpopulasi pada setiap kompartemen.} Selanjutnya dinotasikan Fi sebagai laju peningkatan infeksi sekunder pada kompartemen ke-i dan V_i sebagai laju pergerakan penyakit, kematian dan penurunan kesembuhan dari kompartemen ke-i. Model kompartemen dapat ditulis sebagai

 

 

 

; 1, 2,..., , ; 1, 2,..., .

i i i

j j

i n

j m

  

 

a F a,b V a,b

b G a,b

7

0

R dapat diperoleh dengan memandang kompartemen penyakit dari sistem persamaan diferensial taklinear _{x = f x x}

 

, _n _{yang dapat ditulis sebagai}





a = F - V a

dengan F dan V adalah matriks-matriks berukuran n n , di mana

 0

1 1 1

1 2

2 2 2

1 2

1 2

n

n

n n n

n

F F F

a a a

F F F

a a a

F F F

a a a

     _{  }         _{  }       _{  }       

  0,b

F        dan

 0

1 1 1

1 2

2 2 2

1 2

1 2

n

n

n n n

n

V V V

a a a

V V V

a a a

V V V

a a a

     _{  }         _{  }       _{  }       

  0,b

V





   



dengan



0,b0



adalah titik tetap tanpa penyakit.

The Next Generation Matrix K untuk suatu sistem persamaan diferensial pada titik tetap tanpa penyakit berbentuk

1_. 

K = FV

Berdasarkan Van den Driessche dan Watmough (2008), diperoleh



1



0 .

R _



_FV

dengan





_FV1



_{adalah maksimum dari modulus nilai-nilai eigen FV}1_. (Van den Driessche & Watmough 2008).

Bifurkasi Definisi Bifurkasi

Bifurkasi adalah perubahan kestabilan titik tetap akibat perubahan nilai parameter, sedangkan titik bifurkasi merupakan titik di mana terjadinya bifurkasi (Strogatz 1994, Murray 1993).

Kurva Bifurkasi

Kurva bifurkasi merupakan kurva yang mendeskripsikan titik tetap dan stabilitas dari titik tetap untuk setiap nilai parameter yang berbeda. Kemiringan pada kurva bifurkasi disebut sebagai arah bifurkasi. Jika kurva memiliki kemiringan negatif, maka terjadi bifurkasi mundur dan jika memiliki kemiringan positif, maka terjadi bifurkasi maju (Seydel 1988).

Teorema 1: Akar-akar persamaan polinomial orde-3

Diberikan fungsi polinomial _{h z}

 

_{az bz}3_ 2_{ cz d dengan a0, maka} berlaku

1. Jika d0, maka h z

 

0 memiliki paling sedikit satu akar positif.

(2.11)

8

2. Jika d0_{, maka} h z

 

0 memiliki akar-akar positif jika dan hanya jika



2



1 ₃1 3 0

z b b ac

a

     dan h z

 

1 0

3. Jika d0 dan _{ b}2_{3ac0 , maka h z}

 

_{0 tidak memiliki akar yang} positif

9

3

MODEL MATEMATIKA

Model matematika membantu memahami proses dinamis yang mengatur kepadatan nyamuk dan penularan malaria. Model matematika yang digunakan untuk mengetahui penyebaran malaria di daerah tertentu dikenal dengan model epidemi. Seperangkat persamaan bertujuan untuk menyimulasikan proses interaksi manusia-nyamuk dengan bantuan variabel dan parameter yang dipilih untuk membangun sebuah model yang berarti sedekat mungkin dengan fenomena nyata.

Model epidemi diperkenalkan oleh Daniel Bernoulli tentang penyebaran penyakit cacar (smallpox). Model epidemi matematika modern diperkenalkan pada tahun 1927 oleh McKendrick & Kermarck tentang model SIR, di mana SIR merupakan singkatan dari Susceptible Infected Recovered. Dalam model SIR populasi manusia terdiri atas tiga kelas yaitu manusia rentan (S) artinya manusia yang belum terjangkit penyakit, manusia terinfeksi (I) artinya manusia yang sudah terjangkit penyakit dan manusia sembuh (R) artinya manusia yang kebal atau imun terhadap penyakit.

Model SIR tersebut kemudian terus dikembangkan dengan mengubah asumsi atau menambah kompartemen. Beberapa contoh model dari pengembangan tersebut ialah model SI dan SIS. SI merupakan singkatan dari Susceptible Infected, sedangkan model SIS merupakan singkatan dari Susceptible Infected Susceptible. Dalam model SIS, individu dalam kelas infeksi dapat sembuh dengan pengobatan medis atau proses alam, tetapi kesembuhan itu tidak mengakibatkan individu tersebut kebal, sehingga memungkinkan terinfeksi kembali dan masuk kelas infeksi.

Penelitian Sebelumnya

Pemodelan matematika untuk penyakit malaria diperkenalkan oleh Ross pada tahun 1911. Menurut Ross, jika populasi nyamuk dapat dikurangi hingga di bawah ambang batas tertentu, maka malaria dapat diberantas. Model sederhana yang dibangun dikenal sebagai Model Ross telah dikembangkan selama bertahun-tahun. Pada tahun 1957, McDonald mengembangkan lebih lanjut dengan mempertimbangkan populasi manusia dan nyamuk pada suatu daerah dan tanpa memperhitungkan pola mobilitas manusia dan nyamuk. Perumusan model ini kemudian dikenal dengan nama Model Ross-McDonald.

10

Penelitian Abdullahi et al. (2013)

Model SIR-SI yang dirumuskan oleh Abdullahi et al. (2013) menggambarkan penyebaran penyakit malaria. Populasi manusia dibagi menjadi tiga kelas, yaitu kelas manusia yang rentan (Susceptible) _Sh_{, kelas manusia terinfeksi (Infected) I}h dan kelas manusia pulih (Recovered) ._Rh _{Manusia yang rentan ialah manusia yang} bukan imun dan tidak terkena infeksi. Manusia yang terkena infeksi ialah manusia yang terkena malaria dan dapat menularkan kepada individu lain dengan perantara nyamuk. Manusia sembuh ialah manusia yang sembuh dari penyakit malaria.

Populasi nyamuk dibagi menjadi dua kelas, yaitu kelas nyamuk rentan (Susceptible) _Sv _{dan kelas nyamuk terinfeksi (Infected) I}v_{. Nyamuk yang rentan} adalah nyamuk yang berpeluang terkena penyakit malaria. Sementara itu, nyamuk terinfeksi adalah nyamuk yang di dalam tubuhnya telah terdapat infeksi parasit dan dapat menularkan ke individu lain.

Adapun asumsi-asumsi yang digunakan dalam penelitian ini antara lain a. semua bayi yang baru lahir sangat rentan terhadap penyakit;

b. jangka hidup dari nyamuk tidak tergantung pada infeksi; c. nyamuk yang baru lahir semua sehat;

d. manusia yang terinfeksi akan berpindah ke manusia sembuh karena pemberian obat-obatan;

e. manusia yang rentan akan berkurang karena kematian;

f. manusia yang rentan akan berpindah ke manusia terinfeksi karena digigit nyamuk terinfeksi;

g. manusia yang rentan akan berpindah ke manusia terinfeksi akibat transfusi darah;

h. ibu yang melahirkan dalam keadaan terinfeksi akan melahirkan anak yang terinfeksi juga

Dari asumsi-asumsi tersebut, individu yang lahir dan bermigrasi pada kelas rentan

 

_Sh _{memiliki laju konstan sebesar}

h

 . Manusia yang berada di kelas rentan dapat berpindah ke kelas terinfeksi

 

_Ih _{akibat transfusi darah dengan laju}

1

 atau akibat gigitan nyamuk terinfeksi dengan laju 2. Manusia yang berada di kelas rentan dapat mati dengan laju kematian sebesar h. Lahirnya bayi yang terinfeksi malaria akibat bawaan pada kelas terinfeksi

 

_Ih _{memiliki laju sebesar}



_{. Manusia} yang berada di kelas terinfeksi dapat berpindah ke kelas pulih

 

_Rh _karena penggunaan obat-obatan anti malaria dengan laju k. Manusia di kelas terinfeksi dapat mati dengan laju kematian h dan mati akibat malaria dengan laju



. Manusia di kelas pulih

 

_Rh _{dapat mati dengan laju}

h

 .

Untuk populasi nyamuk, nyamuk yang lahir dan bermigrasi pada kelas rentan

 

_Sv _{memiliki laju konstan sebesar}

v

 . Nyamuk di kelas rentan dapat berpindah ke kelas terinfeksi

 

_Iv _{karena menggigit manusia terinfeksi dengan laju}

3

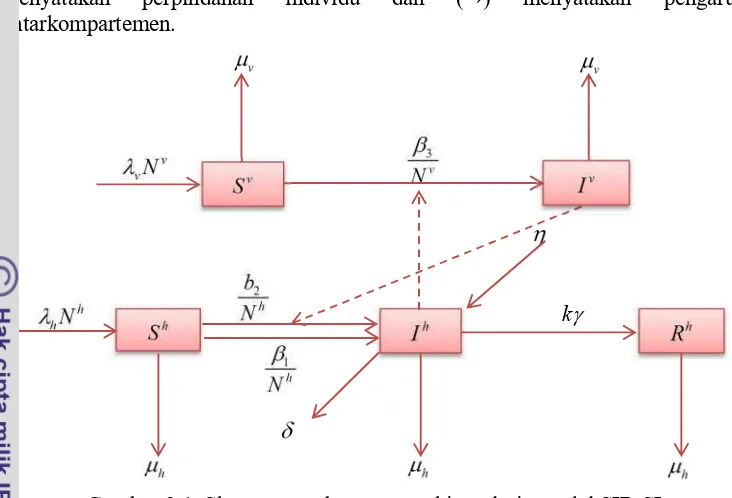
11 Pola penyebaran penyakit malaria dapat dilihat pada Gambar 3.1, dengan (→) menyatakan perpindahan individu dan (⇢) menyatakan pengaruh antarkompartemen.

Gambar 3.1 Skema penyebaran penyakit malaria model SIR-SI

Berdasarkan skema Gambar 3.1, diperoleh sistem persamaan diferensial untuk masing-masing kompartemen sebagai berikut





1 2 1 2 3 3 _, h

h h v h

h h h h

h

h h v h h

h h h h h h h v

v h v

v h v

v

h v v v h

b

dS _{N I I S}

dt N N

b

dI _{I I I S k I}

dt N N

dR _{k I R} dt

dS _{N I S}

dt N

dI _{I S I}

dt N               _    _   _      _  _           _  _     dengan

h h h h

N S I R dan _Nv_Sv_Iv_,

di mana _Nh _{adalah total populasi manusia dan N}v _{adalah total populasi nyamuk.} Dengan memisalkan

, , ,

h h h v

h h h h h h v v

S I R S

S I R S

N N N N

    dan I_v Iv_v

N  ,

maka diperoleh Sh Ih Rh 1 dan Sv  Iv 1 sehingga sistem persamaan diferensial (3.1) dapat disederhanakan menjadi

12



 



1 2

3

( ) 1

(1 ) ,

h

h h v h h h h

h

h h h

v

v h v v

dI _{I I I I R k I}

dt

dR _{k I R} dt

dI _{I I I}

dt

     

 

 

       

 

  

dengan 2b n2 dan n N N v h.

Proses penyederhanaan sistem persamaan diferensial (3.1) menjadi sistem persamaan (3.2) dapat dilihat pada Lampiran 1.

Penelitian Safan et al. (2014)

Model yang dirumuskan oleh Safan et al.(2014) ini merupakan model yang melihat pola penyebaran penyakit epidemi. Model ini menggambarkan populasi manusia terdiri dari tiga kelas, yaitu manusia yang rentan

 

_Sh , _{manusia yang}

terinfeksi

 

_Ih _{dan manusia yang tervaksinasi}

 

_Vh _{. Model ini mempelajari} tentang penyebaran penyakit menggunakan model SIS dengan memperhatikan dampak vaksinasi taksempurna. Dalam hal ini, diasumsikan kemanjuran vaksinasi adalah e

 

0,1 . Vaksinasi dianggap berhasil jika e1 dan gagal jika e0. Kelas rentan dilahirkan dengan laju _h dengan proporsi p dari yang dilahirkan tersebut langsung diberikan vaksin. Populasi rentan memiliki laju kematian h juga, laju tervaksinasi



dan laju terinfeksi adalah _Ih, _{di mana}



_{adalah laju kontak} antara individu terinfeksi dengan individu rentan. Individu terinfeksi juga mati dengan laju h atau disembuhkan dengan laju . Individu vaksinasi juga mati dengan laju h dan terinfeksi dengan laju



1e I





h dengan e adalah kemanjuran vaksin.

Adapun asumsi-asumsi yang digunakan dalam penelitian ini antara lain a. laju kelahiran manusia sama dengan laju kematian;

b. manusia rentan yang baru lahir akan berkurang sebesar p karena pemberian vaksin;

c. manusia yang terinfeksi akan berpindah ke manusia rentan karena pemberian obat-obatan;

d. manusia yang rentan akan berkurang karena kematian;

e. manusia yang rentan akan berkurang karena pemberian vaksinasi; f. manusia rentan yang gagal vaksin akan berpindah ke manusia terinfeksi. Pola vaksinasi taksempurna dapat dilihat pada Gambar 3.2, di mana (→) menyatakan perpindahan individu.

13

Gambar 3.2 Skema penyebaran penyakit model SIS

Skema pada Gambar 3.2 dapat dituliskan dalam sistem persamaan diferensial sebagai berikut

(1 )

(1 ) ( )

(1 ) .

h

h h h h

h h h

h

h h h h h

h

h h

h

h h h h h

h h h

h h h h

dS _{p N I I S}

dt N

dI _{S I e V I I}

dt N N

dV _{p N S V e V I}

dt N

N S I V

       _{ }          _   _                Dengan memisalkan , h h

h h h h

S I

S I

N N

  dan h hh

V V

N  ,

maka Sh I Vh h1 sehingga sistem persamaan diferensial (3.3) dapat disederhanakan menjadi













1 (1 ) ( )

1 1 .

h

h h h h h h h

h

h h h h h h h

dI _{I V I e V I I}

dt

dV _{p I V V e V I}

dt

   

  

      

      

Penyederhanaan sistem persamaan diferensial (3.3) menjadi sistem persamaan (3.4) dapat dilihat pada Lampiran 2.

Modifikasi Model Matematika

Model SIR-SI yang dirumuskan oleh Abdullahi et al. (2013) selanjutnya dimodifikasi dengan mengubah asumsi menjadi individu terinfeksi yang sembuh karena pemberian obatan akan berpindah ke manusia rentan disebabkan obat-obatan hanya bersifat menyembuhkan, tidak memberi kekebalan.

Pada penelitian ini juga melihat pengaruh faktor vaksinasi taksempurna, di mana manusia yang telah diberi vaksin belum tentu menjadi kebal terhadap (3.3)

14

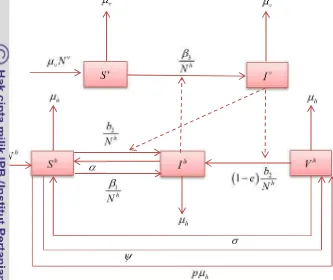
[image:30.612.132.465.185.465.2]

penyakit malaria. Hal ini dikarenakan belum ditemukannya vaksin yang benar-benar manjur dalam memberikan imunitas terhadap penyakit malaria. Selain itu, manusia rentan yang baru lahir akan langsung diberi vaksinasi dengan laju p seperti yang diperkenalkan oleh Safan et al. (2014). Model ini selanjutnya disebut model SIS-SI. Selain itu model modifikasi juga mengasumsikan bahwa manusia yang vaksinnya efektif dapat rentan kembali karena kehilangan kekebalan tubuh (Mandal et al. 2011).

Gambar 3.3 Skema penyebaran penyakit malaria model modifikasi Adapun asumsi-asumsi yang digunakan dalam penelitian ini antara lain  manusia sembuh masih dapat tertularkan penyakit;

 laju kelahiran manusia dan nyamuk dianggap sama dengan laju kematian;  manusia yang vaksinasinya efektif akan berpindah ke manusia rentan apabila

kekebalan tubuhnya hilang.

Secara skematis pola penyebaran penyakit malaria dengan asumsi-asumsi di atas digambarkan dalam diagram kompartemen pada Gambar 3.3.

Model matematika penyebaran penyakit malaria dengan asumsi tersebut dapat dinyatakan dengan persamaan-persamaan berikut













1 2

1 2 2

1 S

1 h

h h h h v h

h h h h

h

h v h h h v

h

h h h

b

dS _{p N I V I I}

dt N N

b b

dI _{I I S I e V I}

dt N N N



    

 _{ }

 

    _    _

 

 

_  _    

 

15









2

3

3

1

. h

h h h h v

h h h

h h h h

v

v h v

v h v

v

h v v v h

v v v

b

dV _{p N S V e V I}

dt N

N S I V

dS _{N I S}

dt N

dI _{I S I}

dt N N S I

        _             _  _       Dengan memisalkan , , ,

h h h v

h h h h h h v v

S I V S

S I V S

N N N N

    dan v vv

I I

N

 ,

maka diperoleh Sh I Vh h1 dan Sv Iv 1 sehingga sistem persamaan diferensial (3.5) dapat disederhanakan menjadi





 









 











1 2 2

2 3 1 1 1 1 1 , h

h v h h h h h v

h

h h h h h h v

v

v h v v

dI _{I I I V I e V I}

dt

dV _{p I V V e V I}

dt

dI _{I I I}

dt                               

dengan 2b n2 dan n N N v h.

Penyederhanaan sistem persamaan diferensial (3.5) menjadi sistem persamaan (3.6) dapat dilihat pada Lampiran 3.

[image:31.612.120.507.58.547.2]

Keterangan dari parameter-parameter dan nilai-nilai parameter yang digunakan pada model-model di atas diberikan pada Tabel 3.1.

Tabel 3.1 Nilai parameter pada model SIS-SI dan satuannya

Variabel Keterangan Parameter Satuan Nilai Sumber

p Proporsi manusia rentan _{yang baru lahir langsung}

divaksin 0.8

tanpa

satuan Asumsi

h

 Laju kematian manusia _{yang dianggap sama}

dengan laju kelahiran 0.041

1

waktu _Labadin et al. (2009)

v

 Laju kematian nyamuk _{yang dianggap sama}

dengan laju kelahiran 0.13

1

waktu _Labadin et al. (2009)

 Laju manusia terinfeksi yang sembuh karena obat-obatan

1

16

Variabel Keterangan Parameter Satuan Nilai Sumber



Laju manusia rentan yang

divaksin 0.4 waktu1 Asumsi

 Laju manusia yang telah divaksin menjadi rentan kembali

1

730 waktu1 Agusto (2012) et al.

1



Laju perpindahan manusia dari kelas rentan ke kelas infeksi akibat transfusi darah

0.022 _waktu1 _Asumsi

2 b

Laju perpindahan manusia dari kelas rentan ke kelas infeksi akibat gigitan nyamuk terinfeksi

0.05 _waktu1 _Pongsumpun (2006)

3



Laju perpindahan nyamuk dari kelas rentan ke kelas infeksi akibat menggigit manusia terinfeksi

0.024 _waktu1 _Labadin et al. (2009)

n Perbandingan populasi _{nyamuk dengan manusia} 10 _satuan tanpa Pongsumpun ₍₂₀₀₆₎

e Efektivitas vaksinasi 0.4 _satuan tanpa Asumsi

17

4

ANALISIS DAN SIMULASI

Penentuan Titik Tetap

Analisis titik tetap pada sistem persamaan diferensial (3.6) diperoleh dengan mengatur dIh 0,

dt  h 0 dV

dt  dan v 0. dI

dt  Dengan menyelesaikan sistem persamaan diferensial tersebut, maka diperoleh dua jenis titik tetap, yaitu titik tetap tanpa penyakit (disease free equilibrium) xdfe dan titik tetap endemik (endemic equilibrium) xee. Titik tetap tanpa penyakit adalah titik tetap yang memuat nilai

0 h

I  . Titik tetap endemik adalah titik tetap yang memuat nilai Ih0.

Dengan menggunakan software berbasis fungsional diperoleh titik tetap xdfe sebagai



_{, ,}





_{0, ,0}*



dfe h h v h

x I V I  V ,

di mana

* h

h

h p

V  

  

 

  . Sementara itu, titik tetap x_ee dapat ditulis sebagai



_{, ,}





**_, **_, **



ee h h v h h v

x I V I  I V I _,

di mana









** ** ** 2 1 1 h h h h v p I V e I         

    dan

** ** 3 ** 3 . h v h v I I I







 

Pencarian nilai ** h

I akan dilakukan melalui persamaan bifurkasi yang akan dibahas pada bagian berikutnya, sehingga **

h

V dan ** v

I pada persamaan (4.3) dapat diperoleh. Proses penentuan titik tetap dapat dilihat pada Lampiran 4.

Analisis Kestabilan Titik Tetap Tanpa Penyakit

 

xdfe

Pada bagian ini akan dilakukan analisis untuk melihat sifat kestabilan pada titik tetap tanpa penyakit xdfe. Misalkan sistem persamaan diferensial (3.6) ditulis sebagai berikut













1 2 3 , , ; , , ; , , . h

h h v

h

h h v

v

h h v dI _{f I V I}

dt

dV _{f I V I} dt

dI _{f I V I} dt







Dengan melakukan pelinearan, maka diperoleh matriks Jacobi sebagai berikut (4.1)

(4.2)

18













1 1 1

2 2 2

3 3 3

* *

1 2

* 2 3

1 0 1

1 .

0

dfe

h h v

h h v

h h v _x

h h h

h h

v

f f f

I V I

f f f

J

I V I

f f f

I V I

V eV e V                _{  }    _{  }   _{  }    _{  }    _{  }                     _     

Nilai eigen matriks Jacobi dapat ditentukan dengan menyelesaikan





det Jx_dfe 



I 0, sehingga diperoleh persamaan karakteristik sebagai berikut

  

a5

 



a1



a9



a a3 7



0

 

 











  , di mana













* 1 1 * 3 2 5 1 1 h h h h a V a eV a                  7 3

9 v. a a





  

Nilai-nilai eigen untuk matriks J diperoleh sebagai berikut



 





 



1 5

2

1 9 1 9 3 7

2

2

1 9 1 9 3 7

3 4 2 4 2 a

a a a a a a

a a a a a a

             

Sistem persamaan diferensial (3.6) akan stabil lokal jika dan hanya jika semua nilai eigen bernilai negatif. Untuk 1 selalu bernilai negatif, sedangkan

 untuk 2 bernilai negatif jika



a a1 9



0 dan a a1 9 a a3 7; dan  untuk 3 bernilai negatif jika



a a1 9



0.

Dengan demikian, sistem persamaan diferensial (3.6) bersifat stabil lokal jika dan hanya jika



a a1 9



0 dan a a1 9 a a3 7.

Kestabilan Global

Selain kestabilan lokal dari titik tetap, pada penelitian ini juga melihat kestabilan global dari titik tetap. Kestabilan global adalah kestabilan dalam waktu jangka panjang. Untuk mengetahui eksistensi kestabilan global dari sistem persamaan diferensial (3.6) pada daerah Σ, di mana







I V Ih, ,h v :Ih 0,Vh 0,I Vh h 1,0 Iv 1



        dan Σ ⊆ ℝ , maka digunakan

(4.5)

(4.6)

19 Kriteria Bendixson (2.10). Dengan menuliskan sistem persamaan diferensial (3.6) menjadi (4.4) dan dengan menggunakan persamaan (2.10b), maka diperoleh

(i) 1 3 1 3





1

sup h v

h v h h

f f

f f

I I V V    

    

 _{  } _{   }

_{   } 

 

 

(ii) 2 3 2 3





3

sup h v

h v h h

f f

f f

V I I I    

    

 _{  } _{   }

_{   } 

 

  .

Dengan demikian, berdasarkan Kriteria Bendixson, sistem persamaan diferensial (3.6) tidak memiliki solusi periodik pada daerah Σ, sehingga selalu memiliki titik tetap yang bersifat stabil global, jika memenuhi 1h v atau

3 h v .

    Hal ini dapat dilihat pada Lampiran 6.

Penentuan Bilangan Reproduksi Dasar

Bilangan reproduksi dasar, dinotasikan dengan R0, merupakan nilai harapan banyaknya populasi rentan yang menjadi terinfeksi selama masa infeksi berlangsung. Penentuan bilangan reproduksi dasar dilakukan dengan pendekatan The Next Generation Matrix.

The Next Generation Matrix K untuk sistem persamaan (3.6) didefinisikan sebagai

1  

K FV

dengan F dan V adalah sebagai berikut



*





*



1 2 3 1 1 0 h h V eV     _{ }    _{ }  

F dan 0 .

0 h v            V

Bilangan reproduksi dasar merupakan nilai eigen taknegatif terbesar matriks K yang ditulis sebagai

2

1 1

0 k₂ k₄ 2 3,

R   k k

di mana



*



1 1 1 , h h V k  _{ } 



*



2 2 1 , h v eV k     3 3 . h k     

Proses penentuan bilangan reproduksi dasar dapat dilihat pada Lampiran 7.

Kondisi yang memungkinkan dari bilangan reproduksi dasar menurut Van den Driessche & Watmough (2008) adalah

1. Jika R0 1, maka jumlah manusia terinfeksi akan menurun pada infeksi berikutnya, sehingga penyakit tidak akan menyebar.

(4.9)

(4.10) (4.8a)

20

2. Jika R0 1, maka jumlah manusia terinfeksi akan meningkat pada masa infeksi berikutnya, sehingga penyakit akan menyebar.

Berdasarkan teorema Bendixson, sistem persamaan diferensial (3.6) selalu memiliki titik tetap yang bersifat stabil global, jika memenuhi 1h v atau 3h v  . Dengan demikian, jika kondisi 1h v atau

3 h v

    terpenuhi maka dapat disimpulkan bahwa jika R01, maka sistem persamaan diferensial (3.6) akan bersifat stabil global ke titik tetap bebas penyakit xdfe. Jika R0 1, maka sistem persamaan diferensial (3.6) akan bersifat stabil global ke titik tetap endemik xee.

Analisis Bifurkasi

Bifurkasi adalah perubahan kestabilan sistem akibat perubahan parameter. Persamaan bifurkasi dapat ditentukan dengan menggunakan dIv 0

dt  pada sistem persamaan (3.6) sehingga diperoleh

3 3 h v h v I I I      .

Kemudian dengan menggunakan dVh 0

dt  pada sistem persamaan (3.6) dan persamaan (4.11), sehingga diperoleh





2 3

3 1 h h h h h h v p I

V _{e I}

I                   .

Dengan menyubstitusikan persamaan (4.11) dan persamaan (4.12) ke dalam 0

h dI

dt  pada sistem persamaan (3.6), maka diperoleh

















3 1 2 3 3 2 3 3 2 3 3 2 3 1 1 1 0. 1

h h h

h h

h v h

h

h v

h h h

h h

h v h

h

h v

I p I

I I

I _e I

I

p I I

I e I I e I         _{   }                           _  _{  }   _     _{  }  _{ }  _{       }    _{   }      _{ }        _{  }   _{  }      _{ }  _{  }  

Dengan menyelesaikan persamaan (4.13) untuk Ih0, maka diperoleh persamaan bifurkasi sebagai

     

_{** **} 3 _** 2 _**

0

h h h h

F I a I b I cI  d _,

di mana

(4.11)

(4.12)

(4.13)

21



  

2

1 3 h 1- 2 0

a

   

  e





2 2 2 2 2 2 2 2

2 3 2 3 1 2 3 1 2 3 2 3 2 3 1 3

2 2 2 2 2 2 2 2

3 3 2 3 3 2 3 3 1 3 1 3 2 3

2 2 2 2 2 2 2 2 2

3 1 2 3 1 2 3 1 3 1 3 2 3 2 3 3

2

2 2

v h h

h h v

h v h h v h h

b   e e  e   e    e  e   p  

                                                                 3

2 2 2 2

2 3 2 3 2 3 2 3 1 2 3 2 2 3

2

1 3 3 3 2 3 3 2 3 2 3

2 2

3 1 3 1 2 3 2 3 3 1 2 3

2

1 3 1

2 2 2 2

2 2 2

2

h v v v h v

h v v v v h v v

h v v v v h v v

h v h v

e e e e e

c e e

p

p                    

                                                                           

2 2 2 2

2 3 h 2 3 2 h v 2 3 2 h v 3

           

   

2 2 2 2

2 3 2 3 1 2 3

2 2 2 2 2 2

1 2 3 1 2 3 .

h v v h v v v h v v

h v v v h v h v h v h v

e

d ep       p         

                                        

Persamaan bifurkasi digunakan untuk menentukan ** h

I sehingga ** h

V dan ** v I pada persamaan (4.3) dapat ditentukan. Dengan demikian, titik tetap endemik dapat diperoleh dari setiap parameter yang diberikan.

Pada penelitian ini, hanya akan dilihat pengaruh perubahan parameter , 1,2,3,

i i

   yang merupakan laju penyebab terjadinya penularan penyakit malaria, terhadap perubahan eksistensi titik tetap endemik dan perubahan kestabilan titik tetap. Dalam hal ini, parameter yang akan dianalisis dianggap sebagai peubah sedangkan parameter lainnya dianggap konstan. Dengan demikian, nilai a, b, c dan d dapat ditulis sebagai a

     



i ,b



i ,c



i dan d

 



i yang merupakan fungsi dalam i, sehingga persamaan bifurkasi untuk setiap parameter bifurkasi i diberikan sebagai berikut



_**



 

 

_** 3

 

 

_** 2

 

_**

 

, 0

i h i h i h i h i

F



I a



I b



I c



I d



 ;  i 1, 2,3.

Daerah untuk setiap parameter i yang memberikan titik tetap endemik dapat diperoleh dengan menggunakan Teorema 1 terhadap persamaan (4.15). Dengan demikian, selang untuk setiap parameter bifurkasi yang mengakibatkan sistem persamaan diferensial (3.6) memiliki titik tetap endemik diberikan pada kasus-kasus di bawah ini

o Kasus 1: d 0

Kasus ini memberikan persamaan (4.15) paling sedikit memiliki satu akar positif. Oleh karena itu, pada kasus ini sistem persamaan diferensial (3.6) juga memiliki paling sedikit satu titik tetap endemik. Dengan menyelesaikan

0

d untuk setiap parameter bifurkasi yang diberikan, maka diperoleh  untuk parameter 1







1



1 1 ₁

h v q p





  

    , di mana























1 2 3 1 h 1 h h v;

q  

 

ep



 e

 

 

    

  



 parameter 2

(4.15)

22











2



2 2

3 1 h 1

q ep e







  

      , di mana



















2 1 h h h v;

q   p

  

 

 



   

 

 parameter 3











3



3 3

2 1 h 1

q ep e







  

      , d