PROYEKSI CADANGAN KLAIM DENGAN METODE
MUNICH CHAIN-LADDER
IKHWAN ABIYYU
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Proyeksi Cadangan Klaim dengan Metode Munich Chain-Ladder adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Mei 2015
Ikhwan Abiyyu
ABSTRAK
IKHWAN ABIYYU. Proyeksi Cadangan Klaim dengan Metode Munich Chain-Ladder. Dibimbing oleh I GUSTI PUTU PURNABA dan RUHIYAT.
Perusahaan asuransi wajib mempersiapkan cadangan klaim secara tepat untuk menutupi pengeluaran dari klaim yang akan terjadi di masa yang akan datang. Salah satu metode estimasi cadangan klaim yang sering digunakan adalah metode chain-ladder. Karena kesederhanaan dari metode tersebut, banyak perusahaan asuransi menggunakannya dalam estimasi cadangan klaim di masa yang akan datang. Namun, metode chain-ladder tidak bisa mengurangi gap antara proyeksi IBNR (Incurred but Not Reported) dari kerugian yang dibayarkan dan kerugian yang sebenarnya terjadi. Metode Munich chain-ladder adalah pengembangan metode dari metode chain-ladder yang dikembangkan oleh Gerhard Quarg dan Thomas Mack. Metode Munich chain-ladder dalam aplikasinya dapat mengurangi gap yang terjadi. Karya ilmiah ini menjelaskan cara estimasi cadangan klaim menggunakan metode Munich chain-ladder dan membandingkan hasilnya dengan menggunakan metode chain-ladder, serta memberikan contoh data di mana metode Munich chain-ladder tidak menghasilkan proyeksi yang baik.
Kata kunci: cadangan klaim, chain-ladder, IBNR, outstanding claim.
ABSTRACT
IKHWAN ABIYYU. Projection of Claim Reserves Using the Munich Chain-Ladder Method. Supervised by I GUSTI PUTU PURNABA and RUHIYAT.
Insurance companies are required to manage the appropriate claim reserves to cover the expenses of the claims that will occur in the future. One of the claim reserves estimation method that frequently used is the chain-ladder method. Because of the simplicity of this method, many insurance companies use the method to estimate the claim reserves in the future. However, the chain-ladder method is not able to reduce the gap between the projection of IBNR (Incurred but Not Reported) paid losses and incurred losses. The Munich chain-ladder is the development of the chain-ladder method introduced by Gerhard Quarg and Thomas Mack. The Munich chain-ladder method can be applied to reduce the gap between the projection of IBNR paid losses and incurred losses. This paper describes how to estimate the claim reserves using the Munich chain-ladder method and to compare the results with using the chain-ladder method. In addition, we provide examples of data, where the Munich chain-ladder method does not produce a good projection.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
PROYEKSI CADANGAN KLAIM DENGAN METODE
MUNICH
CHAIN-LADDER
IKHWAN ABIYYU
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah SWT atas segala rahmat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Penulisan karya ilmiah ini juga tidak lepas dari bantuan berbagai pihak. Untuk itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada:
1. Ibundaku tersayang Ibu Mardiana. Terima kasih atas doa, cinta, semangat, pengorbanan, dan segalanya kepada penulis. Terima kasih telah menjadi mama terhebat untuk anak-anaknya.
2. Adik-adikku Sayyid Abyan dan Siti Najwa Assyyfa atas semangatnya kepada penulis.
3. Bapak Dr Ir I Gusti Putu Purnaba, DEA sebagai dosen pembimbing I dan Bapak Ruhiyat, MSi sebagai dosen pembimbing II. Terima kasih atas segala waktu, ilmu, nasihat, dan bantuannya selama penulisan karya ilmiah ini.
4. Bapak Dr Donny Citra Lesmana, SSi, MFinMath sebagai dosen penguji atas kritik dan saran untuk perbaikan skripsi ini.
5. Dosen dan staf penunjang Departemen Matematika FMIPA IPB atas semua ilmu, nasihat, dan bantuannya.
6. Teman-teman satu bimbingan yaitu Lilyani dan Sinta atas semua saran, semangat, dan bantuannya.
7. Sahabat satu kontrakan yaitu Median, Firi, dan Fakhri serta sahabat dekat selama perkuliahan yaitu Adam, Irma, Henny, Restu, Hendar, Hasan, dan Resty. Terima kasih atas kebersamaannya, perhatian, semangat, dan bantuannya kepada penulis selama 4 tahun perkuliahan. 8. Teman-teman Matematika 48, kakak-kakak Matematika 47, dan
adik-adik Matematika 49 atas kebersamaan dan suka-duka selama penulis menempuh studi di Departemen Matematika.
9. Sahabat dari SMA hingga saat ini Fadhlulrahman Azis, serta Sahabat dari TPB yaitu Diko, Adoy, Feber, dan Dody. Terima kasih atas kebersamaannya dan semangatnya kepada penulis.
10.Kak Julianto, SSi yang telah membagi ilmu dan wawasannya tentang teknik cadangan klaim dalam asuransi, khususnya asuransi kerugian. 11.Pihak-pihak lain yang telah membantu penulisan skripsi ini yang tidak
dapat disebutkan satu per satu. Semoga karya ilmiah ini bermanfaat.
Bogor, Mei 2015
DAFTAR ISI
DAFTAR TABEL viii
DAFTAR GAMBAR viii
DAFTAR LAMPIRAN viii
PENDAHULUAN 1
Latar Belakang 1
Tujuan Penelitian 2
TINJAUAN PUSTAKA 2
Teori Peluang 2
Total Klaim 3
Outstanding Claims Liability 3
Teknik Chain-Ladder 5
HASIL DAN PEMBAHASAN 6
Metode Chain-Ladder 6
Metode Munich Chain-Ladder 7
Implementasi Praktis 11
Contoh Penerapan Metode Cadangan Klaim Munich Chain-Ladder 14
SIMPULAN DAN SARAN 26
Simpulan 26
Saran 27
DAFTAR PUSTAKA 27
LAMPIRAN 28
DAFTAR TABEL
1 Run-off triangle data dan future triangle data dalam bentukinkremental 4 2 Run-off triangle data dan future triangle data dalam bentuk kumulatif 4 3 Run-off triangle untuk kerugian yang dibayarkan dari data Quarg dan
Mack 15
4 Run-off triangle untuk kerugian yang terjadi dari data Quarg dan Mack 15 5 Estimasi faktor penundaan rata-rata dan parameter�dari data Quarg
dan Mack 17
6 Rasio (P/I) dan (I/P) serta parameter� dari data Quarg dan Mack 19 7 Hasil perhitunan Reŝ ( , ) dari data Quarg dan Mack 20 8 Hasil perhitunan Reŝ (�, ) dari data Quarg dan Mack 20 9 Hasil perhitunan Reŝ ( −, ) dari data Quarg dan Mack 21 10 Hasil perhitunan Reŝ ( , ) dari data Quarg dan Mack 21 11 Hasil proyeksi untuk kerugian yang dibayarkan dari data Quarg dan
Mack dengan metode Munich chain-ladder 23
12 Hasil proyeksi untuk kerugian yang terjadi dari data Quarg dan Mack
dengan metode Munich chain-ladder 23
13 Gap antara proyeksi untuk kerugian yang dibayarkan dan kerugian yang terjadi dari data Quarg dan Mack dengan metode Munich
chain-ladder 24
14 Gap antara proyeksi untuk kerugian yang dibayarkan dan kerugian yang terjadi dari data Quarg dan Mack dengan metode chain-ladder 25 15 Gap antara proyeksi untuk kerugian yang dibayarkan dan kerugian
yang terjadi dari data Lloyd's dengan metode Munich chain-ladder 26
DAFTAR GAMBAR
1 Plot residual dari kerugian yang dibayarkan dari data Quarg dan Mack 22 2 Plot residual dari kerugian yang terjadi dari data Quarg dan Mack 22 3 Plot residual dari kerugian yang dibayarkan dari data Lloyd’s 25
4 Plot residual dari kerugian yang terjadi dari data Lloyd’s 26
DAFTAR LAMPIRAN
PENDAHULUAN
Latar Belakang
Setiap orang tidak mengetahui bagaimana kehidupan ke depannya akan berjalan seperti apa. Ketidakpastian bisa saja terjadi seperti bahaya, kerusakan, dan kerugian yang pasti akan dialami kapanpun dan oleh siapapun. Risiko ketidakpastian tersebut dapat merusak kestabilan ekonomi yang sangat besar. Salah satu solusi untuk mengantisipasi risiko tersebut adalah melalui asuransi. Asuransi adalah sebuah janji dari pihak penanggung dalam hal ini perusahaan asuransi kepada pihak tertanggung yakni nasabah, bahwa bila terjadi risiko maka perusahaan asuransi tersebut akan memberikan santunan (benefit) dengan jumlah tertentu kepada nasabahnya.
Industri asuransi dewasa ini semakin berkembang dari tahun ke tahun. Ini bisa digambarkan dengan semakin banyaknya orang yang tertarik untuk membeli produk berupa jasa yang ditawarkan oleh suatu perusahaan asuransi. Dengan membayarkan sejumlah uang yang disebut premi, risiko kerugian yang mungkin dapat timbul dari nasabah pada waktu mendatang telah ditanggung oleh perusahaan asuransi tersebut sesuai dengan polis yang berlaku. Perusahaan asuransi wajib mempersiapkan dana siap pakai secara tepat untuk menutupi pengeluaran oleh klaim yang terjadi pada periode ke depan. Dana inilah yang disebut sebagai cadangan klaim.
Pembayaran klaim mungkin dilakukan tidak lama setelah klaim dilaporkan, namun pada beberapa jenis asuransi, terkadang pembayaran klaimnya membutuhkan waktu yang cukup lama diukur dari saat terjadinya klaim. Hubungan antara waktu kejadian dan penundaan terkait klaim ini dikenal dengan istilah outstanding claims. Ada dua jenis outstanding claims, yaitu Incurred but Not Reported (IBNR) yaitu peristiwa yang telah terjadi tetapi belum dilaporkan ke perusahaan asuransi dan Reported but Not Settled (RBNS) yaitu peristiwa yang telah dilaporkan namun pembayarannya belum terselesaikan (Hossack 1999). Taksiran outstanding claims memegang peranan yang penting, mengingat perusahaan asuransi dituntut untuk selalu dapat menyediakan cadangan yang cukup, guna menutup pembayaran klaim di masa yang akan datang. Jika perkiraan
outstanding claims buruk, maka bisa saja perusahaan dapat mengalami kebangkrutan. Ada beberapa metode statistik untuk menaksir outstanding claims
baik secara deterministik maupun stokastik. Metode chain-ladder merupakan metode deterministik yang paling populer untuk menaksir outstanding claims,
karena kesederhanaannya dan bersifat bebas distribusi (Mack 1993).
2
Tujuan Penelitian
Tujuan dari karya ilmiah ini adalah:
1. Menjelaskan cara proyeksi cadangan klaim dengan metode Munich chain-ladder.
2.
Memberikan contoh penerapan proyeksi cadangan klaim dengan metodeMunich chain-ladder.
3.
Membandingkan hasil proyeksi cadangan klaim dengan metode chain-ladder dan metode Munich chain-ladder.TINJAUAN PUSTAKA
Teori Peluang
Nilai Harapan
1. Jika adalah peubah acak diskret dengan fungsi massa peluang maka nilai harapan dari , dinotasikan dengan , adalah:
= ∑
∀�
,
asalkan jumlah tersebut kovergen mutlak.
2. Jika adalah peubah acak kontinu dengan fungsi kepekatan peluang � maka nilai harapan dari adalah:
= ∫∞ �
−∞ � ,
asalkan integral tersebut konvergen mutlak (Hogg et al. 2014).
Nilai Harapan Bersyarat
Misalkan dan adalah peubah acak kontinu dan �| | adalah fungsi kepekatan peluang bersyarat dari dengan syarat = . Nilai harapan dari dengan syarat = adalah:
| = = ∫ � | | ∞
−∞ �
(Hogg et al. 2014).
Ragam
Ragam dari peubah acak dapat ditunjukkan oleh:
3
� = −
(Hogg et al. 2014).
Martingale
Kejadian disebut martingale (relatif terhadap {ℱ�}, Ρ ) jika: 1. bersesuaian,
2. � | �| < ∞, ∀ ,
3. �[ �|ℱ�− ] = �− , ketika (Williams 1991).
Total Klaim
Total klaim (claim amounts) atau bisa juga disebut sekumpulan kerugian (aggregate loss) adalah jumlahan dari total semua klaim yang terjadi dalam periode tertentu dari kontrak asuransi yang telah ditetapkan. Ini merupakan suatu metode yang digunakan untuk merekam pembayaran yang dibuat dan kemudian menambahkannya dengan pembayaran berikutnya. Dalam kasus ini, total klaim direpresentasikan sebagai jumlahan, banyaknya klaim (number of claims) �, dari total pembayaran individu , , … , � , sehingga
= + + ⋯ + �, untuk � = , , , … dengan = jika � = (Yunawan 2013).
Outstanding Claims Liability
Umumnya penaksiran klaim-klaim yang belum terselesaikan (outstanding claims liability) untuk asuransi kelas bisnis jangka panjang (long-tail) didasarkan pada run-off triangle data. Run-off triangle data memuat gambaran klaim keseluruhan (aggregate), dan merupakan ringkasan dari suatu data set klaim-klaim individu (Antonio et al. 2006). Data yang ada dalam run-off triangle data biasanya merupakan besarnya klaim (claims amount) dan juga banyaknya klaim (number of claims), di mana keduanya tersaji dalam bentuk inkremental atau kumulatif.
Misalkan , menyatakan peubah acak besarnya klaim (dalam bentuk inkremental) untuk klaim-klaim yang terjadi pada periode kejadian (accident period) dan dibayarkan pada periode penundaan (development period) , dengan
dan (Olofsson 2006).
4
Tabel 1 Run-off triangle data dan future triangle data dalam bentuk inkremental
Run-off triangle data dalam bentuk kumulatif, , dapat dibentuk berdasarkan inkremental, , , melalui hubungan berikut:
, = ∑ , =
untuk , , dan + + .
, dapat dinyatakan sebagai besarnya klaim kumulatif untuk klaim-klaim yang terjadi pada tahun kecelakaan ke- dan dibayarkan sampai dengan tahun penundaan ke- . Run-off triangle data dalam bentuk kumulatif disajikan dalam Tabel 2. Besarnya klaim kumulatif sampai dengan tahun penundaan ke- , yaitu
,� = ∑ , �
=
untuk = , , … , , disebut ultimate claims (Mack 1993).
5
Outstanding claims liability untuk tahun kecelakaan ke- didefinisikan sebagai
= ∑ , �
=�+ −
atau = ,�− ,�+ − , untuk = , , … , .
Outstanding claims liability untuk tahun kecelakaan ke- merupakan penjumlahan sel-sel , di baris yang ada pada future triangle, sedangkan total outstanding claims liability didefinisikan sebagai penjumlahan outstanding claims liability untuk semua tahun kecelakaan ( = , , … , ), yaitu
= ∑ ∑ , �
=�+ − �
=
dengan kata lain, total outstanding claims liability , merupakaan jumlah semua , dalam future triangle (Mack 1993).
Teknik Chain-Ladder
Misalkan , menunjukkan total klaim yang diakumulasikan dari waktu kejadian , untuk = , , … , , yang dilaporkan sampai dengan waktu penundaan
j, untuk = , , … , . Jika = , , … , dan = , , … , − + maka besarnya , diketahui. Tujuan yang ingin dicapai adalah untuk memberikan estimasi total klaim ,� untuk waktu kejadian = , , … , dan total besarnya klaim , untuk
= , , … , dan = − + , … , .
Asumsi dasar untuk teknik chain-ladder adalah terdapat nilai faktor penundaan (development factor) , , … , � dengan
( , + | , , , , … , , ) = , ,
untuk = , , … , dan = , , … , − + . Teknik chain-ladder terdiri atas estimasi dengan
̂ = ∑�− += ,
∑�− += , −
dan estimasi total besarnya klaim oleh
�− + ,� = �− + , + + … �
untuk = , , … , atau dengan bentuk lain untuk = , , … , berikut:
̂,� = ,�− + �− + … �
6
HASIL DAN PEMBAHASAN
Metode Chain-Ladder
Pertama-tama akan diperkenalkan beberapa notasi dan kemudian merumuskan asumsi dari metode chain-ladder (CL).
Notasi
Misalkan ∈ ℕ adalah tahun terjadinya kecelakaan dan ∈ ℕ adalah tahun penundaan (biasanya = ). Untuk = , , … , , misalkan adalah kerugian yang dibayarkan (paid) oleh perusahaan asuransi pada tahun kecelakaan ke- dan � adalah kerugian yang terjadi (incurred) pada waktu ke- . Dengan demikian, , menyatakan kerugian yang dibayarkan pada tahun kecelakaan ke- yang mengalami penundaan selama tahun, dan �, mengartikan kerugian yang terjadi pada tahun kecelakaan ke- yang mengalami penundaan selama tahun.
Selain itu, � ≔ { , , … , , } menjelaskan kondisi bahwa waktu tunda dari kerugian yang dibayarkan pada tahun kecelakaan ke- diberikan sampai akhir tahun penundaan ke- dan ℐ ≔ {�, , … , �, } menjelaskan kondisi bahwa waktu tunda dari kerugian yang terjadi pada tahun kecelakaan ke- diberikan sampai akhir tahun penundaan ke- .
Asumsi Model
Beberapa asumsi dalam proses metode CL untuk kerugian yang dibayarkan dan kerugian yang terjadi.
1. Asumsi model untuk kerugian yang dibayarkan (P) PE (Asumsi Nilai Harapan)
Untuk , ∈ � dengan = + , terdapat faktor penundaan �→ > sehingga untuk setiap = , , … , ,
( ,
, |� ) = �→ .
PV (Asumsi Ragam)
Untuk , ∈ � dengan = + , terdapat proporsi konstan �→ sehingga untuk setiap = , , … , ,
var ( ,
, |� ) =
�→ , .
PU (Asumsi Kebebasan)
Berbagai tahun kerugian yang independen, yaitu
7 2. Asumsi model untuk kerugian yang terjadi (I)
IE (Asumsi Nilai Harapan)
Untuk , ∈ � dengan = + , terdapat faktor penundaan ��→ >
Berbagai tahun kerugian yang independen, yaitu
{�, | ∈ �}, {� , | ∈ �}, … , {��, | ∈ �} bebas stokastik.
Dengan demikian, asumsi metode CL menjelaskan bahwa tahun kecelakaan yang stokastik independen, tetapi memiliki faktor penundaan yang sama dan parameter σ setiap tahun penundaan. Asumsi di atas dirancang untuk proyeksi segitiga bawah dan untuk menjelaskan tentang hubungan antara proses kerugian yang dibayarkan dan terjadi. Ekspektasi bersyarat menggambarkan kemungkinan terbaik peramalan , jika hanya diketahui proses kerugian yang dibayar dari tahun kecelakaan, sampai dengan saat ini. Hal ini berlaku analog dengan proses kerugian yang terjadi
�,
�, |ℬ dan ��, ��, |ℬ
dengan ℬ = { , , , , … , , , �, , �, , … , �, } adalah himpunan waktu penundaan yang diketahui hingga akhir tahun penundaan dari proses kerugian yang dibayarkan dan kerugian yang terjadi.
Metode MunichChain-Ladder
Untuk metode Munich chain-ladder (MCL), asumsi independensi PU dan IU dari metode chain-ladder diperluas, yaitu dengan menambahkan asumsi PIU (kebebasan dari tahun kerugian yang dibayarkan dan dari tahun kerugian yang terjadi). Set kebebasan stokastik untuk asumsi kebebasan PIU adalah
8
untuk menjelaskan rasio (P/I) dan rasio (I/P).
Selanjutnya, dengan menambahkan konsep residual bersyarat: jika adalah peubah acak, dengan syarat , maka
� | = √var |
menjelaskan standar deviasi bersyarat dari oleh , dan
res | = −� | |
menjelaskan residual bersyarat oleh . Residual bersyarat adalah standardisasi yang berkaitan dengan nilai harapan bersyarat dan ragam bersyarat, dengan
res | | = dan var res | | = .
Asumsi Model
Mengacu pada asumsi model oleh Mack, dilakukan analisis lebih lanjut untuk menghitung faktor nilai harapan bersyarat dari penundaan proses kerugian yang dibayarkan dan kerugian yang terjadi guna mendapatkan residual masing-masingnya, dengan
res ,
, |� dan res
�,
�, |ℐ .
Dibandingkan dengan model CL, kelebihan dari model Munich chain-ladder (MCL) yang menentukan adalah merumuskan asumsi untuk istilah-istilah berikut, yaitu
res ( �,
�, |� ) |ℬ dan res ( ��,
��, |ℐ ) |ℬ .
danresidual dari rasio (I/P) dan rasio (P/I), didefinisikan
res( −, |� ) atau res( , |ℐ ).
Asumsi tambahan untuk rasio (P/I) dan rasio (I/P)
PQ
Terdapat konstanta untuk , ∈ � dengan = + sehingga untuk setiap = , … , ,
(res ,
, |� |ℬ ) = res( ,
− |� )
9
( ,
, |ℬ ) = �→ +
� ( �,
�, |� )
�( −, |� ) −, − ( −, |� ) . (1) IQ
Terdapat konstanta untuk , ∈ � dengan = + sehingga untuk setiap = , … , ,
(res ��,
, |ℐ |ℬ ) = res( , |ℐ )
yang ekuivalan dengan
(�,
�, |ℬ ) = �→
� + � � ( ��,
��, |ℐ )
�( , |ℐ ) , − ( , |ℐ ) .
(2)
Parameter dan � yang merupakan kemiringan garis regresi dari plot residual masing-masing proses, tidak tergantung pada penundaan tahun ke- . Persamaan (1) dan (2) mewakili harapan bersyarat untuk faktor penundaan sebagai jumlah faktor dari chain-ladder dan koreksi dari kedua jenis data. Akan dianalisis lebih rinci istilah tersebut pada bagian berikutnya.
Analisis Asumsi Model
Akan diperiksa lebih dekat model MCL dan khususnya persamaan bentuk PQ dan IQ, dimisalkan , � > . Kondisi nilai harapan yaitu faktor penundaan dari proses kerugian yang terjadi akan digunakaan untuk proyeksi tahun kecelakaan ke- dari ke , adalah monoton naik, fungsi linear dari rasio (P/I) atau , . Hal ini menunjukkan bahwa pengamatan dari praktik dinyatakan sebagai asumsi teoritis. Persamaan IQ merupakan ekspektasi bersyarat dari jumlah chain-ladder faktor penundaan ��→ dan istilah linear dalam , . Terdapat tiga faktor terkoreksi yang dijelaskan sebagai berikut:
Faktor � adalah koefisien korelasi dari residual faktor penundaan dan residual rasio (P/I), yang akan dibuktikan pada bagian selanjutnya. Oleh karena itu � sebagai fakor korelasi atau parameter korelasi. Nilai dari � haruslah di antara
dan , dan mengukur keterkaitan faktor penundaan sebelumnya dari rasio (P/I). Jika hampir tidak ada ketergantungan atau hubungan pada data, maka
� ≈ dan faktor penundaan rata-rata diproyeksikan seperti pada metode CL. Faktor standar deviasi adalah hasil bagi dari standar deviasi bersyarat faktor
penundaan yang terjadi dan rasio (P/I). Hal ini menyebabkan penyimpangan rasio (P/I) dari rata-rata yang diukur sebagai deviasi dari faktor penundaan. Semakin besar standar deviasi dari faktor penundaan, semakin besar kemungkinan akan menjadi deviasi yang signifikan dari rata-rata, dan semakin besar terkoreksi. Semakin kecil standar deviasi dari rasio (P/I), akan semakin
10
Linear , − ( , |ℐ ) meliputi proyeksi rasio (P/I). Jika rasio (P/I) di atas rata-rata memiliki efek memperbaiki faktor penundaan ke atas, dan sebaliknya. Semakin jauh rasio (P/I) dari rata-rata akan semakin besar koreksinya. Jika rasio (P/I) berada pada rata-rata, faktor penundan yang digunakan akan menjadi rata-rata dari data, seperti dalam metode CL. Berlaku untuk faktor penundaan untuk rasio (I/P).
Parameter korelasi dan � memperlihatkan hubungan antara segitiga dari kerugian yang dibayarkan dan segitiga dari kerugian yang terjadi. Besarnya parameter ini menunjukkan sejauh mana waktu penundaan dari kecelakaan yang dibayarkan dan kecelakaan yang terjadi, dipengaruhi oleh jenis data masing-masingnya, karenanya parameter ini sangat penting untuk ukuran proyeksi utama. Karena pendekatan residual memungkinkan untuk mempertimbangkan semua tahun penundaan, yaitu menyediakan jumlah yang cukup di titik data, estimasi ini relatif stabil.
Selanjutnya akan dibuktikan formula dan � sebagai parameter korelasi. Menggunakan informasi cov� , ≔ cov , | untuk koragam bersyarat dari dua variabel acak dan dengan diberikan kondisi
( ,
, |ℬ ) = , , .
Diketahui kondisi martingale jika �,
�, adalah ℬ yang terukur, maka
Mengacu ke pada bentuk berikut:
corr −, , ( �,�, |� ) = dan corr , , (���,
�, |ℐ ) = �
untuk koefisien korelasi bersyarat, maka
corr (res( −, |� ), res ,
11 dan
corr (res( , |ℐ ), res ��,
, |ℐ ) = �.
Dengan demikian, parameter λ model MCL sebagai korelasi antara run-off triangle untuk kerugian yang dibayarkan dan kerugian yang terjadi. Pada pembahasannya selanjutnya akan dijelaskan perkiraan nilai parameter yang digunakan untuk memperoleh residual masing-masing data serta cara memperoleh nilai λ.
Implementasi Praktis
Pada bagian ini, akan dijelaskan lebih rinci tentang semua perkiraan parameter yang diperlukan untuk Metode MCL, sebelum melakukan perhitungan MCL lengkap untuk contoh konkret.
Mengestimasi Parameter
Untuk menghitung residual dan nilai harapan faktor penundaan, harus diperkirakan setiap parameter dari Model MCL.
Parameter Metode Chain-Ladder
Untuk setiap = + , faktor penundaan �→ dan ��→ untuk =
, , … , − digunakan estimasi Metode chain-ladder
12
Parameter Metode MunichChain-Ladder
Untuk menghitung residual bersyarat dari rasio (P/I) dan (I/P), perlu pendugaan untuk nilai harapan bersyarat , |ℐ dan −, |� dan standar deviasi bersyarat � , |ℐ dan � −, |� .Asumsi pertama bahwa , |ℐ adalah konstan, analog dengan model IE chain-ladder untuk kerugian yang terjadi. Selanjutnya, diasumsikan keterkaitan ragam bersyarat dari rasio (P/I) pada kerugian yang terjadi, analog dengan kondisi IV. Untuk =
, , … , , asumsi berikut untuk nilai harapan bersyarat dan ragam bersyarat dari rasio (P/I). Estimasi nilai harapan bersyarat , |ℐ adalah sebagai berikut:
̂ = ∑�− += �, ∑ �,
berlaku sama untuk semua tahun terjadinya kecelakaan. Estimasi untuk
� , |ℐ yaitu Kemudian diasumsikan bahwa estimasi untuk rasio (P/I) berlaku analog dengan nilai harapan bersyarat dan ragam dari rasio (I/P) dengan mengestimasi nilai harapan bersyarat −, |� sebagai berikut:
̂− = ∑ dengan �̂ didefinisikan
�̂ = − ∑ , �− +
=
13 Masalah akan timbul karena mengikuti kondisi bahwa kedua nilai harapan bersyarat , |ℐ dan −, |� menjadi konstan dengan , yang sudah konstan, ini bertentangan dengan kenyataan di lapangan. Oleh karena itu, hal ini tidak dapat diasumsikan, harus ada struktur ketergantungan yang lebih rumit dari nilai harapan yang keduanya tergantung pada ℐ dan � .
Akan diperkirakan , |ℐ dengan rata-rata di atas rasio (P/I) dari , dari kerugian yang terjadi pada tahun ke- untuk ℐ serupa dengan ℐ . Pada aturan chain-ladder, serupa berarti tingkat �, dekat dengan �, , atau faktor penundaan �, /�, − dekat dengan �, /�, − . Setidaknya, akan terjadi kecelakaan tahun ke- dimana ℐ jelas berbeda dengan ℐ . Tentu saja, konsep ini berlaku analog dengan −, |� . Pendekatan ini akan menghasilkan perkiraan untuk nilai harapan bersyarat yang tidak timbal balik dengan definisi dan dengan kecelakaan setiap tahun.
Begitupun untuk ragam bersyarat dengan situasi serupa. Data yang cukup diberikan dari struktur ketergantungan lebih rumit untuk ragam bersyarat dari , dan −, pada ℐ dan � ,sehingga masing-masing dapat diperhitungkan. Kesederhanaan uraian benar jika , |ℐ dan −, |� adalah fungsi tidak konstan terhadap ℐ dan � . Akan diperkirakan residual bersyarat dari
res ( ,
, |� ) , res (
�,
�, |ℐ ) , res ,
− |� , res
, |ℐ
dengan penyederhanaan notasi reŝ ( , ), reŝ (�, ), reŝ ( −, ), dan reŝ ( , ), sehingga
reŝ ( , ) = �,
�, − �→
̂
�→
̂ √ , (11)
reŝ (�, ) = ��,
��, − �→ �
̂
��→
̂ √�, (12)
dan
reŝ ( −, ) = −, − ̂−
�̂ √ ,
(13)
reŝ ( , ) = , − ̂
14
Diestimasikan nilai dugaan dan � sebagai berikut:
̂ = indeks yang diperpanjang hanya sampai akhir periode run-off.
Perubahan tahun penundaan dalam formula estimasi dan � menyimpulkan hanya sejumlah menghasilkan perkiraan tahun penundaan untuk
parameter λ. Parameter λ untuk setiap tahun penundaan harus berfluktuasi secara
acak dan tidak menunjukkan trend yang akan melanggar asumsi model MCL, ini biasanya terjadi dalam praktek.
Menurut asumsi PQ dan IQ, diperoleh formula rekursif untuk menduga , dan �, , yaitu
Contoh Penerapan Metode Cadangan Klaim MunichChain-Ladder
Metode Munich chain-ladder hanya diaplikasikan untuk asuransi kerugian, contohnya asuransi kebakaran dan asuransi kendaraan. Pada bagian ini, akan dilakukan perhitungan MCL lengkap untuk contoh konkret dari data oleh Quarg dan Mack (2006), serta data dari perusahaan insurance market Llyod’s dengan perhitungan lengkap pada Lampiran 3.
15 Tabel 3 Run-off triangle untuk kerugian yang dibayarkan dari data Quarg dan
Mack
Data run-off triangle pada Tabel 3 adalah klaim dalam bentuk besarnya klaim. Sebagai contoh, ambil baris kedua dan kolom ketiga, besaran klaim sejumlah 2162 merupakan total klaim yang dibayarkan dari akumulasi kejadian pada tahun kecelakaan kedua yang dilaporkan sampai dengan tahun ketiga. Data pada Tabel 3, terdapat bagian yang masih kosong berbentuk segitiga di sebelah kanan bawah yang disebut future triangle, ini merupakan pembayaran klaim di masa yang akan datang dan belum diketahui besarnya.
Tabel 4 Run-off triangle untuk kerugian yang terjadi dari data Quarg dan Mack
Ambil contoh baris kedua dan kolom ketiga, besaran klaim sejumlah 2466 merupakan total klaim yang dilaporkan dari akumulasi kejadian pada tahun kecelakaan kedua yang dilaporkan sampai dengan tahun ketiga. Jika dibandingkan nilai-nilai total klaim pada run-off triangle kerugian yang dibayarkan dan kerugian yang terjadi, total klaim pada run-off kerugian yang terjadi lebih besar dari pada besaran klaim pada run-off kerugian yang dibayarkan. Hal ini terjadi karena total klaim pada run-off kerugian yang terjadi adalah penjumlahan dari klaim yang sudah dibayarkan dan klaim yang belum diselesaikan. Klaim yang belum diselesaikan tersebut bisa jadi tidak dibayarkan oleh perusahaan karena beberapa sebab, misalnya besaran klaim tersebut di bawah nilai minimal klaim (deductible). Lain halnya dengan run-off triangle kerugian yang dibayarkan, data klaim yang terdapat di dalamnya adalah penjumlahan dari besaran klaim yang dilaporkan dan sudah dibayarkan oleh perusahaan. Kelebihan dari metode Munich
1 2 3 4 5 6 7
1 576 1804 1970 2024 2074 2102 2131
2 866 1948 2162 2232 2284 2348
3 1412 3758 4252 4416 4494
4 2286 5292 5724 5850
5 1868 3778 4648
6 1442 4010
7 2044
Tahun kejadian
Tahun penundaan
1 2 3 4 5 6 7
1 978 2104 2134 2144 2174 2182 2174
2 1844 2552 2466 2480 2508 2454
3 2904 4354 4698 4600 4644
4 3502 5958 6070 6142
5 2812 4882 4852
6 2642 4406
7 5022
Tahun kejadian
16
chain-ladder ini adalah mengurangi gap seminimal mungkin antara proyeksi IBNR kerugian yang dibayarkan dan kerugian yang terjadi.
Menghitung faktor penundaan rata-rata dan parameter σ
Langkah pertama adalah mengestimasi parameter dengan metode Chain-ladder, yakni menghitung faktor penundaan �̂→ dan �̂�→ serta menghitung parameter �̂→ dan �̂→ .
Sebagai contoh, perhitungan �̂→ dan �̂�→ dengan menggunakan persamaan (3) dan (4). �̂→ adalah estimasi faktor penundaan untuk kerugian yang dibayarkan dari tahun penundaan ke- hingga tahun penundaan ke- , dengan diketahui infomasi , adalah proses kerugian yang dibayarkan pada tahun kecelakaan ke- dan , proses kerugian yang dibayarkan pada tahun kecelakaan ke- , maka infomasi �, adalah proses kerugian yang terjadi pada tahun kecelakaan ke- dan
�, proses kerugian yang terjadi pada tahun kecelakaan ke- , maka
��→
. untuk kerugian yang terjadi.
Sebagai contoh, perhitungan σ̂→ dan σ̂�→ dengan menggunakan persamaan (5) dan (6). σ̂→ adalah estimasi parameter � untuk kerugian yang dibayarkan dari tahun penundaan ke- hingga tahun penundaan ke- , dengan diketahui informasi �̂→ yang telah diperoleh pada perhitungan sebelumnya, serta
17 tahun penundaan ke- hingga tahun penundaan ke- , dengan diketahui informasi
��→
Estimasi parameter � untuk tahun kejadian ke- yang ditunda hingga tahun ke- adalah sebesar . untuk kerugian yang dibayarkan dan . untuk kerugian yang terjadi. Secara keseluruhan faktor penundaan rata-rata dan parameter σ akan disajikan pada Tabel 5.
Tabel 5 Estimasi faktor penundaan rata-rata dan parameter σ dari data Quarg dan Mack
1→2 2→3 3→4 4→5 5→6 6→7
2.437 1.131 1.029 1.021 1.021 1.014
1.652 1.019 1.000 1.011 0.990 0.996
13.456 3.666 0.482 0.210 0.479
9.727 2.544 1.004 0.120 0.860
�̂→ �̂�→
�̂→
18
Menghitung rasio (P/I) dan (I/P) serta parameter ρ
Setelah diperoleh estimasi untuk faktor penudaan dan parameter � untuk masing-masing kecelakaan yang dibayarkan dan terjadi, selanjutnya akan dicari parameter Metode MCL, dengan menghitung nilai harapan bersyarat dan standar deviasi bersyarat.
Menghitung (P/I) atau ̂ serta (I/P) atau ̂− dengan formula yang telah diperoleh dari pembahsan parameter Metode MCL. Sebagai contoh perhitungan
� atau ̂ dan �
= ̂− dengan menggunakan persamaan (7) dan (9). ̂ adalah nilai harapan bersyarat , |ℐ diperoleh dengan diketahui informasi , dan �, , maka
̂ =∑∑=− + , �, − +
= =
∑= ,
∑= �,
= ++ ++ ++ ++ ++ = = . .
Nilai ̂− adalah nilai harapan bersyarat −, |� diperoleh dengan diketahui informasi , dan �, , maka
̂− =∑∑=− + �,
, − +
= =
∑= �,
∑= ,
= ++ ++ ++ ++ ++ = = . .
Diperoleh nilai harapan bersyarat , |ℐ sebesar . dan ,
− |� sebesar . .
Setelah itu, akan dihitung parameter standar deviasi bersyarat ρ. Sebagai contoh perhitungan �̂� dan �̂ dengan menggunakan persamaan (8) dan (10).
��
̂ = ( − ) ∑ �, − +
=
( , − ̂)
= ( ) ∑ �, =
( , − . )
= ( ) [ ( − . ) +. . . + ( − . ) ]
= . + . + . + . + . + . = . = . .
19
�̂ = ( − ) ∑ , − +
=
( −, − ̂− )
= ( ) ∑ �, =
∗ ( −, − . )
= ( ) [ ( − , ) + ⋯ + ( − , ) ]
= . + . + . + . + . + . = . = . .
Jadi, �̂ = √ . = . .
Diperoleh nilai harapan bersyarat � , |ℐ sebesar . dan
� −, |� sebesar . . Secara keseluruhan, hasil perhitungan untuk nilai harapan bersyarat dan standar deviasi bersyarat untuk kerugian yang dibayarkan dan kerugian yang terjadi disajikan pada Tabel 6.
Tabel 6 Rasio (P/I) dan (I/P) serta parameter ρdari data Quarg dan Mack
Menghitung residual masing-masing parameter
Langkah berikutnya adalah menghitung nilai residual masing-masing dari
reŝ ( , ), reŝ (�, ), reŝ ( −, ), dan reŝ ( , ).
Contoh untuk perhitungan reŝ ( , ) dengan menggunakan persamaan (11), akan dihitung reŝ ( , ) dengan mengetahui informasi , , , ,�̂→ dan �̂→ . Hasil perhitungan yang lengkap untuk reŝ ( , ) tersaji pada Tabel 7.
reŝ ( , ) = ,
, − �→
̂
�̂→ (√ ,
) = − .. (√ ) = − . .
s 1 2 3 4 5 6 7
53.3% 84.9% 92.8% 94.5% 94.9% 96.0% 98.0%
187.8% 117.8% 107.8% 105.8% 105.4% 104.2% 102.0%
14.943 4.990 2.167 1.619 1.791 0.236
5.711 3.819 1.918 1.461 1.637 0.222
̂
�̂ �̂� −
20
Tabel 7 Hasil perhitungan reŝ ( , ) dari data Quarg dan Mack
P 1→2 2→3 3→4 4→5 5→6 6→7
1 1.240 -0.454 -0.178 0.846 -0.724 2 -0.410 -0.258 0.293 0.572 0.690 3 0.628 0.004 1.248 -0.979
4 -0.433 -0.985 -1.151 5 -1.330 1.661
6 0.971
7
Contoh untuk perhitungan reŝ (�, ) dengan menggunakan persamaan (12), akan dihitung reŝ (� , ) dengan mengetahui informasi � , ,� , ,�̂�→ dan �̂�→ . Hasil perhitungan yang lengkap untuk reŝ (�, ) tersaji pada Tabel 8.
reŝ (� , ) = � ,
� , − �→ �
̂
�̂ (√��→ ,
) = − .. (√ ) = − . .
Tabel 8 Hasil perhitungan reŝ (�, ) dari data Quarg dan Mack
I 1→2 2→3 3→4 4→5 5→6 6→7
1 1.605 -0.079 0.222 1.131 0.732 2 -1.184 -1.039 0.287 0.096 -0.681 3 -0.846 1.565 -1.415 -0.843
4 0.299 0.005 0.931 5 0.458 -0.681
6 0.082
7
Contoh untuk perhitungan reŝ ( −, ) dengan menggunakan persamaan (13), akan dihitung reŝ ( −, ) dengan mengetahui informasi −, ,̂− , , dan �̂. Hasil perhitungan yang lengkap untuk reŝ ( −, ) tersaji pada Tabel 9.
Reŝ ( −, ) = ,
− − ̂−
�̂ (√ , ) =
, − .
21 Tabel 9 Hasil perhitungan reŝ ( −, ) dari data Quarg dan Mack
Contoh untuk perhitungan reŝ ( , ) dengan menggunakan persamaan (14), akan dihitung reŝ ( , ) dengan mengetahui informasi , ,̂,� , dan �̂�. Hasil perhitungan yang lengkap untuk reŝ ( , ) tersaji pada Tabel 10.
reŝ ( , ) = , − ̂
��
̂ (√� , ) = . .− . (√ ) = − . .
Tabel 10 Hasil perhitungan reŝ ( , ) dari data Quarg dan Mack
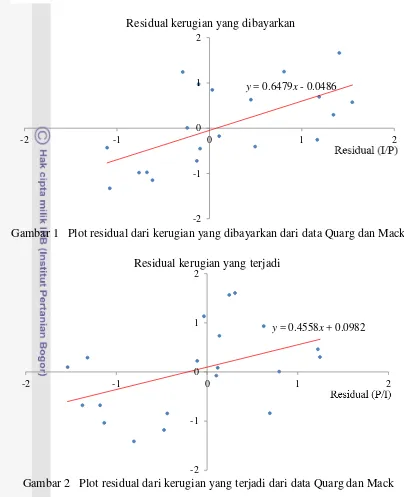
Menggunakan hasil perhitungan residual dari kerugian yang dibayarkan dan residual (I/P) dapat ditarik plot residual kerugian yang dibayarkan (Gambar 3). Sisaan dari kerugian yang dibayarkan menunjukkkan korelasi sebesar 64%. Estimasi slop dari garis regresi melalui titik asal ̂ = . , yang menjelaskan sebagai parameter korelasi yang dijelaskan pada pembahasan sebelumnya.
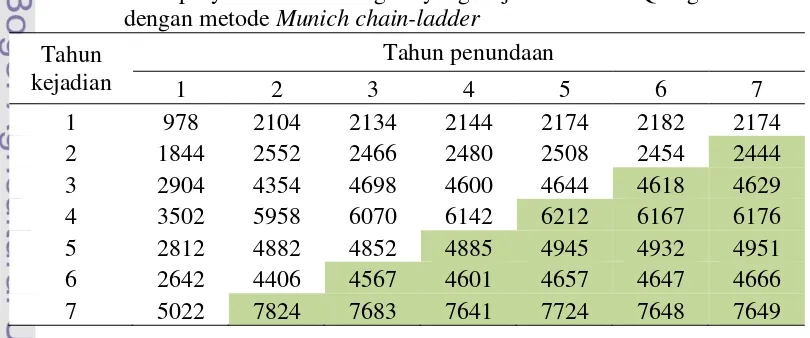
Plot residual dari kerugian yang terjadi (Gambar 4), menunjukkan korelasi 45%. Namun nilai estimasi ̂�yang dipilih adalah sebesar . . ̂ dan ̂� memenuhi syarat dimana parameter bernilai antara sampai .
I/P 1 2 3 4 5 6 7
1 -0.289 -0.100 0.106 0.033 -0.136 -0.726
2 0.496 1.168 1.343 1.547 1.188 0.687
3 0.450 -0.239 0.808 -0.675 -0.755 4 -1.106 -0.761 -0.615 -0.388
5 -1.077 1.406 -1.075 6 -0.116 -1.006
7 1.753
P/I 1 2 3 4 5 6 7
1 0.309 0.103 -0.107 -0.033 0.137 0.728 2 -0.473 -1.131 -1.317 -1.537 -1.177 -0.686 3 -0.437 0.246 -0.805 0.693 0.771
4 1.245 0.795 0.626 0.396
5 1.223 -1.372 1.102
6 0.119 1.065
22
Gambar 1 Plot residual dari kerugian yang dibayarkan dari data Quarg dan Mack
Gambar 2 Plot residual dari kerugian yang terjadi dari data Quarg dan Mack Pada akhirnya digunakan metode Munich chain-ladder untuk proyeksi kerugian yang akan dibayarkan dan kerugian yang akan terjadi. Dengan menggunakan persamaan (15) dan (16) dilakukan perhitungan guna mencari faktor pengali − dan untuk menduga , dan �, . Sebagai faktor penundaan dari kerugian yang dibayar terlebih dahulu, akan digunakan nilai rata-rata
�̂ = .→ untuk menghitung −,
�̂ + → ̂ �̂→
� ( −, − ̂− )
= . + . ( .. ) . − . = . .
y = 0.6479x - 0.0486
-2 -1 0 1 2
-2 -1 0 1 2
Residual kerugian yang dibayarkan
y = 0.4558x + 0.0982
-2 -1 0 1 2
-2 -1 0 1 2
23 sedangkan untuk kerugian yang terjadi dengan informasi �̂ = .�→ untuk menghitung ,
�̂ +�→ ̂ �� ̂�→
�� ( , − ̂)
= . + . ( .. ) . % − . % = . .
Hasil perhitungan lengkap, terdapat di Lampiran 1.
Hasil di atas sebagai estimasi untuk nilai , sebesar . = dan untuk nilai � , sebesar . = . Untuk proyeksi di tahun lainnya, tersaji di Tabel 11 untuk kerugian yang dibayarkan dan Tabel 12 untuk kerugian yang terjadi.
Tabel 11 Hasil proyeksi untuk kerugian yang dibayarkan dari data Quarg dan Mack dengan metode Munich chain-ladder
Tahun kejadian
Tahun penundaan
1 2 3 4 5 6 7
1 576 1804 1970 2024 2074 2102 2131
2 866 1948 2162 2232 2284 2348 2383
3 1412 3758 4252 4416 4494 4573 4597
4 2286 5292 5724 5850 5967 6081 6119
5 1868 3778 4648 4762 4848 4922 4937
6 1442 4010 4387 4492 4573 4642 4655
7 2044 5663 6948 7180 7332 7487 7549
Tabel 11 merupakan hasil akhir dari proyeksi IBNR untuk kerugian yang dibayarkan, dengan melengkapi segitiga bawah dari run-off sebelumnya. Sebagai contoh, perhatikan baris ke-6 kolom ke-4, besarnya cadangan klaim yang harus disediakan adalah sejumlah 4492, merupakan proyeksi total klaim yang dibayarkan dari akumulasi kejadian pada tahun kecelakaan keenam yang dilaporkan sampai dengan tahun keempat.
Tabel 12 Hasil proyeksi untuk kerugian yang terjadi dari data Quarg dan Mack dengan metode Munichchain-ladder
Tahun kejadian
Tahun penundaan
1 2 3 4 5 6 7
1 978 2104 2134 2144 2174 2182 2174
2 1844 2552 2466 2480 2508 2454 2444
3 2904 4354 4698 4600 4644 4618 4629
4 3502 5958 6070 6142 6212 6167 6176
5 2812 4882 4852 4885 4945 4932 4951
6 2642 4406 4567 4601 4657 4647 4666
24
Tabel 12 merupakan hasil akhir dari proyeksi IBNR untuk kerugian yang terjadi, dengan melengkapi segitiga bawah dari run-off sebelumnya. Sebagai contoh, perhatikan baris ke-6 kolom ke-4, besarnya cadangan klaim yang harus disediakan adalah sejumlah 4601, merupakan proyeksi total klaim yang dilaporkan dari akumulasi kejadian pada tahun kecelakaan keenam yang dilporkan sampai dengan tahun keempat.
Langkah selanjutnya yaitu, melihat bagaiamana metode MCL dapat mengurangi gap antara proyeksi IBNR kerugian yang dibayarkan dan kerugian yang terjadi, sebagai kelebihan dari metode ini. Tabel 13, menjelaskan gap antara proyeksi IBNR dari kerugian yang dibayarkan dan kerugian yang terjadi, kolom berwarna putih menunjukkan data klaim sebelum dilakukan proyeksi, dan kolom berwarna biru menunjukkan proyeksi klaim dengan metode MCL.
Tabel 13 Gap antara proyeksi untuk kerugian yang dibayarkan dan kerugian yang terjadi dari data Quarg dan Mack dengan metode Munich chain-ladder
Tahun kejadian
Tahun penundaan
1 2 3 4 5 6 7
1 402 300 164 120 100 80 43
2 978 604 304 248 224 106 61
3 1492 596 446 184 150 45 32
4 1216 666 346 292 244 87 57
5 944 1104 204 124 97 9 14
6 1200 396 180 109 84 5 11
7 2978 2161 735 461 392 161 100
Dibandingkan dengan hasil perhitungan menggunakan metode chain-ladder, hasil proyeksi dari metode MCL jauh lebih baik dalam mengurangi gap antara proyeksi IBNR kerugian yang terjadi dengan kerugian yang dibayarkan. Perhitungan CL jauh lebih sederhana dibandingkan MCL, langkah perhitungan lengkapnya tersaji pada Lampiran 2.
25 Tabel 14 Gap antara proyeksi kerugian yang dibayarkan dan kerugian yang
terjadi dari data Quarg dan Mack dengan metode chain-ladder
Tahun kejadian
Tahun penundaan
1 2 3 4 5 6 7
1 402 300 164 120 100 80 43
2 978 604 304 248 224 106 111
3 1492 596 446 184 150 75 78
4 1216 666 346 292 12 -104 -110
5 944 1104 204 -72 -331 -450 -472
6 1200 396 36 -244 -507 -631 -663
7 2978 2706 2589 2530 2456 2503 2628
Pada contoh kasus yang kedua, digunakan data dari perusahaan Lloyd’s.
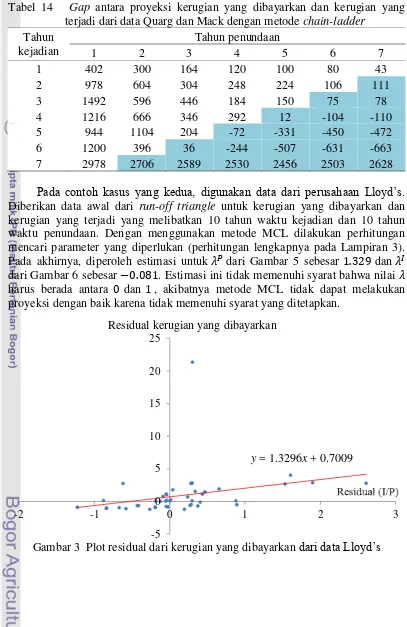
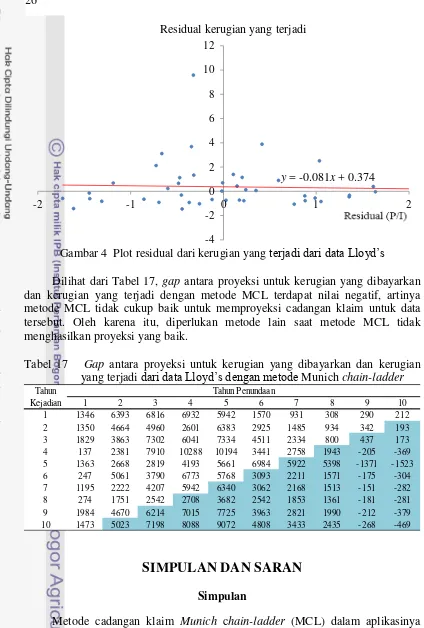
Diberikan data awal dari run-off triangle untuk kerugian yang dibayarkan dan kerugian yang terjadi yang melibatkan 10 tahun waktu kejadian dan 10 tahun waktu penundaan. Dengan menggunakan metode MCL dilakukan perhitungan mencari parameter yang diperlukan (perhitungan lengkapnya pada Lampiran 3). Pada akhirnya, diperoleh estimasi untuk dari Gambar 5 sebesar . dan � dari Gambar 6 sebesar − . . Estimasi ini tidak memenuhi syarat bahwa nilai harus berada antara dan , akibatnya metode MCL tidak dapat melakukan proyeksi dengan baik karena tidak memenuhi syarat yang ditetapkan.
Gambar 3 Plot residual dari kerugian yang dibayarkan dari data Lloyd’s
y = 1.3296x + 0.7009
-5 0 5 10 15 20 25
-2 -1 0 1 2 3
26
Gambar 4 Plot residual dari kerugian yang terjadi dari data Lloyd’s
Dilihat dari Tabel 17, gap antara proyeksi untuk kerugian yang dibayarkan dan kerugian yang terjadi dengan metode MCL terdapat nilai negatif, artinya metode MCL tidak cukup baik untuk memproyeksi cadangan klaim untuk data tersebut. Oleh karena itu, diperlukan metode lain saat metode MCL tidak menghasilkan proyeksi yang baik.
Tabel 17 Gap antara proyeksi untuk kerugian yang dibayarkan dan kerugian yang terjadi dari data Lloyd’s dengan metode Munich chain-ladder
SIMPULAN DAN SARAN
Simpulan
Metode cadangan klaim Munich chain-ladder (MCL) dalam aplikasinya dapat mengurangi gap antara proyeksi IBNR berdasarkan kerugian yang dibayarkan dan kerugian yang terjadi dengan memprediksi pembayaran klaim dimasa yang akan datang. Metode MCL menunjukkan bahwa antara kerugian yang dibayarkan dan kerugian yang terjadi hampir selalu ada korelasi. Dalam
y = -0.081x + 0.374
-4 -2 0 2 4 6 8 10 12
-2 -1 0 1 2
Residual kerugian yang terjadi
1 2 3 4 5 6 7 8 9 10
1 1346 6393 6816 6932 5942 1570 931 308 290 212 2 1350 4664 4960 2601 6383 2925 1485 934 342 193 3 1829 3863 7302 6041 7334 4511 2334 800 437 173 4 137 2381 7910 10288 10194 3441 2758 1943 -205 -369 5 1363 2668 2819 4193 5661 6984 5922 5398 -1371 -1523 6 247 5061 3790 6773 5768 3093 2211 1571 -175 -304 7 1195 2222 4207 5942 6340 3062 2168 1513 -151 -282 8 274 1751 2542 2708 3682 2542 1853 1361 -181 -281 9 1984 4670 6214 7015 7725 3963 2821 1990 -212 -379 10 1473 5023 7198 8088 9072 4808 3433 2435 -268 -469 Tahun
Kejadian
27 penerapannya, metode MCL menghasilkan proyeksi yang baik saat memenuhi kriteria bernilai antara sampai .
Perhitungan dengan metode chain-ladder (CL) lebih praktis dan sederhana jika dibandingkan dengan perhitungan dengan metode MCL. Namun, proyeksi yang dihasilkan oleh metode MCL lebih baik dan lebih dapat diandalkan dibandingkan proyeksi yang dihasilkan oleh metode CL. Oleh karena itu, metode MCL dapat diaplikasikan pada portofolio asuransi di Indonesia, khususnya portofolio asuransi kerugian.
Saran
Langkah selanjutnya adalah menduga kesalahan prediksi klaim dari perhitungan metode Munich chain-ladder dengan teknik bootstrap. Langkah ini perlu untuk melihat ketepatan metode MCL dalam memproyeksikan pembayaran klaim di masa yang akan datang, serta mengkaji metode lainnya yang dapat digunakan saat metode MCL tidak menghasilkan poyeksi yang baik.
DAFTAR PUSTAKA
Antonio K, Beirlant J, Hoedemakers T, dan Verlaak R. 2006. Lognormal mixed models for reported claims reserves. North American Actuarial Journal. 10(1):30−48.doi:10.1080/10920277.2006.10596238.
Hogg RV, McKean J, Craig AT. 2014. Introduction to Mathematical Statistics. Ed ke-7. New Jersey (US): Prentice Hall Inc.
Hossack IB, Pollard JH, Zenwirth B. 1999. Introductory Statistics with Applications in General Insurance. Ed ke-2. Cambridge (UK): University of Cambride Press.
Mack T. 1993. Distribution-free calculation of the standard error of chain-ladder reserve estimates. Astin Bulletin. 23(2):213-225.
Olofsson M. 2006. Stochastic loss reserving testing the new guidelines from the Australian prudential regulation authority (APRA) on Swedish portfolio data using a bootstrap simulation and distribution-free method by Thomas Mack [tesis]. Stockholm (SE): Stockholm University.
Quarg G, Mack T. 2008. Munich chain-ladder:a reserving method that reduces the
gap between IBNR projections based on paid losses and IBNR projections based on incurred losses. Variance. 2(2):266–299.doi: 10.1007/bf02808969. Williams D. 1991. Probability with Martingales. Cambridge (UK): University of
Cambride Press.
28
Lampiran 1 Pengolahan data Quarg dan Mack dengan metode Munich chain-ladder
Hasil perhitungan res( −, ) dari data Quarg dan Mack
Hasil perhitungan res( −, )res( , ) dari data Quarg dan Mack
Hasil perhitungan − dari data Quarg dan Mack
Hasil perhitungan �̂ + ̂ → �̂�→
�� ( −, − ̂
− ) dari data Quarg dan Mack
1 2 3 4 5 6 7
1 0.083 0.010 0.011 0.001 0.018 0.528
2 0.246 1.363 1.802 2.392 1.412 0.472
3 0.203 0.057 0.652 0.456 0.570
4 1.224 0.579 0.378 0.150
5 1.159 1.978 1.156
6 0.013 1.013
7 3.072
1 2 3 4 5 6 7
1 -0.358 0.045 -0.019 0.027 0.098 0.000
2 -0.203 -0.301 0.393 0.884 0.820
3 0.283 -0.001 1.008 0.661
4 0.478 0.749 0.708
5 1.433 2.335
6 -0.112
7
1 2 3 4 5 6 7
1 1.698 1.166 1.083 1.059 1.048 1.038 1.020
2 2.129 1.310 1.141 1.111 1.098 1.045 1.015
3 2.057 1.159 1.105 1.042 1.033 1.018 1.005
4 1.532 1.126 1.060 1.050 1.020 1.019 1.006
5 1.505 1.292 1.044 1.024 1.018 1.015 1.003
6 1.832 1.099 1.094 1.024 1.018 1.015 1.003
7 2.457 2.771 1.226 1.034 1.021 1.021 1.009
1 2 3 4 5 6 7
1
2 1.015
3 1.018 1.005
4 1.020 1.019 1.006
5 1.024 1.018 1.015 1.003
6 1.094 1.024 1.018 1.015 1.003
29 Hasil perhitungan res( , ) dari data Quarg dan Mack
Hasil perhitungan res( , ) res(�, ) dari data Quarg dan Mack
Hasil perhitungan Q dari data Quarg dan Mack
Hasil perhitungan �̂ +�→ ̂ � �̂�→
�� ( , − ̂ ) dari data Quarg dan Mack
1 2 3 4 5 6 7
1 0.095 0.011 0.011 0.001 0.019 0.529
2 0.224 1.280 1.734 2.362 1.386 0.471
3 0.191 0.061 0.648 0.480 0.595
4 1.551 0.633 0.391 0.157
5 1.496 1.883 1.215
6 0.014 1.134
7 2.428
1 2 3 4 5 6 7
1 0.495 -0.008 -0.024 -0.037 0.101 0.000 2 0.560 1.176 -0.378 -0.148 0.802 0.000
3 0.370 0.385 1.139 -0.584 0.000
4 0.373 0.004 0.582 0.000
5 0.560 0.934 0.000
6 0.010 0.000
7 0.000
1 2 3 4 5 6 7
1 0.589 0.857 0.923 0.944 0.954 0.963 0.980
2 0.470 0.763 0.877 0.900 0.911 0.957 0.996
3 0.486 0.863 0.905 0.960 0.968 0.994 1.002
4 0.653 0.888 0.943 0.952 1.011 0.993 1.002
5 0.664 0.774 0.958 1.007 1.012 0.997 1.004
6 0.546 0.910 1.037 1.007 1.012 0.998 1.004
7 0.407 1.558 0.982 0.995 1.011 0.990 1.000
1 2 3 4 5 6 7
1
2 0.996
3 0.994 1.002
4 1.011 0.993 1.002
5 1.007 1.012 0.997 1.004
6 1.037 1.007 1.012 0.998 1.004
30
Lampiran 2 Pengolahan data Quarg dan Mack dengan metode chain-ladder
Hasil pembagi rasio run-off kerugian yang dibayarkan dari data Quarg dan Mack
Hasil perhitungan simple average, weighted average dan faktor pengali untuk kerugian yang dibayarkan dari data Quarg dan Mack
Hasil proyeksi untuk kerugian yang dibayarkan dari data Quarg dan Mack dengan metode chain-ladder
Hasil pembagi rasio dari run-off kerugian yang terjadi dari data Quarg dan Mack
1→2 2→3 3→4 4→5 5→6 6→7
1 3.132 1.092 1.027 1.025 1.014 1.014
2 2.249 1.110 1.032 1.023 1.028
3 2.661 1.131 1.039 1.018
4 2.315 1.082 1.022
5 2.022 1.230
6 2.781
7
P 1→2 2→3 3→4 4→5 5→6 6→7 Tail
Simple Average 2,527 1,129 1,030 1,022 1,021 1,014 1,050
Weighted Average 2,437 1,131 1,029 1,021 1,021 1,014 1,050
Selected 1,291 1,144 1,110 1,087 1,064 1,050 1,000
% Paid 77% 87% 90% 92% 94% 95% 100%
1 2 3 4 5 6 7
1 576 1804 1970 2024 2074 2102 2131
2 866 1948 2162 2232 2284 2348 2465
3 1412 3758 4252 4416 4494 4784 5023
4 2286 5292 5724 5850 6357 6766 7105
5 1868 3778 4648 5161 5608 5969 6268
6 1442 4010 4587 5093 5534 5891 6185
7 2044 2640 3019 3352 3643 3878 4071
Tahun kejadian
Tahun penundaan
1→2 2→3 3→4 4→5 5→6 6→7
1 2.151 1.014 1.005 1.014 1.004 0.996
2 1.384 0.966 1.006 1.011 0.978
3 1.499 1.079 0.979 1.010
4 1.701 1.019 1.012
5 1.736 0.994
6 1.668
31 Hasil perhitungan simple average, weighted average dan faktor pengali untuk
kerugian yang diterjadi dari data Quarg dan Mack
Hasil proyeksi untuk kerugian yang terjadi dari data Quarg dan Mack dengan metode chain-ladder
I 1→2 2→3 3→4 4→5 5→6 6→7 Tail
Simple Average 1,690 1,014 1,000 1,012 0,991 0,996 1,050
Weighted Average 1,652 1,019 1,000 1,011 0,990 0,996 1,050
Selected 1,064 1,049 1,049 1,037 1,046 1,050 1,000
% Inc 94% 95% 95% 96% 96% 95% 100%
1 2 3 4 5 6 7
1 978 2104 2134 2144 2174 2182 2174
2 1844 2552 2466 2480 2508 2454 2577
3 2904 4354 4698 4600 4644 4858 5101
4 3502 5958 6070 6142 6368 6662 6995
5 2812 4882 4852 5089 5276 5520 5796
6 2642 4406 4623 4849 5027 5259 5522
7 5022 5345 5608 5882 6099 6380 6699
Tahun kejadian
32
Lampiran 3 Pengolahan data Lloyd’s dengan metode Munichchain-ladder
Estimasi faktor penundaan rata-rata dan parameter σdari data Lloyd’s
Hasil perhitungan (P/I) dan (I/P) serta parameter ρdari data Lloyd’s
Hasil perhitungan reŝ ( , )dari data Lloyd’s
Hasil perhitungan reŝ ( −, )dari data Lloyd’s
1→2 2→3 3→4 4→5 5→6 6→7 7→8 8→9 9→10
5.185 3.149 1.636 1.359 1.486 1.077 1.031 1.134 1.003
3.776 1.858 1.351 1.248 1.096 1.002 0.983 1.105 0.996
136.558 56.419 23.229 23.295 35.175 5.962 0.401 16.739
131.142 56.711 22.110 19.288 15.944 6.239 1.791 13.455 �̂→
18.1% 25.0% 45.0% 52.7% 58.4% 79.3% 90.4% 96.5% 97.9% 97.9% 553.2% 400.0% 222.3% 189.8% 171.4% 126.1% 110.6% 103.6% 102.2% 102.1%
5.049
9.221 14.118 21.925 17.846 17.167 4.684 2.264 0.881 110.962 101.386 134.467 755.971 465.824 678.318 246.217 119.428 26.556
̂
1 1.523 -1.212 -0.617 -0.694 -0.108 -0.005 0.148 -0.784 2 1.465 -0.836 1.762 -0.959 0.240 0.753 1.121 0.686 3 -0.631 2.745 -0.666 0.119 -0.897 -1.229 -0.887
4 0.041 1.924 -0.516 2.868 2.672 1.078 5 -1.009 -1.123 -0.934 0.093 -0.496
6 2.750 4.012 0.045 0.093 7 0.082 1.107 2.820
8 21.350 -1.072 9 2.782
10
1 2 3 4 5 6 7 8 9 10
1 0.340 0.197 0.271 0.375 0.406 -0.122 -0.039 -0.044 0.278 2 0.469 -0.021 0.043 -0.669 0.014 -0.086 -0.045 0.239 -0.201 3 -0.428 -0.618 -0.411 -0.877 -1.225 -0.263 -0.192 -0.147
4 -0.183 0.659 0.893 1.899 1.532 -0.039 0.334 5 -0.836 -0.578 -0.187 0.005 0.287 0.777
6 0.283 1.606 -0.050 0.299 0.047 7 0.879 0.434 0.298 0.260
8 0.304 -0.840 -0.263 9 2.608 0.880
33 Hasil perhitungan res( −, ) dari data Lloyd’s
Hasil perhitungan res( −, ) res( , )dari data Lloyd’s
Hasil perhitungan − dari data Lloyd’s
Hasil perhitungan �̂ + ̂ → �̂�→
�� ( −, − ̂
− )dari data Lloyd’s
1 2 3 4 5 6 7 8 9 10
1 0.116 0.039 0.074 0.141 0.165 0.015 0.001 0.002 0.077 2 0.220 0.000 0.002 0.447 0.000 0.007 0.002 0.057 0.040 3 0.183 0.382 0.169 0.770 1.499 0.069 0.037 0.022
4 0.034 0.434 0.797 3.606 2.346 0.002 0.112 5 0.698 0.334 0.035 0.000 0.082 0.603
6 0.080 2.579 0.003 0.090 0.002 7 0.773 0.188 0.089 0.067
8 0.092 0.705 0.069 9 6.802 0.774
10 0.002
1 2 3 4 5 6 7 8 9 10
1 0.518 -0.239 -0.167 -0.260 -0.044 0.001 -0.006 0.035 0.000 2 0.687 0.018 0.075 0.641 0.003 -0.064 -0.050 0.164 0.000 3 0.270 -1.697 0.274 -0.104 1.098 0.323 0.170 0.000
4 -0.008 1.268 -0.460 5.445 4.094 -0.042 0.000 5 0.843 0.649 0.174 0.000 -0.142 0.000
6 0.778 6.443 -0.002 0.028 0.000 7 0.072 0.480 0.842 0.000
8 6.490 0.900 0.000 9 7.255 0.000
10 0.000
1 2 3 4 5 6 7 8 9 10
1 8.315 4.465 2.819 2.284 1.954 1.174 1.096 1.031 1.029 1.021 2 9.710 3.946 2.316 1.329 1.721 1.212 1.097 1.059 1.018 1.003
3 3.706 2.689 1.687 1.375 1.331 1.156 1.078 1.026 1.115 1.003
4 3.045 7.488 4.881 4.573 2.611 1.240 1.170 1.033 1.283 1.003
5 2.478 2.576 1.800 1.903 1.880 1.839 1.145 1.042 2.079 1.003
6 12.227 11.371 2.107 2.199 1.738 1.510 1.077 1.033 1.290 1.003
7 16.724 6.108 3.125 2.174 1.472 1.623 1.076 1.033 1.276 1.003
8 12.417 1.983 1.655 1.506 1.181 1.305 1.080 1.033 1.319 1.003
9 51.872 7.268 5.568 1.699 1.399 1.556 1.077 1.033 1.284 1.003
10 5.814 5.646 3.080 1.666 1.365 1.522 1.077 1.033 1.288 1.003
1 2 3 4 5 6 7 8 9 10
1
2 1.003
3 1.115 1.003
4 1.033 1.283 1.003
5 1.145 1.042 2.079 1.003
6 1.510 1.077 1.033 1.290 1.003
7 1.472 1.623 1.076 1.033 1.276 1.003
34
Hasil proyeksi untuk kerugian yang dibayarkan dari data Lloyd’s dengan metode
Munichchain-ladder
Hasil perhitungan reŝ (�, )dari data Lloyd’s
Hasil perhitungan reŝ ( , )dari data Lloyd’s
Hasil perhitungan res( , ) dari data Lloyd’s
1 2 3 4 5 6 7 8 9 10
1 184 1845 3748 5400 6231 9006 9699 10008 10035 10068 2 155 1583 3768 7899 8858 13795 15360 15895 19333 19397 3 676 2287 10635 16102 22177 28825 29828 30700 34233 34346 4 67 367 2038 2879 6329 14366 16201 16730 21465 21535 5 922 1693 3523 4641 6431 8325 9530 9934 20658 20726 6 22 488 3424 5649 7813 11799 12711 13127 16929 16985 7 76 435 1980 5062 7450 12094 13017 13441 17156 17212 8 24 1782 3881 5843 6898 9001 9718 10039 13245 13289 9 39 745 4148 7048 9858 15336 16515 17055 21899 21971 10 306 1728 5321 8864 12096 18410 19831 20480 26381 26468 Tahun
kejadian
Tahun penundaan
1→2 2→3 3→4 4→5 5→6 6→7 7→8 8→9 9→10
1 1.113 -1.043 -0.922 -1.495 -1.465 0.051 -0.732 -0.788 2 0.226 -0.759 -0.685 1.300 0.009 0.114 1.136 0.667 3 -0.790 2.501 -0.783 0.751 0.385 -1.070 -0.391
4 3.875 3.100 -0.142 0.043 -0.153 1.384 5 -0.940 -0.566 0.179 0.686 1.320
6 9.572 -0.835 1.870 -0.937 7 -0.663 0.653 2.029
8 3.662 -0.056 9 -0.617
10
1 2 3 4 5 6 7 8 9 10
1 -0.469 -0.256 -0.692 -0.451 -0.443 0.352 0.175 0.223 -0.810 2 -0.598 0.029 -0.120 1.053 -0.016 0.244 0.204 -1.185 0.587 3 0.883 1.036 1.357 1.359 1.617 0.765 0.879 0.739
4 0.418 -0.662 -1.731 -1.613 -1.444 0.109 -1.468 5 2.108 0.990 0.596 -0.007 -0.318 -1.794
6 -0.321 -1.309 0.149 -0.367 -0.054 7 -0.854 -0.482 -0.724 -0.320
8 -0.343 1.640 0.876 9 -1.438 -0.897
10 -0.073
1 2 3 4 5 6 7 8 9 10
1 0.220 0.066 0.479 0.203 0.196 0.124 0.031 0.050 0.656 2 0.357 0.001 0.014 1.110 0.000 0.059 0.042 1.405 0.344 3 0.780 1.074 1.841 1.848 2.614 0.586 0.772 0.546
4 0.174 0.438 2.997 2.602 2.085 0.012 2.155 5 4.445 0.980 0.355 0.000 0.101 3.219
6 0.103 1.714 0.022 0.134 0.003 7 0.729 0.233 0.524 0.102
8 0.117 2.689 0.768 9 2.069 0.805
35 Hasil perhitungan res( , ) res(�, )dari data Lloyd’s
Hasil perhitungan Q dari data Lloyd’s
Hasil perhitungan �̂ +�→ ̂ � �̂�→
�� ( , − ̂ )dari data Lloyd’s
Hasil proyeksi untuk kerugian yang terjadi dari data Lloyd’s dengan metode
Munichchain-ladder
1 2 3 4 5 6 7 8 9 10
1 -0.522 0.267 0.638 0.674 0.649 0.018 -0.128 -0.175 0.000 2 -0.135 -0.022 0.082 1.369 0.000 0.028 0.232 -0.790 0.000 3 -0.697 2.592 -1.063 1.021 0.623 -0.819 -0.344 0.000
4 1.618 -2.052 0.245 -0.070 0.221 0.151 0.000 5 -1.983 -0.561 0.106 -0.005 -0.420 0.000
6 -3.077 1.093 0.278 0.344 0.000 7 0.566 -0.315 -1.468 0.000
8 -1.255 -0.092 0.000 9 0.887 0.000
10 0.000
1 2 3 4 5 6 7 8 9 10
1 0.120 0.224 0.355 0.438 0.512 0.852 0.912 0.970 0.972 0.979 2 0.103 0.253 0.432 0.752 0.581 0.825 0.912 0.945 0.983 0.996
3 0.270 0.372 0.593 0.727 0.751 0.865 0.927 0.975 1.101 0.996
4 0.328 0.134 0.205 0.219 0.383 0.807 0.855 0.985 1.139 0.996
5 0.404 0.388 0.556 0.525 0.532 0.544 1.009 0.992 1.258 0.996
6 0.082 0.088 0.475 0.455 0.575 1.097 1.002 0.985 1.140 0.996
7 0.060 0.164 0.320 0.460 1.253 1.099 1.002 0.985 1.137 0.996
8 0.081 0.504 0.604 0.996 1.237 1.091 1.002 0.985 1.146 0.996
9 0.019 0.138 1.914 0.996 1.250 1.098 1.002 0.985 1.139 0.996
10 0.172 3.795 1.855 0.996 1.249 1.097 1.002 0.985 1.140 0.996
1 2 3 4 5 6 7 8 9 10
1
2 0.996
3 1.101 0.996
4 0.985 1.139 0.996
5 1.009 0.992 1.258 0.996
6 1.097 1.002 0.985 1.140 0.996
7 1.253 1.099 1.002 0.985 1.137 0.996
8 1.331 1.237 1.091 1.002 0.985 1.146 0.996 9 1.914 1.357 1.250 1.098 1.002 0.985 1.139 0.996 10 3.795 1.855 1.354 1.249 1.097 1.002 0.985 1.140 0.996
1 2 3 4 5 6 7 8 9 10
1 1530 8238 10564 12332 12173 10576 10630 10316 10325 10280 2 1505 6247 8728 10500 15241 16720 16845 16829 19675 19589 3 2505 6150 17937 22143 29511 33336 32162 31500 34670 34519 4 204 2748 9948 13167 16523 17807 18959 18673 21259 21167 5 2285 4361 6342 8834 12092 15309 15452 15332 19287 19203 6 269 5549 7214 12422 13581 14892 14922 14698 16754 16681 7 1271 2657 6187 11004 13790 15156 15184 14954 17005 16930 8 298 3533 6423 8551 10580 11543 11570 11401 13064 13007 9 2023 5415 10362 14063 17583 19299 19336 19045 21687 21592 10 1779 6751 12520 16952 21168 23218 23264 22915 26113 25999 Tahun
kejadian
36
RIWAYAT
HIDUP
Penulis dilahirkan pada hari Rabu, 26 Januari 1994 di Padang. Penulis merupakan putra pertama dari Bapak Agus Darusman dan Ibu Mardiana. Tahun 2011 penulis lulus dari SMA Negeri 10 Kota Padang dan lulus seleksi masuk Institut Pertanian Bogor melalu Seleksi Nasional Masuk Perguruan Tinggi Negeri (SNMPTN) jalur undangan. Penulis diterima di Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam. Selain mengikuti perkuliahan pada mayor Matematika, penulis juga mengikuti perkuliahan minor Statistika Terapan.
Selama mengikuti perkuliahan, penulis aktif dalam kegiatan berorganisasi. Di tahun pertama penulis aktif menjadi anggota Koperasi Mahasiswa (Kopma) IPB, aktif di Organisasi Mahasiswa Daerah (OMDA) yakni Ikatan Pelajar Mahasiswa Minang (IPMM) dan Himpunan Mahasiswa Padang (HIMAPD). Penulis pernah menjabat sebagai Vice President External Relation (VP-ER) di Unit Kegiatan Mahasiswa (UKM) AIESEC IPB, dan menjadi Ketua Departemen
Public Relation di Gugus Mahasiswa Matematika (Gumatika) IPB. Penulis juga pernah menjadi panitia di beberapa kegiatan, di antaranya menjadi ketua pelaksana The � IPB Mathematics Challenges 2014, ketua Divisi Sponsorship
Matematika Ria 2014, dan anggota divisi di beberapa kegiatan Gumatika IPB. Penulis juga pernah tampil bersama grup akustik Elipsoid dan grup nasyid
Guma-voice di beberapa seminar nasional dan acara fakultas.
Penulis pernah menjadi asisten mata kuliah Kalkulus II selama dua periode yaitu periode Semester Ganjil Tahun Ajaran 2013/2014 dan 2014/2015 serta mata kuliah Pemrograman Linear pada periode Semester Genap Tahun Ajaran 2013/2014. Penulis pernah mengikuti program magang profesi di bagian Departemen Aktuaria PT. Asuransi Jiwa Manulife Indonesia selama tiga bulan (Juni-Agustus 2014).
Selama perkuliahan, penulis pernah mendapatkan beasiswa Peningkatan Prestasi Akademik (PPA) dari DIKTI. Penulis juga memperoleh beasiswa AIA