KAJIAN ANALISIS KEPUTUSAN MENGGUNAKAN ANALISIS
SENSITIFITAS DENGAN FUNGSI UTILITY EKSPONENSIAL
SKRIPSI
MISDARWANA NASUTION
080823032
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
KAJIAN ANALISIS KEPUTUSAN MENGGUNAKAN ANALISIS
SENSITIFITAS DENGAN FUNGSI UTILITY EKSPONENSIAL
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
MISDARWANA NASUTION
080823032
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : KAJIAN ANALISIS KEPUTUSAN
MENGGUNAKAN ANALISSIS SENSITIFITAS DENGAN FUNGSI UTILITY EKSPONENSIAL
Kategori : SKRIPSI
Nama : MISDARWANA NASUTION
Nomor Induk Mahasiswa : 082323032
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN
ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di Medan, Juni 2010
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs. Suwarno Ariswoyo Drs. Marwan Harahap M.Eng
NIP: 19500321 198003 1 001 NIP: 19461225 197403 1 001
Diketahui/Diaetujuioleh
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
KAJIAN ANALISIS KEPUTUSAN MENGGUNAKAN ANALISIS SENSITIFTAS DENGAN FUNGSI UTILITY EKSPONENSIAL
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juni 2010
PENGHARGAAN
Puji dan Syukur penulis ucapkan kepada ALLAH SWT yang Maha Pemurah dan Maha Penyayang, dengan limpahan karunia-Nya skripsi ini berhasil diselesaikan dalam waktu yang ditetapkan.
ABSTRAK
STUDY OF DECISION MAKING USING SENSITIVITY ANALYSIS WITH UTILITY EKSPONENSIAL FUNCTION
ABSTRACT
DAFTAR ISI
1.2 Identifikasi Masalah 3
1.3 Tujuan Penelitian 3
1.4 Kontribusi Penelitian 3
1.5 Metode Penelitian 3
Bab 2 Landasan Teori 4
2.1 Beberapa Definisi 4
2.1.1 Teorema Bayes 4
2.1.2 Kemungkinan Bersyarat 6
2.2 Penetuan Pilihan 6
2.2.1 Pilihan Langsung 8
2.2.2 Nilai Ekspektasi 9
2.2.3 Nilai Ekivalen Tetap 12
2.2.4 Utility 12
2.2.4.1 Kurva Utility 13
2.2.4.2 Ekspektasi Utility 13
2.3 Sikap Menghadapi Resiko 15
2.3.1 Sikap Penghindar Resiko 15
2.3.2 Sikap Netral 16
2.3.3 Sikap Penggemar Resiko 16
2.4 Toleransi Resiko dan Fungsi Utility Eksponensial 17
Bab 3 Pembahasan 18
3.1 Analisa Sensitifitas 18
3.1.1 Analisa Sensitifitas Satu Variabel 23
3.1.2 Diagram Tornado 25
3.1.3 Analisa Sensitifitas Dua Peubah 29 3.1.4 Sensitifitas Pada Probabilitas 32 3.1.5 Nilai Ekspektasi dari Permasalahan 37 Cendrawasih Airways
3.1.6 Toleransi Resiko (R) untuk Cendrawasih Airways 39 3.1.7 Menetukan Ekivalen Tetap (NET) 42
Bab 4 Kesimpulan 47
4.1 Kesimpulan 47
4.2 Sarn 47
DAFTAR TABEL
Halaman
Tabel 2.1 Produk yang dapat Dihasilkan 10
Tabel 2.2 Distribusi Kemungkinan Tingkat Penjualan 10 Tabel 3.1 Variabel Input dan Batasan Nilai yang Mungkin 22 untuk Keputusan Pembelian CN-235 oleh Cendrawasih Airways tabel 3.2 Batas bawah dan batas atas keuntungan yang didapat
untuk tiap variabel 27
DAFTAR GAMBAR
Halaman Gambar 2.1 Diagram Keputusan dalam Menghadapi Penjual 8
Sabun Cuci
Gambar 2.2 Diagram Keputusan 11
Gambar 2.3 Kurva Utility untuk contoh 2.1 13 Gambar 3.3 Diagram Tarnado Untuk permasalahan di 27
Cendrawasih Airways
Gambar 3.4 Grafik Sensitifitas Dua Variabel Kapasitas dari 31 Penerbangan Terjadwal dan Biaya Pengoperasian Gambar 3.5 Diagram Keterkaitan dari Cendrawasih Airways 35 Gambar 3.6 Pohon Keputusan untuk Cendrawasih Airways 34
dengan Ketidakpastian untuk Tiga Variabel
Gambar 3.7 Pohon Keputusan untuk Cendrawasih Airways 35 dengan Ketidakpastian untuk Tiga Variabel dengan p = 0,5 dan s = 0,8r
Gambar 3.8 Grafik Sensitifitas Dua Variabel untuk 37 Cendrawasih Airways
Gambar 3.9 Pohon Keputusan untuk Cendrawasih Airways 38 dengan Ketidakpastian untuk Tiga Variabel dengan p = 0,5 dan s = 0,8r
Gambar 3.10 Pohon Keputusan untuk Cendrawasih Airways 41 dengan Memasukkan Utility
Gambar 3.11 Pohon Kcputusan yang Sudah Disederhanakan 42
Gambar 3.12 Grafik Sensitifitas Resiko 46
ABSTRAK
STUDY OF DECISION MAKING USING SENSITIVITY ANALYSIS WITH UTILITY EKSPONENSIAL FUNCTION
ABSTRACT
BAB 1
PENDAHULUAN
1.1Latar Belakang
Pembuatan keputusan pada umumnya berarti memilih satu dari beberapa alternatif yang
tersedia, minimal tersedia dua alternatif yang harus dipilih. Menghadapi dua macam
pilihan, pembuatan keputusan dapat menyatakan persepsinya terhadap kedua alternatif
tersebut yaitu alternatif mana yang lebih ia sukai atau mungkin juga kedua alternatif
tersebut sama-sama disukainya.
Dalam setiap pembuatan keputusan, pembuatan keputusan biasanya akan selalu
berhadapan dengan lingkungan, dimana salah satu karakteristiknya yang paling
menyulitkan dalam proses pembuatan keputusan adalah ketidakpastian di masa depan.
Keputusan yang dibuat setiap individu dalam menghadapi suatu permasalahan
bisa berbeda-beda, tergantung sikap individu tersebut dalam menghadapi resiko yang
mungkin terjadi di dalam permasalahan tersebut. Setiap pribadi mempumyai sikap
sendiri-sendiri terhadap resiko. Ada pribadi yang cenderung untuk menghindari resiko.
Ada pribadi yang lebih memilih untuk mengambil resiko dan juga ada yang netral (tidak
merasa berbeda dalam memilih diantara pilihan yang ada). Dan untuk mengambil
keputusan dengan memasukkan keputusan faktor resiko digunakan nilai ekivalen tetap.
Nilai ekivalen tetap dari suatu kejadian tak pasti adalah suatu nilai tertentu
dimana pembuat keputusan merasa tidak berbeda antara menerima hasil yang tidak
pasti, atau menerima dengan kepastian sesuatu hasil dengan nilai tertentu.
Setelah ditemukan suatu strategi yang optimal dalam suatu permasalahan,
seorang pembuat keputusan harus mengetahui sikapnya dalam menghadapi resiko;
apakah dia seorang penghindar resiko atau pengambil resiko. Seorang penghindar resiko
Artinya, alternatif mana saja yang akan dipilih untuk dapat terhindar dari resiko.
Demikian juga apabila seorang pembuat keputusan adalah pengambil resiko.
Analisa sensitifitas juga disebut sebagai post optimality analysis, karena analisa
ini dilakukan setelah dicapainya suatu strategi yang dianggap optimal. Melalui analisa
sensitifitas, seorang pembuat keputusan dapat mengetahui berapa besar perubahan
angka keputusan dengan mengubah-ubah preferensi terhadap resiko ke dalam fungsi
utilitas eksponensial.
Penerapan nilai ekivalen tetap tidaklah sukar untuk kejadian tak pasti yang
masih sederhana. Tetapi bila kejadian tak pasti yang terlibat semakin kompleks,
penetapan nilai ekivalen tetap secara langsung menjadi sulit. Oleh sebab itu menghitung
nilai ekivalen tetap tidak dapat dilakukan secara langsung, melainkan dengan
melakukan penjajagan terhadap preferensi terhadap pembuat keputusan terhadap resiko
yang didapat dari utility. Hasil penjajagan ini digambarkan dalam suatu kurva yang
disebut kurva utility. Pada umumnya skala utility dinyatakan antara 0 dan 1; dimana
skala utility = 1 menyatakan keadaan atau nilai yang paling disukai dan 0 menyatakan
keadaan atau nilai yang paling tidak disukai. Karena setiap individu mempunyai
preferensi tersendiri dalam menghadapi resiko, maka kurva utility tiap indivdu tidak
akan persis sama.
1.2 Identifikasi Masalah
Di dalam analisis ini akan dicari indikator-indikator atau variabel-variabel yang sangat
sensitif yang mempengaruhi hasil keputusan
Menerapkan analisis keputusan menggunakan analisis sensitifitas dengan fungsi utility
eksponensial untuk mengambil keputusan dalam suatu perusahaan atau organisasi untuk
mengidentifikasi parameter penting yang bisa membuat perubahan pada laba.
1.4 KONTRIBUSI PENELITIAN
• Berguna untuk pengambil keputusan, misalnya pada perbankan
• Lanjutan untuk pengembangan ilmu probabiliy
1.5 METODE PENELITIAN
• Menentukan lingkup keputusan
• Menentukan siklus analisa keputusan
• Membuat diagram keputusan
• Penentuan pilihan
BAB 2
LANDASAN TEORI
2.1. Beberapa Definisi
Kejadian tak pasti adalah kejadian yang munculnya tidak pasti sehingga tidak bisa
diduga terlebih dahulu. Contohnya pada seperti pelemparan sebuah dadu, orang tidak
dapat menduga dengan pasti sisi dadu mana yang akan muncul.
Ruang hasil adalah himpunan dari seluruh hasil yang mungkin muncul dari suatu
kejadian tak pasti. Contohnya seperti pelemparan sebuah dadu, ruang hasilnya adalah 1,
2, 3, 4, 5, dan 6.
Dua kejadian atau lebih disebut saling bertentangan bila kejadian-kejadian
tersebut tidak akan pernah muncul secara bersamaan. Misalnya dalam pelemparan
sebuah mata uang, munculnya gambar atau angka adalah kejadian yang saling
bertentangan (mutually exclusive), atau pada pelemparan sebuah dadu, munculnya dadu
mata 6 dan 3 tidak akan bisa terjadi secara bersamaan.
Kumpulan kejadian dikatakatan bersifat lengkap apabila kumpulan kejadian
tersebut merupakan suatu ruang hasil yang lengkap. Hal ini berarti bahwa jika suatu
percobaan dilakukan, maka hasil yang muncul adalah salah satu dari kejadian yang ada
dalam himpunan. Contohnya dalam hal pelemparan sebuah dadu. Kumpulan 1, 2, 3, 4,
5, dan 6 adalah lengkap. Bila sebuah dadu dilempar, maka salah satu dari kumpulan
angka tersebut pasti akan muncul.
Ada dua pernyataan dasar berkenaan dengan nilai kemungkinan, yaitu:
1. Besarnya nilai kemungkinan bagi munculnya suatu kejadian adalah selalu di
antara nol dan satu. Pernyataan ini dapat ditulis dengan:
( )
1dimana P(A) menyatakan nilai kemungkinan bagi munculnya kejadian A.
2. Jumlah nilai kemungkinan dari seluruh hasil yang mungkin muncul adalah satu.
Jadi, jika suatu ruang hasil yang bersifat lengkap dinyatakan dengan W, maka
jumlah kemungkinan seluruh anggota ruang hasil tersebut adalah satu, atau
dituliskan dengan:
( )
∑
P wi =1 atau P(W) = 1 dimana Wi menyatakan anggota dari ruang hasil.2.1.1 Teorema Bayes
Pengambilan keputusan dalam kondisi ketidakpastian dapat menggunakan teorema
Bayes, dengan kriteria nilai harapan dengan iteratif sehingga ketelitian dan pendekatan
ke keadaan sesungguhnya bisa tercapai, dimana peluangnya mempunyai nilai antara nol
dan satu.
Teorema Bayes yang digunakan pada proses pengambilan keputusan tidak
terlepas dari teori peluang sebagai konsep dasar. Teorema Bayes dikenal sebagai rumus
dasar untuk peluang besyarat yang tidak bebas.
Proses pengambilan keputusan dengan menggunakan kriteria harga harapan
sering disebut sebagai prosedur keputusan Bayes tanpa data. Meskipun kriteria harga
harapan mudah pemakaiannya tetapi mengandung banyak kelemahan diantaranya
ditemukan sumber informasi yang pada umumnya didasarkan pada pertimbangan
subjektif. Oleh karena itu, pengambilan keputusan sering menyadari perlunya tambahan
informasi yang pada umumnya didasarkan pada data sesungguhnya guna membantu
proses pengambilan keputusan. Biasanya ada informasi yang menguntungkan dan ada
informasi yang merugikan. Oleh karena itu, perlu dilakukan seleksi cermat untuk
menentukan informasi yang dapat ditentukan taksiran yang yang lebih realistis dari
Syarat-syarat Teorema Bayes bisa digunakan untuk menentukan pengambilan
keputusan, yaitu:
• Berada pada kondisi ketidakpastian (adanya alternatif tindakan)
• Peluang Prior diketahui dan peluang Posterior dapat ditentukan
• Peluangnya mempunyai nilai antara nol dan satu
Dalil Bayes
Bila A1, A2, …, An adalah kejadian yang saling bertentangan dan lengkap, dan B adalah
kejadian dalam ruang hasil tersebut dengan P
( )
B ≠0 ; i = 1, 2, 3, …, n2.1.2 Kemungkinan Bersyarat
Kemungkinan bersyarat adalah kemungkinan suatu kejadian A terjadi apabila
sebelumnya terlah terjadi kejadian B, atau bisa juga sebaliknya kemungkinan terjadinya
kejadian B apabila sebelumnya telah terjadi kejadian A.
Untuk menghitung nilai kemungkinan bersyarat, digunakan definisi sebagai
berikut:
Definisi
Untuk kejadian A dan B dimana P
( )
B ≠0; maka nilai kemungkinan bersyarat kejadianA jika kejadian B diketahui, ditulis sebagai P A B , adalah:
(
)
Hampir setiap saat manusia membuat atau mangambil keputusan dan melaksanakannya,
dengan asumsi bahwa segala tindakan yang diambil dilakukan secara sadar dan
merupakan hasil proses pengambilan keputusan dalam pikirannya, sehingga sebenarnya
manusia sudah terbiasa dan berpengalaman dalam membuat keputusan. Tetapi proses
Sebuah contoh situasi pembuatan keputusan yang paling sederhana adalah
situasi bagi seorang pegawai sewaktu mulai keluar dari runmah menuju ke kantor, salah
satu contoh pembuatan keputusannya adalah saat pegawai tersebut perlu memutuskan
rute yang sebaiknya diambil. Beragam pemikiran ada didalam benak pegawai tersebut,
berkenaan dengan perempatan yang macet, jalan yang padat dengan becak atau lubang,
atau pintu lintasan kereta api. Semua hal ini mempengaruhi keputusan yang dibuat
dalam beberapa detik tersebut. Keputusan dilaksanakan dalam bentuk perjalanan
melalui rute terpilih tersebut sampai dengan ke kantor. Bila kemudian keputusan
tersebut dievaluasi maka kemungkinan pertanyaan yang muncul adalah “puaskah saya”
atau “bagaimana kalau rute yang lain yang saya ambil” atau “aduh, saya terlambat lagi”.
Semua kemungkinan hasil evaluasi tersebut tidak akan memberikan konsekuensi
apapun selama keputusan yang dibuat tidak perlu dipertanggungjawabkan kepada orang
lain, atau selama prosesnya tidak perlu diminta pengertian dari pihak lain. Apabila tidak
demikian halnya, maka masalah kecil di atas dapat menjadi lebih rumit, karena di dalam
pertanggungjawabannya perlu diuraikan sasaran seperti apa yang ingin dicapai melalui
perjalanan tersebut, alternatif rute yang dapat dipilih, informasi berkenaan dengan
kepadatan dan kualitas jalan pada setiap rute, dan sebagainya. Selain itu, perlu
dijelaskan pula kriteria seperti apa yang digunakan untuk dapat memilih suatu alternatif
rute dikaitkan dengan konsekuensi yang akan diperoleh pada akhir perjalanan. Ini
semua perlu diolah melalui suatu proses yang rasional untuk memperoleh jawaban,
yaitu alternatif rute terbaik guna tercapainya sasaran.
Jelas bahwa untuk permasalahan rute perjalanan dari rumah ke kantor, suatu
proses yang rasional akan kurang bermanfaat, karena secara intuitif saja jawaban akan
dapat diperoleh. Dan mungkin beda 10 menit dengan rute terbaik (bila dapat diketahui)
tidak ada artinya dibandingkan dengan rumitnya perhitungan apabila proses rasional
akan diikuti. Tetapi untuk hal-hal yang besar, untuk keputusan-keputusan yang
dianggap sangat penting, perlu dicari cara yang lebih baik untuk membuat keputusan.
Berikut adalah beberapa cara dalam menentukan pilihan yang digunakan dalam
2.2.1 Pilihan Langsung
Salah satu cara yang umum digunakan dalam menentukan pilihan di atas diantara dua
alternatif yang ada adalah dengan membandingkan keduanya secara langsung,
kemudian menentukan pilihan berdasarkan intuisi.
Sebagian besar keputusan-keputusan yang dibuat dalam kehidupan adalah
berdasarkan intuisi. Manusia mempertimbangkan pilihan-pilihan yang dihadapinya
berdasarkan informasi yang telah dimilikinya sesuai dengan preferensinya terhadap
resiko tindakan yang menunjukkan keputusan terbaik yang dipilihnya.
Berikut ini adalah contoh pengambilan keputusan secara langsung
(menggunakan intuisi).
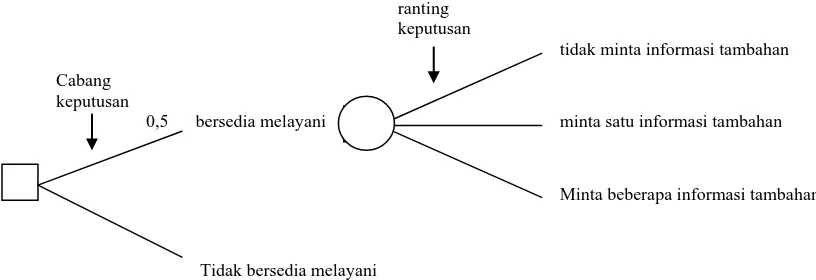
Contoh 2.1 Pengambilan Keputusan Secara Langsung
Seorang wanita penjual barang dari rumah ke rumah menawarkan suatu produk sabun
cuci, maka calon pembeli akan dihadapkan pada dua pilihan; yaitu bersedia atau tidak
melayaninya.
0,5
0,5
2.1 Diagram Keputusan dalam Mnghadapai Penjual Sabun Cuci
Kalau calon pembeli bersedia melayani wanita penjual tersebut maka calon
pembeli tersebut harus memutuskan apakah perlu meminta informasi lebih lanjut dari
wanita tersebut. Pilihan yang tersedia antara lain : tidak meminta informasi tambahan
tetapi langsung membeli (e0), meminta satu informasi tambahan (e1), atau minta
beberapa informasi tambahan (e2). Sekarang ini diagram arus keputusan menjadi lebih
rumit :
Bersedia melayani
ranting
Pengambilan keputusan secara langsung dapat diterapkan untuk kejadian tak pasti yang
sederhana. Tetapi bila kejadian tak pasti yang dilibatkan semakin rumit, sehingga
penerapan pengambilan keputusan secara langsung tidak dapat atau sukar untuk
dilakukan, maka cara yang sering digunakan adalah dengan menggunakan nilai
ekspektsi sebagai dasar pemilihan.
Hasil yang dicerminkan dalam suatu distribusi kemungkinan dapat
dinyatakan dalam harga rata-rata atau nilai ekspektasi, kemudian pembuat keputusan
dapat memilih berdasarkan nilai ekspektasi yang tertinggi. Dengan kata lain, nilai
ekspektasi adalah penjumlahan dari hasil kali probabilitas dengan konstribusinya
(biasanya dalam satuan uang)
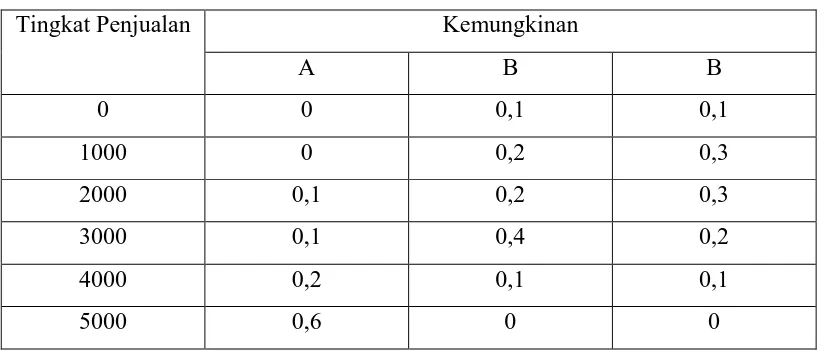
Contoh 2.2 Pangambilan Keputusan Menggunakan Nilai Ekspektasi
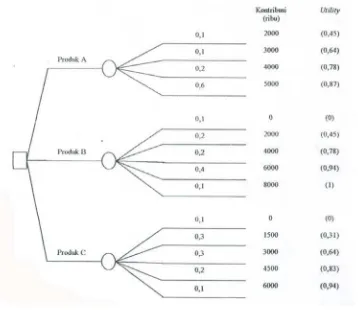
Seorang menajer produksi diharapkan untuk memilih satu diantara tiga jenis produk
baru yang akan dipasarkan. Produk pendahuluan untuk ketiga produk tersebut telah
selesai dilakukan, demikian pula studi tentang harganya. Hasilnya dapat terlihat pada
table 2.1. Selanjutnya dari penelitian pasar dapat pula diketahui distribusi kemungkinan
terlihat pada Tabel 2.2. dan selain itu pimpinan perusahaan telah memutuskan bahwa
hanya satu produk baru dapat dipasarkan.
Tabel 2.1 Produk yang Dapat Dihasilkan
Produk Harga
(unit)
Ongkos
(unit)
Konstribusi
(unit)
A Rp. 2500 Rp. 1500 Rp. 1000
B Rp. 6000 Rp. 4000 Rp. 2000
C Rp. 3750 Rp. 2250 Rp. 1500
Tabel 2.2 Distribusi Kemungkinan Tingkat Penjualan
Tingkat Penjualan Kemungkinan
A B B
0 0 0,1 0,1
1000 0 0,2 0,3
2000 0,1 0,2 0,3
3000 0,1 0,4 0,2
4000 0,2 0,1 0,1
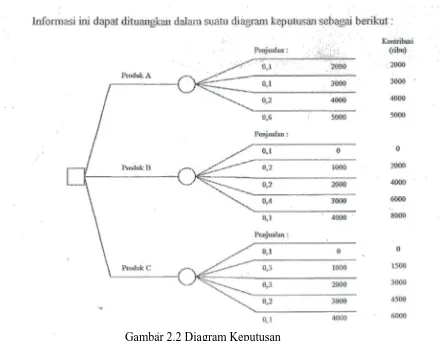
Gambar 2.2 Diagram Keputusan
Untuk contoh di atas, nilai ekspektasi untuk masing-masing produk adalah :
Produk A :
Nilai ekspektasi = (0,1) x (Rp 2.000) + (0,1) x (Rp 3.000) + (0,2) x (Rp 4.000)
+ (0,6) x (Rp. 5.000) = Rp. 4.300 (ribu)
Produk B :
Nilai ekspektasi = (0,1) x (0) + (0,2) x (Rp 2.000) + (0,2) x (Rp 4.000) + (0,4)
x (Rp. 6.000) + (0,1) + (Rp. 8.000) = Rp. 4.400 (ribu)
Produk C :
Nilai ekspektasi = (0,1) x (0) + (0,3) x (Rp 1.500) + (0,3) x (Rp 3.000) + (0,2)
x (Rp. 4.500) + (0,1) + (Rp. 6.000) = Rp. 2.850 (ribu)
Dengan membandingkan nilai ekspektasi ini, maka produk B yang dipilih
karena produk B mempunyai nilai ekspektasi tertinggi.
Membuat keputusan dengan mendasarkan kepada nilai ekspektasi tidaklah sulit. Akan
tetapi cara ini tidak dapat menunjukkan alternatif yang mana yang paling disukai.
Karena kriteria nilai ekspektasi dalam persoalaan ini tidak mencerminkan apa yang
diinginkan oleh sebahagian orang. Hal ini disebabkan karena nilai ekspektasi belum
mencakup faktor resiko. Sedangkan faktor resiko penting untuk diperhitungkan, karena
sikap orang terhadap resiko berbeda-beda.
Untuk menentukan pilihan dengan memasukkan faktor resiko adalah dengan
menggunakan nilai Ekivalen Tetap. Nilai Ekivalen Tetap (NET) dari suatu kejadian tak
pasti adalah suatu nilai tertentu dimana pembuat keputusan merasa tidak berbeda antara
menerima hasil yang dicerminkan dalam ketidakpastian tersebut, atau menerima
dengan kepastian suatu hasil dengan nilai tertentu. Besar nilai inilah yang disebut
dengan Nilai Ekivalen Tetap. Secara singkat dapat dikatakan bahwa Nilai Ekivalen
Tetap adalah nilai batas dimana pembuat keputusan bersedia untuk menukar alternatif
yang dipilih.
2.2.4 Utillity
Utility adalah preferensi pembuat keputusan terhadap suatu nilai dengan
mempertimbangkan faktor resiko. Hasil penjajagan preferensi pembuatan keputusan
terhadap suatu nilai dengan mempertimbangkan faktor resiko tersebut dinotasikan
dalam suatu kurva yang disebut kurva preferensi atau kurva Utility. Kurva utility
memberikan sebuah cara untuk mengkonversikan suatu satuan (misalnya mata uang
Rupiah) menjadi unit utility.
2.2.4.1 Kurva Utility
Kurva Utility menggambarkan bagaimana utility atau preferensi suatu nilai bagi
skala utility = 1 menyatakan keadaan atau nilai yang paling disukai dan 0 menyatakan
keadaan atau nilai yang paling tidak disukai.
Gambar 2.3 Kurva Utility untuk Contoh 2.1
2.2.4.2 Ekspektasi Utility
Karena utility merupakan pencerminan dari preferensi pembuat keputusan; maka untuk
melakukan pemilihan, pembuat keputusan mendasarkan pada ekspektasi utility dari
alternatif-alternatif yang ada, dan memilih berdasarkan ekspektasi utility yang tertinggi.
Sebagai contoh, dalam menghadapi situasi keputusan seperti pada Contoh 2.1 di
Gambar 2.4 Diagram Keputusan dengan Memasukkan Utility
Untuk mencari Utility dari masing konsrtibusi laba seperti pada diagram keputusan di
atas digunakan kurva utility (Gambar 2.4). setelah itu dapat dihitung Ekspektasi Utility
(EU adalah hasil kali probabilitas dengan utility-nya ) dari masing-masing alternatif,
sehingga didapatkan :
Alternatif A :
EUA = (0,1) x (0,45) + (0,1) x (0,6) + (0,2) x (0,78) + (0,6) x (0,87)
= 0,79
Alternatif B :
EUB = (0,1) x (0) + (0,2) x (0,45) + (0,2) x (0,78) + (0,4) x (0,94) + (0,1) x (1) =
0,72
Alternatif C :
EUC = (0,1) x (0) + (0,3) x (0,31) + (0,3) x (0,64) + (0,2) x (0,83) + (0,1) x (0,94)
2.3 Sikap Menghadapi Resiko
Sikap seseorang dalam menghadapi suatu persoalan yang mengandung resiko pada
dasarnya dapat dibedakan menjadi tiga, yaitu : sikap menghindar resiko, netral atau
sikap mengambil resiko.
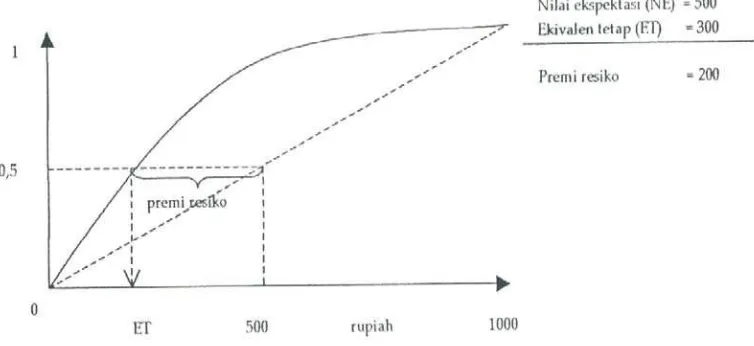
2.3.1 Sikap penghindar Resiko
Bila seseorang bersifat sebagai penghindar resiko maka premi resikonya akan selalu
positif. Dan semakin besar premi resiko tersebut, maka sifat penghindar resiko orang
tersebut akan makin besar pula. Karena sifat penghindar resiko dinyatakan dengan
premi resiko yang positif, maka kurva utility-nya tersebut akan selalu terletak disebelah
kiri atas dari garis netral. Dengan kata lain kurva utility-nya berbentuk concave.
Gambar 2.5 Kurva Utility bagi Penghindar Resiko
Sebuah fungsi Utility bias dispesifikasikan seperti grafik di atas, ataupun dalam
sebuah tabel. Fungsi Utility secara matematis dalapat dinyatakan dlam bentuk
U(x) = 1 – e-x/R 2.3.2 Sikap Netral
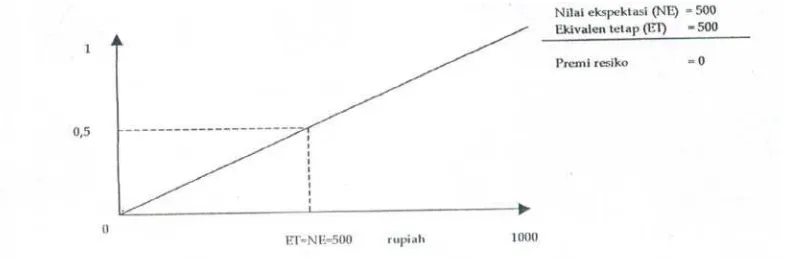
Dilain pihak bila seseorang menyatakan bahwa ekivalen tetap sebuah lotere sama
dengan nilai ekspektasinya, maka dia mempunyai sikap yang netral dalam menghadapi
resiko. Dalam hal ini maka premi resikonya adalah nol. Dan kurva Utilitynya
digambarkan sebagai garis lurus.
Gambar 2.6 Kurva Utility Bagi Sikap Netral
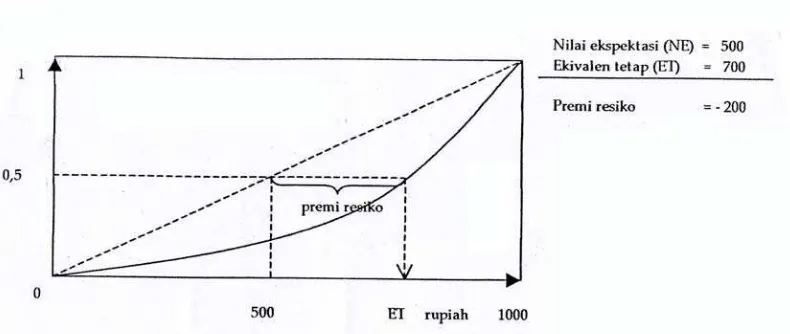
2.3.3 Sikap Penggemar Resiko
Seseorang yang memiliki sifat sebagai penggemar resiko, maka ekivalen tetap atas suatu
kejadian tak pesti baginya akan lebih besar dari pada nilai ekspektasi dari kejadian
tersebut. Untuk orang ini maka premi resikonya adalah negatif, artinya dia
mengharapkan suatu tambahan dari nilai ekspektasi, agar bersedia melepaskan lotere
Gambar 2.7 Kurva Utiliy bagi Pengambil Resiko
2.4 Toleransi Resiko dan Fungsi Utility Eksponensial
Penaksiran utility dapat digunakan untuk menaksir sebuah fungsi utility secara subjektif.
Serta dapat digunakan untuk berbagai situasi, meskipun hal tersebut melibatkan
sejumlah penaksiran. Sebuah alternatif pendekatan berguna untuk mendasarkan
penaksiran sebuah fungsi matematika khusus. Fungsi utility eksponensial sebagi berikut
:
U(x) = 1 – e-x/R
Dalam fungsi utility eksponensial, R disebut dengan toleransi resiko. Semakin
besar nilai R maka akan semakin mendatar pula fungsi utility eksponensialnya,
BAB 3
PEMBAHASAN
3.1 Analisis Sensitifitas
Analisis sensitifitas adalah sebuah pendekatan pemodelan yang dilakukan untuk
mengidentifikasi parameter yang penting dalam sebuah pohon keputusan. Sebagai
konsekuensi hasil dari suatu analisis sensitifitas, seorang pembuat keputusan mungkin
harus mempertimbangkan lebih banyak informasi tentang parameter yang divariasikan,
kemudian efek pada pohon keputusan diperiksa.
Salah satu alasan mendasar mengapa analisis sensitifitas sangat penting bagi
seorang pembuat keputusan adalah karena masalah-masalah yang nyata terdapat di
dalam suatu dunia yang dinamis, terus berubah. Harga bahan baku terus berubah,
permintaan terhadap berbagai jenis produk mengalami naik turun, perusahaan yang
harus harus membeli mesin baru untuk menggantikan yang lama, harga saham yang
fluktuatif, rotasi pegawai yang terus berlangsung, dan lain sebagainya. Analisa
sensitifitas mampu menyediakan informasi yang dibutuhkan untuk merespon
perubahan-perubahan seperti yang disebutkan di atas tanpa harus merevisi solusi
optimal yang sudah ada. Tidak ada prosedur analisa sensitifitas yang terbaik untuk suatu
analisa keputusan. Analisa sensitifitas adalah suatu bagian terpisah dari proses
pengambilan keputusan.
Contoh : Problema Cendrawasih Airways
Sara thoriq, pemilik Cendrawasih Airways telah lama berencana untuk mengembangkan
perusahaan pengangkutannya. Saat ini dirasakan adalah saat yang tetap untuk memulai
karena salah seorang temannya telah memperkenalkannya pada seorang pemilik
menjual pesawatnya. Ada banyak hal yang harus dipertimbangkan sebelum mengambil
keputusan, dan Sara Thotiq merasa sedikit kesulitan dalam menyelesaikannya.
Cendrawasih Airways mempunyai tiga buah pesawat udara bermesin ganda.
Dengan armada ini, Cendrawasih Airways melayani jalur penerbangan carter dan juga
jalur penerbangan terjadwal, khususnya untuk komunitas masyarakat di daerah timur
Indonesia. Rute yang ditempuh adalah rute yang sebelumnya memang belum terjangkau
oleh perusahan pengangkutan lain. Rata-rata 50 % penerbangan rata-rata 1,5 jam
perjalanan dan jarak kurang lebih 483 km. Sisa 50 % lagi adalah penerbangan carter.
Kombinasi dari penerbangan carter dan penerbangan terjadwal yang singkat sudah
terbukti menguntungkan. Thoriq ingin sekali memperbaiki tingkat pelayanan, terutama
pada jalur penerbangan carter, tetapi hal ini terasa mustahil untuk dilakukan tanpa
adanya armada tambahan.
Pemilik penerbangan kecil yang telah dikenalkan oleh temannya tersebut
menawarkan sebuah CN-235 dengan harga Rp. 950.000.000,- dan Thoriq menyadari
kalau dia hanya mampu membeli CN -235 tersebut antara Rp. 850.000.000,- dan
900.000.000 regulasi FAA. Mesinnya masih dapat dikatakan baru, dengan
pengoperasian hanya 150 jam jarak service menyeluruh yang terakhir. Lebih lanjut lagi,
karena telah digunakan oleh perusahaan penerbangan kecil yang mengkhususkan pada
komunikasi yang dibutuhkan oleh Cendrawasih Airways. Ada lima tempat duduk yang
sangat lega untuk penumpang, ditambah ruangan untuk menyimpan barang-barang
penumpang. Kecepatan CN-235 tersebut rata-rata 175 mil laut per jam (knot), atau 201,
4 (mph) atau sekitar 324 km per jam, biaya perawatan, gaji pilot. Biaya tetap tahunan
termasuk asuransi (Rp. 200.000.000,-) dan beban bunga Thoriq sudah memperkirakan
bahwa dia akan mengajukan pinjaman sekitar 40% dari modal yang diperlukan, dan
Thoriq menyadari bahwa tingkat suku bungan pinjaman sekitar 2 % di atas tingkat suku
bungan dasar (tepatnya 9,5 %, dan dapat berubah sewaktu-waktu). Berdasarkan
pengalamannya di Cendrawasih Airways, Thoriq memperkirakan bahwa tarif yang
dapat dikenakan untuk penerbangan carter adalah antara Rp. 3.000.000,- sampai Rp.
3500.000,- per jam, atau harga tiket rata-rata sekitar Rp. 1.000.000,- per orang per jam
kapasitasnya pasti terisi. Dia berharap dapat mengoperasikan armadanya sampai dengan
1000 jam , tapi Thoriq menyadari kalau angka 800 jam akan lebih masuk akal. Dahulu,
rata-tara 50 % dari penerbangan adalah penerbangan carter, tapi sekarang dia ingin
memperbesar persentasenya jika memungkinkan.
Pemilik CN-235 mengatakan pada Thoriq bahwa rencana awalnya dia berencana
menjual pesawat tersebut secara tunai. Tetapi dia juga memberikan pilihan lain yaitu
dengan melakukan pembayaran secara dicicil dalam jangka waktu satu tahun, tentunya
dengan harga yang sedikit lebih mahal jika dibandingkan dibayar secara tunai (dalam
jangka waktu pencicilan tersebut, pemilik lama tetap akan mengoperasikan pesawat
tersebut.) Walaupun mereka belum mendapatkan harga yang telah disepakati untuk opsi
kedua, dalam diskusi yang telah terjadi membuat Thoriq yakin kalau opsi yang kedua
akan memerlukan biaya tambahan antara Rp. 25.000.000,- sampai 40.000.000,-. Selain
pilihan itu memberi pesawat, Thoriq juga mempunyai pilihan berinvestasi yang lain
yaitu menginvestasikan modalnya pada pasar uang dengan harapan tingkat
pengembalian mencapai 8 % dalam setahun. (dengan asumsi suku bunga tidak berubah
dalam 3 tahun).
Dalam mempertimbangkan semua opsi yang ada, Thoriq menyadari bahwa
banyak angka-angka yang di gunakan hanyalah angka-angka penaksiran belaka. Ada
beberapa diantara angka-angka tersebut yang sepenuhnya berada di bawah kendalinya
(seperti seberapa besar jumlah yang akan dibayarkan dan seberapa besar tarif atau harga
tiket yang akan dikenakan), semenntara untuk yang lain seperti biaya asuransi atau
biaya pengoperasian tidak dapat dikendalikannya.
Dalam permasalahan pengambilan keputusan ini, alternatif yang ada adalah
membeli pesawat udara secara tunai, membeli dengan opsi yang diberikan oleh pemlik
awal atau tidak sama sekali. Walaupun masih ada berbagai tujuan objektif lainnya,
seperti pertumbuhan atau perkembangan perusahaan yang mempengaruhi komunitas
masyarakat, dalam konteks menentukan apakah jadi membeli armada pesawat baru,
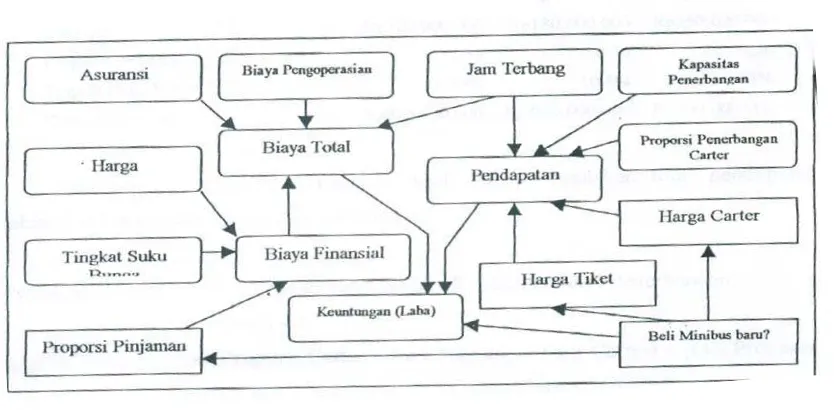
akan sangat berbalasan bagi Thoriq untuk fokus pada satu tujuan, yaitu memaksimalkan
berbagai jenis kuantitas, seperti biaya pengoperasian, dan sebagainya. Hal ini dapat
diperhatikan pada diagram di bawah ini yang menjelaskan tentang alur keuangan
Cendrawasih Airways.
Gambar 3.1 Diagram Keterkaitan Cendrawasih Airways
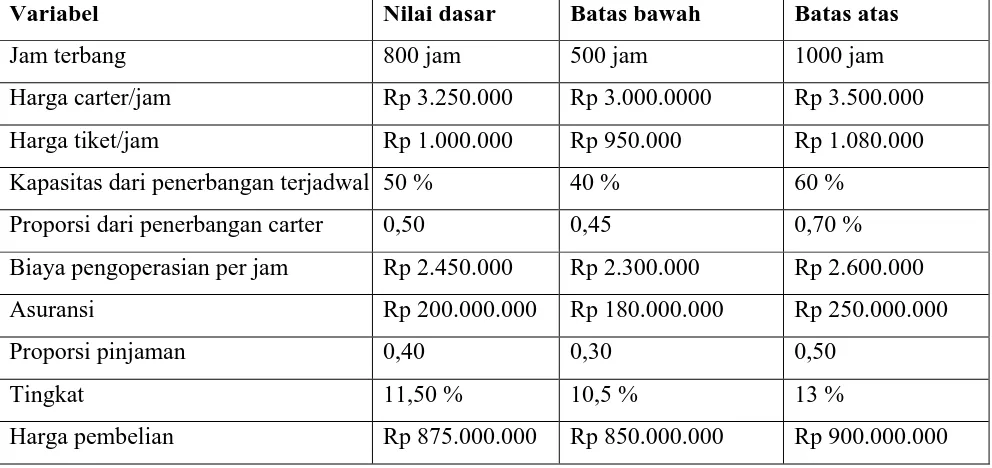
Tabel 3.1 menyediakan data yang menjabarkan tentang variabel-variabel yang
terlibat dalam proses keputusan. Pada tabel ini juga terdapat angka perkiraan (nilai
dasar) serta batas-batas dan batas bawah yang masuk akal. Batas atas dan batas bawah
mewakili hasil pemikiran Thoriq mengenai seberapa tinggi dan seberapa rendah nilai
yang mungkin dicapai oleh masing-masing variabel.
Kolam “ Nilai dasar” pada diagram 3.1 mengindikasikan perkiraan awal Thoriq
untuk 10 variabel input. Nilai dasai ini bisa digunakan untuk memperkirakan
Tabel 3.1 Variabel Input dan Batasan Nilai yang Mungkin untuk Keputusan Pembelian CN-235 oleh Cendrawasih Airways
Variabel Nilai dasar Batas bawah Batas atas
Jam terbang 800 jam 500 jam 1000 jam
Harga carter/jam Rp 3.250.000 Rp 3.000.0000 Rp 3.500.000
Harga tiket/jam Rp 1.000.000 Rp 950.000 Rp 1.080.000
Kapasitas dari penerbangan terjadwal 50 % 40 % 60 %
Proporsi dari penerbangan carter 0,50 0,45 0,70 %
Biaya pengoperasian per jam Rp 2.450.000 Rp 2.300.000 Rp 2.600.000
Asuransi Rp 200.000.000 Rp 180.000.000 Rp 250.000.000
Proporsi pinjaman 0,40 0,30 0,50
Tingkat 11,50 % 10,5 % 13 %
Harga pembelian Rp 875.000.000 Rp 850.000.000 Rp 900.000.000
Kuntungan tahunan merupakan hasil dari penjumlahan total pendapatan tahunan
dikurangi dengan total biaya tahunan :
Pendapatan Total = Pendapatan dari Carter + Pendapatan dari Penerbangan jadwal
= (Proporsi Carter x Jam Terbang x Tarif Carter) + [(1-
Propsorsi Carter) x Jam Terbang x Harga Tiket x Jumlah
Tempat Duduk penumpang x Kapasitas dari Penerbangan
= ( Jam Terbang x Biaya Pengoprasian) + Asuransi + (Harga
x Propporsi Pinjaman x Tingkat Suku Bunga)
= Rp1. 960.000.000 + Rp200.000.000 + (Rp75.000.000 x 0,4
x 11,5%)
= Rp1.96.000.000 + Rp200.0000 + Rp40.250.000
= Rp2.200.250.000,-
Jadi, dengan menggunakan nilai dasar, keuntungan tahunan Thoriq diperkirakan
sebesar : Rp2.200.000.000,- Rp2.200.250.000,- = Rp99.750.000,-. Dengan
memperkirakan bahwa harga beli pesawat yang mampu dibayar oleh Thoriq adalah
Rp75.000.000,- seperti yang telah disebutkan diawal, Thoriq memiliki sekitar 60% dari
harga tersebut, yaitu 60% x Rp75.000.000 = Rp525.000.000,-. Diperkirakan laba yang
diperoleh adalah sekitar 19% Dari modal yang sekarang dimilikinya.
3.1.1 Analisa Sensitifitas Satu Variabel
Dalam permasalahan Cendarawasih Airway, analisa sestifitasnya adalah mencari
variabel mana yang benar-benar dapat membuat perbedaan dalam keputusan yang
dibuat. Analisa sestifitas satu variabel dapat menjawab pertayaan seperti : apakah
tingkat suku bunga berbeda dapat mempengaruhi laba yang diterima atau apakah harga
tiket harus direvisi, atau apakah jika jam terbang diubah akan mempengaruhi banyak
pada laba, dan pertanyaan-pertanyaan lain sebagainya.
Jika diperhatikan tabel 3.1 pada baris jam Terbang, dapat dilihat bahwa
sebenarnya Thoriq tidak terlalu yakin seberapa besar nilai yang tepat untuk jam
Terbang, dimana jam Terbang tersebut dapat bervariasi antara 500 – 1.000 jam.
Tentunya perubahan pada jam Terbang dengan keuntungan dapat digunakan sebuah
Grafik Analisa Sesitifitas Satu Variabel seperti terlihat pada Gambar 3.2.
Garis lurus menuju ke arah kanan atas menunjukkan laba yang mungkin
didapatkan jika jam Terbangnya divariasikan 500 – 1.000. Untuk menggambarkan garis
ini, dimasukan nilai jam Terbang yang berbeda-beda kedalam rumus perhitungan di
menanamkan modalnya di pasar uang. Titik di mana kedua garis ini berpotongan adalah
titik di mana kedua alternatif investasi ini menghasilkan laba yang sama
(Rp525.000.000,-), yaitu Terbang sama dengan 664.
Garis tebal mewakili keuntungan maksimum yang dapat diperoleh oleh Thoriq
untuk tiap nilai Jam Terbang yang berbeda-beda, dan segmen yang berbeda dari garis
ini disesuaikan dengan strategi investasi yang digunakan (apakah membeli pesawat baru
atau mendepositokan uangnya). Pada kenyataannya, Thoriq meyakini bahwa dengan
adanya kemungkinan nilai jam terbang berada di bawah atau di atas 664, menunjukkan
bahwa variabel Jam Terbang adalah termasuk variabel yang penting dan perlu
dipertimbangkan secara hati-hati tentang ketidakpastian yang ada dalam variabel ini.
3.1.2 Diagram Tornado
Dengan menggunakan sebuah diagram tornado, dapat dibandingkan banyak variabel
input pada saat yang bersamaan dengan menggunakan Analisa Sensitifitas Satu
Variabel. Misalnya untuk setiap variabel input pada Tabel 3.1 digunakan nilai batas atas
keuntungan (laba). Gambar 3.2 di atas menunjukan variasi profit yang terjadi saat
variabel inputnya divariasikan antara batas atas dan batas bawahnya. Contohnya dapat
dilihat pada variabel Kapasitas Penerbangan Terjadwal.
Pendapatan Total = Pendapatan dari Carter + Pendapatan dari Penerbangan
Terjadwal
= (Proporsi Carter x Jam Terbang x Tarif Carter) + [(1 - Proporsi
Carter) x Jam Terbang x Harga Tiket x Kapasitas Tempat Duduk
Penumpang x Kapasitas Penerbangan Terjadwal]
= (0,5 x 800 x Rp3.250.000) + (0,5 x 800 x Rpl.000.000 x 5 x
0,4)
= Rpl.300.000.000 + Rp800.000.000 =
Rp2.100.000.000,-
Dengan tidak adanya perubahan pada perhitungan total biaya, sehingga biaya
masih diperkirakan sebesar Rp2.200.250.000,-. Perkiraan kerugian adalah hasil
pengurangan antara total pendapatan dengan total kerugian, yaitu Rp2.100.000.000,
-Rp2.200.250.000,- = - Rp l00.250.000,-. Jadi jika semua variabel lain ditetapkan pada
Nilai dasarnya, sementara variabel Kapasitas Penerbangan Terjadwal ditetapkan pada
batas bawah 0,4 maka akan mengakibatkan kerugian sebesar Rp l00.25 0.000,-. Nilai -
Rpl00.250.000,- ini diletakkan di sebelah ujung kiri pada batang yang variabel
Kapasitas Penerbangan Terjadwal. Untuk mencari nilai batas ujung kanannya,
digunakan nilai batas atas dari variabel Kapasitas Penerbangan Terjadwal, dengan
menggunakan rumus yang sama seperti di atas.
Pendapatan Total = Pendapatan dari Carter + Pendapatan dari Penerbangan
Terjadwal
= (Proporsi Carter x Jam Terbang x Tarif Carter) + [(1 - Proporsi
Carter) x Jam Terbang x Harga Tiket x Kapasitas Tempat Duduk
Penumpang x Kapasitas Penerbangan Terjadwal] = (0,5 x 800 x
Rp3.250.000 ) + (0,5 x 800 x Rpl.000.000 x 5 x
= Rpl.300.000.000 + Rpl.200.000.000
= Rp2.500.000.000,-
Dengan tetap menggunakan asumsi bahwa perkiraan biaya dasar tidak berubah,
maka diperkirakan keuntungan sebesar Rp2.500.000.000 - Rp2.200.250.000 =
Rp299.750.000,-. Sehingga nilai batas ujung kanan batangnya pada diagram tornado
adalah Rp299.750.000,-.
Tabel 3.2 Batas Bawah dan Batas atas Keuntungan yang Didapat untuk Tiap Variabel
Variabel Profit Bawah Profit Atas
Jam terbang Rp (100.250.000) Rp 299.750.000
Harga carter/jam Rp (27.750.000) Rp 184.750.000
Harga tiket/jam Rp (20.250.000) Rp 219.750.000
Kapasitas dari penerbangan terjadwal Rp 250.000 Rp 199.750.000
Proporsi dari penerbangan carter Rp 49.750.000 Rp 119.750.000
Biaya pengoperasian per jam Rp 49.750.000 Rp 179.750.000
Asuransi Rp 69.750.000 Rp 219.750.000
Proporsi pinjaman Rp 89.687.500 Rp 109.812.500
Tingkat Rp 94.500.000 Rp 103.250.000
Harga pembelian Rp 98.600.000 Rp 100.900.000
Jika digunakan cara yang sama untuk setiap variabel yang ada, akan didapat data
Diagram Tarnado untuk permasalahan di Cendrawasih Airyas
Gambar 3.3 Diagram Tornado Untuk permasalahan di Cendrawasih Airways
Panjang dari batang untuk setiap variabel yang diberikan mewakili perluasan
dari keuntungan yang mungkin didapat. Grafik tersebut disusun sedemikian rupa
sehingga variabel yang sangat sensitif; yaitu variabel dengan batang terpanjang, terletak
pada bagian atas, dan yang paling tidak sensitif diletakkan pada bagian bawah. Dengan
susunan batang yang diletakkan berdasarkan panjang ini, dapat dengan mudah dilihat
mengapa grafik ini disebut dengan Diagram Tornado.
Garis vertikal yang memotong sumbu x = 42.000.000 mewakili nominal yang
didapat oleh Thoriq apabila dia menanamkan modalnya sebesar Rp.525.000.000,-pada
pasar uang dengan tingkat pengembalian sebesar 8%. Jika dia tidak yakin keuntungan
yang mungkin akan diperolehnya lebih besar dari Rp42.000.000,- maka mungkin
sebaiknya dia tidak perlu membeli CN-235 tersebut.
Ada banyak hal yang menarik yang dapat dilihat dari Gambar 3.3 di atas.
Contohnya, ketidakpastian yang akan dihadapi Thoriq mengenai Kapasitas Penerbangan
Terjadwal ternyata sangatlah penting. Sementara sebaliknya, keuntungan tahunan
ternyata tidaklah sensitif terhadap harga pesawat terbang. Diagram Tornado dapat
menunjukkan variabel mana saja yang perlu lebih diperhatikan dan mana yang dapat
sehingga untuk proses analisa lebih lanjut, variabel-variabel di atas dapat diasumsikan
tetap berada pada nilai dasarnya. Sementara Kapasitas Penerbangan Terjadwal, Biaya
Pengoperasian, Jam Terbang dan Tarif Carter mempunyai efek yang besar terhadap
keuntungan tahunan; dimana batang untuk keempat variabel ini memotong garis kritis
42.000.000. Proporsi dari Penerbangan Carter, Harga Tiket, dan Asuransi juga
mempunyai efek yang kuat terhadap laba, tetapi batang dari ketiga variabel ini
semuanya terletak di sebelah kanan garis 42.000.000. Untuk tahapan awal, ketiga
variabel ini dapat diasumsikan tetap pada nilai dasarnya.
Terdapat empat variabel yang sensitif karena yang menjadi benchmark-nya.
adalah investasi di pasar uang dengan asumsi suku bunga tidak berubah sebesar 8%.
Tapi jika benchmark investasi lainnya diubah, misalnya ke dalam bentuk tabungan
dengan tingkat suku bunga 3% pertahun, maka keuntungan yang akan diperolehnya
dalam setahun adalah Rp. 15.750.000,- maka tinggal tiga variabel saja yang diagram
tornadonya berpotongan dengan garis benchmark. Artinya hanya tinggal tiga variabel
saja yang sensitif terhadap laba. Demikian sebaliknya, jika modal yang ada
diinvestasikan di dalam instrumen saham, dan kebetulan saham tersebut tidak meraup
keuntungan pada tahun tersebut, tetapi malah minus 10% dalam setahun, maka tinggal
satu variabel saja yang sensitif terhadap laba. Jadi, pada permasalahan ini, terdapat
empat variabel yang sensitif, karena benchmark-nya. adalah investasi di pasar uang
dengan tingkat pengembalian 8% pertahun (fixed 3 tahun).
3.1.3 Analisa Sensitifitas Dua Peubah
Analisa Diagram Tornado memberikan pemahaman yang mendalam, tentang apa yang
akan terjadi, tetapi terbatas jika hanya ada satu variabel yang berubah dalam satu waktu.
Akan sangat rumit, jika ingin dicari akibat dari perubahan beberapa variabel dalam satu
waktu. Tapi ada suatu Tehnik Grafik yang tersedia untuk mempelajari interaksi dari dua
Misalkan, ingin dicari pengaruh gabungan dari perubahan dua variabel yang
paling kritis, yaitu Biaya Pengoperasian dan Kapasitas dari Penerbangan Terjadwal.
Pada Gambar 3.3 terlihat garis lurus yang mewakili semua nilai yang mungkin dari
kombinasi kedua variabel di atas. Kemudian akan dilihat nilai keuntungan tahunan dari
Biaya Pengoperasian dan Kapasitas dari Penerbangan Terjadwal yang kurang dari Rp
42.000.000,-. Untuk mendapatkan nilai tersebut, maka harus dicari dulu total dari
pendapatan setahun dikurang dengan total biaya setahun yang kurang dari Rp
42.000.000,- atau dicari dulu total pendapatan yang kurang dari hasil pengurangan total
biaya ditambah Rp 42.000.000,-
Total Pendapatan < Total Biaya + Rp 42.000.000,-
(Proporsi Carter x Jam Terbang x Tarif < (Jam Terbang x Biaya
Carter) + [(1 - Proporsi Carter) x Jam Pengoperasian) + Asuransi + (Harga
Terbang x Harga Tiket x Jumlah Beli x Pporsi Pinjaman x Tingkat
Tempat Duduk Penumpang x Kapasitas Suku Bunga) + Rp42. 000.000,-
Penerbangan Terjadwal]
Dengan memasukkan nilai dasar pada semua variabel kecuali pada variabel Biaya
Pengoperasian dan Kapasitas dari Penerbangan Terjadwal, akan didapatkan
(0,5 x 800 x 3.250.000) +[0,5 x 800 x (800 x Biaya Pengoperasian ) +
1.000.000 x 5 x Kapasitas dari < 200.000.000 + (875.000.000 x 0,4 x
Penerbangan Terjadwal 0,115)+42.000.000
yang dapat disederhanakan menjadi:
1.300.000.000 + (2.000.000.000 x < (800 x Biaya Pengoperasian) +
Kapasitas Terjadwal) 282.250.000
Kapasitas Terjadwal < 0,0000004 x Biaya Pengoperasian - 0,509
Pertidaksamaan ini mendefenisikan daerah dimana pembelian pesawat akan
menghasilkan keuntungan yang lebih kecil dari Rp 42.000.000. Untuk
menggambarkan garis dari pertidaksamaan ini hanyalah diperlukan dua titik awal. Cara
yang paling gampang adalah dengan memasukkan nilai ekstrim (batas atas dan batas
bawah) dari Biaya Pengoperasian untuk menghitung berapa nilai dari Kapasitas.
Jika Biaya Pengoperasian = Rp2.300.000, maka
Kapasitas Terjadwal = 0,0000004 x 2300000 - 0,509
= 0,411
Jika Biaya Pengoperasian = Rp2.600.000, maka
Kapasitas Terjadwal = 0,0000004 x 2600000 - 0,509
Titik yang diberi label "Nilai Dasar" didapat jika perhitungan keuntungan dengan
menggunakan variabel Kapasitas dari Penerbangan Terjadwal dan Biaya Pengoperasian
yang tetap pada nilai dasarya. Dapat dilihat bahwa titik Nilai Dasar itu terletak pada
daerah keuntungan > Rp42.000.000. Dengan begitu, bisa diambil kesimpulan bahwa
pembelian CN-235 dapat memberikan keuntungan yang menjanjikan. Tapi mungkin
saja Thoriq ingin mengetahui bagaimana perkiraan hasil yang mungkin didapatkan
apabila kedua variabel di atas dikombinasikan, apakah akan mendapatkan keuntungan
yang menarik, atau malah akan menghasilkan kerugian
Misalkan saja, ternyata Biaya Pengoperasian ternyata lebih tinggi dari perkiraan
nilai dasar, katakan sebesar Rp2.480.000, dan Kapasitas dari Penerbangan Terjadwal
lebih kecil dari perkiraan nilai dasar, katakan sebesar 48%. Jika dihitung sendiri-sendiri,
yaitu dengan memasukkan nilai dari salah satu variabel tersebut dalam perhitungan,
sementara nilai variabel yang lain tetap pada nilai dasarnya, kedua nilai tersebut terlihat
tidak menimbulkan kerugian, keuntungan yang diperoleh tetap lebih besar dari Rp
42.000.000. Tapi pada saat kedua variabel tersebut dikombinasikan (titik C pada
Gambar 3.4), ternyata kombinasi kedua variabel tersebut menghasilkan laba yang
untuk tidak membeli CN-235 tersebut. Situasi yang demikian mengindikasikan bahwa
ketidakpastian variabel-variabel ini harus dimodelkan dengan menggunakan metode
probabilitas.
3.1.4 Sensitifitas Pada Probabilitas
Langkah selanjutnya dalam analisis ini adalah memodelkan ketidakpastian yang
melingkupi variabel-variabel kritis yang diidentifikasi dan analisis dengan
menggunakan diagram tornado. Keempat variabel kritis tersebut adalah (1) Kapasitas
dari Penerbangan Terjadwal, (2) Biaya Pengoperasian, (3) Jam Terbang, dan (4) Tarif
Carter. Ketidakpastian yang perlu dipertimbangkan hanyalah untuk ketiga variabel
pertama, karena tarif carter adalah sebuah variabel keputusan yang dapat ditetapkan
langsung oleh Thoriq. Untuk keperluan contoh disini, diasumsikan bahwa untuk awal
percobaan memodelkan ketidakpastian, Thoriq memilih dua nilai untuk masing-masing
variabel, satu mewakili skenario optimistis dan satu lagi mewakili yang pesimistis.
Diagram keterkaitannya seperti yang terlihat pada Gambar 3.4. Diagram tersebut juga
memperlihatkan perubahan dalam model, berdasarkan analisis sensitifitasnya. Biaya
Pengoperasian, Jam Terbang, dan Kapasitas dari Penerbangan Terjadwal telah diubah
menjadi simpul kejadian- Variabel input yang tersisa (Tingkat Suku Bunga, Proporsi
Pinjaman, Harga Beli, Asuransi, Tarif Carter dan Proporsi dari Penerbangan Carter)
telah ditetapkan pada nilai dasarnya dan dengan demikian dapat dianggap sebagai
konstanta. Pohon keputusan pada Gambar 3.5 menunjukkan nilai pesimistis dan
Gambar 3.5 Diagram Keterkaitan dari Cendrawasih Airways
Sekarang masalahnya telah menjadi lebih sederhana. Pada Gambar 3.4 dan 3.5.
distribusi probabilitas untuk Jam Terbang tergantung pada Kapasitas Penerbangan
Terjadwal. Jika Kapasitasnya rendah, maka mungkin dapat mengakibatkan beberapa
penerbangan dibatalkan dengan demikian mengnrangi jumlah jam terbang. Sebuah garis
lengkung yang berhubungan ditarik dari "Kapasitas dari Penerbangan Terjadwal" ke
"Jam Terbang" pada diagram keterkailan, dan dalam pohon keputusan nilai untuk r =
P(Jam Terbang Rendah | Kapasitas Rendah) mungkin tidak sama dengan untuk s =
P(Jam Terbang Rendah |Kapasitas Tinggi). Pendapat awal adalah bahwa nilai r akan
lebih besar dibandingkan s. Sebaliknya, Biaya Pengoperasian ditetapkan independen
terhadap variabel-variabel lainnya.
Gambar 3.6 Pohon Keputusan untuk Cendrawasih Airways dengan
Ketidakpastian untuk Tiga Variabel
Hal berikutnya yang harus dilakukan adalah menaksir beberapa nilai untuk
probabilitas p, q, r, dan s. Bila dianggap bahwa Thoriq merasa yakin dengan penaksiran
nilai p = 0,5, atau bahwa Biaya Pengoperasian dapat setinggi (Rp2.530.000) atau
serendah (Rp2.370.000). Andaikan Thoriq merasa bahwa sebuah cara yang masuk akal
s = 80% r. Sehingga, jika Kapasitas tinggi (55%), maka probabilitas Jam = 650
hanyalah 80% dan probabilitas Jam = 650 pada saat Kapasitas rendah. Dengan dua
spesifikasi ini, sekarang tinggal dua probabuitas lagi yang belum dispesifikasi yang
harus dicari, yaitu q dan r. Gambar 3.7 menunjukkan pohon keputusan yang sudah
dimodifikasi dengan p = 0,5 dan s = 0,8/r.
Gambar 3.7 Pohon Keputusan untuk Cendrawasih Airways dengan Ketidakpastian untuk Tiga Variabel dengan p = 0,5 dan s = 0,8r
Sekarang dapat dibuat sebuah grafik sensitifitas dua variabel untuk q dan r.
Sebagaimana analisis saisitifitas dua variabel di atas, grafiknya akan menunjukkan
daerah mana yang Nilai Ekspektasinya untuk membeli CN-235 lebih besar dari pada
menanamkan modal di pasar uang.
Untuk menggambarkan grafiknya, pertama sekali harus dicari nilai ekspektasi dari
membeli CN-235 dalam nilai q dan r, termasuk spesifikasinya bahwa p = 0,5 dan s
EMV (Pembelian) = 0.5 {[-97.250. OOOr - 42.250.000(l-r)] +
(1-q)[65.250.000(0,8) + 182.750.000(l-0,8r)]} +
0,5{q[6.750.000/- + 101.750.0000-/-)] +
(1-q)[169.250.000(0,8/-) + 326.750.000(l-0,8r)]}
Setelah direduksi secara aljabar, persamaan di atas menjadi:
EMV (Pembelian) =q (35.000.000r - 225.000.000) - 110.000. 000r + 254.750.00
Pesawat terbang akan dibeli jika EMV (pembelian) > 42.000.000. Sehingga bisa
dihitung pertidaksamaan untuk q dengan menggunakan r.
q(350.00.000r - 225.000.000) - 110.000.000r + 254.750.000 > 42.000.000
254.750.000 - 42.000.000 - 110.000.000r > q(225. 000.000 - 35.000.000r)
Kemudian pertidaksamaan di atas menjadi:
(212.750.000 - 110.000.000/-) / (225.000.000 - 35.000.000r) > q
Dengan menggunakan pertidaksamaan ini, sebuah grafik sensitifitas dua variabel
untuk Cendrawasih Airways dapat dibuat (Gambar 5.8). Kurva yang memisahkan dua
daerah yang mewakili nilai dari q dan r untuk EMV (pembelian) = 42.000.000 mewakili
titik-titik nilai r antara 0 dan 1 ke dalam pertidaksamaan di atas. Untuk nilai q dan r ini,
Thoriq haruslah merasa tidak berbeda (dalam hal EMV) antara membeli pesawat atau
tidak. Daerah di bawah garis terdiri dari titik-titik di mana q < (212.750.000 - 110.000.
000r) / (225.000.000 - 35.000.000r); untuk titik (q , r) ini. EMV (pembelian) >
Rp42.000.000. Grafik yang dihasilkan masuk akal karena q dan r adalah probabilitas
dari skenario pesimistis - Kapasitas rendah dan Jam Terbang rendah. Jika Thoriq
berpendapat bahwa skenario pesimistis sangat mungkin terjadi (q dan r mendekati 1)
maka Thoriq mungkin tidak akan mau membeli pesawat terbang.
Hal penting yang dapat dilihat dari Gambar 3.7 adalah bahwa Thoriq mungkin
tidak mempunyai pengalaman untuk menentukan berapa seharusnya probabilitas untuk
probabilitas q mungkin berada antara 0,4 dan 0,5 serta bahwa r mungkin berada di
antara 0,5 dan 0,65. Probabilitas-probabilitas ini diwakili oleh titik-titik yang ada pada
Kotak A dalam Gambar 3.7. Kesemua titik ini berada dalam daerah "Beli CN=235",
sehingga kesimpulaimya adalah CN-235 harus dibeli. Keputusan ini tidak sensitif
terhadap penaksiran dari probabilitas. Jika sebaliknya, Thoriq berpendapat bahwa
bahwa nilai yang masuk akal untuk q dan r ada dalam Kotak B, maka kemudian pilihan
yang optimal belumlah jelas.
Gambar 3.8 Grafik Sensitifitas Dua Variabel untuk Cendrawasih Airways
Grafik analisis Sensitifitas dapat memberikan petunjuk dalam menentukan
seberapa besar usaha yang diperlukan untuk memodelkan ketidakpastian dalam sebuah
pennasalahan keputusan. Grafik juga dapat menunjukkan apakah keputusan yang dibuat
sensitif terhadap ketidakpastian dalam permasalahan dan permodelan dari
ketidakpastian tersebut.
3.1.5 Nilai Ekspektasi dari Permasalahan Cendrawasih Airways
Jika diulang kembali inti permasalahan dari Cendrawasih Airways adalah apakah
sebaiknya pemilik Cendrawasih Airways, dalam hal ini Thoriq, harus membeli
Airways, atau tidak. Setelah sebelumnya dibuat permodelan dari permasalahannya, telah
diketahui bahwa ada tiga variabel ketidakpastian : kapasitas dari penerbangan terjadwal
(proporsi dari tiket yang teriual), biaya pengoperasian, dan total jam terbang dalam
setahun. Gambar 3.9 memperlihatkan pohon keputusan dengan probabilitas tertentu
pada cabang-cabangnya.
Gambar 3.9 Pohon Keputusan untuk Cendrawasih Airways dengan Ketidakpastian untuk Tiga Variabel dengan p = 0,5 dan s = 0,8r
Untuk menghitung nilai ekspektasi dari pembelian pesawat baru, digunakan nilai
probabilitas dari cabang-cabang pohon keputusannya.
Maka Nilai Ekspektasi (pembelian pesawat) adalah:
= -Rpl 1.378.250 + (-Rp6.041.750) + Rp5.637.600 + Rp28.070.400 +Rp789.750 +
Rpl4.550.250 + Rpl4.623.200 + Rp50.
= Rp96.440.000,-
Nilai Ekspektasi untuk investasi pada pasar uang
Dari perhitungan di atas dapat dilihat bahwa nilai ekspektasi membeli pesawat
terbang jauh lebih besar dari pada nilai ekspektasi menginvestasikan modal pada pasar
uang. Jika kriteria memilih yang digunakan adalah nilai ekspektasi, maka yang akan
dipilih adalah membeli pesawat terbang, karena nilai ekspektasi membeli pesawat
terbang jauh lebih tinggi dari pada menginvestasikan modal pada pasar uang. Tetapi
sebagian besar orang tampaknya akan lebih cenderung untuk memilih altematif kedua,
yaitu menginvestasikan modal pada pasar uang. Jadi dapat ditarik kesimpulan, bahwa
penggunaan kriteria nilai ekspektasi dalam permasalahan tidak mewakili apa yang
mungkin diinginkan oleh sebahagian besar orang. Kondisi ini disebabkan karena
membeli pesawat terbang adalah tindakan yang lebih beresiko dibandingkan
menginvestasikan modal pada pasar uang. Jika Thoriq termasuk pembuat keputusan
yang menghindari resiko, ingin diketahui seberapa penghindar resikokah Thoriq dan
apakah dia tetap berkeinginan untuk membeli pesawat terbang tersebut. Atau, jika
Thoriq adalah seorang penggemar resiko, seberapa rendahkan tingkat toleransinya
terhadap resiko yang membuat dia mau menginvestasikan modalnya di pasar uang.
Untuk menjawab pertanyaan di atas, secara konsep cukup sederhana, tapi
perhitungan yang akan dilibatkan sangat lamban dan tidak menarik. Untuk keperluan
perhitungannya digunakan fungsi utilitas eksponensial. Pada konsepnya, yang ingin
dicari adalah nilai kritis untuk R sehingga ekspektasi utility dari membeli pesawat akan
sama dengan ekspektasi utility dari menanamkan modal di pasar uang. Sehingga
kemudian pertanyaannya berubah menjadi : apakah toleransi resiko Thoriq berada di
atas atau di bawah nilai kritis. Jika toleransi resiko Thoriq berada di atas nilai kritis,
maka keputusan yang paling baik adalah membeli pesawat terbang baru, jika di bawah
nilai kritis, maka sebaiknya diambil keputusan yang tidak terlalu beresiko yaitu
menginvestasikan uangnnya pada pasar uang.
3.1.6 Toleransi Resiko (R) untuk Cendrawasih Airways
Seperti yang sudah dijabarkan pada bab sebelumnya, R adalah toleransi resiko. Semakin
sebaliknya semakin kecil nilai R maka akan semakin concave kurvanya atau semakin
menghindari resiko. Dengan demikian, jika seorang pembuat keputusan tidak terialu
penghindar resiko; atau jika pembuat keputusan dapat mentoleransi lebih banyak resiko,
pembuat keputusan tersebut dapat menaksir nilai yang besar untuk R untuk memperoleh
sebuah fungsi utility yang lebih mendatar. Jika seorang pembuat keputusan tidak terialu
dapat mentoleransi resiko, maka pembuat keputusan tersebut dapat menaksir nilai R
yang lebih kecil dan memperoleh sebuah fungsi utility yang lebih melengkung.
Nilai X (keuntungan) yang terbesar, dimana Thoriq merasa lebih baik untuk
melakukan membeli pesawat daripada tidak, kurang lebih hampir mendekati tingkat
toleransi Thoriq terhadap resiko. Ini adalah nilai dimana seorang pembuat keputusan
bisa menggunakannya sebagai nilai R di dalam fungsi utility eksponensialnya. Sebagai
contoh, andaikan setelah memperhatikan pohon keputusan untuk masalah di atas,
pembuat keputusan mengambil keputusan bahwa nilai X yang terbesar yang bisa
membuatnya memutuskan ikut bermainjudi adalah X= Rp142.410.000,-. Sehingga R =
Rp142.410.000,-. Dengan menggunakan penaksiran ini dalam fungsi utility
eksponensial akan menghasil fungsi utility
U(x) =1-e-x4241000
Karena nilai R sudah diperoleh maka utility dan masing-masing variabel dapat dicari
dengan mensubstitusikan nilai R ke dalam fungsi utility eksponensial.
Lalu dicari Ekspektasi Utility-nya.
Jika digambarkan diagram pohonnya adalah sebagai berikut :
Laba (x) U(x) Probabilitas EU
-Rp 97.250.000 -0.97958 0.1170 -0.114611
-Rp 42.250.000 -0.34538 0.1430 -0.049390
Rp 65.250.000 0.36757 0.0864 0.037158
Rp 182.750.000 0.72287 0.1536 0.111033
Rp 6.750.000 0.04629 0.1170 0.005416
Rp 101.750.000 0.51056 0.1430 0.073010
Rp 169.250.000 0.69531 0.0864 0.060075
Rp 326.750.000 0.89918 0.1536 0.138114
Maka:
Ekspektasi Utility (Pembelian Pesawat) = 0,255405 Ekspektasi
Utility (Investasi Pasar Uang) = 0,255411
3.1.7 Menentukan Nilai Ekivalen Tetap (NET)
Untuk mencari Nilai Ekivalen Tetap untuk kejadian tak pasti pada pembelian pesawat
adalah sebagai berikut:
U(x)=1-e-x/R
U(x)=l-e x /142410000
Seperti sudah diketahui sebelumya bahwa Ekspektasi Utility (Pembelian Pesawat)
adalah 0,255405.
Jika masing-masing sisi dikurangi 1, maka :
-0,7444595 = −e−x/142410000
x = -142410000 x -0,294915
x = 41998821,3078
Diperoleh Nilai Ekivalen Tetap untuk kejadian tak pasti pada pembelian pesawat, yaitu
Rp.41.998.821,- ICarena Nilai Ekivalen Tetap-nya sudah diketahui, maka pohon
Gambar3.11 Pohon Kcputusan yang Sudah Disederhanakan
Nilai Ekivalen tetap adalah suatu nilai yang ditetapkan, atau diputuskan bukan
merupakan perkiraan nilai yang akan diterima dari kejadian tak pasti tersebut, Jika
pengambil keputusan mengaambil keputusan berdasarkan Nilai Ekivalen Tetap pada
kasus Cendrawasih Airways, maka yang menjadi keputusan yang diambil adalah "tidak
jadi membeli pesawat, lebih baik menginvestasikan di pasar uang", karena Nilai
Ekivalen Tetapnya lebih tinggi.
3.1.8 Sensitifitas Resiko
Setelah nilai kritis R diperoleh, untuk melihat berapa perubahan angka
keputusan analisis sensitifitas penerima resiko yang dilakukan dengan mengambil nilai
R di bawah dan di atas nilai kritis R untuk memperoleh Nilai Ekivalen Tetap-nya
(NET). Perhitungan untuk mencari nilai ini dilakukan dengan jalan coba-coba (trial and
error). Seperti sudah diketahui sebelumnya bahwa Ekspektasi Utility (Pembelian
Pesawat) adalah 0,255405. Dengan mengambil nilai R dari 2410000 sampai dengan
262410000. Nilai Ekivalen Tetap yang diperoleh adalah sebagai berikut:
0,255405 =l-e-xR - 0,744595 =-e-x/R
0,744595 =e-x/R
In (0,744595)= In (e-x/R) In (0,744595) = - x/R
x= - R x [In (0,744595)]
Untuk R = 2.410.000, maka
x = -2.410.000 x -0,294915 = 710.728,5633
Untuk R = 22.410.000, maka
x = -22.410.000 x -0,294915 = 6.608.890,9142
Untuk R = 42.410.000, maka
x=-42.410.000 x -0,294915 = 12.507.053,2650
Untuk R = 62.410.000, maka
x=-62.410.000 x -0,294915 = 18.405.215,6159
Untuk R = 82.410.000, maka
x= -82.410.000 x -0,294915 = 24.303.377,9668
x=-102.410.000x-0,294915= 30.201.540,3176
Untuk R = 122.410.000, maka
x = -122.410.000 x -0,294915 = 36.099.702,6685
Untuk R = 142.410.000, maka
x = -142.410.000 x -0,294915 = 41.997.865,0194
Untuk R = 162.410.000, maka
x = -162.410.000 x -0,294915 = 47.896.027,3702
Untuk R = 182.410.000, maka
x = -182.410.000 x -0,294915 = 53.794.189,7211
UntukR = 202.410.000, maka
x = -202.410.000 x--0,294915 = 59.692.352,0720
Untuk R = 222.410.000, maka
x=-222.410.000x-0.294915 =65.590.514,4229
Untuk R = 242.410.000, maka
x = -242.410.000 x -0,294915 = 71.488.676,7737
Untuk R = 262.410 000, maka
x = -262,410,009 x -0^294915 = 77.386.839,1246
Untuk R = Z82.410.000, maka
x = -282.410.000 x -0.294915 = 83.285.001,4755
Jika Nilai Ekivalen Tetap di atas dimasukkan dalam sebuah label hasilnya
Tabel 3.3 Nilai Ekivalen Tetap berdasarkan Toleransi Resikonya
Toleransi Resiko Nilai Ekivalen Tetap
2.410.000 710.728,5633
22.410.000 6.608.890,9142
24.410.000 12.507.053,2650
62.410.000 18.405.215,6159
82.102.000 24.303.377,9668
102.410.000 30.201.540,3176
Jika Thoriq hanya dapat menerima resiko di bawah nilai kritis atau R <
142.410.000, maka dia akan mengambil keputusan yang mengandung sedikit resiko.
Keputusan yang akan diambilnya adalah menginvestasikan uangnya pada pasar uang.
Akan tetapi jika Thoriq dapat menerima resiko di atas nilai kritis (R >
142.410.000), artinya Thoriq dapat mentolerir resiko lebih besar dari 142.410.000 maka
keputusan yang akan diambil adalah membeli pesawat terbang CN-23
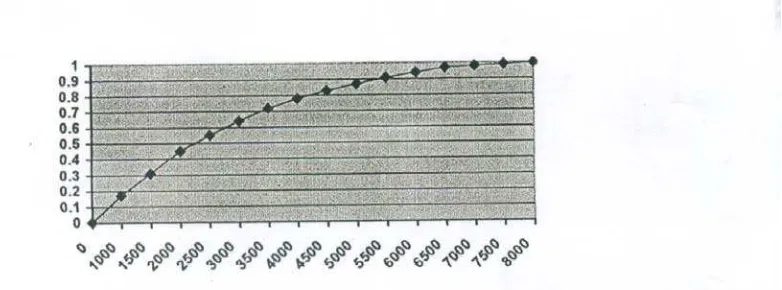
Toleransi resiko ini dapat dinyatakan dalam sebuah grafik dalam hubungannya
dengan Nilai Ekivalen Tetap. Grafik sensitifitas resikonya dap dapat ditunjukkan
Dari grafik ini dapat dilihat, bahwa tenyata Thoriq netral terhadap resiko yang
mungkin terjadi. Artinya, dia tidak merasa berbeda antara menerima resiko di bawah
nilai kritis atau R < 142.410.000 yang akan membuat dia mengambil keputusan yang
mengandung sedikit resiko, ataupun menerima resiko di atas nilai kritis (R >
142.410.000), dimana artinya Thoriq dapat mentolerir resiko lebih besar dari
142.410.000 sehingga keputusan yang akan diambil adalah membeli pesawat terbang
CN-235.
Setelah dilakukan analisa sensitifitas penerima resiko, jika ternyata Thoriq dapat
menerima resiko lebih besar dari nilai kritis atau R > Rpl42.410.000,- maka keputusan
yang diambil adalah membeli pesawat terbang, dengan begitu memperlihatkan bahwa
BAB 4
KESIMPULAN
4.1 Kesimpulan
• Nilai ekivalen tetap digunakan untuk menentukan pilihan dengan memasukkan faktor resiko
• Diagram Tornado dapat digunakan untuk membandingkan Analisis Sensitifitas satu variabel untuk banyak variabel input secara bersamaan
• Diagram tornado disusun sedemikian hingga variabel yang paling sensitif (variabel dengan batang paling panjang), ditempatkan pada bagian paling atas,
dan yang paling tidak sensitif ditempatkan pada bagian bawah
4.2 Saran
• Untuk pembuat keputusan harus mengetahui analisis sensitifitas karena analisis ini dilakukan setelah dicapainya suatu strategi yang dianggap optimal. Dimana
sensitifitas berdasarkan nilai probabilitas dari simpul-simpul keputusan dan
penerapan dalil bayes
• Untuk pembuat keputusan harus mengetahui berapa besar perubahan angka keputusan dengan mengubah-ubah preferensi terhadap resiko ke dalam fungsi
utilitas eksponensial
DAFTAR PUSTAKA
Accel, Amir D. 1999. Complete Business Statistics 4th edition. Singapore McGraw Hill
Bunn, Derek W. 1984. Applied Decision Analysis. San Fransisco. McGraw Hill Book
Company
Clemen, R.T. 1996. Making Hard Decision: An Introduction to Decision Analysis 2nd
Edition. Belmot California. Duxbury Press
Fabrycky, Wotter J. dan Thuesen, G. J. 1980. Economic Decision Analysis 2nd Edition.
New Jersey. Prentice Hall
Kaim, Azhar.1995. Teori pembuatan keputusan. Jakarta. Lembaga Penerbit Fakultas
Ekonomi Universitas Indonesia
Mangkusubroto, Kuntoro dan Trisnadi, Liatiarini. 1987. Analisa Pendekatan Keputusan
dalam Manajemen Usaha dan Proyek. Bandug. Ganeca Exact
Manurung, Adler Haymans. 1991. Pengambilan Keputusan Pendekatan Kuantitatif.
Jakarta. Rineka Cipta
Paul, E. Moody. 1993. decision Making: Proven Methods for Better Decision. New
York. McGraw Hill
Supranto, Johannes. 1998. Teknik Pengambilan Keputusan. Jakatra. Rineka Cipta