ABSTRAK
IQBAL HANIF. Penerapan Algoritme Genetika dalam Pendugaan Parameter Fungsi Cobb-Douglas dengan Galat Aditif. Dibimbing oleh AGUS MOHAMAD SOLEH dan AAM ALAMUDI.
Fungsi Cobb-Douglas dengan galat aditif merupakan fungsi yang dapat digunakan untuk menganalisis hubungan antara hasil produksi dan faktor-faktor produksi. Metode yang dapat digunakan dalam menduga parameter fungsi tersebut adalah metode Nonlinear Least Square (NLS) dan algoritme yang umum digunakan adalah iterasi Gauss Newton (NLS-GN), namun metode tersebut kurang optimal ketika dihadapkan dengan masalah multikolinearitas. Algoritme alternatif yang dapat digunakan pada metode NLS adalah Algoritme Genetika (NLS-GA). Tujuan penelitian ini adalah untuk mengkaji penerapan Algoritme Genetika pada pendugaan parameter fungsi Cobb-Douglas dengan galat aditif. Hasil penelitian menunjukkan bahwa metode NLS-GA belum mampu menghasilkan dugaan parameter yang lebih baik dibanding metode NLS-GN pada data simulasi tanpa masalah multikolinearitas, namun metode NLS-GA mampu mengatasi masalah yang dihadapi metode NLS-GN ketika dihadapkan pada data dengan masalah multikolinearitas. Metode NLS-GA juga mampu menghasilkan model dengan kemampuan prediksi lebih baik dibanding metode NLS-GN pada data riil.
Kata kunci: Algoritme Genetika, Fungsi Cobb-Douglas, Nonlinear Least Square
ABSTRACT
IQBAL HANIF. The Application of Genetic Algorithm to Estimate Parameters of Cobb-Douglas Function with Additive Errors. Supervised by AGUS MOHAMAD SOLEH and AAM ALAMUDI.
Cobb-Douglas function with additive errors is a function which can be used to analyse the relationship between production output and production factors. The method commonly used to estimate the parameter of that function is Nonlinear Least Square (NLS) and a common algorithm for this method is Gauss Newton iteration (NLS-GN). However, NLS-GN method has less-optimum results when analysing multicolinearity data. A possibly better method for this analysis is Genetic Algorithm (NLS-GA). The purpose of this study is to analyse the use of Genetic Algorithm to estimate parameters of Cobb-Douglas function with additive errors. The results show that NLS-GA method could not produce a better parameter estimator than NLS-GN method does but it produced a better parameter estimator in analysing multicolinearity data. NLS-GA method is capable of producing a better model with predictive ability than NLS-GN method does with real data.
PENDAHULUAN
Latar Belakang
Fungsi Cobb-Douglas dengan galat aditif merupakan salah satu fungsi produksi yang dapat digunakan untuk menganalisis hubungan antara hasil produksi dan faktor-faktor produksi. Salah satu metode yang dapat digunakan untuk menduga parameter fungsi tersebut adalah metode Nonlinear Least Square, yaitu menghitung nilai parameter yang mampu meminimumkan Jumlah Kuadrat Galat (Huet et al. 2003).
Algoritme pengoptimuman dibutuhkan dalam pendugaan parameter dengan metode Nonlinear Least Square. Algoritme yang umum digunakan adalah iterasi Gauss Newton, yaitu algoritme yang menerapkan deret Taylor orde pertama untuk memperoleh titik optimum (Chapra dan Canale 2002). Metode Nonlinear Least Square dengan iterasi Gauss Newton mampu menghasilkan dugaan parameter yang baik dengan waktu yang relatif cepat. Namun, ketika dihadapkan dengan data yang memiliki masalah multikolinearitas, metode tersebut tidak dapat memberikan hasil pendugaan parameter yang optimal (Erkoç et al. 2010).
Algoritme pengoptimuman alternatif yang dapat digunakan adalah Algoritme Genetika. Algoritme Genetika meniru proses evolusi makhluk hidup untuk menangani masalah pengoptimuman (Sartono 2010). Algoritme genetika diduga mampu menghindari overfitting, menangani masalah multikolinearitas dengan baik dan memberikan hasil yang mudah diinterpretasikan (Zhang dan Horvath 2006).
Tujuan Penelitian
Penelitian ini bertujuan untuk mengkaji penerapan Algoritme Genetika sebagai algoritme alternatif pendugaan parameter fungsi Cobb-Douglas dengan galat aditif.
TINJAUAN PUSTAKA
Fungsi Cobb-Douglas dengan Galat Aditif
Fungsi Cobb-Douglas dengan galat aditif dikembangkan oleh Goldfeld dan Quandt (1970). Mereka menambahkan komponen stokastik aditif (additive stochastic term) ke dalam fungsi produksi yang ditemukan oleh Cobb dan Douglas (1928), yang kemudian dikenal dengan istilah galat (error). Bentuk fungsi produksi Cobb-Douglas dengan galat aditif adalah sebagai berikut:
PENDAHULUAN
Latar Belakang
Fungsi Cobb-Douglas dengan galat aditif merupakan salah satu fungsi produksi yang dapat digunakan untuk menganalisis hubungan antara hasil produksi dan faktor-faktor produksi. Salah satu metode yang dapat digunakan untuk menduga parameter fungsi tersebut adalah metode Nonlinear Least Square, yaitu menghitung nilai parameter yang mampu meminimumkan Jumlah Kuadrat Galat (Huet et al. 2003).
Algoritme pengoptimuman dibutuhkan dalam pendugaan parameter dengan metode Nonlinear Least Square. Algoritme yang umum digunakan adalah iterasi Gauss Newton, yaitu algoritme yang menerapkan deret Taylor orde pertama untuk memperoleh titik optimum (Chapra dan Canale 2002). Metode Nonlinear Least Square dengan iterasi Gauss Newton mampu menghasilkan dugaan parameter yang baik dengan waktu yang relatif cepat. Namun, ketika dihadapkan dengan data yang memiliki masalah multikolinearitas, metode tersebut tidak dapat memberikan hasil pendugaan parameter yang optimal (Erkoç et al. 2010).
Algoritme pengoptimuman alternatif yang dapat digunakan adalah Algoritme Genetika. Algoritme Genetika meniru proses evolusi makhluk hidup untuk menangani masalah pengoptimuman (Sartono 2010). Algoritme genetika diduga mampu menghindari overfitting, menangani masalah multikolinearitas dengan baik dan memberikan hasil yang mudah diinterpretasikan (Zhang dan Horvath 2006).
Tujuan Penelitian
Penelitian ini bertujuan untuk mengkaji penerapan Algoritme Genetika sebagai algoritme alternatif pendugaan parameter fungsi Cobb-Douglas dengan galat aditif.
TINJAUAN PUSTAKA
Fungsi Cobb-Douglas dengan Galat Aditif
Fungsi Cobb-Douglas dengan galat aditif dikembangkan oleh Goldfeld dan Quandt (1970). Mereka menambahkan komponen stokastik aditif (additive stochastic term) ke dalam fungsi produksi yang ditemukan oleh Cobb dan Douglas (1928), yang kemudian dikenal dengan istilah galat (error). Bentuk fungsi produksi Cobb-Douglas dengan galat aditif adalah sebagai berikut:
2
Nilai parameter di dalam fungsi Cobb-Douglas diinterpretasikan sebagai elastisitas faktor produksi terhadap hasil produksi . Adanya hukum kenaikan hasil yang semakin berkurang (law of diminishing returns) dalam produksi menyebabkan nilai berada pada selang (Soekartawi 2002). Namun, tidak tertutup kemungkinan bagi parameter untuk memiliki nilai negatif. Merujuk pada hasil penelitian Chisasa dan Makina (2013), parameter memiliki nilai positif apabila penambahan faktor produksi mampu meningkatkan hasil produksi (produktif). Namun sebaliknya, parameter memiliki nilai negatif apabila penambahan faktor produksi justru mengurangi hasil produksi (tidak produktif).
Nonlinear Least Square(NLS)
Erkoç et al. (2010) mendefinisikan bentuk umum dari model nonlinear adalah sebagai berikut:
dengan adalah nilai peubah respon pada amatan ke-i, adalah nilai peubah bebas pada amatan ke-i, adalah parameter, dan adalah galat ke-i yang menyebar normal(0, . Metode Nonlinear Least Square (NLS) merupakan salah satu metode yang dapat digunakan untuk menduga parameter fungsi nonlinear. Dasar dari metode ini adalah mencari nilai yang meminimumkan nilai Jumlah Kuadrat Galat (JKG) (Huet et al. 2003), yang didefinisikan dengan fungsi objektif berikut:
∑[ ]
Iterasi Gauss Newton (GN)
Untuk memperoleh nilai parameter yang mampu meminimumkan JKG, fungsi objektif metode NLS perlu diturunkan terlebih dahulu. Turunan orde pertama atau persamaan normal dari fungsi objektif metode NLS adalah sebagai berikut:
∑[ ] [
] ̂
3
∑ [ ]
substitusikan persamaan deret diatas ke dalam bentuk umum model nonlinear:
∑ [ ]
jika:
[ ]
maka persamaan nonlinear dapat dituliskan kembali ke dalam notasi matriks:
Persamaan diatas memiliki bentuk persamaan yang linear, sehingga nilai dapat diduga melalui pendekatan Metode Kuadrat Terkecil (MKT) secara iteratif dengan persamaan sebagai berikut:
̂
dengan adalah matriks turunan parsial dari persamaan nonlinear (jacobian), adalah vektor nilai selisih antara peubah respon dengan dugaannya, adalah vektor nilai awal parameter, dan ̂ adalah vektor nilai dugaan parameter hasil iterasi. Bila ̂ maka
yang merupakan pemenuhan
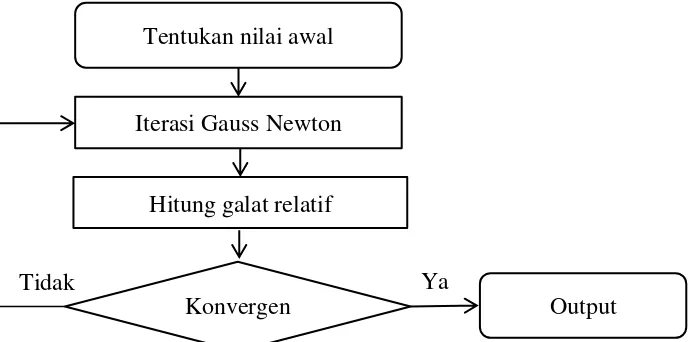
persyaratan persamaan normal metode NLS-GN. Langkah-langkah pendugaan parameter dengan metode NLS-GN diilustrasikan melalui diagram alir pada Gambar 1.
Gambar 1 Diagram alir mekanisme metode NLS-GN Iterasi Gauss Newton
Hitung galat relatif Tentukan nilai awal
Konvergen Output
4
1. Menentukan nilai awal dugaan parameter yaitu .
2. Melakukan iterasi Gauss Newton terhadap , diperoleh nilai dugaan parameter hasil iterasi yaitu ̂ .
3. Hasil dugaan paraemeter dijadikan nilai awal untuk iterasi selanjutnya. Iterasi berhenti apabila konvergen, yaitu ketika | ̂
| .
Masalah Multikolinearitas
Multikolinearitas adalah sebuah kondisi yang terjadi akibat adanya hubungan linear antar peubah bebas, baik itu interkorelasi sempurna (terpaut linear) atau interkorelasi tidak sempurna tetapi cukup kuat (Gujarati dan Porter 2010). Metode NLS-GN tidak dapat memberikan hasil pendugaan parameter yang optimal ketika dihadapkan dengan data yang memiliki masalah multikolinearitas. Misalkan selisih parameter antar iterasi dalam metode NLS-GN ( disimbolkan dengan α, maka kita dapat menghitung nilai Kuadrat Tengah Galat (KTG) dari ̂ dengan persamaan sebagai berikut:
̂ [ ̂ ] [ ̂ ]
∑ ̂
∑ ̂
∑
Korelasi yang cukup kuat antar peubah menyebabkan matriks berada dalam kondisi buruk (ill-conditioned), yang menyebabkan minimal satu akar ciri dari matriks ( ) akan bernilai sangat kecil. Akibatnya, var ̂ dan KTG( ̂) akan bernilai cukup besar (Erkoç et al. 2010).
Algortime Genetika (Genetic Algorithm-GA)
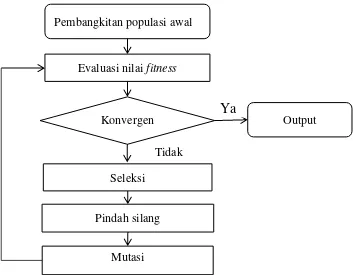
5 yang sama, yaitu meminimumkan selisih antara nilai aktual (titik amatan) dengan nilai dugaannya (titik pada kurva). Langkah-langkah pendugaan parameter metode NLS dengan skema GA rancangan Scrucca (NLS-GA) diilustrasikan melalui diagram alir pada Gambar 2.
Gambar 2 Diagram alir mekanisme metode NLS-GA 1. Pembangkitan populasi awal
Membangkitkan populasi awal sebanyak N individu berupa vektor kromosom [ ̂| ̂ | | ̂ ]. Nilai dugaan parameter dibangkitkan mengikuti sebaran seragam sesuai dengan batasan yang ditentukan.
2. Evaluasi fitness individu
Kriteria fitness yang digunakan adalah nilai JKG. Semakin kecil nilai JKG suatu individu, maka semakin baik individu tersebut. Sebanyak k% individu terbaik dalam populasi dipertahankan untuk generasi selanjutnya, dan proses ini dikenal dengan istilah elitisme (Hopgood 2001).
3. Seleksi individu
Standardisasi nilai fitness dilakukan terlebih dahulu dengan metode Fitness Linear Scaling, yaitu metode standardisasi menggunakan fungsi linear (Hopgood 2001) dengan persamaan sebagai berikut sebagai berikut:
̅
̅
̅( ̅)
̅ ̅
̅
̅
̅
̅ ̅
Evaluasi nilai fitness
Pindah silang
Mutasi Seleksi
Pembangkitan populasi awal
Konvergen
Ya
Output6
Individu kemudian diseleksi dengan metode Roulette Wheel, dengan peluang suatu individu untuk terpilih ( ) dinyatakan dengan persamaan sebagai berikut:
| | ∑ | |
4. Pindah silang (cross-over)
Metode pindah silang yang digunakan adalah Local Arithmetic Crossover, yaitu metode pindah silang dengan cara mengkombinasikan individu induk secara linear (Michalewicz 1992). Persamaan yang digunakan adalah sebagai berikut:
dengan dan adalah individu induk, dan adalah individu anak hasil pindah silang, dan adalah bilangan acak seragam(0, 1). Peluang pindah silang yang ditetapkan adalah sebesar p.
5. Mutasi
Metode mutasi yang digunakan adalah Uniform Random Mutation, yaitu mengganti nilai gen yang terpilih dengan bilangan acak yang mengikuti sebaran seragam sesuai dengan batasan yang ditentukan. Pemilihan gen yang akan dimutasi dilakukan secara acak, dimana setiap gen memiliki peluang yang sama untuk terpilih (Michalewicz 1992). Peluang mutasi yang ditetapkan adalah sebesar q.
6. Langkah 2-5 terus diulangi hingga konvergen, dengan kriteria
kekonvergenan adalah m kali iterasi, kemudian dipilih individu terbaik dari populasi terakhir.
METODE
Data
Penelitian ini menggunakan dua jenis gugus data, yaitu data simulasi dan data produksi pertanian. Data simulasi dibangkitkan berdasarkan skema pembangkitan data yang sama seperti yang dilakukan pada penelitian Goldfeld dan Quandt (1970). Persamaan Cobb-Douglas hasil penelitian Chisasa dan Makina (2013) digunakan untuk membangkitkan data simulasi, dengan rincian persamaan sebagai berikut:
6
Individu kemudian diseleksi dengan metode Roulette Wheel, dengan peluang suatu individu untuk terpilih ( ) dinyatakan dengan persamaan sebagai berikut:
| | ∑ | |
4. Pindah silang (cross-over)
Metode pindah silang yang digunakan adalah Local Arithmetic Crossover, yaitu metode pindah silang dengan cara mengkombinasikan individu induk secara linear (Michalewicz 1992). Persamaan yang digunakan adalah sebagai berikut:
dengan dan adalah individu induk, dan adalah individu anak hasil pindah silang, dan adalah bilangan acak seragam(0, 1). Peluang pindah silang yang ditetapkan adalah sebesar p.
5. Mutasi
Metode mutasi yang digunakan adalah Uniform Random Mutation, yaitu mengganti nilai gen yang terpilih dengan bilangan acak yang mengikuti sebaran seragam sesuai dengan batasan yang ditentukan. Pemilihan gen yang akan dimutasi dilakukan secara acak, dimana setiap gen memiliki peluang yang sama untuk terpilih (Michalewicz 1992). Peluang mutasi yang ditetapkan adalah sebesar q.
6. Langkah 2-5 terus diulangi hingga konvergen, dengan kriteria
kekonvergenan adalah m kali iterasi, kemudian dipilih individu terbaik dari populasi terakhir.
METODE
Data
Penelitian ini menggunakan dua jenis gugus data, yaitu data simulasi dan data produksi pertanian. Data simulasi dibangkitkan berdasarkan skema pembangkitan data yang sama seperti yang dilakukan pada penelitian Goldfeld dan Quandt (1970). Persamaan Cobb-Douglas hasil penelitian Chisasa dan Makina (2013) digunakan untuk membangkitkan data simulasi, dengan rincian persamaan sebagai berikut:
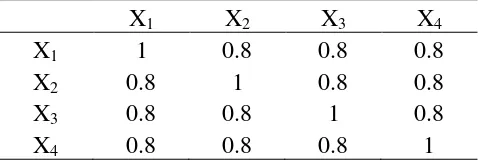
7 bilangan untuk setiap peubah bebas ) dengan nilai rataan = 50 dan matriks kovarian dengan menggunakan matriks korelasi seperti pada Tabel 1.
Tabel 1 Matriks korelasi untuk pembangkitan bilangan acak multivariat normal
X1 X2 X3 X4
X1 1 0.8 0.8 0.8
X2 0.8 1 0.8 0.8
X3 0.8 0.8 1 0.8
X4 0.8 0.8 0.8 1
Langkah selanjutnya adalah membangkitkan sisaan (u) yang mengikuti sebaran normal(0, 1) sebanyak 1.000 bilangan untuk masing-masing jenis data serta membangkitkan peubah respon dengan rumus:
Data produksi pertanian yang digunakan di dalam penelitian ini adalah data hasil produksi tanaman yang tergolong tanaman biji-bijian (serealia) beserta faktor-faktor produksinya, yaitu luas lahan, jumlah alat pertanian yang digunakan, dan konsumsi pupuk. Data produksi pertanian yang digunakan merupakan data cross-section yang diperoleh berdasarkan hasil produksi tahun 2004 dan diambil dari 45 negara yang berbeda. Data diunduh dari database World Bank yang dapat diakses melalui website World Bank (http://data.worldbank.org/indicator). Rincian data produksi pertanian yang digunakan dapat dilihat pada Lampiran 1.
Minimum Variance Unbiased Estimator (MVUE)
Suatu dugaan parameter dapat dikatakan sebagai dugaan parameter terbaik apabila memenuhi kriteria Minimum Variance Unbiased Estimator (MVUE). Misalkan adalah dugaan parameter bagi Hogg dan Craig (2005) berpendapat bahwa dapat dikatakan sebagai MVUE bagi apabila memenuhi kriteria sebagai berikut:
1. (tidak berbias).
2. lebih kecil atau sama dengan ragam dari semua penduga bagi parameter (ragam minimum).
K-Fold Cross Validation
8
tes digunakan untuk menghitung KTG dari model yang terbentuk dari gugus data latih. Proses ini diulang sebanyak kali hingga semua bagian digunakan satu kali sebagai gugus data tes. Nilai sisaan validasi silang diduga dengan persamaan berikut:
∑ ∑ ̂
dengan adalah peubah respon ke-i pada gugus data tes dan ̂ adalah dugaan untuk pada saat bagian ke- tidak digunakan dalam pembentukan model. Nilai yang biasa digunakan adalah lima atau sepuluh (Izenman 2008)
Metode
Proses analisis yang digunakan di dalam penelitian ini secara umum terdiri atas tiga poin utama:
1. Penerapan metode NLS-GA untuk pendugaan parameter fungsi Cobb-Douglas dengan galat aditif pada data simulasi tanpa masalah multikolinearitas, serta membandingkan hasilnya dengan dugaan parameter hasil metode NLS-GN.
2. Penerapan metode NLS-GA untuk pendugaan parameter fungsi Cobb-Douglas dengan galat aditif pada data simulasi dengan masalah multikolinearitas, serta membandingkan hasilnya dengan dugaan parameter hasil metode NLS-GN.
3. Penerapan metode NLS-GA pada kasus riil, serta mebandingkan kemampuan prediksi antara model hasil pendugaan dengan metode NLS-GA dengan model hasil pendugaan dengan metode NLS-GN.
Penelitian dilakukan dengan menggunakan komputer dengan spesifikasi CPU Intel Core-i3 1.8 GHz dan RAM sebesar 2 GB. Perangkat lunak (software) yang digunakan adalah R 3.1.3 dan RStudio. Fungsi-fungsi R yang digunakan di dalam penelitian antara lain fungsi “nls” untuk menerapkan metode NLS-GN, fungsi “GA” pada paket “GA” yang dikembangkan oleh Scrucca (2013) untuk menerapkan metode NLS-GA, dan fungsi “mvrnorm” pada paket “lestat” untuk pembangkitan bilangan acak menyebar multivariat normal. Beberapa ketetapan untuk masing-masing metode yang digunakan di dalam penelitian adalah sebagai berikut:
1. Untuk metode NLS-GN, nilai awal untuk semua parameter ( ) = 1 dan toleransi galat ( ) sebesar 10-5.
9 Prosedur Analisis pada Data Simulasi
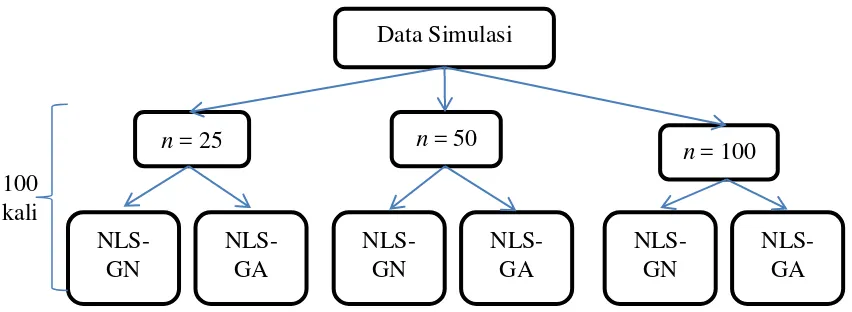
Prosedur analisis untuk data simulasi di dalam penelitian ini digambarkan pada diagram alir pada Gambar 3 dengan rincian sebagai berikut:
1. Melakukan resampling tanpa pengembalian sebanyak n data dari data populasi.
2. Melakukan pendugaan parameter untuk setiap metode. 3. Menyimpan hasil pendugaan parameter ke dalam matriks.
4. Mengulangi langkah 1-3 sebanyak 100 kali, kemudian menghitung rataan dan simpangan baku dari parameter hasil pendugaan.
5. Melakukan langkah 1-4 dengan ukuran contoh yang berbeda-beda (n = 25, n = 50, dan n = 100).
Prosedur diatas dilakukan sebanyak satu kali untuk setiap jenis data (data simulasi tanpa masalah multikolinearitas dan data simulasi dengan masalah multikolinearitas). Metode terbaik untuk data simulasi adalah metode yang menghasilkan dugaan yang memenuhi kriteria MVUE, yaitu nilai rataan dugaan parameter yang mendekati nilai parameter sebenarnya dan nilai ragam (dalam penelitian ini diwakilkan oleh simpangan baku) dugaan parameter yang paling kecil. Rincian program R untuk prosedur analisis pada data simulasi dapat dilihat pada Lampiran 2 dan Lampiran 3.
Gambar 3 Prosedur analisis pada data simulasi Prosedur Analisis pada Data Riil
Prosedur analisis untuk data riil di dalam penelitian ini digambarkan pada diagram alir pada Gambar 4 dengan rincian sebagai berikut:
1. Melakukan pendugaan parameter untuk setiap metode.
2. Melakukan K-Fold Cross Validation dengan k=5 (empat bagian terdiri dari sepuluh baris data dan satu bagian sisanya terdiri dari lima baris data) Metode terbaik untuk data riil adalah metode yang menghasil persamaan dengan kemampuan prediksi yang lebih baik, yaitu persamaan yang menghasilkan nilai sisaan validasi silang yang paling kecil. Rincian program R untuk prosedur analisis pada data riil dapat dilihat pada Lampiran 4.
n = 25
Data Simulasi
n = 50
n = 100
NLS-GN
NLS-GA
NLS-GN
NLS-GA
NLS-GN
NLS-GA 100
10
Gambar 4 Prosedur analisis pada data riil
HASIL DAN PEMBAHASAN
Aplikasi Algoritme Genetika pada Data Simulasi tanpa Masalah Multikolinearitas
Hasil 100 kali pendugaan parameter untuk setiap ukuran contoh (n = 25, n = 50 dan n = 100) menunjukkan bahwa metode NLS-GA mampu melakukan pendugaan parameter dengan cukup baik. Hal ini terlihat dari rataan dugaan parameter hasil metode NLS-GA mendekati nilai parameter ( = 0.1835,
= 0.5932, = −0.0065, = 0.4153, = −0.0431) dan simpangan baku dugaan parameter yang cukup kecil. Namun jika dibandingkan dengan metode NLS-GN, metode NLS-GA belum mampu menghasilkan dugaan parameter yang lebih baik dibanding metode NLS-GN. Hal ini terlihat dari rataan dugaan parameter hasil metode NLS-GN lebih mendekati nilai parameter bila dibandingkan dengan rataan dugaan parameter hasil metode NLS-GA. Metode NLS-GN juga menghasilkan dugaan parameter dengan simpangan baku yang lebih kecil bila dibandingkan dengan simpangan baku dugaan parameter hasil metode NLS-GA. Rincian rataan dan simpangan baku dugaan parameter hasil metode NLS-GN dan NLS-GA dapat dilihat pada Tabel 2 dan Tabel 3.
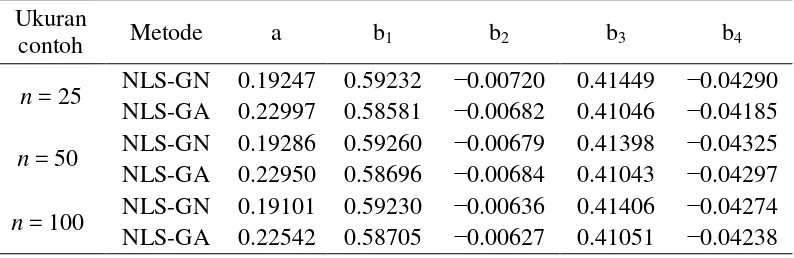
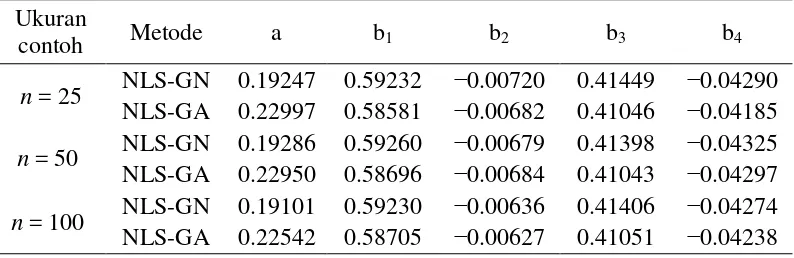
Tabel 2 Rataan hasil dugaan parameter untuk masing-masing metode di setiap ukuran contoh pada data simulasi tanpa masalah multikolinearitas
Ukuran
contoh Metode a b1 b2 b3 b4
n = 25 NLS-GN 0.19247 0.59232 −0.00720 0.41449 −0.04290 NLS-GA 0.22997 0.58581 −0.00682 0.41046 −0.04185 n = 50 NLS-GN 0.19286 0.59260 −0.00679 0.41398 −0.04325 NLS-GA 0.22950 0.58696 −0.00684 0.41043 −0.04297 n = 100 NLS-GN 0.19101 0.59230 −0.00636 0.41406 −0.04274 NLS-GA 0.22542 0.58705 −0.00627 0.41051 −0.04238
Data Riil
NLS-GN NLS-GA
K-Fold Cross Validation (k=5)
10
Gambar 4 Prosedur analisis pada data riil
HASIL DAN PEMBAHASAN
Aplikasi Algoritme Genetika pada Data Simulasi tanpa Masalah Multikolinearitas
Hasil 100 kali pendugaan parameter untuk setiap ukuran contoh (n = 25, n = 50 dan n = 100) menunjukkan bahwa metode NLS-GA mampu melakukan pendugaan parameter dengan cukup baik. Hal ini terlihat dari rataan dugaan parameter hasil metode NLS-GA mendekati nilai parameter ( = 0.1835,
= 0.5932, = −0.0065, = 0.4153, = −0.0431) dan simpangan baku dugaan parameter yang cukup kecil. Namun jika dibandingkan dengan metode NLS-GN, metode NLS-GA belum mampu menghasilkan dugaan parameter yang lebih baik dibanding metode NLS-GN. Hal ini terlihat dari rataan dugaan parameter hasil metode NLS-GN lebih mendekati nilai parameter bila dibandingkan dengan rataan dugaan parameter hasil metode NLS-GA. Metode NLS-GN juga menghasilkan dugaan parameter dengan simpangan baku yang lebih kecil bila dibandingkan dengan simpangan baku dugaan parameter hasil metode NLS-GA. Rincian rataan dan simpangan baku dugaan parameter hasil metode NLS-GN dan NLS-GA dapat dilihat pada Tabel 2 dan Tabel 3.
Tabel 2 Rataan hasil dugaan parameter untuk masing-masing metode di setiap ukuran contoh pada data simulasi tanpa masalah multikolinearitas
Ukuran
contoh Metode a b1 b2 b3 b4
n = 25 NLS-GN 0.19247 0.59232 −0.00720 0.41449 −0.04290 NLS-GA 0.22997 0.58581 −0.00682 0.41046 −0.04185 n = 50 NLS-GN 0.19286 0.59260 −0.00679 0.41398 −0.04325 NLS-GA 0.22950 0.58696 −0.00684 0.41043 −0.04297 n = 100 NLS-GN 0.19101 0.59230 −0.00636 0.41406 −0.04274 NLS-GA 0.22542 0.58705 −0.00627 0.41051 −0.04238
Data Riil
NLS-GN NLS-GA
K-Fold Cross Validation (k=5)
11 Tabel 3 Simpangan baku hasil dugaan parameter untuk masing-masing metode di setiap ukuran contoh pada data simulasi tanpa masalah multikolinearitas Ukuran
contoh Metode a b1 b2 b3 b4
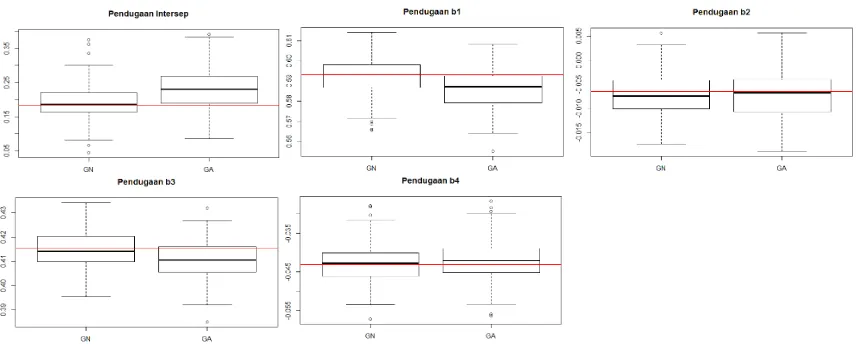
n = 25 NLS-GN 0.05670 0.00994 0.00441 0.00722 0.00517 NLS-GA 0.06205 0.01060 0.00459 0.00806 0.00554 n = 50 NLS-GN 0.04604 0.00668 0.00273 0.00473 0.00353 NLS-GA 0.05090 0.00765 0.00298 0.00505 0.00382 n = 100 NLS-GN 0.02688 0.00426 0.00164 0.00320 0.00216 NLS-GA 0.03248 0.00510 0.00178 0.00393 0.00259 Hasil pendugaan parameter juga disajikan dalam bentuk boxplot. Boxplot hasil pendugaan parameter dari masing-masing metode untuk ukuran contoh n = 25 dapat dilihat pada Gambar 5, sedangkan untuk semua ukuran contoh dapat dilihat pada Lampiran 5. Pada Gambar 5, terlihat bahwa garis tengah boxplot dugaan parameter yang dihasilkan oleh metode NLS-GN lebih mendekati nilai parameter (garis merah) dibanding boxplot dugaan parameter hasil metode NLS-GA, yang menunjukkan bahwa dugaan parameter hasil metode NLS-GN memiliki bias yang lebih kecil dibanding dugaan parameter hasil metode NLS-GA. Boxplot dugaan parameter yang dihasilkan oleh metode NLS-GN juga memiliki lebar kotak yang lebih kecil dibanding boxplot dugaan parameter hasil metode NLS-GA, yang menunjukkan bahwa dugaan parameter hasil metode NLS-GN memiliki keragaman yang lebih kecil dibanding dugaan parameter hasil metode NLS-GA.
Gambar 5 Boxplot dari dugaan parameter hasil metode NLS-GN dan NLS-GA pada data simulasi tanpa masalah multikolinearitas (n = 25)
Aplikasi Algoritme Genetika pada Data Simulasi dengan Masalah Multikulinearitas
12
metode NLS-GA cukup jauh dari nilai parameter ( = 0.1835, = 0.5932, = −0.0065, = 0.4153, = −0.0431). Hal yang sama juga terjadi pada metode NLS-GN, tetapi jika dibandingkan dengan metode NLS-GA, hasil metode NLS-GN memiliki bias yang lebih kecil. Hal ini terlihat dari rataan dugaan parameter hasil metode NLS-GN lebih mendekati nilai parameter bila dibandingkan dengan rataan dugaan parameter hasil metode NLS-GA.
Namun, berbeda dengan metode NLS-GN yang menghasilkan dugaan parameter dengan simpangan baku yang besar karena masalah multikolinearitas, metode NLS-GA mampu mengatasi masalah multikolinearitas dalam melakukan pendugaan parameter. Metode NLS-GA menghasilkan dugaan parameter dengan simpangan baku yang jauh lebih kecil bila dibandingkan dengan metode NLS-GN. Rincian rataan dan simpangan baku dugaan parameter hasil metode NLS-GN dan NLS-GA dapat dilihat pada Tabel 4 dan Tabel 5.
Tabel 4 Rataan hasil dugaan parameter untuk masing-masing metode di setiap ukuran contoh pada data simulasi dengan masalah multikolinearitas Ukuran
contoh Metode a b1 b2 b3 b4
n = 25 NLS-GN 0.39820 0.57469 0.03605 0.41718 −0.12420 NLS-GA 0.41833 0.40224 0.13691 0.32453 0.03486 n = 50 NLS-GN 0.31305 0.58799 0.05814 0.34554 −0.06631
NLS-GA 0.32870 0.44426 0.12586 0.27463 0.07661 n = 100 NLS-GN 0.32137 0.50925 0.09230 0.39478 −0.07310
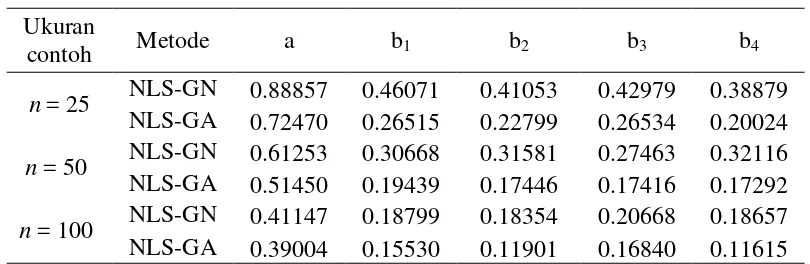
NLS-GA 0.32877 0.42415 0.12277 0.33630 0.03808 Tabel 5 Simpangan baku hasil dugaan parameter untuk masing-masing metode di
setiap ukuran contoh pada data simulasi dengan masalah multikolinearitas
Ukuran
contoh Metode a b1 b2 b3 b4
13 bias yang lebih kecil dibanding dugaan parameter hasil metode NLS-GA. Namun dugaan parameter metode NLS-GA mampu menghasilkan boxplot dengan lebar kotak yang lebih kecil dibanding boxplot dugaan parameter hasil metode NLS-GN, yang menunjukkan bahwa dugaan parameter hasil metode NLS-GA memiliki keragaman yang lebih kecil dibanding dugaan parameter hasil metode NLS-GN.
Gambar 6 Boxplot dari dugaan parameter hasil metode NLS-GN dan NLS-GA pada data simulasi dengan masalah multikolinearitas (n = 25)
Aplikasi Algoritme Genetika pada Data Riil
Baik metode NLS-GN maupun NLS-GA menghasilkan dugaan parameter yang tidak jauh berbeda pada data riil. Namun, hasil K-Fold Cross Validation menunjukkan bahwa nilai sisaan validasi silang dari model yang dihasilkan metode NLS-GA lebih kecil bila dibandingkan dengan model yang dihasilkan metode NLS-GN, sehingga disimpulkan bahwa metode NLS-GA mampu menghasilkan model dengan kemampuan prediksi lebih baik dibanding metode NLS-GN. Rincian hasil pendugaan parameter dan K-Fold Cross Validation untuk masing-masing metode dapat dilihat pada Tabel 6 dan Tabel 7.
Tabel 6 Hasil dugaan parameter untuk masing-masing metode pada data riil
Metode a b1 b2 b3
NLS-GN 6.69072 0.04271 0.29299 −0.02379 NLS-AG 6.70112 0.04276 0.29031 −0.02361
Tabel 7 Nilai sisaan validasi silang untuk setiap model yang dihasilkan oleh masing-masing metode pada data riil
14
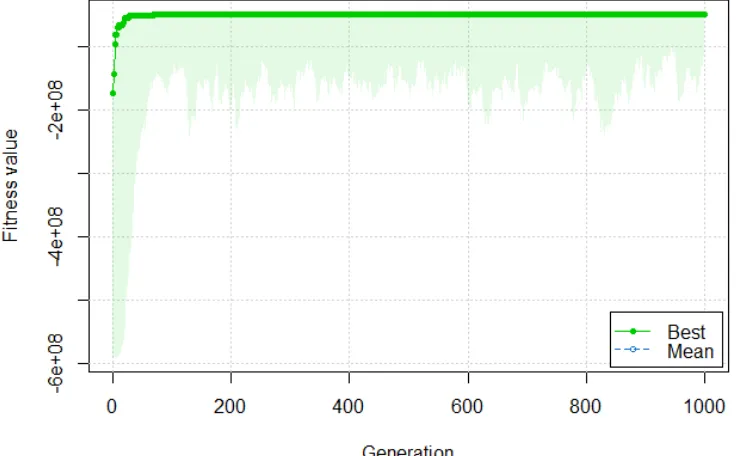
Metode NLS-GA membutuhkan waktu yang lebih lama dibanding metode NLS-GN. Metode NLS-GN hanya membutuhkan waktu 0.02667 detik untuk melakukan proses pendugaan parameter, sedangkan metode NLS-GA membutuhkan waktu 1.98653 menit untuk melakukan proses pendugaan parameter. Grafik iterasi proses pendugaan dengan metode NLS-GA dapat dilihat pada Gambar 7.
Gambar 7 Grafik iterasi metode NLS-GA
SIMPULAN DAN SARAN
Metode NLS-GA mampu menghasilkan dugaan parameter yang cukup baik pada data simulasi tanpa masalah multikolinearitas, namun tidak lebih baik bila dibandingkan dengan metode NLS-GN pada data yang sama. Metode NLS-GA menghasilkan dugaan parameter yang kurang baik pada data simulasi dengan masalah multikolinearitas, namun mampu mengatasi problem yang dihadapi metode NLS-GN ketika dihadapkan pada data dengan masalah multikolinearitas, dengan menghasilkan dugaan parameter dengan simpangan baku yang jauh lebih kecil dibanding metode NLS-GN. Metode NLS-GN maupun NLS-GA menghasilkan dugaan parameter yang tidak jauh berbeda pada data riil, namun hasil K-Fold Cross Validation menunjukkan bahwa bahwa metode NLS-GA mampu menghasilkan model dengan kemampuan prediksi lebih baik dibanding metode NLS-GN.
14
Metode NLS-GA membutuhkan waktu yang lebih lama dibanding metode NLS-GN. Metode NLS-GN hanya membutuhkan waktu 0.02667 detik untuk melakukan proses pendugaan parameter, sedangkan metode NLS-GA membutuhkan waktu 1.98653 menit untuk melakukan proses pendugaan parameter. Grafik iterasi proses pendugaan dengan metode NLS-GA dapat dilihat pada Gambar 7.
Gambar 7 Grafik iterasi metode NLS-GA
SIMPULAN DAN SARAN
Metode NLS-GA mampu menghasilkan dugaan parameter yang cukup baik pada data simulasi tanpa masalah multikolinearitas, namun tidak lebih baik bila dibandingkan dengan metode NLS-GN pada data yang sama. Metode NLS-GA menghasilkan dugaan parameter yang kurang baik pada data simulasi dengan masalah multikolinearitas, namun mampu mengatasi problem yang dihadapi metode NLS-GN ketika dihadapkan pada data dengan masalah multikolinearitas, dengan menghasilkan dugaan parameter dengan simpangan baku yang jauh lebih kecil dibanding metode NLS-GN. Metode NLS-GN maupun NLS-GA menghasilkan dugaan parameter yang tidak jauh berbeda pada data riil, namun hasil K-Fold Cross Validation menunjukkan bahwa bahwa metode NLS-GA mampu menghasilkan model dengan kemampuan prediksi lebih baik dibanding metode NLS-GN.
15 dengan masalah heteroskedastisitas atau data dengan masalah autokorelasi. Kendala utama dalam penelitian ini adalah terbatasnya sumber daya, yaitu spesifikasi komputer yang digunakan cukup rendah, sehingga untuk penelitian selanjutnya disarankan untuk menggunakan komputer dengan spesifikasi yang lebih baik.
DAFTAR PUSTAKA
Chapra SC, Canale RP. 2002. Numerical Methods for Engineers: With Software and Programming Applications. Ed ke-4. New York (US): McGraw-Hill. Chisasa J, Makina D. 2013. Bank Credit And Agricultural Output In South Africa:
A Cobb-Douglas Empirical Analysis. International Business & Economics Research Journal. 12(4): 387-398.
Cobb CW, Douglas PH. 1928. A Theory of Production. The American Economic Review. 18(1): 139-165.
Erko A, Tez M, Akay KU. 2010. On Multicolinearity in Nonlinear Regression Models. Sel uk Journal of Applied Mathematics. Special Issue: 65-72
Goldfeld SM, Quandt RE. 1970. The Estimation of Cobb-Douglas Type Functions with Multiplicative and Additive Errors. International Economic Review. 11(2): 251-257.
Good PI. 2006. Resampling Method: A Practical Guide to Data Analysis. Ed ke-3. Boston (US): Birkh user.
Gujarati DN, Porter DC. 2010. Basic Econometrics. Ed ke-5. New York (US): McGraw-Hill.
Hogg RV, McKean JW, Craig AT. 2005. Introduction to Mathematical Statistics. Ed ke-6. New Jersey (US): Pearson Prentice Hall.
Hopgood AA. 2001. Intelligent Systems for Engineers and Scientists. Boca Raton (US): CRC Press.
Huet S, Bouvier A, Poursat MA, Jolivet E. 2003. Statistical Tools for Nonlinear Regression: A Practical Guide with S-PLUS and R Examples. Ed ke-2. New York (US): Springer.
Izenman AJ. 2008. Modern Multivariate Statistical Techniques: Regression, Classification, and Manifold Learning. New York (US): Springer.
Michalewicz Z. 1992. Genetic Algorithms + Data Structures = Evolution Programs. Ed ke-2. New York (US): Springer.
Sartono B. 2010. Pengenalan Algoritme Genetik untuk Pemilihan Peubah Penjelas dalam Model Regresi Menggunakan SAS/IML.Forum Statistika dan Komputasi. 15(2): 10-15.
Scrucca L. 2013. GA: A Package for Genetic Algorithms in R. Journal of Statistics Software. 53(4): 1-37.
Soekartawi. 2002. Prinsip Dasar Ekonomi Pertanian: Teori dan Aplikasi. Jakarta (ID): Raja Grafindo Persada.
15 dengan masalah heteroskedastisitas atau data dengan masalah autokorelasi. Kendala utama dalam penelitian ini adalah terbatasnya sumber daya, yaitu spesifikasi komputer yang digunakan cukup rendah, sehingga untuk penelitian selanjutnya disarankan untuk menggunakan komputer dengan spesifikasi yang lebih baik.
DAFTAR PUSTAKA
Chapra SC, Canale RP. 2002. Numerical Methods for Engineers: With Software and Programming Applications. Ed ke-4. New York (US): McGraw-Hill. Chisasa J, Makina D. 2013. Bank Credit And Agricultural Output In South Africa:
A Cobb-Douglas Empirical Analysis. International Business & Economics Research Journal. 12(4): 387-398.
Cobb CW, Douglas PH. 1928. A Theory of Production. The American Economic Review. 18(1): 139-165.
Erko A, Tez M, Akay KU. 2010. On Multicolinearity in Nonlinear Regression Models. Sel uk Journal of Applied Mathematics. Special Issue: 65-72
Goldfeld SM, Quandt RE. 1970. The Estimation of Cobb-Douglas Type Functions with Multiplicative and Additive Errors. International Economic Review. 11(2): 251-257.
Good PI. 2006. Resampling Method: A Practical Guide to Data Analysis. Ed ke-3. Boston (US): Birkh user.
Gujarati DN, Porter DC. 2010. Basic Econometrics. Ed ke-5. New York (US): McGraw-Hill.
Hogg RV, McKean JW, Craig AT. 2005. Introduction to Mathematical Statistics. Ed ke-6. New Jersey (US): Pearson Prentice Hall.
Hopgood AA. 2001. Intelligent Systems for Engineers and Scientists. Boca Raton (US): CRC Press.
Huet S, Bouvier A, Poursat MA, Jolivet E. 2003. Statistical Tools for Nonlinear Regression: A Practical Guide with S-PLUS and R Examples. Ed ke-2. New York (US): Springer.
Izenman AJ. 2008. Modern Multivariate Statistical Techniques: Regression, Classification, and Manifold Learning. New York (US): Springer.
Michalewicz Z. 1992. Genetic Algorithms + Data Structures = Evolution Programs. Ed ke-2. New York (US): Springer.
Sartono B. 2010. Pengenalan Algoritme Genetik untuk Pemilihan Peubah Penjelas dalam Model Regresi Menggunakan SAS/IML.Forum Statistika dan Komputasi. 15(2): 10-15.
Scrucca L. 2013. GA: A Package for Genetic Algorithms in R. Journal of Statistics Software. 53(4): 1-37.
Soekartawi. 2002. Prinsip Dasar Ekonomi Pertanian: Teori dan Aplikasi. Jakarta (ID): Raja Grafindo Persada.
16
Lampiran 1 Data produksi pertanian beserta rincian peubah
No Negara X1 X2 X3 Y
1 Albania 7574 100.59862 143900 3466.3
2 Algeria 97809 25.09516 3000600 1344.1
3 Belarus 55330 146.91781 2201996 2992.8
4 Brazil 791191 150.94595 20426199 3131.5
5 Bulgaria 30962 80.85180 1830123 4077.8
6 Canada 732915 54.63277 16161700 3141.9
7 Chile 53850 491.35267 706925 5657.5
8 Cuba 75562 18.53022 304417 2921.5
9 Czech Republic 89350 87.00808 1617101 5444.5
10 Denmark 115360 144.78449 1490600 6013.1
11 Estonia 37178 84.52124 260979 2330.3
12 Fiji 5644 45.28824 6439 2374.6
13 Finland 174000 132.74553 1127100 3210.6
14 Ghana 1912 13.20050 1332718 1373.3
15 Greece 258476 176.41765 1261210 4034
16 Hungary 119044 98.52110 3001698 5589.9
17 Latvia 55697 64.12884 432900 2447.4
18 Lithuania 107800 173.76021 878500 3254.9
19 Luxembourg 6787 333.61290 27981 6396.6
20 Macedonia, FYR 53700 53.48156 189597 3596.7
21 Madagascar 550 2.20305 1441159 2354.2
22 Mali 700 52.04158 3292388 864.1
23 Mexico 253546 73.29420 10496782 3078.6
24 Moldova 39600 8.31522 1039038 2832
25 Nigeria 23000 4.54511 17716000 1372.8
26 Norway 132951 215.23015 328200 4401.5
27 Paraguay 23470 78.42196 843935 2445.8
28 Poland 1365400 129.13561 8377273 3537.6
29 Portugal 175150 208.31490 462756 2945.5
30 Romania 171811 42.62524 6107605 3995.3
31 Russian Federation 531973 11.41978 40493400 1882.6
32 Senegal 645 12.50247 1083525 973.3
33 Slovak Republic 22053 83.66691 818331 4640.8
34 Slovenia 105250 358.69886 100729 5815.1
35 South Africa 63200 60.28759 4321204 2782.7
36 Spain 966598 165.40261 6597267 3760.5
37 Sudan 16639 4.60897 5349940 657.2
38 Suriname 988 141.03774 49044 3559
39 Sweden 160600 97.85392 1125672 4892.9
17 Lampiran 1 (lanjutan)
No Negara X1 X2 X3 Y
41 Togo 96 3.39312 729829 1094.8
42 Trinidad and Tobago 5129 84.88462 3000 1573.3
43 Tunisia 34982 36.14296 1654901 1307.9
44 Ukraine 370404 16.41802 14409100 2845.2
45 Uruguay 36465 138.88769 587066 4298.9
Rincian peubah:
Peubah Deskripsi
Y Hasil produksi biji-bijian (kg/ha) X1 Jumlah traktor dan mesin pertanian
X2 Konsumsi pupuk (kg/ha)
18
Lampiran 2 Program R untuk proses analisis pada data simulasi tanpa masalah multikolinearitas
#Mengaktifkan paket “GA”
library(GA)
#Membuat matriks penampung dugaan parameter a<-1:100 b1<-1:100 b2<-1:100 b3<-1:100 b4<-1:100 hasil1<-data.frame(a,b1,b2,b3,b4,waktu) a<-1:100 b1<-1:100 b2<-1:100 b3<-1:100 b4<-1:100 hasil2<-data.frame(a,b1,b2,b3,b4,waktu)
#Pembangkitan data populasi
beta<-c(0.1835,0.5932,-0.0065,0.4153,-0.0431) e<-rnorm(1000,0,1) pop1<-runif(1000,0.1,100) pop2<-runif(1000,0.1,100) pop3<-runif(1000,0.1,100) pop4<-runif(1000,0.1,100) resp<-exp(beta[1])*(pop1^beta[2])*(pop2^beta[3])*(pop3^beta[4])* (pop4^beta[5])+e popgab1<-data.frame(resp,pop1,pop2,pop3,pop4)
#Fungsi untuk proses simulasi 100 kali dengan ukuran contoh n simulasi1<-function(n){
for (i in 1:100){
#Proses resampling data<-popgab1[sample(nrow(popgab1),n),] colnames(data)<-c("y1","x1","x2","x3","x4") rownames(data)<-NULL y1<-data$y1 x1<-data$x1 x2<-data$x2 x3<-data$x3 x4<-data$x4
#Pendugaan parameter dengan metode NLS-GN GN<-nls(y1~exp(a)*x1^b1*x2^b2*x3^b3*x4^b4, data=data,
start=list(a=1, b1=1, b2=1, b3=1, b4=1),
19 Lampiran 2 (lanjutan)
hasil1[i,3]<-parameter[3] hasil1[i,4]<-parameter[4] hasil1[i,5]<-parameter[5]
#Pendugaan parameter dengan metode NLS-GA
fit.cd <- function(data=data, a, b1, b2, b3, b4){ Y_hat <- exp(a) * x1^b1 * x2^b2 * x3^b3 * x4^b4 SSE = t(y1-Y_hat) %*% (y1-Y_hat)
return(SSE) }
GA<-ga(type="real-valued", min=c(-10,-1,-1,-1,-1), max=c(10,1,1,1,1),
fitness=function(b) -fit.cd(data,b[1],b[2],b[3],b[4], b[5]),
popSize=1000, maxiter=1000, pcrossover=0.8, pmutation=0.05,
elitism = base::max(1, round(1000*0.05)) )
summary(GA)
solusi<-print(summary(GA2)$solution) hasil2[i,1]<-solusi[1]
hasil2[i,2]<-solusi[2] hasil2[i,3]<-solusi[3] hasil2[i,4]<-solusi[4] hasil2[i,5]<-solusi[5] }
20
Lampiran 3 Program R untuk proses analisis pada data simulasi dengan masalah multikolinearitas
#Mengaktifkan paket “GA” dan “lestat”
library("lestat") library("GA")
#Membuat matriks penampung dugaan parameter a<-1:100 b1<-1:100 b2<-1:100 b3<-1:100 b4<-1:100 hasil1<-data.frame(a,b1,b2,b3,b4,waktu) a<-1:100 b1<-1:100 b2<-1:100 b3<-1:100 b4<-1:100 hasil2<-data.frame(a,b1,b2,b3,b4,waktu)
#Pembangkitan data populasi
beta<-c(0.1835,0.5932,-0.0065,0.4153,-0.0431) e<-rnorm(1000,0,1)
corr<-matrix(1:64,4,4) for (i in 1:4){
for (j in 1:4){
ifelse (i==j, corr[i,j]<-1, corr[i,j]<-0.8) } } dist<-mvrnorm(1000,rep(50,4), corr) dist pop1<-dist[,1] pop2<-dist[,2] pop3<-dist[,3] pop4<-dist[,4] resp<-exp(beta[1])*(pop1^beta[2])*(pop2^beta[3])*(pop3^beta[4])* (pop4^beta[5])+e popgab2<-data.frame(resp,pop1,pop2,pop3,pop4)
#Fungsi untuk proses simulasi 100 kali dengan ukuran contoh n simulasi2<-function(n){
for (i in 1:100){
#Proses resampling data<-popgab2[sample(nrow(popgab2),n),] colnames(data)<-c("y2","x1","x2","x3","x4") rownames(data)<-NULL y2<-data$y2 x1<-data$x1 x2<-data$x2 x3<-data$x3 x4<-data$x4
21 Lampiran 3 (lanjutan)
start=list(a=1, b1=1, b2=1, b3=1, b4=1),
nls.control(maxiter = 1000, tol = 1e-05, warnOnly=TRUE), trace=TRUE
)
summary(GN)
parameter<-print(summary(GN)$parameters[,1]) hasil1[i,1]<-parameter[1]
hasil1[i,2]<-parameter[2] hasil1[i,3]<-parameter[3] hasil1[i,4]<-parameter[4] hasil1[i,5]<-parameter[5]
#Pendugaan parameter dengan metode NLS-GA
fit.cd <- function(data=data, a, b1, b2, b3, b4){ Y_hat <- exp(a) * x1^b1 * x2^b2 * x3^b3 * x4^b4 SSE = t(y2-Y_hat) %*% (y2-Y_hat)
return(SSE) }
GA<-ga(type="real-valued", min=c(-10,-1,-1,-1,-1), max=c(10,1,1,1,1),
fitness=function(b) -fit.cd(data4,b[1],b[2],b[3],b[4], b[5]),
popSize=1000, maxiter=1000, pcrossover=0.8, pmutation=0.05,
elitism = base::max(1, round(1000*0.05)) )
summary(GA) waktu2<-t2-t1
solusi<-print(summary(GA)$solution) hasil2[i,1]<-solusi[1]
hasil2[i,2]<-solusi[2] hasil2[i,3]<-solusi[3] hasil2[i,4]<-solusi[4] hasil2[i,5]<-solusi[5] }
22
Lampiran 4 Program R untuk proses analisis pada data riil
#Membuat matriks penampung dugaan parameter a<-1 b1<-1 b2<-1 b3<-1 waktu<-1 hasil1<-data.frame(a,b1,b2,b3,waktu) a<-1 b1<-1 b2<-1 b3<-1 waktu<-1 hasil12<-data.frame(a,b1,b2,b3,waktu)
#Fungsi pendugaan parameter untuk data riil (format data [x1|x2|x3 |y] aplikasi<-function(data){ y<-data$y x1<-data$x1 x2<-data$x2 x3<-data$x3
#Pendugaan parameter dengan metode NLS-GN Sys.time()->t1
GN<-nls(y~exp(a)*x1^b1*x2^b2*x3^b3, data=data,
start=list(a=1, b1=1, b2=1, b3=1),
nls.control(maxiter = 1000, tol = 1e-05, warnOnly=TRUE), trace=TRUE ) Sys.time()->t2 summary(GN) waktu1<-t2-t1 parameter<-print(summary(GN)$parameters[,1]) hasil1[,1]<-parameter[1] hasil1[,2]<-parameter[2] hasil1[,3]<-parameter[3] hasil1[,4]<-parameter[4] hasil1[,5]<-waktu1
#Pendugaan parameter dengan metode NLS-GA fit.cd <- function(data=data, a, b1, b2, b3){ Y_hat <- exp(a) * x1^b1 * x2^b2 * x3^b3 SSE = t(y-Y_hat) %*% (y-Y_hat)
23 Lampiran 4 (lanjutan)
elitism = base::max(1, round(1000*0.05)) ) Sys.time()->t2 summary(GA) plot(GA) waktu2<-t2-t1 solusi<-print(summary(GA)$solution) hasil2[,1]<-solusi[1] hasil2[,2]<-solusi[2] hasil2[,3]<-solusi[3] hasil2[,4]<-solusi[4] hasil2[,5]<-waktu2
#Pengacakan data untuk validasi silang
coba<-data[sample(nrow(data),45,replace=FALSE),] rownames(coba)<-NULL y<-coba[,1] x1<-coba[,2] x2<-coba[,3] x3<-coba[,4]
#Proses validasi silang untuk metode NLS-GN solusi1<-matrix(1:20,5,4)
GN<-nls(y~exp(a)*x1^b1*x2^b2*x3^b3, data=coba[-(1:10),],
start=list(a=1, b1=1, b2=1, b3=1),
nls.control(maxiter = 1000, tol = 1e-05, warnOnly=TRUE), trace=TRUE
)
solusi1[1,]<-print(summary(GN)$parameters[,1])
GN<-nls(y~exp(a)*x1^b1*x2^b2*x3^b3, data=coba[-(11:20),],
start=list(a=1, b1=1, b2=1, b3=1),
nls.control(maxiter = 1000, tol = 1e-05, warnOnly=TRUE), trace=TRUE
)
solusi1[2,]<-print(summary(GN)$parameters[,1])
GN<-nls(y~exp(a)*x1^b1*x2^b2*x3^b3, data=coba[-(21:30),],
start=list(a=1, b1=1, b2=1, b3=1),
nls.control(maxiter = 1000, tol = 1e-05, warnOnly=TRUE), trace=TRUE
)
solusi1[3,]<-print(summary(GN)$parameters[,1])
GN<-nls(y~exp(a)*x1^b1*x2^b2*x3^b3, data=coba[-(31:40),],
start=list(a=1, b1=1, b2=1, b3=1),
nls.control(maxiter = 1000, tol = 1e-05, warnOnly=TRUE), trace=TRUE
)
solusi1[4,]<-print(summary(GN)$parameters[,1])
24
Lampiran 4 (lanjutan)
data=coba[-(41:45),],
start=list(a=1, b1=1, b2=1, b3=1),
nls.control(maxiter = 1000, tol = 1e-05, warnOnly=TRUE), trace=TRUE
)
solusi1[5,]<-print(summary(GN)$parameters[,1]) solusi1
yduga<-1:45
for (i in 1:10){
yduga[i]<-exp(solusi1[1,1])* x1[i]^solusi1[1,2]*
x2[i]^solusi1[1,3]* x3[i]^solusi1[1,4] }
for (i in 11:20){
yduga[i]<-exp(solusi1[2,1])* x1[i]^solusi1[2,2]*
x2[i]^solusi1[2,3]* x3[i]^solusi1[2,4] }
for (i in 21:30){
yduga[i]<-exp(solusi1[3,1])* x1[i]^solusi1[3,2]*
x2[i]^solusi1[3,3]* x3[i]^solusi1[3,4] }
for (i in 31:40){
yduga[i]<-exp(solusi1[4,1])* x1[i]^solusi1[4,2]*
x2[i]^solusi1[4,3]* x3[i]^solusi1[4,4] }
for (i in 41:45){
yduga[i]<-exp(solusi1[5,1])* x1[i]^solusi1[5,2]* x2[i]^solusi1[5,3]* x3[i]^solusi1[5,4] } yduga jkg<-1:45
for (i in 1:45){
25 Lampiran 4 (lanjutan)
cv1[5]<-sum(jkg[41:45]/5)
#Proses validasi silang untuk metode NLS-GA solusi2<-matrix(1:20,5,4)
fit.cd <- function(data=coba[-(1:10),], a, b1, b2, b3){ Y_hat <- exp(a) * x1^b1 * x2^b2 * x3^b3
SSE = t(y-Y_hat) %*% (y-Y_hat) return(SSE) } GA<-ga(type="real-valued", min=c(-10,-1,-1,-1), max=c(10,1,1,1), fitness=function(b) -fit.cd(coba[-(1:10)],b[1],b[2],b[3], b[4]), popSize=1000, maxiter=1000, pcrossover=0.8, pmutation=0.05,
elitism = base::max(1, round(1000*0.05)) )
solusi2[1,]<-print(summary(GA)$solution)
fit.cd <- function(data=coba[-(11:20),], a, b1, b2, b3){ Y_hat <- exp(a) * x1^b1 * x2^b2 * x3^b3
SSE = t(y-Y_hat) %*% (y-Y_hat) return(SSE) } GA<-ga(type="real-valued", min=c(-10,-1,-1,-1), max=c(10,1,1,1), fitness=function(b) -fit.cd(coba[-(11:20)],b[1],b[2],b[3], b[4]), popSize=1000, maxiter=1000, pcrossover=0.8, pmutation=0.05,
elitism = base::max(1, round(1000*0.05)) )
solusi2[2,]<-print(summary(GA)$solution)
fit.cd <- function(data=coba[-(21:30),], a, b1, b2, b3){ Y_hat <- exp(a) * x1^b1 * x2^b2 * x3^b3
SSE = t(y-Y_hat) %*% (y-Y_hat) return(SSE) } GA<-ga(type="real-valued", min=c(-10,-1,-1,-1), max=c(10,1,1,1), fitness=function(b) -fit.cd(coba[-(21:30)],b[1],b[2],b[3], b[4]), popSize=1000, maxiter=1000, pcrossover=0.8, pmutation=0.05,
elitism = base::max(1, round(1000*0.05)) )
26
Lampiran 4 (lanjutan)
fit.cd <- function(data=coba[-(31:40),], a, b1, b2, b3){ Y_hat <- exp(a) * x1^b1 * x2^b2 * x3^b3
SSE = t(y-Y_hat) %*% (y-Y_hat) return(SSE) } GA<-ga(type="real-valued", min=c(-10,-1,-1,-1), max=c(10,1,1,1), fitness=function(b) -fit.cd(coba[-(31:40)],b[1],b[2],b[3], b[4]), popSize=1000, maxiter=1000, pcrossover=0.8, pmutation=0.05,
elitism = base::max(1, round(1000*0.05)) )
solusi2[4,]<-print(summary(GA)$solution)
fit.cd <- function(data=coba[-(41:45),], a, b1, b2, b3){ Y_hat <- exp(a) * x1^b1 * x2^b2 * x3^b3
SSE = t(y-Y_hat) %*% (y-Y_hat) return(SSE) } GA<-ga(type="real-valued", min=c(-10,-1,-1,-1), max=c(10,1,1,1), fitness=function(b) -fit.cd(coba[-(41:45)],b[1],b[2],b[3], b[4]), popSize=1000, maxiter=1000, pcrossover=0.8, pmutation=0.05,
elitism = base::max(1, round(1000*0.05)) )
solusi2[5,]<-print(summary(GA)$solution)
yduga<-1:45
for (i in 1:10){
yduga[i]<-exp(solusi2[1,1])* x1[i]^solusi2[1,2]*
x2[i]^solusi2[1,3]* x3[i]^solusi2[1,4] }
for (i in 11:20){
yduga[i]<-exp(solusi2[2,1])* x1[i]^solusi2[2,2]*
x2[i]^solusi2[2,3]* x3[i]^solusi2[2,4] }
for (i in 21:30){
yduga[i]<-exp(solusi2[3,1])* x1[i]^solusi2[3,2]*
27 Lampiran 4 (lanjutan)
}
for (i in 31:40){
yduga[i]<-exp(solusi2[4,1])* x1[i]^solusi2[4,2]*
x2[i]^solusi2[4,3]* x3[i]^solusi2[4,4] }
for (i in 41:45){
yduga[i]<-exp(solusi2[5,1])* x1[i]^solusi2[5,2]*
x2[i]^solusi2[5,3]* x3[i]^solusi2[5,4] }
jkg<-1:45
for (i in 1:45){
jkg[i]<-((y[i]-yduga[i])^2) }
cv2<-1:5
28
Boxplot dari dugaan parameter dengan ukuran contoh n = 25
Boxplot dari dugaan parameter dengan ukuran contoh n = 50
Boxplot dari dugaan parameter dengan ukuran contoh n =100
29
Boxplot dari dugaan parameter dengan ukuran contoh n = 25
Boxplot dari dugaan parameter dengan ukuran contoh n = 50
Boxplot dari dugaan parameter dengan ukuran contoh n = 100
Judul Skripsi: Penerapan Algoritme Genetika dalam Pendugaan Parameter Fungsi
Nama NIM
'
Cobb-Douglas dengan Galat Aditif : Iqbal Hanif
: G14110077
Disetujui oleh
SSi. MT
/
��
�h_ui oleh
�- (', ' .: ' .! �. .,.., � ... // <· �- .. �.' 1 --:v' t a ( /r/ ...
� ..
<-' j
' ' '
/<
i � . /;;::��;> '· ?" - . ,i( :; _1
i,�
. �';-.� \ ( J - ·\\ �;
:·(:;>.
··.�Ir Aam Alamudi, MSi Pembimbing II
' � :
�
�;��
;�·:i
�
: • . .·;.
-.I
:. -:Dr·-nan.unria, SSi, MSi
': . .: � ..
::;.Keiua
De)artemen,. ----. ---·�--��---:.".
PENERAPAN ALGORITME GENETIKA DALAM PENDUGAAN
PARAMETER FUNGSI COBB-DOUGLAS
DENGAN GALAT ADITIF
IQBAL HANIF
DEPARTEMEN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Penerapan Algoritme Genetika dalam Pendugaan Parameter Fungsi Cobb-Douglas dengan Galat Aditif adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
ABSTRAK
IQBAL HANIF. Penerapan Algoritme Genetika dalam Pendugaan Parameter Fungsi Cobb-Douglas dengan Galat Aditif. Dibimbing oleh AGUS MOHAMAD SOLEH dan AAM ALAMUDI.
Fungsi Cobb-Douglas dengan galat aditif merupakan fungsi yang dapat digunakan untuk menganalisis hubungan antara hasil produksi dan faktor-faktor produksi. Metode yang dapat digunakan dalam menduga parameter fungsi tersebut adalah metode Nonlinear Least Square (NLS) dan algoritme yang umum digunakan adalah iterasi Gauss Newton (NLS-GN), namun metode tersebut kurang optimal ketika dihadapkan dengan masalah multikolinearitas. Algoritme alternatif yang dapat digunakan pada metode NLS adalah Algoritme Genetika (NLS-GA). Tujuan penelitian ini adalah untuk mengkaji penerapan Algoritme Genetika pada pendugaan parameter fungsi Cobb-Douglas dengan galat aditif. Hasil penelitian menunjukkan bahwa metode NLS-GA belum mampu menghasilkan dugaan parameter yang lebih baik dibanding metode NLS-GN pada data simulasi tanpa masalah multikolinearitas, namun metode NLS-GA mampu mengatasi masalah yang dihadapi metode NLS-GN ketika dihadapkan pada data dengan masalah multikolinearitas. Metode NLS-GA juga mampu menghasilkan model dengan kemampuan prediksi lebih baik dibanding metode NLS-GN pada data riil.
Kata kunci: Algoritme Genetika, Fungsi Cobb-Douglas, Nonlinear Least Square
ABSTRACT
IQBAL HANIF. The Application of Genetic Algorithm to Estimate Parameters of Cobb-Douglas Function with Additive Errors. Supervised by AGUS MOHAMAD SOLEH and AAM ALAMUDI.
Cobb-Douglas function with additive errors is a function which can be used to analyse the relationship between production output and production factors. The method commonly used to estimate the parameter of that function is Nonlinear Least Square (NLS) and a common algorithm for this method is Gauss Newton iteration (NLS-GN). However, NLS-GN method has less-optimum results when analysing multicolinearity data. A possibly better method for this analysis is Genetic Algorithm (NLS-GA). The purpose of this study is to analyse the use of Genetic Algorithm to estimate parameters of Cobb-Douglas function with additive errors. The results show that NLS-GA method could not produce a better parameter estimator than NLS-GN method does but it produced a better parameter estimator in analysing multicolinearity data. NLS-GA method is capable of producing a better model with predictive ability than NLS-GN method does with real data.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Statistika
pada
Departemen Statistika
PENERAPAN ALGORITME GENETIKA DALAM PENDUGAAN
PARAMETER FUNGSI COBB-DOUGLAS
DENGAN GALAT ADITIF
IQBAL HANIF
DEPARTEMEN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
Judul Skripsi: Penerapan Algoritme Genetika dalam Pendugaan Parameter Fungsi
Nama NIM
'
Cobb-Douglas dengan Galat Aditif : Iqbal Hanif
: G14110077
Disetujui oleh
SSi. MT
/
��
�h_ui oleh
�- (', ' .: ' .! �. .,.., � ... // <· �- .. �.' 1 --:v' t a ( /r/ ...
� ..
<-' j
' ' '
/<
i � . /;;::��;> '· ?" - . ,i( :; _1
i,�
. �';-.� \ ( J - ·\\ �;
:·(:;>.
··.�Ir Aam Alamudi, MSi Pembimbing II
' � :
�
�;��
;�·:i
�
: • . .·;.
-.I
:. -:Dr·-nan.unria, SSi, MSi
': . .: � ..
::;.Keiua
De)artemen,. ----. ---·�--��---:.".
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah SWT karena berkat rahmat dan karunia-Nya lah penulis dapat menyelesaikan karya ilmiah yang berjudul Penerapan Algoritme Genetika dalam Pendugaan Parameter Fungsi Cobb-Douglas dengan Galat Aditif.
Terselesaikannya penyusunan karya ilmiah ini tentunya tidak terlepas dari bantuan, motivasi, saran, dan kerja sama dari berbagai pihak. Oleh karena itu, penulis mengucapkan terima kasih kepada:
1. Bapak Agus Mohamad Soleh, SSi, MT selaku ketua komisi pembimbing yang sangat sabar dan teliti dalam memberikan masukan dan nasihat kepada penulis untuk dapat menghasilkan karya ilmiah yang baik.
2. Bapak Ir Aam Alamudi, MSi selaku anggota komisi pembimbing atas kesempatan yang telah diberikan kepada penulis untuk dapat mengembangkan diri pada topik yang penulis teliti.
3. Ayah, ibu, kakak serta seluruh keluarga atas segala motivasi, nasihat, dan doanya yang selalu ditujukan kepada penulis sehingga penulis selalu bersemangat untuk menyelesaikan karya ilmiah ini.
4. Seluruh Dosen Departemen Statistika IPB atas ilmunya yang tak ternilai sehingga penulis dapat menerapkan ilmu Statistika dengan baik dan benar. 5. Seluruh Staf Tata Usaha Departemen Statistika IPB yang selalu bersedia
direpotkan sehingga segala proses administrasi berjalan dengan lancar. 6. Teman-teman Statistika angkatan 2011 terutama rekan sebimbingan (M.
Fickri Ramadhan dan Fariz Akyas) atas bantuan, motivasi, dan doa mereka sehingga penulis dapat menyelesaikan karya ilmiah ini.
7. Teman-teman se-organisasi di IAAS LC-IPB (terutama departemen STD), GSB IPB (terutama departemen DBC), IMBR IPB, dan Pemuda Indonesia atas kesediaannya untuk saling bekerja sama, berbagi keceriaan, berbagi pengetahuan, dan berbagi pengalaman kepada penulis selama penulis menempuh pendidikan S1 di IPB.
Tak ada gading yang tak retak. Demi penyempurnaan karya ilmiah ini, saran, kritik, dan masukan sangat penulis harapkan dari pembaca. Semoga karya ilmiah ini bermanfaat.
DAFTAR ISI
DAFTAR TABEL vi
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
PENDAHULUAN 1
Latar Belakang 1
Tujuan Penelitian 1
TINJAUAN PUSTAKA 1
Fungsi Cobb-Douglas dengan Galat Aditif 1
Nonlinear Least Square(NLS) 2
Iterasi Gauss Newton (GN) 2
Masalah Multikolinearitas 4
Algortime Genetika (Genetic Algorithm-GA) 4
METODE 6
Data 6
Minimum Variance Unbiased Estimator (MVUE) 7
K-Fold Cross Validation 7
Metode 8
Prosedur Analisis pada Data Simulasi 9 Prosedur Analisis pada Data Riil 9
HASIL DAN PEMBAHASAN 10
Aplikasi Algoritme Genetika pada Data Simulasi tanpa Masalah
Multikolinearitas 10
Aplikasi Algoritme Genetika pada Data Simulasi dengan Masalah
Multikulinearitas 11
Aplikasi Algoritme Genetika pada Data Riil 13
SIMPULAN DAN SARAN 14
DAFTAR PUSTAKA 15
LAMPIRAN 16
DAFTAR TABEL
1 Matriks korelasi untuk pembangkitan bilangan acak multivariat normal 7 2 Rataan hasil dugaan parameter untuk masing-masing metode di setiap
ukuran contoh pada data simulasi tanpa masalah multikolinearitas 10 3 Simpangan baku hasil dugaan parameter untuk masing-masing metode di
setiap ukuran contoh pada data simulasi tanpa masalah multikolinearitas 11 4 Rataan hasil dugaan parameter untuk masing-masing metode di setiap
ukuran contoh pada data simulasi dengan masalah multikolinearitas 12 5 Simpangan baku hasil dugaan parameter untuk masing-masing metode di
setiap ukuran contoh pada data simulasi dengan masalah
multikolinearitas 12
6 Hasil dugaan parameter untuk masing-masing metode pada data riil 13 7 Nilai sisaan validasi silang untuk setiap model yang dihasilkan oleh
masing-masing metode pada data riil 13
DAFTAR GAMBAR
1 Diagram alir mekanisme metode NLS-GN 3
2 Diagram alir mekanisme metode NLS-GA 5
3 Prosedur analisis pada data simulasi 9
4 Prosedur analisis pada data riil 10
5 Boxplot dari dugaan parameter hasil metode NLS-GN dan NLS-GA pada data simulasi tanpa masalah multikolinearitas (n = 25) 11 6 Boxplot dari dugaan parameter hasil metode NLS-GN dan NLS-GA pada
data simulasi dengan masalah multikolinearitas (n = 25) 13
7 Grafik iterasi metode NLS-GA 14
DAFTAR LAMPIRAN
1 Data produksi pertanian beserta rincian peubah 16 2 Program R untuk proses analisis pada data simulasi tanpa masalah
multikolinearitas 18
3 Program R untuk proses analisis pada data simulasi dengan masalah
multikolinearitas 20
4 Program R untuk proses analisis pada data riil 22 5 Boxplot dari dugaan parameter hasil metode NLS-GN dan NLS-GA pada
data simulasi tanpa masalah multikolinearitas. 28 6 Boxplot dari dugaan parameter hasil metode NLS-GN dan NLS-GA pada