Pemrograman Geometrik dan Analisis Sensitivitasnya

(1)

PEMROGRAMAN GEOMETRIK DAN ANALISIS SENSITIVITASNYA

YUDI SURYA LESMANA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(2)

YUDI SURYA LESMANA

G54103027

(3)

ABSTRACT

YUDI SURYA LESMANA. Geometric Programming and Its Sensitivity Analysis. Directed by FARIDA HANUM and TONI BAKHTIAR.

Geometric programming (GP) is one of special form on convex optimization problems. GP is a type of mathematic optimum problem which is indicated by objective function and constraints problems which have special form. Objective function of GP is a posynomial function and its constraints are posynomial functions for inequality problem or monomial functions for equality problem. The objective of GP problem is to minimize posynomial objective function and the problems called primal geometric programming (PGP).

Geometric programming is divided into unconstrained GP and constrained GPs. The dual geometric programming (DGP) has a maximizing objective function and some constraints which satisfy the normality, ortogonality, and positivity conditions. In this paper we present some procedures in determining the solutions of the GP. We show that the optimal solution of the DGP is equivalent with that of the PGP.

(4)

oleh FARIDA HANUM dan TONI BAKHTIAR.

Pemrograman geometrik (PG) merupakan salah satu bentuk khusus dari masalah pengoptimuman konveks. PG adalah suatu tipe masalah optimisasi matematik yang ditandai oleh fungsi objektif dan fungsi-fungsi kendala yang memiliki bentuk khusus. Fungsi objektif PG adalah fungsi posinomial dan fungsi kendalanya berupa fungsi posinomial untuk kendala pertidaksamaan atau fungsi monomial untuk kendala persamaan. Fungsi posinomial merupakan penjumlahan beberapa fungsi monomial. Masalah PG bertujuan meminimumkan fungsi posinomial dan masalahnya disebut pemrograman geometrik primal (PGP).

Pemrograman geometrik dibedakan menjadi dua, yaitu PG takberkendala dan PG berkendala. Untuk menentukan solusinya digunakan dual dari masing-masing PG tersebut. Dual masalah PG disebut pemrograman geometrik dual (PGD). PGD berfungsi objektif memaksimumkan suatu fungsi dan berfungsi kendala yang memenuhi kondisi normalitas, ortogonalitas, dan kepositifan. Dalam penentuan solusi PGD diberikan beberapa prosedur sehingga diperoleh solusinya. Nilai solusi optimum PGD ekuivalen dengan nilai solusi optimum PGP.

(5)

PEMROGRAMAN GEOMETRIK DAN ANALISIS SENSITIVITASNYA

Skripsi

sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada

Departemen Matematika

YUDI SURYA LESMANA

G54103027

(6)

Menyetujui:

Pembimbing I,

Dra. Farida Hanum, M.Si.

NIP. 131 956 709

Pembimbing II,

Dr. Toni Bakhtiar, M.Sc.

NIP. 132 158 750

Mengetahui:

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Prof. Dr. Ir. Yonny Koesmaryono, M.S.

NIP. 131 473 999

(7)

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala rahmat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Penyusunan karya ilmiah ini juga tidak lepas dari bantuan berbagai pihak. Untuk itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada:

1. Allah SWT, atas segala kekuatan yang telah diberikan sehingga tugas akhir ini dapat diselesaikan.

2. Dra. Farida Hanum, M.Si. selaku dosen pembimbing I (terima kasih atas semua ilmu, kesabaran, motivasi, dan bantuannya selama penulisan skripsi ini).

3. Dr. Toni Bakhtiar, M.Sc. selaku dosen pembimbing II (terima kasih atas semua ilmu, saran, dan motivasinya).

4. Donny Citra Lesmana, M.Sc. selaku dosen penguji (terima kasih atas semua ilmu dan sarannya).

5. Semua dosen Departemen Matematika (terima kasih atas semua ilmu yang telah diberikan).

6. Keluargaku tercinta: bapak (terima kasih atas semua doa, nasihat dan motivasinya), ibu (terima kasih banyak atas semua doa, dukungan, dan kasih sayangnya. Ibu memang ibu terbaik sedunia), Aa Hendar, Teh Ela, Aa Dede, Teh Neng, adeku Jajat, Mang Djadjang (terima kasih atas doa dan dukungannya).

7. Nenk Iyank tercinta (terima kasih atas semua bantuan, doa, nasihat, dan motivasinya). 8. Teman-teman Math 40: Rusli (terima kasih telah menjadi pembahas pada seminar skripsi

penulis, terima kasih juga telah menemani mencari sumber pustaka ke UI), Mufti (terima kasih atas bantuannya membuat program dan slide presentasi), Abdillah (terima kasih telah menjadi pembahas pada seminar skripsi penulis), Rama (terima kasih atas bantuannya menerjemahkan abstrak ke bahasa inggris), Elis, Sawa, Lili, Ari, Jayu, Demi, Febrian, Prima, Dimas, Ali, Beri, Aam, Mukafi, Uli, Yuda, Dwi, Sri, Agatha, Herni, Mayang, Mika, Indah, Icha, Ami, Nchi, Marlin, Ulfa, Mitha, Septi, Achie, Ifni, Tiwi, Metha, Vina, Abay, Manto, Anton, Azis (terima kasih atas doa dan dukungannya). 9. Bu Susi, Bu Ade, Bu Marisi, Mas Bono, Mas Deni, Mas Yono (terima kasih atas doa dan

motivasinya)

10. Teman-teman Math 41: Dian (terima kasih telah menjadi pembahas pada seminar skripsi penulis), Uwie (terima kasih atas batuannya mendekor poster), LiaY, Niken, dan lainnya (terima kasih atas doanya).

11. Para Pengajar dan crew MSC : Kak Syam, Kak Hepy, Kak Taufik, Kak Jae, Kak Indra,

Mba Novi, Mba Nuqi, Rina, Dewi, Poppy, Kusnandar, Ikang, Basir, dan lainnya (terima kasih atas doa dan motivasinya).

12. Teman-teman Wapemala : Abdul (terima kasih atas bantuanya menerjemahkan jurnal), Dudi, Egi, Kiyunk, Deri, sandi, Ijal, Sopian, Edi, Rifa (terima kasih atas doanya).

Semoga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan khususnya Matematika dan menjadi inspirasi bagi penelitian-penelitian selanjutnya.

Bogor, Oktober 2007

(8)

bersaudara. Ayah penulis bernama Wandi dan Ibu bernama Aminah.

Pada tahun 1997 penulis menyelesaikan pendidikan SD Negeri Margapala Sumedang Selatan. Penulis melanjutkan pendidikan di SLTP Negeri 7 Sumedang pada tahun yang sama. Pada tahun 2000 penulis melanjutkan pendidikan di SMU Negeri 1 Sumedang. Pada tahun 2003 penulis diterima di Institut Pertanian Bogor (IPB) melalui jalur Undangan Seleksi Masuk IPB (USMI) di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam IPB.

(9)

vii

DAFTAR ISI

Halaman

DAFTAR GAMBAR ... viii

DAFTAR LAMPIRAN ... viii

I PENDAHULUAN 1.1 Latar Belakang ... 1

1.2 Tujuan ... 1

II LANDASAN TEORI 2.1 Fungsi Kalkulus ... 1

2.2 Pengoptimuman Konveks dan Pemrograman Geometrik ... 2

2.3 Fungsi Lagrange ... 4

III PEMROGRAMAN GEOMETRIK 3.1 Pengubahan PG standar ke Bentuk Umum Pengoptimuman Konveks ... 5

3.2 Contoh Aplikasi PG dan Pengubahan ke Bentuk PG standar ... 6

3.3 Jenis Pemrograman Geometrik ... 7

3.4 Derajat Kesulitan ... 7

IV PENENTUAN SOLUSI PG 4.1 PGD untuk PG Takberkendala ... 8

4.2 PGD untuk PG Berkendala ... 11

V ANALISIS SENSITIVITAS ... 15

VI SIMPULAN DAN SARAN 6.1 Simpulan ... 21

6.2 Saran ... 21

DAFTAR PUSTAKA ... 21

(10)

viii

Halaman

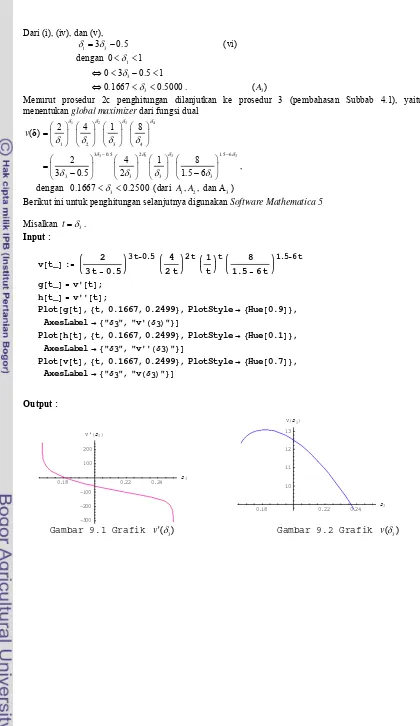
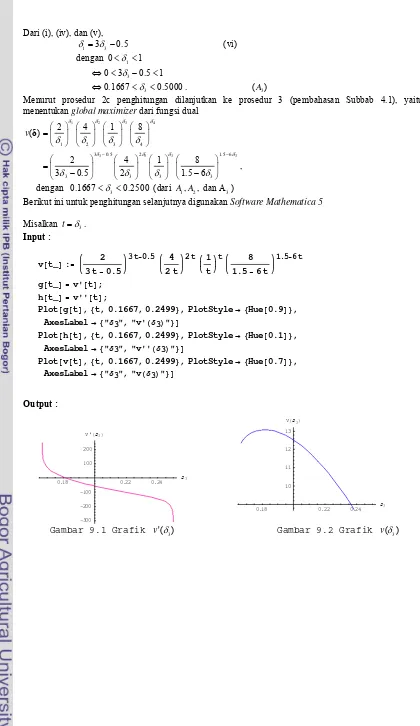
1. Grafik v(δ3)... 33

2. Grafik v'(δ3)... 33

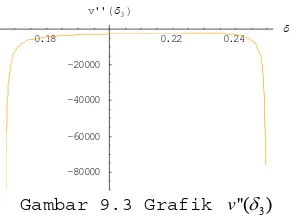
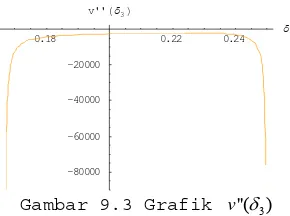
3. Grafik v''(δ3)... 34

4. Grafik v(δ2)... 38

5. Grafik v'(δ2)... 38

DAFTAR LAMPIRAN

Halaman 1. Pembuktian Fungsi Konveks pada Contoh 2.2.2 ... 24

2. Pembuktian Teorema 2.2.3 ... 24

3. Pembuktian Teorema 2.2.4... 26

4. Pembuktian F( )=ln (f ey) y Merupakan Fungsi Konveks ... 27

5. Pembuktian Meminimumkan f0 Ekuivalen dengan Meminimumkan ln(f0) ... 29

6. Pembuktian Teorema 4.1.1... 30

7. Penghitungan Solusi Optimum PGD pada Contoh 4.1.1... 31

11.Penulisan Persamaan (5.7) dan (5.9) ke Bentuk Matriks ... 39

(11)

I PENDAHULUAN

1.1 Latar Belakang

Istilah Pemrograman Geometrik (PG) diperkenalkan oleh Duffin, Peterson, dan Zener pada tahun 1967. Istilah ini diambil dari masalah-masalah geometri yang dapat diformulasikan sebagai PG. Pemrograman Geometrik adalah suatu tipe masalah optimalisasi matematik yang ditandai oleh fungsi objektif dan fungsi-fungsi kendala yang memiliki bentuk khusus.

Dalam karya ilmiah ini PG dibedakan menjadi 2, yaitu PG takberkendala dan PG berkendala. Untuk menentukan solusi optimumnya digunakan metode yang sama,

yaitu menentukan masalah dual terlebih dahulu kemudian dengan prosedur yang ada dihitung solusi optimum dari masalah dual tersebut. Setelah diperoleh solusi optimum masalah dual maka akan diperoleh solusi PG. Selain itu, ingin dicari pengaruh perubahan koefisien fungsi objektif masalah PG terhadap solusi optimumnya.

1.2 Tujuan

Tujuan penulisan karya ilmiah ini adalah mempelajari penyelesaian masalah PG, dan melakukan analisis sensitivitas terhadap PG takberkendala.

II LANDASAN TEORI

Pada bab ini akan diberikan teori yang

menjadi landasan pengerjaan karya ilmiah ini. Berikut diberikan beberapa definisi dan teorema yang digunakan dalam penulisan karya ilmiah ini.

2.1 Fungsi Kalkulus

Dalam subbab ini diberikan beberapa jenis fungsi kalkulus yang digunakan dalam penulisan karya ilmiah ini.

Definisi 2.1.1

(Fungsi Naik dan Fungsi Turun)

Jika f suatu fungsi dengan

( )

1

( )

2

f x < f x , ∀ <x1 x2 dalam suatu selang

I maka f disebut fungsi naik pada selang I. Jika berlaku f x

( )

1 > f x

( )

2 , maka f disebut fungsi turun pada selang I.

(Stewart, 1998) Definisi 2.1.2 (Fungsi Eksponensial)

Fungsi eksponensial adalah fungsi yang berbentuk

( ) x

f x =a

dengan a suatu konstanta positif dan

x

∈

. (Stewart, 1998) Definisi 2.1.3

(Fungsi Eksponensial Natural)

Fungsi eksponensial natural adalah fungsi yang berbentuk

( ) x

f x =e

dengan e≈2.718 dan x∈ .

(Stewart, 1998)

Teorema 2.1.1 (Hukum Eksponen) Jika a>0 dan a≠1, maka ( ) x

f x =a

merupakan fungsi kontinu dengan daerah asal dan daerah nilai (0, )∞ . Khususnya,

0

x

a > untuk setiap x. Jika 0< <a 1 maka ( ) x

f x =a merupakan fungsi turun. Jika a>1 maka ( )f x =ax merupakan fungsi naik. Jika

, 0

a b≠ dan ,x y∈ , maka 1. x y x y

a+ =a a

2. x y x y

a a

a

− ₌

3. ( x)y xy

a =a

4. ( )x x x

ab =a b .

(Stewart, 1998) Definisi 2.1.4 (Fungsi Logaritma)

Jika ( )f x =log_ax, maka f disebut fungsi logaritma dengan bilangan pokok a, dengan a

suatu konstanta positif,x>0dan x∈ . (Stewart, 1998) Definisi 2.1.5 (Fungsi Logaritma Natural)

Jika f x( )=logex=lnx, maka f disebut fungsi logaritma natural, dengan x>0 dan

.

x∈

(Stewart, 1998) Teorema 2.1.2 (Hukum Logaritma)

Jika a>1, fungsi ( )f x =logax

merupakan fungsi naik dengan daerah asal (0, )∞ dan daerah nilai . Jika ,x y>0 dan

(12)

1. log (_a xy)=log_ax+log_ay

2. log_a x log_ax log_ay y

⎛ ⎞₌ ₋

⎜ ⎟ ⎝ ⎠

3. log (_a xr)=rlog_ax.

(Stewart, 1998) Teorema 2.1.3 (Hukum Logaritma Natural) Fungsi ( )f x =lnx merupakan fungsi naik dengan daerah asal (0, )∞ dan daerah nilai . Jika x y, >0 dan r bilangan real sebarang, maka

1. ln(xy)=lnx+lny

2. ln x lnx lny y

⎛ ⎞₌ ₋

⎜ ⎟ ⎝ ⎠

3. ln(xr)=rlnx.

(Stewart, 1998) Definisi 2.1.6 (Global Minimizer)

Misalkanf fungsi bernilai real yang terdefinisi pada himpunan n.

D⊆ Titik * x di D adalah global minimizer untuk f di D jika

* ( ) ( )

f x ≤ f x untuk setiap x di D,dengan x vektor berukuran n.

(Peressini et al., 1988) Definisi 2.1.7 (Global Maximizer)

Misalkanf fungsi bernilai real yang terdefinisi pada himpunan n.

D⊆ Titik * x di D adalah global maximizer untuk f di D jika

* ( ) ( )

f x ≥ f x untuk setiap x di D,dengan x vektor berukuran n.

(Peressini et al., 1988) Teorema 2.1.4 (Pertaksamaan Holder) Misalkan ,x y∈ n, maka untuk p>1,

1

q> , dengan 1 1 1

p+ =q , berlaku

1 1

1 1 1

n n _p n _q p q i i i i i i i

x y x y

= = =

⎛ ⎞ ⎛ ⎞

≤ ⎜ ⎟ ⎜ ⎟

⎝ ⎠ ⎝ ⎠

∑

.

(Boyd & Vandenberghe, 2004)

2.2 Pengoptimuman Konveks dan Pemrograman Geometrik

Pengoptimuman konveks terdiri atas pemrograman linear dan pemrograman nonlinear. Pemrograman geometrik termasuk pemrograman nonlinear. Berikut ini diberikan beberapa landasan yang berhubungan dengan

pemrograman geometrik dan pengoptimuman konveks.

Definisi 2.2.1 (Himpunan Konveks)

HimpunanC⊂ n disebut himpunan konveks jika dan hanya jika untuk setiap x dan y di C, dan setiap λ dengan 0≤ ≤λ 1 maka λx+ −(1 λ)y∈C.

(Peressini et al., 1988) Definisi 2.2.2 (Fungsi Konveks)

Misalkan f fungsi bernilai real yang terdefinisi pada himpunan konveks C di n

maka

1. fungsi f disebut konveks di C jika ( [1 ] ) ( ) [1 ] ( )

f λx+ −λy ≤λf x + −λ f y

untuk setiap x dan y di C dan setiap λ dengan 0≤ ≤λ 1,

2. fungsi f disebut konveks sempurna di C jika (f λx+ −[1 λ] )y <λf( )x +

[1−λ] ( )f y untuk setiap x dan y di C

dan setiap λ dengan 0< <λ 1. (Peressini et al., 1988) Teorema 2.2.1 (Fungsi Konveks untuk Fungsi Satu Variabel)

Jika f terdiferensialkan dua kali pada ,I

maka f fungsi konveks pada I jika dan hanya jika f''( )x ≥0untuk setiap x∈I. Jika

''( ) 0

f x > untuk setiap x∈I, maka f

disebut fungsi konveks sempurna.

(Peressini et al., 1988) Definisi 2.2.3 (Fungsi Afin)

Fungsi : n m

f → disebut fungsi afin jika merupakan penjumlahan fungsi linear dan suatu konstanta, notasinya ( )f x =Ax b+ , dengan A matriks berukuran m n× , x vektor berukuran n, dan b vektor berukuran m.

(Boyd & Vandenberghe, 2004) Contoh 2.2.1

Misalkan didefinisikan fungsi f sebagai berikut

1 2 3 1 2 3

( , , ) 2 1.5 3.2

f x x x = x +x + x +

(

)

12

3

2 1 1.5 3.2

x x x

⎛ ⎞ ⎜ ⎟

= _{⎜ ⎟}+

⎜ ⎟ ⎝ ⎠

,

(13)

3

Teorema 2.2.2

Misalkan f fungsi konveks yang terdefinisi pada himpunan konveks n.

C⊂

Jika λ λ1, 2,...,λk adalah bilangan-bilangan

taknegatif, dengan λ λ1+ 2+ +... λk=1 dan

2 , ,..., k

1

x x x titik di ,C maka

1 1

( ).

k k i i i i i i

f λ λ f

= =

⎛ _{⎞ ≤}

⎜ ⎟

⎝

∑

x ⎠

∑

x

(Peressini et al., 1988) Bukti (lihatPeressini et al., 1988)

Definisi 2.2.4 (Bentuk Umum Pengoptimum an Konveks)

Suatu pengoptimuman konveks didefinisi-kan mempunyai bentuk umum

0

(

Minimumkan ( )

terhadap ( ) 0, 1,..., _i ) 0, 1,...,

f

f_i i m

h i p

⎫ ⎪⎪

≤ = ⎬

⎪

= = _⎪⎭

x

(2.2.1)

dengan f₀,_fi fungsi konveks untuk 1≤ ≤i m, hi fungsi afin untuk 1≤ ≤i p

,

x

adalah vektor berukuran n dengan 0 untuk 1

j

x > ≤ ≤j n.

Minimumkan f0( )x =x12+x22 terhadap

1

1 2

2 2

1 1 2

( ) 0

1

( ) ( ) 0.

x f

x

h x x

= ≤

+

= + =

x x

Terlihat h1 merupakan fungsi kuadrat sehingga menurut Definisi 2.2.3 h1 bukan fungsi afin. Karena salah satu syarat sudah terbukti tidak terpenuhi, maka permasalahan pada Contoh 2.2.2 bukan pengoptimuman konveks.

Tetapi permasalahan pada Contoh 2.2.2 bisa dikonversi menjadi pengoptimuman konveks dengan cara sebagai berikut:

Karena 1+x₂2>0 maka agar pertaksamaan 1

2 2

0 1

x

x ≤

+ terpenuhi haruslah x1≤0

sehingga kendala pertaksamaan menjadi

1( ) 1 0

f x =x ≤ .

(i) Dapat diperlihatkan bahwa f0 dan f1 adalah fungsi konveks.

Bukti (lihat Lampiran 1). (ii)Fungsi kendala 2

1 2

(x +x ) =0 terpenuhi jika dan hanya jika x1+x2 =0, sehingga fungsi h1 menjadi h1( )x = +x1 x2=0, sehingga berdasarkan Definisi 2.2.3, h1 adalah fungsi afin.

Berdasarkan (i) dan (ii) maka permasalahan Contoh 2.2.2 dapat dimodelkan menjadi,

2 2

0 1 2

1 1

1 1 2

0

Minimumkan ( ) terhadap ( )

( ) 0

f x x

f x

h x x

≤

⎫

= +

⎪

= ⎬

⎪

= + _{= ⎭}

x x x

(2.2.2)

Permasalahan (2.2.2) adalah pengoptimuman konveks karena f₀, f₁ fungsi konveks, dan

1

h fungsi afin.

Berikut ini diberikan dua definisi dan dua teorema yang berperan penting dalam pemrograman geometrik.

Definisi 2.2.5 (Fungsi Monomial)

Fungsi g yang terdefinisi untuk 1

( , ...,x x_n) =

x dengan xi>0 untuk setiap 1, 2, 3,...,

i= n disebut fungsi monomial atau monomial jika

1 2

( ) a a... an,

n

g x =cx x x

dengan c konstanta positif dan ai∈R.

Misalkan didefinisikan 2 0.15 1 2 1 2 ( , ) 2.3

f x x = x x−

2 0.15 1 2 1 2

( , ) 2.3 .

h x x = − x x−

Fungsi f adalah fungsi monomial sedangkan h

bukan fungsi monomial, karena koefisien pada h bukan konstanta positif.

Berikut dapat diperlihatkan bahwa fungsi monomial tertutup terhadap operasi perkalian dan pembagian.

Misalkan f dan g fungsi monomial dengan

1 2

( ) a a... an

n

f x =cx x x

1 2

( ) b b... bn

n

g x =dx x x , maka

(i) (fg)( )x = f( ) ( )x g x

1 2 1 2

1 1 2 2

1 2 1 2 ( ) ( ) ( ) 1 2

( ... )( ... )

... .

n n

a b a a b b

n n

a b a b a b

n

cx x x dx x x

cdx + x + x +

(14)

Karena c d, >0 maka cd>0, xi >0, dan untuk setiap a bi, i∈ , maka ai+ ∈bi

untuk i=1, 2,..., ,n sehingga menurut Definisi 2.2.5 fg merupakan fungsi monomial.

(ii)

( )

f f

g = g x x

x

1 2

1 2 ... ...

n

a a a

n b b b

n

cx x x

dx x x

=

(1 1) (2 2) ( )

1 2 ...

n n

a b a b a b

n

c

x x x

d

−

− −

⎛ ⎞

= ⎜ ⎟_{⎝ ⎠} .

Karena c d, >0 maka c 0

d > , xi>0 dan

untuk setiap a bi, i∈ maka ai− ∈bi ,

untuk i=1, 2,...,n sehingga menurut Definisi 2.2.5 f

g merupakan fungsi monomial.

Dari (i) dan (ii) terbukti bahwa fungsi monomial tertutup terhadap operasi perkalian dan pembagian.

Definisi 2.2.6 (Fungsi Posinomial)

Fungsi f yang terdefinisi di x=( , ,...,x x1 )

n

x untuk setiap xj >0 disebut posinomial jika

1 1

( ) ( ) ,ij

n m

a

i j

f c x

= =

=

∑ ∏

x

dengan ci konstanta positif dan aij∈R untuk

1≤ ≤i m dan 1≤ ≤j n.

(Peressini et al., 1988) Dengan perkataan lain fungsi posinomial merupakan penjumlahan dari beberapa fungsi monomial.

Contoh 2.2.4

Didefinisikan fungsi f sebagai berikut 2 0.15 2

1 2 1 2 1 2 2

( , ) 2.3 4 3

f x x = x x− + x x + x

dengan x=( ,x x1 2) di 2

, x x1, 2 >0. Karena 1 2.3 0

c = > , c2= >4 0, c3= 3>0, dan 1, 2 0,

x x > maka berdasarkan Definisi 2.2.6

f adalah fungsi posinomial.

Teorema 2.2.3 (Pertaksamaan Aritmatik-Geometrik (A-G))

Jika x x1, 2,...,xn bilangan-bilangan real positif

dan jika δ δ1, 2,...,δn adalah bilangan-bilangan

positif dengan δ δ1+ 2+ +... δn=1, maka

1 1

( )i

n n i i i

i i

x δ δx

= =

≤

∑

∏

,

dengan persamaannya berlaku jika dan hanya jika x1=x2= =... xn.

(Peressini et al., 1988) Bukti (lihatLampiran 2)

Teorema 2.2.4 (Perluasan Pertaksamaan A-G)

Misalkan x x1, 2,...,xn bilangan-bilangan

positif. Jika δ δ1, 2,...,δn bilangan-bilangan

positif dan λ δ δ= 1+ 2+ +... δn, maka

1 1

,

i

n n

i i

i i i

x x

δ λ

λ λ

δ

= =

⎛ ⎞

⎛ ⎞ _≥

⎜ ⎟

⎝

∑

⎠

∏

⎝ ⎠

persamaannya berlaku jika dan hanya jika

1

n i i j

j

x δ x

λ =

⎛ ⎞

= _⎜ _⎟

⎝

∑

⎠, untuk i=1, 2,...,n.

(Peressini et al., 1988) Bukti (lihat Lampiran 3)

2.3 Fungsi Lagrange

Misalkan diberikan masalah pengoptimuman yang mempunyai bentuk umum sebagai berikut

Minimumkan ( ) terhadap ( ) 0 dengan 1, 2,..., , .

i

n

f g

i m

⎫ ⎪

= _⎬

⎪

= ∈ _⎭

x x

x

(2.3.1)

Salah satu metode yang dapat digunakan untuk menyelesaikan masalah (2.3.1) adalah metode pengali Lagrange. Metode ini dimulai dengan pembentukan fungsi Lagrange yang didefinisikan sebagai berikut.

Definisi 2.3.1 (Fungsi Lagrange)

Misalkan diberikan masalah pengoptimuman (2.3.1). Fungsi Lagrange dari masalah tersebut didefinisikan

1

( , ) ( ) ( )

m i i i

L f λg

=

= −

∑

xλ x x (2.3.2)

dengan λ ≥i 0.

(Kuhn, 2006) Teorema 2.3.1

Syarat perlu bagi sebuah fungsi objektif ( )

(15)

5

maksimum lokal pada titik *

x adalah turunan parsial pertama dari fungsi Lagrange-nya yang didefinisikan pada (2.3.2) terhadap setiap

elemennya 0,

j

L x

∂ ₌

∂ dan i 0

L

λ

∂ ₌

∂ untuk

1, 2,..., ,

i= m dan j=1, 2,..., .n

(Kuhn, 2006)

III PEMROGRAMAN GEOMETRIK

Pemrograman geometrik (PG) merupakan

pengoptimuman suatu fungsi posinomial terhadap kendala monomial atau posinomial.

Suatu PG didefinisikan mempunyai bentuk standar :

0 Minimumkan ( )

terhadap ( ) 1, 1,..., ( ) 1, 1,...,

i i

f

f i k

g i l

⎫ ⎪

≤ = ⎬

⎪

= = _⎭

x x x

(3.1)

dengan f0,fi fungsi posinomial,

g

i fungsi monomial, x vektor berukuran n, dan

0 untuk 1

j

x > ≤ ≤j n.

(Boyd & Vandenberghe, 2004) Contoh 3.1

Misalkan diberikan pemrograman sebagai berikut.

Minimumkan

1 1/ 2 1

0( , , ) 2.3 4

f x y z =x y− − z− + xz+ xyz

terhadap

2 2 1/ 2 1 1

2 1 1/ 2 2

( , , ) (1/ 3) (4 / 3) 1 ( , , ) 2 3 1 ( , , ) (1/ 2) 1,

f x y z x y y z

f x y z xy xyz x z g x y z xy

− − −

− −

= + ≤

= + + ≤

= =

dengan x y z, , >0.

Contoh 3.1 merupakan PG bentuk standar dengan n=3, k = 2 dan l = 1.

Contoh 3.2

Misalkan diberikan suatu permasalahan sebagai berikut.

Minimumkan

1 1/ 2 1

0( , , ) 2.3 4

f x y z =x y− − z− + xz+ xyz

terhadap

2 2 1/ 2 1 1

2

( , , ) (1/ 3) (4 / 3) 1 ( , , ) 3 1

( , , ) ( 1/ 2) 1.

f x y z x y y z

f x y z xyz

g x y z xy

− − −

= + ≤

= ≤

= − =

dengan x y z, , >0.

Contoh 3.2 bukan PG karena g bukan fungsi monomial.

Contoh 3.3

Misalkan diberikan fungsi objektif dari suatu permasalahan sebagai berikut

Maksimumkan f x x x( ,1 2, 3)=x x x1 2 3 dengan x x x1, 2, 3>0.

Dapat diperlihatkan bahwa memaksimumkan 1 2 3

x x x ekuivalen dengan meminimumkan

1 2 3 1

x x x .

Misalkan f mempunyai nilai maksimum di titik * * * *

1 2 3 (x x x, , ) =

x maka

* ( ) ( )

f x ≥ f x (menurut Definisi 2.1.7) * * *

1 2 3 1 2 3

x x x x x x

⇔ ≥

* * *

1 2 3 1 2 3

1 1

x x x x x x

⇔ ≤

(karena x x x x1, 2, 3, 1*, * * 2, 3 0

x x > ), menurut Definisi 2.1.6,

1 2 3 1

x x x minimum

di titik x*=( ,x x x1* 2*, 3*).

Jadi terbukti bahwa memaksimumkan x x x1 2 3 ekuivalen dengan meminimumkan

1 2 3 1

x x x ,

untuk x x x1, 2, 3>0.

3.1 Pengubahan PG Standar ke Bentuk Umum Pengoptimuman Konveks

Dengan menggunakan hukum eksponen-sial dan hukum logaritma maka bentuk PG standar pada (3.1) dapat diubah menjadi pengoptimuman konveks dengan cara sebagai berikut:

(i) Pada fungsi monomial

1 2

( ) ... n

n

a a a

g x =cx x x disubstitusikan

persamaan ln i

i i i

y

y = x ⇔x =e sehingga fungsi g menjadi

1 2 1 1 2 2

1 1 2 2

( , ,..., ) ( ) ( ) ...( ) ... .

n n n

n n

y y

y y y y y y y

a

a a

a

a a

g e e e c e e e

ce e e

(16)

Kemudian dengan mengunakan sifat-sifat fungsi logaritma natural diperoleh,

1 2

1 1 2 2

ln( ( , ,..., ))

ln( ... )

ln ln ln ... ln

n

n n

y y y

a y a y a y

g e e e

ce e e

c e e e

=

= + + + +

1 1 2 2

lnc a y lne a y lne ... a yn nlne

= + + + +

1 1 2 2 . lnc a y a y ... a yn n

= + + + +

Jika _g_{( )}_x = =₁ ₍_{g e}y1_,_ey2_,...,_eyn_),_maka

1 2

ln( ( y

,

y

,...,

yn)) 0

g

e

= , sehingga fungsi monomial g menjadi fungsi afin berbentuk

1 1 2 2

ln ... 0

... ln .

n n n n

c a y a y a y

a y a y a y c

=

= −

+ + + +

⇔ + + +

(ii) Fungsi posinomial

1 1

( ) ( ) ,ij

n m

i j

a

f c x

= =

=

∑ ∏

x

dengan 0ci > dan xj>0 untuk

1, 2,...,

i= m, 1, 2,...,j= n, maka ( ) 0

f x > , dan fungsi kendala fi( )x ≤1, dengan fi fungsi posinomial, maka

0< fi( )x ≤1 untuk setiap i=1, 2,..., .k Terlihat bahwa fi( ) ,

+ ∈

x dengan +

himpunan bilangan real positif, sehingga berlaku

ln(_fi( ))x ≤ln1

(karena fungsi logaritma merupakan fungsi naik di +)

ln(_fi( )) 0

⇔ x ≤

Misalkan

1 2

( ) ln ( y, y,..., yn)

F y = f e e e , dengan f

fungsi posinomial.

Dapat diperlihatkan bahwa F fungsi konveks. Bukti (lihat Lampiran 4 bagian 1). (iii) Dapat diperlihatkan meminimumkan f0

ekuivalen dengan meminimumkan lnf0. Bukti (lihat Lampiran 4 bagian 2). Berdasarkan (i), (ii), (iii), maka bentuk standar PG dapat dikonversi menjadi bentuk umum pengoptimuman konveks yang dapat dimodelkan sebagai berikut

1 2

0 Minimumkan ln ( , ,..., ) terhadap

ln( ( , ,..., )) 0, ln( ( , ,..., )) 0, 1, 2,..., , 1, 2,..., .

n

y y y

y y y j

f e e e

f e_i e e

g e e e

i k j l

⎫ ⎪ ⎪ ⎪ ⎪ ⎬

≤ _⎪

⎪

= _⎪

⎪

= = _⎭

(3.1.1)

3.2 Contoh Aplikasi PG dan Pengubahan ke Bentuk PG Standar

Menentukan volume yang optimum dari sebuah wadah yang berbentuk balok merupakan salah satu contoh aplikasi PG. Misalkan tinggi balok h, panjang w, dan lebar

d, serta rasio masing-masing sisi adalah h/w d/w, dan h/d. Dengan memperhatikan fungsi kendala yang diberikan dan ingin memperoleh volume balok yang maksimum maka masalah ini dapat dimodelkan sebagai berikut

Maksimumkan terhadap 2( ) / / dengan , , 0

w f

wdh

hw hd A

h w

wd A

d w d h w

α β

γ δ

⎫ ⎪

+ ≤ _⎪

⎪

≤ ≤ _⎪

⎬

≤ _⎪

⎪

≤ ≤ _⎪

> _⎪⎭

(3.2.1)

dengan d, h, dan w variabel keputusan, 0

w

A > luas selimut balok, Af >0 luas alas balok, dan , , ,α β γ δ konstanta positif. Dengan menggunakan transformasi, masalah (3.2.1) dapat dikonversi ke bentuk PG standar sebagai berikut.

a) Sebagaimana telah dijelaskan pada Contoh 3.3, maka memaksimumkan wdh

ekuivalen dengan meminimumkan 1 1 1

w d h− − − , dengan h w d, , >0.

b) Fungsi kendala juga dapat dikonversi menjadi

/

2( )

(2 / )( )

hw hd _Aw

A_w hw hd A_w A_w

+ ≤

⇔ + ≤

(karena _Aw>0)

(2 /A_w)hw (2 /A_w)hd 1

⇔ + ≤

c) α≤h w/ ≤β

i _ii

/ dan /

h w h w

α β

⇔ ≤ ≤

1

i. /

(karena 0)

1 (karena 0)

h w

w h w

wh h

α α

α −

≤

⇔ ≤ >

(17)

7

1

ii. /

(1/ ) 1

(karena konstanta positif)

h w

hw

β β

β

−

≤

⇔ ≤

d) wd≤Af

(1/ ) 1

(karena 0)

f f

A wd A

⇔ ≤

>

e) γ ≤d w/ ≤δ

ii i

/ dan /

d w d w

γ δ

⇔ ≤ ≤

i. /γ ≤d w

(karena 0)

w d w

γ

⇔ ≤ >

1 _{1 (karena} ₀₎

wd d

γ −

⇔ ≤ >

ii. /d w≤δ

1

(1/ )δ dw− 1

⇔ ≤

(karena δ konstanta positif). Dari a), b), c.i), c.ii), d), e.i), dan e.ii) terbukti bahwa permasalahan (3.2.1) dapat dikonversi menjadi PG standar sebagai berikut

Minimumkan 1 1 1

h w d− − −

terhadap

1

(2 / ) (2 / ) 1 1

A_w hw A_w hd

h w

α −

+ ≤

≤

1 (1/ )β hw− ≤1 (1/A wdf) ≤1

1

1 1

(1/ ) 1

wd w d

γ δ

−

− ≤

≤

dengan h w d, , >0, α β γ, , ,A Af, w

konstanta positif.

3.3 Jenis Pemrograman Geometrik

Dilihat dari ada atau tidak adanya kendala, maka pemrograman geometrik dapat dibedakan menjadi pemrograman geometrik takberkendala, dan pemrograman geometrik berkendala. Pada dasarnya PG takberkendala dan PG berkendala sama, yaitu sama-sama masalah optimalisasi. Karena PG berkendala disertai dengan fungsi kendala yang mempunyai bentuk khusus sedangkan PG tak berkendala tidak disertai fungsi kendala, maka untuk memudahkan penghitungan kedua masalah ini dibedakan.

Pemrograman geometrik takberkendala adalah masalah meminimumkan suatu fungsi posinomial dengan tidak disertai fungsi kendala. Suatu pemrograman geometrik

tak-berkendala didefinisikan mempunyai bentuk umum sebagai berikut

1 1

1 2 Minimumkan

( ) ( ) dengan

0, 0,..., 0, konstanta real,

dan konstanta positif

ij

m n

a i j i j

m ij

i

g c x

x x x

a c

= =

⎫ ⎪ ⎪ =

⎪ ⎪ ⎬ ⎪ > > > _⎪ ⎪ ⎪ ⎭

∑ ∏

x

(3.3.1)

(Peressini et al., 1988) Pemrograman geometrik berkendala adalah masalah meminimumkan suatu fungsi posinomial dengan disertai fungsi kendala, dan mempunyai bentuk umum sebagai berikut

0

0 1

1

0 1

1 1

1 Minimumkan

( ) ( ) ... ( ) terhadap

( ) ( ) ... ( ) 1

( ) ( ) ... ( ) 1 dengan 0, untuk 1,..., ,

fungsi monomial untuk 1,..., , fungsi posinom

k k

n

n n

k n n

j i

k i

f u u

x j m

u

i n f

−

+

= + +

= + + ≤

> =

=

x x x

0 1

ial untuk 0,..., , dan

misalkan ... k .

i k

n n n p

⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪

= _⎪

⎪

+ + + = _⎭

(3.3.2)

(Peressini et al., 1988) Jika diperhatikan dari bentuknya, PG berkendala termasuk PG bentuk standar. Catatan

Masalah PG yang berfungsi objektif meminimumkan disebut pemrograman geometrik primal (PGP).

3.4 Derajat Kesulitan

Derajat kesulitan merupakan tingkat kesulitan untuk melakukan penghitungan dalam menentukan solusi masalah PG. Derajat kesulitan untuk PG takberkendala dan PG berkendala dirumuskan sebagai berikut 1. Derajat kesulitan PG takberkendala

Misalkan diberikan PG seperti masalah (3.3.1), maka derajat kesulitannya dirumuskan sebagai berikut

1

ST n m

(18)

ST

π = derajat kesulitan PG takberkendala

n= banyaknya suku penjumlahan pada fungsi objektif

banyaknya variabel keputusan.

m=

2. Derajat kesulitan PG berkendala Misalkan diberikan PG seperti masalah (3.3.2), maka derajat kesulitannya dirumuskan sebagai berikut 0 1 1 r SB k k

n n m

π = ⎛ ⎞ =_⎜ + _⎟− − ⎝

∑

⎠ , dengan SB

π = derajat kesulitan PG berkendala 0

n = banyaknya suku penjumlahan pada fungsi objektif

k

n = banyaknya suku penjumlahan pada fungsi kendala ke-k

banyaknya variabel keputusan.

m=

Ditentukannya derajat kesulitan dari suatu permasalahan PG akan bermanfaat dalam penghitungan solusi optimumnya.

1. PG memiliki satu solusi jika dan hanya jika π =i 0, untuk i=ST SB, .

2. PG memiliki banyak solusi jika dan hanya jika π >i 0, untuk i=ST SB, .

3. PG tidak memiliki solusi jika dan hanya jika π <i 0, untuk i=ST SB, .

(Bazaraa et al., 1979)

IV PENENTUAN SOLUSI PG

Untuk melakukan penghitungan dalam

menentukan solusi masalah pemrograman geometrik maka ditentukan masalah dual dari pemrograman geometrik yang disebut pemrograman geometrik dual (PGD).

4.1 PGD untuk PG Takberkendala

Berikut ini dapat ditentukan bentuk PGD dari masalah (3.3.1).

1. Fungsi ( )g x dapat ditulis sebagai

1 1 ( ) ( ) ij m a i j n j i i i c x g δ δ = = ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠

∏

∑

x ,

dengan 0δ >i (kondisi kepositifan)

2. Jika ditambahkan kendala

1 1 n i i δ = =

∑

(kondisi normalitas)

maka menurut Teorema Pertaksamaan A-G diperoleh 1 1 ( ) ( ) i ij m a i j n j i i c x g δ δ = = ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ≥ _⎜ _⎟ ⎜ ⎟ ⎝ ⎠

∏

x

1 1 1

( )

i

ij i

n n m a i

j i i i j

c x δ δ δ = = = ⎛ ⎞ ⎛ ⎞ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠

∏

∏∏

( )

1 1 i ij i i

n n _a i

j i i i

c x δ δ δ = = ⎛ ⎞ ⎛ ∑ ⎞ = _{⎜ ⎟ ⎜} _⎟ ⎝ ⎠ ⎝ ⎠

∏

3. Jika ditambahkan kendala

1 0 n ij i i aδ = =

∑

(kondisi ortogonalitas) 1, 2,...,

j= m

maka diperoleh 1 ( ) , i n i i i c g δ δ = ⎛ ⎞ ≥ ⎜ ⎟ ⎝ ⎠

∏

x

sehingga jika didefinisikan

1 ( ) : , i n i i i c v δ δ = ⎛ ⎞ = _{⎜ ⎟} ⎝ ⎠

∏

δ

maka diperoleh ( ) ( )

g x ≥v δ

untuk sebarang _∈ m

x dengan x>0 dan sebarang _δ_∈ n

yang memenuhi kondisi kepositifan, normalitas, dan ortogonalitas.

Jadi diperoleh PGD dari masalah (3.3.1) adalah 1 1 2 1 1 Maksimumkan ( ) terhadap

0, 0,..., 0 1

0, 1, 2,...,

i n i i i n n i i n ij i i c v

a j m

δ δ δ δ δ δ δ = = = ⎫ ⎪ ⎛ ⎞ ⎪ = _{⎜ ⎟} _⎪ ⎝ ⎠ _⎪ ⎪ ⎪ ⎬ > > >

(19)

9

Vektorδberukuran n yang memenuhi kondisi kepositifan, normalitas, dan ortogonalitas disebut vektor fisibel untuk PGD.

(Peressini et al., 1988) Karena δ>0 dan ci konstanta positif,

maka ( )vδ >0, sehinga ( )v δ ∈ +. Teorema 4.1.1

Misalkan PGP konsisten, maka PGD yang berpadanan adalah konsisten. Jika

* * * * 1 2 ( ,x x,...,xm) =

x adalah solusi PGP,

selanjutnya vektor =(δ δ1*, 2*,...,δn*)

*

δ yang

didefinisikan oleh * *

* ( )

, 1, 2,..., ( )

i i

u

i n

g

δ = x =

x

(dengan 1

1 ( ) i... im

i i m

u x =c xα xα adalah suku ke-i

dari ( )g x ) adalah solusi untuk PGD dan *

( ) ( ).

g =v *

x δ

(Peressini et al., 1988) Bukti (lihat Lampiran 5)

Berdasarkan Teorema 4.1.1, masalah dual akan mempunyai solusi jika himpunan vektor fisibel tidak kosong. Jika solusi untuk masalah (4.1.1) adalah vektor δ*∈ n,

maka solusi untuk masalah (3.3.1) adalah x*∈ m. Berikut diberikan prosedur untuk menentukan solusi pemrograman geometrik takberkendala. Prosedur Pemrograman Geometrik

Takberkendala

Misalkan diberikan PGP Minimumkan

1

( ) ( )

n i i

g u

= =

∑

x x ,

dengan 1

1

( ) ai... im

i i m

u x =c x x adalah fungsi monomial, dan x1>0,x2 >0,...,xm>0.

1. Tentukan himpunan fisibel F dari PGD, yaitu himpunan vektor δ di n

yang memenuhi

1

0,..., 0 (kepositifan) 1 (normalitas)

0, 1, 2,..., (ortogonalitas)

n n

i i

n ij i i

a j m

δ δ

δ

δ =

=

> >

= ∑

= =

∑

2. Jika himpunan vektor fisibel F

a) himpunan kosong maka proses berhenti, masalah PG tidak mempunyai solusi,

b) terdiri atas satu vektor _δ* (solusi tunggal), maka δ*

merupakan solusi dari PGD, lanjutkan ke langkah 4, c) terdiri atas lebih dari satu vektor

(mempunyai banyak solusi) maka lanjutkan ke langkah 3

3. Tentukan vektor δ*

yang merupakan

global maximizer untuk fungsi dual

1 ( )

i

n i i i

c v

δ

δ =

⎛ ⎞

= _{⎜ ⎟}

⎝ ⎠

∏

δ ,

pada himpunan vektor fisibel F, maka δ*

adalah solusi PGD. 4. Jika diberikan solusi δ*,

maka solusi dari masalah primalnya adalah *

x yang diperoleh dari

* *

* ( )

, 1, 2,..., ( )

i i

u

i n

v

δ = x =

δ .

Berdasarkan Teorema 4.1.1, v(δ*)=g( *). x (Peressini et al., 1988) Contoh 4.1.1

Misalkan diberikan masalah PG sebagai berikut

Minimumkan

3 2 3 3 3

1 2 1 2 1 2 1 2

( , ) 60 50 20

g x x = x x− − + x x + x x−

terhadap 1 0, 2 0

x > x > Jawab

Derajat kesulitan pada permasalahan Contoh 4.1.1 adalah 0, karena

1

ST n m

π = − − 3 2 1 0 = − − = .

Jadi masalah PG pada Contoh 4.1.1 mempunyai satu solusi.

Berdasarkan (4.1.1) dual dari masalah pada Contoh 4.1.1 adalah

Maksimumkan

3

1 2

1 2 3

60 50 20

( )

v

δ

δ δ

δ δ δ

⎛ ⎞

⎛ ⎞ ⎛ ⎞

=_⎜ _{⎟ ⎜} _⎟ _⎜ _⎟

⎝ ⎠ ⎝ ⎠ ⎝ ⎠

δ

terhadap

1 2 3 1 (normalitas) δ δ+ +δ =

1 0, 2 0, 3 0 (kepositifan) δ > δ > δ >

1 2 3

3 3 3 0

(ortogonalitas)

2 3 0

δ δ δ

− + − = ⎫

⎬

(20)

Koefisien δi untuk i=1, 2, 3 pada kondisi

ortogonalitas di atas adalah pangkat dari x1 dan x2 pada fungsi objektif g x x( ,1 2).

Dari kondisi normalitas dan ortogonalitas diperoleh sistem persamaan linear (SPL)

1 2 3

1 2 3 1

3 3 3 0

2 3 0

δ δ δ δ δ δ δ δ δ + + = ⎫ ⎪ − + − _{= ⎬} ⎪ − + + _{= ⎭} (4.1.2)

dan solusinya adalah * * * * 1 2 3

2 1 1

( , , ) , ,

5 2 10

δ δ δ ⎛ ⎞

= _{= ⎜} _⎟

⎝ ⎠

δ .

Penghitungan (lihatLampiran 6). Dapat diperhatikan bahwa *

0

i

δ > , dan ini merupakan satu-satunya solusi. Jadi nilai solusi optimum PGD adalah

* * * 3 1 2 3 1 2 * * *

1 2 3

0.4 0.5 0.1 ( )

60 50 20

0.4 0.5 0.1

126.049 c c c v δ δ δ δ δ δ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ =_⎜ _{⎟ ⎜} _⎟ _⎜ _⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ = ⎜_⎝ ⎟ ⎜_{⎠ ⎝} ⎟ ⎜_{⎠ ⎝} ⎟_⎠ = * δ

Langkah 2b menyatakan bahwa proses dapat dilanjutkan ke langkah 4, yaitu menentukan solusi optimum PGP

* * * 1 2 ( ,x x ), =

x dengan menyelesaikan * 3 * 2

1 2

60x− x− =0.4(126.049)=50.420 (i) *3 *

1 2

50x x =0.5(126.049)=63.025 (ii) * 3 *3

1 2

20x−x =0.1(126.049)=12.6049(iii) Persamaan (i) dapat disederhanakan menjadi

* 2 *3

2 1

60x− =50.420x

*3 * 2 1 1.1900 2

x = x− , (iv)

dengan menyubstitusi Persamaan (iv) ke Persamaan (ii) diperoleh

* 2 * 2 2

50(1.1900x−)x =63.025 *

2 0.944

x = , (v)

dengan menyubstitusi Persamaan (v) ke Persamaan (iii) diperoleh

20x1* 3(0.944)3 12.6049

− ₌ *3 1 1.335 x = * 1 1.101

x = ,

sehingga solusi optimum PGP adalah *

(1.101, 0.994) =

x .

Berdasarkan Teorema 4.1.1, nilai solusi optimum PGP sama dengan nilai solusi optimum PGD. Jadi (0.944,1.101)g =

126.049 adalah nilai solusi optimum PGP Contoh 4.1.1.

Contoh 4.1.2 Minimumkan

3 3 2 1

1 2 1 2 1 2 1 2 1 2

( , ) 2 4 8

f x x = x x− + x x− +x x + x x−

dengan x x1, 2>0 Jawab

Derajat kesulitan masalah PG pada Contoh 4.1.2 adalah

1 4 2 1 1.

ST n m

π = − − = − − =

Jadi masalah PG pada Contoh 4.1.2 mempunyai banyak solusi.

Berdasarkan (4.1.1) dual dari masalah pada Contoh 4.1.2 adalah

Maksimumkan

3

1 2 4

1 2 3 4

2 4 1 8

( ) v δ δ δ δ δ δ δ δ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ =⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠ δ terhadap

1 2 3 4 1

δ δ+ +δ +δ = (normalitas) 1 2 3 4

1 2 3 4

3 2 0

3 0

δ δ δ δ

− + + = ⎫

⎬

− + + − _{= ⎭} (ortogonalitas) 0,

i

δ > untuk i=1, 2,..., .n (kepositifan)

Dari kondisi normalitas dan ortogonalitas diperoleh SPL

1 2 3 4

1 2 3 4 1

3 2 0

3 0 δ δ δ δ δ δ δ δ δ δ δ δ + + + = ⎫ ⎪ − + + _{= ⎬} ⎪ − + + − _{= ⎭} (4.1.3)

dan solusi optimum PGD adalah * * * * *

1 2 3 4

( , , , )

(0.0457, 0.3638, 0.1819, 0.4086)

δ δ δ δ

= =

δ

(lihatLampiran 7 ),

sehingga nilai solusi optimum PGD adalah 0.0457 0.3638

* 2 4

( )

0.0460 0.3638

v = ⎜⎛ ⎞_⎟ ⎛_⎜ ⎞_⎟

⎝ ⎠ ⎝ ⎠ δ 0.1819 0.4086 1 8 0.1819 0.4086 ⎛ ⎞ ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ 13.0692. =

Menurut Teorema 4.1.1, * * ( ) ( )

vδ = f x

13.0692

= , dengan f(x*) nilai solusi optimum PGP untuk suatu *

f

D

∈

x , dengan

f

D daerah asal fungsi .f

Menurut prosedur 4 dapat dihitung solusi optimum PGP * * *

1 2 (x x, ) =

x sebagai berikut *3 * 3 * *

1 2 1

2 ( )

0.0457(13.0692)

x x− =δ v

(21)

11

*3 * 3

1 2 0.2986

x x− =

* *

1 2

3lnx −3lnx =ln 0.2986

* * 1 2

lnx −lnx = −0.4028

(i) * * * *

1 2 3 ( )

x x =δ v δ * *

1 2 0.1819(13.0692)

x x =

* * 1 2

lnx +lnx =ln 2.3773

* * 1 2

lnx +lnx =0.8660. (ii)

Dari (i) dan (ii) diperoleh *

1

2 lnx =0.4631 *

1

lnx =0.2316 (iii) * 0.2316

1 1.2606.

x =e =

Dari (ii) dan (iii) diperoleh *

2

lnx =0.6344 * 0.6344

2 1.8859.

x =e =

Jadi diperoleh solusi optimum PGP adalah * * *

1 2

( ,x x ) (1.2606,1.8859)

= =

x .

4.2 PGD untuk PG Berkendala

Untuk mencari solusi dari permasalahan (3.3.2) terlebih dahulu ditentukan dual dari permasalahan tersebut. Berikut dapat ditentukan masalah dual dari permasalahan (3.3.2).

1) Pada fungsi kendala fr( )x ≤1, untuk 1, 2,...,

r= k.

Misalkan λ >r 0, untuk r=1, 2,..., ,k maka diperoleh

(

( )

)

r 1r 1.

r

f x λ ≤ λ =

Karena fr( )x >0, untuk x∈Df, maka

(

)

1 1

( ) r 1 1 1.

k k k r r r f λ = = ≤ = =

∏

x

∏

Karena

(

)

1

( ) r 1,

k r r f λ = ≤

∏

x maka

( )

( ) (

)

0 0

1

( ) r

k r r

f f f λ

=

≥

∏

x x x

( )

(

)

0 1 1 1 ( ) , ij r m _a i j n k j i r

i i r

c x f λ δ δ = = = ⎛ ⎛ ⎞⎞ ⎜ ⎜ ⎟⎟ ⎜ ⎜ ⎟⎟ =_⎜ _⎜ _⎟_⎟ ⎜ ⎜ ⎟⎟ ⎜ _⎝ _⎠⎟ ⎝ ⎠

∏

∑

∏

x

dengan δ >i 0, untuk i=1,...,n0. 2) Jika ditambahkan kendala

0 1 1 n i i δ = =

∑

(kondisi normalitas), maka menurut Teorema Pertaksamaan A-G (Teorema 2.2.3), diperoleh

(

)

0 1 0 1 1 ( ) ( ) ( ) i ij r m a i j n k j r i i r

c x f f δ λ δ = = = ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ≥ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠

∏

x x

(

)

0 0

1 1 1 1

( ) ( )

i

r ij i

n n m k a i

j r i i i j r

c x f δ λ δ δ = = = = ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ = ⎜ ⎟ ⎜ ⎟⎜ ⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠

∏

∏∏

∏

x

( )

0

(

)

0

1

1 1 1

( ) .

n i

ij i r

i

n m _a k i

j r

i i j r

c x f δ δ λ δ = = = = ⎛ ⎞ ⎛ ⎞ _⎜ ∑ _⎟⎛ ⎞ = ⎜ ⎟ _⎜ _⎟⎝⎜ ⎟_⎠ ⎝ ⎠ ⎝ ⎠

∏

x

Jadi

( )

0

(

)

0

1

0

1 1 1

( ) .

n i

ij i r

i

n m _a k i

j r

i i j r

f c x f δ δ λ δ = = = = ≥ ⎛ ⎞ ⎛ ⎞ _⎜ ∑ _⎟⎛ ⎞ ⎜ ⎟ _⎜ _⎟⎝⎜ ⎟_⎠ ⎝ ⎠ ⎝ ⎠

∏

x x (4.2.1) Diperhatikan fungsi kendala

( )

(

)

( )

0 1 1

, r aij i r r n m

r i j

i n j

f c x

δ λ λ = + = ⎛ ⎞ = ⎜_⎜ ⎟_⎟ ⎝

∑ ∏

⎠

x untuk

1, 2,...,

r= k

Misalkan δ >i 0, untuk i=n0+1,...,nr,

dan λr =λr

( )

δ =δn₀+1+δn₀+2+ +... δnr,

untuk 1, 2,..., ,r= k maka menurut Teorema 2.2.4, diperoleh

( )

(

)

0 1 1 ( ) i ij r r _r m a i j n j r r

i n i

c x f δ λ _λ λ δ = = + ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ≥ _⎜ _⎟ ⎜ ⎟ ⎝ ⎠

∏

x

0 1 0 1 1

( )

i

r r

ij i r

n n m a i

r j

i n i i n j

c x δ δ λ λ δ = + = + = ⎛ ⎞ ⎛ ⎞ = _{⎜ ⎟ ⎜}⎜ ⎟_⎟ ⎝ ⎠ ⎝ ⎠

∏

∏ ∏

( )

1

0 1 1

nr i r ij i r i no n m a i r j

i n i j

c x δ δ λ λ δ = + = + = ⎛ ⎞ ⎛ ⎞ _∑ = _{⎜ ⎟ ⎜}⎜ ⎟_⎟ ⎝ ⎠ ⎝ ⎠

∏

. Jadi

( )

(

)

( )

1

0 1 1

nr i r ij i r r i no

n m _a

i

r r j

i n i j

(22)

¾ Misalkan r=1, maka menurut (4.2.2), berlaku

( )

(

)

( )

1 1 1 1 1 0 0 1 1 1 1 . n i ij i i n

n m _a

i

j i n i j

f c x λ δ δ λ λ δ = + = + = ≥ ⎛ ⎞ ⎛ ⎞ _⎜ ∑ _⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠

∏

x

( )

(

)

( )

2 2 2 2 1 1 1 2 2 1 1 . n i ij i i n

n m _a i

j i n i j

f c x λ δ δ λ λ δ = + = + = ≥ ⎛ ⎞ ⎛ ⎞ _⎜ ∑ _⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠

∏

x

( )

(

)

( )

3 3 3 3 1 2 2 3 3 1 1 . n i ij i i n

n m _a

i

j i n i j

f c x λ δ δ λ λ δ = + = + = ≥ ⎛ ⎞ ⎛ ⎞ _⎜ ∑ _⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠

∏

x

¾ Jika dilakukan terus sampai dengan

r=k, k∈ , dengan himpunan bilangan asli, maka menurut (4.2.2) berlaku

( )

(

)

( )

11

1 1 1

. k nk i k ij i k i nk k k

n m _a

i

k j

i n i j

f c x λ δ δ λ λ δ = −+ − = + = ≥ ⎛ ⎞ ⎛ ⎞ _⎜ ∑ _⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠

∏

x

Karena fr( )x >0, untuk x∈Df, maka

( )

(

)

1

(

( )

)

2

(

( )

)

1 2 ...

k

f x λ f x λ f x λ ≥

( )

1 1 1 1 0 0 1 1 1 n i ij i i n

n m _a

i

j i n i j

c x δ δ λ λ δ = + = + = ⎛ ⎞ ⎛ ⎞ _⎜ ∑ _⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠

∏

( )

2 2 2 1 1 1 2 1 1 ... n i ij i i n n m a i j i n i j

c x δ δ λ λ δ = + = + = ⎛ ⎞ ⎛ ⎞ _⎜ ∑ _⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠

∏

( )

11

11 1

nk i k ij i k i nk k n m a i k j

i n i j

c x δ δ λ λ δ = −+ − = + = ⎛ ⎞ ⎛ ⎞ _∑ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠

∏

( )

(

)

1 r k r r f λ =

⇔

∏

x ≥

( )

01

0

1 1 1

nr i r ij i r i n n

k m _a

i

r j

r i n i j

c x δ δ λ λ δ = + = = + = ⎛ ⎞ ⎛ ⎞ _∑ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠

∏

(4.2.3) Jika (4.2.3) disubstitusikan ke (4.2.1), maka diperoleh

( )

0 0 1 1 0 0 0

1 1 1

1 1 n i ij i r i nr i r ij i i n

n m _a k i

j r

i i j r

n m _a

i

j i n i j

c f x c x δ δ _λ δ δ λ δ δ = = + = = = = + = ⎛ ⎞ ⎛ ⎞ _⎜ ∑ _⎟ ≥ _{⎜ ⎟ ⎜} _⎟ ⎝ ⎠ ⎝ ⎠ ⎛ ⎞ ⎛ ⎞ _⎜ ∑ _⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠

∏

x

( )

0 1 0

1 1 1

1 . nr i i r ij i i r

n n m _a

i i

j i i i n i j

k r r c c x δ δ δ λ δ δ λ = = = + = = ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ∑ = _{⎜ ⎟} _{⎜ ⎟ ⎜}⎜ ⎟_⎟ ⎝ ⎠ _{⎝ ⎠ ⎝} ⎠

∏

Jadi

( )

0 1 0 0

1 1 1

1 . nr i i r ij i i r

n n m _a

i i

j i i i n i j k r r c c f x δ δ δ λ δ δ λ = = = + = = ⎛ ⎞ ⎛ ⎞ ⎛ ⎞ ∑ ≥ _{⎜ ⎟} _{⎜ ⎟ ⎜}⎜ ⎟_⎟ ⎝ ⎠ _{⎝ ⎠ ⎝} ⎠

∏

x

3) Jika ditambahkan kendala

1 0, r n ij i i aδ = =

∑

(kondisi ortogonalitas), maka diperoleh

( )

0

( )

0

1 1 1

i i

r

n n k i i

r i i i n i r

c c f δ δ λ λ δ δ = = + = ⎛ ⎞ ⎛ ⎞ ≥ _{⎜ ⎟} _{⎜ ⎟} ⎝ ⎠ ⎝ ⎠

∏

x .

Karena

( )

0 1 0 2 ... r,

r r n n n

λ =λ δ =δ + +δ + + +δ maka

( )

0

(

)

0

( ) 0

1 1 1

( )

i i

r

n n k i i

r i i i n i r

c c f δ δ λ λ δ δ = = + = ⎛ ⎞ ⎛ ⎞ ≥ _{⎜ ⎟} _{⎜ ⎟} ⎝ ⎠ ⎝ ⎠

∏

δ x δ Jika didefinisikan

( )

0

(

)

0

( )

1 1 1

: ( )

i i

r

n n k i i

r i i i n i r

c c v δ δ λ λ δ δ = = + = ⎛ ⎞ ⎛ ⎞ = _{⎜ ⎟} _{⎜ ⎟} ⎝ ⎠ ⎝ ⎠

∏

δ δ δ

(

( )

)

1 1 ( ) i r r n k i r i i r

c δ _λ λ

δ = = ⎛ ⎞ = ⎜ ⎟ ⎝ ⎠

∏

_δ δ _, maka

( ) ( )

0 ,

f x ≥v δ (4.2.4) untuk sebarang _∈ m

x dengan komponen-komponen positif, dan sebarang δ_∈ n

yang memenuhi kondisi kepositifan, normalitas, dan ortogonalitas.

(23)

13

(

)

0 ( ) 1 1 1 2

11 1 21 2 1

1 1 2 2

0 Maksimumkan

( ) ( )

terhadap ... 1

... 0

dengan 0 untuk 1,..., , da j i p k j i j j i

n p p m m pm p

i

c v

a a a

i n δ λ λ δ δ δ δ δ δ δ δ δ δ δ = = ⎛ _⎛ _⎞ ⎞ ⎜ ⎟ =_⎜ ⎜_⎜ ⎟_⎟ _⎟ ⎝ ⎠ ⎝ ⎠ + + + = + + + = + + + = > =

∏

δ δ δ 1 1 1

n 0 untuk 1 ,

1,

( ) ... untuk 1,...,

i i

i k k

i n n

n i n

k i k δ λ δ ₋ δ − + ⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ≥ + ≤ ≤ ⎪ ∀ ≥ ⎪ ⎪ = + + = _⎭ δ (4.2.5)

(Peressini et al., 1988) Teorema 4.2.1

Misalkan PG berkendala konsisten dan * x adalah solusi untuk PGP berkendala, maka PGD yang berpadanan konsisten dan memiliki solusi δ*_{yang memenuhi}

* *

0( ) ( )

g x =vδ

dan * 0 * * 0 * 1 ( )

, 1, 2,..., ( )

( ) ( ), 1,..., ,

1,..., .

i i

j i j j

u

i n

g

u i n n

j k δ λ ₋ ⎧ = ⎪ = ⎨ ⎪ ₌ ₊ ⎩ = * x x δ x

(Peressini et al., 1988) Bukti (lihat Peressini et al., 1988).

Berikut ini diberikan prosedur untuk menentukan solusi PG berkendala.

Prosedur PG Berkendala

Misalkan diberikan PGP seperti masalah (3.3.2), maka untuk menentukan solusinya diberikan prosedur sebagai berikut

1. Tentukan vektor fisibel F dari PGD, yaitu himpunan vektor δdi nyang memenuhi

0 0, untuk 1,...,

i i n

δ > = (kepositifan) 0

0, untuk 1,...,

i i n p

δ ≥ = + 0 1 1 n i i δ = =

∑

(normalitas)

1 0 p ij i i aδ = =

∑

,

j=1,...,m

(ortogonalitas)

2. Jika himpunan vektor fisibel F

a) himpunan kosong, maka proses berhenti, masalah PG tidak mempunyai solusi,

b) terdiri atas satu vektor _δ*

, maka

*

δ merupakan solusi dari PGD. Penghitungan dilanjutkan ke langkah 4, c) terdiri atas lebih dari satu vektor

(mempunyai banyak solusi), maka lanjutkan ke langkah 3.

3. Tentukan vektor δ*

yang merupakan

global maximizer untuk fungsi dual

(

)

( ) 1 1 ( ) ( ) j i p k j i j j i

c v δ λ λ δ = = ⎛ _⎛ _⎞ ⎞ ⎜ ⎟ = ⎜_⎜ ⎟_⎟ ⎜ _⎝ _⎠ ⎟ ⎝

∏

⎠

∏

δ δ δ .

4. Jika diberikan solusi _δ*

, maka solusi dari masalah primalnya adalah *

x yang diperoleh dari * 0 * * 0 * 1 ( )

, 1, 2,..., ( )

( ) (