Algoritma dan struktur data II
Teks penuh
Gambar
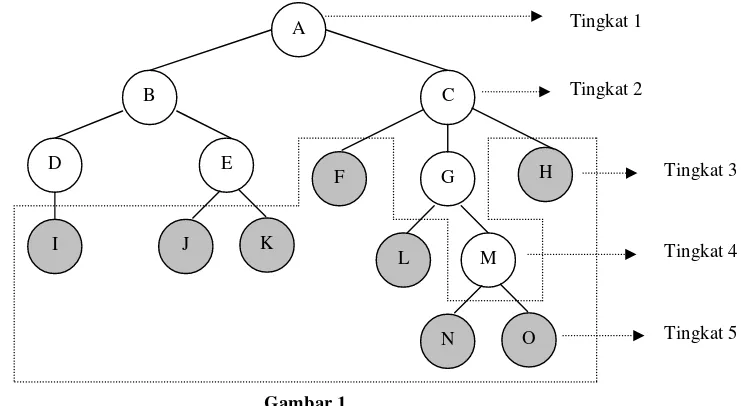
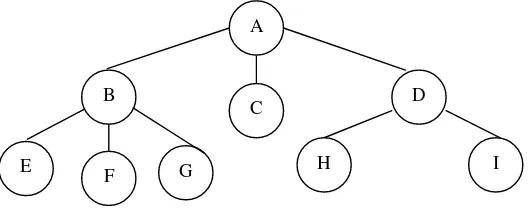
Dokumen terkait
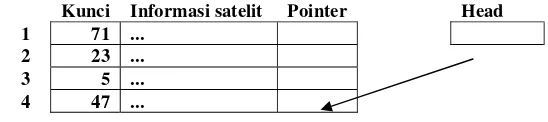
Kondisi linked list masih kosong atau posisi penyisipan kurang dari atau sama dengan 1 Jika kondisi ini terjadi, maka langkah yang dilakukan adalah sangat mudah yaitu dengan
Perulangan yang lebih dalam akan diproses terlebih dahulu sampai habis, kemudian perulangan yang lebih luar baru akan bertambah, mengerjakan perulangan yang lebih
Antara tipe pointer (sesuai dengan pendeklarasian pointer) dan tipe obyek yang akan ditunjuk oleh pointer haruslah sejenis.Kalau misalnya pointer pu dimaksudkan untuk
Untuk menyisipkan sebuah elemen baru ke dalam sebuah linked list pada posisi tertentu kita harus menemukan terlebih dahulu alamat memori dari elemen yang akan disisipi..
Tanpa adanya array doubling, setiap operasi memiliki waktu konstan, dan tidak bergantung pada jumlah item di dalam stack. Dengan adanya array doubling, satu operasi push
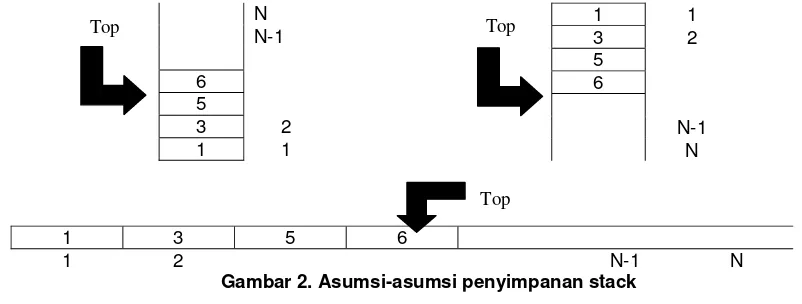
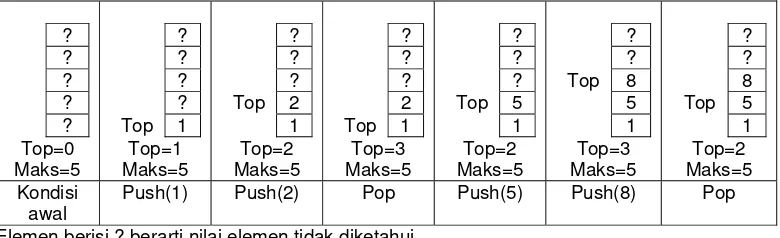
Dalam struktur stack dikenal dengan istilah PUSH, dan POP. - PUSH adalah istilah yang digunakan untuk memasukkan, menyimpan, menulis atau menginsert data kedalam stack. -
Dengan circular array, meskipun posisi terakhir telah terpakai, elemen baru tetap dapat ditambahkan pada posisi pertama jika posisi pertama dalam keadaan kosong.Jika
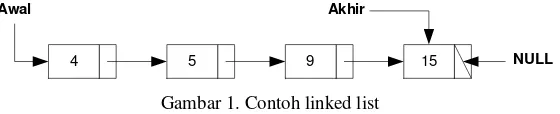
Menghapus Node di Depan Dengan Head dan Tail Penghapusan node tidak boleh dilakukan jika keadaan node sedang ditunjuk oleh pointer, maka harus dilakukan penunjukkan terlebih dahulu