PELABELAN SUPER EDGE MAGIC PADA GRAF CYCLE
, GRAF PLANAR
, GRAF
JALINAN, DAN GRAF UBUR-UBUR
ANISA TRIAGRINA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudulPelabelan Super Edge Magic Pada Graf Cycle , Graf Planar , Graf Jalinan, dan Graf Ubur-ubur adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Oktober 2014
ABSTRAK
ANISA TRIAGRINA. Pelabelan Super Edge Magic pada Graf Cycle
, Graf Planar , Graf Jalinan, dan Graf Ubur-ubur.
Dibimbing oleh TEDUH WULANDARI MAS’OED dan MUHAMMAD ILYAS.
Pelabelan pada graf adalah pemetaan bijektif yang memetakan unsur himpunan simpul atau himpunan sisi ke himpunan bilangan asli. Suatu graf
dengan banyaknya simpul dan banyaknya sisi dapat dikatakan memiliki pelabelan super edge magic jika dan hanya jika terdapat fungsi bijektif yang memetakan label setiap simpul pada bilangan asli 1 sampai , dan setiap sisi pada bilangan asli sampai . Selain itu, terdapat konstanta sehingga jumlah label dua simpul yang adjacent dan satu sisi di antaranya adalah konstanta . Dalam karya ilmiah ini terdapat satu lema dan empat teorema yang akan dibahas. Lema membuktikan bahwa graf dengan pelabelan super edge magic memiliki himpunan sisi yang terdiri dari bilangan asli yang berurutan. Masing-masing dari keempat teorema tersebut membuktikan bahwa graf cycle
, graf planar , graf jalinan, dan graf ubur-ubur
memiliki pelabelan super edge magic. Hal ini diketahui berdasarkan pada lema sebelumnya.
Kata kunci: Himpunan Sisi yang Berurutan, Pelabelan Graf, Super Edge Magic
ABSTRACT
ANISA TRIAGRINA. SuperEdge Magic Labeling of Cycle Graph , Planar Graph , Braid Graph and Jellyfish Graph. Supervised by TEDUH WULANDARI MAS’OED and MUHAMMAD ILYAS.
Labeling in graph theory is a bijection mapping that maps each elements of a set of vertices and a set of edges to the set of natural number. A graph denoted by with p vertices and q edges is called a super edge magic if and only if there is a bijective function that maps each of vertices labels to the natural numbers range 1 to and each of edges labels to the natural numbers range to . Also, there is a constant so that the number of two adjacent vertices and one of edges is equal to . In this paper, there are one lemma and four theorems were discussed. The lemma proves that graph with super edge magic labeling has a set of edges that consists of consecutive integers. Each of the four theorems proves that cycle graph , planar graph , braid graph and jellyfish graph has super edge magic labeling. This was proved using the fact indicated in the lemma previously mentioned.
PELABELAN SUPER EDGE MAGIC PADA GRAF CYCLE
, GRAF PLANAR , GRAF JALINAN,
DAN GRAF UBUR-UBUR
ANISA TRIAGRINA
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
Judul Skripsi : Pelabelan Super Edge Magic Pada Graf Cycle , Graf Planar , Graf Jalinan, dan Graf Ubur-ubur Nama : Anisa Triagrina
NIM : G54100010
Disetujui oleh
Teduh Wulandari Mas’oed, MSi Pembimbing I
Muhammad Ilyas, MSi, MSc Pembimbing II
Diketahui oleh
Dr Toni Bakhtiar, MSc Ketua Departemen
PRAKATA
Segala puji serta syukur bagi Alloh AWT yang telah memberikan nikmat dan karunia-Nya kepada kita semua. Shalawat serta salam semoga senantiasa tercurahkan kepada Nabi Muhammad SAW, beserta keluarga, sahabat serta para pengikutnya yang setia sampai akhir zaman. Alhamdulillah penulis bersyukur karena berkat rahmat dan karunia-Nya penulis dapat menyelesaikan skripsi dengan judul “Pelabelan Super Edge Magic Pada Graf Cycle , Graf Planar , Graf Jalinan, dan Graf Ubur-ubur”.
Terima kasih penulis ucapkan kepada Ibu Teduh Wulandari Mas’oed, M.Si selaku dosen pembimbing I, Bapak Muhammad Ilyas M.Si, M.Sc selaku dosen pembimbing II, dan Bapak Drs Siswandi, M.Si selaku dosen penguji yang telah memberikan bimbingan yang sangat berharga juga untuk semua waktu, nasehat, dukungan dan ilmu yang telah diberikan kepada penulis. Ungkapan terima kasih juga disampaikan kepada ayah, ibu, mba, mas, adik serta Bagus, atas segala doa dan saran kepada penulis dalam penyusunan skripsi ini. Terima kasih juga disampaikan untuk teman satu kontrakan, yaitu Vina, Tari, Susi, Amal dan Ai atas segala saran dan masukan kepada penulis. Tidak lupa juga terima kasih sebesar-besarnya kepada teman-teman di Departemen Matematika IPB angkatan 47, keluarga besar GUMATIKA IPB dan IKAHIMATIKA Indonesia Wilayah III yang selalu memberikan semangat dan dukungan dalam menulis skripsi.
Akhirnya dengan segala kerendahan hati, penulis menyadari bahwa dalam skripsi ini masih terdapat banyak kekurangan untuk menuju kesempurnaan. Penulis mencoba berusaha semaksimal mungkin dengan harapan skripsi dapat memperoleh hasil yang baik dan dapat bermanfaat bagi penelitian-penelitian selanjutnya.
Bogor, Oktober 2014
DAFTAR ISI
DAFTAR GAMBAR vi
PENDAHULUAN 1
Latar Belakang 1
Tujuan 1
LANDASAN TEORI 1
Teori Graf 2
Jenis-jenis Graf 3
Pelabelan Graf 5
PEMBAHASAN 8
SIMPULAN DAN SARAN 28
Simpulan 28
Saran 28
DAFTAR PUSTAKA 28
DAFTAR GAMBAR
1 Graf G 2
2 Walk 3
3 (a) , (b) , (c) 4
4 4
5 (a) , (b) , (c) 5
6 (a) , (b) , (c) 5
7 Pelabelan edge magic pada graf 6
8 Pelabelan edge magic pada graf dengan (a) dan (b) 7 9 Pelabelan super edge magic pada graf dengan 8 10 Graf dan memiliki himpunan yang terdiri dari 5 bilangan asli yang
berurutan 10
11 Graf cycle ber-order 3 11
12 Graf cycle dan memiliki himpunan yang terdiri dari 3 bilangan asli yang
berurutan 12
13Graf 13
14Graf cycle dan memiliki himpunan yang terdiri dari 5 bilangan
asli yang beurutan 14
15Graf 14
16Graf cycle dan memiliki himpunan yang terdiri dari 5 bilangan
asli yang berurutan 15
17 Graf planarber-order 5 15
18 Graf planar ber-order 5 dan memiliki himpunan yang terdiri dari 7 bilangan
asli yang beurutan 16
19 Graf 17
20 Graf dan memiliki himpunan yang terdiri dari 9 bilangan
asli yang berurutan 18
21 Graf 18
22 Graf dan memiliki himpunan yang terdiri dari 11 bilangan
asli yang berurutan 19
24Graf jalinan ber-order 6 dan memiliki himpunan yang terdiri dari 7 bilangan
asli yang berurutan 20
25 Graf 21
26 Graf dan memiliki himpunan yang terdiri dari 11 bilangan asli yang
berurutan 22
27 Graf 22
28 Graf dan memiliki himpunan yang terdiri dari 15 bilangan asli yang
berurutan 23
29 Graf ubur-uburber-order 6 24
30 Graf ubur-uburber-order 6 dan memiliki himpunan yang terdiri dari 7
bilangan asli yang beurutan 24
31 Graf ubur-ubur 26
32 Graf ubur-ubur dan memiliki himpunan yang terdiri
dari 9 bilangan asli yang berurutan 26
33 Graf ubur-ubur 27
34 Graf ubur-ubur dan memiliki himpunan yang terdiri
PENDAHULUAN
Latar Belakang
Teori graf adalah salah satu cabang ilmu matematika yang mempelajari sifat-sifat graf. Teori ini ditemukan pertama kali oleh ahli matematika asal Swiss, Leonhard Euler pada tahun 1736 saat menyelesaikan masalah jembatan Konigsberg.
Graf merupakan pasangan himpunan simpul dan himpunan sisi sehingga membentuk pola graf tertentu. Pola-pola yang terbentuk didefinisikan dan dikategorikan dalam kelas-kelas graf. Salah satu bahasan dalam graf adalah pelabelan graf.
Pelabelan graf adalah pemetaan bijektif yang memetakan unsur himpunan simpul dan atau himpunan sisi ke himpunan bilangan asli. Pelabelan dapat dilakukan dengan dua cara, yaitu pelabelan simpul dan atau pelabelan sisi. Pelabelan simpul adalah pelabelan dengan domain himpunan simpul, sedangkan pelabelan sisi adalah pelabelan dengan domain himpunan sisi. Pelabelan total adalah pelabelan dengan domain gabungan himpunan simpul dan himpunan sisi. Terdapat beberapa jenis pelabelan pada graf, antara lain pelabelan gracefull¸ pelabelan harmoni, pelabelan beraturan, pelabelan tak beraturan, pelabelan ajaib (magic labeling) dan pelabelan anti ajaib (antimagic labeling). Tulisan ini merupakan rekonstruksi ulang dari tulisan S. M. Lee dan A. N-T Lee dalam artikel “On Super Edge-Magic Graphs with Many Odd Cycles”.
Masalah yang akan dibahas pada penelitian ini adalah apakah graf dengan pelabelan super sisi ajaib (super edge magic) memiliki himpunan sisi yang berurutan dan apakah graf cycle , graf planar , graf jalinan, dan graf ubur-ubur dengan cycle ganjil memiliki pelabelan super edge magic.
Tujuan Penelitian
Tujuan dari penulisan karya ilmiah ini adalah untuk:
1. Membuktikan bahwa graf dengan pelabelan super edge magic memiliki himpunan sisi yang berurutan.
2. Membuktikan bahwa graf cycle , graf planar
, graf jalinan, dan graf ubur-ubur dengan cycle ganjil memiliki pelabelan super edge magic.
LANDASAN TEORI
2
Teori Graf
Definisi 1 (Graf)
Suatu graf G adalah pasangan terurut (V,E) dengan V adalah himpunan tak kosong dan berhingga dan E adalah himpunan pasangan tak terurut yang menghubungkan elemen-elemen V. Graf G dinotasikan G = (V,E). Elemen V disebut simpul atau vertex sedangkan elemen E disebut sisi atau edge. Himpunan dari simpul-simpul pada graf G dinotasikan dengan V(G) atau V, sedangkan himpunan dari sisi-sisi pada graf G dinotasikan dengan E(G) atau E.
(Foulds 1992)
Definisi 2 (Graf Tak Berarah)
Graf G disebut graf tak berarah apabila anggota himpunan sisi dari graf G bukan merupakan pasangan terurut dari simpul-simpul G.
(Chartrand & Oellermann 1993)
Graf yang akan dibahas dalam karya ilmiah ini adalah graf tak berarah. Contoh graf tak berarah dapat dilihat pada Gambar 1.
Gambar 1 Graf G = (V,E)
Himpunan simpul pada graf G = (V,E) adalah { } dan himpunan sisi pada graf G adalah { }.
Definisi 3 (Order dan Size)
Misalkan diberikan graf G. Banyaknya simpul dari suatu graf G disebut order dari G, dan banyaknya sisi dari G disebut size dari G. Order dari graf G dinotasikan dengan | | dan size dari graf G dinotasikan dengan | |.
(Chartrand & Oellermann 1993)
Pada Gambar 2.1, banyaknya simpul adalah 3, dituliskan | | = 3, sedangkan banyaknya sisi juga 3, dituliskan | | = 3.
Definisi 4 (Walk)
Suatu walk pada graf G adalah suatu barisan simpul dan sisi dari graf G dengan bentuk { }. Suatu walk yang menghubungkan dengan dikatakan tertutup jika . Jika , maka walk tersebut dikatakan terbuka.
(Chartrand & Oellermann 1993)
Contoh walk dapat dilihat pada Gambar 2.
{ }
c b
3
Gambar 2 Walk.
Definisi 5 (Cycle)
Cycle pada suatu graf G adalah walk tertutup yang mengandung setidaknya tiga simpul dan semua simpulnya berbeda.
(Foulds 1992)
Contoh cycle dapat dilihat pada Gambar 1.
Definisi 6 (Graf Cycle)
Suatu graf ber-order dengan yang membentuk sebuah cycle disebut graf cycle dan dinotasikan dengan .
(Chartrand & Oellermann 1993)
Gambar 1 dapat dinotasikan dengan .
Definisi 7 (Cycle Ganjil)
Cycle dikatakan ganjil jika banyaknya sisi atau simpul dari suatu cycle bernilai ganjil.
(Foulds 1992)
Jenis-jenis Graf
Jenis graf sangat beragam, dan dapat dikelompokkan menjadi beberapa kategori, bergantung pada pengelompokannya. Jenis graf yang akan dibahas dalam karya ilmiah ini ada empat sesuai dengan banyaknya teorema yang akan dibahas, yaitu graf cycle , graf planar (planar graph)
, graf jalinan (braid graph), dan graf ubur-ubur (jellyfish graph).
Definisi 8 (Graf Cycle )
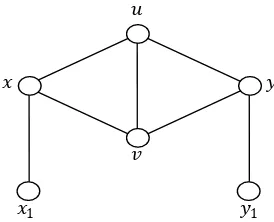
Graf cycle adalah graf dengan banyaknya simpul dan banyaknya sisi , . Dengan himpunan simpulnya dibagi menjadi dua jenis, yaitu dan . Himpunan simpul dari adalah { } dengan himpunan simpul dari adalah { } dan himpunan simpul dari adalah { }. Dan
himpunan sisi dari adalah himpunan sisi dari , dimana sisi dari
adalah sisi antar simpul , digabung dengan
{ }.
(Lee dan Lee, 2003)
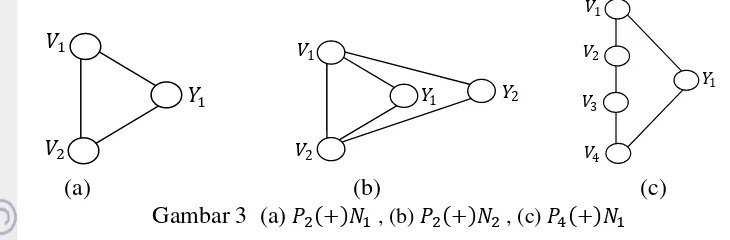
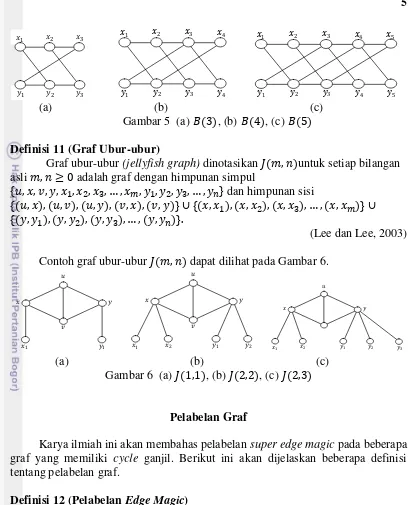
Beberapa contoh graf dapat dilihat pada Gambar 3. 1
2
3
4
4
(a) (b) (c)
Gambar 3 (a) , (b) , (c)
Definisi 9 (Graf Planar)
5
Karya ilmiah ini akan membahas pelabelan super edge magic pada beberapa graf yang memiliki cycle ganjil. Berikut ini akan dijelaskan beberapa definisi tentang pelabelan graf.
Definisi 12 (Pelabelan Edge Magic)
Misalkan graf G dengan banyaknya simpul p dan banyaknya sisi q. Suatu pemetaan satu-satu dari himpunan simpul digabung himpunan sisi ke himpunan { } disebut sebagai pelabelan edge magic pada G jika ada konstanta (disebut magic number ) sehingga untuk setiap .
(Enomoto, et al. 1998)
6
Gambar 7 Pelabelan edge magic pada graf
Misal dan masing-masing edge dipadankan dengan suatu nilai :
maka diperoleh label sisi, sehingga
Maka, adalah magic number. Dan pelabelan edge magic dapat digambarkan seperti Gambar 8 (a).
Sedangkan, apabila dipadankan dengan suatu nilai:
7
Maka, adalah magic number. Dan pelabelan edge magic dapat digambarkan seperti Gambar 8 (b).
(a) (b)
Gambar 8 Pelabelan edge magic pada graf dengan (a) dan (b)
Definisi 13 (Pelabelan Super Edge Magic)
Misalkan graf G dengan simpul p dan sisi q, dan G memiliki pelabelan edge magic . Jika { } dan { } maka disebut pelabelan super edge magic.
(Enomoto, et al. 1998)
8
Gambar 9 Pelabelan super edge magic pada graf dengan
Definisi 14 (Graf Edge Magic)
Suatu graf G disebut edge magic jika terdapat sebuah pelabelan edge magic. (Enomoto, et al. 1998)
Gambar 8 (a) dan (b) merupakan contoh graf edge magic karena memiliki pelabelan edge magic.
Definisi 15 (Graf Super Edge Magic)
Suatu graf G disebut super edge-magic jika terdapat sebuah pelabelan super edge magic dari G. membuktikan bahwa graf dengan pelabelan super edge magic memiliki himpunan sisi yang berurutan dan beberapa graf dengan cycle ganjil memiliki pelabelan super edge magic.
Berikut ini akan diberikan lema yang akan menunjukkan bahwa graf yang memiliki himpunan beranggotakan hasil penjumlahan label dua simpul adjacent dan himpunan tersebut terdiri dari bilangan asli yang berurutan merupakan graf dengan pelabelan super edge magic.
Lema 3.1
9
Bukti
Misalkan graf G merupakan graf super edge magic. Akan dibuktikan bahwa graf G memiliki fungsi bijektif { } sedemikian sehingga himpunan { } merupakan himpunan yang terdiri dari bilangan asli yang berurutan.
Misalkan G memiliki simpul dan sisi. Karena G graf super edge magic, artinya ada { }, { } dan konstanta sehingga untuk setiap . Karena maka dapat diperoleh
{ } dan Karena { }, maka dapat diperoleh
{ } yang merupakan himpunan yang terdiri dari bilangan asli yang berurutan.
Misalkan graf G memiliki fungsi bijektif { } sedemikian sehingga himpunan { } merupakan himpunan yang terdiri dari bilangan asli yang berurutan. Akan dibuktikan bahwa graf G memiliki pelabelan super edge magic dengan konstanta magic .
Misalkan graf G memiliki simpul dan sisi . Graf G memiliki fungsi bijektif { } sedemikian sehingga { } merupakan himpunan yang terdiri dari bilangan asli yang berurutan. Misal . Diketahui { }.
Akan dibuktikan { } dan ada sedemikian sehingga , untuk setiap .
Pilih Akibatnya diperoleh fungsi pelabelan sisi
( ) ( )
( ) , untuk { } dan .
Untuk suatu dan dapat diperoleh
( ) dengan sehingga ( ) ( )
( ) Akibatnya diperoleh
{ } Jadi { }
Berikutnya akan ditunjukkan ada sehingga Pilih ,
10
Berikut ini diberikan dua ilustrasi untuk lebih memahami Lema 3.1. Ilustrasi pertama akan ditunjukkan graf yang super edge magic dan memiliki himpunan yang terdiri dari bilangan asli yang berurutan.
Misalkan diberikan graf seperti Gambar 7, banyaknya simpul dan sisi
Gambar 10 Graf dan memiliki himpunan yang terdiri dari 5 bilangan asli yang berurutan
11
Selanjutnya akan dibahas beberapa teorema yang digunakan untuk membuktikan bahwa graf dengan cycle ganjil memiliki pelabelan super edge magic dengan menggunakanLema 3.1.
Sebelum membuktikan Teorema 3.2, berikut diberikan contoh graf cycle dengan himpunan sisi terdiri dari bilangan asli yang berurutan.
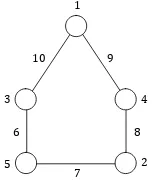
Misalkan diberikan graf cycle ber-order 3 dengan bentuk seperti pada Gambar 11.
Gambar 11 Graf cycle ber-order 3
12
Dari label-label simpul tersebut, dapat ditunjukkan bahwa himpunan sisi dari graf tersebut terdiri dari bilangan asli yang berurutan dan dapat digambarkan sebagai berikut.
Gambar 12 Graf cycle dan memiliki himpunan yang terdiri dari 3 bilangan asli yang berurutan
Cara pelabelan tersebut merupakan salah satu contoh cara memperoleh himpunan sisi yang terdiri dari bilangan asli yang berurutan pada suatu graf. Cara ini juga digunakan untuk membuktikan Teorema 3.2.
Berikut akan dibuktikan Teorema 3.2 yang menyatakan bahwa graf memiliki pelabelan super edge magic.
Teorema 3.2
adalah super-edge magic, untuk setiap .
(Lee dan Lee, 2003)
Bukti
Diketahui graf memiliki jumlah simpul sebanyak dan jumlah sisi sebanyak .
Didefinisikan fungsi { } dengan aturan : ;
;
� ;
Akan dibuktikan bahwa graf memiliki fungsi bijektif
{ } sedemikian sehingga himpunan { }
merupakan himpunan yang terdiri dari bilangan asli yang berurutan. Dari definisi fungsi umum simpul, diperoleh fungsi umum sisi, yaitu:
� ;
;
( ) ;
� ;
1
2
3 4
13
Sehingga, dapat diperoleh :
{ � � �
�
( ) � �
� }
Karena dan , maka dapat diperoleh :
{
}
{
}
{
}
{
}
{
} merupakan himpunan yang berurutan.
Jadi, sesuai Lema 3.1 graf merupakan super-edge magic karena memiliki himpunan yang terdiri dari bilangan asli yang berurutan.
Berikut ini diberikan ilustrasi untuk lebih memahami Teorema 3.2. Ada beberapa ilustrasi yang akan diberikan. Pada dasarnya proses menunjukkan bahwa graf memiliki himpunan sisi yang terdiri dari bilangan berurutan dengan mencoba semua kemungkinan dengan mengikuti aturan yang ada.
Ilustrasi pertama, diberikan graf ber-order 4 dengan bentuk seperti pada Gambar 13.
Gambar 13 Graf 1
2
14
Diketahui dan , maka simpul-simpul pada graf dapat dipadankan dengan suatu nilai menurut aturan yang berlaku sebagai berikut :
Dari label-label simpul tersebut, dapat ditunjukkan bahwa himpunan sisi dari graf terdiri dari bilangan asli yang berurutan. Sehingga, graf tersebut memiliki pelabelan super edge magic dan dapat digambarkan sebagai berikut.
Gambar 14 Graf cycle dan memiliki himpunan yang terdiri dari 5 bilangan asli yang berurutan
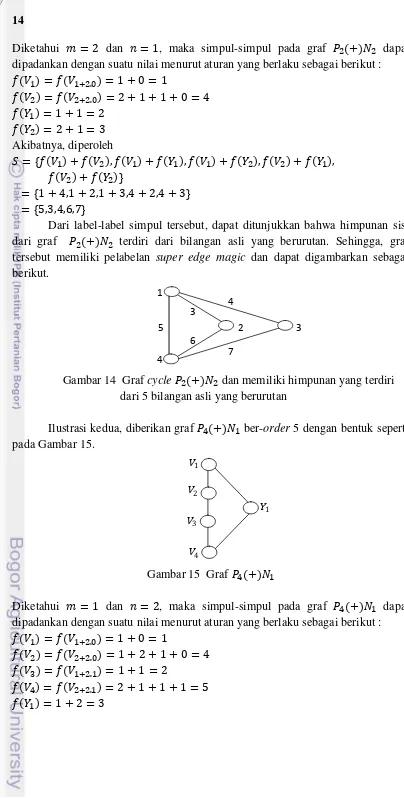
Ilustrasi kedua, diberikan graf ber-order 5 dengan bentuk seperti pada Gambar 15.
Gambar 15 Graf
15
Akibatnya, diperoleh
{ � � }
{ } { }
Dari label-label simpul tersebut, dapat ditunjukkan bahwa himpunan sisi dari graf terdiri dari bilangan asli yang berurutan. Sehingga, graf tersebut memiliki pelabelan super edge magic dan dapat digambarkan sebagai berikut.
Gambar 16 Graf cycle dan memiliki himpunan yang terdiri dari 5 bilangan asli yang berurutan
Sebelum membuktikan Teorema 3.3, berikut diberikan contoh graf planar yang memiliki himpunan sisi yang terdiri dari bilangan asli yang berurutan.
Misalkan diberikan graf planar ber-order 5 dengan bentuk seperti pada Gambar 17.
Gambar 17 Graf planarber-order 5
Misalkan simpul-simpul pada graf planar ber-order 5 dipadankan dengan suatu nilai, yaitu :
1
2 4 5
6
8
3
7
4
5
1 2
16
Dari label-label simpul tersebut, dapat ditunjukkan bahwa himpunan sisi dari graf tersebut terdiri dari bilangan asli yang berurutan dan dapat digambarkan sebagai berikut.
Gambar 18 Graf planar ber-order 5 dan memiliki himpunan yang terdiri dari 7 bilangan asli yang berurutan
Contoh ini digunakan untuk membuktikan Teorema 3.3.
Berikut akan dibuktikan Teorema 3.3 yang menyatakan bahwa graf planar memiliki pelabelan super edge magic.
} merupakan himpunan yang terdiri dari bilangan asli yang berurutan.
17
Dari definisi fungsi umum simpul, diperoleh fungsi umum sisi, yaitu:
;
; Sehingga, dapat diperoleh :
{
}
Karena , maka dapat diperoleh :
{ }
{ }
{ }
merupakan himpunan yang berurutan.
Jadi, sesuai Lema 3.1 graf planar merupakan super-edge magic karena memiliki himpunan yang terdiri dari bilangan asli yang berurutan.
Berikut ini akan diberikan beberapa ilustrasi untuk lebih memahami Teorema 3.3.
Ilustrasi pertama, diberikan graf planar ber-order 6 dengan bentuk seperti pada Gambar 19.
Gambar 19 Graf )
1 2
2 2 1
18
Diketahui , maka simpul-simpul pada graf dapat dipadankan dengan suatu nilai menurut aturan yang berlaku sebagai berikut :
19
Diketahui , maka simpul-simpul pada graf dapat dipadankan dengan suatu nilai menurut aturan yang berlaku sebagai berikut :
Dari label-label simpul tersebut, dapat ditunjukkan bahwa himpunan sisi dari graf terdiri dari bilangan asli yang berurutan. Sehingga, graf tersebut adalah graf super edge magic dan dapat digambarkan sebagai berikut.
Gambar 22 Graf dan memiliki himpunan yang terdiri dari 11 bilangan asli yang berurutan
Sebelum membuktikan Teorema 3.4, berikut diberikan contoh graf jalinan yang memiliki himpunan sisi yang terdiri dari bilangan asli yang berurutan.
20
Misalkan simpul-simpul pada graf jalinan ber-order 6 dipadankan dengan suatu nilai, yaitu :
Akibatnya, diperoleh
S { } { }
{ }
Dari label-label simpul tersebut, dapat ditunjukkan bahwa himpunan sisi dari graf tersebut terdiri dari bilangan asli yang berurutan dan dapat digambarkan sebagai berikut.
Gambar 24 Graf jalinan ber-order 6 dan memiliki himpunan yang terdiri dari 7 bilangan asli yang berurutan
Contoh ini digunakan untuk membuktikan Teorema 3.4.
Berikut akan dibuktikan Teorema 3.4 yang menyatakan bahwa graf jalinan memiliki pelabelan super edge magic.
Teorema 3.4
Graf jalinan adalah super-edge magic untuk setiap .
(Lee dan Lee, 2003)
Bukti
Diketahui graf memiliki jumlah simpul sebanyak dan jumlah sisi sebanyak .
Didefinisikan fungsi { } dengan aturan :
4
6
1 3 5
2 4 6
8
21
Akan dibuktikan bahwa graf B(n) memiliki fungsi bijektif { } sedemikian sehingga himpunan { } merupakan himpunan
yang terdiri dari bilangan asli yang berurutan.
Dari definisi fungsi umum simpul, diperoleh fungsi umum sisi, yaitu:
Sehingga, dapat diperoleh :
{ ,
,
}
Karena , maka dapat diperoleh :
{
}
{ }
{ }
merupakan himpunan yang berurutan.
Jadi, sesuai Lema 3.1 graf merupakan super-edge magic karena memiliki himpunan yang terdiri dari bilangan asli yang berurutan.
Berikut ini akan diberikan beberapa ilustrasi untuk lebih memahami Teorema 3.4.
Ilustrasi pertama, diberikan graf jalinan ber-order 8 dengan bentuk seperti pada Gambar 25.
Gambar 25 Graf
2 3 4
1
2 3 4
22
Diketahui , maka simpul-simpul pada graf dapat dipadankan dengan suatu nilai menurut aturan yang berlaku sebagai berikut :
Dari label-label simpul tersebut, dapat ditunjukkan bahwa himpunan sisi dari graf terdiri dari bilangan asli yang berurutan. Sehingga, graf tersebut merupakan graf super edge magic dan dapat digambarkan sebagai berikut.
23
Diketahui , maka simpul-simpul pada graf dapat dipadankan dengan suatu nilai menurut aturan yang berlaku sebagai berikut :
Dari label-label simpul tersebut, dapat ditunjukkan bahwa himpunan sisi dari graf terdiri dari bilangan asli yang berurutan. Sehingga, graf tersebut merupakan graf super edge magic dan dapat digambarkan sebagai berikut.
Gambar 28 Graf dan memiliki himpunan yang terdiri dari 15 bilangan asli yang berurutan
Sebelum membuktikan Teorema 3.5, berikut diberikan contoh graf ubur-ubur yang memiliki himpunan sisi yang terdiri dari bilangan asli yang berurutan.
24
Gambar 29 Graf ubur-uburber-order 6
Misalkan simpul-simpul pada graf ubur-ubur ber-order 6 dipadankan dengan suatu nilai, yaitu :
Akibatnya, diperoleh :
S { } { }
{ }
Dari label-label simpul tersebut, dapat ditunjukkan bahwa himpunan sisi dari graf tersebut terdiri dari bilangan asli yang berurutan dan dapat digambarkan sebagai berikut.
Gambar 30 Graf ubur-ubur ber-order 6 dan memiliki himpunan yang terdiri dari 7 bilangan asli yang berurutan
Contoh ini digunakan untuk membuktikan Teorema 3.5.
Berikut akan dibuktikan Teorema 3.5 yang menyatakan bahwa graf ubur-ubur memiliki pelabelan super edge magic.
1 1
2
3 4
5
1 6
5 6
7
8 9
25
Teorema 3.5
Graf ubur-ubur adalah super-edge magic untuk setiap .
(Lee dan Lee, 2003)
Bukti
Diketahui graf memiliki jumlah simpul sebanyak dan jumlah sisi sebanyak .
Didefinisikan fungsi { } dengan aturan :
Akan dibuktikan bahwa graf B(n) memiliki fungsi bijektif
{ } sedemikian sehingga himpunan { }
merupakan himpunan yang terdiri dari bilangan asli yang berurutan. Dari definisi fungsi umum simpul, diperoleh fungsi umum sisi, yaitu:
Sehingga, dapat diperoleh :
{ ,
}
Karena , maka dapat diperoleh :
{
}
{
} merupakan himpunan yang berurutan.
Jadi, sesuai Lema 3.1 graf merupakan super-edge magic karena memiliki himpunan yang terdiri dari bilangan asli yang berurutan
26
Berikut ini akan diberikan beberapa ilustrasi untuk lebih memahami Teorema 3.5.
Ilustrasi pertama, diberikan graf ubur-ubur ber-order 8 dengan bentuk seperti pada Gambar 31.
Gambar 31 Graf ubur-ubur
Diketahui dan , maka simpul-simpul pada graf dapat dipadankan dengan suatu nilai menurut aturan yang berlaku sebagai berikut :
ubur-27
Ilustrasi kedua, diberikan graf ubur-ubur ber-order 9 dengan bentuk seperti pada Gambar 33.
Gambar 33 Graf ubur-ubur
Diketahui dan , maka simpul-simpul pada graf dipadankan dengan suatu nilai menurut aturan yang berlaku sebagai berikut :
ubur-28
SIMPULAN DAN SARAN
Simpulan
Dalam karya ilmiah ini telah dibuktikan bahwa suatu graf adalah graf super edge magic jika dan hanya jika graf tersebut memiliki himpunan yang beranggotakan hasil penjumlahan label dua simpul yang adjacent dan terdiri dari bilangan asli yang berurutan.
Dalam karya ilmiah ini juga ditunjukkan bahwa graf cycle , graf planar , graf jalinan, dan graf ubur-ubur dengan cycle ganjil memiliki himpunan beranggotakan hasil penjumlahan label dua simpul yang adjacent dan terdiri dari bilangan asli yang berurutan. Sehingga, graf tersebut merupakan graf yang memiliki pelabelan super edge magic.
Saran
Karya ilmiah ini membahas pelabelan super edge magic pada beberapa graf dengan cycle ganjil. Bagi yang berminat membuat karya ilmiah yang berhubungan dengan pelabelan super edge magic dapat mencari penyelesaian masalah pelabelan pada graf lainnya.
DAFTAR PUSTAKA
Chartrand G, Oollermann OR. 1993, Applied and Algorithm Graph Theory. New York (US) : Mc Graw-Hill.
Enomoto H, Llado AS., Nakamigawa T, Ringel G. 1998. Super edge-magic graphs. SUT J. Math, 34(2), 105-109.
Figueroa-Centeno RM, Ichishima R, Muntaner-Batle FA. 2001. The place of super edge-magic labelings among other classes of labelings. Discrete Mathematics, 231(1), 153-168.
Foulds LR. 1992. Graph Theory Applications. New York (US): Spinger-Verlag.
Lee SM, Lee ANT. 2003. On super edge-magic graphs with many odd cycles. Congressus Numerantium, 65-80.
RIWAYAT HIDUP
Penulis dilahirkan di Jakarta pada tanggal 21 Agustus 1992 dari ayah H. Ikhwan Darmawan dan ibu Hj. Sumiyati. Penulis adalah putri ketiga dari empat bersaudara. Tahun 2010 penulis lulus dari SMA Negeri 82 Jakarta dan pada tahun yang sama penulis lulus seleksi masuk Institut Pertanian Bogor (IPB) melalui jalur Undangan Seleksi Masuk IPB dan diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
Selama mengikuti perkuliahan, penulis aktif mengajar privat mata kuliah kalkulus TPB di bimbingan belajar dan privat mahasiswa Smart Quantum dan mengajar privat untuk tingkat SD, SMP, SMA dan D3 IPB di bimbingan belajar dan privat. Penulis juga aktif sebagai bendahara Departemen Komunikasi dan Informasi BEM FMIPA pada tahun 2011/2012 dan staf Departemen Pengembangan Sumber Daya Mahasiswa Gugus Mahasiswa Matematika pada tahun 2012/2013. Penulis juga pernah aktif di organisasi luar kampus sebagai staf Departemen Komunikasi dan Informasi Ikatan Himpunan Mahasiswa Matematika Wilayah 3, yaitu Jawa Barat, Banten, DKI Jakarta dan Kalimantan Barat. Selain itu, penulis juga aktif dalam berbagai kepanitiaan di antaranya panitia IPB Mathematics Challenge (IMC) sebagai bendahara Divisi Humas pada tahun 2012, panitia Sport Competition and Art Festival on MIPA Faculty (SPIRIT) sebagai anggota Divisi Humas pada tahun 2012, Community Development (COMDEV) IKAHIMATIKA INDONESIA Wilayah 3 Regional Jabodetabek dan Banten sebagai Sekretaris Umum pada tahun 2012, dan aktif membantu di berbagai kepanitiaan lainnya.