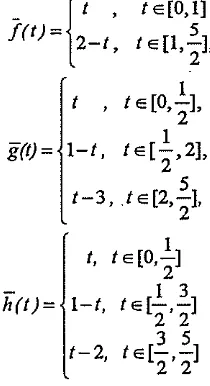Rendezvous Search Pada Garis Dengan Tiga Pemain

(1)

RENDEZVOUS SEARCH

PADA G M S

DENGAN TIGA PEMATN

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAElUAN

AWM

INSTlTUT PERTANIAN BOGOR

BOGOR

(2)

ABDUL LATIP. Rendezvous Search pada Garis dengan Tiga Petnain (Rendezvous Search on the Line with Three Players). Dibimbiug oleli FARDA HANUM dan TEDUH WULANDARI.

Pada suatu lapangan luas de~igan lintasan kereta api melintasi seluruh daerah tersebut, tiga orang penerjun ditejunkan. Mereka telah menyepakati sebelu~nnya untuk berte~nu di ILntasan kereta api tersebut, tetapi belum taliu letak yang sebenarnya untuk bettemu. P e n k a n dilakukan di sepanjang lintasan kereta api dan untuk memecalhn masalah ini diynakan re~zdezvoussearch pada garis.

Tiap pe~nain tidak mengetahui arah pe rjalanan pemain lainnya, hanya jarak di &tara dua pemain terdekat diketahui, yaitu 1. Mereka bergerak dengan kecepatan paling besar 1 untuk saling bertemu. Pertemuan yang te jadi lebih dahulu antara dua pemain akan mengakhiri permainan.

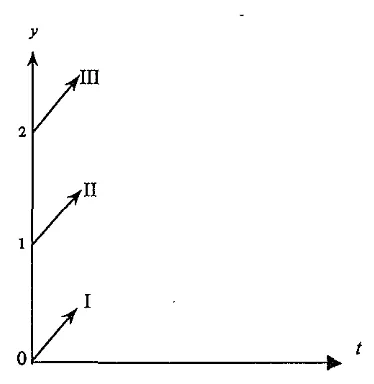
Rangkaian permainan digambarkan &lam bidang Cartesius, dengan sumbu horisontal menyatakan waktu clan sumbu vertikal menyatakan posisi pemain pa& garis lurus. Penelitian ini dilakukan untuk membantu ketiga pemain menentukan strategi yang liarus diynakan agar mereka dapat bertemu dalam waMu yang minimum.

Nilai randevu dapat diperoleh &lam dua bentuk yaitu bentuk simetrik dan asimettik. Bentuk simetrik membatasi pemain untuk mengynakan strategi pencarian p i g sama sedangkan bentuk asimetrik niemungkinkan pemain untuk membicarakan terlebih dahulu strategi yang akan mereka gunakan sehingga mereka boleh memilih strategi yang berbeda. Dalam tulisan ini yang dibicatakan adalah bentuk asimetrik.

(3)

RENDEZVOUS SEARCH

PADA GARIS

DENGAN TIGA PEMAIN

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains

PA

Program Studi Matematika

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN

ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

(4)

Judul : Re~?dezvous Search pada Garis dengan Tiga Pemain Nama : Abdul Latip

NRP : G31.0883

' I

-

Dra. ~ a h d a Hanum, M.Si. Pembimbing I

Menyetujui,

Teduh Wulandari, S.Si. Pembimbing I1

(5)

RIWAYAT HIDUP

Penulis dilahirkan di Bogor pada tanggal 16 September 1975 sebagai anak ketiga dari empat

bersaudara, anak dari pasangan H. U. Zakaria dan Khopipah.

Tahun 1994 penulis lulus dari SMA Negeri I Ciawi danpada tahun yang sama lulus Seleksi masuk IPB

melalui jalur undangan seleksi masuk IPB. Penulis memilih Program Studi Matematika, Jurusan

Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

Selama mengikuti perkuliahan penulis aktif pada salah satu lembaga pendidikan. Selain itu, penulis

(6)

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya sehingga karya ilmiah

ini berhasil diselesaikan. Judul yang dipilih dalam tulisan ini adalah Rendezvous Search pada Garis

dengan Tiga Pemain.

Terima kasih penulis ucapkan kepada berbagai pihak yang telah membantu penyelesaian karya ilmiah

ini, antara lain Ibu Dra. Farida Hanum, M.Si. dan Ibu Teduh Wulandari, S.Si. selaku pembimbing, serta

Bapak Dr. Ir. D.S. Priyarsono sebagai penguji luar. Di samping itu terima kasih penulis sampaikan pada

teman-teman angkatan 31 atas kebersamaannya selama ini, warga Cidangiang 30, khususnya Ahnled

Hendra, yang tefah banyak membantu menyelesaikan karya ilmiah ini. Ungkapan terima kasih juga

disampaikan kepada bapak, umi, serta kakak-kakak dan adik tercinta, atas segala doa dan kasih sayangnya.

Semoga karya ilmiah ini dapat bermanfaat.

Bogor, Februari 2001

(7)

Halaman

DAFTAR TABEL

...

... ... . . . ix

DAFTAR GAMBAR ..

...

ix

DAFTAR LAMPIRAN

...

ix

1. PENDAHULUAN 1.1 Latar Belakang ..

...

. 1

1.2 Tujuan ...

.

1

11. MODEL FORMAL 2.1 Notasi dan Asumsi

...

.

...

1

2.2 Hubuugan Antara Kasus dan Tipe

...

3

2.3 Ruang Strategi

...

:

...

3

111. KELAS STRATEGI YANG BERHINGGA

...

7

IV. ALGORITMA UNTUK

MENENTUKAN

R&

...

9

(8)

DAFTAR TABEL

Halaman

1. Anggota-anggota 2

2. Anggota-anggota B

...

3

3. Himpunan image

4

...

4

4. Garis-garis untuk menentukan 7 n ~ ~ ~ h . h ~ ... 5

.

*

- - - 5. Nilai-nlla~ T ( f , g , h ) untuk b E B

...

.

...

6

. .

. - 6. Nilai-nllal T C ( f

, g ,

h ) untuk c e C

...

.

...

.

...

6

DAFTAR GAMBAR

Halaman I. Posisi dan arah pemain untuk (0, I ,2,-,+,+) 2. Posisi dan arah pemain untuk (2,1,0,+,-,-) 3. Permainan yang dimulai dengan kasus cl . 4. Garis LI,, dan L , _ , untuk bl 6 5. Garis LJ,, dan Lz, untuk c, dengan a = I

...

7

6. Garis LI,, dan L2,) untuk cl dan a = 1 dengan shategi f yang baru

... .

.

...

8

7. Proses kemungkinan 1 dalam bentuk gambar 22

DAFTAR LAMPIRAN

Halaman I. Bidang Cartesius untuk b , b,, b,, ..., b,, ... 13

2. Diagram alir algoritma untuk menentukan Ry,,

...

15

3. Tahap-tahap algoritma untuk menentukan R;,>

..

... 17

(9)

I. PENDAHULUAN

1.1 Latar Belakang

Rendezvous search adalah suatu kwrdinasi tanpa komunikasi dau mernpakan proses paralef. Masalah rendezvous search (Alpern, 1995) menjelaskan bagaimana para pemain yang ditempatkan secara acak dalam suatn daerah

pencarian diketahui dapat bergerak dengan kecepatan maksimal 1 untuk saling bertemu dalam waktn harapan terkecil. Pada awal peuempatan dalam permainan, tiap pemain tahu posisinya masing-masing tapi tidak tahu posisi pemain lainnya.

Masalah rendezvous search pertama kali secara formal didefinisikan oleh Alpern (1995). Untuk menyederhanakan masalah, apilih kasus pada

garis lurns sebagai daerah pencarian.

Cerita yang melatarbelakangi pennasalahan ini adalah sebagai berikut: Misalkan ada dua orang penejnn ingin. bertemu yang ditejunkan pada

snatu lapangan luas dan terdapat lintasan kereta api yang melintasi daerah tersebut. Mereka telah menyepakati sebelumnya unhk bertemu, tetapi

belum tahu di mana letak yang sebenarnya pada lintasau kereta api tersebut. Masalahnya adalah bagaimana mereka hams bertindak agar memperoleh waktu harapan ya* minimum Cerita

di atas tersebut kemudian dikembangkan untnk pemaiu yang terdiri atas tiga orang.

Nilai randew dapat diperoleh dalam dua bentuk, yaitn benhlk simetrik dan b e n a asimetrik. Bentuk simetrik membatasi pemain untuk mengguuakan strategi pencarian yang Sam% sedangkan bentuk asimetrik memungkinkan pemain untuk memilih strategi yang berbeda. Pada

tnlisan ini yang akan dipelajari adalah rendezvous search tiga pemain dengan bentuk asimetrik.

1.2 Tujnan

Tujuan penulisan karya ilmiah ini adalah: 1. mempelajari jaminan pertemuan antara tiga

orang pemain,

2. mempelajari koudisi yang dibutuhkan untnk strategi optimal, dan

3. menentukan nilai randew asimetrik untuk tiga orang pemain.

II.

MODEL FORMAL

2.1 Notasi dan Asnmsi

Permainan dimulai dengan menempatkan tiga orang pemain secara acak pada suatu daerah.

Untnk menyederhanakan masalah, dipilih garis lurns sebagai daerah pencarian, setiap pemain tidak mengetahui posisi dari pemain lainnya, tetapi jarak di antara 2 pemain terdekat diketahui, yaitn 1 satnan jarak. Mereka bergerak dengan kecepatan paling besar 1 satuan jaraklsatnan waktu untuk saling bertemu. Pertemuan yang tejadi lebih dahulu antara dua orang pemain akan mengakhiri permainan.

Diasumsikan bahwa permainan ini asimetrik, artinya masing-masing pemain mengetahui sebelumnya strategi yang akan digunakan oleh pemain laiunya.

Rangkaian permainan digambarkan dalam bidang Cartesius, dengan sumbn horizontal menyatakan waktn dan sumbu vertikal menyatakan posisi pemain pada garis lurns.

Definisi 1

Orientasi awal w pada pemain adalah rangkap-3

(01, 02.03) dengan

+

jika pemain i bergerak naik pa&

={

awal permainan

-

jika pemain i bergerak t n m pada

awal permainan

Definisi 2

Posisi awal p pada pemain adalah rangkap3 @ I , p2, p3) dengan P adalah permumi

himpunan {0, 1,2) danpl menyatakan posisi awal pemain i, i=l, 2,3.

Definisi 3

Suatu permainan dengan tiga pemain dikatakan berakhir jika:

a) pemain yang ditempatkan pada 0 bertemu dengan pemain yang ditempatkan pada 1,

atau

b) pemain yang ditempatkan pada 2 bertemu dengan pemain yang ditempatkan pada 1, atau

(10)

sedangkan pemain yang ditempatkan pada 0 bertemu dengan pemain yang ditempatkan pada 2 tidak dibahas karena sebelum kedua pemain tersebut bertemu, maka terlebih dahnlu saiah satu di antara mereka akan beitemu dengan pemain yang ditempatkan pada 1 sehingga menjadi bentuk a) atau b) pada pemyataan di atas.

Misalkan himpunan C mempakan kumpulan semua anggota c = @, w ) yang menyatakan posisi dan arah saat permainan dimnlai. Perhatilotnbahwa suatu permainan yang dimnlai dengan @,,pz,p3, - , o z , w ~ ) "berakl~ir sama" dengan permainan yang dimulai dengan ( 2 - p ~ , 2-pz, 2-p3,

+,

-w2,-w3 ). Untuk menjelaskan hal ini, misalkan diambil contoh pl=O, ~ = l , p3=2, dengan arahpemain

II

danpemain

111 keduanya

+.

Contoh ini menghasilkan :

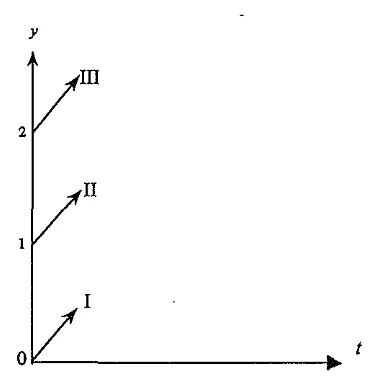
( P I . PZ, ~ 3 . - . ma, a s ) = (0,1,2,-,+,+). Ddam bidang Cartesius dapat dilihat pada Gambar 1 .

[image:10.599.68.510.69.811.2]

( Z-PI, 2-pz, 2-p3,

+

,*z, -m3 )= (2,1,0,+,-,-I. Dalam bidang Cartesius dapat dilihat pada Gambar 2.

Gatnbar 1. Posisi dan arah pemain untuk (0,1,2,-,+,+).

,l

0

III

(11)

Tanpa memperlliitikan a r d ~ masing-masing pemain itu naik atau turun, dari kedua gambar tersebut terlihat bahwa pemain I1 dan pemain I11

sama-sama bergerak menjauhi pemain I, sehingga dapat dikatakan bahwa kedua permainan berakhir sama. Hal yang sama juga berlaku jika masing- masing nilai p l ,

n,

p3, atau 02 dan 03 diubah. Ini

berarti bal~wa w, selalu dapat dibuat +. Jadi nntuk kasus ini diasumsikan bahwa wl =

+

sehingga himpunan C hanya mempunyai 24 anggota

(=3!x2'). Semua anggota himpnnan C disebut kasus clan diperlihatkan pada Tabel 1.

Misalkan (a,, a*) menyatakan pasangan tak teNNt dari pemain-pemain yang ditempatkan setelah pemain lain ditempatkan pada am1 permaiuan. Misalkan b, =-(al, a2, dl, d2), dengan di

menyatakan arah relatif pemain a, terhadap pemain

a,. (i#j), yaitu,

to jika pemain a, bergerak kearah

pem$n a, pada awal permainan mu jika @main a, bergerak menjauhi

pemain a) pada awal permainan

dengan i, j = 1, 2 dan i # j. Misalkan B={b,l

i=1, ..., 12). Semua anggota B disebut tipe clan B

mempunyai 12 anggota yang diperlihatkan pada

Tabel 2.

2.2 Hubungau Antara Kasus dan Tipe

Sebelumnya telah diuraikan bahwa permainan berakhir jika dua pemain yang letaknya berdekatan pada awal permainan sudah bertemu. Misalkan suatu permainan dimulai dengan kasus

cl

.

( pernain 11 terletak antara pemain I dan

pemain III), maka permainan akan berakhir jika pemain I dan I1 bertemu, atau jika pemain I1 dan 111

[image:11.599.310.497.137.329.2]

bertemu. Misalkan posisi awal pemain diberikan sebagai c, yang diperlihatkan pada bidang Cartesius dalam Gambar 3.

Gambar 3. Permainan yang dimulai dengan kasus c,.

Dalam Gamba~ 3 terlihat b a h m pemain I bergerak menuju pemain I1 sedangkan pemain II bergerak menjauhi pemain I dan pemain 11 bergerak menuju pemain 111 sedangkan pemain 111 bergerak menjauhi pemain 11, sehingga kasus cl &pat dihubungkan menjadi dua tipe, yaitu

b2 = (I, II, to, mu) dan blo = (II, III, to, mu). Suatu pertemuan antara dua pemain Cyang terjadi lebih dahulu) akan mengakhiri permainan.

Misalkan pemetaan

4

menya- hubungan antara kasus dan tipe, yaitu:

4

: C-tBxB, Kc) = (b,, bJ), V c e C , i < j ,

maka himpnnan image dari

4

&pat dilihat dalam Tabel 3.

2 3 Ruang Strategi

Dalam pembahasan permainan ini, strategi adalah fungsi yang menyatakan arah dan jar& pergerakan pemain. Strategi yang digunakan hanya yang terdapat pada mang strategi yang didefinisikan sebagai berikut :

(12)

Tabel 3. Himpunan image

4

kontinn b a d clan P adalah iumpunan kompak. (Alpern, 1995), maka nilai pa& ( 2 ) selalu dijamin ada (Goldberg, 1976).

Misalkan p(fg,h) menyatakan waktu saat pemain dalam tipe b saling bertemu (6 E B). Untuk

semua c E C, didefinisikan: T a g & = min plb~t;g,h)

bsrplc) (3)

Diberikan tiga strategi Cfg,h) sembarang, dengan delapan garis lintasan berikut ini:

Garis-garis di atas menyatakan lintasan masing-masing pemain. Lintasan Ll,,(f)

menyatakan garis untuk pemain dengan strategif; lintasan &(t) menyatakan garis untuk pemain dengan strategi g, sedangkan lintasan LO,&) dan

L3,,(f) menyatakan garis untuk pemain dengan strategi h. Untuk semua b E B,

p(L

g, h) &pat

ditentukan dengan menggunakan garis Lk, dan

Definisi 4 L*+,,p dalam (4), sehingga

Misalkan pemain I memilih strategi

f;

pemain

I1 memilih srategi g dan pemain

EI

memilih _{p ~ ; g , h )}₌_min_{{ t}_:_{L k d t )}₌_L&l,p(f)} _{( 5 )} strategi h, denganf; g, h E P. Misalkan

TXf;

g, h)

menyatakan peamuan ~ a n g betpadanan _dengan

P

₌_{+ I ,}_k=0,1,2_dan_k_{menyatakan letak} dengan kasus c, dengan c E C. Maka waktu _{pemain. Garis-garis untuk menentukan}

PV;

_g,_h)

pertemuan harapan ? a h ) dinyatakan sebagai : dengan b E B diberikan dalam Tabel 4.

dengan R:, adalah nilai randevu, yaihl waMu

harapan pertemuan asimetrik dengan tiga pemain

[image:12.602.72.286.56.838.2]

(13)

[image:13.595.303.408.250.443.2]

Tabel 4. Garis-garis untuk menentnkan _pemainI turun atau

p

=-I. Akhirnya diperoleh m k h ) (k, a)= (0+1) dan (lctl,n = ( 1 ~ 1 ) . Demikianpula dalam menentnkan garis-garis untuk bs, b? dan b, dilakukan dengan cara seperti untnk b5.

3) Untuk tipe bs, bla, b11 dan bl;

Untuk tipe bg, ~ I O , b11 dan b12

,

garis yang

diambil pemain 111 adalah L3,,karena garis tersebut letaknya lebih dekat terhadap garis strategi pemain 11 (L2,0) dibandingkan dengan Lo,,.

Ilustrasi

Diberikan contoh kasus berikut ini. Misalkan:

Penjelasan Tabel 4

1) Untnk tipe bl, b2, b3 dan b4

Contoh: Untuk tipe bl (I, 11, to, to), pemain I

dan pemain I1 saling mendekat. Garis yang diambil adalah garis yang memuat strategi pemain I (f) dan pemain 11 (g), yaitn LI,, dan L%,.(jadi k 1 ) Letak pemain I berada di bawah pemain I1 (pemain I di 1 dan pemain I1 di 2), sehingga agar keduanya saling mendekat, maka pemain I naik atau a =+l dan

pemain II tnrun atau

p -1.

Akhirnya diperoleh (k, a)=(l+l) dan (lctl, p) = (2;l). Demikian pula dalam menentukan garis-garis untuk b2, b3 dan

b4 dilakukan dengan cara seperti untuk bl.

2) Untuk tipe b,, bs, b, dan b8

Contoh: Untuk tipe b5 (I, 111, to, to), pemain I clan pemain 111 saling mendekat, garis yang diambil adalah garis yang memuat strategi pemain I (f) dan

pemain 111 (h). Garis yang memuat strategi pemain 111 ada dua yaitn Loao dan L,,,. Tetapi garis yang terdekat dengan garis untuk stmtegi pemain I (LIJ adalah Lo,, sehingga pada tipe b, ini, garis yang diambil pemain III adalah Lq, Dengan demikian

,

pemain 111 terletak di bawah pemain I (pemain 111 pada 0 sedaugkan pemain I pada 1) sehingga agar saling mendekat, pemain III naik atau a =+1 dan

dengan

f,g,

h

berturut-turut merupakan strategi pemain I, pemain 11, dan pemain 111.

B e r k k a n Tabel 4, untuk bl diambil garis L1.1 dan

LZ-,

Apabila strategi-strategi pemain I dan

pemain U disubstitusikan ke (4) diperoleh : L1,1= f(t) +1

(14)

[image:14.595.71.518.58.772.2]

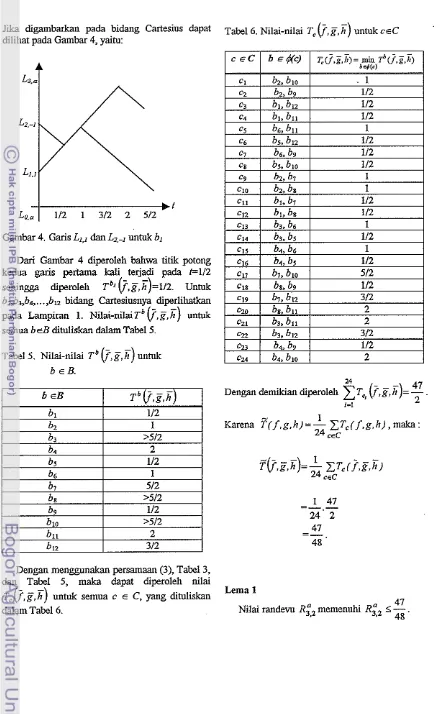
Jika digambarkan pa& bidang Cartesius dapat dilihat pada Gambar 4, yaitu:

Gambar 4. Garis

4-1

dan LZ.-, untuk bl

Dari Gambar 4 diperoleh bahwa titik potong kedua garis peitama kali tejadi pada t-112 sehingga diperoleh Tbl @,g,h)=112. Untuk

bZ,b3,b4,.

. .

,b12 bidang Cartesiusnya diperlihatkan pada Lampiran 1. ~ilai-nilaiTb

@,

g.

F)

untuk semua b e B dituliskan dalam Tabel 5.

Tabel 5. Nilai-nilai T

*

@,

c,

h)

untuk

b € B.

Dengan menggunakan persamaan (3), Tabel 3, dan Tabel 5, maka &pat diperoleh nilai

T, 6 ,

g,

h)

untuk semua c E C, yang dituliskan dalam Tabel 6.

Tabel 6. Nilai-nilai T, @,g,h) untuk ceC

21

47

Dengan demikian diperoleh _T,

@,g,

h)=

-

f=1 2

Lema 1

47

Nilai randevu R12 memenuhi R12 5

-

[image:14.595.286.518.77.655.2]

(15)

Bukti _Karena

f,g,l;~P,

_maka_R:,

sT(f,g,h).

Karena R& = min

T"(

f , g , h ) (dari persamaan

f

.g.heP _{Terbukti bahwa}_R,4,₅

-

47

.

2), makaR& 2 T"(f ,g.h), V f , g , h E P. 48

III.

KELAS STRATEGI YANG BEREWGGA

Misalkan pemain I memilih strategg pemain I1

memilih strategig, dan pemain In memilih strategi

4 ,

t E [ ~ , ; l h, dengan I;

g,

E

>.

Dengan menggunakan

persamaan (4), maka misalkan Ll,,(,, dinamakan lintasan agen-agen pemain I; L2,,0, dinamakan lintasan agen-agen pemain 11; Lo,,fl dan L3,,(,, dinamakan lintasan agen-agen pemain In; dengan

a = + l .

Lema 2

Misalkan x g , h ) adalah strategi-strategi pemain. Misalkanti < t 2 <

...

< tk(k58)adalah

waktu pertemuan pemain i dengan beberapa agen pemain terdekat untuk pertama kalinya. Maka

strategi pemain i &pat d i m m i sehingga untuk setiap j, agen pemain i dapat bergerak dengan kecepatan 1 menuju agen pemain terdekat (dengan waktu pertemuan t = $+I ) dalam selang waktu ( 9 . $1) dengan menggrinakan strategi baru tersebut untuk semua j E {O, 1,

...,

k-1) (to = O),

dan waktu pertemuan harapan paling besar adalah T"(f ,g, h).

Bukti

(Lihat Lampiran 4)

llustrasi Lema 2

Misalkan strategi pemain I dengan kecepatan kurang dari 1 akan bertemu dengan pemain terdekatnya pada waktu (misalkan) t4

.

Maka strategi pemain I ini dapat d i m m i dengan kecepatan 1 sehingga waktu pertemuan dengan pemain terdekatnya bisa kurang dari t4. Sebagai contoh misalkan g g , h ) adalah strategi-strategi pemain dengan f adalah strategi pemain I.

Misalkan diambil cl, yaitu (0,1,2,+,+,+) dengan

a=1, jika digambarkan pada bidang Cartesius untuk L1,, clan L2,1 &pat dilihat pada Gambar 5

berikut ini:

Gambar 5. Garis dan LZ,I untuk c, dengan

a=I.

Strategi a w l :

Dad Garnbar 5 terlihat bahm ti* p p t o n g a n

2512 sehinga waktu pertemnannya >512. Jika saategi

[image:15.602.300.505.376.620.2]

(16)

(17)

Lema 5

ldisalkan &g,l~) adalah strategi-strategi optimal

maka T,&, h)

<

4 untnk semua c G C.

IV.

ALGORITMA UNTI

Akibat 4 dalam bahasan sebelumnya memungkinkan untuk mengkonstruksi sebuah atgoritma untuk menemukan selumh strategi- strategi optimum dan nilai randevu R&

.

Misalkan

s(k) menyatakan strategi-strategi yang

didefinisikan sampai waktu (k+1)/2. Jika s(k)

memennhi syarat yang diberikan dalam Lema 2,

maka s(k) dapat dituliskan dalam bentuk mat*

3xk dengan elemen-elemennya:

i

+

1, jika pemaini m e l a n j u h

sv ( k ) =

-

arahsebelumnppada t = j / 2

1, jikapemain i mengubah arahpada t = j / 2

untuk i=1,2,3 dan j = 1 2

,...

jc. Banyaknya matriks

s(k) adalah

2)*.

Berdasarkan Lema 5, maka strategi dapat dibatasi sampai waktu yang didefinisikan kurang dari 4. Tanpa menghilangkan keumuman dapat diasumsikan bahwa untuk interval waktu [0,1/2], semua pemain bergerak dengan amh asal yang diberikan oleh a. Pada saat j/Z fjkl), s&)

akan menentukan apakah pemain i mengubah arah

pa& setengah unit waktu berikutnya. Jika pemain menggunakan strategi s(@, ia dapat menentukan apakah pertemuan telah tejadi pada waktu

(k+1)/2. Misalkan untuk semua c EC didefinisikan:

{

t, jikapermainanberakhir

T ( c , s ( ~ ) ) = pada t I;

lk

+

l ) / 2

m, selaimya

Artinya, T(c,s(k)) ada nilainya jika saat k diberikan maka pemain telah bertemu, tetapi jika tidak bertemu maka

akan

bemilai m. Misalkan:

T'(c,s(k))=min (T(c,s(k)), (k+1)/2+1/2).

T(c,s(k)) dapat diinterpretasikan sebagai waktu

pertemuan aktual jika s(k) digunakan dengan asumsi bahwa posisi semna pemain pada waktu (k+1)/2

dan

T (c,s(k)) sebagai waktu pertemuan paling mungkin yang menggunakan strategi s(W,

karena jika pemain belum bertemu pada fk+1)/2,

maka perkiraan waktu pertemuan paling optimis adalah (k+l)/2+1/2. Misalkan M(s(W adalah indikator apakah permainan telah berhenti pada W u (k+1)/2 dalam ke-24 kasus saat strategi s(kJ

diguuakan, yaitu :

Bukti

(Lihat Lampiran 4)

K

MENENTUKAN

R:2

M(s(k,) =

{

1, jika maksc,cT(c, s(k)J < m

0, selainnya

Artinya, M(s(!$) bemilai 1 jika saat k diberikan, maka pemain telah bertemu nntuk tiap kasus tetapi bila a& satu atau lebih kasus yang menyebabkan pemain tidak bertemu saat k diberikan, maka

M(s(k)) akan bemilai 0.

Algoritma didefinisikan dalam tahaptahap sedemikian sehingga setiap tahap k (k=1,2 ,..., 7),

hanya strategi-strategi s(1) yang digunakan. Misalkan Ak menyatakan batas atas terkecil untuk

R&

yang diperoleh pada tahap

k,

clan Ak

mempakan barisan tak naik Lema 1 berakibat bahwa A. &ah 47/48 dan tiap strategi s(kJ

berpotensi menjadi strategi optimal jika

ET*(sO) SAk-1;

2 4 1

*

dengan EP(sfk)j= x - T (ci , s ( k ) )

.

Misalkan

i-I 24

Dl menyatakan himpunan selnruh matriks s(1)

(bernilai sama terhadap permutasi baris)

,

Dk

menyatakan himpunan matriks HOG-1) dengan tambahan satu kolom matriks s(l), dan

didefinisikan:

Hk=@(k)

&.

Ey(s(k))

ax-I

clan M(s(kJJ=Ol, Rk=ls(k) E Dk:

~ET'lso

> A*-11,

E ~ = ( s ( ~ ) E D ~ : EETS(~JJ I; A ~ - , dan M ( s ( ~ J J = ~ ) .

Jadi

Hk

menyatakan himpunan strategi s(k) dengan dugaan paling mungkin ~T'(s(k)) Ak-1 yang berpotensi menghasilkan strategi optimal; Rk

menyatakan himpunan strategi s(k) yang ditolak pada tahap k karena memilii waktu harapan lebih dari sehingga tidak optimal, Ek menyatakan himpunan strategi s(k) yang memiliki waktu

pertemuan harapan ET6(k)J (paling besx &ah Arti dari bemilai sama terhadap permutasi

1 1 )

baris misalnya suatu matriks

-

1 dianggap sama

(18)

artinya dengan ma& karena apabila pada

salah satu matriks tersebut dilakukan permutasi baris, maka akan menghasilkan matriks yang sama dengan matriks yang lainnya. Begitu pula matriks

- 1

-

1 akan dianggap sama artinya dengan

I:

matriks

[

Ma& s(1) didefinisikan, -1 -1

Perhatikan bahwa strategi-strategi dalam himpunan Ek optimal kecuali bila waktu pertemuan harapan yang lebih kecil diperoleh pada tahap

tahap berikutnya pada algoritma, yaitu terdapat sebuah kf(k' > k) dan A , < ET(s(k))

,

dengan

24 1

ET(s(kJJ= x - - ~ ( c , ,s(k)) . Dengan kata lain,

1-1 24

hams diperoleh Ak = minaCk,,, ET(s(k)) untuk

k=1,2,

...

,7. Perhatikan bahwaAk=Ak-~ kecuali bila terdapat s(k) dengan M(s(k.)=l dan ET(s(k))+lk-~.

Ide utama algoritma ini adalah bahwa pada

setiap tahap k, matriks s(k) dipartis1 menjadi stmtegi-strategi optimal potensial @aim himpunan

Ek uHk) dan selainnya (yaitu Rt). Partisi banyaknya matriks yang harus diperhatikan pada

tahaptahap berikutnya dalam algoritma Untuk setiap s(kJ dalam H(kJ @emilai sama terhadap permutasi baris), s k ) diperluas sampai matriks

3x(k+I) dengan menambeMan kolom tambahan

(k+1) sedemikian sehingga kesimpulan tentang waktu pertemuan harapan dapat diperoleh dari

matriks pada tahap k' (k' > k). Tiap s(kJ dalam Hk

meningkat paling tin@ 8 kemungkinan s(k+l)

&lam tahap (k+l). Algoritma berhenti pada langkah k saat Hk merupakan himpunan kosong. Secara singkat, algoritma tersebut adalah sebagai berikut:

Dimuiai dengan k=l

I). Tentukan s(k) yang banyaknya

z3*

matriks

2). Apakah k=l? jika ya maka Dl=s(l) dan

dilanjutkan ke 3)

,

tetapi jika k#l maka langsung ke 3)

3). Tentukan matriks anggota Dk

4). Apakah s(k)~Dk? jika ya maka dilanjutkan ke 5), tetapi jika tidak maka proses tidak dilanjutkan

6). ~entukan s(k) yang menjadi anggota Hb Rk.

dan

Ek

7). Apakah Ek merupakan himpunan kosong? Jika ya maka dilanjutkan ke 8) sedangkan bila tidak maka langsung ke 9)

8). Ak-Ak-1 dan dilanjutkan ke 10)

9). Hitung ETfs(kU dan

Ak = m ( s ( k ) ) kemudian dilanjutkan ke 10)

lo). Apakah Hk merupakan himpunan kosong? Jika ya maka proses selesai

dan

tentukan nilai Ak, jika tidak maka proses dilanjutkan untuk k=k+l

11). Apakah k+1<81 J i i ya maka proses diteruskan jika tidak maka proses tidak usah dilanjutkan

Diagram alir algoritmauntuk menentukan R',2 dituliskan dalam Lampiran 2 sedangkan penjelasan tahaptahap algoritma untuk menentukan R& dituliskan dalam Lampiran 3.

Teorema 6

(19)

Bukti k=4, d e w A,=47/48. Sehingga diprole11 Dengan menggunakan algoritma. untuk 47

R & = - .

.

tne~~entukan R& , maka proses berhenti pada saat 48

V. KESIMPULAN DAN SARAN

Pertexnuan antara ti@ pemain yang berada pada mengakhiri permainan menghasilkan nilai randevu suatu garis &pat dihitung secara matematik asimetrik R& 47,48, .

cnengynakan Rendezvous search.

w a h

pertemuan antara tiga pemain akan Tulisan ini dapat dikembangkan nntuk pemain minimum jika strategi yang mereka gun&n Ymg terdiri atas lebih dari tiga orang (n pemain). merupakan yaitu skate@ yang Selain itu jnga bisa dicari nilai randevu untuk memenuhi syarat kondisi optimal, D~~ orang simetrik baik untuk tiga pemain maupun pemain bertemu lebih dahulu yang kemudian akan nntuk pmain.

DAFTAR PUSTAKA

Alpern, S. 1995. The rendezvous search problem. SIAM Journal of Control and optimization 33(3): 673683.

Alpern, S. & A. Beck. 1997. Rendezvous search problem on the line with bounded resource: expected time minimization. European Journal of Operations Research 101: 558597.

Alpern, S. & S. Gal. 1995. Rendezvous search on the liue with distinguishable players. SIAM Jozmial of Control and Optimization 33(4):

12701276.

Anderson, E.J. & S. Essegaier. 1995. Rendezvous search problem on the line with

indistinguishable players. SLAM Journal of Control and Optimization 33(3): 16371642.

Goldberg, RR. 1976. Methods ofReal Analysis. Ed2. John Willey, New York.

Lim, W.S. & S. Alpern. 1996. Minimax rendezvous search on the line. SIAMJournal of Control and Optimization 34(5): 16501665.

Lim,

W.S.,

S. Alpern & A. Beck. 1997. Rendezvous search on the line with more than

two players. Operations Research 45(3): 357362.

(20)

(21)

Latnpiran 1. Bidang Cartesius untuk b.,, b3, b,, ..., b12

I

b

I b - 1

Diperoleh T ( f ,g, h ) = -

Lo,,' 112 1 312 2 512 2

b2

- - -

Diperoleh T ( f , g , h ) = 1

L , - I

+ I

L4-I

LI,-I Diperoleh ~ * ~ ( j , g , h j = 1

. I

Lo,, 112 1 312 2 512

t

- 5

Diperoleh T ( f , g , h j z -

2

L J . /

L , I

I

Lo, 1 L1,-1

5 Diperoleh Tb7 ( j , g , h ) = -

2

LII, a 112 1 312 2 512

(22)

Diperoleh

Tb"(f.g,h)

= 2

1 Diperoleh

~ ~ ( f , g , h )

=

-

2

3 Diperoleh

T b k 2 ( f , g ,

h )

= - 2

(23)

Lampiran 2. Diagram alir algoritma untuk menentukan

R&

-

Tentukan matriks

angora

Dk

Tidak

(24)

$.

Tentukan anggota

Hk,

Rk,

Ek

Ya

Ak=Aa,

Ak = min ET(s(k))

r(k)e&

(25)

Lampiran 3. Tahap-tahap algoritma untnk menentukan R$

Tahap inisialisasi : Ao=47/48 cia1 s(1) = [[l)2[;j,[;i)3[! 1

~ ] 7 [ - ~ ] * [ ~ ] 3 [ ~ ~ ) 7 [ ~ 1 ) ]

,

* Tahap 1: Diketahui k = l sehingga s(k) = s(1). Banyaknya matriks s(1) adalah 2 * ' = ~ ~ = 8 ,

yaitu:

sfl)=[~),[~),[~l),[~~),[j],[~],[j~),[~l)]

1 -1 -1 -1

,

Karena k = l maka jelas bal~wa Dl =s(l). Dari kedelapau matriks itu akan ditentukan yang menjadi

anggota HI ,RI, dan El. Karena matriks bernilai sama dengan

d i d [:jnntnk &;roses selanjutnya. Begitu pula mat&

maka bisa diarnbil matriks

.

Untuk s(l)=

[:I

1 ; artinya pemain I, pemain 11, &II pemain 111 melanjntkan arah sebelumnya

. .

pada t=1/2. T(cI,s(l)) menyatakau waktu pertemuan peltama kali dari dua pemain yang berdekatan dengan posisi awal pa& cl (0,1,2,+, 1. +) untnk [0,1/2] dan dilanjutkan dengan

s(1) untuk [112,1]. Apabila digambarkan pada bidang Cartesius diperolel~ l~asil sebagai berikut:

(26)

(27)

24

.

makadiperoleh hasil ~ T * ( c ~ , s ( l ) ) = 21

,

sehingga i=l

Dari hasil ini, diperoleh bahwa ET'(~(I))<A,, Apabila T(c,s(l)) digambarkan pada bidang Cartesius diperoleh hasil :

sehingga T(c,s(l))= m. Hal ini menghasilkan maksCec T(c,s(I)) =a, sehingga M(s(l))=O. / I \

Karena ET'(s(1)) 410 dan M(s(l))=O

,

maka s(1) = 1 mempakan anggota HI

.

Dengan

I-J

cara perhitungan yang sama seperti

[:]

1 dan

[IJ,

maka untuk dua matriks yang lain diperoleh :

-

1 E HI dan - 1 E R,. Pada tahap ini El tidak mempunyai anggota.

I-lj

.

,

I-lj

.

,

Karena El himpunan kosong, maka A1=A0=47/48. Pada tahap ini ada dua matriks anggota ( 1 ) 1 1 )

1 dan -1 sehingga HI bukan himpunan kosong. Akibatnya proses

-"

1-

J

1-

J

ditemskax pada tahap berikutnya untuk k=2.

Tahap 2:Diketahui k=2 selungga s(k) = s(2). Pada tahap 2 ini, matriks s(2) yang diproses adalah anggota

Dz

yaitu matriks anggota HI dengan tambahan satu kolom matriks s(1). Pada tahap

(28)

(29)

Lampiran 4. Pembuktian Lema 2 dan Leilia 5

Bukti Lema 2:

Misalkan pemain terdekat dengan peinain i adalah pemain r dan s, dengan MS. Diasumsikan bahwa

pemain i menggunakan strategi J dan mengikuti lintasan Ll,,(.), sehigkan pemain r dan s

n~enggunakan strategi g dan h dan mengikuti lintasan

Lp(.)

dan Lo,&), dengan

fi

y €{+I; -1). Bukti dibagi menjadi kemungkinan-kemungkinan berikut:

Kemunglunan 1: Satu agen pemain i bertemu dengan agen pemain r pada

fi,~

sedangkan agen lain pemain i tidak bertemu dengan agen peinain manapun pa& tPl,

Kemunglunan 2: Satu agen pemain i bertemu dengan agen penlain r pada tj,~, sedan- agen lain pemain i bertemu agen pemain s pada

t,,).

Kemungkinan 3: Hanya satu agen pemain i yang bertemu dengan agen kedna pemain r dan s pada $+I, sedangkan agen pemain i yang lain tidak bertemu dengan agen pemain manapun.

Kejadian dimana satu agen pemain i memenuhi kemungkinan 3 sedangkan agen pemain i lainnya bertemu agen pemain lain tak mungkin terjadi. Hal ini karena jika kemungkinan 3 berlaku, maka :

af($+d

+ 1 = .Bg($+3 + 2 = yh ($+I) yang berakibat -aJ($+J + 1 = -.Bgft,,J = -yh

($+3

+ 2

sehi~igga diperoleh -a f ($+I)

+

1 # -,13g($+I)

+

2 clan -a J($+))

+

1 t -yh ($+I). Oleh karena itu lintasan

pada Ll,., tidak berpotongan dengan lintasan agen-agen pemain lain pada

ti,).

Kemungkinan dimana agen pemain i bertemu dengan agen kedua pemain r ( atau s

,

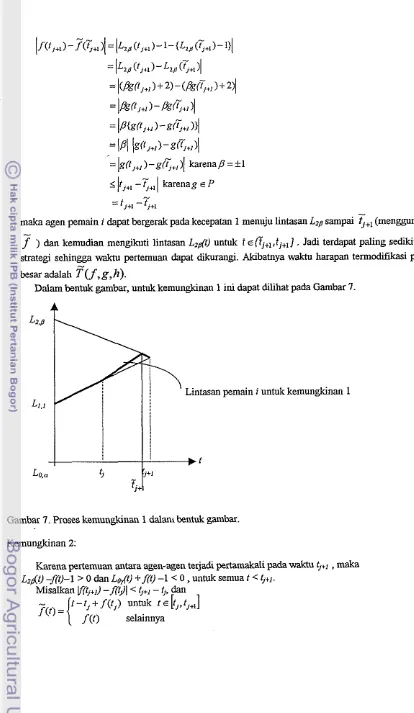
tapi bukan kednanya), &pat diperlakukan dengan cara yang sama seperti kemungkinan 1. Unmk keperluan pembuktian lema, maka tanpa mengurangi keumuman &pat diasumsikan bahwa satu agen pemain i yang dibahas adatall agen yang mengikuti lintasan strategi L1,1(1).

Kemungkinan 1:

Misalkan

1

J($+I) - J(tJ

1

< $+I

-

4,

maka $-$+~<fl$+~)

-f$<

$+I

-

$.

Perhatihi bahwa jika penlain i bertemu deiigan pemain r di $+I, maka

Lzpt$+l)=fl$+l) + 1 ( 6 )

sehingga

LZptt)- J(t)

-

1 > 0, Vf<lj+~. Akibatnya, &pat dituliskan strategi baru : t - t j

+

J(tj) u n t u k t ~ [ t ~ , t ~ + , ]

r ( t ) =

J(t) selainnya, sehingga

&,(tj+1)-7(t,+,)-1= &p(f+l)-f+l + t j - J(tj)-l

< &p(tj+I)- t,+~ + tj + t j + ~ -tj - J(tj+1)-1 = 0

-

Karena L2P(.) dan

f

(.)

kontinu yang berakibat bahwa terdapat

q+,

E (t, .tj+,) sedemikian sehingga

(30)

= [L2@ @,+1)-L2fl

)I

= l ( k f t j + l ) + 2 ) - (&(T+l) + 211

= ] k ( t j + I I-&(<+,

11

= l ~ { g ( t , + ~ ) - a < + , )>I

=\PI

[ g ( t j + , ) - g K + l ) [

= Ig(t,+l)-g(<+l)[ karenap = +l

5 Itj+,

-<.+lI

karenag E P

-

tj+1

-

f j + l

maka agen pemain i &pat bergerak pada kecepatan 1 menuju lintasan Lz8 sampai

<+,

(menggunakan

-

f

) clan kemudian mengikuti lintasan L2dt) untuk t E ( T ~ + , , ~ ~ + ~ ]

.

Jadi terdapat paling sedikit satu strategi sehingga waktu pertemuan &pat dikurangi. Akibatnya waktu harapan termodifikasi paling besar adalah

T"(

f

,g,h).

Dalam bentuk gambat, untuk kemungkinan 1 ini &pat dilihat pa& Gambar 7.

[image:30.602.70.484.44.757.2]

4

Gambar 7. koses kemungkinan 1 dalanl bentuk gambar

Kemungkinan 2:

Karena pertemuan antara agen-agen tejadi pertamald pada waktu $+I

,

maka L2/Xt) -J(t)-1 > 0 dan L d t )

+

f(t) -1 < 0

,

untuk semua t < t j t l .

Misalkan V(tj+,)

-flvl<

5+1

-ti.

dan

t

-

t j

+

J ( t j ) untuk t E [t,, t j U ]

(31)

maka dillasilkan : ~ , ~ ( t ) - f " ( t ) - l > 0 dan

{

~ o ~ ( t ) + ? ( t ) - l < o

~ 2(fj+l )-7(tj+l)- , 1 < 0, Lor (fj+,)+ 7(fj+,) > 0.

-

Karena Lzd.), LO&.) dan

f

() kontinu yang menmbatkan terdapat <+j,i,+l E (tj,tj+j)

.

sedemikian sehinga

L,, (q+,) =

+

1 L,, (ij+,) = -7(ij+,)

+

1.

Misalkan f' = maks(i;+,

,Fit,),

maka

\f(t,+,)-7(t.)\ =lf(tj+,)-t. + t j

-JV,)l

= I f ( t j + , ) - f ( f j ) - t . + f j l

<Ij+,-t, -t

-

+ t j

I

-t-1 = t . -t

J+l

Jadi

1

f(tl+,)-7(t*4 < t l i l - t ' ,

maka satu agen pemain

-

i dapat bergerak pada kecepatan 1 menuju lintasan Lzp sampai

t j , (menggunakan

7

) dan kemudian mengikuti lintasan Lzdt) untuk t E ( ~ + l , t , + l ] , sedangkan satn

agen yang lain bergerak menuju lintasan LO,, sampai

i1+,

dan kemudian mengikuti lintasan Lo,#)

untuk t ~(i,+~,t,+,]. Jadi terdapat paling sedikit satn strategi sehingga waktu pertemuan dapat

dikurangi. Akibatnya waMu harapan temodifikasi paling besar adalah

T"(

f

,g,h).

Karena pertemuan antara satu agen pemain i dengan agen pemain r dan s terjadi pertamakali pa& waktuIi,~.maka

Lzdf) -/It)-1 > 0 dan L d t ) -/It)-1 < 0 , untuk semua 1 < $+,. Misalkan

Ifl$+~)

-flII,l< $1

-

r/,

dan

t-t,+j(t,) untuk t c [ t j , t j + , ] f ( t ) selainnya

maka dihasilkan :

-

Karena Lzd.), L d . ) dan

f

()

kontinu yang mengahbatkan terdapat

T+,

E (t,. t,,) dengan

<+,

< t _,

(32)

(33)

-

1 1 2 3 m

T ( f ; g , h ) = - ( a , x - + a , x - + a , x - + a m x-)

24 2 2 2 2

1 1 2 3 m

= - ( 1 2 x - + 6 x - + 5 x - + - )

24 2 2 2 2

1 39 m

=-(-+-)

24 2 2 1

= -(39+m). 48

Berdasarkan Lema 1, maka diperoleh:

47

1 47

- ( 3 9 + m ) < -

48 48 m

<

8,

(34)

RENDEZVOUS SEARCH

PADA G M S

DENGAN TIGA PEMATN

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAElUAN

AWM

INSTlTUT PERTANIAN BOGOR

BOGOR

(35)

(36)

I. PENDAHULUAN

1.2 Tujnan

orang pemain,

II.

MODEL FORMAL

Definisi 1

(01, 02.03) dengan

+

={

awal permainan

-

awal permainan

Definisi 2

Definisi 3

atau

(37)

I. PENDAHULUAN

1.2 Tujnan

orang pemain,

II.

MODEL FORMAL

Definisi 1

(01, 02.03) dengan

+

={

awal permainan

-

awal permainan

Definisi 2

Definisi 3

atau

(38)

sedangkan pemain yang ditempatkan pada 0 bertemu dengan pemain yang ditempatkan pada 2 tidak dibahas karena sebelum kedua pemain tersebut bertemu, maka terlebih dahnlu saiah satu di antara mereka akan beitemu dengan pemain yang ditempatkan pada 1 sehingga menjadi bentuk a) atau b) pada pemyataan di atas.

Misalkan himpunan C mempakan kumpulan semua anggota c = @, w ) yang menyatakan posisi dan arah saat permainan dimnlai. Perhatilotnbahwa suatu permainan yang dimnlai dengan @,,pz,p3, - , o z , w ~ ) "berakl~ir sama" dengan permainan yang dimulai dengan ( 2 - p ~ , 2-pz, 2-p3,

+,

-w2,-w3 ). Untuk menjelaskan hal ini, misalkan diambil contoh pl=O, ~ = l , p3=2, dengan arahpemain

II

danpemain

111 keduanya

+.

Contoh ini menghasilkan :

( P I . PZ, ~ 3 . - . ma, a s ) = (0,1,2,-,+,+). Ddam bidang Cartesius dapat dilihat pada Gambar 1 .

[image:38.599.68.510.69.811.2]

( Z-PI, 2-pz, 2-p3,

+

,*z, -m3 )= (2,1,0,+,-,-I. Dalam bidang Cartesius dapat dilihat pada Gambar 2.

Gatnbar 1. Posisi dan arah pemain untuk (0,1,2,-,+,+).

,l

0

III

(39)

Tanpa memperlliitikan a r d ~ masing-masing pemain itu naik atau turun, dari kedua gambar tersebut terlihat bahwa pemain I1 dan pemain I11

sama-sama bergerak menjauhi pemain I, sehingga dapat dikatakan bahwa kedua permainan berakhir sama. Hal yang sama juga berlaku jika masing- masing nilai p l ,

n,

p3, atau 02 dan 03 diubah. Ini

berarti bal~wa w, selalu dapat dibuat +. Jadi nntuk kasus ini diasumsikan bahwa wl =

+

sehingga himpunan C hanya mempunyai 24 anggota

(=3!x2'). Semua anggota himpnnan C disebut kasus clan diperlihatkan pada Tabel 1.

Misalkan (a,, a*) menyatakan pasangan tak teNNt dari pemain-pemain yang ditempatkan setelah pemain lain ditempatkan pada am1 permaiuan. Misalkan b, =-(al, a2, dl, d2), dengan di

menyatakan arah relatif pemain a, terhadap pemain

a,. (i#j), yaitu,

to jika pemain a, bergerak kearah

pem$n a, pada awal permainan mu jika @main a, bergerak menjauhi

pemain a) pada awal permainan

dengan i, j = 1, 2 dan i # j. Misalkan B={b,l

i=1, ..., 12). Semua anggota B disebut tipe clan B

mempunyai 12 anggota yang diperlihatkan pada

Tabel 2.

2.2 Hubungau Antara Kasus dan Tipe

Sebelumnya telah diuraikan bahwa permainan berakhir jika dua pemain yang letaknya berdekatan pada awal permainan sudah bertemu. Misalkan suatu permainan dimulai dengan kasus

cl

.

( pernain 11 terletak antara pemain I dan

pemain III), maka permainan akan berakhir jika pemain I dan I1 bertemu, atau jika pemain I1 dan 111

[image:39.599.310.497.137.329.2]

bertemu. Misalkan posisi awal pemain diberikan sebagai c, yang diperlihatkan pada bidang Cartesius dalam Gambar 3.

Gambar 3. Permainan yang dimulai dengan kasus c,.

Dalam Gamba~ 3 terlihat b a h m pemain I bergerak menuju pemain I1 sedangkan pemain II bergerak menjauhi pemain I dan pemain 11 bergerak menuju pemain 111 sedangkan pemain 111 bergerak menjauhi pemain 11, sehingga kasus cl &pat dihubungkan menjadi dua tipe, yaitu

b2 = (I, II, to, mu) dan blo = (II, III, to, mu). Suatu pertemuan antara dua pemain Cyang terjadi lebih dahulu) akan mengakhiri permainan.

Misalkan pemetaan

4

menya- hubungan antara kasus dan tipe, yaitu:

4

: C-tBxB, Kc) = (b,, bJ), V c e C , i < j ,

maka himpnnan image dari

4

&pat dilihat dalam Tabel 3.

2 3 Ruang Strategi

Dalam pembahasan permainan ini, strategi adalah fungsi yang menyatakan arah dan jar& pergerakan pemain. Strategi yang digunakan hanya yang terdapat pada mang strategi yang didefinisikan sebagai berikut :

(40)

Tabel 3. Himpunan image

4

kontinn b a d clan P adalah iumpunan kompak. (Alpern, 1995), maka nilai pa& ( 2 ) selalu dijamin ada (Goldberg, 1976).

Misalkan p(fg,h) menyatakan waktu saat pemain dalam tipe b saling bertemu (6 E B). Untuk

semua c E C, didefinisikan: T a g & = min plb~t;g,h)

bsrplc) (3)

Diberikan tiga strategi Cfg,h) sembarang, dengan delapan garis lintasan berikut ini:

Garis-garis di atas menyatakan lintasan masing-masing pemain. Lintasan Ll,,(f)

menyatakan garis untuk pemain dengan strategif; lintasan &(t) menyatakan garis untuk pemain dengan strategi g, sedangkan lintasan LO,&) dan

L3,,(f) menyatakan garis untuk pemain dengan strategi h. Untuk semua b E B,

p(L

g, h) &pat

ditentukan dengan menggunakan garis Lk, dan

Definisi 4 L*+,,p dalam (4), sehingga

Misalkan pemain I memilih strategi

f;

pemain

I1 memilih srategi g dan pemain

EI

memilih _{p ~ ; g , h )}₌_min_{{ t}_:_{L k d t )}₌_L&l,p(f)} _{( 5 )} strategi h, denganf; g, h E P. Misalkan

TXf;

g, h)

menyatakan peamuan ~ a n g betpadanan _dengan

P

₌_{+ I ,}_k=0,1,2_dan_k_{menyatakan letak} dengan kasus c, dengan c E C. Maka waktu _{pemain. Garis-garis untuk menentukan}

PV;

_g,_h)

pertemuan harapan ? a h ) dinyatakan sebagai : dengan b E B diberikan dalam Tabel 4.

dengan R:, adalah nilai randevu, yaihl waMu

harapan pertemuan asimetrik dengan tiga pemain

[image:40.602.72.286.56.838.2]

(41)

[image:41.595.303.408.250.443.2]

Tabel 4. Garis-garis untuk menentnkan _pemainI turun atau

p

=-I. Akhirnya diperoleh m k h ) (k, a)= (0+1) dan (lctl,n = ( 1 ~ 1 ) . Demikianpula dalam menentnkan garis-garis untuk bs, b? dan b, dilakukan dengan cara seperti untnk b5.

3) Untuk tipe bs, bla, b11 dan bl;

Untuk tipe bg, ~ I O , b11 dan b12

,

garis yang

diambil pemain 111 adalah L3,,karena garis tersebut letaknya lebih dekat terhadap garis strategi pemain 11 (L2,0) dibandingkan dengan Lo,,.

Ilustrasi

Diberikan contoh kasus berikut ini. Misalkan:

Penjelasan Tabel 4

1) Untnk tipe bl, b2, b3 dan b4

Contoh: Untuk tipe bl (I, 11, to, to), pemain I

dan pemain I1 saling mendekat. Garis yang diambil adalah garis yang memuat strategi pemain I (f) dan pemain 11 (g), yaitn LI,, dan L%,.(jadi k 1 ) Letak pemain I berada di bawah pemain I1 (pemain I di 1 dan pemain I1 di 2), sehingga agar keduanya saling mendekat, maka pemain I naik atau a =+l dan

pemain II tnrun atau

p -1.

Akhirnya diperoleh (k, a)=(l+l) dan (lctl, p) = (2;l). Demikian pula dalam menentukan garis-garis untuk b2, b3 dan

b4 dilakukan dengan cara seperti untuk bl.

2) Untuk tipe b,, bs, b, dan b8

Contoh: Untuk tipe b5 (I, 111, to, to), pemain I clan pemain 111 saling mendekat, garis yang diambil adalah garis yang memuat strategi pemain I (f) dan

pemain 111 (h). Garis yang memuat strategi pemain 111 ada dua yaitn Loao dan L,,,. Tetapi garis yang terdekat dengan garis untuk stmtegi pemain I (LIJ adalah Lo,, sehingga pada tipe b, ini, garis yang diambil pemain III adalah Lq, Dengan demikian

,

pemain 111 terletak di bawah pemain I (pemain 111 pada 0 sedaugkan pemain I pada 1) sehingga agar saling mendekat, pemain III naik atau a =+1 dan

dengan

f,g,

h

berturut-turut merupakan strategi pemain I, pemain 11, dan pemain 111.

B e r k k a n Tabel 4, untuk bl diambil garis L1.1 dan

LZ-,

Apabila strategi-strategi pemain I dan

pemain U disubstitusikan ke (4) diperoleh : L1,1= f(t) +1

(42)

[image:42.595.71.518.58.772.2]

Jika digambarkan pa& bidang Cartesius dapat dilihat pada Gambar 4, yaitu:

Gambar 4. Garis

4-1

dan LZ.-, untuk bl

Dari Gambar 4 diperoleh bahwa titik potong kedua garis peitama kali tejadi pada t-112 sehingga diperoleh Tbl @,g,h)=112. Untuk

bZ,b3,b4,.

. .

,b12 bidang Cartesiusnya diperlihatkan pada Lampiran 1. ~ilai-nilaiTb

@,

g.

F)

untuk semua b e B dituliskan dalam Tabel 5.

Tabel 5. Nilai-nilai T

*

@,

c,

h)

untuk

b € B.

Dengan menggunakan persamaan (3), Tabel 3, dan Tabel 5, maka &pat diperoleh nilai

T, 6 ,

g,

h)

untuk semua c E C, yang dituliskan dalam Tabel 6.

Tabel 6. Nilai-nilai T, @,g,h) untuk ceC

21

47

Dengan demikian diperoleh _T,

@,g,

h)=

-

f=1 2

Lema 1

47

Nilai randevu R12 memenuhi R12 5

-

[image:42.595.286.518.77.655.2]

(43)

Bukti _Karena

f,g,l;~P,

_maka_R:,

sT(f,g,h).

Karena R& = min

T"(

f

-

47

.

2), makaR& 2 T"(f ,g.h), V f , g , h E P. 48

III.

KELAS STRATEGI YANG BEREWGGA

4 ,

t E [ ~ , ; l h, dengan I;

g,

E

>.

Dengan menggunakan

a = + l .

Lema 2

...

< tk(k58)adalah

...,

k-1) (to = O),

Bukti

(Lihat Lampiran 4)

llustrasi Lema 2

.

berikut ini:

a=I.

Strategi a w l :

[image:43.602.300.505.376.620.2]

(44)

Bukti _Karena

f,g,l;~P,

_maka_R:,

sT(f,g,h).

Karena R& = min

T"(

f

-

47

.

2), makaR& 2 T"(f ,g.h), V f , g , h E P. 48

III.

KELAS STRATEGI YANG BEREWGGA

4 ,

t E [ ~ , ; l h, dengan I;

g,

E

>.

Dengan menggunakan

a = + l .

Lema 2

...

< tk(k58)adalah

...,

k-1) (to = O),

Bukti

(Lihat Lampiran 4)

llustrasi Lema 2

.

berikut ini:

a=I.

Strategi a w l :

[image:44.602.300.505.376.620.2]

(45)

(46)

Lema 5

ldisalkan &g,l~) adalah strategi-strategi optimal

maka T,&, h)

<

4 untnk semua c G C.

IV.

ALGORITMA UNTI

Akibat 4 dalam bahasan sebelumnya memungkinkan untuk mengkonstruksi sebuah atgoritma untuk menemukan selumh strategi- strategi optimum dan nilai randevu R&

.

Misalkan