BAB III LIMIT DAN FUNGSI KONTINU 3.1 Pengertian Limit 3.2 Teknik Aljabar Untuk Menghitung Limit 3.3 Limit Satu Sisi 3.4 Limit Tak Hingga dan Limit Menuju Tak Hingga 3.5 Limit Fungsi Trigonometri

BAB III

LIMIT DAN FUNGSI KONTINU

3.1 Pengertian Limit

3.2 Teknik Aljabar Untuk Menghitung Limit 3.3 Limit Satu Sisi

3.4 Limit Tak Hingga dan Limit Menuju Tak Hingga 3.5 Limit Fungsi Trigonometri

3.6 Bilangan Alam 3.7 Fungsi Kontinu

Konsep limit mempunyai peranan yang sangat penting di dalam kalkulus dan berbagai bidang matematika. Oleh karena itu, konsep ini sangat perlu untuk dipahami. Meskipun pada awalnya konsep limit sukar untuk dipahami, tetapi dengan sedikit bantuan cara numeris kemudian konsep ini bisa dimengerti. Dan kenyataannya, setelah dipraktekkan masalah hitung limit relative mudah. Mengingat hal itu, maka pada bagian pertama Bab ini limit diterangkan secara intuitive (numeris). Kemudian pada bagian selanjutnya, dikembangkan teknik penghitungan limit.

3.1 Pengertian Limit

Apa yang terjadi dengan f(x) _{apabila x cukup dekat dengan 2? Perhatikan table 3.1.1 berikut.}

Tabel 3.1.1

x f(x)x23 x f(x)x23

3 12 1,5 5,25

2,05 7,2025 1,95 6,8025

2,001 7,004001 1,999 6,996001

2,0001 7,00040001 1,9999 6,99960001

Dari table terlihat bahwa apabila x cukup dekat dengan 2, maka f(x) _{mendekati 7. Hal ini tidak} mengherankan, karena apabila dihitung f(2)2237. Dalam hal ini dikatakan bahwa limit f(x) x

mendekati 2 sama dengan 7, ditulis:

7 ) ( lim

2 

 f x x

Selanjutnya, perhatikan fungsi f yang ditentukan oleh rumus:

1 1 )

( 2

  

x x x f Gambar 3.1.1

●

Fungsi f tersebut tidak terdefinisikan di x = 1 karena di titik ini f(x) berbentuk 0 0

. Tetapi masih dapat dipertanyakan apa yang terjadi pada f(x) bilamana x mendekati 1 tetapi x1. Untuk x1,

) ( 1 1

) 1 )( 1 ( 1

1 )

( 2 x g x

x x x x

x x

f   

    

 

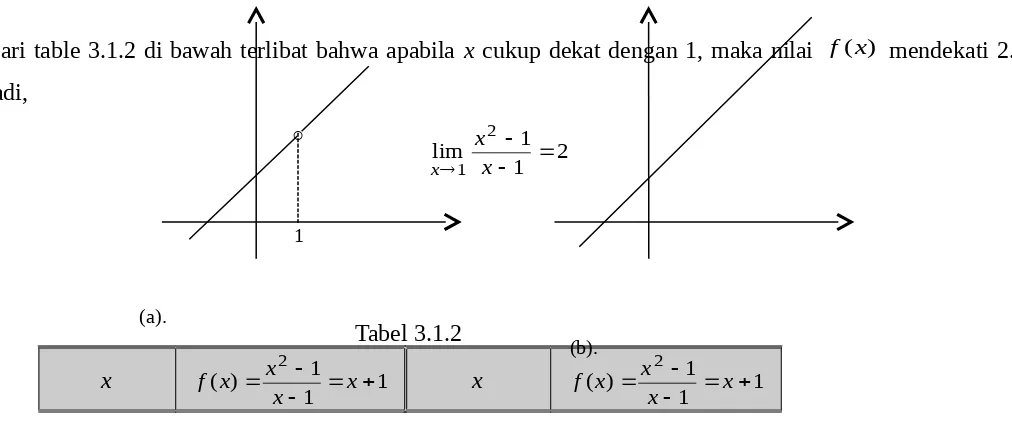
Dari table 3.1.2 di bawah terlibat bahwa apabila x cukup dekat dengan 1, maka nilai f(x) _{mendekati 2.} Jadi,

2 1

1 lim 2

1  

  x

x x

Tabel 3.1.2

x 1

1 1 )

( 2  

 

 x

x x x

f x 1

1 1 )

( 2  

 

 x

x x x f ○

(a).

2 3 0,5 1,5

1,05 2,05 0,99 1,99

1,001 2,001 0,999975 1,999975

1,00000017 2,00000017 0,9999999 1,9999999

Dari beberapa uraian di atas, berikut diberikan definisi limit.

Secara matematis definisi di atas dapat ditulis sebagai berikut.

Catatan: Pada definisi limit di atas, fungsi f tidak perlu terdefinisikan di c. Limit f(x) untuk x mendekati

c mungkin ada walaupun f tidak terdefinisikan di c.

Contoh 3.1.2 Buktikan bahwa _xlim_4(2x –5) = 3.

Penyelesaian:

|(2x –5) – 3| = |2x – 8| = |2(x – 4)| = |2| |x – 4| = 2|x – 4| Definisi 3.1.1 Limit f(x) x mendekati c sama dengan L, ditulis:

L x f c

xlim ( )

jika untuk setiap x yang cukup dekat dengan c, tetapi x c, maka f(x) mendekati L.

L x f c

Diberikan bilangan  > 0 sebarang. Apabila diambil  = /2, maka untuk setiap x di dalam domain f yang memenuhi 0 <|x – 4| <  berlaku:

|(2x – 5) – 3| = 2 |x – 4| < 2  = 2./2 = .█

Contoh 3.1.3 Buktikan bahwa untuk c > 0, _{x c} x  c 

lim _.

Penyelesaian:

(3.1.1) x c



x c



_xx _cc _xx c_c

     

 

Ditinjau x >0dengan sifat

2 c c

x  _{. Menurut ketidaksamaan segitiga:}

2 2

c c c c x c x

x      

Hal ini berakibat: (3.1.2)

2 c x 

Selanjutnya, dari (3.1.1) dan (3.1.2) diperoleh:

c c x c

x c x c x

3 2     

 _,

untuk setiap x>0. Diberikan bilangan  > 0 sebarang. Apabila diambil

  

   

2 3 , 2

min c  c

 _{maka untuk}

setiap x>0 dengan 0 x c  _berlaku:

       

c c x c

x c x c x

3 2

Jadi, untuk setiap  > 0 terdapat δ>0 sehingga untuk setiap x>0 dengan 0 x c  _berlaku: 

      

c c x c

x c x c x

3 2

.█

Bukti: Misalkan _xlim_c f(x)L dan _xlim_c f(x)K. Akan ditunjukkan bahwa LK. Diberikan  0 sebarang, maka terdapat ₁,₂ 0 _sehingga:

i.

2 )

(x  L 

f , untuk setiap xDf dengan 0 x c 1.

ii.

2 )

(x  K 

f , untuk setiap xDf dengan 0 x c 2.

Apabila diambil  min



₁,₂



maka untuk setiap xDf dengan 0 x c  _berlaku: 

   



 K L f x f x K

L ( ) ( )

Hal ini berarti LK .█

Contoh 3.1.5 Tunjukkan bahwa

x x

xlim0 tidak ada.

Penyelesaian: Untuk x0,

1 lim lim

0

0   

 x

x x

x x x

Sementara, untuk x0,

1 lim

lim

0

0 

 



 x

x x

x x x

Karena nilai limit tidak tunggal maka

x x

xlim0 tidak ada.█

3.2 Teknik Aljabar Untuk Menghitung Limit

Sifat-sifat dasar limit yang dinyatakan dalam beberapa teorema berikut ini sangat diperlukan dalam hitung limit. (Dengan berbagai pertimbangan bukti teorema tidak disertakan dalam buku ini).

Teorema 3.1.4 Jika _xlim_c f(x) ada maka nilainya tunggal.

Contoh 3.2.3

(a). lim (2 7 6) lim 2 lim 7 lim 6

2 2

2 2 ) i ( 2 . 2 . 3 2

2   

    x  x x

x x x x x

0 6 2 . 7 2 . 2

6 lim lim

7 lim

2

6 lim lim

7 lim 2

2 1 . 2 . 3

2 2

2

2 )

v.a ( 2 . 2 . 3

2 2

2 2 ) ii ( 2 . 2 . 3

   

 

   

  

 



 



 



x x

x

x x

x

x x

x x

(b). _xlim_17x 2x1 _3.2.2_{(iii) x}lim_17x._xlim_1 2x1

Teorema 3.2.2 Jika _xlim_c f(x) dan _xlim_c g(x) keduanya ada dan kR maka berlaku pernyataan-pernyataan berikut:

i. _xlim_c



f(x)g(x)



_xlim_c f(x)_xlim_c g(x) ii. _xlim_c kf(x)k _xlim_c f(x)

iii. _xlim_c f(x)g(x)_xlim_c f(x)._xlim_c g(x)

iv. _{lim ( )}

) ( lim

) (

) ( lim

x g

x f

x g

x f

c x

c x c

x

 

  , asalkan

0 ) (

lim 

c g x x

v. Untuk nN : (a).   n

c x n c

x f x f x 

 

  



 ( ) lim ( )

lim

(b).   n

c x n c

x f x f x

 



 

 

 

 lim ( ) )

(

lim , asalkan lim ( )0

c f x x

(c).   n

c x n c

x f x f x

1

1 _{lim ( )}

) (

lim 

  

  



 , asalkanuntuk n genap

0 ) (

lim 

7lim lim (2 1) 7.1 2.1 1 7 1 1 ) (v.c & ii) ( 2 . 2 .

3     

     

 x x x

x

(c). _{lim (5 2) 5}2_.(.( ₁1₎) ₂3 1₃ ) 3 2 ( lim 2 5 3 2 lim 1 1 ) iv ( 2 . 2 . 3

1   

              x x x x x x x .█

Contoh 3.2.4 Hitung

4 2 3 lim 2 ₂

2     _x x x x .

Penyelesaian: Karena limit penyebut sama dengan 0, maka Teorema 3.2.2 (iv) tidak dapat digunakan. Akan tetapi, hal ini bukan berarti limit di atas tidak ada. Pada soal di atas, yang akan dihitung adalah nilai limit untuk x mendekati 2, bukan nilai untuk x sama dengan 2. Oleh karena itu, dengan memanfaatkan teknik-teknik aljabar, untuk x2 diperoleh:

2 1 ) 2 )( 2 ( ) 1 )( 2 ( 4 2 3 2 2            x x x x x x x x x Sehingga: 4 1 2 2 1 2 2 1 lim 4 2 3 lim ) iv ( 2 . 2 . 3 2 2 2

2  

          x x x x x x x .█

Contoh 3.2.5 Tentukan lim 1₁

1    x x x . Penyelesaian:







_lim



₁



_{1 1 2}

1 1 1 lim 1 1 lim 1 1

1      

      

 x x

x x x x x x x .█

Contoh 3.2.6 Tentukan

16 8 lim 4 3 2 _    _x x x . Penyelesaian:















3 2 2 3



2 2 2 4 4 3 3 2 4 3

2 _{( 2) .( 2) .( 2) ( 2)}

) 2 ( ) 2 .( ) 2 ( lim ) 2 ( ) 2 ( lim 16 8 lim                           

 _{x x x x}









8 3 8 8 8 8

4 4 4 8 4 2

4 2 lim ₃ 2 ₂

2     

     

  



 _{x x x}

x x

x .█

Pada contoh-contoh di atas telah digambarkan bagaimana teknik-teknik aljabar dapat digunakan untuk menyelesaikan soal hitung limit. Namun demikian tidak semua soal limit dapat diselesaikan dengan

cara demikian. Sebagai contoh, misalnya

x x x

sin lim

0

 .

Dalam berbagai hal, teorema di bawah ini sangat membantu dalam penyelesaian soal hitung limit.

Contoh 3.2.8 Tentukan 

  

 

 x x

x

1 sin lim

0 .

Penyelesaian: Untuk x0, sin1 1

x . Oleh karena itu, untuk x 0 berlaku: x

x x x

xsin1  sin1 

Hal ini berakibat:

x x x

x  

 sin1

Selanjutnya, karena lim₀







lim₀ 0 

 x x x

x maka 0

1 sin lim

0 

 

 

 x x

x .█

Soal Latihan

Untuk soal 1 – 6, tunjukkan pernyataan berikut dengan definisi limit.

Teorema 3.2.7 (Teorema Apit) Misalkan f, g, dan h fungsi-fungsi sehingga f(x)g(x)h(x)

untuk semua x di dalam interval terbuka yang memuat c, kecuali mungkin di c. Jika

L x h x

f

c x c

1. _xlim_1(x2)3 2. lim 1 1₂

2 

 x

x 3.

1

lim 2

1 

  x

x

4. 2

1 2 lim

0   

 x

x

x 5.

2 lim

4 

 x

x 6. ₁ 2

1 lim 2

1  

  x

x x

7. Jika

    

 

 

0 ,

1

0 ,

1 ) (

x x x

f _{, tunjukkan bahwa x}lim_0 f(x) _{tidak ada.}

Untuk soal 8 – 20, hitunglah masing-masing limit jika ada. 8. lim( 2 20)

5 

 x

x 9. lim ( 3 1)

2

2  



 x x

x 10. ₃

2 lim

0    x

x x

11.

4 8 2 lim

2 2

2 _

 

 _x

x x

x 12. 1

1 lim

1 



 x

x

x 13. ₈

64 lim

3 6

2 _

  _x

x x

14.

1 1 lim ₃

4

1 _



  _s

s

s 15. u

u

u 



 1

1 lim

2 3

1 16. 2

2

1 ₁

3 2

lim

x x

x _

 

 

17.

5 3

4 lim

2 2

2 _{ }



 _x

x

x 18. _{x a}

a xn n a

x 





lim 19.

a x

a xn n a

x 



  lim

20.

h x h x h

 

0

lim 21.

2 ) 2 1 ( ) 1 ( lim

2 



 x

x

x 22. x

x x

1 1

lim 3 0

  

3.3 Limit Satu Sisi

Kiranya mudah dipahami bahwa _xlim_0 x tidak ada, karena x tidak terdefinisikan untuk x0.

Secara matematis, definisi di atas dapat dituliskan sebagai berikut:

(i). _xlim_c f(x)L jika dan hanya jika untuk setiap  0 ada  0 sehingga untuk setiap x(c,c)

berlaku f(x) L _.

(ii). _xlim_c f(x)L jika dan hanya jika untuk setiap  0 ada  0 sehingga untuk setiap x(c ,c)

berlaku f(x) L _.

Definisi 3.3.1 (i). Misalkan f(x) terdefinisikan pada suatu interval (c,c)_{. Apabila untuk x di}

dalam (c,c) yang cukup dekat dengan c, nilai f(x) mendekati L, maka dikatakan bahwa L merupakan limit kanan f(x) untuk x mendekati c, ditulis:

L x f c

x  

) ( lim

(ii). Misalkan f(x) terdefinisikan pada suatu interval (c ,c)_{. Apabila untuk x di dalam} (c ,c)

yang cukup dekat dengan c, nilai f(x) mendekati L, maka dikatakan bahwa L merupakan limit kiri f(x)

untuk x mendekati c, ditulis:

L x f c x







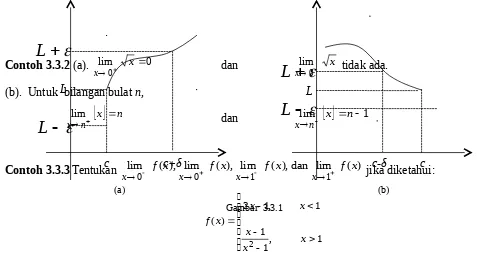
Contoh 3.3.2 (a). _xlim_0 x 0 dan _xlim₀ x tidak ada.

(b). Untuk bilangan bulat n,

_xlim_n

 

x n dan _xlim_n

 

x n1

Contoh 3.3.3 Tentukan _xlim_0 f(x), _xlim_0 f(x), _xlim_1 f(x),dan _xlim_1 f(x) jika diketahui:

      

 



 



1 ,

1 1

1 ,

1 2 ) (

2 x

x x

x x

x f

Penyelesaian:

(a). Untuk x cukup dekat dengan 0 (baik x < 0 maupun x > 0), f(x) 2x 1_{. Oleh karena itu,}

1 ) 1 2 ( lim ) ( lim

1 ) 1 2 ( lim ) ( lim

0 0

0 0

   

   

 

 

 

 

x x

f

x x

f

x x

x x

(b). Untuk x cukup dekat dengan 1 dan x < 1, f(x) 2x 1_{. Sehingga:}

L





L





L

c c+δ





L

L





L

c-δ c

Gambar 3.3.1

1 ) 1 2 ( lim ) ( lim

1

1     



x x

f

x x

Tetapi, untuk x cukup dekat dengan 1 dan x > 1,

1 1 )

( ₂

  

x x x

f _{. Sehingga:}

2 1 1 1 lim ) 1 )( 1 (

1 lim

1 1 lim ) ( lim

1 1

2 1

1     

 

  

 



 _{  }

 x x x

x x

x x

f

x x

x

x .█

Dari beberapa contoh di atas, diperoleh beberapa kenyataan. Limit kiri suatu fungsi ada tetapi limit kanannya tidak ada (atau sebaliknya), limit kiri dan kanan suatu fungsi ada tetapi nilainya tidak sama, dan limit kiri dan kanan suatu fungsi ada dan nilainya sama. Selanjutnya, karena ketunggalan limit maka diperoleh pernyataan berikut.

Sebagai akibat langsung dari Teorema di atas, diperoleh:

Pada Contoh 3.3.3 di atas, karena _xlim_1 f(x)_xlim_1 f(x) maka _xlim_1 f(x) tidak ada.

Contoh 3.3.6 Diberikan:

    

  



1 ,

1 ,

1 2 ) (

3 _x

x

x x

x f

Karena untuk x1, f(x)2x 1_{, maka:}

1 ) 1 2 ( lim ) ( lim

1

1  _   



x x

f

x

x .

Secara sama,

1 lim

) (

lim 3

1

1  _  



x x

f x

x .

Selanjutnya, karena _xlim_1 f(x)1_xlim_1 f(x) maka: _xlim_1 f(x)1.█

Teorema 3.3.4 _xlim_c f(x)L jika dan hanya jika _xlim_c f(x)_xlim_c f(x)L.

Contoh 3.3.7 Tentukan _xlim_2 f(x) jika diketahui:

 

    

  

2 ,

2 ,

) (

x x

x x

x f

Penyelesaian:

2 lim ) ( lim

2

2  _  



x x

f x

x lim2 ( ) lim2

 

2

 



 _



x x

f

x x

Jadi, _xlim_2 f(x)2.█

3.4 Limit Tak Hingga dan Limit Menuju Tak Hingga

Terlebih dahulu diperhatikan masalah hitung limit berikut: ₂ 0

1 lim

x

x . Untuk nilai-nilai x yang cukup

dekat dengan 0, maka nilai-nilai ( ) 1₂ x x

f  _{diberikan pada table berikut ini.}

Tabel 3.4.1

x 1₂

x x 2

1 x

1 1 −1 1

0,5 4 −0,5 4

0,01 10.000 −0,01 10.000

0,0001 100.000.000 −0,0001 100.000.000

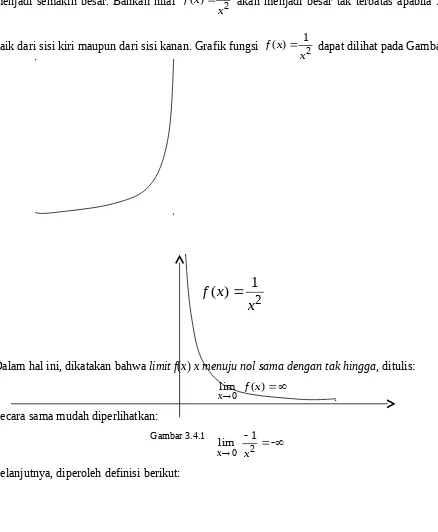
Dari Tabel 3.4.1 di atas dapat dilihat bahwa apabila nilai x semakin dekat dengan 0, maka nilai ( ) 1₂ x x

f 

menjadi semakin besar. Bahkan nilai ( ) 1₂ x x

f  _{akan menjadi besar tak terbatas apabila x mendekati 0,}

baik dari sisi kiri maupun dari sisi kanan. Grafik fungsi ( ) 1₂ x x

f  _{dapat dilihat pada Gambar 3.4.1.}

Dalam hal ini, dikatakan bahwa limit f(x) x menuju nol sama dengan tak hingga, ditulis:

   ( ) lim

0 f x x

Secara sama mudah diperlihatkan:

   0 2

1 lim

x x Selanjutnya, diperoleh definisi berikut:

2

1

)

(

x

x

f



Secara matematis, Definisi di atas dapat ditulis sebagai:

Contoh 3.4.2

(a). 





 1

1 lim

1 x

x (b). _

   

 

 

 1

1 1 lim 1

lim ₂

0 2 3

0 _{x x} x _x x

x .

Di atas telah diterangkan pengertian limit untuk

x



c

, dengan c suatu bilangan berhingga. Akan tetapi, dalam berbagai aplikasi sering ditanyakan bagaimana nilai f(x) _{apabila nilai x cukup besar.} Sebagai contoh, bagaimana nilai

x x

f( )1 _{apabila nilai x cukup besar? Tabel 3.4.2 di bawah}

memperlihatkan nilai f untuk berbagai nilai x. Ternyata semakin besar nilai x (arah positif), nilai f(x) semakin kecil mendekati nol. Dalam hal ini dikatakan:

0 1 lim 

  x x

Tabel 3.4.2

(a) (b)

x

x x

f( ) 1 _x

x x f( )1

10 0,1 −1 −1

Definisi 3.4.1 (i). jika untuk setiap x cukup dekat dengan c, tetapi , maka f(x) menjadi besar tak terbatas arah positif.

(ii). jika untuk setiap x cukup dekat dengan c, tetapi , maka f(x) menjadi besar tak terbatas arah negatif.

1.000.000 0,000001 −1.000.000 −0,000001

5.000.000 0,0000002 −5.000.000 −0,0000002

100.000.000 0,00000001 −100.000.000 −0,00000001

Secara sama, apabila x besar tak terbatas arah negative ternyata berakibat f(x) _{mendekati nol, yaitu:}

0 1

lim 



 x

x

Kemudian dapat diturunkan pengertian limit menuju tak hingga. Hal itu dituliskan dalam definisi berikut.

Secara matematis, Definisi 3.4.3 dapat ditulis sebagai:

Mudah ditunjukkan bahwa: 0

1 lim 

  x

x dan 0

1 lim 



 x

x

Definisi 3.4.3 (i). _xlim_ f(x)L jika f(x) _{terdefinisikanuntuk setiap nilai x cukup besar (arah positif)}

dan jika x menjadi besar tak terbatas (arah positif) maka f(x) _{mendekati L.}

(ii). _xlim_ f(x) jika f(x) _{terdefinisikanuntuk setiap nilai x cukup besar (arah negatif) dan jika x}

menjadi besar tak terbatas (arah negatif) maka f(x) _{mendekati L.}

(i). _xlim_ f(x)L jika untuk setiap bilangan real  0 terdapat bilangan M 0 sehingga untuk setiap xM berlaku f(x) L _.

Contoh 3.4.4 Tentukan 9 1 lim ₃    _x x .

Penyelesaian: Untuk x0, x39x. Sehingga _x

x

1 9 1

0 ₃ 



 _{. Selanjutnya, karena} lim 1 0   x

x maka

dengan Teorema Apit diperoleh: 0 9 1 lim ₃ 

   _x

x .█

Contoh 3.4.5 Hitung

7 4 2 3 2 lim ₂ 2     

 _{x x}

x x x . Penyelesaian: Karena:



 







 



   

 2 3 lim ( 2) 3

lim x2 x x x

x

x lim



2 4 7





2 _x

x x

maka sifat limit perbagian tidak dapat digunakan. Namun demikian apabila pembilang dan penyebut sama-sama dibagi dengan _x2 _maka:







2



2

2 2 2 2 7 4 2 3 2 lim 7 4 2 3 2 lim x x x x x x x x x x x

x  

           2 1 0 0 2 0 0 1 7 4 2 lim 3 2 1 lim 7 4 2 3 2 1 lim 2 2 2 2                                   x x x x x x x x x x x .█

Contoh 3.4.6 Tentukan

10 7 2 6 7 lim 3 5 3      

 x x x

x x

x .

Penyelesaian: Dengan membagi pembilang dan penyebut dengan _x5_{, diperoleh:}

5 3 5 5 3 3 5 3 10 7 2 6 7 lim 10 7 2 6 7 lim x x x x x x x x x x x x x

x _{  }

0 0 0 0 1 0 0 0 10 7 2 1 lim 6 7 1 lim 5 4 2 5 4 2                              x x x x x x x x .█

Contoh 3.4.7 Hitung

10 7 2 6 7 2 lim ₅6 ₃3

      

 x x x

x x x

x .

Penyelesaian: Dengan membagi pembilang dan penyebut dengan _x5_{, diperoleh:}

5 3 5 5 3 6 3 5 3 6 10 7 2 6 7 2 lim 10 7 2 6 7 2 lim x x x x x x x x x x x x x x x

x   

                                               0 0 0 1 0 0 0 10 7 2 1 lim 6 7 2 lim 5 4 2 5 4 2 x x x x x x x x x .█ Soal Latihan

Untuk soal 1 – 20, tentukan nilai limitnya jika ada. Jika tidak ada limitnya, terangkan alasannya!

1. x

xlim_2 2 2. _xlim_1 x1 3. _{x 3 x}

1 lim

3

4. _{2 ( 2)}2

1 lim



 x

x 5. lim (x a)2

a x

a

x _



 6. lim1 _{1 x}2

x

x_  _

7. lim1 _{1 x}2

x

x_  _ 8. 2

2 lim 2 _     x x

x 9. 2

2 lim 2 _    x x x

10. 3 2 ₃

5 2 8 7 5 3 lim x x x x

x _{ }

 



 11. 3 4 11 21

11 5 7

lim _{5 2}

2      

 x x x

x x

x 12. x

x x x _    1 2 3 lim

13. lim ₃2 ₂5

 



 x

x

x 14. _xlim



x 1 x 2x



2

2 _{  }



 15. _{7 5}

7 lim 2      x x x x 16. 3 2 2 5 lim 3 2 3     

 _{x x}

x x

x 17. 

        

 2 1 2 1

lim 2 2 x x x x

x 18. 2

19.



x x x



x 2

lim _ 2 _ 

 20. xlim



x 2x 5x



2 _{ }

 

21. Tentukan lim_x1 f(x), lim_x0 f(x), dan lim_x3 f(x) jika diberikan:

   

    

 

 



  



 



3 ,

1 5

3 0

, 3 3

0 ,

1 2

)

( 2

2

x x

x x

x x x

x x

x f

22. Fungsi f yang terdefinisikan pada [ a,a] _{dikatakan genap (atau ganjil) jika} f(x)f(x) _(atau

) ( )

( x f x

f   _{) untuk setiap} x[a,a]_{. Jika} f x L

xlim_0 ( ) maka tentukan _xlim_0 f(x) jika: (a). f

genap, (b). f ganjil.

3.5 Limit Fungsi Trigonometri

Dengan memanfaatkan Teorema Apit, dapat ditunjukkan teorema di bawah ini.

Contoh 3.5.2 Hitung

 

 tan3

5 sin lim

0

 .

Penyelesaian:

  

 

 

   

 



 

 

 3

5 lim . 3 tan

3 lim . 5

5 sin lim 3

1 3 tan

3 5 5

5 sin lim 3

tan 5 sin lim

0 0

0 0

0    

  

Tetapi untuk   0 berakibat 3  0 dan 5  0, sehingga:

Teorema 3.5.1 (i). 1

sin lim sin

lim

0

0   

 x

x x

x x

x .

(ii). 1

tan lim tan

lim

0

0   

 x

x x

x x

3 5 3 5 . 1 . 1 3 5 lim . 3 tan 3 lim . 5 5 sin lim 3 tan 5 sin lim 0 0 3 0 5

0      

             .█ Soal Latihan

Untuk soal 1 – 12, hitunglah nilai limitnya. 1.

x x

x tan2 5 sin lim

0

 2.



2



cos lim 2 _  _  x x

x 3. _{x x}

x

x tan3

4 sin lim 2 0  4. x x xlim _3sin2₂

3 0

 5. x x

x

x sin3

cos 1 lim

0



 6. x a

x a a x    ) sin( lim 7. x x x x sin3 sin4

2 lim

0 

 8. x x

x x

x cos2 cos7 5 tan lim

0 

 9. x

x x cos sin 1 lim 2   10. a x a x a x    sin sin

lim _11. 

     

 x x

x tan

1 sin

1 lim

0 12. 

 

 



 x x x

x cos

1 1 lim

0

3.6 Bilangan Alam

Pada bagian ini, pembaca diingatkan kembali pada rumus binomium Newton. Untuk sebarang

R

 b

a, _dan n_N :

(3.6.1)





n k k n n n n

n

k

n _{a b a na b} n n _{a b b}

k n b

a      

               



... ! 2 ) 1

( 2 2

1 1

Apabila diambil

n b

a1 dan 1_{, maka dari (3.6.1) diperoleh:}

                                                                                                       _  



n n n n n n n n n n n n n n n k n n n k k n n k n 1 1 2 1 ... 2 1 1 1 ! 1 ... 2 1 1 1 ! 3 1 1 1 ! 2 1 2 1 ... 1 ! 2 ) 1 ( 1 1 1 1 1 1 2 1

Karena 1 1 1 3        n

n maka menurut Teorema Apit nilai

n

n n

       1 1

lim ada. Berdasarkan perhitungan,

untuk

n





diperoleh:

e n

n

n _       

    _



 4! ... 2,718...

1 ! 3 1 ! 2 1 2 1 1 lim

(3.6.2) e n

n

n  

  

 _ 

 

1 1 lim

Mudah ditunjukkan bahwa untuk nm berlaku:

m n

m

n 

    _      

_11 ₁ 1

Selanjutnya, apabila diberikan sebarang bilangan real positif x maka dapat dicari bilangan asli m dan n

sehingga nxm. Hal ini berakibat:

m x

n

m x

n 

    _        _      

_11 ₁ 1 ₁ 1

dan karena e

m n

m

m n

n  

   

 

     



  



1 1 lim 1

1

lim maka sekali lagi dengan Teorema Apit diperoleh:

(3.6.3) e

x x

x  

   

  

1 1 lim

Berdasarkan (3.6.2), tentunya mudah dipahami bahwa:

(3.6.4) e

x x

x  

    _  

1 1 lim

Selanjutnya, apabila diambil substitusi

x

u 1_{, maka untuk} u 0 berakibat x . Sehingga, dari (3.6.3) dan (3.6.4) diperoleh:

(3.6.5)   e

x u

x

x u

u  

   

 



  

1 1 lim 1

lim 1

0

Contoh 3.6.1 Hitung 3 5

1 2 1 lim





 

 

 

 

x

x x .

Penyelesaian: Apabila diambil substitusi ₁2_x 1_y

 maka berturut-turut diperoleh:

(i). x1 2y_{, sehingga} 3x 56y 2_.

(ii). Karena

2 1 x

y   _{maka untuk}

x





_berakibat y   _.

2 6 2 6 5 3 ₁ 1 1 1 lim 1 1 lim 1 2 1 lim            _                              y y y x y y y y x x 2 6 1 1 lim 1 1 lim       _                      y y y y y

2 6 6 6 1 . 1 1 lim 1 1

lim  

      _                            

 e e

y

y y

y

y .█

Contoh 3.6.2 Tentukan lim₁



2



1 1

 

x

x x .

Penyelesaian: Soal dapat ditulis:





 





1 1

1 1

1

1 2 lim 1 (1 )

lim         x x x

x x x

Diambil substitusi y 1 x_{. Jika} x1 maka y 0_{. Selanjutnya, menurut (3.6.5) diperoleh:}

            e y y x x y y y y x x x x 1 1 lim 1 lim ) 1 ( 1 lim 2 lim 1 1 0 1 0 1 1 1 1 1

1 _ 

                    .█

Teorema berikut ini sangat bermanfaat untuk menyelesaikan soal-soal hitung limit yang berkaitan dengan bilangan alam. Bukti diserahkan kepada pembaca sebagai latihan.

Contoh 3.6.4 Tentukan

2 3 1 1 lim    _       x x _x x . Penyelesaian: Soal dapat ditulis:

2 3 2 3 1 2 1 lim 1 1 lim       _                 x x x

x x x

x

Apabila berturut-turut diambil

1 2 ) (    x x

f dan g(x)3x 2 _maka:

Teorema 3.6.3 Apabila _xlim_c f(x)0 dan _xlim_c g(x) (atau  ) maka:



_{1 ( )}



( ) lim ( ). ( ) lim g x f x g x

c x c x e x

f _ 

     

 ( ) 0 dan lim ( )

lim f x g x

x x

Selanjutnya, menurut Teorema 3.6.3:

6 ) 2 3 ( 1 2 lim 2 3 2 3 1 2 1 lim 1 1

lim   

       _                 

 e  e

x x x x x x x x x x .█

Contoh 3.6.5 Hitung 3 2 1

2 lim  

 x x x x x . Penyelesaian:









2 3 2

2 1 1 lim lim 1 2 3 1          x x x x x x x x x x

Selanjutnya, jika diambil f(x)x 1 dan

2 3 ) ( ₂    x x x x

g maka:

  



 ( ) 0 dan lim ( )

lim

1

1 f x x g x

x

Sehingga menurut Teorema 3.6.3:









lim( 1). 3 2

1 2 3 1 2 1 2 3 2 2 1 1 lim

lim   

         

 x x

x x x x x x x x x x x e x x 1 ) 1 )( 2 ( ) 1 ( lim

1    



 

e

e x x

x x

x .█

Contoh 3.6.6 Selesaikan

x x x x 3 3 2 lim 0   . Penyelesaian: Tulis: x x x x x x x x x x x x x x 3 1 3 lim 3 1 2 lim 3 3 1 1 2 lim 3 3 2 lim 0 0 0 0             

Berturut-turut diambil substitusi:

1 3 dan

1

2   

 x _v x

u

(i). lim 2₃ 1 lim _{3. log(1 )} 1_{3lim log}1



₁



1_{3 loglim}1



₁



1 ₃1.2_log1 1₃ln2 0

2 1

2 0 2

0

0  _  _  _  



 



 u _{u u} e

u

x u

u u

u u

x

x

(ii). lim3₃ 1 lim_{3. log(1 )} 1_{3lim log}1



₁



1_{3 loglim}1



₁



1 ₃1.3_log1 1₃ln3 0

3 1

3 0 3

0

0  _  _  _  



 



 u u u e

u

x u

u u

u u

x

x

Selanjutnya, dari (i) dan (ii) diperoleh:



ln2 ln3



3

1 3

3 2 lim

0  



 x

x x

x .█

Soal Latihan

Untuk soal 1 – 10, hitunglah nilai limitnya.

1. 3 1

2 2 1 lim





 

 

 

 

x

x x 2.





1( 2)

2 1

lim 

 

x

x x

3. x

x x

x 2

2 1 lim





 

   



 _4.



2



1( 1)

1 3 3

lim 

  

x

x x x

5.

x x

x

1 2 lim

0 

 6. x

x x

x 2

2 1 3 lim

1 2

0





 

7. x _x

x ln

1 lim

1



 8.

5 7 1 3

1 3 lim





 

 

 



 x

x x

x

9.

2

1

2 2

0 _{2 1}

1 lim

x

x _{x x}

x

    

  

 



 10.

) 7 ( 1 3

0

2

1 1 lim

x x

x _{x x}

x 

 _

 

 

 



Seperti telah dijelaskan pada bagian sebelumnya, kadang-kadang nilai_xlim_c f(x) sama dengan )

(c

f _{, kadang pula tidak sama. Pada kenyataannya, meskipun} f(c) _{tidak terdefinisikan akan tetapi} )

( lim f x

c

x mungkin ada. Apabila xlimc f(x)= f(c) maka dikatakan fungsi f kontinu di c.

Definisi 3.7.1 di atas secara implisit mensyaratkan tiga hal agar fungsi f kontinu di a, yaitu: (i). f(a) ada atau terdefinisikan,

(ii). lim_xa f

 

x ada, dan (iii). lim_x_a f

 

x f

 

a

Secara grafik, fungsi f kontinu di

x



a

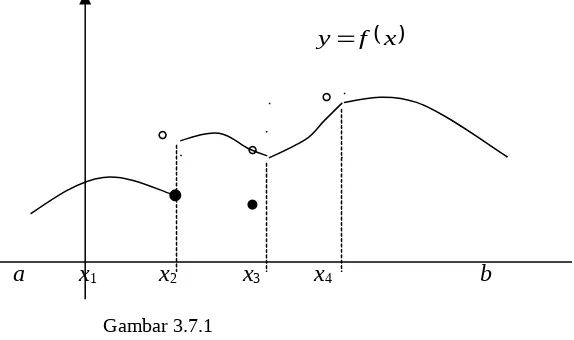
jika grafik fungsi f pada suatu interval yang memuat a

tidak terpotong di titik (a, f(a))_{. Jika fungsi f tidak kontinu di a maka dikatakan f diskontinu di a. Pada} Gambar, f kontinu di x1 dan di setiap titik di dalam (a,b) kecuali di titik-titik x2, x3, dan x4. Fungsi f

diskontinu di x2 karena lim ( )

2

x f x

x tidak ada, diskontinu di x3 karena nilai lim3 ( )

x f x

x tidak sama dengan

nilai fungsi di x3 (meskipun keduanya ada), dan diskontinu di x4 karena nilai fungsi di titik ini tidak ada.

 

x f y

a x1 x2 x3 x4 b

Gambar 3.7.1

Definisi 3.7.1 Fungsi f dikatakan kontinu di aDf jika lim_xa f(x)f (a).







Fungsi f dikatakan kontinu pada interval I jika f kontinu di setiap titik anggota I.

Contoh 3.7.2

(a). Fungsi f dengan rumus   ₁1

2

  

x x x

f _{diskontinu di x = 1 karena f (1) tidak terdefinisi.}

(b). Fungsi HeavysideH yang didefinisikan oleh

 

  

  

0 1

0 0

x jika

x jika x

H

diskontinu di x = 0 sebab lim_x0 H

 

x tidak ada. (c). Fungsi g dengan definisi:

 

     

  





2 jika 1

2 jika

2 4

2

x x x

x x g

diskontinu di x = 2 sebab g(2) = 3 sedangkan

 

lim



2



4 2

4 lim

lim

2 2

2

2 _   

 

 

 x x

x x

g

x x

x . Namun

demikian fungsi g kontinu di x = 1 sebab lim_x1 g

 

x 3g

 

1 .█

Berikut sifat-sifat dasar fungsi kontinu.

Seperti halnya pada hitung limit, dalam kekontinuan juga dikenal istilah kontinu satu sisi. Hal itu diberikan pada definisi berikut ini.

Teorema 3.7.3 Jika fungsi f dan g kontinu di a, dan k sebarang konstanta real, maka f+g,

f – g, kf, dan fg kontinu dia. Demikian pula, _gf kontinu di a asalkan g

 

a 0_.

Contoh 3.7.5 Diberikan f x ₁ x2 . 

 Selidikilah kekontinuan fungsi f.

Penyelesaian:

Jelas f tidak kontinu pada



 , 1



_{dan pada}



1,



_{sebab f tidak terdefinisi pada interval tersebut.}

Untuk nilai-nilai a dengan –1 < a <1 diperoleh:

 x x



x



a f a

f

a x a

x a

x         

2 2

2 _{lim 1 1}

1 lim lim

Jadi, f kontinu pada (1, 1). Dengan perhitungan serupa didapatkan:

 

0



1



lim

1   

 

f x

f

x dan lim1

 

0

 

1

f x

f x

 





sehingga f kontinu dari kanan di x = 1 dan kontinu dari kiri di x = 1. Jadi, f kontinu pada



 1,1



.█

Contoh 3.7.7

(a). f x x2 x1 kontinu pada R .

(b).  

1 5

2 3

  

x x x x

f _{kontinu pada}



x _{R ;} x1, x  1  _.

(c). f x  x1 _{kontinu pada}



1,



_.█

Hubungan antara fungsi kontinu dan hitung limit dinyatakan dalam teorema berikut.

Teorema 3.7.6 Fungsi polinomial, fungsi rasional, fungsi akar, fungsi logaritma, fungsi eksponen, dan fungsi trigonometri kontinu pada domainnya masing-masing.

Teorema 3.7.8 Jika f kontinu di b dan _xlim_a g

 

x b, maka _xlim_a f



g

 

x



f

 

b. Dengan kata lain

 

g x f lim g x  f

Contoh 3.7.9 Hitung _xlim_1 ln



1x



.

Penyelesaian: Namakan f

 

x lnx _dan g

 

x 1x_{. Karena x}lim_1g

 

x 2 _{dan f kontinu di x = 2}

maka lim ln1  lim    lim   ln lim   ln 2

1 1

1

1 _

 

        

    



 



 x x f g x f x g x x g x

x .█

Soal Latihan

Untuk soal 1 – 8, tentukan titik-titik di mana fungsi berikut diskontinu. 1.

x x x

h( ) 3 _{2. f(x)}3 _x2 _{1 3.}

1 2 )

( ₃

  

x x x f

4. g(x) xtanx _5.

3 2 )

( ₂

 

s s s

f _6.

2 4 )

( 2

  

t t t h

7.

     

 

 

 



1 , 2 3

3 1 , 5

3 , 1 3 ) (

2

x x

x x x

x

g _8.

    

    

3 1 ,

3

3 1 0 , 2

0 ,

) (

2 _x

x

x x

x x x

f

9. Selidiki kontinuitas f x _x  

1 1 )

( _pada [1,5]

10.Jika

  

  

  

7 3 , 15

3 0

, 2 )

( ₂

x x

x x

x

f maka tunjukkan bahwa f kontinu pada [0,7]_.

11.

      

  

  





5 ,

2

5 ,

5 3 )

(

2

x bx

x x

ax x

f _12.

   

    

 

 

 



0 ,

0 ,

4

0 ,

tan tan

) (

x b

ax

x x bx

ax