DAFTAR PUSTAKA
Aribowo, Agus Sasmito. 2008. Visualisasi Teori Optimalisasi Biaya Transportasi Untuk Pembelajaran Riset Operasi. Jurnal Informatika.
Kertiasih, Ni Ketut. 2009. Penggunaan Metode Transportasi dalam Program Linier Untuk Pendistribusian Barang. UNDIKSHA. Bali
Nasution, M.N. 2008. Manajemen Transportasi. Ghalia Indonesia. Jakarta.
Nur Hamin, Ismaillia. (2007). “Identifikasi Alternatif Pengadaan Bahan Baku di
Perusahaan Daerah Air Minum (PDAM) Kabupaten Boyolali”. Tersedia pada http://www.etd.eprints.ums.ac.id/1743/2/ D600030127.pdf. (diakses tanggal 16 Septeember 2016).
Sitorus, Parlin. 1997. Program Linier. Universitas Trisakti, Jakarta.
Subagyo, Pangestu., Asri, Marwan., Handoko, Tani. 1984. Dasar-dasar Operations Research. BPFE. Yogyakarta
Susanta, B. (1994). Program Linear. Yogyakarta: Departemen Pendidikan dan Kebudayaan.
Wijaya, Andi. 2012. Pengantar Operasi riset. Mitra Wacana Media. Bogor
BAB 3
HASIL DAN PEMBAHASAN
Data yang diperoleh dari perusahaan adalah sebagai berikut:
Tabel 3. 1 Jumlah Laptop yang akan Dikirim dari Tempat Asal
Sumber Jumlah yang Akan Dikirim
Medan 1400 unit
Binjai 900 unit
Tebing Tinggi 1000 unit
Total 3300 unit
Tabel 3. 2 Jumlah Permintaan di Tempat Tujuan
Lokasi Tujuan Jumlah Permintaan
Sibolga 700 unit
Pematang Siantar 950 unit
Tanjung Balai 750 unit Sidikalang 800 unit
Total 3200 unit
Tabel 3. 3 Tabel Biaya angkut dalam Tabel Transportasi (dalam rupiah)
Perhatikan, bahwa:
1. Selanjutnya tabel di atas akan disebut dengan tabel transportasi. 2. Kolom mewakili daerah atau tempat tujuan distribusi.
3. Baris mewakili sumber daya yang dimiliki perusahaan
4. Selanjutnya yang dimaksud dengan sel x14 adalah baris 1 dan kolom 4.
5. Angka yang terdapat pada pojok kanan atas setiap sel menunjukkan biaya transportasi di sel tersebut.
Alokasi produk laptop yang telah dilakukan oleh perusahaan adalah sebagai berikut:
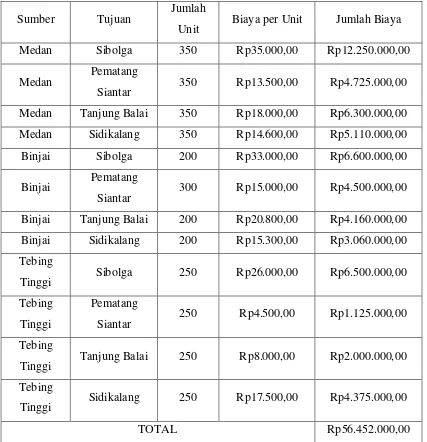
Tabel 3.4 Alokasi dan Biaya Distribusi Produk Laptop pada PT. IT Master
Sumber Tujuan Jumlah
Unit Biaya per Unit Jumlah Biaya
Medan Sibolga 350 Rp35.000,00 Rp12.250.000,00
Medan Pematang
Siantar 350 Rp13.500,00 Rp4.725.000,00 Medan Tanjung Balai 350 Rp18.000,00 Rp6.300.000,00
Medan Sidikalang 350 Rp14.600,00 Rp5.110.000,00
Binjai Sibolga 200 Rp33.000,00 Rp6.600.000,00
Binjai Pematang
Siantar 300 Rp15.000,00 Rp4.500.000,00
Binjai Tanjung Balai 200 Rp20.800,00 Rp4.160.000,00 Binjai Sidikalang 200 Rp15.300,00 Rp3.060.000,00
Tebing
Tinggi Sibolga 250 Rp26.000,00 Rp6.500.000,00 Tebing
Tinggi
Pematang
Siantar 250 Rp4.500,00 Rp1.125.000,00
Tebing
Masalah di atas dapat dirumuskan dalam masalah program linier sebagai berikut:
= 35000 + 13500 + 18000 "+ 14600 %+ 33000 & + 15000 &'+ 20800 &"+ 15300 &%+ 26000 ( + 450 (' + 800 ("+ 17500 (%
Dengan batasan
* + , =
+ '+ "+ % = 1300
& + &'+ &"+ &% = 900 ( + ('+ ("+ (%= 1000
./0 , =
+ & + ( = 700
'+ &'+ (' = 950 "+ &"+ (" = 750 %+ &%+ (% = 800 Keterangan :
x1 = Medan
x2 = Binjai
x3 = Tebing Tinggi
x4 = Sibolga
x5 = Pematang Siantar
x6 = Tanjung Balai
3. 1 Penyelesaian Awal dengan Metode Least Cost
Jumlah permintaan berdasarkan tabel di atas adalah 3200 unit, sedangkan jumlah kapasitas atau barang yang akan didistribusikan adalah 3300 unit. Hal ini berarti
bahwa masalah transportasi pada penelitian ini adalah masalah transportasi tidak seimbang karena jumlah permintaan tidak sama dengan jumlah kapasitas. Untuk dapat melakukan penyelesaian masalah maka ditambahkan satu kolom semu (dummy) dengan biaya transportasi sebesar 0.
Tabel 3.5 Tabel Transportasi Awal dengan Dummy
Tujuan
Penyelesaian dimulai dengan cara mengisikan alokasi produk sebanyak-banyaknya sesuai dengan permintaan dan kapasitas. Sel dengan biaya distribusi terendah adalah sel x35. Isikan produk sebanyak kapasitas.
Tabel 3.6 Hasil Tahap 1
B. Tahap 2
Jumlah permintaan pada x5 telah terpenuhi. Selanjutnya alokasikan kembali
produk sebanyak-banyaknya pada sel dengan biaya terendah berikutnya. Sel yang terpilih adalah sel x36.
Tabel 3.7 Hasil Tahap 2
Tujuan
Tentukan kembali sel dengan biaya transportasi terkecil lainnya untuk dapat dialokasikan produk sebanyak mungkin sesuai kapasitas dan permintaan. Sel terpilih adalah sel x17.
Tabel 3.8 Hasil Tahap 3
Tabel 3.9 Hasil Tahap 4
Berdasarkan tabel 3. 9, permintaan dan kapasitas belum terpenuhi seluruhnya. Lakukan kembali pengalokasian barang pada sel dengan biaya yang kecil selanjutnya.
Tabel 3.10 Hasil Tahap 5
Tujuan
Dari tabel 3. 10, permintaan pada kolom x6 telah terpenuhi namun kapasitas belum
terpenuhi. Lakukan pengalokasian produk pada kolom x24 sesuai kapasitas dan
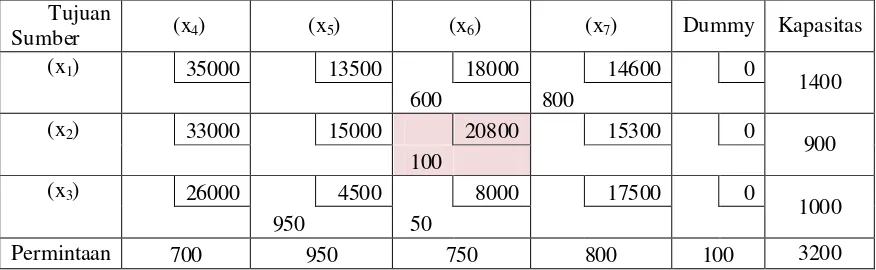
Tabel 3.11 Hasil Tahap 6
Berdasarkan tabel 3. 11 seluruh permintaan telah terpenuhi, tetapi kapasitas masih ada. Kolom dummy berguna dalam hal ini. Maka dari itu sisa alokasi barang di tempatkan pada kolom dummy.
Tabel 3.12 Hasil Tahap Akhir dengan Metode Least Cost
Gambar 3. 1 Jalur Pendistribusian Laptop Menggunakan Metode Least Cost
Total biaya pengiriman menggunakan Metode Least Cost sebagai berikut:
Tabel 3. 13 Jumlah Biaya dan Alokasi dngan Metode Least Cost
Sumber Tujuan Jumlah Unit Biaya per Unit Jumlah Biaya
Medan Tanjung
Balai 600 Rp18.000,00 Rp10.800.000,00
Medan Sidikalang 800 Rp14.600,00 Rp11.680.000,00 Binjai Sibolga 700 Rp33.000,00 Rp23.100.000,00
Binjai Tanjung
Balai 100 Rp20.800,00 Rp2.080.000,00 Tebing
Tinggi
Pematang
Siantar 950 Rp4.500,00 Rp4.275.000,00
Tebing Tinggi
Tanjung
Balai 50 Rp8.000,00 Rp400.000,00
3. 2 Penyelesaian Optimal dengan Metode Stepping Stone
A. Tahap 1
Sebelum melanjutkan ke tahap optimal, terlebih dahulu harus di teliti apakah terjadi redundansi atau degenerasi. Jumlah sel yang terisi harus berjumlah m (sumber) + n (tujuan) – 1. Dari hasil penyelesaian menggunakan metode Least Cost dapat dilihat bahwa jumlah sel yang terisi adalah 7 sel. Hal ini menunjukkan bahwa tidak terjadi permasalahan degenerasi maupun redundansi. Maka penyelesaian optimal dapat dilanjutkan.
Dari Tabel 3.12 pilih sel-sel yang kosong untuk mencari nilai indeks perbaikannya dengan cara melakukan loncatan searah jarum jam dengan pijakannya berupa sel basis (berisi) sehingga terbentuk sebuah loop terdekat yang memungkinkan untuk kembali ke sel semula dengan memuat tanda (+) dan (−)
secara bergantian pada setiap sudut sel dari loop tersebut. Mulai dengan tanda (+) pada sel kosong terpilih. Setelah semua sel-sel kosong dievalusi dan didapat nilai indeks perbaikannya selanjunya dilihat apakah masih ada nilai yang < 0. Jika tidak ada, maka pemecahan awal sudah optimal tetapi bila masih ada nilai yang negatif pilih sel yang mempunyai nilai negatif terbesar (penurunan biaya terbesar) untuk dilakukan perbaikan jalur.
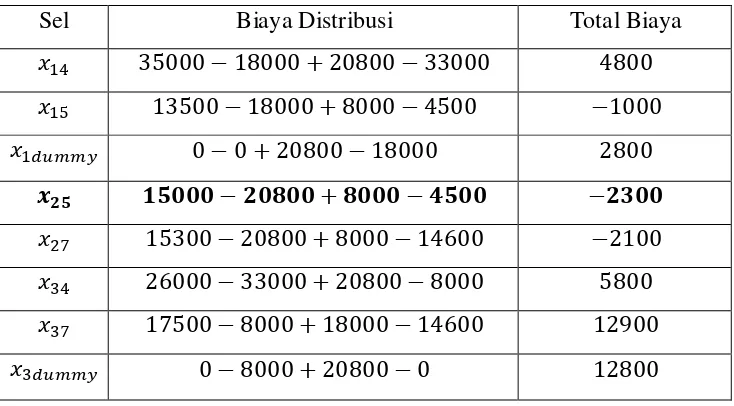
Tabel 3. 14 Indeks Perbaikan Sel Kosong pada Tabel 3. 12
Sel Biaya Distribusi Total Biaya
Dari tabel 3. 13 diketahui bahwa ada biaya distribusi bernilai negatif. Maka dari itu perlu dilakukan perbaikan alokasi. Sel yang akan dilakukan perubahan adalah sel yang memiliki biaya distribusi terkecil yaitu sel x25.
(x5) (x6)
(x1) 13500 18000
600
(x2) 15000 20800
(+) 100
(-)
(x3) 4500 8000
950 (-) 50 (+)
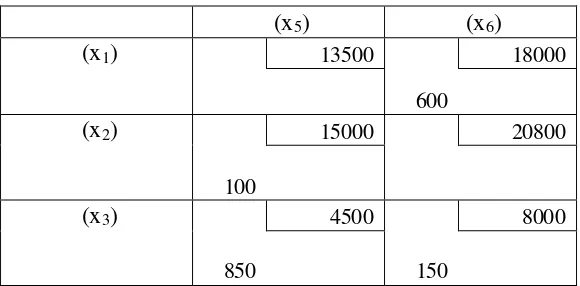
Gambar 3. 2 Loop pada Sel x25
(x5) (x6)
(x1) 13500 18000
600
(x2) 15000 20800
100
(x3) 4500 8000
850 150
Tabel 3. 15 Hasil Tahap 1
Lakukan kembali evaluasi pada sel yang kosong untuk mengetahui biaya distribusi pada jalur tertutup.
Tabel 3. 16 Indeks Perbaikan Sel Kosong pada tabel 3. 15
Sel Biaya Distribusi Total Biaya
(x5) (x6) (x7) Dummy
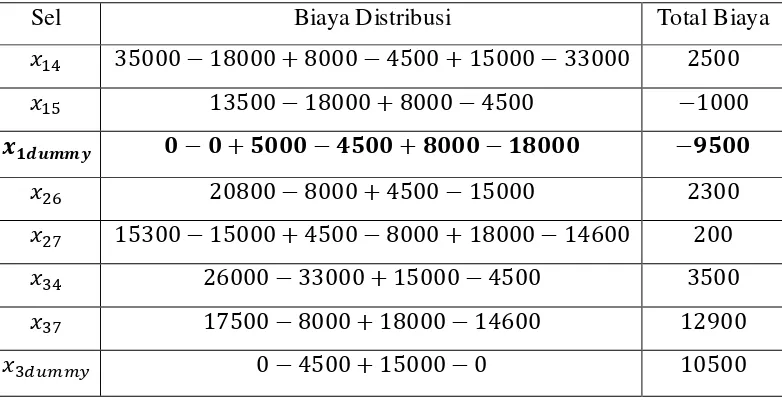
Gambar 3. 5 Hasil Perbaikan Sel x1dummy
Tabel 3. 17 Hasil Tahap 2
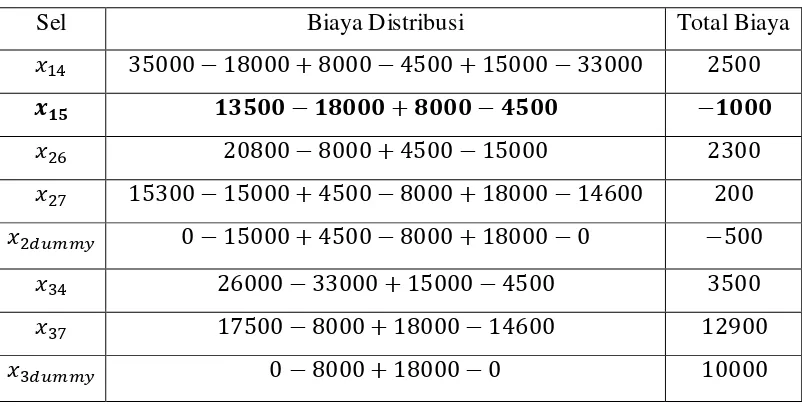
Tabel 3. 18 Indeks Perbaikan Sel yang Kosong pada Tabel 3.17
Sel Biaya Distribusi Total Biaya
35000 − 18000 + 8000 − 4500 + 15000 − 33000 2500
587 8<799 − 8:999 + :999 − ;799 −8999
&" 20800 − 8000 + 4500 − 15000 2300 &% 15300 − 15000 + 4500 − 8000 + 18000 − 14600 200 &23 4 0 − 15000 + 4500 − 8000 + 18000 − 0 −500
( 26000 − 33000 + 15000 − 4500 3500 (% 17500 − 8000 + 18000 − 14600 12900
(23 4 0 − 8000 + 18000 − 0 10000
Dari tabel 3. 18 dapat dilihat bahwa ada sel yang memiliki biaya negatif. Lakukan kembali perbaikan sel yang memiliki biaya distribusi terendah yaitu sel x15.
(x5) (x6)
(x1) 13500 18000
(+) 500
(-)
(x2) 15000 20800
200
4500 8000
(x3)
750 (-) 250 (+)
(x5) (x6)
(x1) 13500 18000
500
(x2) 15000 20800
200
4500 8000
(x3)
250 750
Gambar 3. 7 Hasil Perbaikan Sel x15
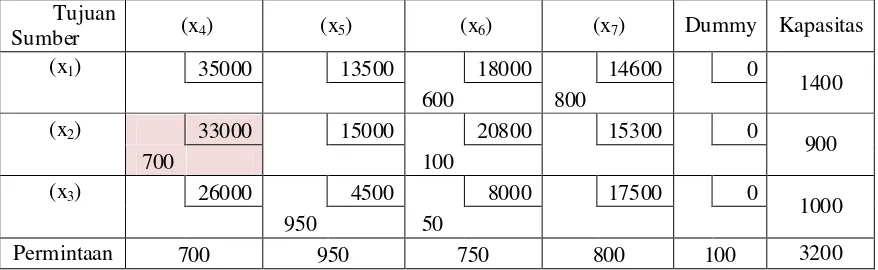
Tabel 3. 19 Hasil Tahap 3
Tujuan
Sumber (x4) (x5) (x6) (x7) Dummy Kapasitas (x1) 35000 13500 18000 14600 0
1400
500 800 100
(x2) 33000 15000 20800 15300 0
900 700 200
(x3) 26000 4500 8000 17500 0
1000
250 750
Permintaan 700 950 750 800 100 3200
D. Tahap 4
Tabel 3. 20 Indeks Perbaikan Sel yang Kosong pada Tabel 3. 19
Sel Biaya Distribusi Total Biaya 35000 − 13500 + 15000 − 33000 3500 evaluasi pada sel dengan nilai terkecil yaitu sel x2dummy.
(x5) (x6) (x7) Dummy
Tabel 3. 21 Hasil Tahap 4
Tabel 3. 22 Indeks Perbaikan Sel Kosong pada Tabel 3.21
(x5) (x6) (x7)
Gambar 3. 11 Hasil Perbaikan Sel x27
Tabel 3.23 Hasil Tahap 6
Tujuan
Tabel 3. 24 Indeks Perbaikan Sel Kosong pada Tabel 3. 23
Sel Biaya Distribusi Total Biaya
35000 − 14600 + 15300 − 33000 2700
Berdasarkan tabel di atas diketahui bahwa semua biaya bernilai positif. Penyelesaian menggunkan metode Stepping Stone telah selesai.
Tabel 3. 25 Hasil Alokasi Menggunakan Metode Stepping Stone
Tujuan
Berdasarkan hasil penyelesaian menggunkan metode Stepping Stone, barang didistribusikan dari Medan menuju Pematang Siantar sebanyak 700 unit dan ke Sidikalang sebanyak 700 unit. Barang dikirim dari Binjai menuju Sibolga sebanyak 700 unit dan ke Sidikalang sebanyak 100 unit. Barang dari Tebing
Gambar 3. 12 Jalur Pendistribusian Laptop Menggunakan Metode Stepping Stone
Total biaya distribusi menggunakan metode Stepping Stone sebagai berikut:
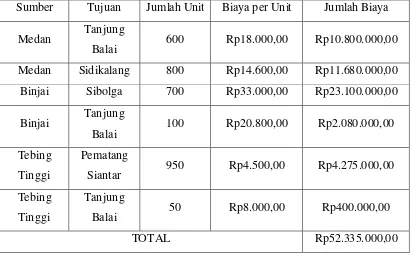
Tabel 3. 26 Jumlah Biaya dan Alokasi Menggunakan Metode Stepping Stone
Sumber Tujuan Jumlah
Unit Biaya per Unit Jumlah Biaya
Medan Pematang
Siantar 700 Rp13.500,00 Rp9.450.000,00 Medan Sidikalang 700 Rp14.600,00 Rp10.220.000,00
Binjai Sibolga 700 Rp33.000,00 Rp23.100.000,00
Binjai Sidikalang 100 Rp15.300,00 Rp1.530.000,00 Tebing
Tinggi
Pematang
Siantar 250 Rp4.500,00 Rp1.125.000,00
Tebing
Tinggi Tanjung Balai 750 Rp8.000,00 Rp6.000.000,00
TOTAL Rp51.425.000,00
Medan
Binjai
Tebing Tinggi
Sidikalang Tanjung Balai Pematang Siantar
Dari perhitugan di atas dapat diteliti bahwa proses pengalokasian barang menggunakan metode Least Cost dilakukan dengan mengisi sel yang memiliki biaya distribusi terendah hingga semua kapasitas dan permintaan terpenuhi. Karena jumlah permintaan tidak sama dengan jumlah kapasitas maka perlu ditambahkan kolom dummy untuk dapat dilakukan pengalokasian. Hasil yang diperoleh dengan metode Least Cost dioptimalkan dengan metode Stepping Stone. Sebelum memulai pengoptimalan menggunakan metode Stepping Stone, harus diteliti terleih dahulu jumlah sel yang terisi pada penyelesaian awal. Jika terjadi persoalan degenerasi atau redundansi, penyelesaian optimal belum dapat dilanjutkan. Setelah dipastikan jumlah sel berisi berjumlah m+n-1 dimana pada penelitan ini jumlah m+n-1 adalah sel, penyelesaian optimal menggunakan
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Berdasarkan hasil penelitian, penulis mengambil kesimpulan:
1. Kombinasi Metode Least Cost dan Metode Stepping Stone dapat menyelesaikan permasalahan transportasi agar pengalokasian produk menghasilkan biaya yang lebih minimum.
2. Total biaya yang diperoleh menggunakan kombinasi Metode Least Cost dan Metode Stepping Stone adalah Rp51.425.000,00, lebih murah
Rp5.027.000,00 dari alokasi perusahaan sebelumnya.
3. Berdasarkan hasil penyelesaian optimal, laptop didistribusikan dari Medan menuju Pematang Siantar sebanyak 700 unit dan ke Sidikalang sebanyak 700 unit. Barang dikirim dari Binjai menuju Sibolga sebanyak 700 unit dan ke Sidikalang sebanyak 100 unit. Barang dari Tebing Tinggi dikirim sebanyak 250 unit menuju Pematang siantar dan 750 unit ke Tanjung Balai.
4.2 Saran
BAB 2
LANDASAN TEORI
2.1 Riset Operasi
Istilah Riset Operasi (Operation Research) pertama kali digunakan pada tahun 1940 oleh Mc Closky dan Trefthen di suatu kota kecil Bowdsey Inggris. Riset Operasi adalah suatu metode pengambilan keputusan yang dikembangkan dari studi operasi-operasi militer selama Perang Dunia II. Pada masa awal perang 1939, pemimpin militer Inggris memanggil sekelompok ahli-ahli sipil dari berbagai disiplin dan mengkoordinasi mereka ke dalam suatu kelompok yang diserahi tugas mencari cara-cara yang efisien untuk menggunakan alat yang baru ditemukan yang dinamakan radar dalam suatu sistem peringatan dini menghadapi serangan udara. Kelompok ahli Inggris ini dan kelompok-kelompok lain berikutnya melakukan penelitian (research) pada operasi-operasi (operations) militer.
Setelah kesuksesan tim riset operasi ini, militer Inggris dan Amerika Serikat melanjutkan mengaktifkan tim riset operasi. Sebagai hasilnya, tim riset operasi
semakin banyak yang disebut dengan “peneliti operasi militer” yang mengaplikasikan pendekatan riset operasi pada permasalahan pertahanan nasional. Beberapa teknik yang dikembangkan memasukkan ilmu politik, matematik, ekonomi, teori probabilitas dan statistik.
dinamis, teori antrian dan teori inventori telah dikembangkan dengan baik di akhir tahun 1950-an.
Dalam riset operasional, masalah optimasi dalam pengambilan keputusan diperoleh dengan menerapkan teknik matematika dan statistika. Model matematika yang digunakan dalam metode riset operasional bersifat menyederhanakan masalah dan membatasi faktor-faktor yang mungkin berpengaruh terhadap suatu masalah. Jika riset operasi akan digunakan untuk memecahkan suatu permasalahan, maka harus dilakukan lima langkah sebagai berikut: 1. Memformulasikan persoalan.
2. Mengobservasi sistem.
3. Memformulasikan model matematis dari persoalan yang dihadapi.
4. Mengevaluasi model dan menggunakannya untuk prediksi.
5. Mengimplementasikan hasil studi.
Arti riset operasi (operations research) telah banyak didefinisikan oleh beberapa ahli, diantaranya:
1. Morse dan Kimball mendefinisikan riset operasi sebagai metode ilmiah (scientific method) yang memungkinkan para manajer mengambil keputusan mengenai kegiatan yang mereka tangani dengan dasar kuantitatif. Definisi ini kurang tegas karena tidak tercermin perbedaan antara riset operasi dengan disiplin ilmu yang lain.
2. Churchman, Arkoff dan Arnoff pada tahun 1950-an mengemukakan
pengertian riset operasi sebagai aplikasi metode-metode, teknik-teknik dan peralatan-peralatan ilmiah dalam menghadapi masalah-masalah yang timbul di dalam operasi perusahaan dengan tujuan ditemukannya
pemecahan yang optimum masalah-masalah tersebut.
3. Miller dan M.K. Starr mengartikan riset operasi sebagai peralatan
Dari ketiga definisi tersebut dapat disimpulkan bahwa riset operasi berkenaan dengan pengambilan keputusan yang optimal dalam, dan penyusunan model dari sistem-sistem baik yang diterministik maupun probabilistik yang berasal dari kehidupan nyata. Atau dunia pengelolaan atau dunia usaha yang memakai pendekatan ilmiah atau pendekatan sistematis disebut riset operasi (Operations Resech).
2.2 Program Linier
Program Linier adalah suatu cara untuk menyelesaikan permasalahan mengenai pengalokasian atau penempatan sumber-sumber yang terbatas di antara beberapa aktivitas yang bersaing, dengan cara yang terbaik yang mungkin dilakukan agar memperoleh suatu solusi yang optimal. Selain persoalan program linier seperti masalah optimaslisasi, metode grafik, metode simplex dan dualitas, ada persoalan
program linier yang bertipe khusus, yang kekhususannya terletak pada karakteristik utama. Tipe khusus persoalan program linier yang paling penting ialah apa yang dikenal sebagai masalah transportasi. Masalah transportasi secara umum berhubungan dengan masalah pendistribusian suatu komoditas atau produk dari sejumlah sumber (supply) ke sejumlah tujuan (demand) dengan tujuan meminimumkan ongkos pengangkutan yang terjadi (biaya distribusi).
Pengertian program linier menurut beberapa ahli, sebagai berikut:
1. Menurut T. Hani Handoko Program Linier ialah suatu metode analitik paling terkenal dan yang merupakan suatu bagian pada kelompok teknik-teknik yang disebut dengan programisasi matematik.
2. Menurut Sofjan Assauri Program Linier adalah suatu teknik perencanaan
yang dengan menggunakan model matematika dengan tujuan untuk
3. Menurut Zainal Mustafa, EQ, dan juga Ali Parkhan Program Linier ialah suatu cara yang lazim digunakan dalam pemecahan suatu masalah pengalokasian sumber-sumber yang terbatas dengan secara optimal. 4. Menurut Zulian Yamit Program Linier ialah metode ataupun teknik
matematis yang digunakan untuk dapat membantu manajer dalam
pengambilan keputusan. Ciri khusus dalam penggunaan metode matematis ini ialah berusaha untuk mendapatkan maksimisasi atau juga minimisasi.
2.3 Masalah Transportasi
Transportasi adalah suatu proses pemindahan manusia atau barang dari suatu tempat ke tempat lain dengan menggunakan suatu alat bantu kendaraan darat, kendaraan laut, maupun kendaraan udara, baik umum maupun pribadi dengan menggunakan mesin atau tidak menggunakan mesin. Pada masalah tranportasi, biasanya jumlah barang yang disalurkan dari setiap lokasi permintaan bervariasi.
Atas dasar kenyataan bahwa rute pengiriman yang berbeda akan menghasilkan biaya kirim yang berbeda, maka tujuan pemecahan kasus ini adalah menentukan berapa unit barang yang arus dikirim dari setiap sumber ke setiap tujuan sehingga permintaan dari setiap tujuan terpenuhi dan total biaya kirim minimum.
Ciri dari masalah transportasi antara lain:
1. Terdapat sejumlah sumber dan sejumlah tujuan.
2. Kuantitas komoditas sumber atau tujuan besarnya tertentu.
3. Jumlah pengiriman komoditas sesuai kapasitas sumber atau tujuan. 4. Biaya yang terjadi besarnya tertentu.
Dalam transportasi, terdapat beberapa masalah yang dihadapi apabila terdapat kesalahan dalam pengalokasi maupun dalam jumlah kapasitas pemasok dan kapasitas permintaan. Masalah khusus yang di hadapai dalam transportasi adalah sebagai berikut:
Apabila terjadi penawaran lebih besar dari permintaan atau unbalance, maka diperlukan tambahan tempat tujuan semu atau sering disebut dummy. Tambahan tempat tujuan diperlukan agar penawaran sama dengan
permintaan, sehingga tabel awal yang fleksibel dapat dibentuk. Biaya transportasi untuk setiap sel dummy sama dengan nol.
b. Permintaan lebih besar dari penawaran
Seperti halnya pada masalah pertama, apabila terjadi permintaan lebih besar dari penawaran, maka diperlukan tambahan tempat asal semu dengan biaya transportasi sama dengan nol. Tambahan tempat asal semu diperlukan agar tabel awal yang fleksibel dapat dibentuk.
c. Maksimalisi keuntungan
Sasaran pokok yang hendak dicapai dari model transportasi adalah mengalokasikan produk yang tersedia di tempat asal ke tempat tujuan agar diperoleh total biaya minimum. Namun apabila orientasi berubah menjadi keuntungan maksimum maka diperlukan konversi terhadap tujuan dari minimisasi biaya ke maksimalisasi keuntungan.
d. Masalah prioritas
Tujuan yang hendak dicapai dalam permasalahan transportasi adalah mencari alokasi dengan total biaya minimum, oleh karena itu biaya persatuan barang terkecil merupakan dasar alokasi.
e. Masalah pemblokiran
Sebagai lawan dari prioritas adalah pemblokiran, di mana perusahaan menetapkan untuk tidak mengalokasikan produk ke suatu daerah tertentu. f. Masalah multi commodity
Masalahnya adalah pengalokasian barang terdiri dari berbagai jenis produk, Persoalannya bagaimana mengatur alokasi produk dari beberapa pabrik ke daerah pemasaran dengan biaya total transportasi minimum. g. Masalah transshipment
2.4 Metode Transportasi
Metode Transportasi adalah suatu metode yang digunakan untuk mengatur distribusi dari sumber-sumber yang menyediakan produk-produk yang sama di tempat-tempat yang membutuhkan secara optimal. Alokasi produk ini harus diatur sedemikian rupa karena terdapat perbedaan biaya transportasi (alokasi) dari suatu sumber ke beberapa tujuan yang berbeda- beda dan dari beberapa sumber ke suatu tujuan juga berbeda- beda.
Adapun tujuan dari penggunanaan metode transportasi sebagai upaya untuk pendistribusian barang adalah agar supply dari beberapa sumber dapat dilakukan secara efektif dan biaya murah ke beberapa tempat tujuan. Persediaan atau penawaran maksimum pada setiap sumber dan permintaan minimum pada setiap tujuan. Distribusi ini dilakukan sedemikian rupa sehingga permintaan dari beberapa tempat tujuan dapat dipenuhi dari beberapa sumber, yang masing-masing dapat memiliki permintaan atau kapasitas yang berbeda. Alokasi ini
dilakukan dengan mempertimbangkan biaya pengangkutan yang bervariasi karena jarak dan kondisi antar lokasi yang berbeda. Dengan menggunakan metode transportasi, dapat diperoleh suatu alokasi distribusi barang yang dapat meminimalkan total biaya transportasi (Susanta, 1994).
Model transportasi merupakan suatu teknik riset operasi yang dapat membantu dalam pembuatan keputusan-keputusan lokasi pabrik atau gudang. Model transportasi adalah suatu model penentuan lokasi untuk menentukan pola
2.5 Metode Penyelesaian Awal Least Cost
Metode Least Cost adalah metode yang membuat alokasi berdasarkan kepada biaya yang terendah. Metode ini menyusun tabel awal dengan cara pengalokasian distribusi barang dari sumber ke tujuan mulai dari sel yang memiliki biaya distribusi kecil. Metode ini merupakan sebuah pendekatan yang sederhana, yang menggunakan langkah-langkah berikut:
a. Identifikasi sel dengan biaya yang paling rendah. Pilih salah satu jika terdapat biaya yang sama.
b. Alokasikan unit sebanyak mungkin untuk sel tersebut tanpa melebihi pasokan atau permintaan. Kemudian coret kolom atau baris itu (atau keduanya) yang sudah penuh terisi.
c. Dapatkan sel dengan biaya yang paling rendah dari sisa sel (yang belum dicoret).
d. Ulangi langkah ke 2 dan 3 sampai semua unit habis dialokasikan.
2.6 Metode Penyelesaian Optimal Stepping Stone
Metode Stepping Stone atau metode batu loncatan merupakan langkah lanjutan dari salah satu metode dasar untuk mendapatkan solusi optimal yaitu total biaya minimum. Metode Stepping stone merubah alokasi produk untuk mendapatkan alokasi produksi yang optimal menggunakan cara trial and error atau coba – coba. Stepping Stone menguji optimalitas tabel awal dengan cara perhitungan Cij sel-sel
Beberapa hal penting yang perlu diperhatikan dalam penyusunan jalur Stepping Stone:
a. Arah yang diambil boleh searah atau berlawanan arah jarum jam. b. Hanya ada satu jalur tertutup untuk setiap kotak kosong.
c. Jalur harus mengikuti kotak terisi, kecuali pada kotak kosong yang sedang dievaluasi.
Langkah-langkah penyelesaiannya adalah sebagai berikut : 1. Pilihlah sel manapun yang tidak terisi untuk dievaluasi.
2. Telusurilah sebuah jalur tertutup yang kembali ke kotak awal melalui kotak-kotak yang sekarang ini yang sedang digunakan (yang diizinkan hanyalah gerakan vertikal dan horizontal). Walaupun demikian, boleh melangkahi kotak manapun baik kosong ataupun berisi.
3. Mulai dengan tanda plus (+) pada kotak yang tidak terpakai, tempatkan secara bergantian tanda plus dan tanda minus pada setiap kotak pada jalur yang tertutup yang baru saja dilalui.
4. Hitunglah indeks perbaikan dengan cara: pertama, menambahkan biaya unit yang ditemukan pada setiap kotak yang berisi tanda plus, dan kemudian dilanjutkan dengan mengurangi biaya unit pada setiap kotak berisi tanda minus. 5. Ulangi langkah 1 hingga 4 sampai semua indeks perbaikan untuk semua kotak yang tidak berisi sudah dihitung. Jika semua indeks yang dihitung lebih besar atau
sama dengan nol, maka solusi optimal sudah tercapai. Jika belum, maka solusi sekarang dapat terus ditingkatkan untuk mengurangi biaya pengiriman total.
2. 6 Redundansi dan Degenerasi
1.1 Latar Belakang
Masalah transportasi berhubungan dengan pendistribusian barang-barang dari beberapa sumber ke beberapa tujuan. Biasanya memiliki sejumlah kapasitas barang dari masing-masing sumber dan sejumlah kapasitas kebutuhan barang dari masing-masing daerah tujuan. Masalah pokok dalam alokasi pendistribusian produk adalah bagaimana caranya agar produk tersebut dapat melewati jalur–jalur tertentu, dari sumber–sumber yang menyediakan produk ke tempat–tempat tujuan, sehingga biaya yang dikeluarkan dapat ditekan seminimal mungkin. Pengiriman produk dapat dikatakan optimal jika didukung dengan adanya rencana pengalokasian yang tepat, sehingga akan menghasilkan biaya transportasi yang minimum.
Sasaran transportasi adalah mengalokasikan produk yang ada pada sumber asal sedemikian rupa hingga terpenuhi semua kebutuhan pada tempat tujuan. Sedangkan tujuan utama dari persoalan transportasi adalah untuk mencapai biaya yang serendah-rendahnya (minimum) atau mencapai keuntungan yang
sebesar-besarnya (maksimal). Persoalan transportasi terdapat pada pemilihan rute dalam jaringan distribusi produk antara pusat industri dan distribusi gudang atau antara distribusi gudang regional dan distribusi pengeluaran lokal. Dalam menggunakan metode transportasi, pihak manajemen mencari rute distribusi yang akan mengoptimalkan tujuan tertentu, misalnya tujuan meminimumkan total biaya transportasi, memaksimalkan laba, atau meminimumkan waktu yang digunakan.
Ada beberapa metode transportasi yang dapat digunakan untuk menyelesaikan masalah transportasi, di antaranya Metode Least Cost Combination dan Metode Stepping Stone. Metode transportasi yang digunakan
dengan menggunakan Metode Stepping Stone untuk membuktikan bahwa proses pengalokasian hasil produksi yang dilakukan sudah optimal.
PT. IT Master merupakan salah satu perusahaan distributor laptop yang ada di Sumatera Utara. Perusahaan ini mengirim laptop ke berbagai kota yang ada di Sumatera Utara. Dalam penelitian ini, sumber yang diteliti adalah dari kota Medan, Binjai dan Tebing Tinggi. Di mana barang akan didistribusikan ke kota-kota disekitarnya. Kota tujuan yang diteliti adalah Sibolga, Pematang Siantar, Tanjung Balai dan Sidikalang. Pengiriman dilakukan menggunakan kendaraan roda empat. Pada penelitian ini akan diteliti alokasi optimal dari sumber-sumber ke tujuan-tujuan agar biaya yang dihasilkan menjadi optimal.
Berdasarkan uraian di atas, penulis membuat judul mengenai Metode Transportasi yaitu Metode Least Cost Combination dan Metode Stepping Stone untuk menyelesaikan masalah transportasi, dengan mengambil tugas akhir yang berjudul Optimasi Biaya Distribusi Menggunakan Metode Least Cost dan Metode
Stepping Stone (Studi Kasus PT. IT Master).
1.2Perumusan Masalah
Berdasarkan latar belakang di atas, maka permasalahan dari penelitian ini dirumuskan bagaimana mengoptimalkan pengalokasian produk laptop PT. IT Master dan menentukan jumlah biaya minimum.
1.3Batasan Masalah
Batasan masalah dalam penelitian ini adalah:
3. Lokasi yang diteliti terdiri dari 3 sumber dan 4 tujuan.
1.4 Tujuan Penelitian
Tujuan dari penelitian ini adalah meminimumkan biaya distribusi laptop pada PT. IT Master yang dialokasikan secara optimal.
1.5Tinjauan Pustaka
Salah satu permasalahan khusus dalam program linier adalah masalah transportasi. Untuk menyelesaikan permasalahan ini digunakan metode transportasi. Dikatakan khusus, karena terletak pada karakteristik utama, yaitu bahwa masalah-masalah tersebut cenderung membutuhkan sejumlah pembatas dan variabel yang sangat banyak sehingga penggunaan komputer dalam menyelesaikan metode simpleksnya akan sangat mahal dibandingkan secara manual (Fien Zulfikarijah, 2003).
Metode transportasi digunakan untuk memecahkan masalah dalam dunia usaha seperti masalah pembelanjaan modal, analisis lokasi dan alokasi dana untuk investasi. Metode transportasi diharapkan mampu meminimumkan biaya tempat tujuan dengan biaya yang paling minimum. Masing-masing sumber tersebut mempunyai kapasitas pengiriman tertentu, sedangkan masing-masing tempat tujuan ini mempunyai permintaan dalam jumlah tertentu pula (M.N Nasution, 2008).
Metode transportasi merupakan bagian dari program linier yang digunakan untuk mengatur dan mendistribusikan sumber-sumber yang menyediakan produk ke tempat-tempat yang membutuhkan untuk mencapai efisiensi biaya transportasi. Alokasi produk harus memperhatikan biaya distribusi dari satu tempat ke tempat
menyamakannya ditambahkan variabel dummy dengan biaya distribusi sebesar nol (Andi Wijaya, 2012).
Menurut P. Sitorus, masalah transportasi untuk mencari nilai minimum dapat dirumuskan sebagai berikut:
=
Dengan kendala
= ; = 1,2,3, … ,
= ; = 1,2,3, … ,
Keterangan:
xij = jumlah barang yang harus diangkut dari tempat asal i ke tempat tujuan j
cij = biaya angkut per unit barang dari tempat asal i ke tempat tujuan j
si = banyaknya barang yang tersedia di tempat asal i
dj = banyaknya permintaan terhadap barang dari tempat tujuan j
i = sumber ke i
j = tujuan ke j
kedua, dan seterusnya sampai semua suplai yang dialokasikan memenuhi kebutuhan permintaan solusi awal mendekati solusi optimal. (Agus, 2008).
Langkah-langkah pada metode Least Cost Combination adalah (Andi Wijaya, 2012) :
a. Membuat tabel transportasi.
b. Dimulai dari mengisi sel pada biaya terendah dengan angka sebanyak-banyaknya yang disesuaikan dengan kapasitas dan permintaan (pilih yang paling kecil).
c. Lakukan langkah yang sama pada langkah b untuk mengisi sel-sel lain yang disesuaikan dengan kapasitas dan permintaan sampai seluruh kapasitas permintaan terpenuhi.
Metode Stepping Stone merupakan metode yang digunakan untuk menguji solusi awal yang telah dilakukan sebelumnya. Metode Stepping Stone ditemukan oleh W. W Cooper dan A. Charnes (Pangestu Subagyo dkk, 1984).
Langkah-langkah metode Stepping Stone adalah (Andi Wijaya, 2012) :
a. Mencari sel yang kosong
b. Melakukan loncatan pada sel yang terisi
Keterangan :
1. Loncatan dapat dilakukan secara vertikal atau horizontal.
2. Dalam suatu loncatan tidak boleh dilakukan lebih dari satu kali loncatan pada baris atau kolom yang sama tersebut.
3. Loncatan dapat dilakukan melewati sel lain selama sel tersebut terisi.
4. Setelah loncatan pada baris langkah selanjutnya pada kolom dan sebaliknya.
5. Jumlah loncatan bersifat genap.
6. Perhatikan sel yang terisi pada loncatan berikutnya untuk memastikan proses tidak terlambat
d. Perhitungan dilakukan dengan cara menghitung biaya, sel yang kosong diberi tanda positif selanjutnya negatif, positif, negative dan seterusnya. e. Apabila semua telah bernilai positif berarti solusi awal yang telah
dikerjakan sebelumnya telah menghasilkan biaya transportasi minimum, tetapi apabila masih terdapat nilai negatif, maka dicari nilai negatif terbesar (penghematan terbesar).
f. Apabila terdapat tanda negatif, alokasikan produk dengan melihat proses e,akan tetapi yang dilihat adaah isi dari sel tersebut. Tambahkan dan kurangkan dengan isi sel negatif terkecil pada seluruh sel.
g. Lakukan langkah yang sama dengan mengulang dari langkah b sampai hasil perhitungan biaya tidak ada bernilai negatif.
1.6Kontribusi Penelitian
Manfaat dari penelitian ini adalah sebagai berikut:
1. Membantu menentukan jumlah pengalokasian produk pada PT. IT Master agar biaya distribusi minimum.
2. Sebagai informasi bagi penelitian selanjutnya yang berhubungan dengan masalah transportasi.
1.7Metodologi Penelitian
Langkah-langkah yang akan dilakukan dalam menyelesaikan penelitian ini adalah :
1. Mencari literatur dari beberapa buku, jurnal dan karya tulis yang
berhuungan dengan Metode Least Cost Combination dan Metode Stepping Stone.
2. Pengumpulan Data
3. Pengolahan Data
Tahapan yang dilakukan dalam pengolahan data adalah sebagai berikut: a. Definisikan masalah yang dihadapi ke dalam model matematika
program linier.
b. Menyusun tabel transportasi awal.
c. Kembangkan penyelesaian awal dengan menggunakan Metode Least Cost Combination
d. Cari penyelesaian optimal dengan menggunakan Metode Stepping Stone
ABSTRAK
Masalah transportasi berhubungan dengan pendistribusian barang-barang dari beberapa sumber ke beberapa tujuan. Biasanya memiliki sejumlah kapasitas barang dari masing-masing sumber dan sejumlah kapasitas kebutuhan barang dari masing-masing daerah tujuan. Masalah pokok dalam alokasi pendistribusian produk adalah bagaimana caranya agar produk tersebut dapat melewati jalur–jalur tertentu, dari sumber–sumber yang menyediakan produk ke tempat–tempat tujuan, sehingga biaya yang dikeluarkan dapat ditekan seminimal mungkin. Tujuan penelitian ini adalah meminimumkan biaya distribusi laptop pada PT. IT Master menggunakan solusi awal Least Cost yang dilanjutkan dengan penyelesaian optimal menggunakan metode Stepping Stone. Hasil yang diperoleh dengan kombinasi metode transportasi ini adalah Rp51.425.000,00.
(Case Studi PT. IT Master)
ABSTRACT
Transportation problems relating to the distribution of goods from multiple sources to multiple destinations. Usually has a freight capacity of each source and the amount of capacity needs of goods from each region of interest. The main problems in the allocation of product distribution is how to make the product can pass through certain lines, from the sources that provide the products to places of interest, so the cost can be minimized. The purpose of this study is to minimize distribution costs at PT. IT Master laptops using Least Cost initial solution method, followed by optimal completion method Stepping Stone. The results obtained with the combination of transportation methods is Rp51.425.000,00..
SKRIPSI
PURNOMO S G PASARIBU
120803079
DEPARTEMEN MATEMATIKA
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar
Sarjana Sains
PURNOMO S G PASARIBU
120803079
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
Judul : Optimasi Biaya Distribusi Menggunakan Metode Least Cost dan Metode Stepping Stone (Studi Kasus PT. IT Master)
Kategori : Skripsi
Nama : Purnomo S G Pasaribu Nomor Induk Mahasiswa : 120803079
Program Studi : Sarjana (S1) Matematika Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam (FMIPA) Universitas Sumatera Utara
Diluluskan di
Medan, November 2016
Komisi Pembimbing:
Pembimbing 2, Pembimbing 1,
Dra. Normalina Napitupulu, M. Sc Drs. Marihat Situmorang, M.Kom NIP. 19631106 198902 2 001 NIP. 19631214 198903 1 001
Disetujui oleh:
OPTIMASI BIAYA DISTRIBUSI MENGGUNAKAN METODE LEAST
COST DAN METODE STEPPING STONE
(Studi Kasus PT. IT Master)
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil karya saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, November 2016
PURNOMO S G PASARIBU
Puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus dengan kasih dan berkatNya penulis dapat menyelesaikan penyusunan skripsi ini dengan judul Optimasi Biaya Distribusi Menggunakan Metode Least Cost dan Metode Stepping Stone (Studi Kasus PT. IT Master).
Terima kasih juga penulis sampaikan kepada :
1. Bapak Drs. Marihat Situmorang, M. Kom selaku pembimbing 1 dan Ibu Dra. Normalina Napitupulu, M. Sc selaku pembimbing 2 yang telah membimbing penulis selama penulisan skripsi ini.
2. Ibu Asima Manurung, S. Si, M. Si dan Bapak Dr. Pasukat Sembiring, M. Si selaku dosen penguji yang telah memberikan kritik dan saran yang membangun dalam penyempurnaan skripsi ini.
3. Bapak Prof. Dr. Tulus, M.Si. Ph.D dan Ibu Dr. Mardiningsih, M.Si selaku Ketua dan Sekretaris Departemen Matematika FMIPA-USU Medan.
4. Bapak Dr. Kerista Sebayang, M. S selaku Dekan FMIPA USU serta seluruh civitas akademika di lingkungan FMIPA USU.
5. Ayahanda Pontas Pasaribu dan Ibunda Patarida Sitanggang serta saudara dan saudari penulis Pryanto Pasaribu, Pendikary Pasaribu, Purwanto Pasaribu, Putra Pasaribu dan Penina Pasaribu yang selama ini memberikan bantuan dan dorongan kepada penulis.
6. Teman-teman saya Alosyus, Manotar, Fransiskus, Willy, Daniel, Ayen, Fauzi, Karsa, Samuel, Mega, Goklim, Oka, Agustina, Desi, Dedi dan
Mexander atas motivasi, semangat dan bantuannya dalam menyelesaikan tulisan ini.
ABSTRAK
Masalah transportasi berhubungan dengan pendistribusian barang-barang dari beberapa sumber ke beberapa tujuan. Biasanya memiliki sejumlah kapasitas barang dari masing-masing sumber dan sejumlah kapasitas kebutuhan barang dari masing-masing daerah tujuan. Masalah pokok dalam alokasi pendistribusian produk adalah bagaimana caranya agar produk tersebut dapat melewati jalur–jalur tertentu, dari sumber–sumber yang menyediakan produk ke tempat–tempat tujuan, sehingga biaya yang dikeluarkan dapat ditekan seminimal mungkin. Tujuan penelitian ini adalah meminimumkan biaya distribusi laptop pada PT. IT Master menggunakan solusi awal Least Cost yang dilanjutkan dengan penyelesaian optimal menggunakan metode Stepping Stone. Hasil yang diperoleh dengan kombinasi metode transportasi ini adalah Rp51.425.000,00.
(Case Studi PT. IT Master)
ABSTRACT
Transportation problems relating to the distribution of goods from multiple sources to multiple destinations. Usually has a freight capacity of each source and the amount of capacity needs of goods from each region of interest. The main problems in the allocation of product distribution is how to make the product can pass through certain lines, from the sources that provide the products to places of interest, so the cost can be minimized. The purpose of this study is to minimize distribution costs at PT. IT Master laptops using Least Cost initial solution method, followed by optimal completion method Stepping Stone. The results obtained with the combination of transportation methods is Rp51.425.000,00..
PERSETUJUAN i
1. 6 Kontribusi Penelitian 6
1. 7 Metodologi Penelitian 6
BAB 2 LANDASAN TEORI 8
2. Riset Operasi 8
2. 2 Program Linier 10
2. 3 Masalah Transportasi 11
2. 4 Metode Transportasi 13
2. 5 Metode Penyelesaian Awal 13
2. 6 Metode Penyelesaian Optimal 16
2. 7 redundansi dan Degenerasi 18
BAB 3 HASIL DAN PEMBAHASAN 20
3. 1 Gambaran Perusahaan 20
3. 2 Model Transportasi 20
Nomor Judul Halaman Tabel
3.1 Jumlah Laptop yang akan Dikirim dari Tempat Asal 21 3.2 Jumlah Permintaan di Tempat Tujuan
21 3.3 Tabel Biaya angkut dalam Tabel Transportasi (dalam rupiah) 21 3.4 Tabel Transportasi Awal dengan Dummy
3.11 Hasil Tahap Akhir dengan Metode Least Cost 26 3.12 Jumlah Biaya dan Alokasi dngan Metode Least Cost 27 3.13 Indeks Perbaikan Sel Kosong pada Tabel 3. 11 28 3.14 Hasil Tahap 1
30 3.15 Indeks Perbaikan Sel Kosong pada tabel 3. 14 30 3.16 Hasil Tahap 2
31 3.17 Indeks Perbaikan Sel yang Kosong pada Tabel 3.16 32 3.18 Hasil Tahap 3
33 3.19 Indeks Perbaikan Sel yang Kosong pada Tabel 3. 18 34 3.20 Hasil Tahap 4
35 3.21 Indeks Perbaikan Sel Kosong pada Tabel 3.20 35 3.22 Hasil Tahap 6
Nomor Judul Halaman Gambar
3.1 Jalur Pendistribusian Laptop Menggunakan Metode Least Cost 27
3.2 Loop pada Sel x25 29
3.3 Hasil Perbaikan Sel x25 29
3.4 Loop pada Sel x1dummy 31
3.5 Hasil Perbaikan Sel x1dummy 31
3.6 Loop pada Sel x15 32
3.7 Hasil Perbaikan Sel x15 33
3.8 Loop pada Sel x2dummy 34
3.9 Hasil Perbaikan Sel x2dummy 34
3.10 Loop pada Sel x27 36
3.11 Hasil Perbaikan Sel x27 36