Analisis kestabilan model penyebaran gonorrheae

ANALISIS KESTABILAN

MODEL PENYEBARAN, GONORRHEAE

Oleh:

AT1 ROHAYATI

JURUSAN MATEMATIKA

HAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

*

,

. .

RINGKASAN

. .

..

.

AT1 ROHAYATI. Analisis Kestabilan Model Penyebaran Gonorrheae. (Analysis of Stabil* on

Spread of Gonorrheae Modelf. Dibimbing oleh MUHAMMAD NUR AID1 dan PAlAN SIANTUN.

Gonorrheae merupakan sejenis penyakit kelamin yang disebabkan oleh bakteri gonococcus yang

menyebar melalui hubungan seksual. Penderita 'penyakit ini umumnya para pekerja seks atau mereka yang melakukan seks tak wajar. Penyakit ini memiliki karakteristik unik yang mendasar yakni tidak ada kekebalan, artinya bahwa bila penderita yang dinyatakan sembuh kemungkinan untuk terjangkit sangat besar dan setiap individu yang rentan akan terinfeksi jika berhubungan seksual dengan penderita penyakit

ini. Martin Braun (1975) membuat suatu model epide~nik Lentang penyebaran penyakit gonorrheae.

Pernodelan ini hanya menibahas penyebaran gonorrheae yang disebabkan oleh hubungan seksual lawan

jenis (heteroseksual).

Pada tulisan ini akan dibahas suatu analisis yang berguna untuk mengetahui kondisi kestabilan dan

pendekatan solusi kualitatif .model penyebaran gonorrheae, yaitu kecenderungan naik turunnya kurva

solusi, ha1 ini disebabkan oleh kondisi kestabilan model tersebut. Analisis kestabilan dilakukan dengan dua cara, yaitu secara analitik dan numerik. Solusi analitik dilakukan dengan metode isoklin dan solusi

numerik diperoleh berdasarkan diagram fase melalui bantuan sofhvare Locbif. Berdasarkan kedua cara

tersebut diperoleh hasil yang sama. Pendekatan solusi kualitatif model untuk mengetahui perkembangan penderita laki-laki atau perempuan berdasarkan kondisi-kondisi tertentu. Hal ini dilakukzn dengan

ANALISIS KESTABILAN MODEL PENYEBARAN GONORRHEAE

AT1 ROHAYATI

Skripsi

Sebagai salah satu syarat untuk ~ne~nperoleli

gelar

Sarjana Sains

Pada

Program Studi Mate~natika

JURUSAN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

Judul

:

Analisis Kestabilan Model Penyebaran

Gonorrheae

Nana

:

Ati Rohayati

NRP

:

GO5311727

Menyetujui,

Dr. Ir. Muhammad Nur Aidi. MS.

Pembimbing I

Dr. Paian Sianturi

Petnbimbing I1

Penulis dilalurkan dl Punvakarta pada tanggal 13 Mei 1976 sebagai anak penalla dari linua

bersaudan, anak dari pasangan Castluita dan Yoyoh Mal~n~udal~. Tallun 1988 penulis nlenyelesaikan

pendidikan dasar di SD Negeri Cilandak I, kenuudian pada taluun 1991 menyelesaikru~ pendidikan

~nenengal~ pertanla di

S M P

Negeri Calnpaka Punvakarta.

Tahun 1994 Penulis lulus dari SMA Negeri 2 Punvakarta dan pada taluun yang sama lulus seleksi masuk IPB nlelalui jalur Undangau Seleksi Masuk IPB. Penulis ~nenlilih Progranl Studi Matematika,

PRAKATA

Alhan~dulillah, puji dan syukur penulis panjatkan kepada Allah SWT atas segala ralunat &I

karunia-Nya, sellingga penulisan karya ilmiah ini dapat diselesaikan. Penulisan ini dilakukan sejak bulan

Septenlber 1999, dengan judul skripsi "Analisis KestabilanModel Penyebaran Gonorrheae".

Terima kasih penulis ucapkan kepada senlva pihak yang telah men~banlu peuyelesaian @a ilnliall

ini, antara lain kepada Bapak Dr. Ir. Mul~amnlad Nur Aidi, MS. dan Bapak Dr. Paian Sianturi selaku dosen pembinlbing, selta Ibu Dra. Farida tianurn yang telal~ memberikan saran. Ucapan terin~a kasih penulis sanlpaikan kepada Mainah, Bapak, Engkih dan Ema, Dede, Yeye, Utie, Oppie, Bapak dan Ibu Drs. Endi Suhendi (keluarga Kalijati), dan keluarga Wantilan alas segala do'a, dukuugan dan kasill

sayangnya. Selain itu terinla kasilt penulis ucapkan pada teman-leman, antara lain: Oni dan Sri (atas

pinjaman ko~nputenlya), Ade, Yuni, Cansilatie, Ifah, Inne, Enno, warga Barcela, anak-anak IMA AT-

TAQWA, Invan, anak-anak Matenlatika 32 dan 33, alas doa, persahabatan dan dukungamya.

Scn~oga m a ilnlial~ ini bennanfaal.

Bogor, April 2001

DAFTAR IS1

Halaman

DAFTAR GAMBAR

...

viii

I PENDAHULUAN

1.1 Latar Belakang

...

...

I

1.2 Tujuan Penulisan

...

1

1.3 Penjelasan Singkat tentang Gonorrheae

...

1

I1 LANDASAN TEORI

. .

2.1 Sistem Persamaan Linear Mandm

...

.

.

.

...

2

...

2.2 Pelinearan 2

. . .

2.3 Vektor Eigen dan Nlla~ Elgen ... 2 2.4 Bentuk Kanonik Jordan

...

2

2.5 Kestabilan Titik Tetap

. .

2.5.1 A n a l ~ s ~ s Kestabilan Titik Tetap

. .

...

....

...

3 2.5.2 Perilaku T l t ~ k Tetap ... 4 2.5.3 Bentuk Umum Kestabilan

...

4

...

2.6 Bidang Fase dan Orbit Solusi 6

...

2.7 Garis Isoklin dan Arah Gerak Solusi 6

...

111 PEMODELAN DINAMIKA PENYEBARAN GONORRHEAE 7

IV ANALISIS MODEL PENYEBARAN GONORRHEAE

4.1 Penentuan Titik Tetap

...

4.2 Matriks Jacobi

...

4.3 Analisis Kestabilan di Sekitar Titik Tetap

...

9

4.4 Plot Bidang Fase ...

4.5 Orbit dan Kestabilan Sist

4 Solusi Model

...

V KESIMPULAN

...

14

DAFTAR PUSTAKA

...

.

.

.

... 14

DAFTAR

GAMBAR

1. Bentuk umum kestabilan di sekitar titik tetap

untuk tipe nilai eigen real (a. Stabil, b. Takstabil, c. Sadel)

...

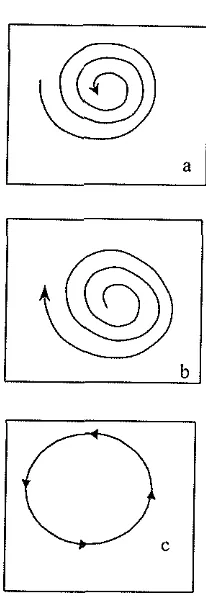
5

2. Bentuk umum kestabilan di sekitar titik tetap

...

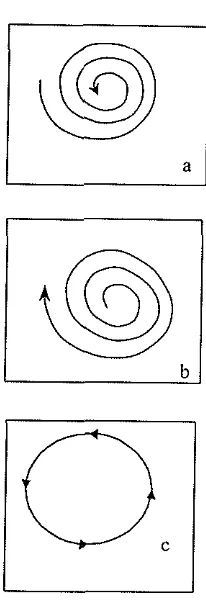
untuk tipe nilai eigen kompleks (a. Spiral stabil, b. Spiral takstabil, c. Stabil netral) 5

3. Isoklin dan kemiringan orbit yang melaluinya

...

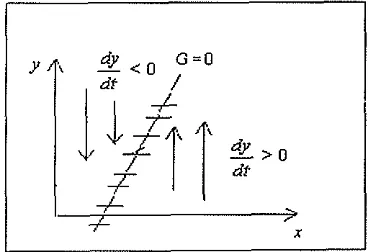
6

4. Isoklin F = 0 beserta arah gerak orbit

...

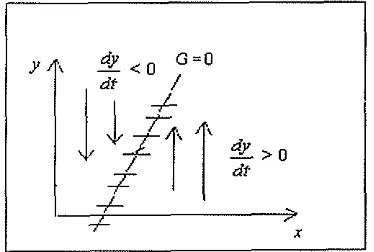
6

5 . Isoklin G = 0 beserta arah gerak orbit

...

.

.

.

.

...

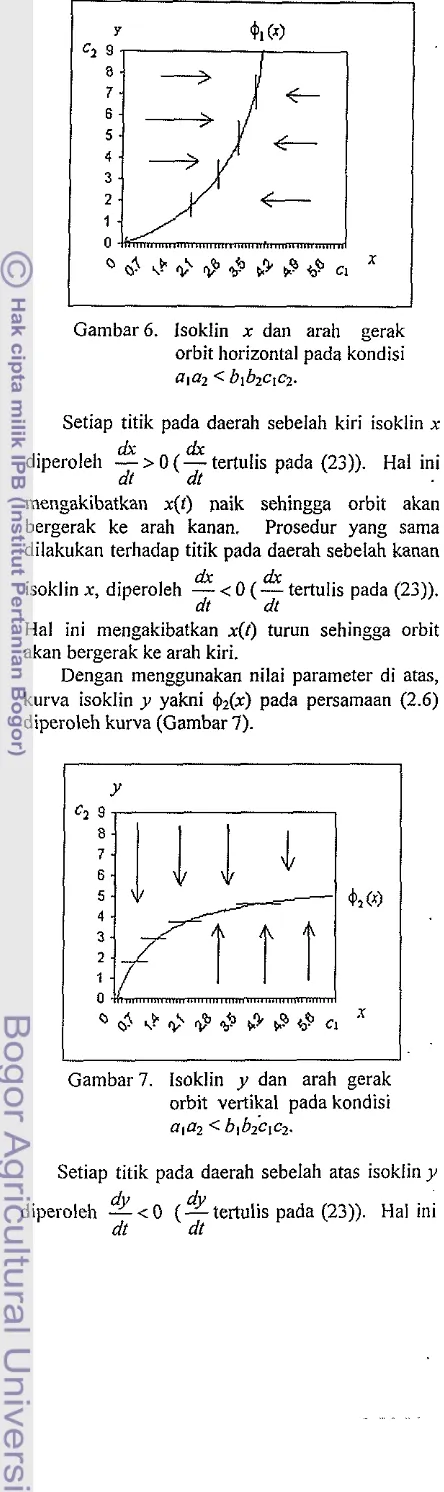
6

6. Isoklin x dan dan arah gerak orbit horizontal

pada kondisi a, a, < blb2cIc2

...

I0

7. Isoklin y dan dan arah gerak orbit horizontal

...

...

pada kondisi a, a, < blb2c1c2

.

.

.

.

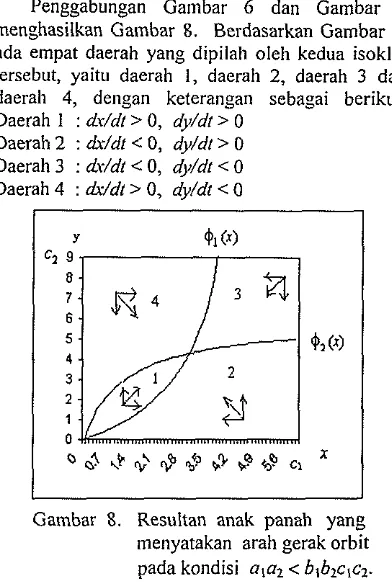
10

8. Resultan anak panah yang menyatakan arah gerak orbit

pada kondisi a , a, < blb2c,c2

...

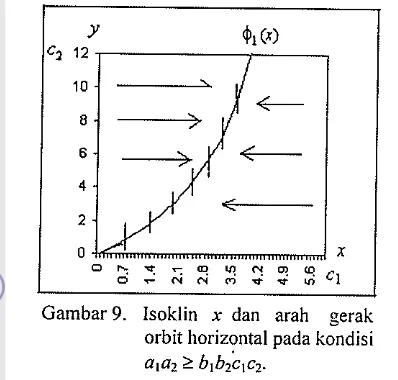
10

9. Isoklin x dan dan arah gerak orbit horizontal

pada kondisi a1 a2

>

blb2clc2 ... 1 I

10. Isoklin y dan dan arah gerak orbit horizontal

...

pada saat a l a2

>

blb2cIc2 1 1

11. Resultan anak panah yang menyatakan arah gerak orbit

pada kondisi a, a2 2 blb2clc2

...

11

12. Orbit penderita laki-laki ( x ) dan penderita perempuan

pada kondisi a, a2 < blb2clc2

...

12

I Orbit penderita laki-laki (x) dan penderita perempuan

...

...

pada kondisi a, a2

>

blb2cIc2

.

.

.

.

12

14. Perkembangan penderita laki-laki (x)

kondisi a l a2 < blb2cIc2

...

13

15. Perkembangan penderita perempuan (Y)

pada kondisi a, a,

<

blb2clc2

...

13

16. Perkembangan penderita laki-laki (x)

...

padakondisi a,a2 2 b,b2c,c 13

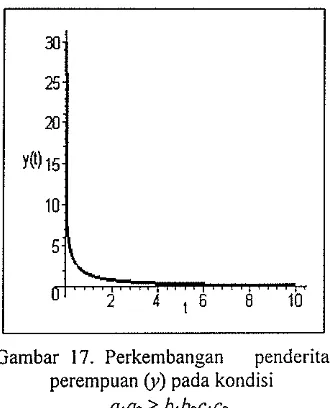
17. Perkembangan penderita perempuan (v)

I. PENDAHULUAN

1.1 L a t a r belakang

Meningkatnya jumlah penderita penyakit yang

disebabkan oleh hubungan seksual seperti

gonorrheae, cl~lamydia, syphilis dan AIDS merupakan masalah utama di bidang kesehatan pada negara maju maupun negara berkembang. Sebagai contoh, di Amerika Serikat setiap tahunnya lebih dari dua juta orang menderita

penyakit gonorrheae. Jumlah tersebut jauti lebih

besar dari total penderita penyakit lainnya [Fahmi, S. 19971.

Penderita penyakit gonorrheae ini umumnya

para pekerja seks dan mereka yang melakukan seks tak wajar. Untuk mengetahui apakah seseorang tersebut terjangkit atau tidaknya, dibutuhkan waktu

yang cukup lama. Hal ini disebabkan masa

terinfeksinya yang cukup lama.

Seseorang yang telah dinyatakan sembuh dari

penyakit gonorrheae ini kemungkinan

terjangkitnya kembali sangat besar, karena belum ditemukannya vaksin pencegah penyakit tersebut.

Pennasalahan tersebut merupakan masalah yang menarik untuk dimodelkan. Oleh karena itu diperkenalkan model epidemik sederhana yang menggambarkan penyebarannya.

Sehubungan dengan masalah penyebaran dari

penyakit gonorrheae ini, maka pada tulisan ini

akan dibuat suatu analisis yang membahas kestabilan dan solusi model dinamik penyebaran gonorrheae berdasarkan diagram fase. Analisis

kualitatif model penyebaran gonorrheae dilakukan

karena model tersebut merupakan sistem

persamaan diferensial taklinear yang terlalu rumit untuk diaualisis secara kuantitatif.

Analisis kualitatif model penyebaran

gonorrheae ini dilakukan melalui pendekatan sistem dinamik dengan menggunakan bantuan sofhvarc Locbif dan Maple.

1.2 Tujuan Penulisan

Tujuan penulisan karya ilmiah ini adalah untuk ~nenganalisis kestabilan dan menganalisis solusi kualitatif dari model dinamik penyebaran gonorrl?eae.

1.3 Penjelasan Singkat tentang Gonorrlreae

Gonorrheae adalah sejenis penyakit kelamin

yang disebabkan oleh bakteri gonococcus yang

menyebar melalui hubungan seksual. Bakteri gonococcus ini ditemukan oleh Neisser pada tahun

1879. Gonococcus termasuk golongan diplokok

(Genus bakteri dari famili Actabacillaceae yang

terdiri dari dua sel kokkus yang kembar), berbentuk biji kopi dengan lebar 0.8 dan panjang

1.6 p. Bakteri ini bersifat negatif-Gram (dinding

sel bakteri mempunyai kandungan lipida yang tinggi), bersifat tahan asam, tampak di luar dan di dalam leukosit, tidak tahan lama di udara bebas, cepat mati pada keadaan kering, tidak tahan suhu di atas 39°C dan tidak tahan zat disinfektan (anti

kuman / pembersih).

Daerah yang paling mudah terinfeksi adalah daerah dengan mukosa epitel kuhoid atau lapis gepeng yang belum berkembang (imatur), yakni pada vagina wanita sebelum pubertas. Masa tunas gonorrheae sangat singkat, pada pria umumnya

berkisar antara 2 - 5 hari, kadang-kadang lebih

lama. Sedangkan pada wanita masa tunas

gonorrheae sulit untuk ditentukan karena pada umumnya bersifat asimtomatik (berubah-ubah).

Pada pria, kuman masuk ke uretra. Hal ini akan menimbulkan radang pada uretra (uretritis), yang paling sering adalah uretritis anterior akuta dan dapat menjalar ke proksimal (depan atau ujung pangkal) yang mengakibatkan komplikasi lokal, asenden (menuju ke depan) dan diseminata (pangkal uretra). Keluhan subyektif berupa rasa gatal, panas di bagian distal (pangkal) uretra di

sekitar lubang luar uretra, kemudian disusul

disuria, polakisuria, keluar cairan dari ujung uretra yang kadang-kadang disertai darah, dapat pula disertai nyeri pada waktu ereksi. Pada beberapa kasus dapat terjadi pembesaran kelenjar getah

bening. lnfeksi pada wanita, pada mulanya

hanya mengenai leher rahim, kadang-kadang menimbulkan rasa nyeri pada panggul bawah.

Diagnosa pada penyakit ini dilakukan atas dasar perbandingan, pemeriksaan klinis dan pemeriksaan pembantu. Secara epidemiologis pengobatan yang dianjurkan adalah obat dengan dosis tunggal. Jika tidak diobati dengan segera akan mengakibatkan kemandulan, cacat, gangguan pertumbuhan, radang sendi, kanker bahkan juga kematian.

11.

LANDASAN TEORI

2.1 Sistem Persamaan Diferensial Linear

Mandiri n111 ... "'I,,

Perhatikan sistem persamaan diferensial (SPD) berikut ini:

dengan fungsi ~ ( x ) mempunyai sifat

XI =

h

(xi (tb

...

>X.(f)) lim,,, cp(x) = 0. Bentuk Mx disebut pelinearan

i 2 =

f2

(11 (11, ... ,.,,(I)) dari (4).

(1) [Tu, 19941

dengan

fi, fi,

...

,

sebagai fungsi dari

XI (I), x 2 (t);.., x,, (I), yang kontinu, bernilai real,

dan mempunyai turunan parsial kontinu disebut sistem persamaan diferensial mandiri, karena perubahan x dan y dinyatakan sebagai fungsi dari x

dan y sendiri yang tidak mengandung t secara

eksplisit.

Sistem persamaan diferensial mandiri dapat dinyatakan dalam bentuk matriks berikut:

x = A x (2)

.

_,

dengan x =

11,

. . = ! I , d a n A a d a l a b

x,,

x,, matriks berukuran nxn.

[Hasibuan, 19891

Definisi: (Titik Tetap)

Sisteln persamaan diferensial (1) dapat ditulis

dalam bentuk :

i = f ( x ) (3)

dengan

f

fungsi yang terturunkan. ~ i t i k x ' dengan

x = 0 disebut titik h i t i s atau titik tetap.

f(')

[Tu, 19941

2.2 Pelinearan

Dengan menggunakan perluasan Taylor pada suatu titik tetap x', maka diperoleh persamaan

berikut :

k

= Mx

+

cp(x), ₍₄₎

dengan M inatriks Jacobi, yaitu

M E D f (x') E

D

f (x)IF.".

2.3 Vektor Eigen d a n Nilai Eigen

Misalkan A matriks berukuran nxn, maka suatu vektor taknol X di R" disebut vekror eigen dari A, jika untuk suatu skalar h, yang disebut nilai eigen dari A, berlaku:

Ax=

M.

Vektor X disebut vektor eigen yang bersesuaian dengan nilai eigen h. Untuk mencari nilai eigen

dari matriks A yang berukuran nxn maka

persamaan AX =

LY

dapat dituliskan kembali

sebagai berikut:

A X = A X ~ ( A - X I ) = O

Persamaan terakhir akan mempunyai solusi tak-no1

jika dan banya jika :

det (A-hl) = /A-A4 = 0 ₍₅₎

Persamaan (5) disebut persamaan karakreristik dari A.

[Anton, H., 199.51

2.4 Bentuk Kanonik J o r d a n

Misalkan diberikan sistem

-

persamaan

-

diferensial dua dimensi untuk A =

I:::

1::

J

mempunyai persamaan karakteristik sebagai

berikut :

C(h) = d e t ( A - X I ) = h 2 - y h + 6 = 0

dengan y = a l l + a2, dan S = det (A)

-

- all a22-a12 021.

Nilai eigen yang diperoleh dari persamaan karakteristik di atas adalah:

( 6 )

Misalkan matriks real Pzx2 mempunyai

balikan sehingga P.'AP = J, dengan J adalah

salah satu dari matriks dalam bentuk kanonik

Jordan :

Dalam penjelasan selanjutnya, bentuk kanonik Jordan (i), (ii) dan (iii) akan disebut Jordanl, Jordan2, dan Jordan3. Bentuk Jordan1 adalah kasus

untuk dua nilai eigen real yang berbeda (XI # h2).

Bentuk Jordan2 adalah kasus untuk dua nilai eigen

yang sama yaitu: h l = h 2 = h =

1

, dengan

y'=

46.

2

Bentuk Jordan3 adalah kasus untuk nilai eigen Y

kompleks yaitu hl,,= a

+

ip, dengan a =

-,

dan

2

, 3 46-y 2 7

,

a dan (3 keduanya bernilai real

2

dengan

P

> 0. J adalah matriks simetrik dengan

elemen diagonalnya adalah bagian real dari nilai eigen dan elemen yang bukan diagonal adalah bagian imajiner dari nilai eigen.

[Tu, 19941

2.5 Kestabilan Titik Tetap

2.5.1 Analisis Kestabilan Titik Tetap

Analisis kestabilan titik tetap berdasarkan nilai eigen dilakukan dengan cara menganalisis nilai eigen tersebut. Perhatikan nilai eigen pada

persamaan (6). Ada beberapa kasus untuk

menganalisis kestabilan titik tetap, tergantung

pada nilai y2

-

46.

KASUS 1 (y2 -46)> 0

Nilai eigen yang diperoleh adalah real dan

berbeda (hl =L hz), dengan bentuk kanonik Jordan

i

=[hl

O

1.

Solusi umum yang diperoleh

0 h2

adalah :

A? r

x(t)= C, v, cA1' +C2 v2

"

₍₇₎

dengan Al dan

A,

adalah nilai eigen dari matriks

Jacobi, v , dan v2 berturut-turut adalah vektor eigen

yang bersesuaian dengan nilai eigen.

Pada kasus ini kestabilan titik tetap

mempunyai 3 sifat yaitu:

I . Bila kedua nilai eigennya negatif (hl < 0 dan

h2 < 0), maka diperoleh nilai y < 0 dan 6 > 0.

Dari solusi (7) diperoleh bahwa jika t

mendekati takhingga maka x mendekati no1 sehingga titik tetap bersifat stabil.

2. Bila semua nilai eigennya bernilai positif

( h , > 0 dan h2 > 0), maka diperoleh nilai y > 0

dan 6 > 0. Dari solusi (7) diperoleh bahwa

jika 1 mendekati takhingga maka x mendekati

takhingga. Hal ini menunjukkan bahwa x(t) merupakan titik tetap bersifat takstabil.

3. Bila nilai eigennya berlainan tanda (misalkan

A, < 0 <

h2

), maka diperoleh nilai 7 < 0 dan 6

<

0. Dari solusi (7) diperoleli bahwa jika 1

mendekati takhingga maka x(t) mendekati takhingga, sehingga lintasan kurva membentuk

suatu asimtot pada bidang v , dan 12. Titik

tetap ini bersifat titik sadel dan bersifat titik takstabil.

KASUS2 (y2-46)=0

Nilai eigen yang diperoleh nilai eigen real ganda ( & I = h2= h), dengan bentuk kanonik Jordan

J

=[h

I]. Bentuk solusi umumnya adalah:

0 A

x(t) = (c, + c 2 1)

2'

₍₈₎

Pada kasus ini kestabilan titik tetap

mempunyai 2 sifat, antara lain:

1. Bila kedua nilai eigen negatif (i., < 0 dan

h2 < 0). Dari solusi (8) diperoleh bahwa jika r

mendekati takhingga maka x(l) menuju nol, sehingga titik tetap bersifat stabil.

2. Bila nilai eigen bernilai positif (i., > 0 dan

2.1 > 0). Dari solusi (8) diperoleh bahwa jika I

mendekati takhingga maka x(r) menuju takhingga sehingga titik tetap tersebut bersifat takstabil.

KASUS 3 (y2 -46)< 0

Pada kasus ini nilai eigen yang diperoleh

adalah nilai eigen kompleks dengan bentuk _{- -}

kanonik Jordan J =

!I.

Misalhn nilai

eigen yang diperoleh adalah = a

+

iP ( a # 0,

p

# O), dengan a dan

P

adalah bilangan real dan

p

> 0. Sistem yang mempunyai nilai eigen a

+

iP

dapat dilambangkan dengan

x

,

dengan .? =

[:

1

$=[-;

PI-

atau dalarn bentuk skalar adalah:

Dalam bentuk koordinat polar, x l dan x? dapat

dinyatakan dalam bentuk x, = r cos (8) dan

menghasilkan

Dengan menurunkan (10) terhadap waktu t akan

diperoleh :

Kemudian jika persamaan (9) disubstitusikan ke dalam persamaan (12) maka diperoleh:

Dengan menurunkan (1 1) terhadap t, maka akan diperoleh:

Bentuk x12sec2(8) dapat diperoleh dari persamaan (10) dan (11) yang menghasilkan

x12sec2(@)= r 2 . Kemudian dengan

lnensubstitusikan persamaan (9) dan

xI2sec2 (€I)= r 2 ke dalam persamaan (14) maka

diperoleh:

Solusi di atas mempunyai beberapa kasus yang

hergantung pada nilai a dan

0

seperti pada

persamaan (13) dan (15) yaitu: a. a < O

Jika

a

< 0 maka r(f) pada persamaan (13)

berkurang pada saat t bertambah. Jika

0

> 0

Inaka @(1) pada persamaan (15) akan

berkurang, pada saat t semakin hesar, sehingga arali gerak orbit akan hergerak searah jamm

jam lnenuju titik tetap. Jika

p

< 0 maka arah

gerak orbit berlawanan dengan arab jarum jam

menuju titik tetap. Dalam ha1 ini titik tetap merupakan titik tetap bersifat spiral srabil.

b. azO

Jika a > 0 maka r(t) pada persamaan (13) akan

bertamhah pada saat t semakin besar. Jika

p

> 0 maka B(t) pada persamaan (15) akan berkurang, pada saat t semakin besar. sehingga arah gerak orbit akan bergerak searah jamm

jam menjauhi titik tetap. Jika

P <

0 maka arah

gerak orbit akan bergerak berlawanan dengan

arah jarum jam menjauhi titik tetap. Titik

tetap tersehut hersifat spiral fakrfabil. c. a=O

Jika a = 0 maka r(f) pada persamaan (13) tidak

berubah sepanjang waktu. Jika

P

< 0 maka €I(!)

pada persamaan (15) akan naik, dan jika

p

> 0

maka e(t) akan turun. Karena r(t) tetap maka gerak orbit membentuk suatu lingkaran dengan titik tetap sebagai pusat. Titik tetzp tersehut bersifat slabil nefral.

2.5.2 Perilaltu Titik Tetap

Berdasarkan uraian di atas maka dapat

disimpulkan hahwa kestabilan titik tetap

mempunyai 3 perilaku, yaitu:

I . Stahil jika:

a. Setiap nilai eigen real adalah negatif

(A;< 0 untuk semua I].

h. Setiap komponen real nilai eigen

kompleks adalah takpositif, (Re (A, )

< 0

untuk semua I ] .

2. Takstabil jika:

a. Setiap nilai eigen real adalah positif

(Ai> 0 untuk semua I].

b. Setiap komponen real nilai eigen

kompleks adalah positif, (Re (A, ) > 0

untuk semua I ] .

3. Sadel jika:

Perkalian dua buah nilai eigen real sembarang

adalah negatif (A; A, < 0, untuk i dan j

sembarang). Titik tetap sadel ini bersifat

takstabil.

2.5.3 Bentuk Umum Kestabilan

Bentuk ulnum kestabilan di sekitar titik tetap herdasarkan perilaku orbit di sekitarnya, dibedakan berdasarkan dua tipe nilai eigen, nilai eigen real dan nilai eigen kompleks.

Bentuk umum kestabilan untuk tipe nilai eigen real adalah:

1. Jika setiap orbit mendekati titik tetap, maka

2. Jika setiap orbit bergerak menjauhi titik tetap, maka titik tetap itu disebut titik tetap takstabil. Tipe ini ditunjukkan oleh Gambar

1 .b.

3. Jika ada orbit yang bergerak mendekati dan

ada orbit yang menjauhi titik tetap, maka titik tetap itu disebut titik pelana (sadel). Tipe ini ditunjukkan oleh Gambar 1.c.

Bentuk umum kestabilan untuk tipe nilai eigen kompleks adalah:

1. Jika setiap orbit mendekati titik tetap secara

spiral, maka titik tetap tersebut merupakan titik tetap spiral stabil. Tipe ini ditunjukkan ole11 Gambar 2.a.

2. Jika setiap orbit ~nenjauhi titik tetap secara

spiral, lnaka titik tetap tersebut merupakan

titik tetap spiral takstabil. Tipe ini

ditunjukkan oleh Gambar 2.b.

3. jika orbit-orbit bergerak mengelilingi titik

tetap sehingga membentuk kurva tertutup, maka titik tetap tersebut merupakan titik tetap

[image:13.599.53.516.55.820.2] [image:13.599.353.456.70.370.2]

stabil netral. Tipe ini ditunjukkan oleh

Gambar 2.c.

[Hasibuan, K. M. 19891

Teorema Kestabilan

Misalkan x = Ax adalab suatu sistem

persamaan diferensial dengan A matriks real

berukuran 2x2. Misalkan juga persamaan

karakteristik dari matriks A diberikan oleh h 2 + B h + C = 0 , d e n g a n B = t r ( ~ ) dan C = d e t A . Kestabilan sistem persamaan diferensial di atas diperoleh dari:

1. Jika B > 0 dan C > 0, maka titik tetap bersifat

stabil.

2. Jika B < 0 dan C > 0, maka titik tetap bersifat

tak-stabil.

3. Jika C < 0, maka titik tetap bersifat sadel

takstabil.

4. Jika B = 0 dan C > 0, maka titik tetap bersifat

stabil netral.

Bukti : [Indaryani, L. 19991

Gambar 2. Bentuk umum kestabilan titik tetap untuk tipe nilai eigen kompleks (a. Spiral stabil, b. Spiral takstabil, c. Stabil netral).

2.6 Bidang Fase dan Orbit Solusi

Perhatikan sistem persamaan diferensial berikut ini:

Solusi sistem persamaan diferensial (16)

lnelnbentuk suatu kurva berdimensi 3 dengan

koordinat (t,x,y). Karena secara eksplisit t tidak ada

dalam sistem tersebut, maka setiap solusi sistem

(16) untuk to < t < t, membentuk kurva di bidang

(x, y), atau jika t bergerak dari to ke t,, gugus titik-

titik (x(t), y(t)) membentuk suatu kurva di bidang

(x, y). Kurva ini disebut orbit (trayektori) yang merupakan solusi persamaan (16). Sedangkan bidang (x, y) disebut bidang fuse solusi tersebut. Dengan kata lain orbit solusi suatu sistem persamaan diferensial adalah lintasan yang dilakukan oleh solusi di bidang (x, y).

[Hasibuan, K. M. 19891

[image:14.605.321.504.77.224.2]

2.7 Garis Isnklin dan Arah Gerak Solusi

Kurva dengan F (xa) = k, k konstanta, disebut

suatu isoklin dari persamaan diferensial(l6). Salah satu cara untuk memperoleh gambaran orbit sistem persamaan diferensial (SPD) (16), terutama untuk persamaan diferensial yang solusi persamaan diferensialnya tidak dapat dicari secara eksplisit, adalah dengan menggunakan metode

isoklin dan arah gerak solusi. Hal ini dapat

dilakukan karena SPD (16) membentuk suatu

medan arah di bidang (x, y), sehingga orbit yang

baik dapat diperoleh dengan cara memplot sejumlah kemiringan orbit pada titik-titik di bidang fase.

Isoklin-isoklin dari persamaan (16) adalah

kurva yang seluruh unsur-unsur garisnya

melnpunyai kemiringan tertentu. Jadi setiap orbit solusi suatu persamaan diferensial yang melalui suatu isoklinnya memiliki kemiringan yang sama.

Misalkan 0 adalah sudut antara arah gerak orbit yang terletak pada garis isoklin terhadap sumbu x. Ada dua isoklin yang paling penting,

yaitu isoklin &/dt = 0 yang berpadanan dengan

B

= ~ 1 2 , dan isoklin &/dt = 0 yang berpadanan

dengan 0 = 0. Perhatikan Gambar 3 berikut ini:

[image:14.605.314.502.388.519.2]

I I

Gambar 3. Isoklin dan kemiringan orbit

yang melaluinya

Pada isoklin F = 0 dengan 0 = xni, orbit

lnemiliki arah gerak vertikal karena x tetap.

Sedangkan pada isoklin G = 0 dengan 0 = 0, orbit

memiliki arah gerak horizontal karena y tetap. Dari penjelasan tadi diperoleh bahwa

-- ok - F = 0 atau

-

&

= G = 0 pada garis isoklin.

dt dl

dr

_dv

Akibatnya, nilai

-

atau - menjadi negatif

dt dt

~.. ...

[image:14.605.318.505.546.672.2]

pada salah satu daerah yang dipilah oleh garis isoklin. Perhatikan arah panah pada Gambar 4 dan

Gambar 5.

I I

Gambar 4. Isoklin F = 0 beserta arah gerak orbit

Arah gerak orbit pada suatu anak gugus _{resultan anak panah pada kedua isoklin tersebut.}

bidang fase (x, y), ditentukan berdasarkan nilai _{[Hasibuan, K. M. 19891}

111

PEMODELAN DINAMIK PENYEBARAN

GONORRHEAE

Model penyebaran gonorrheae dikembangkan oleh Martin Braun (1975). Asurnsi dari pemodelan ini adalah sebagai berikut:

I. Penyebaratlnya melalui hubungan seksual lawan jenis (heteroseksual).

2. Setiap individu yang rentan akan tertular jika

berhubungan seksual dengan orang yang terinfeksi gonor-rheae.

3. Conorrheae tidak memberikan kekebalan

terhadap penderita yang telah melakukan pengobatan, artinya bahwa kemungkinan terinfeksinya kembali masih ada.

4. Setelah pengobatan, penderita tidak

berinteraksi (berhubungan seksual) lagi

dengan orang yang terinfeksi.

Perhatikan sistem persamaan diferensial berikut:

dengan,

nlr

-

: laju pe~?umbuhan penderita laki-laki per

cN

satuan waktu

: laju pe~tumbuhan penderita perempuan

dl

per satuan waktu.

x : banyaknya penderita laki-laki.

y : banyaknya penderita perempuan.

a , : tingkat keberhasilan pengobatan penderita

laki-laki.

o2 : tingkat keberhasilan pengobatan penderita

perempuan.

b~ : tingkat resiko penularan terhadap laki-

laki.

b~ : tingkat resiko penularan terhadap

perempuan

C I : banyaknya populasi laki-laki.

cz : banyaknya populasi perempuan.

c l

-x

: banyaknya populasi laki-laki yang

mudah tertular (rentan).

c?

-

y : banyaknya populasi perempuan yang

mudah tertular (rentan).

Menurut Martin Braun (1975), kondisi yang

biasanya dipenuhi adalah al > q, yakni tingkat

keberhasilan pengobatan penderita laki-laki lebih besar daripada tingkat keberhasilan pengobatan

penderita perernpuan, karena jika laki-laki

terinfeksi maka gejalanya akan cepat timbul,

dengan demikian akan cepat melakukan

pengobatan.

Nilai-nilai a l , a2, b l , b,, c l , c,, x dan y selalu positif, dengan 0 < x < c, dan 0 < y < c,. Nilai-

nilai al,a2 masing-masing sebanding dengan

banyaknya populasi laki-laki dan perempuan. Nilai-nilai bl, b, masing-masing sebanding dengan banyaknya populasi laki-laki atau perempuan yang mudah tertular (rentan) dan banyaknya penderita laki-laki atau penderita perempuan.

Nilai-nilai parameter a,, a>, b13 b~ yang

IV. ANALISIS MODEL DINAMIK PENYEBARAN GONORRHEAE

4.1 Penentuan Titik Tetap

Pemodelan ini hanya didefinisikan pada kuadran pertama, dengan demikian titik tetap pada model ini didefioisikan pada kuadran pertama, dengan kata lain terjadi keseimbangai~ positif, karena x(t) dan At) tidak pernah negatif. Nilai- nilai x(t) dan At) masing-masing tidak pernah

melebihi

c l

dan

c2.

Perhatikan sistem persamaan diferensial (17).

cl:

dY

Titik tetap diperoleh apabila

-

=

-

= 0 , atau

dt dl

dari persamaan (18) dan (19) diperoleh:

'IX dan x = '7, Y

=

b, (c,

-

x)

b2(~2

-Y) (20)

Dengan mensubstitusikan nilai y ke dalain

persamaan x =

,

maka diperoleh:

b2

( ~ 2

-

Y )

Kemudian nilai x disubstitusikan ke dalam

persamaan y = bl (cl alx maka diperoleh:

Dari sistem persamaan diferensial (17) diperoleh dua titik tetap, yaitu:

TI

(x, y) = (0, 0) dan

T2

(x, 11) =

T2

(x',

Dengan x' dan y' sesuai dengan persamaan (21) dan (22) di atas.

Selanjutnya dari kedua titik tetap yang

diperoleh, akan ditinjau dua kasus yang

membedakan nilai komponen petnbilang pada persamaan (21) dan (22) yakni:

1. Kasus

a,@

<

b,b2c,c2

Pada kondisi ini, titik tetap yang diperoleh

ada dua, yaitu

TI

dan

T2,

karena

T2

bernilai

positif dan berada pada kuadran pertama.

2. Kasus ala2

>

blb2cIc2

Pada kondisi ini, titik tetap yang diperoleh hanya ada satu, yaitu titik tetap TI. Titik tetap

T2

bemilai negatif (1' < 0 dan

y'

< 0) dan tidak berada pada kuadran pertama. Oleh

karena itu,

T2

tidak akan dibahas.

4.2 Matriks Jacobi

Perhatikan persamaan (IS) dan (19) yang dapat dituliskan kembali berikut ini:

Dengan melakukan pelinearan pada sistem

persamaan diferensial (23) maka akan diperoleh

matriks Jacobi berikut ini :

Untuk titik tetap TI : (0,0), diperoleh matriks

Jacobi berikut ini :

Untuk titik tetap

Tz

(xa) = (x', ye), diperolell

matriks Jacobi sebagai berikut:

J. = [ - q - 4 ~

k-b]

dengan

Jika a102 < blb2cIcZ, maka B = - Gll+ ja2) > 0 dan

C =

GI

I j12) -

GI,

j2,) > 0. Berdasarkan Teorema

Kestabilan pada 2.5.3, titik tetap T2 bersifat stabil.

b. Kasus ala2 2 blb2cIca

Pada kasus ini, sistem persamaan diferensial (17) hanya memiliki satu titik tetao vaitu titik tetao

TI (0,0), karena T2 berada di 'liar kuadran

i.

j 1 2 = ~ I ~ Z C I (b1c2 + a ~ ) - b l (h b 2 ~ 1 ~ 2 -ala2) Perhatikan nilai eigen pada persamaan (24), karena

b2 (b1~2 + 01 ) ala2 2 blb2clc2 maka diperoleh kedua nilai eigen

negatif (hl < 0 dan ha < 0). Berdasarkan definisi

blbzc2(b?c1 +a2)-bz(bib2~1~2 -0102)

,

dan kestabilan (lihat 2.5.1 pada landasan teori), titik

J21 =

-

bi(b2 CI + a d tetap TI (0,O) bersifat stabil.

4.4 Plot Bidang Fase

Perhatikan kembali sisteln persamaan

diferensial (23). Definisikan isoklin 41(x) adalah

dr

kurva

f

(xa) = 0, yaitu yang tnemenuhi

-

= 0,

4.3 Analisis Kestabilan di Sekitar Titik Tetap dl

Analisis kestabilan pada titik tetap untuk sehinggamenghasi'kan:

sisteln persamaan diferensial (17) dibagi menjadi

dua kasus yaitu kasus yang telah dijelaskan pada _{Y= -- a'x}

-

_4!(x).

sub bab 4.1, yakni: (CI - X) (25)

a. Kasus ala2 ; blb2cIc2 Persamaan ini disebut isoklinx.

Pada kasus ini terdapat aua titik tetap, TI (0,O)

dan T, (x'a'). Definisikan isoklin 4?(x) adalah kurva

Dari rnatriks Jl di atas diperoleh persamaan

karakteristik di bawah ini: g (xa) = 0, yaitu kurva yang memenuhi d~ = 0,

(11

C(h) = det (J,-hl) = 0 _{sehingga menghasilkan:}

(-al - A) (-a2-h)

-

blclb2c2 = 0

A'+ (al+a2) A+ ala2- blb2c1c2=0 _bzc2x

Dari persatnaan karakteristik ini diperoleh:

= (02

+

b2X) = dz(x). (26)

2

-(a, +9)+d(al +a2) -4(oIa2 -6,b2CIC2)) (24,) Persamaan ini disebut isoklin y

Jika ala2

<

blb2clc2, maka diperoleh nilai

eigen bernilai A, < 0 dan h2 > 0. Berdasarkan

definisi kestabilan (liliat 2.5.1 pada landasan

teori), titik tetap TI bersifat sadel takstabil. Dari ~natriks J2 untuk titik tetap T,, maka akan diperoleh persamaan karakteristik berikut ini:

C(A) = det (J2-hl) = 0 .

A'-0

1 1

+.

122) 1 +

O'II

J Z Z ) - G I ~ J Z I ) = 0 Persa~naan karakteristik di atas analog dengan

bentuk persamaan h% B h + C = 0,

di~nana : B =

-

GI

jZ2) dan

C =

0'11

~ z ~ ) - G I z

jd.

Selanjutnya akan ditinjau kemungkinan bentuk isoklin dan arah gerak orbit. Pembentukan isoklin ini dilakukan secara manual, yaitu dengan cara

~nengambil nilai-nilai sembarang berdasarkan

kondisi tertentu yang harus dipenuhi. Dalam ha1 ini, berapapun pengambilan nilai-nilai tersebut akan menghasilkan pola kurva yang sama.

I . Kondisi ala2 < blO2c1c2

Dengan memilih nilai parameter yang sesuai

dengan kondisi di atas (al = 0.99, aa = 0.85,

b l = 0.325, b, = 0.425, c l = 5, c2 = 4) diperoleh

I I

Gambar 6. isoklin x dan arah gerak orbit horizontal pada kondisi ala2 < blbrc,cz.

Setiap titik pada daerah sebelah kiri isoklin x

dx

dx

diperoleh

-

> 0 (- tertulis pada (23)). Hal ini

dt dt

mengakibatkan x(t) naik sehingga orbit akan

bergerak ke arah kanan. Prosedur yang sama

dilakukan terhadap titik pada daerah sebelah kanan

dr

dx

isoklin x, diperoleh

-

< 0 (- tertulis pada (23)).

dl dl

Hal ini mengakibatkan x(!) turun sehingga orbit

akan bergerak ke arah kiri.

Dengan menggunakan nilai parameter di atas,

kurva isoklin y yakni +&) pada persamaan (2.6)

diperoleh kurva (Gambar 7).

Gambar 7. lsoklin y dan arah gerak

orbit vertikal pada kondisi alaz < blb2Clcz.

Setiap titik pada daerah sebelah atas isoklin JJ

dv d~

diperoleh

-

< 0 (- tertulis pada (23)). Hal ini

dt dt

mengakibatkan A t ) turun sehingga orbit akan

bergerak ke arah bawah. Prosedur yang sama

dilakukan terhadap titik pada daerah sebelah bawah

dy dy

isoklin y, diperoleh

-

> 0 (- termlis pada

dl dl

(23)). Hal ini mengakibatkan y(f) naik sehingga

orbit akan bergerak ke arah atas.

Penggabungan Ga~nbar 6 dan Gambar 7

men%asilkan Gatnbar 8. Berdasarkan Gambar 8,

ada empat daerah yang dipilah oleh kedua isoklin

tersebut, yaitu daerah I , daerah 2, daerah 3 dan

daerah 4, dengan keterangan sebagai berikut: Daerah 1 : dr/dt> 0, dy/d/> 0

Daerah 2 : &/dl < 0, dy/dl > 0 Daerah 3 : dr/dt< 0, dy/dr < 0 Daerah 4 : Wd1> 0, dy/dr < 0

Y

41

(r) [image:18.608.75.297.80.826.2] [image:18.608.84.293.81.321.2] [image:18.608.313.509.177.468.2]

I J

Gambar 8. Resultan anak panab yang

menyatakan arah gerak orbit

pada kondisi a l q < b1bIclc2

Perhatikan anak panah pada Gambar 8,

Resultan anak panah tnenyatakan arah gerak orbit.

Berdasarkan resultan anak panab pada Gambar 8,

arah gerak orbit niendekati titik keseimbangan,

2. Kondisi alaz 2 blb2c1cz

Nilai parameter yang dipilih secara

sembarang tapi memenuhi kondisi di atas ialah a l = 0 . 9 9 , a 2 = 0 . 8 5 , b l = 0 . 1 5 5 , bz=0.025, c 1 = 6 ,

cz = 12. Pada kondisi ini, akan dibahas dua isoklin,

yaitu isoklin x dan isoklin y, untuk isoklin x

bergerak ke arah bawah. Prosedur yang sama dilakukan terhadap titik pada daerah sebelah bawah

du dy

isoklin y, diperoleh

-

> 0 (- tenulis pads

dt dl

(23)). Hal ini ~nengakibatkan y(t) naik sehingga orbit akan bergerak ke arah atas.

Penggabungan Gambar 9 dan Gambar 10

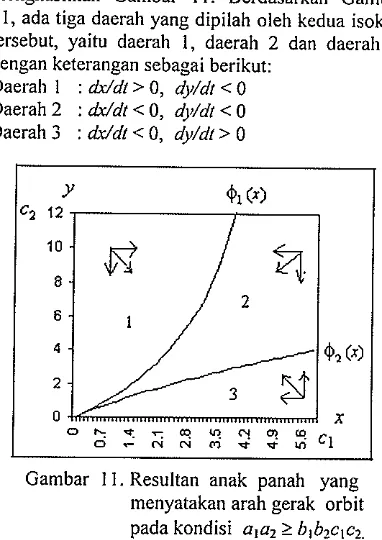
menghasilkan Gambar 1 1 . Berdasarkan Gambar 11, ada tiga daerah yang dipilah oleh kedua isoklin

tersebut, yaitu daerah 1, daerah 2 dan daerah 3.

dengan keterangan sebagai berikut: Daerah 1 : dx/dt > 0, dy/dt < 0

Gambar 9. Isoklin x dan arah yerak Daerah 2 : < 0, a$/df < 0

orbit horizontal oada kondisi Daerah 3 : < 0, dy/dl> 0

Setiap titik pada daerah sebelah kiri isoklin x

dr

ak

diperoleh

-

> 0 (- tertulis pada (23)). Hal ini

d! dt

mengakibatkan x(t) naik sehingga orbit akan

bergerak ke arah kanan. Prosedur yang sama

dilakukan terhadap titik pada daerah sebelah kanan

ak

ak

isoklin x, diperoleh

-

< 0 (- tertulis pada (23))

dl dt

Hal ini mengakibatkan x(t) turun sehingga orbit

akan bergerak ke arah kiri.

-

Dengan menggunakan nilai parameter di atas,

kurva isoklin y yakni $&) pada persamaan (2.6) Gambar I I . Resultan anak panah yang

diperoleh kurva (Gambar 10). menyatakan arah gerak orbit

pada kondisi a,a2 t blb2cIc2.

Perhatikan anak panah pada Gambar 8.

Resultan anak panah menyatakan arah gerak orbit.

Berdasarkan resultan anak oanah oada Gambar 8.

arah gerak orbit mendekati titik keseimbangan (0,0).

4.5 Orbit dan Kestabilan Sistem

Analisis kualitatif melalui diagram fase untuk menunjukkan kondisi kestabilan sistem pada titik tetapnya dapat diilust-asikan dengan bantuan sofiware Locbif. Adapun diagram fase tersebut

merupakan orbit solusi sistem persatnaan

[image:19.595.88.287.69.259.2]

diferensial (17) yang tnenggambarkan lintasan

Gambar 10. Isoklin y dan arah gerak orbit yang dilalui pada bidang (x, y).

orbit vertikal pada kondisi Untuk menghasilkan suatu diagram fase

ala2 2 blb2cIc2. dengan bantuan Locbif diperlukan nilai-nilai

parameter yang memenuhi syarat yang

Setiap titik pada daerah sebelah atas isoklin y disubstitusikan ke dalam sistem persamaan

dy d. diferensial (17). Nilai-nilai parameter tesebut

-<O (-tertufis ~ a d a (23)). Hal diatnbil berdasarkan syarat-syarat tertentu, Adapun

dt dt .

[image:19.595.75.290.75.782.2] [image:19.595.313.504.167.437.2]

ala; t blb;clc,. Tanda panah menunjukkan arah gerak sepanjang lintasan solusi selama waktu berjalan.

Ilustrasi kestabilan sistem untuk kondisi

ala; < blb;cIc2, dengan nilai parameter c l = c, =20

juta, a, = 0.99, a; = 0.95, bl = 0.049, dan

62 = 0.575 dapat ditunjukkan pada Gambar 12

berikut ini:

Gambar 12. Orbit penderita laki-laki ( x )

dan penderita perempuan Q

pada kondisi ala2 < b,b2clc2.

Gambar 12 menunjukkan bahwa titik tetap T;

bersifat stabil, untuk titik awal sembarang di setiap daerah akan bergerak ke arah titik tetap

(1.21, 1.21) pada pada waktu I = 88.3. Pada

kondisi ini bahwa sistem stabil pada titik

kesetimbangan, artinya bahwa banyaknya

penderita penyakit gonorrheae berada pada jumlah yang tetap. Sedangkan untuk titik tetap TI pada kondisi ini bersifat sadel pada kuadran 11, 111, dan IV.

Gambar 13. Orbit penderita laki-laki ( x )

dan penderita perempuan (y)

pada kondisi ala; 2 blb2clc;.

Gambar 13 menunjukkan bahwa titik tetap TI bersifat stabil, karena untuk titik awal sembarang di setiap daerah akan bergerah ke arah titik tetap

( 0, 0 ) pada waktu 1 z 80.4. Hal ini menunjukkan

sistem stabil, artinya tidak ada lagi yang terinfeksi.

4.6 Solusi Model

Solusi kualitatif dari persamaan (17)

dilakukan melalui grafik yang diperoleh dengan

menggunakan sofware Maple, dengan

memasukkan nilai-nilai parameter a,, a,, 61, 62. CI.

c,, Nilai-nilai parameter tersebut diambil

berdasarkan pada kondisi tertentu. Dalam ha1 ini, ada dua kondisi yang harus dipenuhi, yaitu ala2 < blbzclc, dan ala; t b1b2cIc2 dengan a l >a;.

Pada kondisi a l a 2 < blb2cIc2, dengan nilai

parameter sama dengan nilai pada orbit dan kestabilan sistem (lihat 4 3 , sehingga diperoleh grafik sebagai berikut:

Selanjutnya ilustrasi kestabilan sistem untuk

kondisi ala2 t blb;cIc2, dengan nilai parameter

adalah c, = c2 = 20 juta al = 0.99, a2 = 0.9,

bl = 0.0435 dan b2= 0.037 dapat ditunjukkan pada

[image:20.602.330.499.72.274.2]

Gambar 14. Perkembangan penderita

laki-laki (x) pada kondisi

ala2 < blb2clc2.

Gambar 14 menunjukkan bahwa pada selang

waktu 1 tertentu lintasan kuwa semakin menurun

hingga mencapai titik minimum. Selanjutnya

lintasan kurva akan konstan sampai t mendekati

tak hingga. Hal ini menunjukkan bahwa selama

selang waktu tertentu banyaknya penderita

gonorrheae untuk laki-laki (x(r)) akan semakin berkurang hingga mencapai jumlah yang minimum dan selanjutnya akan berada pada jumlah yang tetap.

Ga~nbar 15. Perkembangan penderita

perelnpuan (v) pada kondisi

a1a2 < b l b l c ~ c ~ .

Gambar 15 lnenunjukkan bahwa pada selang

waktu r tertentu lintasan kurva semakin menurun

liingga mencapai titik minimum, selanjutnya lintasan kurva akan konstan. Hal ini menunjukkan bahwa selama selang waktu tertentu banyaknya

penderita gonowl7eae untuk pereliipuan @(I)) akan

semakin berkurang hingga mencapai jumlah yang minimum dan selanjutnya akan berada pada jumlah yang tetap.

Pada kondisi a,a2 2 blb2cIc2, dengan nilai

parameter sama dengan nilai pada orbit dan kestabilan sistem (lihat 4 . 9 , sehingga diperoleh grafik sebagai berikut:

Gambar 16. Perkembangan penderita laki-laki (x) pada kondisi

a l q 2 blb2cIc2.

Gambar 16 menunjukkan bahwa lintasan

kurva semakin menurun selama selang waktu t.

Pada saat waktu t mendekati takhingga maka x(r)

akan mendekati 0. Hal ini menunjukkan bahwa

banyaknya penderita gonorrheae untuk laki-laki

( ~ ( 1 ) ) akan semakin berkurang sehingga pada

akhirnya banyaknya penderita go~torrheae untuk

laki-laki tersebut nol.

Gambar 17. Perkembangan penderita

perempuan pada kondisi

[image:21.595.114.289.63.286.2] [image:21.595.335.500.157.366.2] [image:21.595.335.500.479.683.2]

Gambar 17 menunjukkan bahwa lintasan banyaknya penderita gonorrheae untuk perempuan

kurva semakin menurun selama selang waktu t. W t ) ) akan semakin berkurang sehingga pada

Pada saat waktu t mendekati takhingga makay(t) akhirnya banyaknya penderita gonorrl7eae untuk

akan mendekati 0. Hal ini menunjukkan bahwa perempuan tersebut nol.

V.

KESIMPULAN

Model dina~nika tentang penyebaran

gonorrhcae dikembangkan . oleh Martin Braun

(1975). Pemodelan ini membahas penyebaran

penyakit gonorrheoe yang disebabkan oleh

hubungan seksual lawan jenis individu rentan mudah tertular jika berhubungan seksual dengan orang yang terinfeksi.

Analisis kestabilan yang dilakukan pada model ini diinterpretasikan ke dalam suatu contoh di~nana permasalahan yang ada dibagi dua kasus.

Kasus pertama yaitu pada saat ala2 < b1b2cIc2, dan

kasus kedua yaitu n,a2 2 blb2cIc2.

Kasus pertama, sistem memiliki dua titik

tetap, titik tetap TI = (0, 0) yang bersifat sadel

takstabil dan titik tetap T2 = (x8,y'). dengan

yang bersifat stabil. Hal ini menunjukkan bahwa

untuk kasus ini banyaknya penderita gonorrheae

baik laki-laki maupun perempuan pada akhirnya akan mengalami jumlah yang tetap (konstan).

Kemudian untuk kasus kedua, sisteln hanya

memiliki satu titik tetap TI = (0, 0) yang bersifat

stabil. Hal ini menunjukkan bahwa banyaknya

penderita gonorrheae untuk laki-laki dan

perempuan semakin lama akan semakin berkurang sampai akhirnya penyakit tersebut sembuh (tidak ada lagi yang terinfeksi).

DAFTAR PUSTAKA

Anton, H. 1987. Aljabar Linear Eletnenler.

Terjemahan Pantur Silaban. Erlangga, Jakarta

Braun, M. 1975. Differential equations and

their applications, Applied Marhea~atical

Sciences Series. 15: 208 - 2 16.

Braun, M., S. C.Courtney, dan A. D. Donald.

1983. D~fferential Equation Models.

Springer-Verlag, New York.

Falimi, S. ' 1997. Gonore, hal. 44-51. Di dalam

Bahaya Penyakit K~rlit don Kelanzh. Lukrnan Hakim (penyunting). FKUI-RSUPN Dr. Cipto Mangunkusumo, Jakarta.

Frauenthal, J. C. 1980. Mathematical

Modeling in Epidenziology. Springer-Verlag, New York.

Hasibuan, K. M. 1989. Dinamika Populasi,

Penzodela~z Matenzatika didalanl Biologi Populasi. PAU IPB, Bogor.

Indaryani, L. 1999. Bifurkasi lokal pada titik

tetap non-hiperbolik. Skripsi. Jurusan

Matematika FMlPA IPB, Bogor.

Tu, N. V. 1994. Dynamical Sysrenz. .In

LISTlNG PROGRAM MAPLE

# Bidang Fase Perkembangan Penderita Laki-laki pada Kondisi ala2 < blb2clc2 (Gambar 14)

> Restart;

> a,:=0.99:a2:=0.95:b1:=0.049:b2:=0.575:cl:=20:c2:=20:

> with (DEtools):

G

Phaseportrait ([D(x)(t)=-a1 *x(t)+b I *(c l-x(t))*y(t),D(y)(t)=-a2*y(t)+b2*(~2-y(t))*x(t)].\[x(t),y(t)J,

t=O.. 10,[[x(0)=1O,y(0)=1OJ],stepsize=0.05,\scene=[t,x(t)],linecolo~[blue],

tnetl~od=classical[foreuler]);

# Bidang Fase Perkembangan Penderita Perempuan pada Kondisi a l a 2 < blb2cIc: (Gambar 15)

> Restatt;

> a1:=0.99:a~:=0.95:~:=0.049:b~:=0.575:c~:=20:~~:=20:

> with (DEtools):

G

Phaseportt.ait ([D(x)(t)=-ai*x(t)+bi*(cl-x(t))*y(t),D(y)(t)=-a2*y(t)+b2*(c2-y(t))*x(t)J,\[x(t),y(t)],

t=O.. lO,[[x(O)=lO,y(O)=lO]],stepsize=O.O5,\scene=[t,y(t)],linecolor=[blue],

metliod=classical[foreuler]);

# Bidang Fase Perkembangan Penderita Laki-laki pada Kondisi ala2 2 blbZcIc2 (Gambar 16)

> Restatt;

> al:=0.99:a2:=0.9:bl:=0.0435:b2:=0.037:cl:=20:c2:=20:

9 with (DEtools):

G

phaseportrait ([D(x)(t)=-al*x(t)+bl*(cl-x(t))*y(t), D(y)(t)=-a2*y(t)+b2*(c2-(t))*x(t)],\[x(t),y(t)],

t=O.. 1 O,[[x(O)=lO,y(O)=lO]J,stepsize=O.O5,kcene=[t,x(t)],linecolo~[blue~,

metl~od=classical[foreuler]);

# Bidang Fase Perkembangan Penderita Perempuan pada Kondisi a l a 2 2 blb2cIc2 (Gambar 17)

> Restart;

> al:=0.99:a2:=0.9:bl:=0.0435:b2:=0.037:cl:=20:c2:=20:

9 with (DEtools):

G

phasepo~.trait

([D(x)(t)=-al*x(t)+bI*(cl-x(t))*y(t),

D(y)(t)=-aZ*y(t)+b2*(~2-(t))*x(t)],\[x(t),y(t)],

t=O.. lO,[[x(O)=lO,y(0)=1O]],stepsize=0.05,\scene=[t,y(t)J,linecolor=[blueJ,

ANALISIS KESTABILAN

MODEL PENYEBARAN, GONORRHEAE

Oleh:

AT1 ROHAYATI

JURUSAN MATEMATIKA

HAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

I. PENDAHULUAN

1.1 L a t a r belakang

Meningkatnya jumlah penderita penyakit yang

disebabkan oleh hubungan seksual seperti

gonorrheae, cl~lamydia, syphilis dan AIDS merupakan masalah utama di bidang kesehatan pada negara maju maupun negara berkembang. Sebagai contoh, di Amerika Serikat setiap tahunnya lebih dari dua juta orang menderita

penyakit gonorrheae. Jumlah tersebut jauti lebih

besar dari total penderita penyakit lainnya [Fahmi, S. 19971.

Penderita penyakit gonorrheae ini umumnya

para pekerja seks dan mereka yang melakukan seks tak wajar. Untuk mengetahui apakah seseorang tersebut terjangkit atau tidaknya, dibutuhkan waktu

yang cukup lama. Hal ini disebabkan masa

terinfeksinya yang cukup lama.

Seseorang yang telah dinyatakan sembuh dari

penyakit gonorrheae ini kemungkinan

terjangkitnya kembali sangat besar, karena belum ditemukannya vaksin pencegah penyakit tersebut.

Pennasalahan tersebut merupakan masalah yang menarik untuk dimodelkan. Oleh karena itu diperkenalkan model epidemik sederhana yang menggambarkan penyebarannya.

Sehubungan dengan masalah penyebaran dari

penyakit gonorrheae ini, maka pada tulisan ini

akan dibuat suatu analisis yang membahas kestabilan dan solusi model dinamik penyebaran gonorrheae berdasarkan diagram fase. Analisis

kualitatif model penyebaran gonorrheae dilakukan

karena model tersebut merupakan sistem

persamaan diferensial taklinear yang terlalu rumit untuk diaualisis secara kuantitatif.

Analisis kualitatif model penyebaran

gonorrheae ini dilakukan melalui pendekatan sistem dinamik dengan menggunakan bantuan sofhvarc Locbif dan Maple.

1.2 Tujuan Penulisan

Tujuan penulisan karya ilmiah ini adalah untuk ~nenganalisis kestabilan dan menganalisis solusi kualitatif dari model dinamik penyebaran gonorrl?eae.

1.3 Penjelasan Singkat tentang Gonorrlreae

Gonorrheae adalah sejenis penyakit kelamin

yang disebabkan oleh bakteri gonococcus yang

menyebar melalui hubungan seksual. Bakteri gonococcus ini ditemukan oleh Neisser pada tahun

1879. Gonococcus termasuk golongan diplokok

(Genus bakteri dari famili Actabacillaceae yang

terdiri dari dua sel kokkus yang kembar), berbentuk biji kopi dengan lebar 0.8 dan panjang

1.6 p. Bakteri ini bersifat negatif-Gram (dinding

sel bakteri mempunyai kandungan lipida yang tinggi), bersifat tahan asam, tampak di luar dan di dalam leukosit, tidak tahan lama di udara bebas, cepat mati pada keadaan kering, tidak tahan suhu di atas 39°C dan tidak tahan zat disinfektan (anti

kuman / pembersih).

Daerah yang paling mudah terinfeksi adalah daerah dengan mukosa epitel kuhoid atau lapis gepeng yang belum berkembang (imatur), yakni pada vagina wanita sebelum pubertas. Masa tunas gonorrheae sangat singkat, pada pria umumnya

berkisar antara 2 - 5 hari, kadang-kadang lebih

lama. Sedangkan pada wanita masa tunas

gonorrheae sulit untuk ditentukan karena pada umumnya bersifat asimtomatik (berubah-ubah).

Pada pria, kuman masuk ke uretra. Hal ini akan menimbulkan radang pada uretra (uretritis), yang paling sering adalah uretritis anterior akuta dan dapat menjalar ke proksimal (depan atau ujung pangkal) yang mengakibatkan komplikasi lokal, asenden (menuju ke depan) dan diseminata (pangkal uretra). Keluhan subyektif berupa rasa gatal, panas di bagian distal (pangkal) uretra di

sekitar lubang luar uretra, kemudian disusul

disuria, polakisuria, keluar cairan dari ujung uretra yang kadang-kadang disertai darah, dapat pula disertai nyeri pada waktu ereksi. Pada beberapa kasus dapat terjadi pembesaran kelenjar getah

bening. lnfeksi pada wanita, pada mulanya

hanya mengenai leher rahim, kadang-kadang menimbulkan rasa nyeri pada panggul bawah.

Diagnosa pada penyakit ini dilakukan atas dasar perbandingan, pemeriksaan klinis dan pemeriksaan pembantu. Secara epidemiologis pengobatan yang dianjurkan adalah obat dengan dosis tunggal. Jika tidak diobati dengan segera akan mengakibatkan kemandulan, cacat, gangguan pertumbuhan, radang sendi, kanker bahkan juga kematian.

11.

LANDASAN TEORI

2.1 Sistem Persamaan Diferensial Linear

Mandiri n111 ... "'I,,

Perhatikan sistem persamaan diferensial (SPD) berikut ini:

dengan fungsi ~ ( x ) mempunyai sifat

XI =

h

(xi (tb

...

>X.(f)) lim,,, cp(x) = 0. Bentuk Mx disebut pelinearan

i 2 =

f2

(11 (11, ... ,.,,(I)) dari (4).

(1) [Tu, 19941

dengan

fi, fi,

...

,

sebagai fungsi dari

XI (I), x 2 (t);.., x,, (I), yang kontinu, bernilai real,

dan mempunyai turunan parsial kontinu disebut sistem persamaan diferensial mandiri, karena perubahan x dan y dinyatakan sebagai fungsi dari x

dan y sendiri yang tidak mengandung t secara

eksplisit.

Sistem persamaan diferensial mandiri dapat dinyatakan dalam bentuk matriks berikut:

x = A x (2)

.

_,

dengan x =

11,

. . = ! I , d a n A a d a l a b

x,,

x,, matriks berukuran nxn.

[Hasibuan, 19891

Definisi: (Titik Tetap)

Sisteln persamaan diferensial (1) dapat ditulis

dalam bentuk :

i = f ( x ) (3)

dengan

f

fungsi yang terturunkan. ~ i t i k x ' dengan

x = 0 disebut titik h i t i s atau titik tetap.

f(')

[Tu, 19941

2.2 Pelinearan

Dengan menggunakan perluasan Taylor pada suatu titik tetap x', maka diperoleh persamaan

berikut :

k

= Mx

+

cp(x), ₍₄₎

dengan M inatriks Jacobi, yaitu

M E D f (x') E

D

f (x)IF.".

2.3 Vektor Eigen d a n Nilai Eigen

Misalkan A matriks berukuran nxn, maka suatu vektor taknol X di R" disebut vekror eigen dari A, jika untuk suatu skalar h, yang disebut nilai eigen dari A, berlaku:

Ax=

M.

Vektor X disebut vektor eigen yang bersesuaian dengan nilai eigen h. Untuk mencari nilai eigen

dari matriks A yang berukuran nxn maka

persamaan AX =

LY

dapat dituliskan kembali

sebagai berikut:

A X = A X ~ ( A - X I ) = O

Persamaan terakhir akan mempunyai solusi tak-no1

jika dan banya jika :

det (A-hl) = /A-A4 = 0 ₍₅₎

Persamaan (5) disebut persamaan karakreristik dari A.

[Anton, H., 199.51

2.4 Bentuk Kanonik J o r d a n

Misalkan diberikan sistem

-

persamaan

-

diferensial dua dimensi untuk A =

I:::

1::

J

mempunyai persamaan karakteristik sebagai

berikut :

C(h) = d e t ( A - X I ) = h 2 - y h + 6 = 0

dengan y = a l l + a2, dan S = det (A)

-

- all a22-a12 021.

Nilai eigen yang diperoleh dari persamaan karakteristik di atas adalah:

( 6 )

Misalkan matriks real Pzx2 mempunyai

balikan sehingga P.'AP = J, dengan J adalah

salah satu dari matriks dalam bentuk kanonik

Jordan :

Dalam penjelasan selanjutnya, bentuk kanonik Jordan (i), (ii) dan (iii) akan disebut Jordanl, Jordan2, dan Jordan3. Bentuk Jordan1 adalah kasus

untuk dua nilai eigen real yang berbeda (XI # h2).

Bentuk Jordan2 adalah kasus untuk dua nilai eigen

yang sama yaitu: h l = h 2 = h =

1

, dengan

y'=

46.

2

Bentuk Jordan3 adalah kasus untuk nilai eigen Y

kompleks yaitu hl,,= a

+

ip, dengan a =

-,

dan

2

, 3 46-y 2 7

,

a dan (3 keduanya bernilai real

2

dengan

P

> 0. J adalah matriks simetrik dengan

elemen diagonalnya adalah bagian real dari nilai eigen dan elemen yang bukan diagonal adalah bagian imajiner dari nilai eigen.

[Tu, 19941

2.5 Kestabilan Titik Tetap

2.5.1 Analisis Kestabilan Titik Tetap

Analisis kestabilan titik tetap berdasarkan nilai eigen dilakukan dengan cara menganalisis nilai eigen tersebut. Perhatikan nilai eigen pada

persamaan (6). Ada beberapa kasus untuk

menganalisis kestabilan titik tetap, tergantung

pada nilai y2

-

46.

KASUS 1 (y2 -46)> 0

Nilai eigen yang diperoleh adalah real dan

berbeda (hl =L hz), dengan bentuk kanonik Jordan

i

=[hl

O

1.

Solusi umum yang diperoleh

0 h2

adalah :

A? r

x(t)= C, v, cA1' +C2 v2

"

₍₇₎

dengan Al dan

A,

adalah nilai eigen dari matriks

Jacobi, v , dan v2 berturut-turut adalah vektor eigen

yang bersesuaian dengan nilai eigen.

Pada kasus ini kestabilan titik tetap

mempunyai 3 sifat yaitu:

I . Bila kedua nilai eigennya negatif (hl < 0 dan

h2 < 0), maka diperoleh nilai y < 0 dan 6 > 0.

Dari solusi (7) diperoleh bahwa jika t

mendekati takhingga maka x mendekati no1 sehingga titik tetap bersifat stabil.

2. Bila semua nilai eigennya bernilai positif

( h , > 0 dan h2 > 0), maka diperoleh nilai y > 0

dan 6 > 0. Dari solusi (7) diperoleh bahwa

jika 1 mendekati takhingga maka x mendekati

takhingga. Hal ini menunjukkan bahwa x(t) merupakan titik tetap bersifat takstabil.

3. Bila nilai eigennya berlainan tanda (misalkan

A, < 0 <

h2

), maka diperoleh nilai 7 < 0 dan 6

<

0. Dari solusi (7) diperoleli bahwa jika 1

mendekati takhingga maka x(t) mendekati takhingga, sehingga lintasan kurva membentuk

suatu asimtot pada bidang v , dan 12. Titik

tetap ini bersifat titik sadel dan bersifat titik takstabil.

KASUS2 (y2-46)=0

Nilai eigen yang diperoleh nilai eigen real ganda ( & I = h2= h), dengan bentuk kanonik Jordan

J

=[h

I]. Bentuk solusi umumnya adalah:

0 A

x(t) = (c, + c 2 1)

2'

₍₈₎

Pada kasus ini kestabilan titik tetap

mempunyai 2 sifat, antara lain:

1. Bila kedua nilai eigen negatif (i., < 0 dan

h2 < 0). Dari solusi (8) diperoleh bahwa jika r

mendekati takhingga maka x(l) menuju nol, sehingga titik tetap bersifat stabil.

2. Bila nilai eigen bernilai positif (i., > 0 dan

2.1 > 0). Dari solusi (8) diperoleh bahwa jika I

mendekati takhingga maka x(r) menuju takhingga sehingga titik tetap tersebut bersifat takstabil.

KASUS 3 (y2 -46)< 0

Pada kasus ini nilai eigen yang diperoleh

adalah nilai eigen kompleks dengan bentuk _{- -}

kanonik Jordan J =

!I.

Misalhn nilai

eigen yang diperoleh adalah = a

+

iP ( a # 0,

p

# O), dengan a dan

P

adalah bilangan real dan

p

> 0. Sistem yang mempunyai nilai eigen a

+

iP

dapat dilambangkan dengan

x

,

dengan .? =

[:

1

$=[-;

PI-

atau dalarn bentuk skalar adalah:

Dalam bentuk koordinat polar, x l dan x? dapat

dinyatakan dalam bentuk x, = r cos (8) dan

menghasilkan

Dengan menurunkan (10) terhadap waktu t akan

diperoleh :

Kemudian jika persamaan (9) disubstitusikan ke dalam persamaan (12) maka diperoleh:

Dengan menurunkan (1 1) terhadap t, maka akan diperoleh:

Bentuk x12sec2(8) dapat diperoleh dari persamaan (10) dan (11) yang menghasilkan

x12sec2(@)= r 2 . Kemudian dengan

lnensubstitusikan persamaan (9) dan

xI2sec2 (€I)= r 2 ke dalam persamaan (14) maka

diperoleh:

Solusi di atas mempunyai beberapa kasus yang

hergantung pada nilai a dan

0

seperti pada

persamaan (13) dan (15) yaitu: a. a < O

Jika

a

< 0 maka r(f) pada persamaan (13)

berkurang pada saat t bertambah. Jika

0

> 0

Inaka @(1) pada persamaan (15) akan

berkurang, pada saat t semakin hesar, sehingga arali gerak orbit akan hergerak searah jamm

jam lnenuju titik tetap. Jika

p

< 0 maka arah

gerak orbit berlawanan dengan arab jarum jam

menuju titik tetap. Dalam ha1 ini titik tetap merupakan titik tetap bersifat spiral srabil.

b. azO

Jika a > 0 maka r(t) pada persamaan (13) akan

bertamhah pada saat t semakin besar. Jika

p

> 0 maka B(t) pada persamaan (15) akan berkurang, pada saat t semakin besar. sehingga arah gerak orbit akan bergerak searah jamm

jam menjauhi titik tetap. Jika

P <

0 maka arah

gerak orbit akan bergerak berlawanan dengan

arah jarum jam menjauhi titik tetap. Titik

tetap tersehut hersifat spiral fakrfabil. c. a=O

Jika a = 0 maka r(f) pada persamaan (13) tidak

berubah sepanjang waktu. Jika

P

< 0 maka €I(!)

pada persamaan (15) akan naik, dan jika

p

> 0

maka e(t) akan turun. Karena r(t) tetap maka gerak orbit membentuk suatu lingkaran dengan titik tetap sebagai pusat. Titik tetzp tersehut bersifat slabil nefral.

2.5.2 Perilaltu Titik Tetap

Berdasarkan uraian di atas maka dapat

disimpulkan hahwa kestabilan titik tetap

mempunyai 3 perilaku, yaitu:

I . Stahil jika:

a. Setiap nilai eigen real adalah negatif

(A;< 0 untuk semua I].

h. Setiap komponen real nilai eigen

kompleks adalah takpositif, (Re (A, )

< 0

untuk semua I ] .

2. Takstabil jika:

a. Setiap nilai eigen real adalah positif

(Ai> 0 untuk semua I].

b. Setiap komponen real nilai eigen

kompleks adalah positif, (Re (A, ) > 0

untuk semua I ] .

3. Sadel jika:

Perkalian dua buah nilai eigen real sembarang

adalah negatif (A; A, < 0, untuk i dan j

sembarang). Titik tetap sadel ini bersifat

takstabil.

2.5.3 Bentuk Umum Kestabilan

Bentuk ulnum kestabilan di sekitar titik tetap herdasarkan perilaku orbit di sekitarnya, dibedakan berdasarkan dua tipe nilai eigen, nilai eigen real dan nilai eigen kompleks.

Bentuk umum kestabilan untuk tipe nilai eigen real adalah:

1. Jika setiap orbit mendekati titik tetap, maka

2. Jika setiap orbit bergerak menjauhi titik tetap, maka titik tetap itu disebut titik tetap takstabil. Tipe ini ditunjukkan oleh Gambar

1 .b.

3. Jika ada orbit yang bergerak mendekati dan

ada orbit yang menjauhi titik tetap, maka titik tetap itu disebut titik pelana (sadel). Tipe ini ditunjukkan oleh Gambar 1.c.

Bentuk umum kestabilan untuk tipe nilai eigen kompleks adalah:

1. Jika setiap orbit mendekati titik tetap secara

spiral, maka titik tetap tersebut merupakan titik tetap spiral stabil. Tipe ini ditunjukkan ole11 Gambar 2.a.

2. Jika setiap orbit ~nenjauhi titik tetap secara

spiral, lnaka titik tetap tersebut merupakan

titik tetap spiral takstabil. Tipe ini

ditunjukkan oleh Gambar 2.b.

3. jika orbit-orbit bergerak mengelilingi titik

tetap sehingga membentuk kurva tertutup, maka titik tetap tersebut merupakan titik tetap

[image:30.599.53.516.55.820.2] [image:30.599.353.456.70.370.2]

stabil netral. Tipe ini ditunjukkan oleh

Gambar 2.c.

[Hasibuan, K. M. 19891

Teorema Kestabilan

Misalkan x = Ax adalab suatu sistem

persamaan diferensial dengan A matriks real

berukuran 2x2. Misalkan juga persamaan

karakteristik dari matriks A diberikan oleh h 2 + B h + C = 0 , d e n g a n B = t r ( ~ ) dan C = d e t A . Kestabilan sistem persamaan diferensial di atas diperoleh dari:

1. Jika B > 0 dan C > 0, maka titik tetap bersifat

stabil.

2. Jika B < 0 dan C > 0, maka titik tetap bersifat

tak-stabil.

3. Jika C < 0, maka titik tetap bersifat sadel

takstabil.

4. Jika B = 0 dan C > 0, maka titik tetap bersifat

stabil netral.

Bukti : [Indaryani, L. 19991

Gambar 2. Bentuk umum kestabilan titik tetap untuk tipe nilai eigen kompleks (a. Spiral stabil, b. Spiral takstabil, c. Stabil netral).

2.6 Bidang Fase dan Orbit Solusi

Perhatikan sistem persamaan diferensial berikut ini:

Solusi sistem persamaan diferensial (16)

lnelnbentuk suatu kurva berdimensi 3 dengan

koordinat (t,x,y). Karena secara eksplisit t tidak ada

dalam sistem tersebut, maka setiap solusi sistem

(16) untuk to < t < t, membentuk kurva di bidang

(x, y), atau jika t bergerak dari to ke t,, gugus titik-

titik (x(t), y(t)) membentuk suatu kurva di bidang

(x, y). Kurva ini disebut orbit (trayektori) yang merupakan solusi persamaan (16). Sedangkan bidang (x, y) disebut bidang fuse solusi tersebut. Dengan kata lain orbit solusi suatu sistem persamaan diferensial adalah lintasan yang dilakukan oleh solusi di bidang (x, y).

[Hasibuan, K. M. 19891

[image:31.605.321.504.77.224.2]

2.7 Garis Isnklin dan Arah Gerak Solusi

Kurva dengan F (xa) = k, k konstanta, disebut

suatu isoklin dari persamaan diferensial(l6). Salah satu cara untuk memperoleh gambaran orbit sistem persamaan diferensial (SPD) (16), terutama untuk persamaan diferensial yang solusi persamaan diferensialnya tidak dapat dicari secara eksplisit, adalah dengan menggunakan metode

isoklin dan arah gerak solusi. Hal ini dapat

dilakukan karena SPD (16) membentuk suatu

medan arah di bidang (x, y), sehingga orbit yang

baik dapat diperoleh dengan cara memplot sejumlah kemiringan orbit pada titik-titik di bidang fase.

Isoklin-isoklin dari persamaan (16) adalah

kurva yang seluruh unsur-unsur garisnya

melnpunyai kemiringan tertentu. Jadi setiap orbit solusi suatu persamaan diferensial yang melalui suatu isoklinnya memiliki kemiringan yang sama.

Misalkan 0 adalah sudut antara arah gerak orbit yang terletak pada garis isoklin terhadap sumbu x. Ada dua isoklin yang paling penting,

yaitu isoklin &/dt = 0 yang berpadanan dengan

B

= ~