Study Tentang Fuzzy Linear Programing Dengan Metode Modifikasi Subgradient

STUDI TENTANG FUZZY LINEAR PROGRAMMING

DENGAN METODE MODIFIKASI SUBGRADIENT

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

SURYANI NAZMI

020803027

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

ii

PERSETUJUAN

Judul : STUDI TENTANG FUZZY LINEAR PROGRAMMING

DENGAN METODE MODIFIKASI SUBGRADIENT

Kategori : SKRIPSI

NIM : 020803027

Program Studi : SARJANA (S1) MATEMATIKA Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di

Medan, Desember 2008

Komisi Pembimbing

Pembimbing 2 Pembimbing 1

Drs. Suwarno Ariswoyo M.Si Drs. Djakaria Sibayang NIP.130810774 NIP. 131474685

Diketahui oleh :

Departemen Matematika FMIPA USU Ketua,

Dr. Saib Suwilo, M.Sc NIP. 131796149

iii

PERNYATAAN

STUDI TENTANG FUZZY LINEAR PROGRAMMING DENGAN

METODE MODIFIKASI SUBGRADIENT

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Desember 2008

iv

PENGHARGAAN

Segala puji dan syukur kehadirat ALLAH SWT, atas berkat dan rahmat-Nyalah sehingga saya dapat menyelesaikan skripsi ini dengan judul, Studi Tentang Fuzzy Linear Programming Dengan Metode Modifikasi Subgradient.

Skripsi ini merupakan salah satu mata kuliah wajib yang harus diselesaikan oleh seluruh mahasiswa/I Departemen matematika, guna untuk melengkapi syarat memperoleh gelar sarjana Matematika di Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.

Dalam kesempatan ini, saya mengucapkan terima kasih yang sebesar-besarnya kepada Bapak Dr. Eddy Marlianto, M. Sc, selaku Dekan FMIPA USU. Bapak Dr. Saib Suwilo, M. Sc dan Drs. Henry Rani Sitepu, M. Si, selaku Ketua dan Sekretar is Departemen Matematika di FMIPA USU Medan . Bapak Suwarno Ariswoyo, M.Si selaku dosen pembimbing I dan Drs. Djakaria Sebayang selaku dosen pembimbing II yang telah memberikan dukungan moral, motivasi, waktu, tenaga, pikiran dan bantuannya sehingga penulis dapat menyelesaikan penelitian ini. Seluruh Staf Pengajar Matemaika di FMIPA USU beserta pegawai Administrasi. Keluargaku tercinta terutama kedua orang tuaku, bapakku (Alm), ibuku, serta kakak, abang dan adiku yaitu kak Sari, kak Dani, bang Abi, bang Jaya, bang Jun, bang Riki, dan Ayu yang selalu memberikan dukungan moral dan memberi kasih sayang serta semangat. Tak lupa pula untuk rekan-rekan mahasiswa Departemen Matematika khususnya angkatan 2002 yang tak mungkin disebutkan satu persatu.

Penulis menyadari masih banyak kekurangan dalam penulisan ini, untuk itu penulis meminta kritik dan saran yang membangun dari pembaca sekalian.

Akhir kata penulis mengucapkan terima kasih atas perhatiannya, semoga tulisan ini berguna bagi pembaca sekalian.

Medan, Desember 2008

v

ABSTRAK

Masalah fuzzy linear programming terdiri dari dua macam masalah yaitu masalah linear programming dengan fuzzy koefisien teknologikal dan masalah linear program - ming ruas kanan,yang koefisien tekhnologikal adalah bilangan fuzzy.Untuk memecah- kan masalah optimisasi fuzzy linear programming digunakan Metode Modifikasi Subgradient yang diilustrasikan dalam bentuk contoh dan solusi numerik.

vi

ABSTRACT

The fuzzy linear programming problems consisten of two kind problems, i.e., linear programming problems with only fuzzy technological coefficients and linear programming problems in which both the right-hand side, the technological coefficient are fuzzy number. For solve the fuzzy linear programming optimization problem were usedthe modified subgradient method which illustratived in example and numerical solutions.

vii

DAFTAR ISI Halaman PERSETUJUAN……... ii

PERNYATAAN... iii

PENGHARGAAN... iv

ABSTRAK... v

ABSTRACT... vi

DAFTAR ISI... viii

BAB I Pendahuluan... 1

1.1 Latar Belakang... 1

1.2 Perumusan Masalah... 2

1.3 Tinjauan Pustaka... 2

1.4 Maksud Dan Tujuan... 3

1.5 Kontribusi Penelitian... 4

1.6 Metode Penelitian... 4

BAB II Landasan Teori... 5

2.1 Fuzzy Set... 5

2.2 Perbedaaan Antara Himpunan Crisp Dengan Himpunan Fuzzy... 5

2.3 Fungsi Keanggotaan………. 6

2.4 Domain Himpunan Fuzzy………. 8

2.5 Membangkitkan Nilai Keanggotaan Fuzzy... 9

2.6 Program Linear... 10

2.7 Fuzzy Linear Programming... 10

BAB III Pembahasan……… 14

3.1 Program Linear Dengan Koefisien Fuzzy teknologikal…….. 14

3.2 Program Linear Dengan Koefisien fuzzy Teknologikal Dan Fuzzy Ruas Kanan... 16

3.3 Metode Modifikasi Subgradient... 19

viii

BAB IV Kesimpulan Dan Saran... 25

4.1 Kesimpulan... 25

4.2 Saran... 25

v

ABSTRAK

Masalah fuzzy linear programming terdiri dari dua macam masalah yaitu masalah linear programming dengan fuzzy koefisien teknologikal dan masalah linear program - ming ruas kanan,yang koefisien tekhnologikal adalah bilangan fuzzy.Untuk memecah- kan masalah optimisasi fuzzy linear programming digunakan Metode Modifikasi Subgradient yang diilustrasikan dalam bentuk contoh dan solusi numerik.

vi

ABSTRACT

The fuzzy linear programming problems consisten of two kind problems, i.e., linear programming problems with only fuzzy technological coefficients and linear programming problems in which both the right-hand side, the technological coefficient are fuzzy number. For solve the fuzzy linear programming optimization problem were usedthe modified subgradient method which illustratived in example and numerical solutions.

BAB I PENDAHULUAN

1.1 Latar Belakang

Pada fuzzy linier programming, akan dicari suatu nilai z yang merupakan fungsi objektif yang akan dioptimisasikan sedemikian hingga tunduk pada batasan-batasan yang dimodelkan dengan menggunakan himpunan fuzzy.

Teori himpunan fuzzy, yang dikembangkan oleh L.Zadeh pada abad pertengah -an tahun 60 -an, telah banyak berhasil dalam menangani masalah pengambilan keputusan dalam lingkungan kabur atau tidak pasti karena faktor subjektif ataupun karena intuitif.

Dalam pemodelan programa linier salah satu asumsi dasar adalah asumsi kepastian yaitu setiap parameter, data-data dalam pemodelan programa linier yang terdiri dari koefisien-koefisien fungsi tujuan, konstanta-konstanta ruas kanan dan koefisien-koefisien teknologis diketahui secara pasti. Tetapi dalam prakteknya asumsi ini jarang dipenuhi. Karena, kebanyakan model programa linier dirumuskan untuk memilih suatu tindakan atau keputusan diwaktu yang akan datang. Jadi, parameter-parameter yang akan dipakai didasarkan atas suatu prediksi mengenai kondisi masa datang. Karena ketidakpastian tersebut, biasanya dilakukan analisa kepekaan setelah di dapat penyelesaian optimal. Tujuannya adalah untuk mengetahui parameter -parameter yang sensitif, untuk mencoba mengestimasinya dengan lebih baik dan kemudian memilih suatu pemecahan yang tetap atau lebih baik untuk nilai-nilai yang mungkin dimiliki oleh parameter-parameter sensitif tersebut.

Dalam tulisan ini akan dibahas tentang permasalahan optimisasi dari pemrogra ma linier yang koefisien teknologis dan konstanta-konstanta ruas kanan yang termasuk bilangan fuzzy akan diselesaikan dengan metode modifikasi subgradient.

1.2 Perumusan Masalah

Permasalahan yang dapat diambil berdasarkan uraian diatas adalah bagaimana menyelesaikan masalah optimisasi dalam fuzzy linear programming dengan menggu- nakan metode modifikasi subgradient.

1.3 Tinjauan Pustaka

Sebagai penunjang teori dalam penulisan tugas akhir ini penulis menggunakan beberapa buku antara lain :

Gasimove menyatakan bahwa pendekatan algoritma dari metode modifikasi subgradient dapat diaplikasikan untuk memecahkan permasalahan nonconvex dan nonsmooth dari permasalahan optimisasi. Metode ini mengatur kontruksi dari masalah dual dengan menggunakan fungsi lagrangian.

Klir dan Yuan menyatakan bahwa Lofti A.Zadeh mengemukakan tentang teori himpunan fuzzy, dimana anggota - anggotanya tidak berdasarkan pada masalah ketegasan atau penguatan, tetapi juga pada masalah kederajatan (degree),

Klir dan Yuan menyatakan nilai optimal dari fuzzy set,yang mana G subset

Dari Rn

       − − =

∑

= 1 ) /( ) ( 0 ) ( 1 1 1 n j u j j

G x c x z z z

µ didefinisi

∑

∑

∑

= = = ≥ < ≤ < n j u j j n j u j j n j j j z x c if z x c ifz z x c if 1 1 1 1 1

       − =

∑

= 1 ) ( 0 ) ( 1 n j j ij i

i x b a x C µ

∑

∑

∑

∑

= = = = + ≥ + < ≤ < n j j ij ij i n j n j j ij ij i j ij n j j ij i x d a b x d a b x a x a b 1 1 1 1 ) ( , ) ( , ,

Sakawa dan Yauchi menyatakan pemakaian bilangan fuzzy yang digunakan dalam konteks pengambilan keputusan, khususnya dalam masalah program linier tidak konveks (non convex).

Sri kusumadewi menyatakan bahwa himpunan kabur (fuzzy set) menurut Lofti A.Zadeh adalah memodifikasi teori himpunan dimana setiap anggotanya memiliki derajat keanggotaan yang bernilai kontinu antara 0 sampai 1, alasan menggunakan logika fuzzy yaitu konsep logika fuzzy mudah dimengerti, sangat fleksibel, memiliki toleransi terhadap data-data yang tidak tepat, mampu memodelkan data-data nonlinier yang sangat kompleks, dapat membangun dan mengaplikasikan pengalaman-pengalaman para pakar secara langsung tanpa harus melalui proses pelatihan, dapat bekerjasama dengan teknik kendali secara konvensional pada bahasa alami.

Dubois dan Prade menyatakan bahwa parameter-parameter fuzzy diasumsikan

sebagai bilangan fuzzy yaitu bilangan fuzzy −

Pdengan fungsi keanggotaan merupakan

pemetaan kontinu dari ke interval tertutup [0.1], μ −

P(P) = 0 semua P ε (-∞, P], μP− (P) tidak turun sempurna dan kontinu pada tertutup [P1, P2],) μ

−

P(P) =1 untuk

semua P ε , [P2, P3], μ

−

P(P) tidak naik sempurna dan kontinu pada [P3,P4] dan μ

−

P(P) = 0 untuk semua P ε [ P4,∞).

1.4 Maksud Dan Tujuan

Adapun maksud dan tujuan dari penelitian ini adalah :

2. Mencari solusi optimal dengan menggunakan penerapan metode modifikasi subgradient .

1.5 Kontribusi Penelitian

Dengan adanya tulisan ini sangatlah bermanfaat dalam memecahkan persoalan non linier dengan parameter fuzzy serta mendapatkan gambaran mengenai metode pendekatan baru yang akan digunakan untuk memecahkan permasalahan optimisasi. Selain itu, Penelitian ini juga bermanfaat untuk menambah wawasan dan pengetahuan bagi penulis.

1.6 Metode Penelitian

Pada penelitian ini, terdapat beberapa metode pengumpulan data yang digunakan, yaitu :

1. Metode kepustakaan

Metode pengumpulan data kepustakaan dilakukan dengan mengumpulkan data-data dari sumber atau buku yang relevan dan jurnal terhadap penelitian. 2. Referensi internet

BAB II

LANDASAN TEORI

2.1 Fuzzy Set

Pada tahun 1965, Zadeh memodifikasi teori himpunan dimana setiap anggotanya memiliki derajat keanggotaan yang bernilai kontinu antara 0 sampai 1. Himpunan ini disebut dengan himpunaan kabur (Fuzzy Set). Selama beberapa dekade yang lalu, himpunan fuzzy dan hubungannya dengan logika fuzzy telah digunakan pada lingkup domain permasalahan yang cukup luas.Lingkup ini antara lain mencakup kendali proses, klasifikasi dan pencocokan pola, manajemen dan pengambilan keputusan, riset operasi, ekonomi, dll. Sejak tahun 1985, terjadi perkembangan yang sangat pesat pada logika fuzzy tersebut terutama dalam hubungannya dengan penyele-saian masalah kendali, terutama yang bersifat non-linear, ill-defined, time-varying, dan situasi-situasi yang sangat kompleks.

Logika fuzzy dikatakan sebagai logika baru yang lama, sebab ilmu tentang logika fuzzy modern dan metodis baru ditemukan beberapa tahun yang lalu, padahal sebenarnya konsep tentang logika fuzzy itu sendiri sudah ada pada diri kita sendiri. Logika fuzzy adalah suatu cara yang tepat untuk memetakan suatu ruang input kedalam suatu ruang output.

Ada beberapa alasan mengapa orang menggunakan logika fuzzy, antara lain: konsep logika fuzzy mudah dimengerti, logika fuzzy sangat fleksibel, logika fuzzy memiliki toleransi terhadap data - data yang tidak tepat, logika fuzzy mampu memodelkan fungsi – fungsi nonlinear yang sangat kompleks, logika fuzzy dapat membangun dan mengaplikasikan pengalaman – pengalaman para pakar secara langsung tanpa harus melalui proses pelatihan, logika fuzzy dapat bekerjasama dengan teknik-teknik kendali secara konvensional, logika fuzzy didasarkan pada bahasa alami.

2.2 Perbedaan Antara Himpunan Crips Dengan Himpunan Fuzzy

A berisi item x dengan P(x) benar. Jika XA merupakan fungsi karakteristik A dan

property p, maka dapat dikatakan bahwa P(x) benar, jika dan hanya jika XA(x)=1.

Himpunan fuzzy didasarkan pada gagasan untuk memperluas jangkauan fungsi karakteristik sedemikian hinnga fungsi tersebut akan mencakup bilangan real pada interval [0,1]. Nilai keanggotaannya menunjukkan bahwa suatu item dalam semesta pembicaraan tidak hanya berada pada 0 atau 1, namun juga nilai yang terletak diantaranya. Dengan kata lain, nilai kebenaran suatu item tidak hanya bernilai benar atau salah. Nilai 0 menunjukkan salah, nilai 1 menunjukkan benar, dan masih ada nilai - nilai yang terletak antara benar atau salah.

Misalkan diketahui klasifikasi sebagai berikut: MUDA umur < 35 tahun SETENGAH BAYA 35 ≤ umur ≤ 55 tahun TUA umur > 55 tahun

Dengan menggunakan pendekatan crips, amatlah tidak adil untuk menetapkan nilai SETENGAH BAYA. Pendekatan bisa saja dilakukan untuk hal-hal yang bersifat diskontinu. Misalkan klasifikasi untuk umur 55 dan 56 sangat jauh berbeda, umur 55 th termasuk SETENGAH BAYA, sedangkan umur 56 th sudah termasuk tua. Demikian pula untuk kategori MUDA dan TUA. Orang yang berumur 34 tahun dikatakan MUDA, sedangkan orang yang berumur 35 tahun sudah TIDAK MUDA lagi. Orang yang berumur 55 tahun termasuk SETENGAH BAYA, orang yang berumur 55 tahun lebih 1 hari sudah TIDAK SETENGAH BAYA lagi. Dengan demikian pendekatan crips ini sangat tidak cocok untuk diterapkan pada hal - hal yang bersifat kontinu, seperti umur.

Selain itu, untuk menunjukkan suatu umur pasti termasuk SETENGAH BAYA, atau tidak termasuk SETENGAH BAYA, dan menunjukkan suatu nilai kebenaran 0 atau 1, dapat digunakan nilai pecahan, dan menunjukkan 1 atau nilai yang dekat dengan 1 untuk umur 45 th, kemudian perlahan menurun menuju ke 0 untuk umur dibawah 35 th dan diatas 55 th.

2.3 Fungsi Keanggotaan

(sering juga disebut dengan derajat keanggotaan) yang memiliki interval antara 0 sampai 1.

Sebagai contoh, Misalkan akan membuat himpunan tinggi badan orang. Kata TINGGI menunjukkan derajat seberapa besar orang dikatakan tinggi. Dengan menggunakan crisp (tegas), misalkan seseorang dikatakan tinggi jika memiliki tinggi badan diatas 165 cm.

Secara tegas dapat dikatakan bahwa orang yang memiliki tinggi badan diatas 165 cm dikatakan Tinggi dengan nilai keanggotaan (μ) = 1. Sebaliknya, apabila seseorang memiliki tinggi badan kurang dari atau sama dengan 165 cm, maka secara tegas dikatakan bahwa orang tersebut Tidak Tinggi dengan μ=0 . Hal ini menjadi tidak adil, karena untuk orang yang memiliki tinggi badan 165,1 cm dikatakan Tinggi, sedangkan orang yang memiliki tinggi badan 165 cm dikatakan Tidak Tinggi.

Dengan menggunakan himpunan fuzzy, dapat dibuat suatu fungsi keanggotaan yang bersifat kontinu. Orang yang memiliki tinggi badan 160 cm sudah mendekati tinggi, artinya dia dikatakan Tinggi dengan μ=0,75. Sedangkan orang yang memiliki tinggi badan 153 cm, dia memang kurang tinggi, artinya dia dikatakan Tinggi dengan μ=0,2.

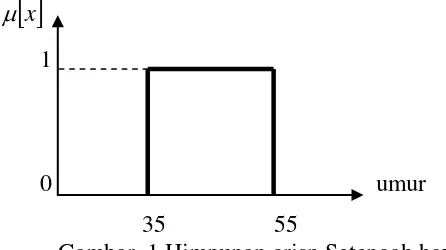
Contoh lain, untuk variabel umur menunjukkan himpunan crisp untuk setengah Baya, dimana orang yang berumur kurang dari 35 tahun atau lebih dari 55 tahun disebut bukan Setengah Baya (nilai keanggotaan =0). Sedangkan orang yang berumur antara 35 dan 55 tahun disebut Setengah Baya (nilai keanggotaan = 1). Ini dapat dilihat pada gambar 1 .

µ

[ ]

x

1

0 umur 35 55

[ ]

x

µ 1

0.5

0

25 35 45 55 65 umur

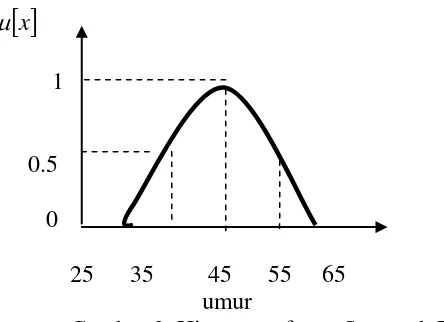
Gambar 2. Himpunan fuzzy Setengah Baya

Gambar 2 ini menunjukkan fuzzy set untuk setengah baya . Orang yang berumur 25 sampai 65 tahun dikatakan Setengah Baya dengan nilai keanggotaan yang berbeda. Orang dikatakan benar-benar Setengah Baya (nilai keanggotaan = 1) jika berumur 45 tahun.

Himpunan fuzzy yang berhubungan dengan Muda,Setengah Baya, dan tua, dapat didefenisikan secara bersama. Himpunan-himpunan tersebut kelihatan overlap.Umur 60 tahun termasuk Setengah Baya dan Tua. Jika umur semakin bertambah maka keanggotaan Mudanya semakin mendekati 0. Tiap-tiap himpunan fuzzy dapat disebutkan sesuai dengan nilai linguistik yang bersesuaian, dalam hal ini Muda, Setengah Baya, dan Tua.

2.4 Domain Himpunan Fuzzy

BERAT 1

derajat keanggotaan

µ

[ ]

x

0

40 45 50 55 60 berat badan (kg)

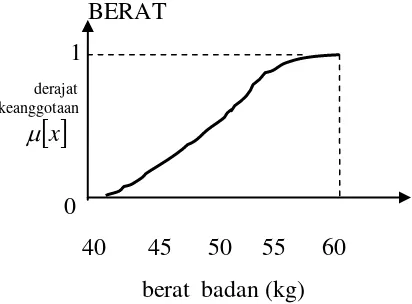
Gambar 3. Himpunan Fuzzy berat ; berdasarkan berat badan dalam kg.

2.5 Membangkitkan Nilai Keanggotaan Fuzzy

Setelah diketahui himpunan fuzzy, maka yang harus diketahui lagi yaitu bagaimana himpunan fuzzy tersebut merepresentasikan pengetahuan. Sebagai contoh, himpunan fuzzy TINGGI konsisten terhadap suatu garis lurus dari domain false ke true. Pemukaan himpunan fuzzy yang merupakan bagian dari himpunan tersebut yang mendefinisikan fungsi keanggotaan, dapat dibuat dalam berbagai bentuk. Biasanya, permukaan tersebut berupa garis kontinu yang bergerak dari kiri kekanan. Kontur dari suatu himpunan fuzzy menunjukkan properti semantik dari konsep fuzzy tersebut.

DEKAT DENGAN 5 Derajat

Keanggotaan

[ ]

x

µ

0 5 10

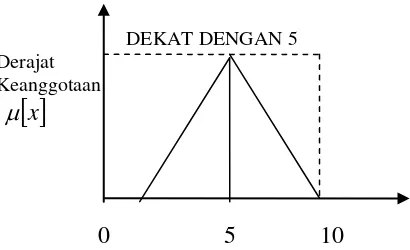
Gambar 4. Dekat Dengan 5 sebagai kurva lonceng

DEKAT DENGAN 5 Derajat

Keanggotaan

[ ]

x

µ

0 5 10

Gambar 5. Dekat Dengan 5 sebagai kurva segitiga

2.6 Program linear

Program linear yang diterjemahkan dari linear programming (LP) adalah suatu cara untuk menyelesaikan persoalan pengalokasian sumber - sumber yang terbatas diantara beberapa aktivitas yang bersaing, dengan cara yang terbaik yang mungkin dilakukan. Misalnya pengalokasian fasilitas produksi, sumber daya nasional untuk kebutuhan dosmetik, penjadwalan produksi, dan lain-lain.

Program linear menggunakan model matematis untuk menjelaskan

persoalan yang dihadapinya. Sifat ”linear ” disini memberi arti bahwa seluruh fungsi matematis dalam model ini merupakan fungsi linear, sedangkan kata program merupakan sinonim untuk perencanaan. Dengan demikinan, program linear (LP) adalah perencanaan aktivitas-aktivitas untuk memperoleh hasil yang optimum, yaitu suatu hasil yang mencapai tujuan terbaik di antara seluruh alternatif yang feasible.

2.7 Fuzzy Linear Programming

Salah satu contoh model linear programming klasik, adalah: Maksimumkan :

f(x) = cT

∈

x dengan batasan :

Ax ≤ b X ≥ 0

Dengan c, x ℜn, b∈ℜm, A∈ℜ

f(x) = c

mxn

Atau

Minimumkan :

T

dengan batasan : Ax ≥ b

X ≥ 0

dengan c, x∈ ℜn, b∈ℜm, A∈ℜmxn

A, b dan c adalah bilangan-bilangan crisp, tanda ≤ pada kasus maksimasi dan tanda ≥ pada kasus minimasi juga bermakna crisp, demikian juga perintah ”maksimumkan” atau ”minimumkan ” merupakan bentuk imperatif tegas.

Pada fuzzy linear programming ,akan dicari suatu nilai z yang merupakan fungsi objektif yang akan dioptimasikan sedemikian hingga tunduk pada batasan-batasan yang dimodelkan dengan menggunakan himpunan fuzzy

Sehingga untuk kasus maksimasi akan diperoleh : Tentukan x sedemikian hingga:

cTx

~

≥

z

Ax ~

≤ B

X ≥ 0

Dengan tanda, ~

≥, merupakan bentuk fuzzy dari, ~

≥, yang menginterpretasikan ‘pada

dasarnya kurang dari atau sama dengan’. Demikian pula, tanda, ~

≥, merupakan bentuk

fuzzy dari , ~

≥, yang menginterprestasikan pada dasarnya lebih dari atau sama dengan.

Untuk kasus minimisasi akan diperoleh : Tentukan x sedemikian hingga :

cTx

~

≥

z

Ax ~

≤ B

X ≥ 0

Kedua bentuk dan dapat dibawah ke suatu bentuk, yaitu Tentukan x sedemikian hingga :

Bx ~

≤ d

X ~

≤ 0

B = _     − A c ; dan

d = _

    − b z

; untuk kasus maksimasi

atau

B = _

     −A c ; dan

d = _

     −b z

; untuk kasus minimasi

Tiap-tiap baris / batasan (0,1,2….,m) akan direpresentasikan dengan sebuah himpunan fuzzy, dengan fungsi keanggotaan pada himpunan ke-i adalah µi [x].

Fungsi keanggotaan untuk model ‘keputusan” himpunan fuzzy dapat dinyatakan sebagai :

µD

i min [x] = {µi

{

[ ]

}

min max ] [ max 0

0 D x x i i x

x≥ µ = ≥ µ [x]}

Tentu saja diharapkan, kita akan mendapatkan solusi terbaik, yaitu suatu solusi dengan nilai keanggotaan yang paling besar, dengan demikian solusi sebenarnya adalah :

Dari sini terlihat bahwah µi[x] = 0 jika batasan ke-i benar-benar dilanggar. Sebaiknya,

µi[x] = 1 jika batasan ke – i benar-benar dipatuhi (sama halnya dengan batasan

bernilai tegas). Nilai µi[x] akan naik secara monoton pada selang (0,1), yaitu :

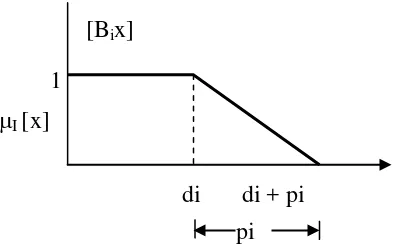
µi      + > + ≤ < ≤ ∈ pi d x B p d x B d d x B jika jika jika 0; [0,1]; 1; i i i i i i i [x] =

i = 0,1,2,…………, m

1

Gambar 6. Fungsi Keanggotaan

µi      + > + ≤ < ≤ − pi d x B p d x B d d x B jika jika jika ; pi B 0; 1 1; i i i i i i i ix di

[x] =

i = 0,1,2,…………, m

dengan pi adalah toleransi interval yang diperbolehkan untuk melakukan pelanggaran baik pada fungsi obyektif maupun batasan. Dengan mensubstitusikan kedua persamaan diatas akan diperoleh :

      − − = ≥ ≥ _pi d x B x i i x D

x [ ] maxmin 1 max

0 0 µ

Dari gambar di atas dapat dilihat bahwa, semakin besar nilai domain, akan memiliki

nilai keanggotaan yang cenderung semakin kecil. Sehingga untuk mencari nilai λ-cut

dapat dihitung sebagai λ = 1-t, dengan : di + tpi = ruas kanan batasan ke – i

dengan demikian akan diperoleh bentuk linear programming baru sebagai berikut : Maksimumkan : λ

Dengan batasan : λ pi + Bix ≤ di + pi i = 0,1,……….m

x ≥ 0

[Bix]

di + pi di

µI [x]

BAB III

PEMBAHASAN

Pada bab ini akan dibahas mengenai optimisasi metode modifikasi subgradient

3.1 Program Linear Dengan Koefisien Fuzzy Teknologikal

Suatu persamaan program linier dengan koefisien fuzzy tekhnologikal dirumuskan sebagai berikut :

Maksimumkan:

∑

= n 1 j j jx c

dengan kendala:

∑

= ≤ n j i j ij x b a

1 ~

(1.1)

1 ≤ i ≤ m xj

( )

x =

aij

µ

≥ 0, 1 ≤ j ≤ n

Dimana xj > 0 untuk yang lainnya Dengan asumsi-asumsi

Asumsi 1. aij adalah bilangan fuzzy dengan fungsi keanggotaan linier yaitu :

     − + 0 / ) ( 1 ij ij

ij d x d

a if if if ij ij ij ij ij ij d a x d a x a a x + ≥ + < ≤ <

dimana x ∈ R dan dij> 0 untuk semua i = 1,..., m, j = 1,..., n. untuk defuzzifikasi dari masalah ini, pertama fuzzify fungsi objektif. Ini dilakukan dengan menghitung batas bawah dan batas atas dari nilai optimal pertama, batasan dari nilai optimal, z1 dan zu termuat dengan pemecahan masalah program linear

standar yaitu :

z1

∑

dengan kendala

∑

= ≤ n j i j ijx b a

1

,i =1,…,m, (1.2)

x_j≥ 0, j= 1, …,n

dan

z2

∑

= n j j jx c 1 = max

dengan kendala

∑

= ≤ + n j i j ij

ij d x b a

1

)

( (1.3)

x_j≥ 0

Fungsi objektif bernilai antara z1 & z2

ij

a

yang koefisien tekhnologikalnya berbeda

antara dana_ij +d_ij. Misalkan z1 = min (z1, z2) dan zu = max (z1, z2) maka z1

dan zu

ℜ

disebut batas bawah dan batas atas.

Asumsi 2. masalah linear crisp pada persamaan (1.2) dan (1.3) mempunyai nilai optimal terbatas. Dalam kasus ini nilai optimal, G, dimana subset dari n

       − − =

∑

= 1 ) /( ) ( 0 ) ( ₁ 1

1 z z

z x c x _u n j j j G µ didefinisi sebagai :

∑

∑

∑

= = = ≥ < ≤ < n j u j j n j u j j n j j j z x c if z x c ifz z x c if 1 1 1 1 1 (1.4)

himpunan fuzzy darii, kontain C_i,dimana subset ℜm

       − =

∑

∑

= = 1 / ) ( 0 ) ( 1 1 n j j ij n j j ij i

i x b a x d x c

µ

didefinisikan sebagai :

,

∑

∑

∑

∑

= = = = + ≥ + < ≤ < n j j ij ij i n j n j j ij ij i j ij n j j ij i x d a b x d a b x a x a b 1 1 1 1 ) ( )

( (1.5)

Dengan menggunakan definisi keputusan fuzzy yang dikembangkan oleh Bellman dan Zadeh, maka diperoleh:

(x) min( (x),min( (x))).

i

C i G

D µ µ

Dalam kasus ini keputusan fuzzy optimal adalah solusi optimal dari permasalahan

max( ( )) maxmin( ),min( ( ))). 0

0 D x _x G _i Ci x

x≥ µ = ≥ µ µ (1.7)

sebagai akibat, persamaan (1.1) ini menjadi permasalahan optimisasi:

, ) ( ) ( max λ µ λ µ λ ≥ ≥ x x i C

G (1.8)

1≤i≤m, x≥0, 0≤λ≤1

Dengan menggunakan persamaan (1.4) dan (1.5) persamaan (1.8)dapat ditulis sebagai berikut:

∑

∑

= = ≤ − + ≤ + − − n j i j ij ij n j j j b x d a z x c z z 1 1 2 2 1 0 ) ( , 0 ) ( max λ λ λ (1.9)

1≤i≤m, x_j ≥0, j = 1,...,n, 0≤λ ≤1

Dengan catatan, bahwa persamaan (1.9) memuat cross product ,λ_xj tak convex. Oleh

karena itu, dibutuhkan solusi dari persamaan ini sehingga pemecahaan umum dari persoalan optimisasi nonconvex dapat diselesaikan

3.2 Program Linear Dengan Koefisien FuzzyTeknologikal Dan Fuzzy Ruas

Kanan

Pada persoalan program linear dengan fuzzy koefisien teknologikal dan fuzzy ruas kanan didefinisikan :

Max

∑

= n 1 j j jx c

∑

= ≤ n j i j ijx b a

1

, ~

(2.1)

1≤i≤m, x_j ≥0

Asumsi 3. a_ijdan b_iadalah bilangan fuzzy dengan fungsi keanggotaan linier, yaitu :      − + = 0 / ) ( 1 )

( _{ij ij ij}

aij x a d x d

µ , ij ij ij ij ij ij d a x d a x ifa a ifx + ≥ + < ≤ < dan      − + = 0 / ) ( 1 )

( i i i_,

i x b p x p

b µ , , , pi bi ifx p b x ifb b ifx i i i i + ≥ + < ≤ <

dimana x ∈ R. Untuk defuzzifikasi dari persamaan (2.1) dapat dihitung nilai optimal dari batas bawah dan batas atas. Nilai optimal z1 dan zu dapat

didefinisikan dengan pemecahan menurut persamaan linear programming standar, untuk itu diasumsikan nilai optimal terbatas yaitu:

z1

∑

= n 1 j j jx c = max

∑

= ≤ + n j i j ij

ij d x b a

1

, )

( (2.2)

1≤i≤m

xj ≥ 0

z2

∑

= n 1 j j jx c = max

∑

= + ≤ n j i i j

ijx b p a

1

, (2.3)

1≤i≤m

xj ≥ 0

z3

∑

= n 1 j j jx c = max

∑

= + ≤ + n j i i j ij

ij d x b p a

1

, )

( (2.4)

xj ≥ 0 dan

z4

∑

= n 1 j j jx c = max

∑

= ≤ n j i j ijx b a

1

, (2.5)

1≤i≤m xj ≥ 0

andaikan zl = min (z1, z2, z3, z4) & zu = max (z1, z2, z3, z4). Fungsi objektif bernilai

antara zl dan zu, koefisien teknologi bernilai antara aijdan aij +dij dan ruas kanan

bernilai antara b_idan b_i + p_i. Maka, himpunan fuzzy dari nilai optimal G yang mana subset dari Rn

       − − =

∑

= 1 ) /( ) ( 0 ) ( 1 1 1 n j u j j

G x c x z z z

µ

, yang didefinisikan sebagai :

∑

∑

∑

= = = ≥ < ≤ < n j u j j n j u j j n j j j z x c if z x c ifz z x c if 1 1 1 1 1 (2.6)

himpunan fuzzy dari kontrain Ci, dimana subset Rn didefinisikan sebagai :

       + − =

∑

∑

= = 1 ) /( ) ( 0 ) ( 1 1 n j i j ij n j j ij i

C_i x b a x d x p

µ

∑

∑

∑

∑

= = = = + + ≥ + + < ≤ < n j i j ij ij i n j n j i j ij ij i j ij n j j ij i p x d a ifb p x d a b x a if x a ifb 1 1 1 1 , ) ( )

( (2.7)

Dengan menggunakan metode defuzzifikasi sebagai permasalahan dari persamaan (2.8), persamaan (2.1) direduksi ke persoalan crisp sehingga :

Max λ

λ (z2 – z1

∑

= n 1 j j jx c

) - + z1

∑

= + n 1 j dij) (aij λ ≤ 0

xj + λpi – bi ≤ 0, (2.8)

, 1 ≤ i ≤ m x ≥ 0,

0 ≤ λ≤ 1

Dengan catatan bahwa, persamaan (2.8) juga persoalan non convex programming.

3.3 Metode modifikasi subgradient

Metode modifikasi subgradient dikembangkan oleh Gasimov yang mana dapat menyelesaikan pemecahan kelompok nonconvex dan nonsmooth pada persoalan optimisasi. Metode ini berdasarkan pada konstruksi permasalahan dual dengan menggunakan fungsi lagrangian.

Andaikan X topologikal linier, S⊂X, Y suatu bentuk real dan Y* adalah dual. Anggap masalah program matematika primal didefinisikan sebagai berikut :

Inf P = Inf f(x) xeS

dengan kendala g (x) = 0

Dimana f adalah nilai fungsi real yang didefinisikan di S dan g adalah pemetaan dari S ke Y. untuk setiap x ∈ X dan y ∈ Y andaikan :

didefinisikan lagrange function dengan persoalan (p) menjadi

L (x, µ, c) = inf {Φ (x,y) + (II y II – (y, µ)} y∈Y

untuk x ∈ X, µ ∈ Y* dan c ≥0. Dengan menggunakan persamaan (3.1)diperoleh :

L (x, µ, c) = f(x) + c II g (x) II – (g (x), µ ) (3.2)

Dimana x ∈ S, µ ∈ Y* dan c ≥ 0

Ini mudah untuk ditunjukkan bahwa: Inf P = Inf sup L (x, µ,c)

xeS(µ,c), ∈ Y* x ℜ+

fungsi dual H didefinisikan :

H(µ,c) = inf L(x, µ,c) (3.3)

x∈S

Untuk u ∈ Y* dan c ≥ 0, maka persoalan dual (p) diperoleh :

(P*) sup P* = sup H (µ,c) (µ,c) ∈ Y* x ℜ+

Elemen (,µ,c ) ∈ Y* x Rt dengan H (µ,c ) = Sup P* adalah solusi (P*)

Teorema 1. Andaikan (P) diketahui f dan g kontinu, S adalah solusi yang mudah. Maka Inf P= Sup P* dan terdapat solusi di (P). Fungsi H di (P*) konkav dan terbatas di Y*x ℜ+, sehingga masalah maksimisasi tidak efisiensi.

Teorema 2. Andaikan Inf P = Sup P*

− −

c

,

µ

dan parameter ( )∈ Y* x ℜ+,

S x∈ inf

− −

c

,

µ

L(x, ) = f ( −

x) + ( −

c)║ g(x)║ - (g ( −

x), −

µ)

Maka −

xadalah suatu solusi (P) dan ( − −

c

,

µ ) adalah solusi (P*

µ

) jika dan hanya jika

g(x) = 0.

Bila diasumsikan dari teorema sebagaimana yang telah dipaparkan diatas, Maksimasikan fungsi dual H dengan menggunakan metode subgradient sehingga diperoleh nilai optimal dari persoalan primal. Sehingga:

S ( ,c ) = { −

x │

−

x minimasi f(x) + c ║ g(x)║- μ1 g(x), x S} ∈

Algoritma

Langkah 1 : (µk,ck ).pemecahan subproblema :

Min (f(x) + ck║ g(x) ║ - (g(x)), µk

∈

))

dengan kendala x S

andaikan xk suatu solusi. Jika g(xk) =0 lalu berhenti; (µk,ck ) adalah solusi masalah

dual (P*), xk

µ

adalah solusi untuk masalah primal (P) lanjutkan ke langkah 2. Langkah 2 : Andaikan k+1 = µk – skg(xk), ck+1 = ck + (sk+ εk ) ║ g(xk) ║

Dimana sk dan εk adalah skalar positif, gantikan k dengan k+1, dan ulangi kembali langkah 1.

3.4 Aplikasi metode modifikasi subgradient ke fuzzy linier programming

Untuk menggunakan metode subgradient ke persoalan (1.9), harus diformulasikan ke dalam persamaan konstrain dengan menggunakan slack variabel po dan pi menjadi :

max λ

go (x, λ, po) = x (z1 – z2

∑

= n 1 j j jx c

) - + z2

∑

= ≤ ≤ = + + n 1 j m 1 1 0, pi bi xj dij) λ (aij

+ Po = 0

gi (x, λ, pi) = (4.1)

x ≥ 0, Po, Pi ≥ 0, 0 ≤λ≤ 1

Untuk persoalan himpunan S dapat didefinisikan sebagai berikut :

S = {(x, p, λ) | x = (x1 ………, xn), p = (P0, P1, …Pn), xi ≥ 0, P0, Pi ≥ 0, 0 ≤ λ ≤ 1}

Maksimunkan λ = - min (-x) dan g (x, λ, p) = (go, gi, ……gm) Fungsi lagrangian di kelompokkan ke persoalan (4.1) menjadi :

L (x, μ, c) = - λ+ c [(λ (z1-z2

∑

= n 1 j j jx c

) - + z2 + Po)2

∑

= n 1 j + (

∑

= + n 1 j dij) xi aij

( λ xj –

bi + pi )2]1/2 – 40 (λ (z1 – z2

∑

= n 1 j j jx c

) + z2

∑

= m 1 j i µ

+ po) -

∑

= + n 1 j dij) xi aij

Contoh :

Pemecahan persoalan optimisasi Max 2x1 + 3x2

1x1 + 2x2≤ 4

3x1 + 1x2≤ 6

x1, x2

     

1 3

2 1

≥ 0

Ambil parameter fuzzy

1 = L(1,1), 2 = L (2,3), 3 = L (3,2) dan 1 = (1,3)

(aij) = (dij) = _

    

3 2

3 1

⇒ (aij + dij) = _

    

4 5

5 2

Untuk persoalan ini harus diselesaikan menurut dua sub persoalan yaitu : z1 = max 2x1 + 3x2

x1 + 2x2≤ 4

3x1 + x2≤ 6

x1 , x 2 ≥ 0

dan z2 = max 2x1 + 3x2

2x1 + 5x2≤ 4

5x1 + 4x2≤ 6

x1 , x 2 ≥ 0

Solusi optimal :

x1 = 1,6 dan x1 = 0,82

x2 = 1,2 x2 = 0,47

z1 = 6,8 z2

λ 3,06 6,8

3,06 3x

2x_{1 2}

≥ −

− +

= 3,06

Dengan menggunakan nilai optimal ini dapat direduksi ke persoalan program non linear ekivalen, yaitu :

Max λ

λ 3x

x

2x x 4

2 1

2

1 ≥

λ 3x 2x

x x 3 6

2 1

2

1 ≥

+ − −

0 ≤ λ≤ 1 x1, x2≥ 0

Bahwa :

Max λ

2x1 + 3x2≥ 3,06 + 3,74λ

(1 + λ) x1 + (2 + 3λ) x2 ≤ 4

(3 + 2λ) x1 + (1 + 3λ)x2 ≤ 6

0 ≤ λ≤ 1 x1 , x2 ≥ 0

Po, P1, P2≥ 0

Sebelum pemecahan masalah, maka pertama kali harus diformulasikan kedalam bentuk:

Max λ = - min (-λ)

3.74 λ -2x1 – 3x2 + 3.06 + po =0

(1 + λ) x1 + (2 + 3λ) x2 – 4 + p1 =0

(3 + 2λ) x1 + (1 + 3λ)x2 - 6 + p2 =0

0 ≤ λ≤ 1 x1 , x2 ≥ 0

Po, P1, P2≥ 0

Dimana, P0, P1 dan P2 adalah slack variabel

Fungsi lograngian untuk masalah ini :

L(x,u,c) = λ + c [ c 3,74 λ - 2x1 – 3x2 + 3,06 + po)2 + (1 + λ) x1 + (2 + 3λ) x2 –

4 + p1)2 + ( 3 + 2λ) x1 + (1 + 3λ) x2 – 6 + p2)2]1/2 – μ0 (3,74 λ - 2x1 – 3x2 + 3,06 + P0)

– μ1 ((1 + λ) x1 + (2 + 3λ) x2 – 4 + p1) – μ2 ((3 + 2λ) x1 + (1 + 3λ) x2 – 6 + P2

1 1 2 1 1 1

0,µ ,µ ,c

µ

)

Andaikan inisial vektor ( ) = (0,0,0,0) dan andaikan pemecahan menurut

0,82 ≤ x1 ≤ 1,6

0,47 ≤ x2 ≤ 1,2

Solusi optimal dari sub persoalan yaitu : x1 = 1

x2 = 0 λ = 1

g1 (x1, p1, λ1) = 4,8

g2 (x1, p1, λ1) = -2

g3 (x1, p1, λ1) = -1

Jadi, g (x1, p1, λ1) ≠ 0, hitung nilai baru dari perkalian lagrange (µ₀1,µ₁1,µ₂1,c1)

dengan menggunakan langkah 2 dari metode modifikasi sub gradient. Solusi dari iterasi kedua yaitu :

x1 = 1,1475877

x2 = 0,75147 λ* = 0,3973723

g1 (x2, p2, λ2) = 9 x 10-6

g2 (x2, p2, λ2) = 3,8 x 10-6

g3 (x2, p2, λ2) = 2,31 x 10-6

Jadi, II g (x) II lebih kecil , dengan :

x1* = 1,1475877, x2* = 0,75147 dan λ = 0,3973723 ini berarti bahwa (x1*, x2*)

BAB IV

KESIMPULAN DAN SARAN

4.1 Kesimpulan

1. Bahwa metode modifikasi subgradient mampu menyelesaikan persoalan dengan memilih solusi yang terbaik tetapi dalam hal ini digunakan hanya sampai koefisien fuzzy teknologikal dan fuzzy ruas kanan.

2. Untuk contoh soal digunakan pendekatan fungsi lagrange. Metode ini dipilih karena prinsip kerja dari fungsi lagrange sederhana dan tidak sulit untuk dimengerti.

3. Metode modifikasi subgradient ini mempunyai beberapa keuntungan antara lain: dualitas bilangan nol dapat digunakan untuk masalah yang rumit, nilai dari fungsi dual naik terus setiap iterasi, metode ini tidak menggunakan parameter penghabisan, dan metode ini mempunyai kriteria pemberhentian alami.

4. Nilai optimal λ dari metode modifikasi subgradient hanya dapat ditemukan pada iterasi kedua sedangkan bila memakai metode decesive set harus mencari sampai nilai optimalnya diperoleh.

4.2 Saran

DAFTAR PUSTAKA

1. Azimov, A. Y., Gasimove, R. N. 1999. : Onweak Conjugacy, Weak

Subdifferentials and Duality with Zero -Gap in Non-Convex Optimization.

Internasional Journal of Applied Mathematics Vol (1999) 171-192.

2. Bellman, R.E. dan L.A.Zadeh,1970, Decision Making in Fuzzy Envirotment. Jurnal of Management Science, vol. 17 (1970), B141-B165.

3. Klir, G.J. dan B.Yuan, 1995, Fuzzy Sets And Fuzzy Logic – Theory And Aplications, Prentince – Hall.

4. Kusumadewi, Sri, 2002, Analisa dan Desain Sistem Fuzzy menggunakan

Toolbox Matlab, Graha Ilmu, Jakarta.

5. Libermann, G. j. dan F.S. Hillier,1990, Introduction to Operation Research Fifth Edition, McGraw-Hill.

6. Sakawa, M., Yana, H., 1985: Interactive Decision Making For Multi - Objective Linear Fractional Programming Problems with Fuzzy

Parameter, Cybernetics systems 16 (1985) 377 -397.

7. Zimmermann, H.J.,1983 : Fuzzy Mathematical Programming, Comput. & Ops. Res. vol 10 No. 4 (1983) 291 – 298.