GENERALISASI METODE PENCABANGAN PADA
PROGRAM INTEGER CAMPURAN
TESIS
Oleh
ALI KADIR LUBIS
117021002/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
GENERALISASI METODE PENCABANGAN PADA
PROGRAM INTEGER CAMPURAN
T E S I S
Diajukan Sebagai Salah Satu Syarat
untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Sumatera Utara
Oleh
ALI KADIR LUBIS
117021002/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2013
Judul Tesis : GENERALISASI METODE PENCABANGAN PADA PROGRAM INTEGER CAMPURAN Nama Mahasiswa : Ali Kadir Lubis
Nomor Pokok : 117021002
Program Studi : Magister Matematika
Menyetujui, Komisi Pembimbing
(prof. Dr. Saib Suwilo, M.Sc) (Prof. Dr. Tulus, M.Si)
Ketua Anggota
Ketua Program Studi Dekan
(Prof. Dr. Herman Mawengkang) (Dr. Sutarman, M.Sc)
Telah diuji pada Tanggal 5 Juni 2013
PANITIA PENGUJI TESIS
Ketua : Prof. Dr. Saib Suwilo, M.Sc
Anggota : 1. Prof. Dr. Tulus, M.Si
2. Prof. Dr. Herman Mawengkang
3. Prof. Dr. Opim Salim S, M.Sc
PERNYATAAN
GENERALISASI METODE PENCABANGAN PADA PROGRAM INTEGER CAMPURAN
TESIS
Saya mengakui bahwa tesis ini adalah hasil karya sendiri, kecuali beberapa kuti-pan dan ringkasan yang masing-masing dituliskan sumbernya
Medan, 5 Juni 2013 Penulis,
Ali Kadir Lubis
ABSTRAK
Penelitian ini mendiskusikan persoalan generalisasi metode pencabangan pada program integer campuran. Mehrotra dan Li (2004) menunjukkan bahwa permasalahan mene-mukan pencabangan hyperplane yang baik pada program integer campuran dapat diru-muskan pada adjoint lattice dari Kernel lattice dari kendala kesetaraan tanpa memer-lukan pengurangan dimensi. Sebagai akibat algoritma vektor kisi menemukan, seperti algoritma Lenstra, Lenstra, Lovasz (algoritma-LLL) atau algoritma pengurangan basis umum dari Lovasz dan Scarf (algoritma-LS) digambarkan dalam variabel ruang asli. Dengan memberikan cara heuristik baru yang alami dalam menghasilkan pencabangan hyperplanes, dan mendiskusikan hubungan dengan teknik reformulasi terbaru Aardal dan Lenstra. Baravykaite dan Ciegis (2007) menyampaikan implementasi template paradigm BnB, C++ untuk semua langkah utama algoritma BnB.
Kata kunci : Program linier, Program integer linier campuran, Branch-and bound
ii
ABSTRACT
This study discusses the generalization branching method on mixed integer program. Mehrotra and Li (2004) showed that the problem of finding a good branching hyperplane on mixed integer program can be formulated on the adjoint lattice of Kernel lattice of equality constraints without the need for dimensional reduction. As a result of finding lattice vector algorithm, such as algorithms Lenstra, Lenstra, Lovasz (LLL algorithm) or general basis reduction algorithm of Lovasz and Scarf (algorithm-LS) is described in the original variable space. They provide a natural way of generating new heuristic branch-ing hyperplanes, and discuss the relationship with the latest reformulation techniques of Aardal and Lenstra. Baravykaite and Ciegis (2007) presents a template implementation of the BnB paradigm, C + + for all the major steps on BnB algorithms.
Keyword : Linear programming, Mixed integer linear programming,Branch-and bound
KATA PENGANTAR
Puji syukur kepada Allah SWT yang selalu memberikan rahmat dan hidayah yang luar biasa sehingga penulis dapat menyelesaikan tesis dengan judul : GENERALI-SASI METODE PENCABANGAN PADA PROGRAM INTEGER CAM-PURAN. Penulis menyampaikan terima kasih yang sebesar-besarnya kepada :
Bapak Prof. Dr. dr. Syahril Pasaribu, DTM&H, M.Sc(CTM), Sp.A(K) selaku Rektor Universitas Sumatera Utara.
Bapak Dr. Sutarman, M.Sc, Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara, yang telah memberikan kesempatan kepada penulis untuk mengikuti Program Magister Matematika di FMIPA Universitas Sumatera Utara.
Bapak Prof. Dr. Herman Mawengkang, Ketua Program Studi Magister Mate-matika FMIPA Universitas Sumatera Utara sekaligus Pembanding-II yang memberikan saran dan kritik dalam penyempurnaan tesis ini.
Bapak Prof. Dr. Saib Suwilo, M.Sc, selaku Sekretaris Program Studi Magister Matematika FMIPA Universitas Sumatera Utara, yang juga sebagai pembimbing I, dan banyak memberikan bimbingan dan arahan dalam menyelesaikan tesis ini.
Bapak Prof. Dr. Tulus, M.Si, yang juga sebagai pembimbing II yang telah mem-berikan bimbingan, arahan dan ilmu pengetahuan dalam menyelesaikan tesis ini.
Bapak Prof. Dr. Opim Salim S, M.Sc, Pembanding-I yang telah memberikan saran dan kritik dalam penyempurnaan tesis ini.
Bapak / Ibu Dosen Program Studi Magister Matematika FMIPA Universitas Sumatera Utara yang telah memberikan ilmunya selama masa perkuliahan.
Ibu Misiani, S.Si, sebagai staf administrasi Program Studi Magister Matematika FMIPA Universitas Sumatera Utara yang banyak membantu proses administrasi.
iv
Ucapan terimakasih juga penulis sampaikan kepada :
Ibunda dan ayahanda tercinta, Almarhumah Rodiah Nasution dan Kadi Lubis serta keluarga tercinta, isteri : Sri Susilawati, S.Pddan anak anak : Alisha Rizki Andini Lubis dan Fadhil Anugrah Lubisyang telah memberikan kasih sayang dan dukungan baik moril maupun materil selama penulis dalam pendidikan dan penyele-saian tesis ini.
Rekan-rekan mahasiswa Program Studi Magister Matematika FMIPA Universitas Su-matera Utara khususnya angkatan reguler tahun 2011 Ganjil, dan semua pihak yang tidak dapat penulis sebutkan satu persatu pada tesis ini. Semoga Allah SWT membalas segala kebaikan dan bantuan yang telah diberikan.
Medan, Juni 2013 Penulis,
Ali Kadir Lubis
RIWAYAT HIDUP
Ali Kadir Lubis, dilahirkan di Muara Bungo Jambi pada tanggal 4 Mei 1971, merupakan anak kedua dari delapan bersaudara dari ayah Kadi Lubis dan ibunda Rodiah Nasution. Penulis menyelesaikan pendidikan Sekolah Dasar (SD) di SD Negeri 066056 Medan pada tahun 1984, Sekolah Menengah Pertama (SMP) di SMP Swasta Hang Kesturi Medan pada tahun 1987, dan Sekolah Menengah Atas (SMA) di SMA Negeri 6 Medan pada tahun 1990.
Pada tahun 1990 penulis melanjutkan pendidikan Diploma III pada Fakultas Pen-didikan Matematika dan Ilmu Pengetahuan Alam jurusan PenPen-didikan Matematika di IKIP Medan dan melanjut pada tingkatan strata-1 pada Fakultas Pendidikan Matema-tika dan Ilmu Pengetahuan Alam jurusan Pendidikan MatemaMatema-tika Universitas Negeri Medan, dan memperoleh gelar Sarjana Pendidikan pada tahun 2001. Pada September 2011 penulis melanjutkan studi pada Program Studi Magister Matematika di FMIPA Universitas Sumatera Utara. Saat ini penulis, bertugas sebagai tenaga pengajar pada Sekolah SMP Swasta NU Medan, SMK Swasta NU Medan dan SMK Negeri 1 Patumbak Kab. Deli Serdang.
vi
DAFTAR ISI
Halaman
PERNYATAAN i
ABSTRAK ii
ABSTRACT iii
KATA PENGANTAR iv
RIWAYAT HIDUP vi
DAFTAR ISI vii
DAFTAR GAMBAR ix
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 3
1.3 Tujuan Penelitian 3
1.4 Manfaat Penelitian 3
1.5 Metode Penelitian 4
BAB 2 TINJAUAN PUSTAKA 5
2.1 Program Integer 5
2.2 Metode Branch and Bound 6
2.3 AlgoritmaBranch and Bound untuk Program Integer 8
2.4 Kelayakan Program Integer 13
2.5 Algoritma Pencabangan Hyperplane 14
BAB 3 PEMBAHASAN 15
3.1 Permasalahan Program Integer Linier Campuran 15
3.2 Menemukan Pencabangan Hyperplane untuk Kasus Integer Campuran 16
3.3 Pembulatan Matriks Pusat 17
BAB 4 KESIMPULAN DAN SARAN 21
4.1 Kesimpulan 21
4.2 Saran 22
DAFTAR PUSTAKA 23
viii
DAFTAR GAMBAR
Nomor Judul Halaman
2.1 Prinsip branch and bound 8
2.2 Calon solusi 1 10
2.3 Calon solusi 2 11
2.4 Calon solusi 3 11
ABSTRAK
Penelitian ini mendiskusikan persoalan generalisasi metode pencabangan pada program integer campuran. Mehrotra dan Li (2004) menunjukkan bahwa permasalahan mene-mukan pencabangan hyperplane yang baik pada program integer campuran dapat diru-muskan pada adjoint lattice dari Kernel lattice dari kendala kesetaraan tanpa memer-lukan pengurangan dimensi. Sebagai akibat algoritma vektor kisi menemukan, seperti algoritma Lenstra, Lenstra, Lovasz (algoritma-LLL) atau algoritma pengurangan basis umum dari Lovasz dan Scarf (algoritma-LS) digambarkan dalam variabel ruang asli. Dengan memberikan cara heuristik baru yang alami dalam menghasilkan pencabangan hyperplanes, dan mendiskusikan hubungan dengan teknik reformulasi terbaru Aardal dan Lenstra. Baravykaite dan Ciegis (2007) menyampaikan implementasi template paradigm BnB, C++ untuk semua langkah utama algoritma BnB.
Kata kunci : Program linier, Program integer linier campuran, Branch-and bound
ii
ABSTRACT
This study discusses the generalization branching method on mixed integer program. Mehrotra and Li (2004) showed that the problem of finding a good branching hyperplane on mixed integer program can be formulated on the adjoint lattice of Kernel lattice of equality constraints without the need for dimensional reduction. As a result of finding lattice vector algorithm, such as algorithms Lenstra, Lenstra, Lovasz (LLL algorithm) or general basis reduction algorithm of Lovasz and Scarf (algorithm-LS) is described in the original variable space. They provide a natural way of generating new heuristic branch-ing hyperplanes, and discuss the relationship with the latest reformulation techniques of Aardal and Lenstra. Baravykaite and Ciegis (2007) presents a template implementation of the BnB paradigm, C + + for all the major steps on BnB algorithms.
Keyword : Linear programming, Mixed integer linear programming,Branch-and bound
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Dalam semua permasalahan minimisasi, sejauh ini menganggap masing-masing desain variabel (termasuk variabel slack, jika ada) diperbolehkan untuk mengambil nilai nyata (atau pecahan). Dalam banyak situasi, sangatlah tepat dan mungkin untuk memiliki solusi pecahan. Misalnya, sangat mungkin untuk menggunakan ketebalan plat 2,66 mm dalam pembangunan struktur, waktu kerja 3,34 jam dalam proyek, dan nitrat 1,78 kg untuk menghasilkan pupuk. Namun, ada permasalahan praktis tertentu dimana nilai-nilai pecahan dari variabel desain tidak praktis dan tidak bermakna secara fisik. Misalnya, tidak mungkin untuk menggunakan 1,6 boiler pada termal pembangkit listrik, sebanyak 1,9 laki-laki dalam suatu proyek, dan 2,76 bubut di bengkel.
Jika solusi bilangan bulat yang diinginkan, adalah mungkin untuk menggunakan salah satu teknik dan pembulatan dari nilai optimum dari desain variabel ke nilai inte-ger terdekat. Namun, dalam banyak kasus sangat sulit untuk melengkapi solusi tanpa melanggar salah satu kendala. Seringkali, pembulatan solusi dapat memberikan nilai fungsi tujuan yang sangat jauh dari nilai optimum asli. Semua kesulitan ini dapat dihin-dari jika permasalahan optimasi yang diajukan dan diselesaikan sebagai permasalahan program integer (Rao 1984).
Program Integer merupakan pengembangan dari Program Linier yang menyele-saikan suatu persoalan dengan persyaratan tambahan bahwa variabel keputusan me-ngambil nilai bilangan bulat (integer). Program Integer ini sangat diperlukan karena banyaknya problema-problema yang timbul di dalam suatu perusahaan maupun dalam sistem ekonomi masyarakat yang peubah keputusannya harus mengambil nilai bilangan bulat. Ini dikarenakan adanya komoditas yang tak dapat terbagi, misalnya : jumlah gedung, jumlah jembatan, produksi mobil, kebutuhan tenaga kerja, dan sebagainya.
Untuk persoalan diatas, bilangan-bilangan pecahan tidak mempunyai arti, dan sering dalam prakteknya dilakukan pembulatan. Dalam pembulatan sering terjadi keke-liruan yang dapat menyebabkan solusi menjadi tidak layak ataupun nilai optimal tidak
1
2
tercapai, terlebih jika Program Integer mempunyai banyak variabel keputusan yang bernilai pecahan.
Sehingga, seharusnya metode pembulatan dihindarkan, karena ada kalanya nilai optimal itu dapat diperoleh tidak hanya dengan membulatkan bilangan pecahan saja tetapi justru harus mengubah nilai bilangan bulat yang sudah ada. Jadi untuk menda-patkan hasil optimal perlu dicari suatu cara untuk mengubah nilai variabel keputusan yang pecahan menjadi bilangan bulat. Proses untuk menentukan solusi yang demikian inilah yang menjadi kerangka dasar utama munculnya model Program Integer.
Dalam permasalahan optimisasi ketika semua variabel yang dibatasi untuk me-ngambil hanya nilai integer, hal itu disebut permasalahan pemrograman bilangan bulat. Ketika beberapa variabel hanya dibatasi untuk mengambil nilai integer, permasalahan optimasi itu disebut permasalahan program integer campuran. Ketika semua variabel desain permasalahan optimasi diperbolehkan untuk mengambil nilai-nilai baik nol atau satu, permasalahan ini disebut permasalahan pemrograman nol-satu (Rao, 1984).
Memecahkan permasalahan optimasi program integer, yaitu menemukan sebuah solusi optimal untuk berbagai jenis permasalahan, bisa menjadi tugas yang sulit. Tidak ada algoritma yang tepat, yang dapat memecahkan permasalahan ini dalam waktunya, tergantung secara polynomial pada permasalahan masukan panjang data atau per-masalahan ukuran data (Arora dan Barak, 2009).
Menurut Genova dan Vassil (2011) program integer linier mengacu pada kelas masalah optimasi kombinatorial terkendala dengan variabel integer, dimana fungsi tu-juannya adalah fungsi linier dan kendala ketaksamaan. Permasalahan optimasi program integer linier (ILP) dapat dinyatakan sebagai berikut:
(1) Maksimalkan cx
(2) Dengan kendala : Ax ≤b,
(3) x∈Zn,
dimana solusi x ∈ Zn adalah vektor dari variabel integer n; x = (x1, x2, . . . , xn)T dan
3
Pengembangan metode optimasi yang tepat untuk permasalahan optimasi pro-gram integer linier setidaknya, ada tiga pendekatan berbeda untuk memecahkan per-masalahan program integer, meskipun seringkali digabungkan menjadi prosedur solusi ”hybrid” dalam praktek komputasi ( Chen, etal.,2010), yaitu:
1. Algoritma cutting plane berdasarkan kombinatorik polyhedral
2. Pendekatan enumerative dan metode branch and bound, branch and cut, dan branch and price
3. Teknik relaksasi dan dekomposisi
Metode branch and bound merupakan metode yang paling sering dipakai untuk menyelesaikan problema Program integer. Metode branch and boundmemakai strategi dimana daerah layak dibagi menjadi himpunan bagian yang lebih kecil. Setiap him-punan bagian berurutan diperiksa sehingga penyelesaian layak yang menghasilkan nilai optimal dari fungsi objektif diperoleh.
1.2 Perumusan Masalah
Metodebranch and bounddalam menyelesaikan program integer campuran, pada prin-sipnya sama dengan pada program integer murni, hanya perlu modifikasi dalam penca-bangan pada variabel-variabel yang harus berharga bilangan bulat. Maka yang menjadi rumusan masalah dari penelitian ini adalah menggeneralisasi metode pencabangan un-tuk program integer campuran.
1.3 Tujuan Penelitian
Penelitian ini mempelajari masalah kelayakan campuran integer. Penelitian ini bertu-juan mendiskusikan metode pencabangan pada program integer campuran.
1.4 Manfaat Penelitian
Adapun manfaat yang diharapkan dari penelitian ini adalah dapat memberikan infor-masi memecahkan permasalahan umum dalam pemrograman integer. Mendiskusikan penggeneralisasian metode pencabangan dalam pemecahan persoalan program integer
4
campuran. Dan membuka sejumlah kemungkinan untuk bagaimana algoritma perca-bangan hyperplane dapat diimplementasikan.
1.5 Metode Penelitian
Metode penelitian ini bersifat literatur dan kepustakaan dengan mengumpulkan infor-masi dari beberapa jurnal. Langkah-langkah yang dilakukan adalah sebagai berikut:
1. Memperkenalkan masalah dalam pertimbangan
2. Mempertimbangkan masalah kelayakan program integer campuran
3. Menguraikan penemuan algoritma pencabangan hyperplane
BAB 2
TINJAUAN PUSTAKA
2.1 Program Integer
Program Integer merupakan pengembangan dari Program Linear dimana beberapa atau semua variabel keputusannya harus berupa integer. Jika hanya sebagian variabel kepu-tusannya merupakan integer maka disebut Program Integer campuran (Mixed Integer Progamming). Jika semua variabel keputusannya bernilai integer disebut Program In-teger Murni (Pure Integer Progamming). Sedangkan Program Integer 0-1 merupakan bentuk Program Integer dimana semua variabel keputusannya harus bernilai integer 0 atau 1 (binary).
Bentuk umum Program Integer adalah: (Mehrotra dan Li 2004)
maxPn
Suatu metode yang sederhana dan praktis untuk menyelesaikan program integer adalah dengan membulatkan hasil variabel keputusan yang diperoleh melalui LP. Pen-dekatan ini mudah dan praktis dalam hal usaha, waktu dan biaya yang diperlukan un-tuk memperoleh suatu solusi. Bahkan, pendekatan pembulatan dapat merupakan cara yang sangat efektif untuk permasalahan program integer yang besar dimana biaya-biaya hitungan sangat tinggi atau untuk permasalahan nilai-nilai solusi variabel keputusan yang sangat besar.
Dengan kata lain, solusi pembulatan dapat lebih jelek dibanding solusi integer optimum yang sesungguhnya atau mungkin merupakan solusi tak layak. Ini membawa konsekuensi besar jika jumlah produk-produk seperti pesawat angkut komersial atau kapal perang yang harus diproduksi dibulatkan ke bilangan bulat terdekat.
5
6
Meskipun IP dibatasi sejumlah solusi layak yang berhingga, namun karena peubah-nya mengambil nilai bilangan bulat membuatpeubah-nya sulit untuk menemukan algoritma yang efisien yang dapat mencari secara langsung titik layak yang integer di dalam ru-ang solusi. Dalam beberapa hal kesulitan ini sudah dapat diatasi oleh para ahli dengan menghasilkan sebuah prosedur solusi yang didasarkan pada penyelesaian problema LP.
Strategi yang dimaksud dapat disimpulkan dalam tiga langkah berikut :
1. Mengkonversi IP menjadi LP biasa
2. Menyelesaikan model LP yang direlaksasi dan mengidentifikasi titik optimum yang kontinu (yang bernilai pecahan)
3. Dimulai dari titik optimum yang kontinu, dengan menambahkan kendala khusus berturut-turut yang dapat memaksa titik optimum dari hasil model LP ke arah pembatasan integer yang diinginkan.
Ada dua metode umum yang digunakan untuk menghasilkan kendala khusus yang memaksa titik optimum dari LP yang direlaksasi ke arah solusi integer yang diinginkan, yakni metode :
a. Cutting plane
b. Branch and bound
2.2 Metode Branch and Bound
Salah satu metode yang dapat digunakan dalam menyelesaikan persoalan program in-teger (IP) adalah metode Branch and Bound. Menurut Winston (2000) metode branch and bound adalah suatu metode mencari solusi optimal dari suatu persoalan IP dengan mengenumerasi titik-titik dalam daerah fisibel dari suatu subpersoalan.
Pada metode branch and bound berlaku :
7
a. Apabila subpersoalan itu tidak fisibel
b. Apabila subpersoalan itu memberikan solusi optimal dimana seluruh vari-abelnya berharga bilangan bulat
c. Apabila nilai Z optimasi untuk subpersoalan itu tidak lebih baik dari nilai Z optimal (dalam persoalan maksimal berarti nilai Z optimal dari subpersoalan itu tidak lebih besar daripada batas bawah yang telah diperoleh)
2. Suatu subpersoalan dapat diabaikan (dieliminasi dari pertimbangan selanjutnya) apabila subpersoalan itu berada dalam situasi berikut :
a. Tidak fisibel
b. Batas bawah (LB) (menyatakan nilai Z dari calon solusi terbaik) sekurang-kurangnya berharga sama dengan nilaiZ dari subpersoalan yang bersangku-tan
Menurut Winston (2004), dikatakan terukur jika terdapat kondisi sebagai berikut:
1. Subpersoalan menghasilkan solusi tak fisibel, sehingga tidak dapat menghasilkan solusi optimal bagi IP
2. Subpersoalan tersebut menghasilkan suatu solusi optimal dengan semua variabel-nya bernilai integer. Jika solusi optimal ini mempuvariabel-nyai nilai fungsi objektif yang lebih baik daripada solusi fisibel yang diperoleh sebelumnya, maka solusi ini men-jadi kandidat solusi optimal dan nilai fungsi objektifnya menmen-jadi batas bawah nilai fungsi objektif optimal bagi masalah IP pada saat itu. Bisa jadi subper-soalan menghasilkan solusi optimal untuk masalah IP.
3. Nilai fungsi objektif optimal untuk subpersoalan tersebut tidak melebihi (untuk masalah maksimisasi) batas bawah saat itu, maka subpersoalan ini dapat dieli-minasi.
8
2.3 Algoritma Branch and Bound untuk Program Integer
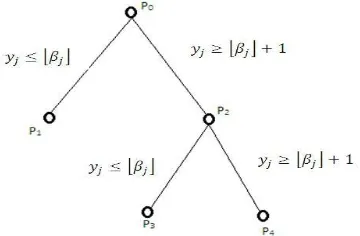
Dalam banyak usaha pemecahan permasalahan program integer campuran (atau per-masalahan optimasi diskrit lainnya, misalnya pedagang keliling, penjadwalan job shop) metode branch and bound paling berhasil diterapkan hingga saat ini. Misal permasala-han ini disebutP0. Langkah pertama adalah untuk memecahkan masalah LP ’berkelan-jutan’ diperoleh dengan mengabaikan kendala integralistik. Jika pada solusi optimal, satu atau lebih dari variabel-variabel bilangan bulat berubah menjadi non-integer, pilih salah satu variabel tersebut dan menggunakannya untuk membagi soal yang diberikan P0 menjadi dua ’sub-masalah’P1 dan P2. Misalkan variabel yang dipilih adalah yj dan
mengambil nilai non-integral βj di optimalkan terus menerus.
Kemudian P1 dan P2 didefinisikan sebagai berikut: P1 ≡P0 dengan penambahan kendalayj ≤ ⌊βj⌋
P2 ≡P0 dengan penambahan kendalayj ≥ ⌊βj+ 1⌋
Setiap solusi untuk P0 adalah juga solusi untuk P1 atau P2 dan sehingga P0 dapat diselesaikan dengan menyelesaikan P1 dan P2. Dilanjutkan dengan memecahkan per-masalahan LP terkait dengan P1 dan P2. Kemudian pilih salah satu masalah dan jika perlu membaginya menjadi dua sub-masalah seperti yang dilakukan dengan P0. Prinsip branch and bound diillustrasikan dalam gambar 2.1 berikut ini.
9
Proses ini dapat dilihat sebagai pembangunan sebuah pohon biner dari sub-masalah yang untuk terminal node yang sesuai dengan persub-masalahan yang masih harus diselesaikan. Dalam perhitungan yang sebenarnya, satu menyimpan daftar masalah yang belum terpecahkan dimana masalah utama telah terpecahkan. Satu juga me-nyimpan catatan nilai MIN tujuan solusi integer terbaik yang ditemukan sejauh ini.
Langkah 0: Awalnya, persoalan terdiri dari masalah awal P0. Masukkan MIN sama dengan salah satu nilai dari beberapa solusi bilangan bulat yang diketahui, atau jika salah satu tidak memberikan hasil pada beberapa batas atas dihitung dari data awal, jika tidak ada kemungkinan adalah tidak mungkin menempatkan MIN. Meme-cahkan masalah LP terkait dengan P0. Jika solusi memiliki nilai integer untuk semua variabel bilangan bulat maka akhiri, jika tidak
Langkah 1: Hapus masalah P dari daftar yang nilai fungsi tujuan optimalx0 lebih besar dari MIN. Jika tidak ada masalah akhiri. Solusi bulat terbaik yang ditemukan sejauh ini adalah optimal. Jika tidak ada ditemukan, maka permasalahan adalah tidak layak.
Langkah 2: Di antara variabel integer dalam masalah P dengan nilai-nilai non-integer dalam solusi optimal terus menerus untuk P, pilih satu untuk percabangan. Biarkan variabel ini menjadiyp dan biarkan nilai tersebut dalam solusi seterusnya menjadi
β.
Langkah 3: Buat dua masalah baru P′ dan P′′ dengan menambahkan pembatasan ekstra
masing-masing yp ≤ β dan yp ≥ β + 1. Selesaikan masalah LP terkait dengan
P′ dan P′′ dan menambahkan masalah ini ke dalam daftar. Jika solusi bilangan
bulat baru dan lebih baik ditemukan, simpan dan memperbarui MIN. Masalah LP baru tidak harus dipecahkan dari awal tetapi dapat kembali dioptimalkan dengan menggunakan algoritma ganda (atau secara parametris mengubah batasan pada yp). Jika selama re-optimasi dari persoalan LP, nilai fungsi tujuan melebihi MIN
masalah ini dapat diabaikan. Kembali ke langkah 1.
10
Jika dianggap bahwa setiap variabel integer dalamP0 memiliki batas atas terbatas (sama dengan beberapa nilai besar untuk variabel nominal yang tak terbatas) maka algoritma harus berhenti pada akhirnya, karena sebagai salah satu hasil yang lebih rendah, pohon dari masalah batas-batas pada variabel semakin ketat dan ketat, dan ini akhirnya akan menjadi tepat jika solusi LP tidak pernah integer.
Perhatikan contoh berikut:
MaksimumkanZ =−7x1−3x2−4x3
Kendala :
x1+ 2x2+ 3x3−x4 = 8 (2.1)
3x1+x2+x3−x5 = 5 (2.2)
x1, x2, . . . , x5 ≥0 dan integer (2.3)
Penyelesaian :
Awalnya persoalan ini diselesaikan sebagai persoalan LP. Solusi optimal LP adalah x1 = 2/5, x2 = 19/5, x3 =x4 =x5 = 0 dengan ¯Z0 = [−71/5] =−15.
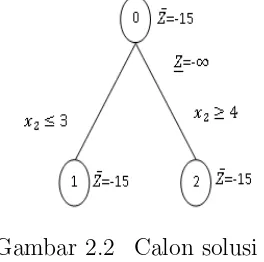
Selanjutnya P0 dipisahkan pada x1 atau x2 dan pilih sembarang x2. Hasilnya ditunjukkan pada gambar 2.2 berikut :
Gambar 2.2 Calon solusi 1
11
Gambar 2.3 Calon solusi 2
Dengan mengambil pencabangan sebelah kiri dan menyelesaikan LP-nya, diper-oleh solusi yang semuanya integer : x1 = 0, x2 = 3, x3 = 2, x4 = 4, x5 = 0 dengan
¯
Z1 =−17. Selanjutnya batas bawah baru Z0 = max{z1}=-17. Node 3 difathom dan kembali ke node 4. Hasilnya diperoleh ¯Z4 =−18 < z0, maka node 4 difathom. Kembali ke node 2.
Solusi optimal dari LP-nya x1 = 1/3, x2 = 4, x3 = 0,x4 = 1/3,x5 = 0 dengan ¯
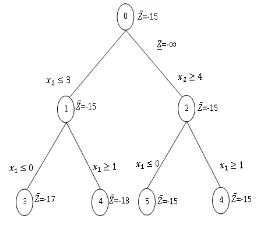
Z2 = [−43/3] =−15. Pencabangan dipilih pada x1 dan hasilnya terlihat pada gambar 2.4 berikut:
Gambar 2.4 Calon solusi 3
Pada node 5, solusi optimal dari LP-nya semuanya integer dan Z5 =−15. Selan-jutnyaZ0 = max{z5}=-15 dan node 5 dan 6 difathom. Sebuah solusi optimal diberikan dengan solusi pada node 5 : x1 = 0, x2 = 5, x3 = 0, x4 = 2, x5 = 0 dan Z =−15.
12
Sementara Baravukaite dan Ciegis (2007), memberikan algoritma branch and bound sebagai berikut :
Algoritma BnB()
begin
(1) cover solution space D by L=
Lj|D⊆Ujm=1Lj using covering rule
(2) S =∅, U B(D) =∞
(3) while (subspace list is not emptyL6=∅) do
(4) choose I ∈L using selection rule, excludeI fromL
(5) if (LB(I)⊂U B(D) +ǫ
(6) Branch I intop subspace Ij using branching rule
(7) for all (Ij, j = 1,2, . . . , p) do
(8) find U B(Ij∩D) and LB(Ij) using branching rules
(9) U B(D) = min(U B(D), U B(Ij ∩D))
(10) if (LB(Ij)< U B(D) +ε)
(11) if (Ij is a possible solution) thenS =Ij
(12) else L=LU{Ij}
(13) end if
(14) end if
(15) end for
(16) end if
13
end AlgoritmaBnB
Dimana L menunjukkan sebagai calon himpunan, S adalah solusi, UB (Di) dan LB (Di) menunjukkan sebagai batas atas dan batas bawah untuk nilai minimum dari fungsi objektif atas sub ruang Di.
Baravukaite dan Ciegis (2007)mendeskripsi dari sebuah template baru ke algorit-ma parallelbranch and bound. Kelas C++ untuk semua langkah utama algoritma BnB termasuk banyak contoh untuk seleksi, estimasi bound dan langkah-langkah pencaban-gan.
2.4 Kelayakan Program Integer
Masalah kelayakan program integer linier murni (FILP) adalah untuk
{x∈Zn+|Ax=a} (2.4)
dimana A ∈ Zm×n, a ∈ Zm, dan A diasumsikan matriks memiliki peringkat tertinggi. Jika tidak, maka baris linier dari A akan dihapus (Mehrotra dan Li 2004).
Masalah kelayakan program integer linier campuran (FMILP) adalah untuk
n
Kolom A sebagai variabel integer, dan kolom C sebagai variabel riil. Tanpa menghilangkan asumsi umum bahwa matriks C memiliki peringkat tertinggi. Jika hal ini tidak terjadi, maka dimiliki π sedemikian rupa sehingga πTC = 0, memungkinkan
untuk menghapus kendala untuk setiapπi 6= 0, dan menggantinya dengan kendalaπTB
= πTb.
Superscript T merupakan transpose dari vektor atau matriks. Untukx∈
Rn,kxk merupakan norml2, dankxkQmerupakan norm ellipsoid
p silkan oleh vektor kolom bi, i= 1, . . . , k. Dual dariA didefinisikan sebagai himpunan
14
A⊥ =
z ∈Rn|Az= 0, zTx∈Z,untuk semua x∈A .
Suatu latticeK∗(AT) disebut adjoin lattice dariA jika untuk setiap basisZ dariA ada
sebuah basis Z∗ dari K∗(AT) sehingga
ZTZ∗ =I (2.6)
Adjoint lattice adalah integral jika setiap anggotanya integral.
Proposisi 2.1 (Mehrotra dan Li, 2004)
Misal ˜Z adalah basis dari lattice A. Maka terdapat matriks integral ˜Z∗ sedemikian
rupa sehingga
˜
Z∗TZ˜ =I (2.7)
Mehrotra dan Li (2004) membuktikan dengan mengasumsikan sebuah basis Z dari A dipenuhi dari perhitungan HNF dari A, danZ∗ terbentuk seperti yang diuraikan diatas.
Karena Z dan ˜Z adalah basis untuk A dimiliki sebuah matriks unimodularV sehingga ˜
Z =ZV. Ambil ˜Z∗ =Z∗V−T. SejakV adalah unimodular, V−T juga unimodular.
2.5 Algoritma Pencabangan Hyperplane
Menurut Mehrotra dan Li (2004) masalah persoalan percabangan hyperplane ε(w, Q) adalah untuk menyelesaikan masalah minimasi :
min
u∈A∗\0W(u, ε(w, Q)) atau ekivalen minu∈A∗\0W(u, ε(0, Q)) (2.8)
dimana ε(0, Q) =nx∈Rn| kxkQ ≤1, Ax = 0o.
Adjoint kisi adalah paling sederhana untuk menghasilkan percabangan hyper-planes dalam ruang asli. Untuk sebuah kisi A∗, sejak A∗ ⊕ L(AT) adalah juga
meru-pakan adjoint kisi, memungkinkan seseorang untuk mengurangi unsur-unsur sebelumA∗
melakukan perhitungan apapun. Numerik ini menguntungkan terutama ketika menam-bahkan pencabangan hyperplane pada kendala yang ada.
BAB 3
PEMBAHASAN
Dalam bab ini akan dibahas tentang permasalahan dalam program interger linier cam-puran, penemuan pencabangan hyperplane pada program integer camcam-puran, dan pem-bulatan matriks pusat.
3.1 Permasalahan Program Integer Linier Campuran
Permasalahan program integer linier campuran, oleh Mehrotra dan Li (2004) ditun-jukkan dalam bentuk berikut, misalkan
¯
Menurut Mehrotra dan Li (2004), permasalahan menemukan solusi layak dari ¯P adalah setara dengan menemukan solusi layak dalam P rojxz( ¯P). Melalui proposisi berikut
menunjukkan bahwa kendala kesetaraan Axz = a dipertahankan dalam perhitungan
proyeksi himpunan.
Proposisi 3.1 (Mehrotra dan Li, 2004)
P rojxz( ¯P) =P rojxz( ˆP)∩ {xz ∈R
n|Ax z=a}
Menurut (Mehrotra dan Li, 2004) perhitungan eksplisit dari P rojxz( ¯P) seperti
yang diusulkan oleh Lenstra (1983) tidak praktis, dan dapat menghasilkan jumlah yang eksponensial dari kendala-kendala. Dalam hal ini, standar metode log-barrier memung-kinkan tidak lagi menghasilkan polinomial perkiraan-γ dari P rojxz( ¯P).
15
16
3.2 Menemukan Pencabangan Hyperplane untuk Kasus Integer Campuran
Lemma berikut memberikan cara untuk menghitung lebar himpunan polyhedral sepan-jang arah yang menarik tanpa menghitung proyeksi dari ¯P.
Lemma 3.1 (Mehrotra dan Li, 2004)
Misalkan Z, Z∗ memenuhi ZTZ∗ = I sebagai basis untuk masing-masing Λ dan Λ∗,
dimana Λ adalah kernel lattice dari A dan Λ∗ adalah adjoint lattice dari A. Untuk
setiap u∈Zn,
Mehrotra dan Li (2004) membuktikan sebagai berikut:
Bagian pertama dari Lemma ini dengan mengingat (ˆxz,xˆc) ∈ P¯, jika dan hanya jika
ˆ
xz ∈P rojxz( ¯P), dan nilai-nilai obyektif dalam ¯P dan P rojxz( ¯P) adalah sama.
Misalkan U = [UA :Z] adalah sebuah matriks unimodular yang memenuhiAU =
[H :O], dimana H adalah bentuk Hermite normal dari A. Misalkan U−T = [U∗
A :Z∗].
Jelas, UTU−T =I, maka ZTU∗
A = 0. Sejak U adalah matriks unimodular, maka U−T
juga matriks unimodular, karena itu adalah basis untuk Zn.
Oleh karena itu, untuk setiap u ∈ Zn, dimiliki vektor bilangan bulat p∗ ∈ Zk
17
Sebagai konsekuensi Lemma 3.1 merumuskan permasalahan menemukan arah tip-is dari ktip-isi Λ∗. Misalkan E(w, Q) = nx∈Rn+¯n| kx−wk
Q ≤1, Rx =r} menjadi
ellipsoid dinyatakan dalam ¯P dan E(w, Q) ⊆ P¯ ⊆ E(w, Q/γ), dimana γ adalah para-meter pendekatan.
Permasalahan menemukan percabangan hyperplane bagi ellipsoidE(w, Q) adalah
min
Maka, dapat menggunakan algoritma LLL-dan variannya bersama-sama dengan algo-ritma GBR untuk menghitung u yang cocok seperti dalam kasus PILP, dengan perbe-daan bahwa perhitungan dilakukan dengan menggunakan proyeksi matriksPRQ−1/2 yang berbeda dan pendekatan-nya. Pembahasan tentang aproksimasi Z∗ dengan ZF mana
F adalah himpunan dari variabel bilangan bulat pecahan pada solusi optimum dari masalah relaksasi terus berlaku.
3.3 Pembulatan Matriks Pusat
Misalkanwz menjadi komponen variabel integer dan wc menjadi komponen
varia-bel kontinu. Misalkan v menjadi solusi sehingga Rv =r, dimana v = h ¯vz
vc
menjadi solusi untuk masalah :
min
tunjukkan bahwa ada arah tipis dalam adjoin kisi Λ∗. Proposisi berikut menunjukkan
bahwa ellipsoid dalam ruang asli diproyeksikan menjadi ellipsoid dalam ruang bilangan bulat murni.
18
Proposisi 3.2 (Mehrotra dan Li, 2004) Misalkan Q = h QQTz Qzc
Mehrotra dan Li membuktikan; misal w = 0, maka wz = 0. Karena baris dalam
himpunan asli diproyeksikan ke baris, batas P rojxz(E(0, Q)) adalah sebuah ellips yang
didefinisikan oleh ˜Q. Untuk setiap xz yang diberikan memenuhi Axz = 0,
pertim-bangkan masalah optimasi berikut :
max
Solusi dari persamaan adalah dalam batasan dari E(0, Q). Berikut ditunjukkan bahwa ρ∗x
z adalah batas dari ˜E(0,Q). Sebuah solusi optimal (x˜ ∗c, ρ∗, λ∗, µ∗) dari
per-samaan (3.3-3.4) memenuhi kondisi optimal KKT :
λ∗(2ρ∗QTzcxz+ 2Qcx∗c) +CTu∗ = 0,
−1 +λ∗(2ρ∗(xTzQzxz) + 2xTzQzcx∗c) +µ∗TBxz = 0,
(ρ∗xz)TQz(ρ∗xz) + 2ρ∗xTzQTzcx∗c +x∗cTQcx∗c = 0,
ρ∗Bx
z+Cx∗c = 0,
dimana λ∗ dan µ∗ adalah pengganda Langrange sesuai dengan masing-masing kendala
3.4 dan 3.5. ρ∗x
z memenuhi kondisi KKT :
(ρ∗xz)TQ(ρ˜ ∗xz) = 1, Axz = 0,
Karena wz adalah proyeksiw, dan karena baris dalam ruang asli adalah proyeksi
untuk garis, ˜E(wz,Q) dan ˜˜ E(w,Q/γ) seperti tertulis dan yang melingkupi ellipsoid dari˜
P rojxz( ¯P), yaitu :
˜
19
Oleh karena itu, sebuah pendekatan-γ dari P rojxz( ¯P) tersedia. Log penghalang untuk
pusat analitik Hessian, dalam kasus terburukγ =n+ ¯n. Lebih buruk dari kemungkinan γ = n saat P rojxz( ¯P) dihitung secara eksplisit, dan kemungkinan γ = n− m jika
dianggap himpunan berdimensi lengkap dengan menghilangkan kendala kesetaraan.
Dari Proposisi 3.2 pemeriksaan kelayakan dari ˜vdapat dilakukan dengan memerik-sa apakah vz dalam ˜E(wz,Q). Dan sebaliknya.˜
Colorally 3.1 (Mehrotra dan Li, 2004)
Jikakwz−vzkQ˜ ≤1, maka dengan menyelesaikan persamaan (3.2) diperolehkwz−v˜kQ˜ ≤ 1. Selanjutnya, jika kwz−v˜kQ˜ >1 maka kwz −v˜kQ˜ >1.
Menggunakan proposisi 3.2 dan mengikuti argumen dalam lemma 3.1, dapat di-tunjukkan bahwa
untuk setiap u ∈ Zn. Oleh karena itu, masalah menemukan pencabangan hyperplane (3.1) setara dengan memecahkan
Jika ¯vdibangun pada persamaan (3.2) adalah bukan merupakan solusi yang layak, maka pencabangan hyperplane yang baik dapat diperoleh dengan menyelesaikan (3.1).
Teorema 3.1 (Mehrotra dan Li, 2004) Misalkan ˜Q1/2
Z menjadi pengurang basis LLL. Jika ¯v memenuhi kw−¯vkQ>1. Maka
ada sebuah arah pencabangan u∈ K∗(A)T sehingga
Wh u0 i,P¯≤γ(3/√2)k
Khususnya, satu dari u diberikan oleh Z∗e
20
Teorema 3.1 dan pembangunan prosedur pembulatan dapat memberikan kesan bahwa perlu menghitung ˜Q, dan secara terpisah pengurang-LLL ˜Q1/2
Z perlu dihitung. Proposisi berikut menunjukkan bahwa basis tersebut tersedia Z∗ dihasilkan untuk lebar
minimum permasalahan (3.1).
Proposisi 3.3 (Mehrotra dan Li, 2004)
Misalkan Z menjadi basis dari Λ, danZ∗ menjadi basis dari adjoint latticeAmemenuhi
ZTZ∗ = I. Diasumsikan bahwa vektor dari P Maka, vektor ˜Q1/2Z adalah pengurang-2 dalam urutan terbalik.
Bukti :
Dari Lemma 3.1 bagian (2) dimiliki
W(u,E˜(wz,Q)) =˜ W
Z∗. Setelah pengurang-2
Z dihitung, dalam rangka untuk menghitung ukuran pengurang ˜Q1/2
Z dapat dibentuk ZTQZ, dan bekerja dengan faktor Choleskynya. Perhitungan˜ ZTQZ˜ membutuhkan
pengerjaan dengan invers dari Qc atau CQ1CC. Dalam kasus linier Qc adalah matriks
diagonal, dan perhitungan dengan CQ−
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Berbagai permasalahan besar kehidupan nyata yang berbeda dalam praktek dirumuskan sebagai permasalahan optimasi bilangan bulat. Jumlah dan ukuran meningkat terus menerus. Terlepas dari kenyataan, bahwa produktivitas algoritma yang tepat dirancang untuk memecahkan permasalahan bilangan bulat telah jauh meningkat selama bebera-pa tahun terakhir, sangat sering tidak dabebera-pat diterapkan untuk memecahkan permasala-han praktis dari ukuran menengah dan besar karena waktu operasional berlebipermasala-han dan persyaratan memori.
Penyelidikan teoritis dan algoritmik juga diterbitkan yang dikhususkan untuk per-masalahan kombinatorial atau biner. Akibatnya, prosedur heuristik yang paling luas untuk memperoleh solusi awal yang cocok, evaluasi calon-solusi, cutting planes, strategi pencarian khusus, dll, terintegrasi dalam produk pemrograman komersial, efektif untuk permasalahan dengan variabel 0-1 atau permasalahan yang memiliki struktur khusus.
Solusi dari permasalahan bilangan bulat dalam kasus umum masih jauh lebih sulit. Metode hibrid adalah alat yang menjanjikan, karena menggabungkan fitur ter-baik dari metode yang berbeda (teknik yang tepat atau metaheuristik) dalam mode saling melengkapi (Bertacco, et. al (2007), Hansen, et. al (2006)). Sejak memper-oleh solusi layak baik dalam waktu yang wajar benar-benar memuaskan untuk banyak permasalahan praktis, pengembangan algoritma heuristik, memiliki komputasi kom-pleksitas polinomial, masih menjadi permasalahan hari ini.
Banyak permasalahan ukuran besar yang nyata dapat tidak diselesaikan dengan algoritma yang tepat karena komputasi eksponensial kompleksitas. Dalam kasus seperti ini, satu-satunya cara adalah penggunaan algoritma perkiraan waktu polynomial.
21
22
4.2 Saran
Meskipun uraian di atas dari penemuan ini telah ditunjukkan dan dijelaskan dengan mengacu pada perwujudan dan aplikasi tertentu, telah disajikan untuk tujuan ilustrasi dan deskripsi dan tidak dimaksudkan untuk menjadi pelengkap atau untuk membatasi penemuan ini pada perwujudan tertentu dan pengungkapan aplikasi. Maka akan jelas bagi yang memiliki ketrampilan dalam bidang sejumlah perubahan, modifikasi, variasi, atau perubahan dengan penemuan seperti yang dijelaskan di sini mungkin dibuat, tidak ada yang berangkat dari semangat atau ruang lingkup dari penemuan ini.
DAFTAR PUSTAKA
Aardal K dan A. K. Lenstra. 2004. Hard Equality Constrained Integer Knapsacks, Mat-hematical of operational Research, 29(3), 724–738.
Arora, S,. dan B. Barak. 2009. Computational Complexity: A Modern Approach. Cam-bridge University Press.
Barvykaite, M. dan R. Ciegis. 2007. ”An Implementation of a Parallel Generalized Branch and Bound Template”, Mathematical Modelling and Analysis, 12:3, 277– 289.
Bertacco, L., M. Fischetti, A. Lodi. 2007. A Feasibility Pump Heuristic for General Mixed-Integer Problems. -Discrete Optimization, Vol. 4, 2007, No 1, 63–76. Chen, D., R. G. Batson, Y. Dang. 2010. Applied Integer Programming: Modelling and
Solution. John Wiley & Son.
Gao L. dan Y. Zhang. 2002. Computational Experience with Lenstra’s Algorithm”, TR02–12, Department of Computational and Applied Mathematics, Rice Univer-sity.
Genova, K. dan Vassil Guliashki. 2011. ”Linear Integer Programming Methods and Approaches”.Cybernatics and Imformation Technologies, vol 11.
Hansen, P., N. Mladenovic, D. Urosevic.2006. Variable Neighborhood Search and Local Branching.Computers & Operational Research, Vol. 33, 2006, No 10, 3034–3035. Lenstra H.W. 1983. Integer programming with a Fixed number of variables,”
Mathema-tics of Operations Research, 8(4), 538–548.
Mehrotra S. dan Z. Li. 2004. On Generalized Branching Methods for Mixed Integer Linier Programming,Technical Report 2004-15, Dept. ofIE/MS, Northwestern University, Evanston, IL60208.
Rao, SS. 1984.”Optimazation: Theory and Aplications”, Second edition, San Diago State University, USA.
Winston,L.W. 2000.Operation Research: Application and Algorithm, third edition, Wadewort Publishing Company, Belmont California.
Wolsey, L. 1998. Integer Programming - In:Wiley - Interscience Series in Discrete Ma-thematics and Optimization. John Wiley & Sons, Inc.
23