SELEKSI HYPERSPECTRAL BAND MENGGUNAKAN RECURSIVE
FEATURE ELIMINATION UNTUK PREDIKSI PRODUKSI PADI
DENGAN SUPPORT VECTOR REGRESSION
HENDRA GUNAWAN
DEPARTEMEN ILMU KOMPUTER
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ii
SELEKSI HYPERSPECTRAL BAND MENGGUNAKAN RECURSIVE
FEATURE ELIMINATION UNTUK PREDIKSI PRODUKSI PADI
DENGAN SUPPORT VECTOR REGRESSION
HENDRA GUNAWAN
Skripsi
Sebagai salah satu syarat untuk memperoleh gelar
Sarjana Komputer pada
Departemen Ilmu Komputer
DEPARTEMEN ILMU KOMPUTER
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRACT
HENDRA GUNAWAN. Hyperspectral Band Selection using Recursive Feature Elimination
for Yield Prediction with Support Vector Regression. Supervised by HARI AGUNG ADRIANTO and SIDIK MULYONO.
Hyperspectral is a new technology in remote sensing that exploits hundreds of bands. Pusat Teknologi Inventarisasi Sumber Daya Alam Badan Pengkajian dan Penerapan Teknologi (PTISDA BPPT) applies hyperspectral in agriculture for yearly yield prediction. Hyperspectral images consist of large number of bands that require analysis to select features. One approach to reduce computational cost is to eliminate bands that do not add value to the regression and analysis method to be applied. In this research, we use a Recursive Feature Elimination (RFE) algorithm that is tailored to operate with Support Vector Regression (SVR) to perform band selection and regression simultaneously. Annual yield of paddy has been predicted with hyperspectral data using Support Vector Regression (SVR) algorithm. Regions used are Indramayu and Subang, and the altitude of the spectral acquisition is 2000 m (Hymap). This data is owned by PTISDA BPPT.
RFE-SVR used in hyperspectral data was able to reduce about 30% of the bands, resulting in 70 bands out of 109 original bands with an RMSE value of 0.0901 and R2 value of 0.9874. Radial Basis Function (RBF) is the best kernel used in RFE-SVR having an RMSE value less than those of other kernels tested.
ii Judul : Seleksi Hyperspectral Band Menggunakan Recursive Feature Elimination untuk Prediksi
Produksi Padi dengan Support Vector Regression
Nama : Hendra Gunawan NRP : G64070073
Menyetujui:
Pembimbing I,
Hari Agung Adrianto, S.Kom., M.Si. NIP. 19760917 200501 1 001
Pembimbing II,
Ir. Sidik Mulyono, M.Eng. NIP. 19670124 198602 1 001
Mengetahui:
Ketua Departemen Ilmu Komputer,
Dr. Ir. Sri Nurdiati, M.Sc. NIP. 19601126 198601 2 001
iii
RIWAYAT HIDUP
Penulis dilahirkan pada tanggal 13 Desember 1989 di Sumedang, Jawa Barat, dengan nama Hendra Gunawan dari pasangan Ibu Imas Masriah dan Bapak Atang Tahyana. Penulis lulus dari Sekolah Menengah Atas (SMA) Negeri 1 Sumedang pada tahun 2007. Tanggal 2 Juli 2007, penulis diterima sebagai mahasiswa Institut Pertanian Bogor melalui jalur Undangan Seleksi Masuk IPB (USMI). Tahun 2008, penulis resmi menjadi mahasiswa Departemen Ilmu Komputer, Fakultas Matematika dan Ilmu Pemgetahuan Alam.
Penulis aktif di organisasi Himpunan Mahasiswa Ilmu Komputer (HIMALKOM) sebagai divisi Marketing dan Relationship (MR) tahun 2008 sampai 2009. Tahun 2010, penulis menjalankan praktek kerja lapangan di Pusat Teknologi Inventarisasi Sumber Daya Alam Badan Pengkajian dan Penerapan Teknologi (PTISDA BPPT) selama 35 hari kerja.
iv
PRAKATA
Puji dan syukur penulis panjatkan ke hadirat Allah Subhanahuwata'ala atas limpahan rahmat dan hidayah-Nya sehingga laporan tugas akhir ini dapat diselesaikan dengan baik. Tulisan dengan judul Seleksi Hyperspectral Band Menggunakan Recursive Feature Elimination untuk Prediksi Produksi Padi dengan Support Vector Regression merupakan hasil penelitian tugas akhir di Departemen Ilmu Komputer. Salawat serta salam juga penulis ucapkan kepada junjungan Nabi Muhammad Shallalahu 'Alaihi Wasallam beserta seluruh sahabat dan umatnya hingga akhir zaman.
Pembuatan laporan ini tentu tidak lepas dari bantuan berbagai pihak. Oleh karena itu, penulis menyampaikan terima kasih kepada Bapak Hari Agung Adrianto, S.Kom, M.Si selaku pembimbing I dan Bapak Ir. Sidik Mulyono, M.Eng selaku pembimbing II atas bimbingan dan arahannya selama pengerjaan tugas akhir ini. Selain itu penulis juga mengucapkan terima kasih kepada semua pihak yang telah membantu dalam penyelesaian tugas akhir ini, yaitu:
1 Kedua orang tua tersayang atas segala do’a, kasih sayang, dan dukungannya.
2 Kakakku Heri Taufik beserta keluarga dan Rina Rosdiana beserta keluarga yang selalu memberi motivasi untuk dapat menyelesaikan tugas akhir ini.
3. Bapak Mushtofa, S. Kom, M.Sc selaku dosen penguji yang memberikan saran dalam penyelesaian skripsi ini.
4. Ibu Dr. Ir. Sri Nurdiati, M.Sc sebagai ketua departemen Ilmu Komputer yang selalu memberi nasihat dan motivasi kepada semua mahasiswa Ilmu Komputer.
5. Bapak Dr. Muhammad Evri, M.Sc, Bapak Dr. M. Sadly, M.Eng dan segenap karyawan PTISDA-BPPT sebagai tempat penelitian tugas akhir ini.
6. Erna, Eneng, Otri, Fauzi, Ana dan Nova teman seperjuangan mulai dari PKL dan selalu memberi semangat dalam penelitian ini.
7. Seluruh teman-teman Program Studi S1 Ilmu Komputer angkatan 44 yang tidak dapat disebutkan namanya satu-persatu.
Penulis juga mengucapkan terima kasih kepada semua pihak yang telah membantu selama pengerjaan penyelesaian tugas akhir ini yang tidak dapat disebutkan satu-persatu. Semoga penelitian ini dapat memberikan manfaat.
Bogor, Januari 2012
v
DAFTAR ISI
Halaman
DAFTAR TABEL ... vi
DAFTAR GAMBAR ... vi
DAFTAR LAMPIRAN ... vi
PENDAHULUAN Latar Belakang ... 1
Tujuan Penelitian ... 1
Ruang Lingkup Penelitian... 1
TINJAUAN PUSTAKA Hyperspectral ... 1
Support Vector Machine (SVM) ... 2
Support Vector Regression ... 3
Kernel Trick ... 4
LIBSVM ... 5
Recursive Feature Elimination (RFE) ... 5
Bootstraping (8-fold) ... 5
Koefisien Determinasi (R2) ... 6
Root Mean Square Error (RMSE)... 6
P-Norm ... 6
METODE PENELITIAN Pra-proses ... 6
Bootstraping (8-fold) ... 7
Support Vector Regression (SVR) ... 7
Bootstraping (8-fold) ... 6
Evaluasi Error ... 7
Recursive Feature Elimination... 7
Evaluasi Hasil ... 7
Lingkungan Pengembangan ... 7
HASIL DAN PEMBAHASAN Pra-proses ... 7
Bootstraping (8-fold) ... 8
Implementasi RFE-SVR ... 8
Parameter � (Gamma), epsilon, C ... 8
Penggunaan Kernel... 10
a Kernel Linear ... 10
b Kernel Sigmoid ... 11
c KernelRadial Basis Function ... 11
d Kernel Polinomial ... 12
Simpang Error ... 12
KESIMPULAN DAN SARAN Kesimpulan ... 13
Saran ... 13
DAFTAR PUSTAKA ... 13
vi
DAFTAR TABEL
Halaman
1 Beberapa jenis kernel yang digunakan. ... 5
2 Penyerapan gas di atmosfer... 8
3 Hasil dataset8-fold train-test... 8
4 Perbandingan seleksi fitur menggunakan kaidah p-norm ... 13
5 Konfigurasi band terbaik ... 13
DAFTAR GAMBAR
Halaman 1 Grafik sebaran nilai aktual dan prediksi yield 10 cm. ... 12 Perbandingan data multispectral dan hyperspectral tanaman Eucalyptus grandis. ... 2
3 Penyerapan gelombang elektromagnetik pada daun ... 2
4 Pemisah antar-kelas (hyperplane) ... 3
5 Linear SVR. ... 4
6 Pemetaan ruang vektor. ... 4
7 Tahap metode penelitian. ... 6
8 Grafik sebaran yield terbaik. ... 8
9 Perbandingan epsilon. ... 9
10 Perbandingan koefisien C. ... 9
11 Perbandingan parameter gamma. ... 10
12 Perbandingan jumlah band terhadap error dan weightkernel linear. ... 10
13 Sebaran prediksi yieldkernel linear. ... 11
14 Perbandingan jumlah band terhadap error dan weightkernel sigmoid... 11
15 Sebaran prediksi yieldkernel sigmoid. ... 11
16 Perbandingan jumlah band terhadap error dan weightkernel RBF. ... 12
17 Sebaran prediksi yieldkernel RBF. ... 12
18 Perbandingan jumlah band terhadap error dan weightkernel Polinomial. ... 12
19 Sebaran prediksi yieldkernel polinomial. ... 12
20 Perbandingan jumlah band dengan error norm-1. ... 13
21 Perbandingan jumlah band dengan error norm-∞. ... 13
DAFTAR LAMPIRAN
Halaman 1 Contoh data yield dan reflectance beberapa band ... 162 Koneksi Library SVM ke IDL ... 17
3 Contoh Pembagian Data training dan testing ... 20
4 Pemilihan epsilon ... 21
1 PENDAHULUAN
Latar Belakang
Prediksi jumlah produksi padi yang dilakukan saat ini masih bersifat tradisional, yaitu dengan melakukan survei ke lapangan dengan menghitung secara ubinan dan eyes estimate. Perhitungan secara ubinan dilakukan secara manual dengan menghitung berat hasil panen padi dalam ukuran 4 x 4 m. Eyes estimates hanya menghitung dengan perkiraan penglihatan seseorang, sehingga hasil yang diperoleh tidak akurat. Keadaan ini dapat menyulitkan proses penghitungan prediksi panen padi yang akan diserahkan ke pihak pemerintahan. Perkembangan pengetahuan dan teknologi menjadi salah satu faktor yang dapat mengatasi masalah ini. Salah satu cara yang dapat diterapkan yaitu dengan menggunakan teknologi hyperspectral. Teknologi ini menggunakan citra satelit berupa data pantulan cahaya (spectrum) dari objek yang ada di bumi. Data ini dapat digunakan untuk prediksi biofisik tanaman padi, seperti nitrogen dan klorofil.
Prediksi suatu nilai dapat diperkirakan dengan menggunakan regresi. Teknik regresi yang sering digunakan dalam berbagai bidang, contohnya regresi linear sederhana dan regresi linear multi variabel. Support Vector Machine
(SVM) merupakan salah satu learningmachine
yang ditemukan oleh Boser, Guyon, dan Vapnik pada tahun 1992. SVM ini berusaha mencari pemisah antar-kelas (hyperplane) yang maksimum. Kelebihan teknik ini dibandingkan dengan teknik klasifikasi lain adalah meminimalkan error pada training-set dan tingkat generalisasi dari SVM tidak dipengaruhi oleh dimensi dari input vektor (Nugroho et al. 2003). Konsep SVM dapat diadaptasi dalam masalah regresi, yang digunakan untuk memprediksi nilai yang diharapkan. Klasifikasi menghasilkan nilai diskret, sedangkan regresi menghasilkan nilai yang kontinu. Teknik ini biasa disebut dengan Support Vector Regression
(SVR).
Komputasi yang kompleks dalam teknik SVR dapat mengakibatkan cost yang tinggi, sehingga diperlukan teknik seleksi fitur. Seleksi fitur dapat digunakan untuk meningkatkan kecepatan komputasi dan model yang baik dengan melibatkan fitur-fitur yang diperlukan saja. Recursive Feature Elimination (RFE) adalah salah satu metode seleksi fitur yang dapat digunakan untuk memecahkan masalah tersebut.
Penelitian ini mencari fitur atau band terbaik pada data hyperspectral tanaman padi. Hasil
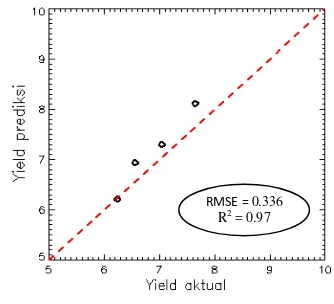
selanjutnya dapat digunakan untuk menghitung prediksi jumlah produksi padi (yield). Penelitian sebelumnya telah dilakukan oleh Yohan (2010) pada data hyperspectral ground tanaman padi dengan ketinggian 10 cm dari kanopi tanaman padi. Hasil prediksi masih kurang baik dengan nilai RMSE di atas 0.5 dan R2 kurang dari 0.5 (Gambar 1).
Gambar 1 Grafik sebaran nilai aktual dan prediksi yield 10 cm.
Tujuan Penelitian
Penelitian ini bertujuan untuk
1 Melakukan seleksi band pada data
hyperspectral padi menggunakan teknik
Recursive Feature Elimination (RFE) dan prediksi yield menggunakan Support Vector Regression (SVR).
2 Mendapatkan kernel yang cocok untuk
Support Vector Regression.
3 Membandingkan kaidah p-norm pada hasil SVR.
Ruang Lingkup Penelitian
Data yang digunakan adalah data
hyperspectral milik PTISDA - BPPT yaitu data
airbone (hymap) dengan ketinggian 2000 m dari permukaan bumi pada tahun 2008 di kawasan Indramayu dan Subang. Data hyperspectral ini terdiri atas nilai-nilai reflectance dan panjang gelombang (wavelength) tanaman padi.
Hasil seleksi fitur dan prediksi dengan
Recursive Feature Elimination – Support Vector Regression akan dievaluasi menggunakan Root Mean Square Error (RMSE) dan sebagai pembanding juga digunakan koefisien determinasi (R2).
TINJAUAN PUSTAKA Hyperspectral
2 yang diperoleh dengan menggunakan alat, tanpa
kontak langsung dengan objek, daerah atau gejala yang akan dikaji (Lillesand & Kiefer 1990). Contoh teknologi yang digunakan yaitu
multispectral dan hyperspectral.
Multispectral menghasilkan gambar dengan beberapa band panjang gelombang yang relatif luas, sedangkan hyperspectral mengumpulkan data gambar dalam ratusan atau ribuan band
spektral yang berdekatan secara bersamaan. Data citra hyperspectral dihasilkan oleh alat yang disebut spektrometer yang melibatkan konvergensi dua teknologi yaitu spektroskopi dan pencitraan jauh (Smith 2006).
Citra hyperspectral memiliki data spektrum puluhan hingga ribuan band. Lebar band data memiliki interval 1 nm - 15 nm, sedangkan pada
multispectral lebar band berkisar antara 50 sampai 120 nm. Data multispectral bisa memiliki celah atau renggang antar-spektral
band yang dikumpulkan, sedangkan data
hyperspectral memiliki kumpulan band yang kontinu (Borengasser et al. 2008). Gambar 2 memperlihatkan perbandingan antara data
multispectral dan hyperspectral. Data
hyperspectral (ASD FieldSpec 3 spectroradiometer) memiliki 150 band dengan rentang sebesar 350 nm sampai dengan 2500 nm, sedangkan data multispectral (Landsat ETM+) merupakan pendekatan rentang band
dari data hyperspectral, tidak merepresentasikan semua sensor (Mutanga et al. 2009).
Gambar 2 Perbandingan data multispectral dan
hyperspectral tanaman Eucalyptus grandis (Mutanga et al. 2009).
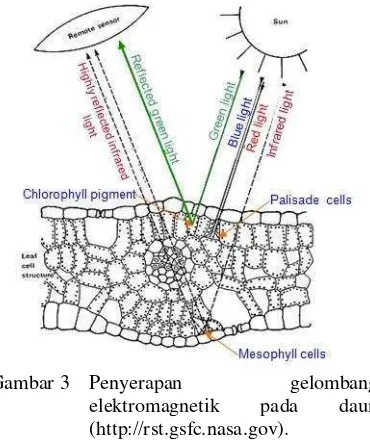
Reflectance adalah persentase cahaya yang dipantulkan oleh suatu material. Nilai
reflectance bervariasi untuk setiap benda dengan bahan yang berbeda (Borengasser et al.
2008). Gelombang elektromagnetik yang diterima oleh daun dapat dilihat pada Gambar 3. Klorofil menyerap cahaya tampak secara efektif. Akan tetapi, penyerapan berpusat pada panjang gelombang merah (sekitar 650 nm) dan
gelombang biru pada bagian palisade daun. Gelombang hijau hanya diperlukan sedikit dan dipantulkan kembali, sehingga warna daun tanaman sehat tampak hijau. Reflektansi naik tajam 40-50% antara gelombang infrared dan
near infrared (NIR) sekitar 700-1000 nm karena interaksi yang terjadi pada sel internal daun. Daun menyerap gelombang merah dan biru pada saat pertumbuhan, sedangkan reflektansi NIR menurun dan memantulkan gelombang merah pada akhir pertumbuhan (gugur), sehingga warna daun terlihat merah, kuning atau kecoklatan (Smith 2006).
Gambar 3 Penyerapan gelombang elektromagnetik pada daun (http://rst.gsfc.nasa.gov).
Support Vector Machine (SVM)
Support Vector Machine (SVM) pertama kali diperkenalkan oleh Boser, Guyon, dan Vapnik pada tahun 1992. Konsep dasar SVM merupakan kombinasi dari teori-teori komputasi yang telah ada, seperti marginhyperplane oleh Duda dan Hart pada tahun 1973, kernel yang diperkenalkan oleh Aronszajn pada tahun 1950, dan konsep pendukung lainnya.
Menurut Nugroho et al. (2003), prinsip dasar SVM adalah linear classifier, dan selanjutnya dikembangkan agar dapat bekerja pada masalah non-linear, dengan memasukkan konsep kernel trick. Gambar 4a memperlihatkan beberapa pola yang merupakan anggota dari dua buah kelas : +1 dan -1. Pola yang tergabung pada kelas -1 disimbolkan dengan kotak, sedangkan pola pada kelas +1 disimbolkan dengan lingkaran. Masalah klasifikasi ini dapat diselesaikan dengan usaha menemukan garis (hyperplane) maksimum yang memisahkan antara kedua kelas tersebut (Nugroho et al.
3 (a)
(b)
Gambar 4 Pemisah antar-kelas (hyperplane) (Nugroho et al. 2003).
Data yang tersedia dinotasikan sebagai ∈
d
, sedangkan label masing-masing dinotasikan
yi∈{-1,+1} untuk i = 1, 2,…, l, dengan l adalah
banyaknya data. Diasumsikan kedua kelas -1 dan +1 dapat terpisah secara sempurna oleh
hyperplane berdimensi d, yang didefinisikan
. + = 0 (1)
Pola yang termasuk kelas -1 (sampel negatif) dapat dirumuskan sebagai pola yang memenuhi pertidaksamaan
. + −1 (2)
Sedangkan pola yang termasuk kelas +1 (sampel positif)
. + +1 (3)
Margin terbesar dapat ditemukan dengan memaksimalkan nilai jarak antara hyperplane
dan titik terdekatnya, yaitu 2/|| ||. Hal ini dapat dirumuskan sebagai Quadratic Programming (QP) problem, yaitu mencari titik minimal persamaan (4), dengan memperhatikan
constraint persamaan (5).
� =
1 2
2 (4) . + −1 0,∀ (5) Persoalan ini dapat diselesaikan dengan beberapa teknik komputasi, di antaranya
Lagrange Multiplier (Cristianini & Taylor 2000).
, , =1 2
2
− ( ( . + −1))
=1
(i = 1, 2, …, l) (6) Pada persamaan (6), adalah Lagrange multipliers data yang memiliki nilai 0 atau positif. Nilai optimal dari persamaan (6) dapat dihitung dengan meminimalkan L terhadap dan b, serta memaksimalkan L terhadap . Persamaan (6) dapat dimodifikasi dengan memerhatikan sifat bahwa pada titik optimal
gradient L = 0, sebagai maksimalisasi masalah yang hanya mengandung , sebagaimana persamaan (7).
Memaksimalkan: −12
, =1 =1
(7)
dengan kendala :
0 = 1, 2,…, =1 = 0 (8) Dari hasil perhitungan ini diperoleh yang kebanyakan bernilai positif. Data yang berkorelasi dengan yang positif ini yang disebut sebagai support vector (Nugroho et al. 2003).
Support Vector Regression
SVR merupakan penerapan konsep Support Vector Machine (SVM) untuk kasus regresi. Output berupa bilangan riil atau kontinu dalam kasus regresi. SVR merupakan metode yang dapat mengatasi overfitting, sehingga akan menghasilkan kinerja yang bagus. SVR digunakan untuk menemukan suatu fungsi f(x)
yang mempunyai deviasi paling besar dari nilai aktual y, untuk semua data training. Jika nilai = 0, maka kita dapatkan suatu regresi yang sempurna (Santosa 2007).
Diketahui suatu data training regresi = 1, 1 , 2, 2 ,…, , ⊆ × , dapat menghitung model SVR yang optimal
∗ = ∗⋅ − ∗ dengan masalah optimasi dual
max , ′ � ,
′ =
, 1 1
1 max
2
l l
i j i i j j i j x x
1 1 l li i i i i
i i
y
Discrimination boundariesKelas -1 Kelas +1
4 dengan kendala
− ′
=1
= 0,
, ′ 0
untuk i = 1, …,l, dengan
∗= ∗− ′∗ =1
,
∗=1 ∗⋅ −
=1
,
Model SVR dapat menginterpretasikan , untuk koefisien − ′ yang tidak bernilai nol merupakan support vector. Perhatikan solusi untuk model regresi yang optimal
∗ = ∗⋅ − ∗
= ∗− ′∗ =1
⋅
−1 ∗− ′∗ =1
=1
⋅ −
hanya tergantung pada support vector. Oleh karena itu, Support Vector Regression dapat mengacu pada model tersebut.
Penggunaan regresi linear dengan SVR dapat diterapkan pada kasus regresi non linear dengan menggunakan kernel trick, sehingga penggunaan dot product pada model optimasi tersebut dapat diganti dengan fungsi kernel
(Hamel 2000). Konstanta C > 0 menentukan
trade off antara ketipisan fungsi f dan batas atas deviasi lebih dari masih ditoleransi. Semua deviasi lebih besar dari akan dikenakan pinalti C (Gambar 5). ekuivalen dengan akurasi dan aproksimasi terhadap training (Santosa 2007).
Gambar 5 Linear SVR (Santosa 2007). Kernel Trick
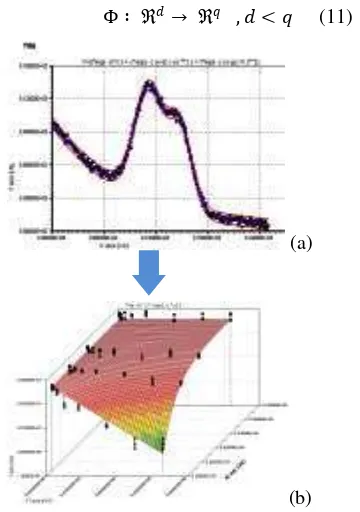
Data dipetakan oleh fungsi Φ( ) ke ruang vektor yang berdimensi lebih tinggi.
Hyperplane yang menjadi garis regresi dapat dikonstruksikan dalam ruang vektor yang baru ini. Ilustrasi dapat dilihat pada Gambar 6.
Gambar 6a memperlihatkan data pada regresi non-linear berdimensi dua. Selanjutnya, Gambar 6b menunjukkan bahwa fungsi Φ memetakan tiap data pada input space tersebut ke ruang vektor baru yang berdimensi lebih tinggi (dimensi 3). Notasi matematika dari pemetaan ini adalah
Φ ∶ → , < (11)
(a)
(b) Gambar 6 Pemetaan ruang vektor. Selanjutnya proses pembelajaran pada SVM regresi dalam menemukan titik-titik support vector, hanya bergantung pada dot product dari data yang sudah ditransformasikan pada ruang baru yang berdimensi lebih tinggi, yaitu Φ( Ԑ.Φ( ). Oleh karena transformasi Φ ini tidak diketahui, dan sangat sulit untuk dipahami secara mudah, maka perhitungan dot product
tersebut sesuai teori Mercer dapat digantikan dengan fungsi , yang mendefinisikan secara implisit transformasi Φ . Hal ini disebut sebagai Kernel Trick, yang dirumuskan
, = Φ( Ԑ.Φ( ) (12)
5 Tabel 1 Beberapa jenis kernel yang digunakan.
Jenis Kernel Definisi Linear , = ( ′. ) Polynomial , = ( . + 1)
Gaussian/RBF
,
= exp − −
2
2�2
Sigmoid , = tanh . +
LIBSVM
LIBSVM adalah library untuk Support Vector Machines (SVM) yang telah dikembangkan sejak tahun 2000. Tujuannya adalah untuk membantu pengguna supaya mudah menerapkan SVM untuk keperluan berbagai aplikasi, seperti masalah optimasi, klasifikasi multi-kelas, prediksi dan pemilihan parameter (Chang & Lin 2011). LIBSVM mendukung pembelajaran berikut :
1 SVC: support vector classification (dua atau lebih kelas).
2 SVR: support vector regression. 3 One-class SVM.
Penggunaan LIBSVM melibatkan dua langkah. Pelatihan data untuk memperoleh model dan menggunakan model untuk memprediksi informasi dari data pengujian.
Pembelajaran yang dipakai yaitu �-Support Vector Regression. Berdasarkan data training, {(x1, z1Ԑ,…, (xl, zl)}, dengan xi ∈ adalah
vektor fitur dan zi ∈ 1 adalah nilai output.
Parameter C > 0 dan �> 0, memiliki bentuk standar
min , ,�,�∗
1
2 + � +
=1 �∗ =1 dengan kendala: � + − �+�, − � − �+�∗,
�,�∗ 0, = 1,…, .
Permasalahan dual yaitu min
, ∗
1
2 − ∗ − ∗
+� ( + ∗) + =1 ( − ∗) =1 (13) dengan kendala
− ∗ = 0,
0 , ∗ , = 1,…, ,
dengan
, = ( , )≡ � � .
Setelah penyelesaian persamaan 13, pendekatan fungsinya :
−=1 + ∗ , + (14) Recursive Feature Elimination (RFE)
Feature selection adalah upaya untuk memilih fitur subset dari fitur asli yang paling berguna. Feature extraction adalah upaya untuk memetakan semua fitur ke dalam fitur baru yang lebih sedikit. Kelebihan feature selection
dibandingkan feature extraction adalah akusisi data yang lebih cepat. Oleh karena itu, pengurangan fitur pada data hyperspectral yang berupa band akan lebih baik jika menggunkan
feature selection dibandingkan feature extraction (Nakariyakul & Casasent 2004).
Recursive Feature Elimination (RFE) merupakan salah satu teknik seleksi fitur.
Properti yang terkenal dari sebuah SVM yaitu terdapat generalisasi error (GE), yang dibatasi oleh
� 1 22 (15)
dengan R adalah jari-jari terkecil dari data pelatihan yang ditransformasikan, dipisahkan oleh M margin sebanyak data N.
RFE fokus untuk meminimalkan GE dengan menghilangkan fitur-fitur yang memaksimalkan margin. Pengukuran prediksi berbanding terbalik dengan margin pada persamaan
�2 = Φ ,
=1 =1
(16)
Oleh karena itu, margin dapat dimaksimalkan dengan meminimalkan W dengan algoritme RFE. Pengembangan dari persamaan (16) yaitu
�2
− = =1 =1 Φ − , −
dengan − yaitu data pelatihan ke-i dengan dengan membuang fitur f (Archibald & Fann 2007).
Bootstrapping (8-fold)
6 (train set). Proses kalibrasi dilakukan secara
iterasi sebanyak 8 kali pelatihan dan pengujian. Dari hasil pengujian diperoleh 8 alternatif hasil dan model yang terbaik dipilih berdasarkan nilai
error yang paling minimum (Mulyono, dkk 2011).
Koefisien Determinasi (R2)
Koefisien determinasi digunakan untuk menilai kecocokan model regresi yang digunakan dengan data. Koefisien ini disimbolkan dengan R2, sedangkan
persamaannya sebagai berikut: 2= ( − )
2 =1
( − )2 =1
dengan adalah nilai y hasil prediksi dan adalah rata-rata dari y aktual (Sembiring 1995).
Sembiring (1995) menyatakan bahwa semakin dekat 2 dengan 1, maka semakin baik kecocokan data dengan model, sedangkan semakin dekat 2 dengan 0, semakin kurang baik kecocokan data dengan model. Range nilai
2 yaitu dari 0 sampai dengan 1. Root Mean Square Error (RMSE)
Memeriksa error dapat dilakukan dengan menghitung Root Mean Square Error (RMSE) pada sebuah model dengan persamaan sebagai berikut:
= ( − ) 2 =1
dengan n adalah jumlah data, adalah nilai aktual data ke-i, dan adalah nilai prediksi data ke-i.
P-Norm
P-norm didefinisikan sebagai
= ( =1 )1 , dengan 1, ∈ dapat dibuktikan bahwa sifat euclidean norm
berikut berlaku untuk semua p-norm:
0 = 0 ⟺ = 0,
= , ,
+ +
Akan tetapi, kenyataannya hanya tiga bentuk dari p-norm yang digunakan, yaitu
1= =1
,
2= 2 =1
1 2
,
∞= lim
→∞ = lim→∞
=1
1 2
(Max norm) (Meyer 2000).
METODE PENELITIAN
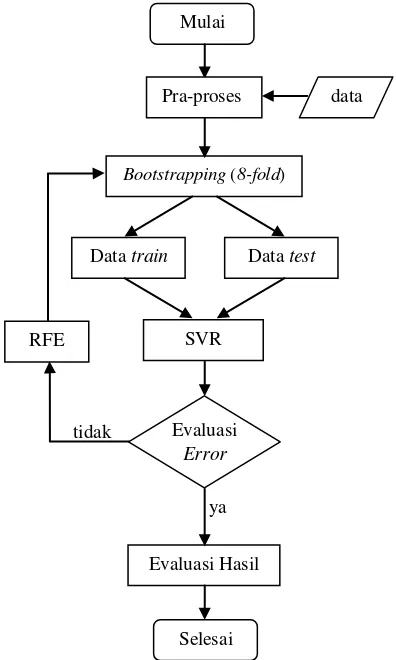
Penelitian ini dilakukan dalam beberapa tahap mengikuti diagram alur Gambar 7.
Gambar 7 Tahap metode penelitian. Pra-proses
Penelitian ini menggunakan data
hyperspectral tanaman padi yang diambil dari ketinggian 2000 m (hymap) dari permukaan bumi yang berisi informasi nilai-nilai
reflectance. Panjang gelombang yang digunakan berkisar antara 350 nm sampai dengan 2500 nm. Jumlah band pada data awal sebanyak 126 band. Data ini diperoleh menggunakan sensor Hyperspectral Mapper. Nilai crop variable yang digunakan disini yaitu nilai prediksi hasil produksi padi (yield). Nilai ini diperoleh melalui pengukuran ubinan saat masa panen.
Data mentah berupa citra yang ditangkap oleh sensor kemudian diekstrak ke format angka
Mulai
data
Evaluasi
Error
Bootstrapping (8-fold)
Pra-proses
Data train Data test
7 dengan menggunakan perangkat lunak ENVI
disimpan dalam file .txt (Lampiran 1). File ini berisi informasi mengenai panjang gelombang dan nilai pantulan (reflectance) objek di permukaan bumi.
Objek yang diperlukan dalam penelitian ini yaitu berupa tanaman padi, sedangkan nilai
reflectance yang diperoleh merupakan pantulan dari semua objek yang ada di permukaan bumi, seperti tanah, air serta zat-zat yang menghalangi sensor di udara. Oleh karena itu, diperlukan proses eliminasi terhadap band yang memiliki derau (noise).
Bootstrapping (8-fold)
Tahap ini menghasilkan data pelatihan dan data pengujian berdasarkan metode
bootstrapping (8-fold). Model yang digunakan diperoleh berdasarkan model yang memiliki nilai error terkecil. Semua data dibagi menjadi 8 subset yang terdiri dari data pelatihan dan data pengujian. Data pelatihan digunakan untuk pembuatan model pada SVR yang akan akan digunakan pada data pengujian.
Support Vector Regression (SVR)
Proses SVR menggunakan library SVM (LIBSVM) dapat dilihat pada Lampiran 2. Secara garis besar, koneksi yang dibuat seperti berikut :
1 LibSVM terdiri dari beberapa file berikut : a svm.h sebagai header file.
b svm.cpp sebagai kode program bahasa C++.
c svm-train.c dan svm-predict.c sebagai kode program bahasa C.
2 Membuat library file svm_train.exe dan svm_predict.exe menggunakan compiler
Code::Blocks.
3 Memanggil fungsi library .exe dari IDL. Data pengujian yang dihasilkan pada proses sebelumnya akan digunakan sebagai input dari proses regresi menggunakan epsilon SVR dan menghasilkan suatu model beserta koefisien α untuk setiap support vector. Data dengan koefisien α bernilai 0, berarti data tersebut bukan merupakan support vector, sedangkan data dengan koefisien α tidak sama dengan 0, maka data tersebut merupakan supportvector. Evaluasi Error
Regresi akan menghasilkan nilai error yang dihitung menggunakan RMSE. RMSE tersebut digunakan sebagai evaluasi untuk hasil akhir. Terdapat aturan mengenai evaluasi error, yaitu jika RMSE yang dihasilkan lebih kecil dibandingkan RMSE sebelumnya, maka proses
feature selection menggunakan Recursive Feature Elimination masih dilakukan. Akan tetapi, jika RMSE yang dihasilkan lebih besar dibandingkan dengan RMSE sebelumnya, maka proses RFE-SVM selesai dan menghasilkan
band yang terbaik pada data ini. Recursive Feature Elimination
Seleksi fitur dilakukan dengan menghitung nilai weight yang menggunakan koefisien alpha ( ) hasil SVR. Band atau fitur yang memiliki nilai weight yang minimum akan dihapus. Oleh karena itu, proses SVR selanjutnya tidak mengikut sertakan band tersebut. Hasil akhir berupa peringkat band terbaik.
Evaluasi Hasil
Hasil prediksi padi akan dievaluasi dengan koefisien determinasi (R2), sedangkan keakuaratan hasil regresi akan dievaluasi dengan Root Mean Square Error (RMSE). Lingkungan Pengembangan
Perangkat keras yang digunakan untuk penelitian yaitu:
1 Processor Intel Core2Duo 2.16 GHz. 2 RAM 2 GB DDR 2.
3 HDD kapasitas 200 GB.
4 Monitor LCD 14.1” dengan resolusi 1280 x 800 piksel.
5 Mouse dan keyboard.
Perangkat lunak yang digunakan untuk penelitian yaitu :
1 Sistem Operasi Microsoft Windows 7 Professional.
2 Interactive Data Language (IDL) versi 6.4.1 terdapat dalam ENVI 4.4 sebagai pengolahan data.
3 Code::Blocks 10 sebagai compiler C++
library SVM.
4 Notepad++ 4.2 dan Microsoft Excel sebagai editor data.
HASIL DAN PEMBAHASAN Pra-proses
Jumlah semua band sebanyak 126 band.
Setelah dilakukan tahap pra-proses yang dilakukan oleh Piantari (2011), yaitu dengan menghilangkan band berupa derauserta adanya
water absorption, menghasilkan band yang efektif digunakan sebanyak 109 band. Water absorption merupakan salah satu faktor yang mempengaruhi data hasil dari teknik penginderaan jauh, khususnya hyperspectral imaging.
8 lainnya. Hal ini berpengaruh, ketika sensor
hyperspectral mengirimkan transmisi gelombang elektromagnetik ke objek di bumi, maka pada rentang tertentu terdapat gelombang atau band yang terganggu oleh gas tersebut, sehingga gelombang elektromagnetik tersebut tidak sampai ke objek di bumi. Akan tetapi, gelombang tersebut diserap oleh uap air di atmosfer. Keadaan ini disebut dengan water absorption. Berdasarkan Lau (2004), terdapat beberapa gas yang menyerap radiasi dan menyebabkan noise pada data hymap (Tabel 2). Tabel 2 Penyerapan gas di atmosfer
Gas Absportion (μm)
H2O
0.94, 1.14, 1.38, 1.88 (Gao et al. 1993)
0.69, 0.72, 0.76 (Aspinall et al. 2002)
O2 0.76, 0.6-1.3 (Gao et al. 1993)
CO2
2.01, 2.08 (Gao et al. 1993)
1.6, 2.005, 2.055 (Aspinall et al. 2002)
O3
0.6 (Gao et al. 1993)
0.35, 9.6 (Aspinall et al. 2002)
N2O 2.0-2.5
CO 2.0-2.5
CH4 2.35 (Gao et al. 1993)
Band derau dan water absorption berada pada panjang gelombang antara 1359-1460 nm, 1774-1970 nm dan 2420-2500 nm. Jumlah data
hymap disesuaikan dengan jumlah data yield
aktual, sehingga dihasilkan sebanyak 34 data. Bootstrapping (8-fold)
Keakuratan model suatu prediksi dilihat dari seberapa besar error yang dihasilkan antara nilai prediksi dan nilai aktual. Semakin kecil atau error mendekati nilai 0, maka keakuratan suatu model prediksi dapat dikatakan baik. Contoh pembagian dataset dapat dilihat pada Lampiran 3.
Teknik ini menghasilkan dataset model yang terbaik dengan memilih nilai error
terkecil, berdasarkan root mean square error
(RMSE). Jumlah resampling data yang digunakan sebanyak 8 dataset. Setiap dataset
terdiri dari data training dan data testing. Contoh bootstrapping (8-fold) pada data dengan 109 band pada Tabel 3.
Tabel 3 Hasil dataset8-fold train-test
Dataset RMSE R2
1 1.027 0.168 2 1.722 0.184 3 1.161 0.499 4 1.336 0.861 5 0.326 0.97 6 0.966 0.046 7 1.762 0.167 8 1.175 0.046
Berdasarkan tabel tersebut, dataset ke-5 merupakan dataset yang memiliki nilai RMSE terkecil sebesar 0.326 dengan nilai korelasi R2 sebesar 0.97 mendekati nilai 1, berarti terdapat korelasi yang hampir sempurna. Oleh karena itu, dataset tersebut yang akan digunakan untuk proses selanjutnya. Gambar 8 menampilkan sebaran nilai yield aktual dan yield prediksi untuk data testing.
Gambar 8 Grafik sebaran yield terbaik. Implementasi RFE-SVR
Penggunaan Recursive Feature Elimination -Support Vector Machine (RFE-SVR) pada data
hyperspectral melibatkan beberapa parameter, seperti γ (GammaԐ, toleransi epsilon, serta koefisien penalti C. Selain ketiga parameter tersebut, terdapat beberapa kernel yang dipakai, yaitu kernel linear, kernel polinomial, kernel radial basis function (RBF) dan kernel sigmoid. Parameter � (Gamma), epsilon, C
Penentuan parameter epsilon digunakan sebagai toleransi akurasi terhadap data training. Konstanta C menentukan trade off antara ketipisan fungsi f pada SVR. Pemilihan nilai parameter tersebut berpengaruh terhadap model dari SVR yang akan dipakai. Model SVR yang baik adalah model dengan nilai error terkecil dan nilai determinasi R2 yang mendekati satu.
9 Penelitian ini mencoba beberapa
penggunaan parameter tersebut sampai dihasilkan model terbaik. Suatu model dikatakan baik apabila data pelatihan yang di
training serta testing menggunakan data yang sama dengan training memiliki nilai error
mendekati nilai 0 dan koefisien determinasi R2 mendekati nilai satu.
Nilai epsilon yang semakin kecil, maka toleransi error yang dibatasi kecil juga. Sebaliknya, nilai epsilon yang besar, maka toleransi error yang dibatasi besar pula. Pemilihan epsilon dilakukan dengan metode
trial and error. Nilai epsilon tidak terlalu berpengaruh terhadap model yang dihasilkan. Hasil percobaan penggunaan beberapa parameter epsilon dapat dilihat pada Gambar 9.
Gambar 9 Perbandingan epsilon. Grafik tersebut memperlihatkan penggunaan beberapa epsilon yang dilihat berdasarkan nilai RMSE. Pemilihan epsilon mempertimbangkan koefisien determinasi R2 juga. Nilai epsilon yang baik yaitu epsilon ( Ԑ < 1. Epsilon yang digunakan yaitu 0.07. Hasil selengkapnya dapat dilihat pada Lampiran 4.
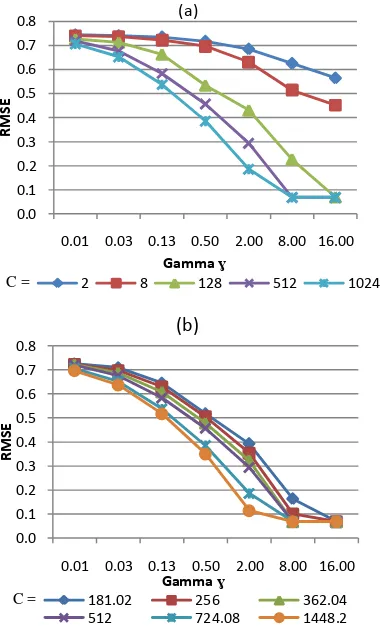
Percobaan yang sama dilakukan terhadap koefisien C dan parameter gamma ( ). Hasil untuk koefisien C pada Gambar 10a. Hasil dengan error minimum terdapat pada koefisien C sebesar 27- 210 (128-1024). Kemudian dilakukan pencarian ulang antara rentang tersebut dan didapatkan hasil pada Gambar 10b. Berdasarkan grafik tersebut dapat dilihat nilai C yang besar menghasilkan error yang kecil. Akan tetapi, tidak terlalu banyak perubahan nilai error-nya. Koefisien C yang ditetapkan yaitu sebesar 210.5 (1448.2).
Hal penting dalam Support Vector Regression yaitu memaksimumkan margin pada prediksi data. Nilai C yang terlalu besar tidak memperhatikan perubahan maksimum margin, sehingga C yang terlalu besar menghasilkan nilai error yang konstan. Sedangkan, nilai C
yang terlalu kecil terlalu memperhatikan nilai penalti dalam SVR.
Gambar 10 Perbandingan koefisien C. Parameter gamma ɣ digunakan dalam pembentukan kernel radial basis function
(RBF) dan kernel sigmoid pada pemetaan data dari dimensi yang rendah ke dimensi yang lebih tinggi. Hasil pemilihan gamma pada rentang 2-7- 24 dapat dilihat pada Gambar 11a. Grafik 11a memperlihatkan gamma dengan error kecil pada rentang 23– 24 (8-16), sehingga dilakukan pemilihan rentang yang lebih kecil lagi. Kurva pada Gambar 11b berhimpit antara perhitungan menggunakan beberapa gamma. Akan tetapi, nilai gamma lebih dari 12.34 dengan nilai C mulai dari 128 menghasilkan nilai yang sama. Oleh karena itu, gamma yang dipilih sebesar 11.31. Perhitungan hasil selengkapanya dapat dilihat pada Lampiran 5.
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
C=8 C=128 C=1024
R
M
S
E
0.001 0.01 0.07 1
= 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
0.01 0.03 0.13 0.50 2.00 8.00 16.00
R
M
S
E
Gamma ɣ
(a)
2 8 128 512 1024
C = 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
0.01 0.03 0.13 0.50 2.00 8.00 16.00
R
M
S
E
Gamma ɣ
(b)
181.02 256 362.04
512 724.08 1448.2
10 Gambar 11 Perbandingan parameter gamma.
Penggunaan Kernel
Kernel yang digunakan dalam RFE-SVR menentukan keakuratan pembuatan model suatu prediksi sehingga memperoleh error yang seminimum mungkin. Penggunaan kernel
bertujuan untuk memetakan data ke dimensi yang lebih tinggi supaya dapat dipisahkan secara linear. Oleh karena itu, perhitungan dengan beberapa kernel digunakan untuk memperoleh kernel yang cocok terhadap data
hyperspectral ini. a Kernel Linear
Kernel linear merupakan kernel yang paling sederhana. Perhitungan kernel tidak melibatkan parameter gamma. Oleh karena itu, hanya digunakan koefisien epsilon � dan penalti C dalam proses SVR. Hasil pengurangan band
terhadap error menggunakan kernel ini dapat dilihat pada Gambar 12.
Gambar 12 Perbandingan jumlah band terhadap
error dan weightkernel linear. Penggunaan kernel linear tidak cocok dengan seleksi fitur RFE. Hal ini terbukti pada saat pengurangan fitur dari 109 band sampai satu band, error yang dihasilkan tidak menurun, tetapi berlaku sebaliknya. Akan tetapi, pengurangan band terhadap weight berlaku sesuai teori, ketika jumlah band berkurang, maka nilai weight meningkat. Hal ini dikarenakan, fitur yang dibuang adalah fitur yang memiliki w minimum. Nilai RMSE semua
band yaitu sebesar 0.5666 dengan R2 sebesar 0.5022, sedangkan pada akhir iterasi satu band
menghasilkan RMSE yang lebih besar yaitu 0.7901 dengan R2 yang jauh lebih kecil yaitu 0.0551. Nilai error ini secara kenyataan di lapangan berpengaruh sebesar 0.5666 ton yield
per hektar. Gambar 13 menunjukkan sebaran nilai yield prediksi terhadap nilai yield aktual pada kernel linear. Sesuai dengan nilai R2 yang diperoleh, sebaran tidak berkumpul ke garis linear, masih terdapat data pencilan yang tidak dapat diprediksi dengan baik.
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
R
M
S
E
Koefisien C
(a)
0.125 0.5 2 8 16
ɣ=
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
0.125 0.5 2 8 32 128 512 1024
R
M
S
E
Koefisien C
(b)
8.72 9.51 10.37
11.31 12.34 13.45
11 Gambar 13 Sebaran prediksi yieldkernel linear.
b Kernel Sigmoid
Pengujian menggunakan kernel sigmoid memerlukan koefisien C dan parameter pada pemetaan input space ke feature space. Penggunaan kernel sigmoid sama dengan kernel
linear, tidak menghasilkan pengurangan band. Nilai RMSE tidak berkurang seiring dengan naiknya weight pada perhitungan RFE (Gambar 14).
Gambar 14 Perbandingan jumlah band terhadap
error dan weightkernel sigmoid. Nilai RMSE saat 109 band yaitu sebesar 0.7958 yang berarti secara riil di lapangan terdapat perbedaan sebanyak 0.7958 ton/ha, dengan R2 yang kecil sebesar 0.0239. Nilai RMSE yang seharusnya turun, saat iterasi terakhir diperoleh hasil yang sebaliknya dengan nilai RMSE = 79.7637 atau setara 79.7637 ton/ha dan R2 = 0.038. Gambar 15 merupakan
sebaran prediksi yield terhadap nilai yield aktual dengan R2 yang sangat kecil. Hasil prediksi menggunakan kernel sigmoid tidak menunjukkan adanya keterkaitan antara yield
prediksi dan yield aktual, sehingga error yang dihasilkan cukup besar.
Gambar 15 Sebaran prediksi yield kernel
sigmoid.
c KernelRadial Basis Function
Pemetaan pada kernelRadial Basis Function
(RBF) membutuhkan parameter gamma . Parameter ini menentukan tebal atau tipisnya jarak antara support vector dengan hyperplane. Parameter yang telah dipilih, yaitu sebesar 11.31 dan C = 1448.2. Hasil menggunakan
kernel RBF terdapat pengurangan band
sebanyak 39 band (Gambar 16).
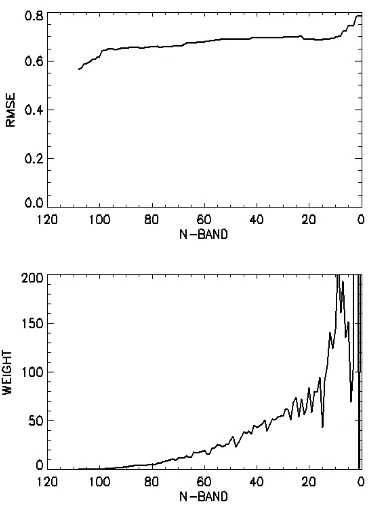
Metode RFE-SVR dengan kernel ini mendapatkan band optimal sebanyak 70 band
dengan RMSE sebesar 0.0901 dan R2 sebesar 0.9874. Perubahan nilai RMSE berkurang seiring dengan berkurangnya jumlah band. Akan tetapi, pada saat pengurangan jumlah
band tertentu, nilai RMSE kembali meningkat. Hal ini mengindikasikan bahwa pada jumlah
band tersebut, band sudah tidak dapat dikurangi lagi. Penggunaan kernel RBF ini menghasilkan RMSE = 0.0901 yang berarti prediksi yield
setiap hektar di lapangan, terdapat kesalahan seberat 0.0901 ton.
RMSE = 0.5666 R2 = 0.5022
12 Gambar 16 Perbandingan jumlah band terhadap
error dan weightkernel RBF. Sebaran nilai yield prediksi terhadap nilai
yield aktual pada kernel RBF dapat dilihat di Gambar 17. Berdasarkan nilai R2 yang mendekati angka 1, sebaran data berkumpul ke satu garis, meskipun ada beberapa data yang masih diluar garis, sehingga masih ada error
sebesar RMSE = 0.0901. Akan tetapi, sebaran prediksi yang diperoleh sudah cukup baik dari pemilihan kernel lainnya.
Gambar 17 Sebaran prediksi yieldkernel RBF. d Kernel Polinomial
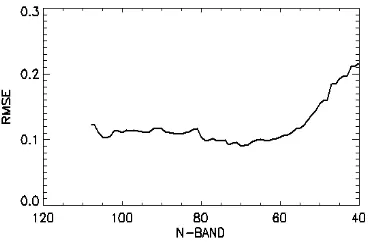
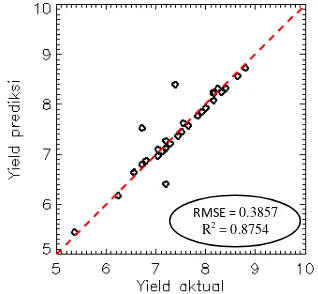
Kernel polinomial yang digunakan yaitu berderajat tiga. Hasil training dengan 109 band
memperoleh nilai RMSE sebesar 0.3857 dan R2 sebesar 0.8014 (Gambar 18). Pengujian kernel
polinomial dengan RFE-SVR hanya berkurang 17 band sehinga hasil akhir yang tersisa sebanyak 92 band optimal dengan RMSE = 0.3055 dan R2 = 0.8754. RMSE sebesar 0.3055 setara dengan kesalahan seberat 0.3055 ton/ha di lapangan.
Gambar 18 Perbandingan jumlah band terhadap
error dan weightkernel Polinomial. Gambar 19 menunjukkan sebaran nilai prediksi yield terhadap nilai yield aktual. Data sebaran cukup baik karena data berkumpul di satu garis, meskipun ada beberapa data jauh dari kumpulan data lainnya karena data tersebut tidak dapat diprediksi dengan baik.
Gambar 19 Sebaran prediksi yield kernel
polinomial. Simpang Error
Selain menggunakan error RMSE, pengujian RFE-SVR pada data hyperspectral ini mencoba beberapa penerapan kaidah error
dalam tiga bentuk norm. Berdasarkan pengujian sebelumnya, kernel terbaik yang digunakan yaitu kernel RBF. Oleh karena itu, pengujian terhadap bentuk norm dilakukan pada kernel
RBF saja.
RMSE 0.0901
R2 = 0.9874
13 Norm ini terdiri dari tiga bentuk yaitu
norm-1, norm-2, dan norm-∞. Hasil training dengan RFE-SVR dengan norm-1 memperoleh error = 2.7486 dan R2 = 0.9859 serta jumlah band
optimal sebanyak 87 band (Gambar 20).
Gambar 20 Perbandingan jumlah band dengan
error norm-1.
Sedangkan, hasil pengujian norm-∞ memperoleh 66 band dengan error = 0.3001 dan R2 = 0.9847 (Gambar 21). Perbandingan lebih lengkap antara semua kaidah norm dapat dilihat pada Tabel 4. Perbandingan menggunakan kaidah p-norm dengan hasil pengurangan band terbaik yaitu dengannorm-∞ karena pada bentuk norm ini, meminimalkan dari error maksimum, yaitu nilai maksimum dari selisih error antara data aktual dengan data prediksi. Selain itu, jumlah band yang diperoleh lebih kecil dengan nilai RMSE yang tidak jauh berbeda dengan bentuk norm lainnya.
Gambar 21 Perbandingan jumlah band dengan
error norm-∞.
Tabel 4 Perbandingan seleksi fitur menggunakan kaidah p-norm
Kaidah band error RMSE R2
Norm-1 87 2.7486 0.0959 0.9859
Norm-2 70 0.0901 0.0901 0.9874
Norm-∞ 66 0.3001 0.0984 0.9847
Konfigurasi band yang didapatkan dengan
kernel RBF dapat dilihat di Tabel 5. Angka 1 menunjukkan bahwa rentang band tersebut adalah band terbaik, sedangkan angka 0
menunjukkan band tersebut tidak terlalu berpengaruh terhadap model prediksi.
Tabel 5 Konfigurasi band terbaik
Band
(nm) Konfigurasi band
459-973 0011111111111111101001100001111111111
989-1623 1100111000100001000111000100111111111
1648-2396 10000000011011111001111111111111110
KESIMPULAN DAN SARAN Kesimpulan
Berdasarkan analisa dalam pembahasan, hasil penelitian ini dapat ditarik kesimpulan, yaitu
1 Penggunaan Recursive Feature Elimination
-Support Vector Machine (RFE-SVR) pada data hyperspectral mampu mengurangi band
sekitar 30% (dari 109 band menjadi 70
band) dengan hasil RMSE yang lebih kecil serta koefisien determinasi (R2) mendekati nilai satu dibandingkan dengan SVR tanpa seleksi fitur.
2 Kernel Radial Basis Function (RBF) merupakan kernel terbaik yang dipakai dalam RFE-SVR dengan nilai RMSE sebesar 0.0901 setara dengan nilai kesalahan seberat 0.0901 ton/ha di lapangan serta korelasi determinasi (R2) sebesar 0.98. 3 Bentuk norm-∞ merupakan bentuk norm
terbaik dengan pengurangan band sebanyak 43 band dari 109 band.
Saran
Beberapa hal yang dapat dilakukan berdasarkan penelitian ini yaitu
1 Penggunaan seleksi fitur lain yang dapat digabung dengan SVR, seperti Embedded Feature Selection (EFS).
2 Penggunaan data untuk proses klasifikasi pada fase tumbuh padi.
3 Penggunaan data yang lebih banyak untuk pembuatan model prediksi yang lebih baik.
DAFTAR PUSTAKA
Archibald R, Fann G. 2007. Feature selection and classification of hyperspectral images with support vector machine.
14 Aspinall RJ, Marcus WA, Boardman JW. 2002.
Considerations in collecting, processing, and analysing high spatial resolution hyperspectral data for environmental investigations. Journal of Geographical Systems 4:15-29.
Borengasser M, Hungate WS, Watkins R. 2008.
Hyperspectral Remote Sensing Principal and Applications. New York: CRC Press.
Casasent D, Nakariyakul S. 2004. Hyperspectral ratio feature selection: agricultural product inspection example. Nondestructive Sensing for Food Safety, Quality, and Natural Resources 5587, Proceedings of SPIE; Philadelphia, 26 Oktober 2004. hlm 133-143.
Chang CC, Lin CJ. 2011. LIBSVM: A Library for Support Vector Machines. Department of Computer Science National Taiwan University.
Cristianini N, Taylor JS. 2000. An Introduction to Support Vector Machine and other kernel-based learning methods. Cambridge: Cambrigde University Press. Gao BC, Heidebrecht KB, Goetz AFH. 1993. Derivation of scaled surface reflectances from aviris data. Remote Sensing of Environment 44:165-178.
Hamel L. 2000. Knowledge Discovery With Support Vector Machines. New Jersey:
John Wiley & Sons, inc.
Lau IC. 2004. Application of atmospheric correction to hyperspectral data: comparisons of different techniques on hymap data. Di dalam: Smith R, Dawbin K, editor. To Measure is to Manage: The 12th Australasian Remote Sensing and Photogrammetry Conference Proceeding; Fremantle, 18-22 Oktober 2004. Fremantle: Spatial Sciences Institute.
Meyer CD. 2000. Matrix Analysis and Applied Linear Algebra. Philadelphia: SIAM. Mulyono S, Piantari E, Fanany MI, Basaruddin
T. 2011. Pemilihan fitur citra hiperspektral hymap dan model prediksi panen padi menggunakan algoritma genetika dan regresi komponen utama.
Pertemuan Ilmiah Tahunan (PIT) MAPIN XVIII; Semarang, 8-9 Juni 2011.
Mutanga O, Aardt JV, Kumar L. 2009. Imaging spectroscopy (hyperspectral remote sensing) in southern Africa: an overview.
South African Journal of Science 105(5-6):193-198.
Nugroho AS, Witarto BA, Handoko D. 2003. Application of support vector machine in Bioinformatics. Proceeding of Indonesian Scientific Meeting in Central Japan; Gifu-Japan, 20 Desember 2003. Piantari E. 2011. Feature selection data
hiperspektral untuk prediksi produktivitas padi dengan algoritme genetika dan support vector regression
[skripsi]. Bogor. Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.
Santosa B. 2007. Data Mining: Teknik Pemanfaatan Data untuk Keperluan Bisnis. Yogyakarta: Graha Ilmu.
Sembiring RK. 1995. Analisis Regresi. Bandung: Penerbit ITB.
Smith RB. 2006. Introduction to Hyperspectral Imaging. Nebraska: MicroImages, Inc. Vijayakumar S, Wu Si. 1999. Sequential
support vector classifiers and regression.
Proceedings International Conference
on Soft Computing (SOCO’99); Genoa, 1999. hlm 610-619.
Yohan. 2010. Prediksi nilai crop variable
tanaman padi pada data hyperprectral
15
16 Lampiran 1 Contoh data yield dan reflectance beberapa band
Yield Band 1 Band 2 Band 3 Band 4 Band 5 Band 6 Band 7 Band 8 7.92 0:0.089980 1:0.088020 2:0.087160 3:0.087930 4:0.091720 5:0.097770 6:0.102050 7:0.103380
6.80 0:0.090600 1:0.087600 2:0.084350 3:0.083930 4:0.088270 5:0.093930 6:0.098070 7:0.099280
7.12 0:0.088110 1:0.086170 2:0.084960 3:0.085150 4:0.088350 5:0.093700 6:0.098360 7:0.100330
5.60 0:0.092210 1:0.091440 2:0.089860 3:0.089690 4:0.092770 5:0.097920 6:0.102150 7:0.103930 6.24 0:0.091650 1:0.088690 2:0.086900 3:0.086800 4:0.089700 5:0.095310 6:0.099460 7:0.100520
7.20 0:0.090550 1:0.089980 2:0.088920 3:0.088770 4:0.091990 5:0.097490 6:0.101710 7:0.103730
5.36 0:0.086960 1:0.085820 2:0.084580 3:0.085090 4:0.088700 5:0.094430 6:0.098850 7:0.099960 8.00 0:0.095660 1:0.094260 2:0.092510 3:0.092560 4:0.095910 5:0.101470 6:0.105550 7:0.107030
8.32 0:0.088220 1:0.086050 2:0.084760 3:0.085350 4:0.088900 5:0.094240 6:0.098170 7:0.099460
8.80 0:0.081510 1:0.077390 2:0.074490 3:0.073910 4:0.078260 5:0.085840 6:0.090810 7:0.090840 7.20 0:0.063040 1:0.062800 2:0.063690 3:0.065850 4:0.070600 5:0.078470 6:0.084770 7:0.088270
7.20 0:0.062210 1:0.061240 2:0.060650 3:0.062330 4:0.066950 5:0.074550 6:0.080070 7:0.082770
6.56 0:0.061440 1:0.061390 2:0.061440 3:0.063810 4:0.069120 5:0.076490 6:0.082000 7:0.085330
6.72 0:0.063260 1:0.066040 2:0.062870 3:0.064260 4:0.069900 5:0.077170 6:0.082700 7:0.085850 8.16 0:0.058340 1:0.061920 2:0.062090 3:0.063050 4:0.068280 5:0.076850 6:0.083040 7:0.085880
8.64 0:0.057320 1:0.062650 2:0.063680 3:0.064660 4:0.070160 5:0.078050 6:0.084310 7:0.087780
8.24 0:0.058600 1:0.054000 2:0.052100 3:0.052000 4:0.057200 5:0.066500 6:0.070400 7:0.070800 7.55 0:0.060260 1:0.055380 2:0.053270 3:0.053750 4:0.058720 5:0.068130 6:0.074160 7:0.074000
7.44 0:0.057170 1:0.056310 2:0.054280 3:0.054150 4:0.060120 5:0.068680 6:0.073070 7:0.072270
7.39 0:0.060970 1:0.056610 2:0.053650 3:0.054140 4:0.060400 5:0.069200 6:0.074260 7:0.074100 7.65 0:0.057080 1:0.052420 2:0.050800 3:0.050980 4:0.055000 5:0.063110 6:0.068760 7:0.068020
8.16 0:0.045700 1:0.042990 2:0.040410 3:0.040380 4:0.043250 5:0.052370 6:0.057890 7:0.057000
7.84 0:0.044000 1:0.041000 2:0.037600 3:0.036300 4:0.041700 5:0.050500 6:0.056400 7:0.055100
6.56 0:0.044200 1:0.042100 2:0.039700 3:0.038500 4:0.041800 5:0.049000 6:0.053200 7:0.051900 6.72 0:0.044290 1:0.042270 2:0.040060 3:0.037880 4:0.042740 5:0.049670 6:0.052280 7:0.051640
7.04 0:0.042270 1:0.040900 2:0.038860 3:0.038370 4:0.042680 5:0.049700 6:0.053800 7:0.052030
7.20 0:0.043960 1:0.041110 2:0.040160 3:0.038940 4:0.041360 5:0.048760 6:0.053130 7:0.052510 6.72 0:0.047400 1:0.045000 2:0.044100 3:0.042200 4:0.047600 5:0.058600 6:0.064800 7:0.063900
7.04 0:0.051930 1:0.044360 2:0.040610 3:0.040840 4:0.046540 5:0.055650 6:0.060920 7:0.059380
7.28 0:0.043520 1:0.040040 2:0.037780 3:0.037200 4:0.041960 5:0.051070 6:0.056020 7:0.054940
7.52 0:0.050490 1:0.045370 2:0.041920 3:0.041410 4:0.045960 5:0.055850 6:0.061600 7:0.059800 7.84 0:0.050570 1:0.044280 2:0.040040 3:0.040450 4:0.045810 5:0.054040 6:0.060300 7:0.059170
17 Lampiran 2 Koneksi Library SVM ke IDL
1 LibSVM terdiri dari beberapa file. File yang dibutuhkan ditandai warna biru.
2 Membuat libraryfile svm-train.exe menggunakan compiler Code::Blocks.
3. Mengubah output menjadi nilai alpha pada svm.cpp (svm-train.exe) a Menghapus syntax berikut:
1 info("\nWarning: using -h 0 may be faster\n"); 2 info(".");
3 info("*");
4 info("\noptimization finished, #iter = %d\n",iter); 5 info("nu = %f\n", sum_alpha/(Cp*prob->l));
6 info("C = %f\n",1/r);
18 Lanjutan Lampiran 2
8 info("epsilon = %f\n",-si->r);
9 info("obj = %f, rho = %f\n",si.obj,si.rho); 10 info("nSV = %d, nBSV = %d\n",nSV,nBSV);
11 info("Line search fails in two-class probability estimates\n");
12 info("Reaching maximal iterations in two-class probability
estimates\n");
13 info("Exceeds max_iter in multiclass_prob\n");
14 info("Prob. model for test data: target value = predicted value +
z,\nz: Laplace distribution e^(-|z|/sigma)/(2sigma),sigma=
%g\n",mae);
15 info("Total nSV = %d\n",total_sv);
b Menambah syntax berikut di fungsi “static void solve_epsilon_svr”
info("%f\n", alpha[i]);
c Hasil nilai alpha
Sebelum diubah
19 Lanjutan Lampiran 2
3 Membuat library svm-predict.exe dengan Code::Blocks tanpa ada perubahan.
20
Dataset 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 … 34 RMSE R2
1 T T T T T T T X T T T T T T T X T T T T … T 1.027 0.168
2 T T T T T T X T T T T T T T X T T T T T … T 1.722 0.184
3 T T T T T X T T T T T T T X T T T T T T … T 1.161 0.499
4 T T T T X T T T T T T T X T T T T T T T … T 1.336 0.861
5 T T T X T T T T T T T X T T T T T T T X … T 0.326 0.97
6 T T X T T T T T T T X T T T T T T T X T … T 0.966 0.046
7 T X T T T T T T T X T T T T T T T X T T … X 1.762 0.167
8 X T T T T T T T X T T T T T T T X T T T … T 1.175 0.046
Keterangan : T = data training
X = data testing
Dataset kelima merupakan dataset yang akan digunakan untuk proses selanjutnya.
L
am
pi
ra
n
3
Cont
oh
p
em
ba
g
ia
n
d
at
a
tr
ai
n
ing
da
n
te
st
ing
21 Lampiran 4 Pemilihan epsilon
Epsilon 0.001 0.01 0.05 0.07 0.09
C=8
ɣ=2
RMSE 0.6279 0.6289 0.6297 0.6303 0.6314 R2 0.3931 0.3905 0.3120 0.3117 0.3088 C=128
ɣ=8
RMSE 0.2389 0.2362 0.2281 0.2269 0.2274 R2 0.9128 0.9145 0.9202 0.9209 0.9207 C=1024
ɣ=12
RMSE 0.0011 0.0100 0.0489 0.0672 0.0855 R2 1.0000 0.9999 0.9969 0.9940 0.9902
Epsilon 0.11 0.13 0.15 0.2 1
C=8
ɣ=2
RMSE 0.6320 0.6313 0.6308 0.6318 0.7145 R2 0.3031 0.3019 0.3014 0.2893 0.1717 C=128
ɣ=8
RMSE 0.2297 0.2314 0.2349 0.2507 0.6117 R2 0.9195 0.9197 0.9188 0.9107 0.4238 C=1024
ɣ=12
22 Lampiran 5 Penggunaan beberapa parameter gamma (ɣԐ dan koefisien C
Gamma(ɣ) pada rentang 2-7 - 24 dan koefisien C pada rentang 2-3 - 211
gamma C 0.125 0.5 2 8 32 128 512 1024 2048
0.007813 RMSE 0.7947 0.7917 0.7813 0.7735 0.7659 0.7633 0.7467 0.7343 0.7244
R2 0.0606 0.0604 0.0604 0.0621 0.0656 0.0696 0.1131 0.1473 0.1726
0.03125 RMSE 0.7918 0.7817 0.7739 0.7649 0.7594 0.7390 0.7198 0.7041 0.6800
R2 0.0604 0.0605 0.0630 0.0680 0.0802 0.1359 0.1752 0.2103 0.2677
0.125 RMSE 0.7832 0.7741 0.7625 0.7514 0.7358 0.7069 0.6582 0.6226 0.5818
R2 0.0606 0.0657 0.0739 0.0993 0.1370 0.2057 0.3213 0.4075 0.4684
0.5 RMSE 0.7737 0.7596 0.7463 0.7280 0.6798 0.6057 0.5573 0.5184 0.4726
R2 0.0654 0.0851 0.1160 0.1558 0.2650 0.4388 0.5047 0.5889 0.6586
2 RMSE 0.7661 0.7477 0.7232 0.6690 0.5845 0.5403 0.4309 0.3427 0.2325
R2 0.0891 0.1199 0.1742 0.3100 0.4631 0.5441 0.7106 0.8233 0.9184
8 RMSE 0.7578 0.7278 0.6711 0.5827 0.5203 0.3790 0.1195 0.1195 0.1195
R2 0.1100 0.1929 0.2946 0.4739 0.5808 0.7866 0.9775 0.9775 0.9775
16 RMSE 0.7520 0.7081 0.6269 0.5341 0.4418 0.1989 0.1584 0.1584 0.1584
R2 0.1418 0.2561 0.3905 0.5651 0.7045 0.9436 0.9646 0.9646 0.9646
Gamma(ɣ) pada rentang 23.125 – 23.75 dan koefisien C pada rentang 27.5 - 210.5
gamma C 181.0193 256 362.0387 512 724.0773 1024 1448.155
8.724062 RMSE 0.2859 0.2074 0.1328 0.1169 0.1169 0.1169 0.1169
R2 0.8884 0.9438 0.9740 0.9788 0.9788 0.9788 0.9788
9.513657 RMSE 0.2593 0.1792 0.1213 0.1165 0.1165 0.1165 0.1165
R2 0.9105 0.9578 0.9780 0.9794 0.9794 0.9794 0.9794
10.37472 RMSE 0.2332 0.1547 0.1184 0.1184 0.1184 0.1184 0.1184
R2 0.9286 0.9669 0.9792 0.9792 0.9792 0.9792 0.9792
11.31371 RMSE 0.2077 0.1404 0.1228 0.1228 0.1228 0.1228 0.1228
R2 0.9434 0.9718 0.9780 0.9780 0.9780 0.9780 0.9780
12.33769 RMSE 0.1840 0.1346 0.1292 0.1292 0.1292 0.1292 0.1292
R2 0.9542 0.9746 0.9761 0.9761 0.9761 0.9761 0.9761
13.45434 RMSE 0.1686 0.1377 0.1377 0.1377 0.1377 0.1377 0.1377
ABSTRACT
HENDRA GUNAWAN. Hyperspectral Band Selection using Recursive Feature Elimination
for Yield Prediction with Support Vector Regression. Supervised by HARI AGUNG ADRIANTO and SIDIK MULYONO.
Hyperspectral is a new technology in remote sensing that exploits hundreds of bands. Pusat Teknologi Inventarisasi Sumber Daya Alam Badan Pengkajian dan Penerapan Teknologi (PTISDA BPPT) applies hyperspectral in agriculture for yearly yield prediction. Hyperspectral images consist of large number of bands that require analysis to select features. One approach to reduce computational cost is to eliminate bands that do not add value to the regression and analysis method to be applied. In this research, we use a Recursive Feature Elimination (RFE) algorithm that is tailored to operate with Support Vector Regression (SVR) to perform band selection and regression simultaneously. Annual yield of paddy has been predicted with hyperspectral data using Support Vector Regression (SVR) algorithm. Regions used are Indramayu and Subang, and the altitude of the spectral acquisition is 2000 m (Hymap). This data is owned by PTISDA BPPT.
RFE-SVR used in hyperspectral data was able to reduce about 30% of the bands, resulting in 70 bands out of 109 original bands with an RMSE value of 0.0901 and R2 value of 0.9874. Radial Basis Function (RBF) is the best kernel used in RFE-SVR having an RMSE value less than those of other kernels tested.
1 PENDAHULUAN
Latar Belakang
Prediksi jumlah produksi padi yang dilakukan saat ini masih bersifat tradisional, yaitu dengan melakukan survei ke lapangan dengan menghitung secara ubinan dan eyes estimate. Perhitungan secara ubinan dilakukan secara manual dengan menghitung berat hasil panen padi dalam ukuran 4 x 4 m. Eyes estimates hanya menghitung dengan perkiraan penglihatan seseorang, sehingga hasil yang diperoleh tidak akurat. Keadaan ini dapat menyulitkan proses penghitungan prediksi panen padi yang akan diserahkan ke pihak pemerintahan. Perkembangan pengetahuan dan teknologi menjadi salah satu faktor yang dapat mengatasi masalah ini. Salah satu cara yang dapat diterapkan yaitu dengan menggunakan teknologi hyperspectral. Teknologi ini menggunakan citra satelit berupa data pantulan cahaya (spectrum) dari objek yang ada di bumi. Data ini dapat digunakan untuk prediksi biofisik tanaman padi, seperti nitrogen dan klorofil.
Prediksi suatu nilai dapat diperkirakan dengan menggunakan regresi. Teknik regresi yang sering digunakan dalam berbagai bidang, contohnya regresi linear sederhana dan regresi linear multi variabel. Support Vector Machine
(SVM) merupakan salah satu learningmachine
yang ditemukan oleh Boser, Guyon, dan Vapnik pada tahun 1992. SVM ini berusaha mencari pemisah antar-kelas (hyperplane) yang maksimum. Kelebihan teknik ini dibandingkan dengan teknik klasifikasi lain adalah meminimalkan error pada training-set dan tingkat generalisasi dari SVM tidak dipengaruhi oleh dimensi dari input vektor (Nugroho et al. 2003). Konsep SVM dapat diadaptasi dalam masalah regresi, yang digunakan untuk memprediksi nilai yang diharapkan. Klasifikasi menghasilkan nilai diskret, sedangkan regresi menghasilkan nilai yang kontinu. Teknik ini biasa disebut dengan Support Vector Regression
(SVR).
Komputasi yang kompleks dalam teknik SVR dapat mengakibatkan cost yang tinggi, sehingga diperlukan teknik seleksi fitur. Seleksi fitur dapat digunakan untuk meningkatkan kecepatan komputasi dan model yang baik dengan melibatkan fitur-fitur yang diperlukan saja. Recursive Feature Elimination (RFE) adalah salah satu metode seleksi fitur yang dapat digunakan untuk memecahkan masalah tersebut.
Penelitian ini mencari fitur atau band terbaik pada data hyperspectral tanaman padi. Hasil
selanjutnya dapat digunakan untuk menghitung prediksi jumlah produksi padi (yield). Penelitian sebelumnya telah dilakukan oleh Yohan (2010) pada data hyperspectral ground tanaman padi dengan ketinggian 10 cm dari kanopi tanaman padi. Hasil prediksi masih kurang baik dengan nilai RMSE di atas 0.5 dan R2 kurang dari 0.5 (Gambar 1).
Gambar 1 Grafik sebaran nilai aktual dan prediksi yield 10 cm.
Tujuan Penelitian
Penelitian ini bertujuan untuk
1 Melakukan seleksi band pada data
hyperspectral padi menggunakan teknik
Recursive Feature Elimination (RFE) dan prediksi yield menggunakan Support Vector Regression (SVR).
2 Mendapatkan kernel yang cocok untuk
Support Vector Regression.
3 Membandingkan kaidah p-norm pada hasil SVR.
Ruang Lingkup Penelitian
Data yang digunakan adalah data
hyperspectral milik PTISDA - BPPT yaitu data
airbone (hymap) dengan ketinggian 2000 m dari permukaan bumi pada tahun 2008 di kawasan Indramayu dan Subang. Data hyperspectral ini terdiri atas nilai-nilai reflectance dan panjang gelombang (wavelength) tanaman padi.
Hasil seleksi fitur dan prediksi dengan
Recursive Feature Elimination – Support Vector Regression akan dievaluasi menggunakan Root Mean Square Error (RMSE) dan sebagai pembanding juga digunakan koefisien determinasi (R2).
TINJAUAN PUSTAKA Hyperspectral
[image:32.595.320.499.189.324.2]2 yang diperoleh dengan menggunakan alat, tanpa
kontak langsung dengan objek, daerah atau gejala yang akan dikaji (Lillesand & Kiefer 1990). Contoh teknologi yang digunakan yaitu
multispectral dan hyperspectral.
Multispectral menghasilkan gambar dengan beberapa band panjang gelombang yang