SKRIPSI
Diajukan dalam Rangka Penyelesaian Studi Strata I Untuk Mencapai Gelar Sarjana Sains
Oleh:
Nama : Meyriska Aulia Harini NIM : 4150401028
Jurusan : Matematika
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS NEGERI SEMARANG
Transformasi Laplace merupakan salah satu metode yang dapat digunakan untuk menyelesaikan persamaan diferensial parsial. Dengan mentransformasikan persamaan diferensial parsial menjadi persamaan diferensial biasa kemudian mentransformasikan balik akan memperoleh penyelesaian dari persamaan diferensial parsial tersebut. Permasalahan yang muncul adalah “Bagaimana menyelesaikan bentuk transformasi Laplace dari masalah nilai batas pada persamaan diferensial parsial?”. Tujuan penulisan skripsi ini adalah untuk mengetahui bentuk transformasi Laplace dari masalah nilai batas pada persamaan diferensial parsial.
Metode penulisan yang digunakan adalah pemilihan masalah, merumuskan masalah, studi pustaka, memecahkan masalah, dan menarik kesimpulan.
Pemodelan matematika untuk masalah konduksi panas menghasilkan persamaan konduksi panas ut =kutt. Penyelesaian bentuk transformasi Laplace dari masalah nilai batas pada persamaan konduksi panas dimensi satu untuk interval tak terbatas pada kasus parabolik adalah
L = ) , (x t
u 1 ⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ −
∫
− − dx e x f e k s k ec kx
s x k s x k s ) ( 2 1 2 ⎪ ⎪ ⎭ ⎪⎪ ⎬ ⎫ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛
∫
− dx e x f e k s k x k s x k s ) ( 2 1sedangkan penyelesaian bentuk transformasi Laplace dari masalah nilai batas pada persamaan konduksi panas dimensi satu untuk interval terbatas pada kasus
parabolik adalah u(x,t)=L-1 ⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + −
−
∫
− xk s dx e e x f k s k
c kx
s x k s cosh ) ( 2 1 1 ⎪ ⎪ ⎭ ⎪⎪ ⎬ ⎫ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + −
+
∫
− xk s dx e e x f k s k
c kx
s x k s sinh ) ( 2 1 2 .
Saran yang dapat disampaikan adalah perlunya penelitian lebih lanjut dalam hal yang sama pada kasus-kasus lain dengan menggunakan metode yang sama maupun dengan metode lainnya.
Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Semarang, pada:
Hari : Senin
Tanggal : 24 Oktober 2005
Panitia Ujian
Ketua Sekretaris
Drs. Kasmadi Imam S., M.S. Drs. Supriyono, M.Si.
NIP. 130781011 NIP. 130815345
Pembimbing I Anggota Penguji
Drs. M. Chotim, M.S. 1. Drs. Khaerun, M.Si
NIP. 130781008 NIP. 131813671
Pembimbing II
2. Drs. M. Chotim, M.S.
NIP. 130781008
Dr. St. Budi Waluya
NIP. 132046848
3. Dr. St. Budi Waluya NIP. 132046848
Motto : “Seseorang dengan tujuan yang jelas akan membuat kemajuan walaupun melewati jalan yang sulit. Seseorang yang tanpa tujuan, tidak akan membuat kemajuan walaupun ia berada di jalan yang lurus.” Thomas Carlyle
Persembahan :
1. Alloh Sesembahanku
2. Mama tercinta dan Alm. Papa tersayang 3. Mas Novi, Mas Roni, Mbak Acik, Daru 4. ‘Seroja’ yang selalu memberi motivasi,
mendukung, mendampingi, mendoakan, dan menyayangi
5. Sahabat-sahabat yang selalu mendukung, mendoakan, dan menyayangi
SWT, yang telah memberikan berkah, rahmat, dan hidayah-Nya sehingga penulis dapat menyelesaikan skripsi dengan judul: “Transformasi Laplace dari Masalah Nilai Batas pada Persamaan Diferensial Parsial”.
Dalam penulisan skripsi ini, penulis mendapat bantuan dari berbagai pihak sehingga penulis ingin menyampaikan terima kasih kepada.
1. Drs. H.A.T. Soegito, SH.,MM., Rektor Universitas Negeri Semarang. 2. Drs. Kasmadi Imam S., M.S., Dekan FMIPA UNNES.
3. Drs. Supriyono, M.Si., Ketua Jurusan Matematika FMIPA UNNES. 4. Drs. M. Chotim, M.S., Dosen Pembimbing I.
5. Dr. St. Budi Waluya, Dosen Pembimbing II.
6. Alm. Ayah, Ibu, kakak-kakak, dan adikku yang selalu mendoakan, mendukung, dan menyayangi.
7. Rina, Woro, Dwi, Lidia, Puput, Nanny, Eli, Taufik, Sigit, Bowo, Ardi, dan teman-teman Math’01 yang selalu mendukung dan membantu.
8. Semua pihak yang telah membantu yang tidak dapat disebutkan satu persatu. Penulis menyadari bahwa skripsi ini masih jauh dari sempurna karena keterbatasan kemampuan dan pengetahuan yang penulis miliki. Oleh karena itu semua kritik dan saran yang membangun sangat penulis harapkan demi perbaikan skripsi ini. Penulis berharap skripsi ini dapat bermanfaat bagi pembaca.
Semarang, Oktober 2005
Penulis
Halaman Judul ……… i
Abstrak ………... ii
Halaman Pengesahan ………. iii
Motto dan Persembahan ………. iv
Kata Pengantar ……… v
Daftar Isi ………. vi
Daftar Lampiran ……….. viii
BAB I Pendahuluan A. Latar Belakang ………... 1
B. Permasalahan ………. 4
C. Batasan Masalah ……….... 4
D. Tujuan Penelitian ………... 4
E. Manfaat Penelitian ………. 5
F. Sistematika Penulisan Skripsi ……… 5
BAB II Landasan Teori A. Persamaan Diferensial Biasa ………. 7
B. Persamaan Diferensial Parsial ………... 14
C. Transformasi Laplace ……….... 17
D. Maple ………. 20
BAB III Metode Penelitian ……….... 22 BAB IV Pembahasan
C. Penyelesaian Umum ………. 30
D. Pemrograman Komputer Persamaan Konduksi Panas Dimensi Satu .. 38
BAB V Penutup A. Simpulan ……….. 53
B. Saran ……… 54
Daftar Pustaka ………. 56
Lampiran ... 57
Tabel 1. Sifat-sifat Umum Transformasi Laplace
A. Latar Belakang
Perkembangan suatu ilmu pengetahuan banyak memegang peranan penting dalam perkembangan suatu teknologi. Tanpa ilmu pengetahuan, teknologi akan sulit bisa berkembang dengan cepat.
Matematika sebagai bahasa simbol yang bersifat universal sangat erat hubungannya dengan kehidupan nyata. Kenyataan membuktikan bahwa untuk menyelesaikan masalah-masalah kehidupan nyata dibutuhkan metode-metode matematika.
Matematika merupakan salah satu cabang ilmu pengetahuan yang mempunyai ciri berbeda dengan disiplin yang dimiliki oleh ilmu pengetahuan lain. Hal-hal yang dipelajari dalam matematika terdiri atas beberapa kelompok ilmu, seperti: aljabar, geometri, analisis, dan matematika terapan. Persamaan diferensial merupakan salah satu cabang matematika yang termasuk dalam kelompok analisis.
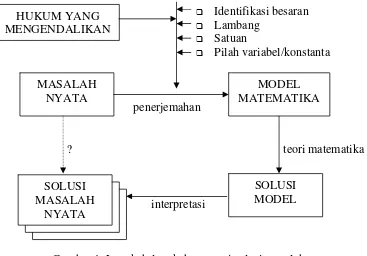
Di dalam dunia nyata kadang terdapat masalah-masalah yang sukar diselesaikan dalam sistemnya. Untuk menyelesaikan masalah tersebut perlu disusun suatu pemodelan matematika yang mirip dengan keadaan sistemnya. Masalah nyata harus dikenali terlebih dahulu melalui beberapa tahapan. Pertama, mengidentifikasi semua besaran yang terlibat. Kedua, memberi lambang pada setiap besaran yang teridentifikasi. Ketiga, menentukan satuan
setiap lambang yang ada dengan menganut suatu sistem satuan. Keempat, memilah-milah dari setiap lambang tersebut, mana yang konstanta dan mana yang variabel. Dan kelima, menentukan hukum yang mengendalikan pada masalah nyata tersebut. Dengan hukum yang mengendalikan masalah nyata tersebut menentukan hubungan antara variabel dan konstanta, yang disebut dengan model matematika. Model matematika dapat berupa persamaan, pertidaksamaan, persamaan diferensial, dan sebagainya. Kemudian dengan memanfaatkan teori-teori dalam matematika diperoleh solusi model. Dengan menginterpretasikan solusi model ditentukan solusi masalah. Pada proses ini satuan muncul kembali.
Untuk lebih jelasnya dapat dilihat pada bagan di gambar 1. Identifikasi besaran Lambang
Satuan
Pilah variabel/konstanta
penerjemahan
? teori matematika
MASALAH NYATA HUKUM YANG MENGENDALIKAN
MODEL MATEMATIKA
interpretasi
SOLUSI MODEL SOLUSI
[image:10.595.133.500.413.669.2]MASALAH NYATA
Gambar 1. Langkah-langkah mencari solusi masalah
Parsial (partial differential equation). Persamaan Diferensial Biasa didefinisikan sebagai suatu persamaan yang mengandung satu atau lebih turunan biasa suatu fungsi yang tidak diketahui dengan dua atau lebih peubah bebas. Sedangkan Persamaan Diferensial Parsial didefinisikan sebagai suatu persamaan yang mengandung satu atau lebih turunan parsial suatu fungsi yang tidak diketahui dengan dua atau lebih peubah bebas.
Setelah suatu model matematika diubah dalam bentuk persamaan diferensial, langkah selanjutnya adalah menyelesaikan persamaan diferensial tersebut dengan menentukan solusinya. Solusi persamaan diferensial adalah suatu fungsi yang memenuhi persamaan diferensial tersebut. Artinya, jika fungsi itu dan turunan-turunannya disubtitusikan ke dalam persamaan diferensial tersebut, diperoleh suatu pernyataan yang benar. Dikatakan solusi umum jika persamaan fungsi masih memuat konstanta, dan disebut solusi khusus jika tidak terdapat konstanta yang didapatkan dengan menggantikan nilai-nilai awal dan syarat batas yang diketahui.
Metode Transformasi Laplace (Laplace Transformation) merupakan salah satu metode yang dapat digunakan untuk menyelesaikan persamaan diferensial parsial. Metode ini pertama kali diperkenalkan oleh Pierre Simon Marquas De Laplace seorang matematikawan Perancis dan seorang guru besar di Paris. Bentuk umum Transformasi Laplace dapat dituliskan dalam bentuk:
F(s)=L{f}
∫
,∞ −
=
0
dimana f(t) adalah suatu fungsi yang terdefinisi untuk 0≤t<∞.
Dalam penulisan ini akan dibahas solusi persamaan diferensial parsial dengan menggunakan metode transformasi Laplace. Transformasi Laplace adalah operasi matematika yang dapat mentransformasikan persamaan diferensial parsial menjadi persamaan diferensial biasa. Kemudian mentransformasikan balik untuk memperoleh penyelesaian dari persamaan diferensial parsial tersebut.
B. Permasalahan
Berdasarkan uraian di atas, maka permasalahan yang timbul adalah “Bagaimana menentukan bentuk transformasi Laplace dari masalah nilai batas pada persamaan diferensial parsial?”
C. Batasan Masalah
Untuk membatasi ruang lingkup penulisan skripsi ini, diberikan batasan-batasan, yaitu menyelesaikan masalah nilai batas pada persamaan diferensial parsial linear orde dua dengan kasus parabolik pada persamaan konduksi panas dimensi satu.
D.Tujuan
E. Manfaat
Manfaat yang diharapkan dalam penulisan skripsi ini adalah:
(1) setelah mengetahui metode transformasi Laplace diharapkan pembaca dapat menyelesaikan persamaan diferensial parsial dengan menggunakan transformasi Laplace;
(2) pembaca diharapkan dapat menentukan bentuk transformasi Laplace dari setiap masalah nilai batas pada persamaan diferensial parsial yang diberikan.
F. Sistematika Penulisan Skripsi
Penulisan sistematika dimaksudkan untuk memberikan arah yang lebih jelas dan lebih memudahkan dalam mempelajari dan memahami isi skripsi.
Adapun sistematika penulisan skripsi yang penulis susun ini terdiri dari 3 (tiga) bagian besar yang merupakan rangkaian dari bab-bab. Dan setiap bab terdiri dari sub bab-sub bab sebagai berikut.
I. Bagian Awal Skripsi 1. Halaman Sampul 2. Halaman Judul 3. Abstraksi
7. Daftar Isi 8. Daftar Lambang 9. Daftar Gambar II. Bagian Isi Skripsi
BAB I : Pendahuluan 1. Latar Belakang 2. Permasalahan 3. Tujuan
4. Batasan Masalah 5. Sistematika Skripsi BAB II : Landasan Teori BAB III : Metode Penelitian BAB IV : Pembahasan
BAB V : Simpulan dan Saran III. Bagian Akhir Skripsi
A. Persamaan Diferensial Biasa
Persamaan diferensial adalah persamaan yang mengandung
turunan-turunan dari suatu fungsi yang tidak diketahui, yang dinamakan
dan yang akan ditentukan persamaan tersebut (Hutahean, 1993).
) (x y
Sebagai contoh, jika laju pertumbuhan suatu populasi (manusia,
hewan, bakteri, dan sebagainya)
dx dy
y'= (x=waktu) sama dengan populasi
, maka model populasi tersebut adalah )
(x
y y'= y, yaitu persamaan
diferensial.
Persamaan diferensial biasa diartikan sebagai suatu persamaan
yang melibatkan turunan pertama atau lebih dari fungsi sembarang y terhadap
peubah x; persamaan ini dapat pula melibatkan y itu sendiri, fungsi x yang diberikan dan konstanta.
Contoh:
1. y'=cosx, 2. y ''+4y=0,
3. x2y"'y'+2exy''=(x2 +2)y2.
Persamaan diferensial biasa dibagi menjadi dua bagian, yakni
persamaan diferensial linear orde satu dan persamaan diferensial linear orde
dua. Persamaan diferensial banyak sekali dikembangkan dalam matematika
teknik.
1. Persamaan Diferensial Linear Orde Satu Definisi 1.
Persamaan Diferensial Orde Satu secara umum dinyatakan
sebagai F(x,y,y')=0. Jika
dx dy
y'= , maka F(x,y,y')=0 dapat ditulis
0 ) , ,
( =
dx dy y x
F . (1)
Persamaan (1) merupakan persamaan dari persamaan diferensial yang
dinyatakan secara implisit. Persamaan (1) dapat dinyatakan secara
eksplisit sebagai
) , (x y f dx dy
= . (2)
Contoh:
Persamaan diferensial implisit: y+y'−2ex =0.
Persamaan diferensial eksplisit: x dx dy y = .
2. Solusi Persamaan Diferensial Linear Orde Satu
Suatu fungsi y= y(x) dinyatakan solusi persamaan diferensial apabila
0 ) ' , ,
(x y y =
F y= y(x) atau turunannya yakni memenuhi persamaan diferensial tersebut.
' y
1
2 +
=x
y adalah solusi persamaan diferensial y'=2x.
Demikian pula untuk c adalah konstanta, merupakan solusi
persamaan diferensial c x y= 2 +
x
y'=2 . Solusi disebut solusi khusus dan disebut solusi umum.
1
2 +
= x y
c x y= 2 +
3. Persamaan Diferensial Linear Orde Dua Definisi 2.
Persamaan diferensial berbentuk disebut
persamaan diferensial orde dua, dimana
0 ) " , ' , ,
(x y y y = f
dx dy
y'= dan
2 2
" dx
y d y =
(Hutahean, 1993).
Contoh:
1. merupakan persamaan diferensial orde
dua,
0 sin tan
' " ) 1
(x+ 2y +y x−y x=
2. xy"'+xy"−xy'+ysinx+2=0 bukan merupakan persamaan diferensial orde dua.
Definisi 3.
Bila f(x,y,y',y")=0 linear dalam y, y’, dan y” maka persamaan diferensial f(x,y,y',y")=0 disebut persamaan diferensial linear orde dua. Secara umum persamaan diferensial orde dua berbentuk:
) ( ) ( ' ) ( " )
(x y b x y c x y g x
dimana koefisien-koefisien dan fungsi merupakan
fungsi-fungsi yang kontinu di dalam selang ),
(x
a b(x),c(x), g(x) b
x
a≤ ≤ dengan di dalam selang ini (Hutahean, 1993).
0 ) (x ≠ a
Definisi 4.
Persamaan diferensial linear orde dua (3) disebut homogen
apabila g(x)=0 dan disebut tidak homogen apabila g(x)≠0 (Hutahean, 1993).
Contoh:
1. Persamaan diferensial xy"+y'sinx+3y=0 adalah persamaan diferensial linear orde dua homogen karena g(x)=0.
2. Persamaan diferensial adalah persamaan
diferensial linear orde dua tak homogen karena . x
y y x
xy"+ 2 '+4 =sin
0 ) (x ≠ g
4. Solusi Persamaan Diferensial Linear Orde Dua
Fungsi ϕ(x) dikatakan solusi persamaan diferensial (3) pada selang I, apabila ϕ(x) mempunyai turunan kedua dan memenuhi hubungan (3) pada selang I, yakni
) ( ) ( ) ( ) ( ' ) ( ) ( " )
(x x b x x c x x g x
a ϕ + ϕ + ϕ = untuk setiap x∈I.
Sekarang perhatikan persamaan diferensial linear orde dua
homogen
0 ) ( ' ) ( " )
(x y +b x y+c x y=
Teorema 1.
Misalkan ϕ(x) solusi persamaan diferensial (4) pada selang I maka )
(x
αϕ juga merupakan solusi persamaan diferensial (4) untuk setiap ℜ
∈
α .
Bukti:
Tulis y=αϕ(x) dimana α suatu konstanta. Jelas y'=αϕ'(x) dan y"=αϕ"(x).
Jelas a(x)(αϕ"(x))+b(x)(αϕ'(x))+c(x)(αϕ(x)).
Jelas α[(a(x)ϕ"(x))+(b(x)ϕ'(x))+(c(x)ϕ(x))]=α(0)=0. Jadi αϕ(x) juga solusi persamaan diferensial (4).
5. Persamaan Diferensial Linear Orde Dua Homogen dengan Koefisien Konstanta
Perhatikan persamaan diferensial yang berbentuk
0 '
"+py+qy =
y , (5)
dimana p dan q konstanta-konstanta. Intuisi merupakan solusi
persamaan diferensial (5) dengan m memenuhi persamaan tersebut.
Untuk itu akan dicari m agar merupakan solusi persamaan
diferensial (5). Dari diperoleh dan
sehingga jika dan disubstitusikan ke persamaan (5) didapat
persamaan . mx
e y =
mx e y= mx e
y = y'=memx y"=m2emx ,
y y', y"
0 )
(
0 2
2 mx + mx + mx = ⇔ + + mx =
e q pm m
qe mpe e
Dengan demikian dikatakan suatu solusi dari persamaan
diferensial (5), jika m merupakan penyelesaian dari persamaan kuadrat
. Dan karena , untuk setiap m dan x, maka
. (6)
mx e y =
0
2 + + =
q pm
m mx ≠0
e 0
2 + + =
q pm m
Persamaan disebut persamaan karakteristik dari
persamaan diferensial (5) dan akar-akarnya disebut akar-akar
karakteristik. Akar-akarnya adalah 0
2 + pm+q =
m
) 4 (
2
1 2
1 a a b
m = − + − dan
) 4 (
2
1 2
2 a a b
m = − − − .
Dari perhitungan di atas jelas bahwa dan
merupakan solusi dari persamaan diferensial
x m e
y 1
1 =
x m e
y 2
2 =
0 '
"+py+qy=
y .
Dari aljabar matematika dapat diketahui bahwa, karena a dan b
merupakan bilangan real, maka akar-akar dari persamaan karakteristik
terbagi dalam tiga kasus, yaitu: dua akar berbeda, dua
akar sama, dan dua akar kompleks. 0
2 + + =
q pm m
1. Akar real berlainan berbeda
Bila m1 dan m2 dua akar real berbeda maka dan adalah
solusi yang bebas linear sehingga merupakan
solusi umum persamaan diferensial (5).
x m
e 1 em2x
x m x m
Be Ae
y = 1 + 2
Contoh:
0 ) 1 )( 2
(m− m− = . Jadi m1 =1 dan m2 =2 merupakan akar real
berbeda maka solusi umumnya adalah y= Aex +Be2x. 2. Kedua akar sama
Misalkan kedua akar persamaan sama, yakni
, maka adalah salah satu solusi persamaan
diferensial (5). Bila
0
2 + + =
q pm m
a m
m1 = 2 = φ1(x)=eax
) ( ) ( )
( 1
2 x W xφ x
φ = solusi lainnya, maka
dx e
e x
W pxdx
ax
∫
⎥⎥⎦ ⎤ ⎢
⎢ ⎣
⎡ ∫
⎟ ⎠ ⎞ ⎜ ⎝ ⎛
= −
2
1 )
(
∫
⎟ ⎠ ⎞ ⎜⎝ ⎛
= −
dx e e
px ax
2
1
.
Karena m1 =m2 =a adalah akar persamaan m2 + pm+q=0, maka p
a m
m1+ 2 =2 =− .
Jadi
∫
⎟ =∫
= ⎠⎞ ⎜
⎝ ⎛
= e dx dx x
e x
W ax 2ax
2
1 )
( .
Hal tersebut memberikan φ2(x)= xφ1(x)⇒φ2(x)= xeax dimana φ1 dan φ2 bebas linear. Jadi solusi umum persamaan diferensial
adalah .
0 '
"+py+qy=
y y= Aeax +Bxeax =(A+Bx)eax Contoh:
Misalkan persamaan diferensial y"−4y'+4y=0. Tentukan solusi persamaan diferensial di atas.
Penyelesaian:
Jelas 2 −4 +4=0 merupakan persamaan karakteristik. m
Jelas (m−2)=0. Jelas m1 =m2 =2.
Jadi suatu solusi umum persamaan diferensial
. x e Bx A
y =( + ) 2 0 4 ' 4
"− y+ y= y
3. Akar kompleks
Misalkan salah satu akar persamaan m2 + pm+q=0 adalah
β α+ =
1
m i, maka akar yang lain yakni m1 =α−βi, sehingga dan adalah solusi basis
untuk persamaan diferensial x
i x
m e e
x ( )
1
1
)
( α β
φ = = + mx i x
e e
x ( )
2
2
)
( α β
φ = = −
0 '
"+py+qy=
y . Jadi solusi umum persamaan diferensial tersebut adalah:
x i x
i
e c e
c
y= 1 (α+β) + 2 (α−β) =c1eαxeβxi+c2eαxe−βxi
=c1eαx(cosβx+isinβx)+c2eαx(cosβx−isinβx) =eαx{(c1+c2)cosβx+(c1 −c2)isinβx}.
Dengan mengambil c1+c2 = A dan i(c1−c2)=B maka solusi umum persamaan diferensial tersebut adalah
. } sin cos
{A x B x e
B. Persamaan Diferensial Parsial
Persamaan diferensial parsial adalah suatu persamaan yang
mengandung satu atau lebih turunan parsial suatu fungsi (yang tidak
diketahui) dengan dua atau lebih peubah bebas.
Tingkat (order) persamaan diferensial parsial adalah pangkat tertinggi dari turunan yang termuat dalam persamaan diferensial parsial. Dan
derajat (degree) persamaan diferensial parsial adalah pangkat tertinggi dari turunan tingkat tertinggi yang termuat dalam persamaan diferensial parsial.
Persamaan diferensial parsial linier adalah suatu bentuk persamaan
diferensial parsial yang berderajat satu dalam peubah tak bebasnya dan
turunan parsialnya (Hutahean, 1993).
Beberapa persamaan diferensial parsial linier orde-2 yang penting.
2 2 2 2 2
x u c t
u
∂ ∂ = ∂ ∂
, disebut persamaan gelombang dimensi satu; (7)
2 2 2
x u c t u
∂ ∂ = ∂ ∂
, disebut persamaan konduksi panas dimensi satu; (8)
0
2 2
2 2
= ∂ ∂ + ∂ ∂
y u x
u
, disebut persamaan laplace dimensi satu; (9)
) , (
2 2
2 2
y x f y
u x
u
= ∂ ∂ + ∂ ∂
, disebut persamaan poisson dimensi satu; (10)
0
2 2
2 2
2 2
= ∂ ∂ + ∂ ∂ + ∂ ∂
z u y
u x
u
Dalam hal ini c adalah konstanta, t adalah waktu dan x,y,z adalah peubah bebas. Untuk memudahkan notasi maka digunakan indeks untuk
menotasikan turunan parsial, seperti
x u ux
∂ ∂
= , 2
2
x u uxx
∂ ∂
= dan sebagainya.
Adapun bentuk umum persamaan diferensial parsial linier orde-2 diberikan
dengan
G Fu Eu Du Cu
Bu
Auxx + xy + yy + x + y + = , (12) dimana A, B, C, D,E, F, dan G adalah fungsi-fungsi yang bergantung pada x
dan y.
Terdapat 3 jenis persamaan diferensial parsial linier yang penting,
yaitu parabolik, hiperbolik dan elliptik. Persamaan diferensial parsial orde
dua dalam persamaan (12);
jika B2 −4AC =0, disebut persamaan parabolik, jika B2 −4AC >0, disebut persamaan hiperbolik,
jika B2 −4AC <0, disebut persamaan elliptik (Pinsky, 1998).
Sedangkan persamaan (8) merupakan persamaan parabolik, persamaan (7)
merupakan persamaan hiperbolik dan persamaan (9) merupakan persamaan
elliptik.
Syarat Batas
Syarat batas adalah syarat-syarat tertentu atau kondisi-kondisi
tertentu yang terlibat dalam persamaan diferensial parsial untuk membantu
yaitu interval terbatas, interval setengah terbatas, dan interval tak terbatas.
Untuk interval terbatas, besarnya interval I adalah sehingga
mempunyai dua syarat batas yaitu pada
L x< < 0
0 =
x dan x= L. Untuk interval setengah tak terbatas, besarnya I adalah 0<x<∞ biasa ditulis , syarat batasnya hanya pada
0 > x 0
=
x . Dan untuk interval tak terbatas, besarnya interval I adalah −∞<x<∞ sehingga tidak punya syarat batas.
Bentuk persamaan syarat batas diberikan dengan
) (x f n u u ⎥⎦⎤= ⎢⎣
⎡
∂ ∂ + β
α , (13)
dimana α,β adalah suatu konstanta dan n u ∂ ∂
didefinisikan sebagai
grad n
x u x
u n u
n . ,..., .
1
⎟ ⎠ ⎞ ⎜
⎝ ⎛
∂ ∂ ∂
∂
= . Terdapat tiga jenis syarat batas yaitu:
(a) persamaan (13) disebut dengan kondisi Dirichlet jika α ≠0 dan 0
=
β ;
(b) persamaan (13) disebut dengan kondisi Neumann jika α =0 dan 0
≠
β ;
(c) persamaan (13) disebut dengan kondisi campuran jika α ≠0 dan 0
≠
C. Transformasi Laplace Definisi 5.
Misalkan adalah suatu fungsi yang terdefinisi pada interval
[0,∞). Transformasi Laplace dari f adalah suatu fungsi F(s) yang
didefinisikan dengan integral ) (t f
∫
∞−
=
0
) ( )
(s e f t dt
F st , (14)
dengan daerah asal F adalah semua nilai dari s sedemikian hingga integral
dari (14) ada. Fungsi asal dinyatakan dengan huruf kecil dan transformasi
Laplacenya dengan huruf yang sama tetapi huruf besar. Transformasi Laplace
dari f dinotasikan dengan F atau L{f}. Selanjutnya fungsi asal f(t) adalah invers dari F(s) dan dinotasikan dengan f(t)= L-1{F(s)} (Hutahean, 1993). Jika L{f}=F(s) maka f(t) disebut invers transformasi Laplace dari F(s) dan
secara simbolis ditulis:
f(t)= L-1{F(s)},
dengan L-1 disebut operator invers transformasi Laplace.
Definisi 6.
Suatu fungsi f(t) dikatakan kontinu bagian demi bagian pada suatu
selang jika f kontinu di sejumlah hingga titik pada selang tersebut
(Hutahean, 1993).
Dari pengertian tersebut berarti selang yang dimaksud dapat dibagi
selang yang terjadi, jadi suatu fungsi f(t) kontinu pada [0,∞) jika f kontinu
pada selang [0,N) untuk semua N >0. Definisi 7.
Suatu fungsi f(t) dikatakan berorde eksponensial jika
terdapat konstanta tak negatif M dan T sehingga
∞ → t t Me t
f( ) ≤ α untuk semua (Hutahean, 1993).
T t≥
Teorema 2.
Diketahui f1 dan f2 suatu fungsi-fungsi. Jika transformasi Laplace dari f1 dan f2 ada dan c merupakan suatu konstanta maka:
(i) L{f1+ f2}=L{f1}+L{f2}; (ii) L{cf1}=cL{f1}.
Bukti:
(i) Jelas L{f1 + f2}=
∫
.∞
− +
0
2
1 )( )
(f f t dt e st
L
⇔ {f1 + f2}=
∫
∞
−
− +
0
2
1( ) ( ) )
(f t e st f t e st dt
L
⇔ {f1 + f2}=
∫
∫
∞ ∞
−
− +
0 0
2
1(t)e dt f (t)e dt
f st st
L L
⇔ {f1 + f2}= {f1}+L{f2}.
(ii) Jelas L
∫
.∞ −
=
0
1
1} ( )( )
{cf e st cf t dt
⇔ L
∫
∞ −
=
0
1
1} ( )( )
⇔ L
∫
∞ −
=
0 1
1} ( )( )
{cf c e st f t dt
⇔ L{cf1}=cL{f1}.
Akibatnya, invers transformasi Laplace jika ada adalah linier.
Bukti:
Tulis f1(t)=L-1{F1(s)} dan f2(t)=L-1{F2(s)}. (a) Jelas L-1{F1(s)+F2(s)}= f1(t)+ f2(t).
⇔ L-1{F1(s)+F2(s)}= L-1{F1(s)}+ L-1{F2(s)}. (b) Jelas L-1{cF1(s)}=cf1(t).
⇔ L-1{cF1(s)}=cL-1{F1(s)}. Jadi L-1 adalah linier.
D. Maple
Maple merupakan salah satu perangkat lunak yang dikembangkan
oleh Waterloo Inc. Kanada untuk keperluan Computer Algebraic System
(CAS). Maple sering digunakan untuk keperluan penyelesaian permasalahan
persamaan diferensial dan visualisasinya, karena mudah untuk digunakan.
Maple memiliki kemampuan menyederhanakan persamaan, hingga suatu
solusi persamaan diferensial dapat dipahami dengan baik. Keunggulan dari
Maple untuk aplikasi persamaan diferensial adalah kemampuan melakukan
persamaan diferensial yang memiliki nilai awal dan syarat batas (Kartono,
2001).
Untuk memulai Maple pada Windows, cukup dengan klik pada
icon Maple yang akan langsung memberikan respon dengan menampilkan
worksheet “>”. Menu-menu yang terdapat pada tampilan Maple terdiri dari
File, Edit, View, Insert, Format, Spreadsheet, Option, Windows, dan Help. Sebagian besar menu di atas merupakan menu standar yang dikembangkan
untuk program aplikasi pada sistem operasi Windows. Bahasa yang
digunakan pada Maple merupakan bahasa pemrograman yang sekaligus
sebagai bahasa aplikasi, sebab pernyataan atau statement yang merupakan
input (masukan) pada Maple berupa deklarasi pada bahasa program dan
command (perintah) yang sering digunakan pada aplikasi. Simbol “>” ini
otomatis dan sebagai tanda bahwa Maple telah siap untuk dioperasikan.
Perintah ke komputer diberikan dengan mengetikkan pada papan ketik
setelah simbol “>”. Perintah ini dicetak dalam warna merah, sedangkan
hasilnya dicetak dalam warna biru. Setiap perintah Maple jika ingin
ditampilkan harus diakhiri dengan simbol titik koma (;) dan simbol titik dua
Peranan metode penelitian dalam suatu penelitian sangat penting. Sehingga dengan metode penelitian dapat mencapai tujuan penelitian yang telah ditetapkan dan agar penelitian yang telah dilakukan berjalan dengan lancar. Melalui metode penelitian, masalah yang dihadapi dapat diatasi dan dipecahkan dari perolehan data yang telah dikumpulkan.
Langkah-langkah yang dilakukan pada penelitian ini meliputi beberapa hal yaitu. A. Pemilihan Masalah
Dalam perkuliahan yang diperoleh penulis, banyak masalah yang perlu dikaji lebih lanjut. Dari beberapa masalah tersebut dihadapkan pada persoalan untuk memilih masalah yang kemudian dijadikan bahan dasar untuk melakukan penelitian lebih lanjut.
B. Merumuskan Masalah
Perumusan masalah diperlukan untuk membatasi permasalahan sehingga diperoleh bahan kajian yang jelas. Sehingga akan lebih mudah untuk menentukan langkah dalam memecahkan masalah tersebut.
C. Studi Pustaka
Setelah diperoleh masalah untuk diteliti, peneliti mengadakan studi pustaka. Studi pustaka adalah penelaahan sumber pustaka yang relevan, digunakan untuk mengumpulkan data informasi yang diperlukan dalam penelitian. Studi pustaka diawali dengan mengumpulkan sumber pustaka yang berupa buku
atau literatur, jurnal, skripsi dan sebagainya. Setelah pustaka terkumpul dilanjutkan dengan pemahaman isi sumber pustaka tersebut yang pada akhirnya sumber pustaka ini dijadikan landasan untuk menganalisis permasalahan.
D. Memecahkan Masalah
Setelah permasalahan dirumuskan dan sumber pustaka terkumpul, langkah selanjutnya adalah pemecahan masalah melalui pengkajian secara teoritis yang selanjutnya disususn secara rinci dalam bentuk pembahasan.
Dalam pembahasan masalah dilakukan beberapa langkah pokok yaitu: 1. memberikan masalah nilai batas pada persamaan diferensial parsial;
2. mentransformasikan masalah nilai batas pada persamaan diferensial parsial dengan menggunakan metode transformasi Laplace;
3. menyelesaikan masalah nilai batas pada persamaan diferensial parsial yang telah ditransformasikan dengan metode transformasi Laplace dengan menggunakan invers transformasi Laplace.
E. Menarik Kesimpulan
A. Pemodelan Persamaan Konduksi Panas Dimensi Satu
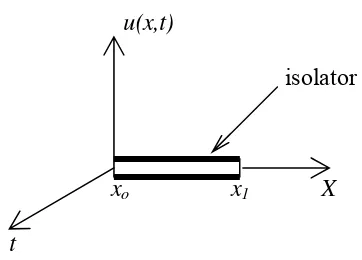
Perhatikan suatu batang kawat tipis dengan ukuran panjang hingga
yang diisolasi dengan irisan melintangnya diasumsikan konstan dan terbuat
dari bahan homogen serta terletak pada sumbu X. Didefinisikan adalah
suhu pada titik x dan waktu t dalam batang kawat tersebut. Ujung-ujung kawat
dan (lihat gambar 1).
) , (x t u
0
x x1
u(x,t)
isolator
xo x1 X
[image:32.595.145.326.399.529.2]t
Gambar 1. Sketsa Batang Kawat pada Sumbu X
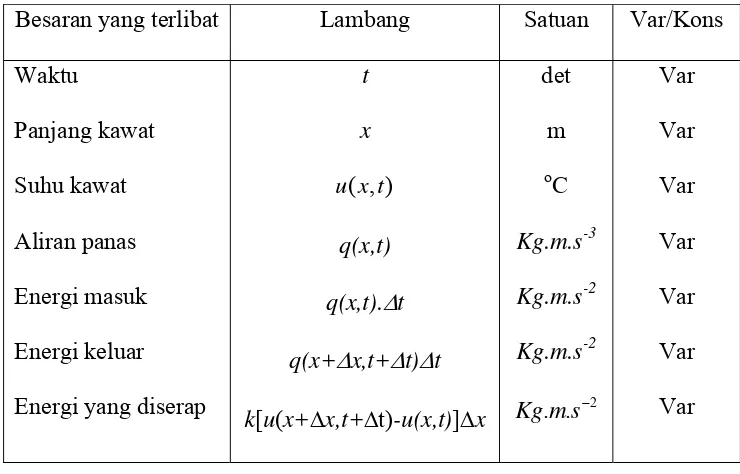
1. Identifikasi Besaran yang Terlibat
Identifikasi besaran yang terlibat pada pemodelan di atas dapat
dilihat dalam tabel 1.
Tabel 1. Identifikasi Besaran yang Terlibat
Besaran yang terlibat Lambang Satuan Var/Kons
Waktu
Panjang kawat
Suhu kawat
Aliran panas
Energi masuk
Energi keluar
Energi yang diserap
t x
) , (x t u
q(x,t) q(x,t).Δt
q(x+Δx,t+Δt)Δt
k[u(x+Δx,t+Δt)-u(x,t)]Δx
det
m
o C
Kg.m.s-3 Kg.m.s-2 Kg.m.s-2
2
. .ms− Kg
Var
Var
Var
Var
Var
Var
Var
2. Hukum yang Mengendalikan
Persamaan konduksi panas sederhana dikarakterisasikan oleh
hukum di bawah ini.
1. Panas mengalir dari tempat yang lebih panas ke tempat yang lebih
dingin.
2. Energi yang masuk sama dengan energi keluar ditambah dengan
energi yang diserap.
3. Energi berbanding lurus dengan laju perubahan suhu persatuan
panjang (Hukum Fourier pada hantaran panas).
3. Model Matematika
energi yang diserap: k[u(x+Δx,t+Δt)−u(x,t)]Δx.
Jadi q(x,t)Δt =q(x+Δx,t+Δt)Δt +k[u(x+Δx,t+Δt)−u(x,t)]Δx −
⇔ (q(x,t) q(x+Δx,t+Δt))Δt =k1[u(x+Δx,t+Δt)−u(x,t)]Δx
t t x u t t x x u k x t t x x q t x q Δ − Δ + Δ + = Δ Δ + Δ + −
⇔ ( , ) ( , ) 1[ ( , ) ( , )]
t t x u t t x x u k x t t x x q t x q t x Δ − Δ + Δ + = Δ Δ + Δ + − ⇔ → Δ → Δ )] , ( ) , ( [ lim ) , ( ) , ( lim 1 0 0 t u k x q ∂ ∂ = ∂ ∂ −
⇔ 1 .
Sesuai dengan hukum Fourier yang menyatakan bahwa energi berbanding
lurus dengan laju perubahan panas terhadap x, maka diperoleh
x u t x q ∂ ∂ − = α ) ,
( , α >0
tanda negatif pada hukum Fourier menunjukkan bahwa panas mengalir
dari tempat yang lebih panas ke tempat yang lebih dingin.
Jadi t u k x u x ∂ ∂ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ − ∂ ∂
− α 1
t u k x u ∂ ∂ = ∂ ∂
⇔α 22 1
t u k x u ∂ ∂ = ∂ ∂ ⇔ α1 2 2 2 2 x u k t u ∂ ∂ = ∂ ∂
⇔ , k
k1 = α 2 2 2 x u c t u ∂ ∂ = ∂ ∂
⇔ , 2. (1)
Persamaan ini disebut dengan persamaan konduksi panas dimensi satu.
Konstanta k dinamakan difusitas yang sama dengan
σρ
K
dengan
konduktifitas termal K, panas jenis σ, dan kerapatan ρ diandaikan konstan. Distribusi temperatur pada saat awal, yaitu saat t =0,
) ( ) 0 ,
(x f x
u = , x∈I
Syarat batas dapat ditentukan pada kedua ujung batang kawat
yaitu dan . Misalnya temperatur pada ujung-ujungnya adalah ,
diperoleh syarat batas Dirichlet: 0
=
x x=l f(t)
⎩ ⎨ ⎧ > = > = 0 ), ( ) , ( 0 ), ( ) , 0 ( t t f t l u t t f t u .
Jika ujung batang kawat diisolasi, maka ( , ) =0 ∂ ∂ x t x u
. Dan jika
panas yang mengalir proporsional terhadap pergantian temperatur pada
ujung batang kawat ) , (x t q x t x u ∂ ∂ ( , )
, maka menurut hukum Fourier konduksi panas
dimensi satu x t x u k t x q ∂ ∂ − = ( , ) ) ,
( , sehingga diperoleh syarat batas Neumann:
⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ > − = ∂ ∂ > − = ∂ ∂ 0 , ) , ( ) , ( 0 ) , 0 ( ) , 0 ( t k t l q x t l u t k t q x t u .
Jika pergantian temperatur pada ujung batang kawat x t x u ∂ ∂ ( , )
proporsional terhadap temperatur , maka diperoleh syarat batas
Campuran:
⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ > = + ∂ ∂ > = + ∂ ∂ 0 ), ( ) , ( ) , ( 0 ), ( ) , 0 ( ) , 0 ( 2 1 t x f t l u x t l u t x f t u x t u β α ,
dimana α, β adalah suatu konstanta yang diberikan.
B. Penyelesaian Persamaan Diferensial Parsial dengan Transformasi Laplace
Interval setengah tak terbatas pada kasus parabolik
Diketahui persamaan konduksi panas 2
2 2 x u c t u ∂ ∂ = ∂ ∂ .
Pada kondisi awal u(x,0)= f(x), x>0 diketahui syarat batasnya adalah:
) ( ) , 0 ( ) , 0
( g t
x t u t u = ∂ ∂ +β
α ; t >0
dengan α,β suatu konstanta yang diberikan.
Diketahui 2 2 2 x u c t u ∂ ∂ = ∂ ∂
⇔L =
⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∂ ∂ ) , (x t t u L ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∂ ∂ ) , ( 2 2 2 t x x u
c , c2 =k
⇔L =
⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∂ ∂ ) , (x t t u kL ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∂ ∂ ) , ( 2 2 t x x u
⇔ ~( , ) ( ,0) 2~(2, ) dx s x u d k x u s x u
s − =
⇔ k x u s x u k s dx s x u
d ( ,0)
) , ( ~ ) , ( ~ 2 2 − =
− . (2)
k x f s x u k s dx s x u
d ( )
) , ( ~ ) , ( ~ 2 2 − =
− , (3)
dengan syarat batas:
) ( ) , 0 ( ) , 0
( g t
x t u t u = ∂ ∂ +β α
⇔L =
⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∂ ∂ + x t u t
u(0, ) β (0, )
α L
{ }
g(t)⇔L
{
αu(0,t)}
+L =⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∂ ∂ x t u(0, )
β L
{ }
g(t)⇔αL
{
u(0,t)}
+βL =⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∂ ∂ x t u(0, )
L
{ }
g(t)⇔ (0, ) ~( )
~ )
, 0 (
~ g s
dx s u d s
u +β =
α . (4)
Interval terbatas pada kasus parabolik Persamaan konduksi panas dimensi satu:
) , ( ) , ( 2 2 t x x u k t x t u ∂ ∂ = ∂ ∂
, 0< x<l, t >0 (5)
pada kondisi awal u(x,0)= f(x), 0<x<ldiketahui syarat batasnya adalah:
) ( ) , 0 ( ) , 0
( g1 t
x t u t u = ∂ ∂ +β
α ; t >0; α,βkonstanta, (6)
) ( ) , ( ) ,
( g2 t
x t l u t l u = ∂ ∂ +β
α ; t >0; α,βkonstanta. (7)
Dengan mentransformasi persamaan (5) diperoleh persamaan yang sama
(2) diperoleh persamaan yang sama dengan persamaan (3), dengan syarat batas: ) ( ) , 0 ( ) , 0
( g1 t
x t u t u = ∂ ∂ +β α
⇔L =
⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∂ ∂ + x t u t
u(0, ) β (0, )
α L
{
g1(t)}
⇔L
{
αu(0,t)}
+L =⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∂ ∂ x t u(0, )
β L
{
g1(t)}
⇔αL
{
u(0,t)}
+βL =⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∂ ∂ x t u(0, )
L
{
g1(t)}
⇔ (0, ) ~ ( )
~ ) , 0 ( ~ 1 s g dx s u d s
u +β =
α , dan (8)
) ( ) , ( ) ,
( g2 t
x t l u t l u = ∂ ∂ +β α
⇔L =
⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∂ ∂ + x t l u t l
u( , ) β ( , )
α L
{
g2(t)}
⇔L
{
αu(l,t)}
+L =⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∂ ∂ x t l u( , )
β L
{
g2(t)}
⇔αL
{
u(l,t)}
+βL =⎭ ⎬ ⎫ ⎩ ⎨ ⎧ ∂ ∂ x t l u(, )
L
{
g2(t)}
⇔ (, ) ~ ( ) ~ ) , ( ~ 2 s g dx s l u d s l
u +β =
α . (9)
C. Penyelesaian Umum
Dengan menggunakan transformasi Laplace (terhadap t atau x)
persamaan-persamaan diferensial parsial tersebut dapat ditransformasikan
menjadi persamaan diferensial biasa berbentuk:
) ( '' y f x
y + = . (10)
Sebagai contoh perhatikan persamaan diferensial y''+y=0. Tulis y1(x) dan y2(x) suatu selesaian.
Jadi .
⎩ ⎨ ⎧
= +
= +
) ( ) ( ' ) ( ' ) ( ' ) ( '
0 ) ( ) ( ' ) ( ) ( '
2 1
2 1
x f x y x B x y x A
x y x B x y x A
Dengan menyelesaikan A’(x) dan B’(x), diperoleh A(x) dan B(x) maka
penyelesaian persamaan (10) di atas adalah:
) ( ) ( ) ( ) ( )
(x A x y1 x B x y2 x
y = + .
Jika pada persamaan (10) tersebut berbentuk eksponensial, polinomial
dan trigonometri (terbatas pada )
(x f
α
sin dan cosα), maka A(x) dan B(x) berupa
suatu konstanta.
Interval setengah tak terbatas pada kasus parabolik Diasumsikan bahwa solusi umum dari persamaan (10) adalah:
x m x
m
e x B e x A x
y( )= ( ) 1 + ( ) 2 . (11)
Dengan mengambil persamaan:
0 )
( ' )
(
' x em1x +B x em2x =
A dan (12)
) ( )
( ' )
(
' 1 2
2
1A x e t B x e f x
t mx+ mx = , (13)
diperoleh:
x m e x f m m x
A'( ) 1 ( ) 1
1 2
−
1 1 2 1 ) ( 1 )
( f x e dx c
m m x
A mx +
− − =
⇔ −
∫
, dan (14)x m e x f m m x
B'( ) 1 ( ) 2
1 2 − − = 2 1 2 2 ) ( 1 )
( f x e dx c
m m x
B mx +
− =
⇔ −
∫
. (15)Jika A(x) dan B(x) dari (14) dan (15) disubstitusikan ke persamaan (11), diperoleh:
mx mx f x e mxdx emx m m c e dx e x f m m c x
y( ) 1 ( ) 2 1 1 ( ) 2 2
1 2 2 1 2 1 ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − + + ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − − =
∫
−∫
− .Dari persamaan (3), akar-akar karakteristik dari persamaan
0 ) , ( ~ ) , ( ~ 2 2 =
− u x s
k s dx s x u d adalah k s t1 = ;
k s t2 =− .
Diasumsikan bahwa solusi umum dari persamaan (3) tersebut adalah:
x k s x k s e x B e x A s x
u~( , )= ( ) + ( ) − . (16) Dengan mengambil persamaan:
0 )
`( )
`( + − kx = s x k s e x B e x
A dan
k x f e x B k s e x A k s x k s x k s ) ( ) `( ) `( − − =− . Diperoleh: x k s e k s k x f x
A =− −
2 ) ( )
1 ) ( 2 1 )
( f x e dx c
k s k x
A kx
s + −
=
⇔
∫
− . (17)x k s e k s k x f x B 2 ) ( ) `( = 2 ) ( 2 1 )
( f x e dx c
k s k x B x k s + =
⇔
∫
. (18)Jika A(x) dan B(x) dari (17) dan (18) disubstitusikan ke persamaan (16) sehingga diperoleh: x k s x k s x k s x k s e dx e x f k s k c e dx e x f k s k c s x
u − −
⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ ⎪ ⎪ ⎭ ⎪⎪ ⎬ ⎫ + + ⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ ⎪ ⎪ ⎭ ⎪⎪ ⎬ ⎫ − =
∫
∫
( ) 2 1 ) ( 2 1 ) , ( ~ 2 1 ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − += −
∫
− e−∫
f x e dxk s k dx e x f e k s k e c e c k s x k s x k s x k s x k s x k s ) ( 2 1 ) ( 2 1 2 1
karena u(x,t) haruslah terbatas bila x→∞ maka L harus pula terbatas bila
= ) , ( ~ x s
u
{
u(x,t)}
∞→
x , maka harus diperoleh c1 =0, sehingga
⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ −
= −
∫
− e−∫
f xe dxk s k dx e x f e k s k e c s x
u kx
s x k s x k s x k s x k s ) ( 2 1 ) ( 2 1 ) , ( ~ 2 .
Untuk mendapatkan penyelesaian persamaan di atas dengan invers
= ) , (x t
u L-1
⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ −
∫
− − dx e x f e k s k ec kx
s x k s x k s ) ( 2 1 2 ⎪ ⎪ ⎭ ⎪⎪ ⎬ ⎫ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛
∫
− dx e x f e k s k x k s x k s ) ( 2 1. (19)
Interval terbatas pada kasus parabolik
Diasumsikan bahwa solusi umum dari persamaan (10) tersebut adalah:
x x B x x A x
y( )= ( )cosh + ( )sinh . (20) Dengan mengambil persamaan:
0 sinh ) `( cosh )
`(x x+B x x=
A dan
) ( cosh ) `( sinh )
`(x x B x x f x
A + = ,
diperoleh:
x x f x
A`( )=− ( )sinh
x x e e x f x
A ( )(( ) 1)
2 1 ) `( 2 − − = ⇔
∫
− + + = ⇔ − 1 ) )( ( 2 1 )(x f x e e dx c
A x x (21)
x x
f
B`= ( )cosh
x x e e x f
B ( )(( ) 1) 2 1 ` 2 + = ⇔
∫
+ + = ⇔ − 2 ) )( ( 2 1 )(x f x e e dx c
Jika A(x) dan B(x) dari (21) dan (22) disubstitusikan ke persamaan (20), diperoleh: ⎩ ⎨ ⎧ ⎩ ⎨ ⎧ ⎭ ⎬ ⎫ + + + ⎭ ⎬ ⎫ + + − =
∫
−∫
− x c dx e e x f x c dx e e x f xy x x ( )( x x) sinh
2 1 cosh ) )( ( 2 1 )
( 1 2 .
Diasumsikan bahwa solusi umum dari persamaan (3) adalah :
x k s x B x k s x A s x
u~( , ) = ( )cosh + ( )sinh . (23)
Dengan mengambil persamaan:
0 sinh ) `( cosh )
`( + x =
k s x B x k s x
A dan
k x f x k s x B k s x k s x A k
s ( )
cosh ) `( sinh ) `( + = − , sehingga diperoleh: x k s k s k x f x
A`( )= ( )sinh
x k s x k s e k s k e x f x A 2 1 ) ( ) `( 2 ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = ⇔
∫
+ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − − =⇔ ( ) − 1
2 1 )
( f x e e dx c
k s k x
A kx
s x k s
. (24)
x k s k s k x f x
x k s x k s e k s k e x f x B 2 1 ) ( ) `( 2 ⎟⎟ ⎟ ⎠ ⎞ ⎜⎜ ⎜ ⎝ ⎛ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − = ⇔ 2 ) ( 2 1 )
( f x e e dx c
k s k x
B kx
s x k s + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − =
⇔
∫
− . (25)Jika A(x) dan B(x) dari (24) dan (25) disubstitusikan ke persamaan (23), diperoleh: x k s dx e e x f k s k c s x
u kx
s x k s cosh ) ( 2 1 ) , ( ~ 1 ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − − =
∫
− x k s dx e e x f k s kc kx
s x k s sinh ) ( 2 1 2 ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + − +
∫
− .Untuk mendapatkan penyelesaian persamaan di atas dengan invers
transformasi Laplace, sehingga diperoleh:
= ) , (x t
u L-1
⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + −
−
∫
− xk s dx e e x f k s k
c kx
s x k s cosh ) ( 2 1 1 ⎪ ⎪ ⎭ ⎪⎪ ⎬ ⎫ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + −
+
∫
− xk s dx e e x f k s k
c kx
s x k s sinh ) ( 2 1
Contoh 1.
Selesaikan masalah nilai batas persamaan konduksi panas pada suatu batang
kawat tipis semi infinite dengan temperatur awal dan ujung kawat pada
mempunyai temperatur konstan .
C o 0
0 =
x to
Penyelesaian:
Diketahui
2 2 2
x u c t u
∂ ∂ = ∂ ∂
, x>0, t >0.
Dipunyai u(x,0)=0, x>0.
Jelas
k x u s x u k s dx
s x u
d ( ,0)
) , ( ~ ) , ( ~
2 2
− = −
( , ) ~( , ) 0 ~
2 2
= −
⇔ u x s
k s dx
s x u d
.
Dipunyai u(0,t)=to, t >0. Jelas L{u(0,t)}=L{to}
s t s
u = o
⇔ ~(0, ) .
Jadi kx
s x
k s
e c e c s x
u~( , )= 1 + 2 − . Tulis c1 =0.
Jelas kx s e c s x
u~( , )= 2 − .
Jadi
s t s u~(0, )= o
0 2
) , 0 (
~ s c e
u =
s t c = o
⇔ 2 .
Jadi kx
s o e s t s x
u~( , )= − .
Jadi u(x,t)=L-1{u~(x,s)}
= ⇔u(x,t) L-1
⎪⎭ ⎪ ⎬ ⎫ ⎪⎩
⎪ ⎨
⎧ − x
k s o e s t
o t t x
u =
⇔ ( , ) L-1
⎪⎭ ⎪ ⎬ ⎫ ⎪⎩
⎪ ⎨
⎧ − x
k s e s 1
⎟⎟ ⎠ ⎞ ⎜⎜
⎝ ⎛ =
⇔
kt x erfc t t x
u o
2 )
,
( .
Jadi ⎟⎟
⎠ ⎞ ⎜⎜
⎝ ⎛ =
kt x erfc t t x
u o
2 )
,
( .
D. Pemrograman Komputer Persamaan Konduksi Panas Dimensi Satu Berikut ini adalah pemrograman Maple untuk persamaan konduksi
panas dimensi satu.
Interval setengah tak terbatas pada kasus parabolik > restart;with(PDEtools):
> p1:=(D@@2)(y)(x)+y(x)=f(x);
:=
p1 (D( )2 )( )y x( ) + y( )x = f( )x
> p2:=y(x)=A(x)*exp(m[1]*x)+B(x)*exp(m[2]*x);
:=
p2 y( )x = A( )x e +
(m )
1x
( ) B x e
(m )
> s1:=D(A)(x)*exp(m[1]*x)+D(B)(x)*exp(m[2]*x)=0;
:=
s1 D( )A x( )e + =
(m )
1x
( ) ( ) D B x e
(m )
2x
0
>s2:=m[1]*D(A)(x)*exp(m[1]*x)+m[2]*D(B)(x)*exp(m[2]*
x)=f(x);
:=
s2 m1D( )A x( )e + =
(m )
1x
m2D( )B x( )e
(m )
2x
( ) f x
> sol1:=solve({s1,s2},{D(A)(x),D(B)(x)});
:= sol1 ⎧
⎩ ⎪⎪ ⎪⎪⎪⎨
⎫
⎭ ⎪⎪ ⎪⎪⎪⎬
,
=
( ) ( )
D A x f( )x
e
(m )
1x
(− + m )
2 m1
=
( ) ( )
D B x − f( )x
e
(m )
2x
(− + m )
2 m1
> sol2:=sol1[1];
:=
sol2 D( )A x( ) = f( )x
e
(m )
1x
(− + m )
2 m1
> sol3:=sol1[2];
:=
sol3 D( )B x( ) = − f( )x
e
(m )
2x
(− + m )
2 m1
> solu1:=dsolve({sol2},A(x));
:=
solu1 A( )x = d + ⌠
⌡ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ e
(−m )
1x
( ) f x
− + m2 m1 x _C1
> solu2:=dsolve({sol3},B(x));
:=
solu2 B( )x = d + ⌠
⌡ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮
− f( )x e
(−m )
2x
− + m
2 m1
x _C1
:=
solu3 B( )x = d + ⌠ ⌡ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮
− f( )x e
(−m )
2x
− + m
2 m1
x _C2
> pers1:=subs(solu1,solu3,p2);
:=
pers1 y( )x = +
⎛ ⎝ ⎜⎜ ⎜⎜ ⎜⎜⎜ ⎞ ⎠ ⎟⎟ ⎟⎟ ⎟⎟⎟ + d ⌠ ⌡ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ e
(−m )
1x
( ) f x
− + m2 m1 x _C1 e
(m )
1x ⎛ ⎝ ⎜⎜ ⎜⎜ ⎜⎜⎜ ⎞ ⎠ ⎟⎟ ⎟⎟ ⎟⎟⎟ + d ⌠ ⌡ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮
− f( )x e
(−m )
2x
− + m2 m1 x _C2 e
(m )
2x
> simplify(pers1);
( ) y x e
(m )
1x d ⌠ ⌡ ⎮ ⎮ ⎮e
(−m )
1x
( ) f x x e
(m )
1x
_C1 m2 e
(m )
1x
_C1 m1 e
(m )
2x d ⌠ ⌡ ⎮ ⎮ ⎮f( )x e
(−m )
2x x − + − ⎛ ⎝ ⎜⎜ ⎜ = e
(m )
2x
_C2 m2 e
(m )
2x
_C2 m1
− + ⎞ − + m2 m1
⎠ ⎟⎟ ⎟ ( ) > restart;with(inttrans): > p:=diff(u(x,s),x$2)-s/k*(u(x,s))=0; :=
p ⎛ − =
⎝
⎜⎜⎜∂∂x22u ,(x s)⎞⎠⎟⎟⎟
su ,(x s)
k 0
> p1:=dsolve(p,u(x,s));
:=
p1 u ,(x s) = _F1( )s e +
⎛ ⎝ ⎜⎜ s k xk ⎞⎠⎟⎟
( ) _F2 s e
⎛ ⎝
⎜⎜− s k x⎞⎠⎟⎟
k
> p2:=subs(_F1(s)=A(x),_F2(s)=B(x),p1);
:=
p2 u ,(x s) = A( )x e +
⎛ ⎝ ⎜⎜ s k xk ⎞⎠⎟⎟
( ) B x e
⎛ ⎝
⎜⎜− s k x⎞⎠⎟⎟
k
>
s1:=D(A)(x)*exp(sqrt(s/k)*x)+D(B)(x)*exp(-sqrt(s/k)*x)=0;
:=
s1 D( )A x( )e + =
⎛ ⎝ ⎜⎜ ks x⎞⎠⎟⎟
( ) ( ) D B x e
⎛ ⎝ ⎜⎜− s ⎞⎠⎟⎟
k x
>
s2:=sqrt(s/k)*D(A)(x)*exp(sqrt(s/k)*x)-sqrt(s/k)*D(B)(x)*exp(-sqrt(s/k)*x)=-f(x)/k;
:=
s2 s − =
k D( )A x( )e
⎛ ⎝ ⎜⎜ sk x⎞⎠⎟⎟
s
k D( )B x( )e
⎛ ⎝ ⎜⎜− s ⎞⎠⎟⎟
k x
− f( )x
k
> s3:=solve({s1,s2},{D(A)(x),D(B)(x)});
:= s3
⎧
⎩ ⎪⎪ ⎪⎪ ⎪⎪ ⎪⎪⎪ ⎨
⎫
⎭ ⎪⎪ ⎪⎪ ⎪⎪ ⎪⎪⎪ ⎬
,
=
( ) ( )
D A x −1 2
( ) f x
s k e
⎛ ⎝ ⎜⎜ sk x⎞⎠⎟⎟
k
=
( ) ( )
D B x 1 2
( ) f x e
⎛ ⎝ ⎜⎜ sk x⎞⎠⎟⎟
s k k
> sol1:=s3[1];
:=
sol1 D( )A x( ) = −1 2
( ) f x
s k e
⎛ ⎝ ⎜⎜ sk x⎞⎠⎟⎟
k
> sol2:=s3[2];
:=
sol2 D( )B x( ) = 1 2
( ) f x e
⎛ ⎝ ⎜⎜ sk x⎞⎠⎟⎟
s k k
> so1:=dsolve({sol1},A(x));
:=
so1 A( )x = d + ⌠
⌡ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮
−1
2 ( ) f x e
⎛ ⎝ ⎜⎜− s ⎞⎠⎟⎟
k x
s k k
x _C1
:=
so2 B( )x = d + ⌠ ⌡ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ 1 2 ( ) f x e
⎛ ⎝ ⎜⎜ sk x⎞⎠⎟⎟
s k k
x _C1
> so3:=subs(_C1=_C2,so2);
:=
so3 B( )x = d + ⌠ ⌡ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ ⎮ 1 2 ( ) f x e
⎛ ⎝ ⎜⎜ sk