Penyelesaian Masalah Gelombang Permukaan dengan Menggunakan Metode Perturbasi Homotopi

(1)

PENYELESAIAN MASALAH GELOMBANG

PERMUKAAN DENGAN MENGGUNAKAN

METODE PERTURBASI HOMOTOPI

ANGGRAENI PUTRISIA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(2)

(3)

PERNYATAAN MENGENAI SKRIPSI DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa skripsi berjudul Penyelesaian Masalah Gelombang Permukaan dengan Menggunakan Metode Perturbasi Homotopi adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Juli 2013

(4)

ABSTRAK

ANGGRAENI PUTRISIA. Penyelesaian Masalah Gelombang Permukaan dengan Menggunakan Metode Perturbasi Homotopi. Dibimbing oleh JAHARUDDIN dan ALI KUSNANTO.

Gelombang permukaan merupakan fenomena yang ditemui ketika mengamati permukaan air laut. Secara umum, gerak gelombang permukaan dalam tiga dimensi dijelaskan secara matematis dalam bentuk persamaan Kadomtsev-Petviashvili (KP). Persamaan Kadomtsev-Kadomtsev-Petviashvili diselesaikan dengan metode perturbasi homotopi. Dalam metode ini, penyelesaian persamaan KP dimisalkan dalam bentuk deret pangkat, dengan suku pertama berupa penyelesaian pendekatan awal. Dikaji penyelesaian persamaan KP dengan dua jenis pendekatan awal, yaitu berupa penyelesaian gelombang soliter dan penyelesaian dalam bentuk fungsi rasional. Penyelesaian dengan metode perturbasi homotopi mendekati penyelesaian eksak yang diperoleh Drazin dan Johnson (1989).

Kata kunci: persamaan Kadomtsev-Petviashvili, metode perturbasi homotopi, gelombang soliter

ABSTRACT

ANGGRAENI PUTRISIA. Surface Wave Solution Using the Homotopy Perturbation Method. Supervised by JAHARUDDIN and ALI KUSNANTO.

Surface wave is a phenomenon that is encountered at the sea surface. Generally, the motion of surface waves in three dimensions could be described mathematically in the form of Kadomtsev-Petviashvili (KP) equation. Kadomtsev-Petviashvili equation is solved using the homotopy perturbation method. In this method, the solution of the KP equation is assumed in the form of power series with the first term of the solution as the initial approach. The solution to the KP equation is studied using two initial approaches. Those are solitary wave solution and solutions in the form of rational functions. The solution of homotopy perturbation method is closed to the exact solution given by Drazin and Johnson (1989).

(5)

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

PENYELESAIAN MASALAH GELOMBANG

PERMUKAAN DENGAN MENGGUNAKAN

METODE PERTURBASI HOMOTOPI

ANGGRAENI PUTRISIA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(6)

(7)

Judul Skripsi : Penyelesaian Masalah Gelombang Permukaan dengan Menggunakan Metode Perturbasi Homotopi

Nama : Anggraeni Putrisia NIM : G54090069

Disetujui oleh

Dr Jaharuddin, MS Pembimbing I

Drs Ali Kusnanto, MSi Pembimbing II

Diketahui oleh

Dr Berlian Setiawaty, MS Ketua Departemen

(8)

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Penulisan karya ilmiah ini juga tidak lepas dari bantuan beberapa pihak. Untuk itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada:

1 Bapak Muhammad Yusuf dan ibu Siti Masfufah, beserta kakak Nina Kirana beserta suami, seluruh keluarga atas semua doa, dukungan, semangat, pengorbanan, nasihat, pendidikan, perhatian, cinta dan kasih sayangnya.

2 Dr Jaharuddin, MS dan Drs Ali Kusnanto, MSi masing-masing sebagai dosen pembimbing I dan dosen pembimbing II atas semua ilmu, kesabaran, motivasi, dan bantuannya selama penulisan skripsi ini.

3 Dosen dan staf penunjang Departemen Matematika atas semua ilmu dan bantuannya.

4 Kakak Matematika 45 dan 44 atas bantuan, saran dan semua ilmunya, teman-teman Matematika 46 atas kebersamaan, bantuan, dukungan dan motivasinya selama ini.

Semoga karya ilmiah ini dapat bermanfaat dan menjadi inspirasi bagi penilitian-penilitian selanjutnya.

Bogor, Juli 2013

(9)

DAFTAR ISI

DAFTAR TABEL ix

DAFTAR GAMBAR ix

DAFTAR LAMPIRAN ix

PENDAHULUAN 1

Latar Belakang 1

Tujuan Karya Ilmiah 2

TINJAUAN PUSTAKA 2

Persamaan Kadomtsev-Petviashvilli 2

Penyelesaian Gelombang Soliter 5

Metode Perturbasi Homotopi 6

HASIL DAN PEMBAHASAN 9

Analisis Metode 9

Aplikasi Metode 10

Kasus Pertama 11

Kasus Kedua 15

SIMPULAN 17

Simpulan 17

DAFTAR PUSTAKA 18

LAMPIRAN 19

(10)

DAFTAR TABEL

1 Galat antara penyelesaian kasus pertama dengan menggunakan MPH

dan penyelesaian eksaknya untuk 12

2 Galat antara penyelesaian kasus pertama dengan menggunakan MPH dan penyelesaian eksaknya untuk dan 14 3 Galat antara penyelesaian kasus kedua dengan menggunakan MPH dan

penyelesaian eksaknya untuk dan 16

DAFTAR GAMBAR

1 Perbandingan antara penyelesaian kasus pertama dengan MPH dan

penyelesaian eksak 12

2 Grafik penyelesaian persamaan KP pada kasus pertama untuk variabel y

tetap 13

3 Grafik penyelesaian persamaan KP pada kasus pertama untuk variabel y

berubah 14

4 Perbandingan antara penyelesaian dengan MPH dan penyelesaian eksak

pada kasus kedua 16

5 Grafik penyelesaian persamaan KP pada kasus kedua untuk t = 0.1 17 6 Grafik penyelesaian persamaan KP pada kasus kedua untuk t = 1 17

DAFTAR LAMPIRAN

1 Penurunan persamaan (34)-(37) 19

2 Penyelesaian kasus pertama (Variabel y tetap) 20 3 Penyelesaian kasus pertama (Variabel y berubah) 21

(11)

PENDAHULUAN

Latar Belakang

Gelombang permukaan merupakan fenomena yang ditemui ketika mengamati permukaan air laut. Gelombang tersebut terjadi karena perbedaan rapat massa air dan udara. Salah satu gelombang permukaan yang akan dikaji dalam karya ilmiah ini adalah gelombang soliter. Gelombang soliter adalah gelombang yang hanya memiliki satu puncak dan bergerak tanpa mengalami perubahan bentuk dan kecepatan. Partikel-partikel air pada gelombang soliter bergerak hanya dalam arah penjalaran gelombang sehingga tidak ada aliran balik.

Pengamatan gelombang soliter pertama kali terdokumentasi oleh ilmuwan Skotlandia pada tahun 1834, John Scott-Russel. Ia mengamati gerak sebuah perahu dari kudanya. Ketika perahu tiba-tiba berhenti, timbullah gelombang air dengan sebuah puncak yang bergerak menjauh dari perahu. Pergerakan gelombang air tersebut kemudian diamati dan ditelusuri olehnya hingga sekitar 2 mil. Bentuk dan kecepatan gelombang air itu nyaris tidak berubah hingga akhirnya menghilang dari pandangan karena masuk ke dalam terowongan air (Newel 1985).

Sebagai suatu fenomena alam, gelombang soliter dapat dijelaskan secara matematis. Salah satu ilmuan yang memformulasikan fenomena ini adalah Korteweg dan de Vries dan menemukan persamaan Korteweg-de Vries (KdV). Persamaan ini menjelaskan tentang fenomena gelombang soliter dimensi dua. Persamaan ini yang menjadi awal motivasi dari studi mengenai gelombang soliter. Secara matematis, penurunan persamaan KdV didasarkan pada persamaan dasar fluida. Penurunan persamaan dasar fluida didasarkan pada hukum kekekalan massa dan hukum kekekalan momentum. Dalam karya ilmiah ini, fluida yang ditinjau tak mampat (incompressible) dengan rapat massa konstan dan gerak partikel fluida yang tak berotasi (irrotasional), serta tidak adanya efek kekentalan (inviscid). Oleh karena itu, dalam karya ilmiah ini diasumsikan bahwa fluida yang ditinjau adalah fluida ideal yang tak berotasi.

(12)

2

Metode perturbasi homotopi merupakan salah satu metode yang banyak digunakan untuk menyelesaikan berbagai masalah taklinear. Metode ini memberikan pendekatan dari penyelesaian dengan tingkat akurasi yang tinggi. Dalam karya ilmiah ini akan dibahas penyelesaian persamaan KP dengan menggunakan metode peturbasi homotopi dengan pendekatan awal berupa penyelesaian gelombang soliter dan penyelesaian dalam bentuk fungsi rasional. Hasil yang diperoleh dengan menggunakan metode ini akan dibandingkan dengan penyelesaian eksak yang diperoleh pada (Drazin dan Johnson 1989).

Tujuan Karya Ilmiah

Berdasarkan latar belakang di atas, maka tujuan penelitian ini adalah:

a Menggunakan metode perturbasi homotopi untuk menyelesaikan persamaan KP dan membandingkan penyelesaian metode tersebut dengan penyelesaian eksak yang diperoleh pada (Drazin dan Johnson 1989).

b Menganalisis penyelesaian dalam bentuk gelombang soliter dan penyelesaian dalam bentuk fungsi rasional.

TINJAUAN PUSTAKA

Pada bagian ini akan dibahas teori-teori yang digunakan dalam menyusun karya ilmiah. Teori-teori tersebut meliputi penurunan persamaan KP (Kadomtsev-Petviashvili) dan penyelesaian eksaknya yang disarikan dari (Pangaribuan 2008) dan (Drazin dan Johnson 1989), konsep dasar metode perturbasi homotopi (He 2000), serta contoh masalah yang diselesaikan dengan metode perturbasi homotopi.

Persamaan Kadomtsev-Petviashvili

Pada bagian ini akan diuraikan secara singkat penurunan persamaan KP berdasarkan sistem Hamiltonian. Bukti penurunan didasarkan pada (Pangaribuan 2008). Domain fluida dibatasi oleh batas bawah di - dan di atas oleh simpangan

Energi total yang dimiliki gelombang terdiri dari energi potensial yang dihasilkan dari ketinggian permukaan air dan energi kinetik yang dihasilkan dari pergerakan partikel fluida. Misalkan Hamiltonian H adalah energi total pada fluida yang didefinisikan sebagai penjumlahan energi kinetik K dan energi potensial P, yaitu

,

dengan K dan P masing-masing adalah

(13)

3

∭ ∬

Fungsi adalah penyelesaian masalah nilai batas berikut : pada dengan |

Sistem Hamilton untuk fluida tersebut dapat dinyatakan oleh

dengan dan masing-masing turunan variasi H terhadap dan (Pudjaprasetya 1996). Jika dan persamaan (1) diturunkan terhadap x, maka diperoleh

( ) ( ₎ Untuk mendapatkan hampiran yang memenuhi sistem Hamilton pada persamaan (2), maka diasumsikan bahwa gelombang yang ditinjau mempunyai panjang gelombang yang cukup panjang dan amplitudo yang cukup kecil. Oleh karena itu diperkenalkan suatu parameter kecil ɛ yang memenuhi

̂ ̂

√ ̂ √ ̂ √ ̂ √ sehingga diperoleh hampiran berikut :

- - -Sehingga berdasarkan sistem Hamilton (2), maka diperoleh sistem Hamilton berikut :

( ₎ ̂

̂ dengan ̂ memenuhi persamaan (4). Persamaan (5) merupakan sistem Hamilton untuk gelombang yang bergerak dalam dua arah. Jika digunakan persamaan (4), maka persamaan (5) dapat dinyatakan dalam bentuk

(14)

4

Misalkan didefinisikan variabel r dan s sebagai berikut :

( ) dengan

dimana r dan s masing-masing menyatakan bentuk gelombang yang merambat ke arah kanan dan ke kiri, dan merupakan kecepatan gelombang linear. Persamaan (5) dapat dinyatakan sebagai sistem Hamilton dalam peubah r dan s berikut :

( ) ( ) Diasumsikan bahwa gelombang yang ditinjau hanya merambat dalam satu arah, misalnya ke arah kanan saja , maka . Sehingga sistem Hamilton pada persamaan (6) memberikan persamaan untuk yang merupakan sistem Hamilton untuk gelombang yang bergerak dalam satu arah sebagai berikut :

- (7) dengan

∬ dan

( )

Berdasarkan , persamaan (7) menjadi

( )

Persamaan (8) merupakan persamaan Kadomtsev-Petviashvili (KP) yang dapat dinyatakan dalam bentuk yang lebih sederhana dengan melakukan transformasi. Untuk itu, misalkan

(15)

5

atau

Persamaan tersebut merupakan bentuk baku dari persamaan Kadomtsev-Petviashvili (KP) yang akan diselesaikan dengan metode perturbasi homotopi.

Penyelesaian Gelombang Soliter

Berikut ini persamaan Kadomtsev-Petviashvili akan diselesaikan secara analitik dengan penyelesaian dimisalkan dalam bentuk gelombang soliter, yaitu gelombang berjalan yang dimisalkan dalam bentuk :

dengan

- dengan masing-masing merupakan kecepatan phase gelombang, panjang gelombang dalam arah X, dan panjang gelombang dalam arah Y. Jika u pada persamaan (11) disubstitusikan ke dalam persamaan (10), kemudian diintegralkan dua kali terhadap , maka diperoleh

( )

dengan K adalah konstanta integrasi. Karena yang akan ditinjau adalah gelombang soliter, maka bentuk dan semua turunannya di sama dengan nol mengakibatkan K = 0 sehingga persamaan (12) menjadi

(16)

6

Berdasarkan persamaan (15) diperoleh bahwa gelombang soliter bergantung pada parameter amplitudo a, kecepatan phase gelombang , panjang gelombang k dalam arah X, dan panjang gelombang l dalam arah Y.

Metode Perturbasi Homotopi (MPH)

Berikut ini diberikan ilustrasi konsep dasar metode perturbasi homotopi berdasarkan pada He (2000). Misalkan diberikan persamaan diferensial sebagai berikut:

(17) dengan suatu operator turunan taklinear dan fungsi yang akan ditentukan yang bergantung pada . Operator secara umum dapat dibagi menjadi dua bagian, yaitu dan yang masing-masing merupakan operator linear dan taklinear. Jadi persamaan diferensial (17) dapat ditulis:

Misalkan pendekatan awal dari penyelesaian dan suatu parameter. Didefinisikan suatu fungsi homotopi sebagai berikut:

( - ) [ - ] (18) Berdasarkan persamaan (18), maka untuk memberikan persamaan

H

-dan untuk p = 1 memberikan persamaan

(17)

7

Hasil ini menunjukkan hubungan antara penyelesaian eksak dari persamaan (17) dengan pendekatan awal dan diperoleh dengan menggunakan metode perturbasi.

Dalam metode perturbasi homotopi, fungsi yang dinyatakan pada persamaan (19) merupakan penyelesaian dari persamaan

atau

( - )[ - ] (20) Jika persamaan (19) disubstitusikan ke dalam persamaan (20), maka diperoleh dengan cara menyamakan koefisien perpangkatan dari .

Untuk lebih memahami metode perturbasi homotopi yang telah dibahas, misalkan diberikan suatu masalah nilai awal yang dinyatakan oleh persamaan berikut : Penyelesaian eksak masalah nilai awal (21) adalah

Berikut ini akan dicari penyelesaian dari masalah nilai awal persamaan (21) dan (22) dengan menggunakan metode perturbasi homotopi. Didefinisikan operator sebagai berikut:

dan

(18)

8

Berdasarkan persamaan (20), maka diperoleh persamaan berikut :

Diasumsikan penyelesaian dari persamaan (23) dinyatakan dalam persamaan berikut:

Jika persamaan (24) disubstitusikan ke dalam persamaan (23), kemudian dipisahkan berdasarkan derajat kepangkatan maka koefisien , perturbasi homotopi diperoleh sebagai berikut :

Penyelesaian pada persamaan (26) dapat ditulis

(19)

9

HASIL DAN PEMBAHASAN

Dalam karya ilmiah ini akan dibahas penggunaan metode perturbasi homotopi untuk menyelesaikan persamaan Kadomtsev-Petviashvili dengan syarat awal berupa gelombang soliter dan gelombang dengan penyelesaian berupa fungsi rasional. Hasil yang diperoleh dengan menggunakan metode ini akan dibandingkan dengan penyelesaian eksak untuk gelombang soliter pada persamaan (15) dan fungsi rasional pada (Drazin dan Johnson 1989).

Analisis Metode

Berikut ini dibahas perluasan dari konsep dasar metode perturbasi homotopi seperti yang diuraikan pada tinjauan pustaka. Misalkan diberikan persamaan diferensial

(20)

10

Karena , maka diperoleh

∑

Hasil ini menunjukkan hubungan antara penyelesaian eksak dari persamaan (27) dengan pendekatan awal dan yang akan ditentukan. Persamaan untuk menentukan diperoleh dengan menggunakan metode perturbasi homotopi. Dalam metode perturbasi homotopi, fungsi yang diberikan pada persamaan (29) merupakan penyelesaian dari persamaan

H( ) atau

(30)

Aplikasi Metode

Pada bagian ini metode perturbasi homotopi yang telah dijelaskan pada bagian sebelumnya akan diaplikasikan untuk menyelesaikan persamaan Kadomtsev-Petviashvili (10) yang dituliskan sebagai berikut :

( Berdasarkan persamaan (30) dan persamaan (31) diperoleh :

( )

dengan suatu parameter dan merupakan pendekatan awal dari penyelesaian. Misalkan penyelesaian dari persamaan (32) dinyatakan dalam deret pangkat berikut:

(33) Jika persamaan (33) dan turunan-turunannya disubstitusi ke dalam persamaan (32), maka koefisien memberikan persamaan

Koefisien memberikan persamaan

(21)

11 Koefisien memberikan persamaan

Koefisien memberikan persamaan

( )

Penurunan persamaan (34)-(37) dapat dilihat pada lampiran 1.

Penyelesaian persamaan (34)-(37) bergantung pada yaitu pendekatan awal dari penyelesaian. Dalam karya ilmiah ini, dibahas dua bentuk yaitu penyelesaian dalam bentuk gelombang soliter dan penyelesaian dalam bentuk fungsi rasional.

Kasus pertama : Penyelesaian dalam bentuk gelombang soliter

Dalam kasus ini akan ditinjau situasi dimana variabel y tetap dan variabel y berubah.

Variabel y tetap

Misalkan diasumsikan bentuk gelombang pada arah sumbu y adalah sama sehingga dipilih pendekatan awal berupa gelombang soliter pada t = 0 berikut

Berdasarkan persamaan (34)-(37) diperoleh penyelesaian ,i = 0,1,2,3,4 sebagai berikut:

Jadi penyelesaian dari persamaan KP dengan pendekatan awal pada persamaan (38) hingga orde keempat sebagai berikut :

(22)

12

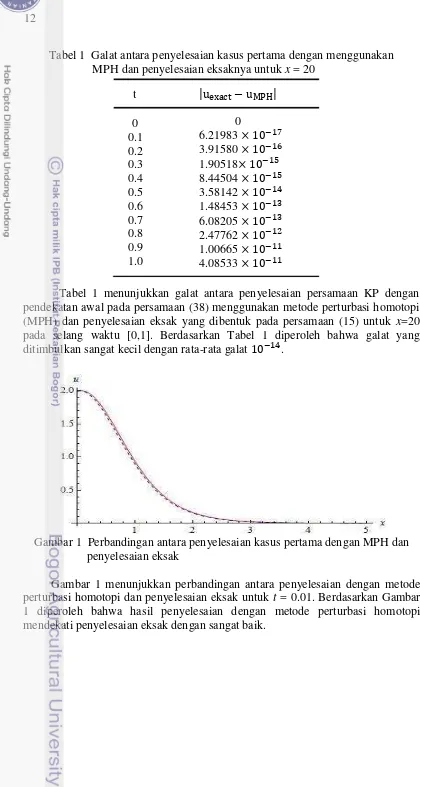
Tabel 1 menunjukkan galat antara penyelesaian persamaan KP dengan pendekatan awal pada persamaan (38) menggunakan metode perturbasi homotopi (MPH) dan penyelesaian eksak yang dibentuk pada persamaan (15) untuk x=20 pada selang waktu [0,1]. Berdasarkan Tabel 1 diperoleh bahwa galat yang ditimbulkan sangat kecil dengan rata-rata galat .

Gambar 1 Perbandingan antara penyelesaian kasus pertama dengan MPH dan penyelesaian eksak

Gambar 1 menunjukkan perbandingan antara penyelesaian dengan metode perturbasi homotopi dan penyelesaian eksak untuk t = 0.01. Berdasarkan Gambar 1 diperoleh bahwa hasil penyelesaian dengan metode perturbasi homotopi mendekati penyelesaian eksak dengan sangat baik.

Tabel 1 Galat antara penyelesaian kasus pertama dengan menggunakan MPH dan penyelesaian eksaknya untuk x = 20

(23)

(24)

(25)

15

Kasus kedua: Penyelesaian dalam bentuk fungsi rasional

Penyelesaian eksak persamaan KP dalam bentuk fungsi rasional adalah

dengan - - (Drazin dan Johnson 1989).

Misalkan dipilih a =1 sehingga pendekatan awal dipilih berbentuk :

Berdasarkan persamaan (34)-(37) diperoleh penyelesaian , i = 0,1,2,3 sebagai berikut :

],

Jadi penyelesaian dari persamaan KP pada kasus kedua dengan pendekatan awal pada persamaan (41) hingga orde ketiga sebagai berikut :

(26)

16

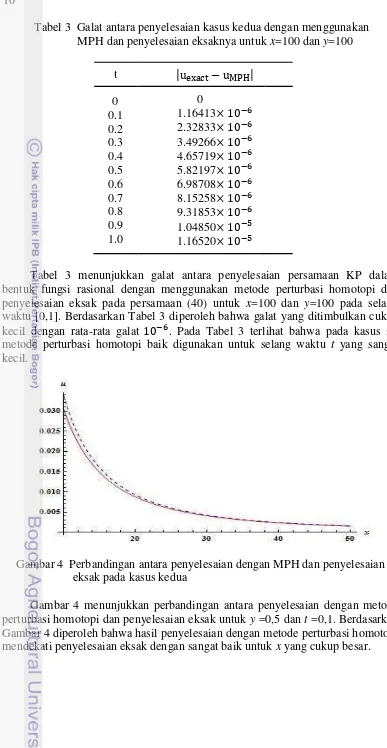
Tabel 3 Galat antara penyelesaian kasus kedua dengan menggunakan MPH dan penyelesaian eksaknya untuk x=100 dan y=100

Tabel 3 menunjukkan galat antara penyelesaian persamaan KP dalam bentuk fungsi rasional dengan menggunakan metode perturbasi homotopi dan penyelesaian eksak pada persamaan (40) untuk x=100 dan y=100 pada selang waktu [0,1]. Berdasarkan Tabel 3 diperoleh bahwa galat yang ditimbulkan cukup kecil dengan rata-rata galat . Pada Tabel 3 terlihat bahwa pada kasus ini metode perturbasi homotopi baik digunakan untuk selang waktu t yang sangat kecil.

Gambar 4 Perbandingan antara penyelesaian dengan MPH dan penyelesaian eksak pada kasus kedua

Gambar 4 menunjukkan perbandingan antara penyelesaian dengan metode perturbasi homotopi dan penyelesaian eksak untuk y =0,5 dan t =0,1. Berdasarkan Gambar 4 diperoleh bahwa hasil penyelesaian dengan metode perturbasi homotopi mendekati penyelesaian eksak dengan sangat baik untuk x yang cukup besar.

(27)

(28)

18

waktu [0,1]. Kemudian kekonvergenan metode perturbasi homotopi pada kasus pertama (pendekatan awal berupa fungsi secan hiperbolik) cepat tercapai. Hal ini disebabkan karena pendekatan awal yang diberikan berupa gelombang soliter. Berdasarkan metode ini pula diperoleh bahwa untuk pendekatan awal berupa gelombang soliter, gelombang yang dihasilkan bergerak tanpa mengalami perubahan bentuk dan kecepatan sesuai dengan sifat gelombang soliter. Untuk pendekatan awal berupa fungsi rasional, diperoleh bahwa gelombang yang dihasilkan bukan berupa gelombang soliter.

DAFTAR PUSTAKA

Bratsos A, Twizell. 1998. An explicit finite difference scheme for the solution of Kadomtsev-Petviashvili. International Journal of Computer Mathematics. 68:175-187. doi: 10.1080/00207169808804685.

Drazin PG, Johnson RS. 1989. Solitons : an Introduction. Cambridge Texts in Applied Mathematics. New York (US): Cambridge University Press. Grubaum F. 1989. The Kadomtsev-Petviashvili equation : an alternative approach

“rank tw ” solutions of Krichever and Novikof. Physics Letters A. 139:146-150. doi: 10.1016/0375-9601(89)90349-6.

He JH. 2000. A coupling method of homotopy technique and perturbation technique for nonlinear problems. International Journal of Nonlinear Mechanic. 1:37-43.

Latham G. 1990. Solutions of the KP equation associated to rank-three commuting differential operators over a singular elliptic curve. Journal Physica D. 41:55-66. doi: 10.1016/0167-2789(90)90027-M.

Mirgolbabaei H, Ganji DD, Taherian H. 2009. Soliton solution of the Kadomtsev-Petviashvili equation by homotopy perturbation method. World Journal of Modelling and Simulation. 1: 38-44.

Newell AC. 1985. Solitons in Mathematics and Physics. Society for Industrial and Applied Mathematics. Philadelphia (US): University of Arizona.

Pangaribuan RU. 2008. Formulasi hamiltonian untuk menggambarkan gerak gelombang soliter dimensi tiga di permukaan laut [skripsi]. Bogor (ID): Institut Pertanian Bogor.

(29)

19

Lampiran 1 Penurunan persamaan (34)-(37)

Berdasarkan persamaan (30) dan persamaan (31), diperoleh

( )

Misalkan penyelesaian persamaan (32) dinyatakan dalam bentuk berikut :

Jika persamaan (33) dan turunan-turunannya disubstitusi ke dalam persamaan (32), maka diperoleh

( )

atau

( )

(30)

20

Koefisien memberikan persamaan berikut :

( )

Koefisien memberikan persamaan berikut :

( )

Lampiran 2 Penyelesaian kasus pertama (Variabel y tetap)

Berikut ini akan ditentukan penyelesaian , , , dan pada persamaan (34)-(37) dengan pendekatan awal berikut :

Dari persamaan (34) diperoleh persamaan

Sehingga penyelesaian untuk sebagai berikut : Dari persamaan (35) diperoleh persamaan

( )

Jika bentuk dan turunan-turunannya digunakan kemudian diintegralkan terhadap x dan t, maka diperoleh

(31)

21 Jika bentuk dan turunan-turunannya digunakan kemudian diintegralkan terhadap x dan t, maka diperoleh

( )

Persamaan masalah nilai batas untuk yaitu

Jadi penyelesaian dari persamaan KP dengan syarat awal pada persamaan (38) hingga orde keempat sebagai berikut :

Lampiran 3 Penyelesaian kasus pertama (Variabel y berubah)

Berikut ini akan ditentukan penyelesaian , , , dan ₅pada persamaan (34)-(37) dengan pendekatan awal berikut :

=

Sehingga penyelesaian untuk yaitu Dari persamaan (35) diperoleh persamaan

(32)

22

( )

Persamaan masalah nilai batas untuk yaitu

Persamaan masalah nilai batas untuk ₅ yaitu

( )

Jadi penyelesaian dari persamaan KP dengan pendekatan awal pada persamaan (39) hingga orde kelima sebagai berikut :

(33)

23

Lampiran 4 Penyelesaian kasus kedua

Berikut ini akan ditentukan penyelesaian , , dan pada persamaan (34)-(37) dengan pendekatan awal dalam bentuk fungsi rasional berikut :

Sehingga penyelesaian untuk yaitu

( )

].

(34)

24

Jadi penyelesaian dari persamaan KP pada kasus kedua dengan pendekatan awal pada persamaan (40) hingga orde ketiga sebagai berikut :

(35)

25

RIWAYAT HIDUP

Penulis dilahirkan di Jakarta pada tanggal 8 Mei 1991 sebagai anak kedua dari dua bersaudara, anak dari pasangan Muhammad Yusuf dan Siti Masfufah.

Pendidikan formal yang telah ditempuh penulis yaitu di TK Islam Annuriyah lulus pada tahun 1997, SD Kartini 1 Jakarta Pusat lulus pada tahun 2003, SMP Negeri 10 Jakarta Pusat lulus pada tahun 2006, SMA Negeri 3 Depok lulus pada tahun 2009 dan pada tahun yang sama penulis diterima di Institut Pertanian Bogor melalui jalur UTMI di Departmen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.