ANALISA PERBANDINGAN JUMLAH MEDAN EKONOMIS
UNTUK JEMBATAN GELAGAR RANGKA BAJA TYPE CURVED
BENTUK TERTUTUP DENGAN BENTANG 48 METER
TUGAS AKHIR
Diajukan untuk melengkapi tugas-tugas dan memenuhi syarat untuk menempuh
Colloqium Doctum/Ujian Sarjana Teknik Sipil
OLEH
ALDESON TOGI MANGIRING SIMATUPANG NIM : 070424005
PROGRAM PENDIDIKAN SARJANA EKSTENSION
DEPARTEMEN TEKNIK SIPIL
ABSTRAK
Dalam perencanaan jembatan rangka selain kuat, stabil dan kaku haruslah ekonomis karena menyangkut masalah pembiayaan yang cukup besar. Untuk itu perlu dicari suatu keadaan jumlah medan (n), pada jembatan rangka dengan suatu bentang tertentu yang akan menghasilkan biaya yang ekonomis pula dengan sistem lalu lintas di bawah sehingga nantinya memberi bobot total struktur yang minimum.
Untuk mencapai tujuan tersebut, pada perhitungan dilakukan dengan cara coba – coba dengan jumlah medan (n) untuk panjang bentang (L) = 48 meter adalah 6, 8, 10. Untuk hal ini dilakukan terhadap rangka type Curved. Dalam proses optimasi sebagai parameter total adalah panjang bentang (L), sedangkan variabel desain adalah jumlah medan (n). Di samping itu bobot total struktur ditetapkan sebagai fungsi tujuan, dan batasan stabilitasnya adalah tegangan ijin tidak dilampaui sehingga ditetapkan sebagai fungsi kendala.
KATA PENGANTAR
Puji dan syukur penulis ucapkan kehadirat Tuhan yang Maha Esa atas berkat
rahmat, karunia dan penyertaan-Nya, sehingga penulis dapat menyelesaikan Tugas Akhir ini yang berjudul “ Analisa Perbandingan Jumlah Medan Ekonomis
Untuk Jembatan Gelagar Rangka Baja Type Curved Bentuk Tertutup Dengan Bentang 48 Meter ”. Tugas Akhir ini merupakan syarat untuk dapat menyelesaikan Program Pendidikan Sarjana Ekstension Departemen Teknik Sipil Fakultas Teknik Universitas Sumatera Utara.
Dalam menyusun dan menyelesaikan Tugas Akhir ini, penulis banyak sekali menerima bimbingan, bantuan, dan dukungan dari berbagai pihak. Maka dalam
kesempatan ini penulis mengucapkan terima kasih dan penghargaan yang setinggi-tinginya kepada:
1. Bapak Ir. Sanci Barus, MT., sebagai Dosen Pembimbingyang telah memberikan
dukungan penuh dari awal hingga selesainya Tugas Akhir ini;
2. Bapak Prof. Dr. Ing. Johannes Tarigan, sebagai Ketua Departemen Teknik Sipil
Fakultas Teknik Universitas Sumatera Utara sekaligus Dosen Wali penulis;
3. Bapak Ir. Zulkarnain A.Muis, M.Eng,Sc., sebagai Koordinator Program
Pendidikan Ekstension Departemen Teknik Sipil Fakultas Teknik Universitas
Sumatera Utara;
4. Seluruh Dosen Staf Pengajar Program Pendidikan Ekstension Departemen
6. Secara khusus penulis mengucapkan terima kasih kepada rekan-rekan
mahasiswa terlebih-lebih kepada rekan-rekan Ekstension 2007, 2006, dan 2008 atas dorongan dan bantuan yang diberikan.
7. Secara khusus penulis berterima kasih kepada orang tua, ayah dan ibunda, adik
beserta seluruh keluarga yang telah memberikan dorongan baik moral, material dan doa restu hingga selesainya Tugas Akhir ini.
Penulis juga menyadari bahwa penulisan ini masih jauh dari kesempurnaan karena keterbatasan pengetahuan dan pengalaman penulis. Maka untuk
menyempurnakan isi dari tugas akhir ini, penulis dengan rendah hati sangat mengharapkan saran-saran serta kritik yang konstruktif dari staf pengajar dan rekan-rekan mahasiswa serta kalangan praktis lainnya.
Akhir kata penulis berharap semoga Tugas Akhir ini dapat memberi manfaat bagi kita semua.
Medan, Maret 2011 Hormat Saya,
Penulis
DAFTAR ISI
Halaman
ABSTRAK ... i
KATA PENGANTAR... ii
DAFTAR ISI ... iv
DAFTAR TABEL ... viii
DAFTAR GAMBAR ... ix
DAFTAR NOTASI ... xi
BAB I PENDAHULUAN ... 1
A. Umum ... 1
B. Latar Belakang ... 1
C. Permasalahan ... 3
D. Maksud dan Tujuan ... 5
E. Pembatasan Masalah ... 5
F. Metode Penulisan ... 6
G. Sistematika Penulisan... 6
BAB II PERILAKU DAN KARAKTERISTIK JEMBATAN ... 8
A. Pendahuluan ... 8
B. Syarat Pelaksanaan ... 8
4. Syarat Ruang Bebas ... 15
C. Elemen-Elemen lantai Kendaraan ... 16
1. Lapisan Aus ... 16
2. Kontruksi Lantai (Deck) ... 16
3. Trotoir ... 16
4. Kerb... 16
5. Sandaran ... 17
D. Elemen-Elemen Bangunan Atas ... 17
1. Gelegar Canai ... 17
2. Gelegar Dinding Penuh ... 18
3. Gelegar Beton ... 18
4. Rangka Batang (Truss)... 18
E. Jenis-Jenis Jembatan berdasarkan Keadaan Perletakan .. 22
F. Jembatan Komposit ... 28
1. Lebar Efektif Lantai Beton ... 29
2. Dimensi Balok Gabungan (Composite Beam).. ... 30
BAB III METODE ANALISIS PADA RANGKA JEMBATAN .. 32
A. Pendahuluan ... 32
B. Perencanaan Rangka Induk ... 32
1. Perhitungan Berat Sendiri Rangka Induk ... 33
2. Gaya Batang Akibat Beban Bergerak ... 37
3. Gaya Batang Akibat Angin ... 38
D. TEORI OPTIMASI... 42
1. Variabel Desain ... 43
2. Fungsi Kendala ... 44
3. Fungsi Tujuan ... 45
E. Metode Minimumnisasi ... 45
BAB IV PEMBAHASAN ... 47
A. Pendahuluan ... 47
B. Batasan Stabilitas ... 47
C. Prosedur ... 50
D. Penentuan Medan Ekonomis ... 54
E. Hasil ... 55
F. Contoh Perhitungan ... 56
1. Sistem Pembebanan Lantai Kendaraan ... 56
2. Perhitungan Gelegar Memanjang ... 57
3. Perencanaan Gelegar Memanjang ... 64
4. Beban yang Bekerja pada Jembatan ... 69
5. Perhitungan Garis Pengaruh... 73
6. Perhitungan Gaya Angin ... 94
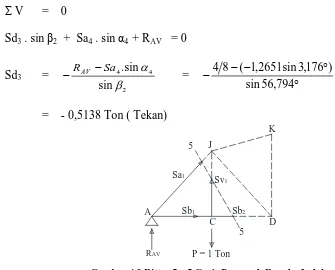
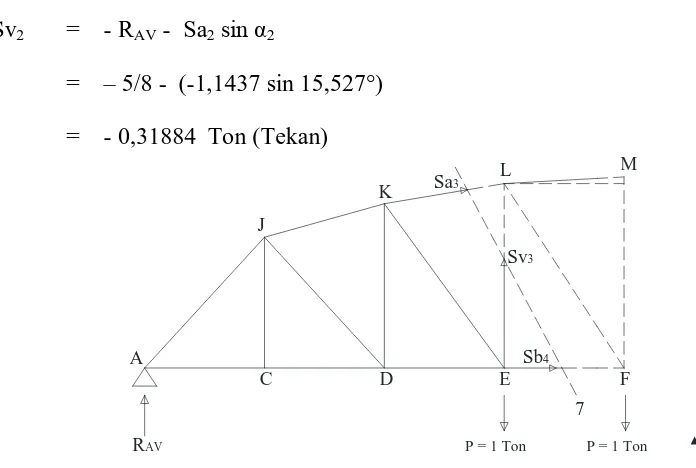
7. Perhitungan Gaya Batang ... 97
8. Kombinasi Gaya Batang... 104
DAFTAR TABEL
Halaman 4.1 Daftar Ordinat Garis Pengaruh Akibat Beban Hidup
Pada Panjang Bentang (L) = 48 m dan Jumlah Medan (n) = 8 ... 85 4.2 Daftar Ordinat Garis Pengaruh Akibat Beban Hidup
Pada Panjang Bentang (L) = 48 m dan Jumlah Medan (n) = 6 ... 86 4.3 Daftar Ordinat Garis Pengaruh Akibat Beban Hidup
Pada Panjang Bentang (L) = 48 m dan Jumlah Medan (n) = 10 .. 87 4.4 Luas Bidang Pengaruh Pada Panjang Bentang (L) = 48 m dan
Jumlah Medan (n) = 8 ... 92 4.5 Luas Bidang PengaruhPada Panjang Bentang (L) = 48 m dan
Jumlah Medan (n) = 6 ... 92 4.6 Luas Bidang PengaruhPada Panjang Bentang (L) = 48 m dan
Jumlah Medan (n) = 10 ... 93 4.7 Gaya Batang Akibat Beban Mati
Pada Panjang Bentang (L) = 48 m dan Jumlah Medan (n) = 6 .. 98 4.8 Gaya Batang Akibat Beban Mati
Pada Panjang Bentang (L) = 48 m dan Jumlah Medan (n) = 10 . 98 4.9 Gaya Batang Akibat Beban Bergerak
Pada Panjang Bentang (L) = 48 m dan Jumlah Medan (n) = 6 .. 100 4.10 Gaya Batang Akibat Beban Bergerak
Pada Panjang Bentang (L) = 48 m dan Jumlah Medan (n) = 10 .. 101 4.11 Gaya Batang Akibat Beban Angin
DAFTAR GAMBAR
Halaman
1.1 Rencana Bentuk Rangka Induk ... 4
1.2 Rangka Jembatan Type CURVED ... 5
2.1 Sietem Pembebanan ” T ” ... 9
2.2 Skema Beban ” D ” untuk Satu Jalur ... 10
2.3 Skema Beban ” D ” untuk Lebar > Dua Jalur ... 11
2.4 Ruang Bebas Jembatan ... 15
2.5 Skematis Rangka Batang ”Through Type” dan ”Deck Type”... 19
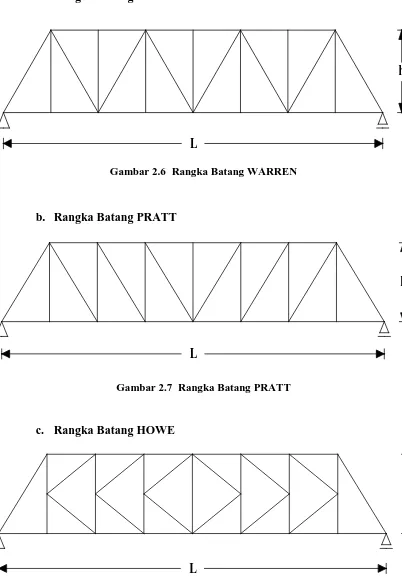
2.6 Rangka Batang WARREN ... 26
2.7 Rangka Batang PRATT ... 26
2.8 Rangka Batang HOWE ... 26
2.9 Rangka Batang CURVED ... 27
2.10 Rangka Batang Menerus ... 27
2.11 Rangka Batang Dinding Penuh Menerus ... 28
2.12 Gelagar Canai Menerus ... 28
2.13 Keadaan Komposit Pada Gelagar Menerus ... 29
3.1 Sistem Pembebanan Berat Sendiri ... 36
3.2 Profil Batang Rangka Induk yang Ditinjau ... 37
3.3 Sistem Pembebanan Akibat Angin ... 38
3.4 Profil Batang Tepi Atas ... 39
3.5 Profil Batang Tepi Bawah ... 40
3.6 Profil Batang Diagonal ... 41
3.8 Diagram Fungsi Maksimum = f(x), Minimum = - f(x) ... 42
3.9 Kendala Permukaan Bidang ... 44
4.1 Grafik Hubungan Berat dengan Jumlah Medan ... 55
4.2 Sistem Pembebanan Lantai Kendaraan ... 56
4.3 Rencana Bentuk Rangka Induk ... 73
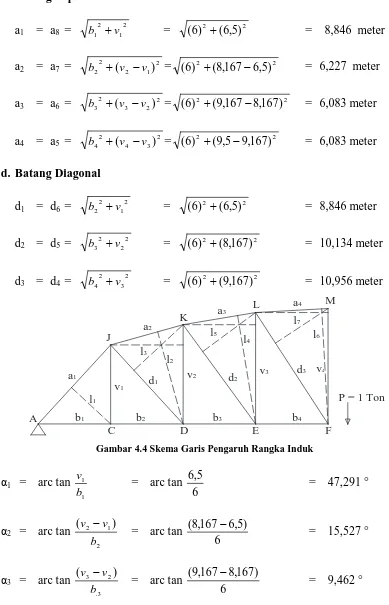
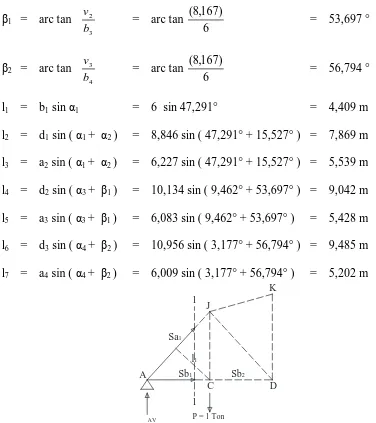
4.4 Skema Garis Pengaruh Rangka Induk ... 74
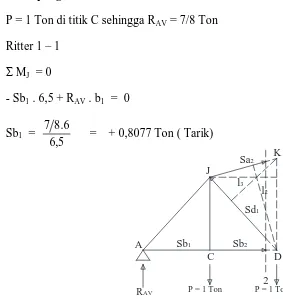
4.5 Ritter 1 – 1 Garis Pengaruh Rangka Induk ... 75
4.6 Ritter 2 – 2 Garis Pengaruh Rangka Induk ... 76
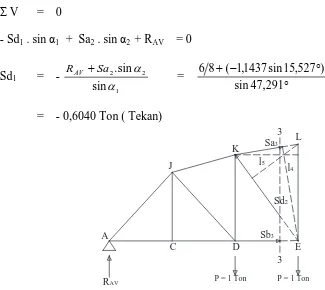
4.7 Ritter 3 – 3 Garis Pengaruh Rangka Induk ... 78
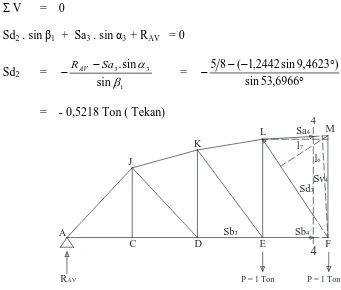
4.8 Ritter 4 – 4 Garis Pengaruh Rangka Induk ... 80
4.9 Ritter 5 – 5 Garis Pengaruh Rangka Induk ... 82
4.10 Ritter 6 – 6 Garis Pengaruh Rangka Induk ... 82
4.11 Ritter 7 – 7 Garis Pengaruh Rangka Induk ... 83
4.12 Ritter 8 – 8 Garis Pengaruh Rangka Induk ... 84
4.13 Garis Pengaruh Batang Tepi Atas ... 88
4.14 Garis Pengaruh Batang Tepi Bawah ... 89
4.15 Garis Pengaruh Batang Diagonal... 90
4.16 Garis Pengaruh Batang Vertikal ... 91
4.17 Skema Beban Angin Pada Jembatan ... 94
DAFTAR NOTASI
L = Panjang Jembatan (Meter)
ω = Koefisien Kejut
H = Tinggi Jembatan (Meter)
T = Lebar Trotoir Minimum (Meter)
B = Lebar Lantai Kendaraan (Meter) Mbs = Momen Akibat Berat Sendiri (T.M) Mbg = Momen Akibat Berat Bergerak (T.M)
Mtb = Momen Akibat Berat Tambahan (T.M) Wpr = Momen Tahanan Baja (Cm³)
Wcomp = Momen Tahanan Composite Elastis (Cm³) W’comp = Momen Tahanan Composite Plastis (Cm³)
Ix = Inersia Baja (Cm4) −
σ = Tegangan Ijin Baja (Kg/cm²)
F (x) = Fungsi Tujuan
NT = Pembebanan Tetap (Ton) NS = Pembebanan Sementara (Ton)
LK = Panjang Tekuk (cm) G = Berat (Ton)
FTotal = Luasan Profil (Cm²)
Fnetto = Luasan Bersih Profil (Cm²)
ABSTRAK
Dalam perencanaan jembatan rangka selain kuat, stabil dan kaku haruslah ekonomis karena menyangkut masalah pembiayaan yang cukup besar. Untuk itu perlu dicari suatu keadaan jumlah medan (n), pada jembatan rangka dengan suatu bentang tertentu yang akan menghasilkan biaya yang ekonomis pula dengan sistem lalu lintas di bawah sehingga nantinya memberi bobot total struktur yang minimum.
Untuk mencapai tujuan tersebut, pada perhitungan dilakukan dengan cara coba – coba dengan jumlah medan (n) untuk panjang bentang (L) = 48 meter adalah 6, 8, 10. Untuk hal ini dilakukan terhadap rangka type Curved. Dalam proses optimasi sebagai parameter total adalah panjang bentang (L), sedangkan variabel desain adalah jumlah medan (n). Di samping itu bobot total struktur ditetapkan sebagai fungsi tujuan, dan batasan stabilitasnya adalah tegangan ijin tidak dilampaui sehingga ditetapkan sebagai fungsi kendala.
BAB I
PENDAHULUAN
A. Umum
Perkembangan ilmu pengetahuan dewasa ini khususnya di bidang teknik, mengakibatkan perubahan dalam system konstruksi baik ditinjau dari segi mutu,
bahan, struktur konstruksi, serta ekonomisnya. Untuk itu perlu disadari dimana nantinya sebagai seorang yang berkecimpung dalam konstruksi harus dapat menganalisis bahan-bahan yang digunakan, agar tercapai suatu efisiensi di dalam
pemakaiannya dan dapat menyesesuaikannya, serta mengembangkannya sejalan dengan perkembangan ilmu pengetahuan teknik tersebut.
Secara umum telah diketahui baja adalah merupakan bahan konstruksi yang terpenting. Dimana sifat-sifatnya maupun kekuatannya yang tinggi dibandingkan dengan bahan lain.
B. Latar Belakang
Jembatan adalah suatu konstruksi yang berfungsi untuk meneruskan lalu lintas melalui suatu rintangan yang berada di bawahnya. Rintangan ini bisa berupa
sungai, lembah, jalan, bahkan laut.
Pada zaman dahulu, jembatan mula-mula di buat untuk menyebrangi
sungai-sungai kecil dengan menggunakan balok-balok kayu atau batang-batang pohon yang cukup besar dan kuat. Perkembangan jembatan semakin maju, antara lain di karenakan penemuan-penemuan material yang baru antara lain kayu atau batu
Untuk memindahkan hasil produksi dari satu tempat ke tempat lain yang di
pisahkan oleh sungai, lembah dan laut maka di bangunlah jembatan. Dengan tujuan agar ongkos dan waktu pengangkutan hasil produksi tersebut semakin kecil. Selain
itu dibangunnya jembatan dari rangka baja agar jembatan tersebut dapat menahan beban yang di akibatkan dari mobilisasi hasil produksi.
Walaupun perkembangan teknologi telah sedemikian maju, seseorang atau
suatu tim perencana jembatan harus dapat memikirkan masalah-masalah yang mungkin terjadi, baik pada saat perencanaaan terlebih lagi pada saat pelaksanaan di
lapangan. Sebelum merencanakan jenis jembatan yang direncanakan, perencanaan jembatan harus mempertimbangkan berbagai faktor yaitu antara lain: lokasi jembatan, bahan yang akan digunakan, waktu pelaksanaan, umur jembatan, biaya
pemeliharaan, estetika terhadap lingkungan, dan biaya pelaksanaan.
Dalam perencanaan jembatan harus diperhatikan lalu lintas di kemudian
hari, terutama peningkatan tekanan gandar maksimumnya. Berhubungan daengan ini, sebaiknya di ambil rencana muatan yang lebih berat daripada yang diperlukan pada saat perencanaan. Namun demikian konstruksi jembatan ini harus disesuaikan
dengan keadaan setempat. Berdasarkan berbagai faktor-faktor tersebut, perencana jembatan kemudian menentukan pilihan akan jenis jembatan yang akan dilaksanakan
di lapangan.
Perencanaan adalah suatu proses untuk menghasilkan penyelesaian optimum. Garis besar prosedur perencanaan adalah perancangan, konfigurasi
Pembangunan jembatan di wilayah dengan fasilitas pendukung yang sangat
minim (seperti jalan), perlu perencanaan yang matang. Mengingat keterbatasan tersebut, maka agak sulit untuk membuat jembatan dengan girder dari beton karena
bobotnya yang berat sehingga sulit untuk mobilitasasi. Sebagai alternative maka dapat dipilih rangka baja dengan bentuk dan jenis yang sesuai dengan kebutuhan.
C. Permasalahan
Estimasi berat sendiri gelagar Rangka Induk Jembatan dengan bentang
tertentu akan tergantung pada berat sendiri gelagar memanjang, berat sendiri gelagar
melintang, berat sendiri lantai kendaraan dan beban-beban lain pada jembatan.
Dimana estimasi bentang gelagar memanjang dan gelagar melintang dipengaruhi
oleh hal berikut :
1. Bertambah banyak jumlah medan, maka bentang gelagar bertambah kecil
yang memberikan dimensiberat sendiri bertambah kecil (berat sendiri
bertambah ringan). Juga dimensi gelagar melintang bertambah (berat sendiri
bertambah ringan). Tetapi jumlah gelagar melintang bertambah banyak.
2. Berkurang jumlah medan, maka bentang gelagar memanjang bertambah
besar yang memberikan dimensi berat sendiri bertambah besar (berat sendiri
bertambah besar). Juga dimensi gelagar melintang bertambah besar (berat
sendiri bertambah besar). Tetapi jumlah gelagar melintang bertambah
9.500 9.167 8.167 6.500
48.000
6.000 6.000
6.000 6.000
6.000 6.000
6.000 6.000
3. Adapun perilaku kasus yang ditinjau dengan bentuk rangka jembatan seperti
gambar, dengan system lantai kendaraan di bawah.
4. Optimasi dilakukan pada rangka jembatan lalulintas biasa lantai beton.
5. Berat sendiri beton, aspal, trotoar, sandaran, ikatan angin dan ikatan-ikatan
lain adalah konstan untuk setiap kasus yang akan dianalisa.
6. Berat sendiri gelagar memanjang, gelagar melintang, gelagar rangka induk
dijadikan sebagai fungsi kendala untuk setiap kajian
7. Pembebanan muatan PU 1987
8. Pembebanan terdiri dari berat sendiri jembatan, beban bergerak seperti dalam
peraturan (PU 1987) dan beban angin
9.500 9.167 8.167 6.500
48.000
6.000 6.000
6.000 6.000
6.000 6.000
6.000 6.000
D. Maksud dan Tujuan
Dengan optimasi rangka jembatan akan dapat diketahui bahwa pada bentang jembatan tertentu, kita menganalisa keadaan jumlah medan jembatan yang
paling ekonomis.
E. Pembatasan Masalah
Supaya pengkajian ini mengarah pad tujuan yang relevan dengan judul Tugas Akhir dank arena keterbatasan pengetahuan, literature dan journal yang dimiliki penyaji, maka perlu diadakan pembatasan masalah untuk memperoleh
analisis yang memadai.
Adapun batasan-batasan sebagai berikut : 1. Proses optimasi dilakukan dengan cara analitis
2. Bahan material baja dan beton masih daerah proporsional bersifat elastis
3. Bahan material baja dan beton masih daerah proporsional bersifat plastis,
isotropik dan homogen
4. Metode optimasi perhitungan struktur berdasarkan batasan elastis
5. Metode ASD (Allowable Stress Design) digunakan dalam perencanaan
6. Rangka batang yang ditinjau adalah Type CURVED 7. Bentang jembatan yang ditinjau adalah 48 meter
8. Pada perhitungan dimensi profil batang rangka induk dipergunakan hanya
batang yang memiliki gaya batang yang paling maksimum untuk
perencanaan pada elemen rangka induk
9. Tujuan akhir yang diinginkan adalah hanya untuk mendapatkan bobot (berat)
yang minimum akibat pengaruh jumlah medan yang paling ekonomis .
F. Metode Penulisan
Di dalam penyelesaian Tugas Akhir ini penyaji mengambil data-data
dengan metode penelitian kepustakaan atau studi literature. Dengan rangka jembatan diberi beban berat sendiri, beban bergerak sehingga diperoleh gaya-gaya batang.
Adapun metode yang digunakan di dalam perhitungan mekanikanya adalah dengan cara analitis.
G. Sistematika Penulisan
Tugas Akhir ini secara garis besar terdiri dari 5 (Empat) Bab yang masing-masing memiliki sub Bab.
Sistematika penulisan Tugas Akhir ini adalah sebagai berikut :
BAB I : Pendahuluan yang meliputi Umum, Latar Belakang, Permasalahan, Maksud dan Tujuan, Pembatasan Masalah,
Elemen-elemen Bangunan Atas, Jenis-jenis Jembatan, dan
Jembatan Komposit.
BAB III : Metode Analisis pada Rangka Jembatan yang meliputi Pendahuluan, Perencanaan Rangka Induk, Dimensi Profil Rangka Induk, Teori Optimasi, dan Metode Minimunisasi.
BAB IV : Pembahasan yang meliputi Pendahuluan, Batasan Stabilitas, Prosedur, Penentuan Medan yang Paling Ekonomis, Hasil, dan Contoh Perhitungan.
BAB II
PERILAKU DAN KARAKTERISTIK JEMBATAN
A. Pengertian Jembatan
Jembatan adalah suatu konstruksi yang gunanya untuk meneruskan jalan melalui rintangan yang permukaannya lebih rendah. Rintangan ini biasanya (jalan,
air, atau jalan lalu lintas). Jembatan merupakan investasi tertinggi dari semua elemen yang dapat di jumpai pada sistem jalan raya. Setiap kerusakan pada konstruksi tidak hanya merupakan suatu reduksi dalam investasi, akan tetapi lebih penting lagi dapat
merupakan penyebab timbulnya gangguan-gangguan dalam kelancaran perputaran roda ekonomi serta dapat menimbulkan kecelakaan bagi manusia.
B. Syarat Pelaksanaan
Untuk merencanakan suatu jembatan, harus diketahui besarnya beban-beban serta gaya-gaya berikut, agar dapat dihitung tegangan-tegangan yang bekerja.
Untuk kemudian menentukan dimensi-dimensi dari bagian-bagiannya. Beban-beban serta gaya-gaya pada jembatan jalan raya tersebut adalah sebagaimana tersebut di bawah ini :
1. Beban Primer
Beban primer adalah beban yang merupakan beban utama dalam perhitungan tegangan-tegangan dalam perencanaan sebuah jembatan. Beban primer
a. Beban Mati
Beban mati adalah semua beban yang berasal dari berat sendiri jembatan atau bagian jembatan yang ditinjau termasuk segala unsur tambahan tetap yang
dianggap merupakan satu-kesatuan tetap dengannya.
b. Beban Hidup
Beban hidup adalah semua beban yang berasal dari berat
kendaraan-kendaraaan yang bergerak (lalu lintas) atau berat orang-orang yang berjalan kaki yang dianggap bekerja pada jembatan. Beban hidup di atas lantai kendaraan dinyatakan dalam dua macam yaitu Beban T dan Beban D.
1) Beban T
Beban “T” adalah beban untuk lantai kendaraan yang dipergunakan untuk
perhitungan kekuatan lantai kendaraan atau sistem lantai kendaraan jembatan. Beban “T” adalah beban oleh kendaraan truk yang mempunyai beban roda sebesar 10 ton dengan ukuran-ukuran serta kedudukan sebagaimana tertera pada gambar
Beban Garis
Beban Merata
2.75 m dimana : a1 = a2 = 30,0 cm
b1 = 12,5 cm b2 = 50,0 cm
MS = Muatan rencana sumbu = 20 ton
2) Beban D
Beban “D” adalah beban untuk jalur lalu-lintas yang dipergunakan untuk
perhitungan kekuatan gelagar-gelagar. Beban “D” atau beban jalur adalah susunan beban pada setiap jalur lalu-lintas yang terdiri dari muatan terbagi rata sebesar “q” ton permeter panjang jalur, dan muatan garis P = 12 ton (belum termasuk kejut)
dalam arah melintang jalur lalu-lintas tersebut.
Gambar 2.2 Skema Beban D untuk Satu Jalur
q = 2,2 Ton/m’ untuk L ≤ 30 meter (2.1)
Dalam penggunaan beban “D” tersebut untuk suatu jembatan berlaku
keadaan, bahwa apabila ketentuan tersebut mempunyai lebar lantai kendaraan lebih besar 50 meter, beban “D” sepenuhnya hanya berlaku pada lebar jalur sebesar 5,50
meter, sedangkan lebar selebihnya dibebani hanya 50 % dari beban “D” tersebut sebagaimana dijelaskan pada gambar 2.3
Gambar 2.3 Skema Beban D untuk Lebar > Dua Jalur
3) Beban pada Trotoir, Kerb, dan Sandaran
Konstruksi dari trotoir harus diperhitungkan terhadap beban hidup sebesar 500 kg/cm². dalam perhitungan kekuatan gelagar-gelagar karena pengaruh beban hidup pad trotoir, diperhitungkan beban 60 % dari muatan hidup trotoir tersebut di atas (Menurut PU 1987)
4) Kejut
Untuk memperhitungkan pengaruh-pengaruh getaran-getaran dan pengaruh dinamis lainnya, tegangan-tegangan akibat beban “D” harus dikalikan dengan
koefisien kejut.
Koefisien kejut itu ditentukan dengan rumus :
φ = 1 +
L + 50
20
(2.4)
dimana :
φ = koefisien kejut
L = panjang jembatan
2. Beban Sekunder
Beban sekunder adalah beban pada jembatan yang merupakan beban sementara, yang selalu bekerja untuk perhitungan tegangan pada setiap perencanaan
jembatan. Pada umumnya beban ini mengakibatkan tegangan-tegangan yang relatif kecil daripada tegangan-tegangan akibat muatan primer, dan biasanya tergantung daripad bentang, sistem jembatan, bahan dan keadaan setempat. Beban sekunder
terdiri dari :
a. Beban angin
b. Gaya akibat rangkak dan susut c. Gaya rem dan traksi
a. Beban angin
Jumlah luas bidang vertikal jembatan yang dianggap terkena oleh angin
ditetapkan sebesar satu setengah kali jumlah luas bagian sisi jembatan.
Apabila ada beban hidup di jembatan, maka luas tersebut ditambah dengan
luas bidang vertikal beban hidup yang tidak terlindung oleh bagian-bagian sisi jembatan. Bidang vertikal beban hidup ditetapkan sebagai suatu permukaan bidang vertikal yang mempunyai tinggi menerus sebesar dua (2) meter di atas lantai
kendaraan.
Dalam memperhitungkanjumlah luas bagian – bagian jembatan pada setiap
sisi dapat digunakan ketentuan sebagai berikut :
1. Untuk jembatan berdinding penuh diambil sebesar 100 % terhadap luas
bidang sisi jembatan yang bersangkutan
2. untuk jembatan rangka diambil sebesar 30 % terhadap luas bidang sisi
jembatan yang bersangkutan
b. Gaya Rangkak dan Susut
Pengaruh rangkak dan susut pada bahan beton dan bahan baja terhadap konstruksi, apabila tidak ditentukan, harus pula ditinjau. Besarnya pengaruh ini,
apabila tidak ada ketentuan lain, dapat dianggap senilai dengan gaya yang timbul akibat turunnya suhu sebesar 15 ºC.
c. Gaya Rem dan Traksi
Bekerjanya gaya-gaya diarah memanjang jembatan, akibat gaya rem dan
koefisien kejut yang memenuhi semua jalur lalu lintas yang ada, dalam arah sumbu
jembatan dengantitik tankap setinggi 1,20 meter di atas permukaan lantai kendaraan.
3. Beban Khusus
Beban khusus adalah beban yang merupakan muatan khusus untuk
perhitungan tegangan pada perencanaan jembatan. Beban ini bersifat : 1. Tidak selalu bekerja pad jembatan
2. Hanya berpengaruh pada sebagian jembatan 3. Hanya bekerja pada system-sistem tertentu
Beban khusus terdiri dari : 1. Gaya akibat gempa 2. Gaya sentrifugal
3. Gaya akibat gesekan pada tumpuan bergerak 4. Gaya dan muatan selama pelaksanaan
5. Gaya akibat aliran air dan benda-benda hanyut
6. Gaya akibat tekanan tanah
T B
T
H
4. Syarat Ruang Bebas
a. Profil Ruang Bebas Jembatan
Yang dimaksud dengan profil ruang bebas jembatan adalah tinggi dan
lebar ruang bebas jembatan dengan ketentuan :
1) Tinggi minimum untuk jembatan tertutup adalah 5 meter
2) Lebar minimum untuk jembatan ditetapkan menurut jumlah jalur lalu
lintas (B) ditambah dengan kebebasan samping minimum 2 x 0,5 meter
Gambar 2.4 Ruang Bebas Jembatan dimana :
H = Tinggi minimum jembatan
C. Elemen-elemen Lantai Kendaraan 1. Lapisan Aus
Lapisan aus berfungsi sebagai lapisan yang langsung menerima lalu lintas kendaraan dan ditempatkan di atas konstruksi lantai. Konstruksi lantai yang dilaksanakan dengan cara demikian itu disebut konstruksi lantai monolit. Lapisan aus dapat terdiri dari bebas aspal atau bebas beton semen Portland yan tidak berfungsi sebagai penahan beban.
2. Konstruksi Lantai (Deck)
Konstruksi lantai (pelat) berfungsi sebagai pemikul beban dari keseluruhan konstruksi lantai kendaraan. Konstruksi lantai terdiri dari :
a. Beton bertulang
b. Pelat baja dengan lapisan aus tipis di atasnya
c. Pelat baja bergelombang yang diisi beton tumbuk di atasnya d. Papan – papan kayu
3. Trotoir
Trotoir digunakan untuk lalu lintas orang. Trotoir terdiri dari : a. Beton bertulang
b. Pelat baja c. Pelat kayu
4. Kerb
Kerb dibuat tergabung menjadi satu dengan trotoir. Kerb terbuat dari : a. Beton bertulang
5. Sandaran
Sandaran jembatan dipasang pada kedua tepi sistem lantai kendaraan serta
berfungsi sebagai konstruksi pengaman bagi lalu lintas kendaraan maupun pejalan kaki. Bentuk konstruksi sandaran banyak variasinya, demikian pula bahan-bahan baku untuk pelaksanaan konstruksinya. Beberapa jenis bahan yang biasanya
digunakan adalah :
a. Beton bertulang
b. Kombinasi beton bertulang pada pipa gas c. Baja siku
d. Pipa gas e. Kayu.
D. Elemen-elemen Bangunan Atas 1. Gelagar Canai
Gelagar canai biasanya digunakan untuk jembatan-jembatan dengan bentang pendek. Gelagar biasanya dipasarkan oleh pabrik sebagai suatu unit lengkap
terdiri dari dua buah flens dan badannya. Kedua flens itu menahan momen lentur sedangkan badannya memikul gaya lintang. Jenis-jenis yang biasa digunakan adalah
:
a. Gelagar standart (Standart Beam, INP)
2. Gelagar Berdinding Penuh (Tersusun)
Gelagar berdinding penuh digunakan pada jembatan-jembatan untuk bentang-bentang sedang yang tidak memerlukan rangka batang akan tetapi
membutuhkan gelagar yang lebih besar daripada gelagar canai. Perhitungan dari sudut ekonomi sebaiknya tidak lebih dari 20 – 30 cm. Elemen-elemen dasar dari gelagar berdinding penuh adalah beban dengan kedua flens yang dilas atau jembatan
statis tertentu di atas dua buah perletakan, ½ bagian atas dari gelagar berdinding penuh akan memikul tekan, sedangkan ½ bagian bawah akan memikul tarik.
3. Gelagar Beton
Gelagar-gelagar beton biasanya diberikan tulangan yang harus memikul tegangan tarik, sedangkan betonnya sendiri harus menahan
tegangan-tegangan tekan dan sedikit geser. Gelagar biasanya berbentuk pelat persegi atau balok T dengan ukuran tinggi lebih besar daripada tebal badannya. Biasanya bentang
yang diijinkan maksimum 20 meter, ditinjau dari segi pelaksanaan dan ekonomisnya.
4. Rangka Batang (Truss)
Rangka batang merupakan suatu bentuk konstruksi yang dapat memikul
beban-beban besar dan dapat digunakan pada jembatan-jembatan dengan bentang yang lebih besar daripad bentang-bentang yang menggunakan gelagar canai atau gelagar dinding penuh. Pada umumnya rangka batang digunakan pada keadaan
(d) (c)
(b) (a)
Jenis – jenis rangka batang dapat dibagi dalam jembatan – jembatan : a. “Through type” dengan rangka batangnya menjulang ke atas dan system
lantai kendaraan di bawah, seperti pada gambar 2.5 (a) dan (b)
b. “Deck type” dengan rangka batangnya dipasang arah ke bawah dan system
lantai kendaraan di atas, seperti pada gambar 2.5 (c) dan (d)
Gambar 2.5 Skematis Rangka Batang “Through Type” dan “Deck Type”
Adapun elemen – elemen dari masing – masing rangka batang dapat diuraikan sebagai berikut :
a. Batang Tepi
Dalam rangka batang, elemen-elemen bagian atas dan bawah yang
membentang pada seluruh panjangnya disebut batang tepi atas dan batang tepi bawah. Untuk jembatan statis tertentu di atas dua (2) perletakan, batang tepi atas
selalu memikul gaya tekan, sedangkan batang tepi bawah memikul gaya tarik. Kedua elemen jembatan ini yaitu batang tepi atas dan batang tepi bawah merupakan bagian utama dari jembatan. Kerusakan-kerusakan pada kedua batang tepi ini dapat
b. Batang Diagonal
Batang-batang diagonal yang dipasang antara kedua batang tepi merupakan unsure-unsur badan dari konstruksi rangka batang. Bergantung kepada bentuk
kerangka batangnya, maka batang-batang diagonal bias mengalami tarik ataupun tekan. Batang–batang diagonal termasuk pula pada bagian-bagian vital dari jembatan. Sehingga apabila timbul kerusakan-kerusakan pada bagian-bagian ini,
konstruksi keseluruhan jembatan menjadi kurang aman.
c. Batang Vertikal
Batang vertival termasuk unsur badan dari jembatan rangka. Batang-
batang dapat menahan gaya tarik atau gaya tekan, bergantun pada konfigurasi rangka batangnya. Sebagian besar dari batang-batang vertikal merupakan unsur penting pada konstruksi jembatan, sehingga apabila terjadi kerusakan dapat
mengakibatkan tidak amannya konstruksi.
d. Ikatan Ayun
Ikatan ayun adalah elemen-elemen sekunder yang menghubungkan kedua rangka batang melalui dua buah titik kumpul panil antara (bukan panil ujung).
Fungsinya adalah memberikan stabilitas dalam arah melintang dan memindahkan gaya geser dari rangka batang satu kepada yang lainnya.
e. Ikatan Angin Atas
Letaknya pada bidang-bidang tepi atas memberikan stabilitas dalam arah
f. Ikatan Angin Bawah
Letaknya pada bidang-bidang tepi bawah memberikan stabilitas dalam arah
melintang kepada kedua rangka batang serta memikul tegangan-tegangan akibat gaya angin.
g. Gelagar Melintang
Dipasang antara titik kumpul panil serta menghubungkan kedua rangka batang. Gelagar melintang menerima gaya-gaya dari konstruksi lantai, gelagar memanjang dan meneruskannya kepad rangka batang.
h. Gelagar Memanjang
Dipasang antara gelagar-gelagar melintang serta memberikan dukungan pada konstruksi lantai. Beban lantai diterima oleh gelagar memanjang kemudian oleh gelagar memanjang diteruskan kepada gelagar melintang dan kepada kedua
rangka batang.
i. Pelat Pertemuan (Buhul)
Pelat ini menghubungkan unsur-unsur konstruksi dari sebuah rangka batang.
Elemen-elemen dari d – h dapat dianggap sebagai unsur-unsur sekunder pada konstruksi, tetapi bukan dianggap tidak penting sehingga apabila salah satu elemen sekunder ini rusak tidak akan mengakibatkan tidak amannya keseluruhan
E. Jenis – jenis Jembatan
Menurut Struyk (Jembatan hal 1-2), jembatan dapat dibagi dalam beberapa
golongan – golongan, yaitu : I. Jembatan-jembatan tetap
II. Jembatan-jembatan dapat digerakkan
Golongan I dapat dibagi dalam beberapa bagian antara lain :
1. Jembatan Kayu, hanya untuk lalu lintas biasa pada bentang kecil dan untuk
jembatan pembantu
2. Jembatan Baja, terbagi atas :
a. Jembatan yang sederhana dimana lantai kendaraannya langsung berada di
atas gelagar. Untuk gelagar itu dipergunakan gelagar-gelagar yang dikonstruir atau gelagar-gelagar-gelagar-gelagar canai
b. Jembatan-jembatan gelagar kembar, hanya untuk lalu lintas kereta api
dengan batang rel di antara balok-balok.
c. Jembatan dengan pemikul lintang dan pemikul memanjang, gelagar
induknya ialah gelagar dinding penuh yang dikonstruir atau gelagar pekerjaan
d. Jembatan Pelengkungan
e. Jembatan Gantung
3. Jembatan-jembatan dari beton bertulang, dalam golongan ini termasuk juga
jembatan-jembatan yang gelagar-gelagarnya di dalam beton
4. Jembatan Batu, hamper tidak ada kecuali dipergunakan untuk lalu lintas
Golongan II (Jembatan-jembatan dapat digerakkan), antara lain adalah: 1. Jembatan-jembatan yang dapat berputar di atas poros mendatar, yaitu
a. Jembatan-jembatan angkat, b. Jembatan-jembatan baskul, c. Jembatan lipat Strauss,
2. Jembatan yang dapat berputar di atas poros mendatar juga termasuk
poros-poros yang dapat berpindah sejajar dan mendatar, seperti yang dinamakan jembatan-jembatan baskul beroda
3. Jembatan-jembatan yang dapat berputar atas suatu poros tegak, atau
jembatan-jembatan putar
4. Jembatan yang dapat berkisar kea rah tegak lurus atau mendatar a. Jembatan angkat,
b. Jembatan beroda,
c. Jembatan gojah atau ponts transbordeur,
Menurut Patar M Pasaribu (Jembatan Rangka hal 1), menjelaskan bahwa konstruksi jembatan baja dapat dilaksanakan dengan berbagai jenis dan bentuk,
antara lain:
1. Jembatan Gelagar Sederhana (Simple Beam Bridge) 2. Jembatan Berdinding Penuh (Plate Girder Bridge) 3. Jembatan Komposit (Composite Bridge)
4. Jembatan Bentuk Kotak (Box Girder Bridge)
5. Jembatan Rangka (Truss Bridge/ Frame Girder Bridge)
8. Jembatan Gantung (Suspension Bridge) 9. Jembatan Kabel Kaku (Cable Stayed Bridge)
Kemudian Patar M Pasaribu (Jembatan Rangka hal 19) membagi jenis-jenis jembatan rangka berdasarkan bebarapa keadaan, antara lain sebagai berikut :
1. Sistem lalu lintas yang melaluinya, a. Jembatan Rangka Tertutup
1) Lalu lintas di atas (Gelagar Melintang di bagian atas rangka utama) 2) Lalu lintas di bawah (Gelagar Melintang di bagian bawah rangka
utama)
b. Jembatan Rangka Terbuka (tidak mempunyai Portal ujung dan ikatan angin Atas)
2. Bentuk Utama Rangka Batang, yaitu
a. Jembatan Rangka dengan Batang dengan Batang Tepi Lurus
b. Jembatan Rangka dengan Batang dengan Batang Tepi Atas Lengkung c. Jembatan Rangka dengan Batang dengan Batang Tepi Bawah Lengkung d. Jembatan Rangka Pelengkung Tiga Sendi
e. Jembatan Rangka Pelengkung dengan Tumpuan Sendi-sendi f. Jembatan Rangka Overhang
g. Jembatan Rangka Gabungan
h. Jembatan Rangka di Atas Beberapa Tumpuan dengan bentuk lurus atau pelengkung yang merupakan konstruksi statis tertentu maupun statis tak tentu
3. Statika Konstruksi, yaitu :
a. Jembatan Rangka Statis Tertentu
b. Jembatan Rangka Statis Tak Tentu
4. Letak dan Bentuk dari Rangka Batang, yaitu : a. Jembatan Rangka dengan Batang Diagonal Naik
b. Jembatan Rangka dengan Batang Diagonal Turun
c. Jembatan Rangka dengan Batang Diagonal Naik dan Turun
d. Jembatan Rangka Batang Diagonal Rangkap e. Jembatan Rangka Batang Bentuk K
f. Jembatan Rangka Batang Bentuk Belah Ketupat
Menurut Peraturan Muatan Untuk Jembatan Jalan Raya, berdasarkan
muatan yang melaluinya jembatan dapat di bagi menjadi beberapa kelas, yaitu : 1. Jembatan Kelas I
2. Jembatan Kelas II 3. Jembatan Kelas III
Selain jenis-jenis di atas ada juga pembagian jembatan. Jenis-jenis
jembatan berdasarkan keadaaan perletakannya dapat dibagi dalam 2 (dua) bagian adalah sebagai berikut :
1. Jembatan Sederhana di atas 2 (dua) Perletakan
Jenis jembatan ini terdiri dari gelagar-gelagar yang terpisah untuk setiap bentang yang pada salah salah satu ujungnya diletakkan di atas tumpuan tetap
h
L
L
h
L
h
a. Rangka Batang WARREN
Gambar 2.6 Rangka Batang WARREN
[image:39.595.108.510.96.683.2]b. Rangka Batang PRATT
Gambar 2.7 Rangka Batang PRATT
c. Rangka Batang HOWE
L
h d. Rangka Batang CURVED
Gambar 2.9 Rangka Batang CURVED
2. Jembatan Menerus di atas Beberapa Perletakan
Bangunan atas dari Jembatan jenis ini diletakkan menerus di atas beberapa
buah perletakan. Keuntungan-keuntungan dari jembatan yang menggunakan konstruksi menerus, adalah sebagai berikut :
a. Reduksi dalam tinggi bangunan atas b. Reduksi dalam jumlah sambungan lantai
c. Gaya dukung cadangan lebih besar
Adapun beberapa contoh dari konstruksi menerus di atas beberapa perletakan adalah sebagai berikut :
a. Rangka Batang Menerus
b. Rangka Batang Dinding Penuh Menerus
Gambar 2.11 Rangka Batang Dinding Penuh Menerus
c. Gelagar Canai Menerus
Gambar 2.12 Gelagar Canai Menerus
F. Jembatan Komposit
Balok gabungan (composite beam) kerjasama antara beton dengan gelagar
baja. Balok gabungan umumnya terdiri dari kerjasama antara lantai beton dengan gabungan baja yang dihubungkan dengan penghubung geser atau shear connector.
Penampang gabungan ini sebaiknya direncanakan sedemikian rupa sehingga garis beratnya terletak di daerah profil baja, untuk menghindarkan adanya bagian beton yang tertarik.
Untuk menghitungkan garis berat balok gabungan tersebut, bagian beton yang bekerjasama dengan profil baja kita ganti dengan membagi luasan beton
Konstruksi Komposit Tanpa tulangan Komposit
-+
+
-+
Pada umumnya tinggi balok gabungan adalah :
a. Gelagar + plat beton = 1/25 L (2.5)
b. Gelagar baja saja = 1/30 L (2.6)
Pada gelagar yang terletak di atas beberapa perletakan (gelagar menerus) yang menjadi bentangnya adalah jarak titik-titik nol akibat momen berat sendiri. Ini gunanya untuk menghindarkan lentur yang terlalu besar. Jadi kita peroleh momen positif dan momen negatif. Dimana momen positif adalah konstruksi composite dan momen negatif adalah konstruksi tanpa composite, atau beton hanya sebagai tempat tulang saja lihat gambar 2.13
Gambar 2.13 Keadaan Komposit pada Gelagar Menerus
1. Lebar Efektif Lantai Beton
Pada perhitungan balok gabungan, lebar plat lantai beton yang dianggap bekerjasama dengan gelagar baja tidak boleh lebih besar dari hal di bawah ini menurut PU adalah :
a) Balok gabungan (composite beam) berbentuk T
1) bef = ¼ L (L = bentang ) (2.7)
b) Balok gabungan (composite beam) berbentuk T
1) bef = ¼ L (L = bentang ) (2.10)
2) bef = Jarak as ke as gelagar baja (2.11) 3) bef = 12 x t (L = Tebal plat beton) (2.12)
2. Dimensi Balok Gabungan (Composite Beam)
Umumnya gelagar baja terdiri dari profil IDIN dengan plat perkuatan sayap
tepi bawah, tetapi gelagar baja biasa tidak mencukupi maka dibuat dari profil tersusun, diman plat sayap dan badan dihubungkan dengan las. Dimensi balok gabungan ini kita hubungan dengan sistem coba-coba. Dengan tebal plat lantai beton
minimum 15 cm sehingga kita kontrol tegangan-tegangan yang terjadi berdasarkan : 1) Bila waktu pemasangan lantai beton tidak diadakan tumpuan pembantu
(perancah/bekesting). Tegangan yang timbul akibat berat sendiri (lantai beton sebelum mengeras + gelagar) dipikul oleh gelagar baja, beban bergerak dengan tumbukan dipikul oleh gelagar composite :
σ
= pr bs W M+ comp
bg
W M
<
σ
(2.13)dimana :
Mbs = Momen akibat berat sendiri (TM)
Mbg = Momen akibat muatan beban bergerak (TM)
Wpr = Momen tahanan baja (cm³)
Wcomp = Momen tahanan composite elastis (cm³)
Tetapi akibat muatan-muatan lainnya seperti (sandaran, aspal, trotoir) karena
pada umumnya dikerjakan setelah bagian-bagian utama selesai/mengeras atau lantai beton yang menimbulkan tegangan tambahan. Perhitungan tegangan
tambahan ini memungkinkan beton dalam keadaan plastis, sehingga kita tidak menggunakan beton dalam keadaan modulus elastis, tetapi menggunakan beton dengan yang lebih besar yaitu n plastis
σ
= prbs W M
+ comp
bg
W M
+ comp
tb W
M
' <
σ
(2.14)dimana :
Mtb = Momen akibat berat sendiri (TM)
W’comp = Momen tahanan composite elastis (cm³)
2) Bila gelagar tersebut diberi tumpuan pembantu (perancah/bekisting) pada saat
pengecoran lantai beton sampai mengering mencapai 75 % dari kekuatan
seharusnya (kekuatan setelah 28 hari) baru tumpuan pembantu tersebut dibuka, sehingga baik akibat berat sendiri maupun beban bergerak maupun beban
bergerak diperhitungkan yang memikul adalah gelagar composite
σ
=comp bg bs
W M
M +
+ comp
tb W
M
BAB III
METODE ANALISIS PADA RANGKA JEMBATAN
A. Pendahuluan
Analisa struktur adalah bagian utama dari formulasi dan solusi suatu desain optimasi, selanjutnya pada beberapa kali selama optimasi. Untuk mengurangi
jumlah waktu untuk keperluan analisis, maka digunakan cara analisis struktur pendekatan.
Dalam hal menghitung gaya-gaya dalam, tegangan, perpindahan atau deformasi pada suatu struktur, kita harus menetapkan model analitik yang menyatakan perilaku struktur akibat beban luar yang bekerja. Suatu model dapat
diterima, harus menggambarkan perilaku fisik dari struktur yang ada tapi mudah atau sederhana untuk dianalisis. Dasar asumsi analisis, yang akan menjamin model
yang menyatakan problem peninjauan, idealisasi dan pendekatan yang memberi hasil pada suatu solusi yang sederhana. Metode analisis struktur yang biasanya digunakan pada desain optimasi
B. Perencanaan Rangka Induk
Dalam merencanakan suatu rangka induk, harus diketahui besarnya beban yang bekerja pada jembatan tersebut, agar dapat menentukan dimensi – dimensi
1. Perhitungan Berat Sendiri Rangka Induk
Berat sendiri rangka induk ditaksir menurut rumus Prof.DR. N.E KIST:
Q =
L f t
L f L M V
. . 9
−
+ (3.1)
dimana :
Q = Berat sendiri gelagar induk dalam satuan ton
V = Berat sendiri jembatan rangka (lantai + gelagar memanjang + gelagar melintang dan lain – lain) dalam satuan ton
L = Bentang jembatan dalam satuan meter
f = Koefisien jembatan rangka di atas dua perletakan (faktor bentuk) berkisar 2,95 – 3 (untuk jembatan di atas dua perletakan pakai f = 2,97)
M = Momen maksimum oleh beban bergerak pada pertengahan bentang dalam satuan ton meter
t = Tegangan ijin rata – rata dalam satuan kg/cm²
Gaya batang akibat berat sendiri dapat dihitung dengan metode sebagai berikut :
a. Metode keseimbangan titik buhul b. Metode ritter
a. Metode Keseimbangan Titik Buhul
Pada suatu konstruksi rangka, konstruksi tersebut harus dalam keadaan seimbang, tetapi setiap titip buhul harus juga dalam keadaan seimbang. Dalam
perhitungan titik buhul mempunyai cara kerja sebagai berikut : 1) Setiap titik buhul dipisahkan
2) Setiap titik buhul harus dalam keadaan seimbang akibat gaya luar yang
bekerja pada titik buhul itu, dan gaya dalam (gaya batang) yang timbul di titik itu
3) Gaya luar gaya batang itu berpotongan di titik buhul tersebut,maka untuk
menghitung gaya-gaya yang blum diketahui kita menggunakan dalil
ΣH = 0 dan ΣV = 0,sedangkan ΣM = 0 tidak ada gunanya dipakai.
4) Syarat mengerjakan no 3 di atas, dibuat suatu perjanjian (konversi) tanda
sebagai berikut :
a). Gaya batang yang menuju titik buhul dinyatakan batang tekan (- )
b). Gaya batang yang meninggalkan titik buhul dinyatakan batang tarik (+) Dari ketentuan di atas ada dua (2) persamaan, maka pada tiap – tiap buhul
yang akan dicari gaya batangnya hanya ada dua (2) batang yang belum diketahui, sehingga tiap–tiap buhul dapat dicari keseimbangannya, satu demi satu sehingag
b. Metode Ritter
Pada suatu konstruksi rangka, konstruksi tersebut harus dalam keadaan seimbang. Dalam perhitungan metode ritter mempunyai cara kerja sebagai berikut:
1) Cari gaya-gaya reaksi akibat gaya-gaya luar 2) Hitung panjang dan sudut batang
3) Syarat ritter, hanya 3 (tiga) buah dari gaya-gaya batang itu belum diketahui 4) Jika kita hendak menghitung salah satu gaya-gaya tersebut maka menurut
cara ritter, kita harus dapatkan gaya batang itu dengan menggunakan dalil
momen terhadap titik potong kedua gaya yang belum diketahui. Dalam hal ini maka momen kedua gaya batang yang belum diketahui itu adalah nol (0). Dan kita menemukan suatu persamaan dimana gaya yang sedang dicari
itu terdapat sebagai satu-satunya gaya yang belum diketahui
5) Syarat mengerjakan no 4 di atas, harus ada pejanjian tanda sebagai berikut
:
a). Gaya-gaya batang yang belum diketahui kita misalkan gaya tarik. b). Dalam pengambilan sigma momen terhadap suatu titik searah putaran
jarum jam disebut positif ( + ) dan berlawan jarum jam disebut negatif ( - )
6) Jika kita menghitung gaya-gaya batang tersebut dengan cara ritter, kalau
kita meritter dari kiri maka dalam pengambilan sigma momen semua gaya-gaya di sebelah kiri ritteran harus kita perhitungkan dan kalau meritter dari
qbs
L
c. Metode Cremona
Pada suatu konstruksi rangka, konstruksi tersebut harus dalam keadaan seimbang. Dalam perhitungan metode cremona mempunyai cara kerja sebagai
berikut :
1) Cari gaya-gaya reaksi akibat gaya-gaya luar
2) Perhatikan dan hitung panjang batang dan sudut 3) Buat gambar induk dari konstruksi dengan skala
4) Dengan skala tertentu juga gambarkan gaya-gaya termasuk gaya-gaya
reaksi dengan syarat harus menutup
5) Urutan penyusunan gaya-gaya dibuat searah putaran jarum jam atau
berlawanan putaran jarum jam
6) Melukis segi banyak gaya-gaya harus pertitik buhul
7) Perjanjian tanda adalah :
a). Meninggalkan titik buhul positif ( + ) b) Menuju titik buhul negatif ( - )
L
b3d2
v2
d1
b2
b1
v1
a3
a2
a1
Cara lain untuk menghoitung berat sendiri dapat juga dihitung
berdasarkan garis pengaruh. Dalam hal ini, pembebanan akibat beban tetap dan beban bergerak digambarkan di atas gambar garis pengaruh, sehingga lebih jelas dan
lebih praktis dalam perhitungan.
2. Gaya Batang Akibat Beban Bergerak
Dalam menghitung gaya batang akibat beban bergerak, dipergunakan garis
pengaruh masing-masing batang. Gaya batang akibat beban bergerak sama dengan luasan bidang garis pengaruh (tanda positif untuk gaya tarik dan tanda negatif untuk gaya tekan) dikalikan dengan beban merata (q), sedang beban bergerak terpusat P
dikalikan dengan ordinat pada posisi yang ekstrim. Untuk gaya batang tarik dibebani garis pengaruh yang bertanda positif, dan untuk gaya batang tekan dibebani
garis pengaruh yang bertanda negatif. Dengan demikian , akan diperoleh kemungkinan gaya-gaya ekstrim maksimum dan gaya-gaya ekstrim minimum.
Batang-batang tertentu yang garis pengaruhnya berubah tanda (ada yang
positif dan ada tanda negatif), dicantumkan panjang bentang positif dan negatif, masing-masing dengan koefisien kejut pada setiap gambar garis pengaruh. Hal ini
diperlukan untuk perhitungan gaya-gaya ekstrim untuk setiap batang.
K K
h
H
Keterangan :
a1,2 = Batang tepi atas b1,2 = Batang tepi bawah
v1,2 = Batang vertikal d1,2 = Batang diagonal
3. Gaya Batang Akibat Angin
Dalam menghitung gaya batang akibat beban angin, dipergunakan garis pengaruh masing – masing batang. Gaya batang akibat angin sama dengan luasan bidang garis pengaruh dikalikan dengan beban angin, tanpa dikalikan dengan
koefisien kejut. Untuk gaya batang tarik dibebani pad garis pengaruh yang bertanda positif, dan untuk gaya batang tekan garis pengaruh yang negatif.
Gambar 3.3 Sistem Pembebanan Akibat Angin
Dengan adanya kombinasi akibat berat sendiri, beban bergerak dan beban
b
h
C. Dimensi Profil Batang Rangka Induk Profil rangka induk terdiri atas : 1. Batang tepi atas
2. Batang tepi bawah 3. Batang diagonal 4. Batang vertikal
Profil penampang batang – batang ini direncanakan sedemikian rupa
dengan mengingat sistem pelaksanaannya di lapangan tidak ada masalah.
1. Profil Batang Tepi Atas
Dalam mendimensi batang tepi atas cukup hanya gaya batang yang paling
besar (ekstrim). Dimensi profil batang tepi atas di buat dari kombinasi pelat profil dengan profil siku.
b
h
2. Profil Batang Tepi Bawah
Dalam menetapkan jarak pelat buhul untuk batang tepi bawah dari segi pertimbangan, praktis pemasangan batang vertikal nantinya, maka jarak pelat buhul
sama untuk batang tepi atas dan batang tepi bawah rangka induk. Dalam mendimensi batang tepi bawah diambil gaya batang yang paling maksimum.
Gambar 3.5 Profil Batang Tepi Bawah
3. Profil Batang Diagonal
Batang diagonal bukanlah batang yang menerus seperti batang tepi atas dan batang tepi bawah, melainkan merupakan batang tersendiri, yang satu dengan
yang lainnya tidak berhubungan. Dengan demikian, dalam mendimensi batang diagonal tidak terikat dengan profil dasar ynag mesti sama sebagaimana halnya
dalam mendimensi batang diagonal cukup hanya batang diagonal yang memikul gaya batang yang maksimum.
b
h
h
Gambar 3.6 Profil Batang Diagonal4. Profil Batang Vertikal
Dalam merencanakan batang vertikal yang perlu diperhatikan kekakuan dan kestabilan sambungan di titik buhul maka batang vertikal dimasukan di bagian
sebelah dalam pelat buhul. Dalam hal ini tinggi profil batang vertikal maksimum sama dengan jarak bersih dari pelat buhul. Dalam mendimensi batang vertical yang
memikul gaya batang yang maksimum
Maksimum
Minimum f(x) f(x)
0 X
f(x) D. Teori Optimasi
Optimasi dapat didefinisikan sebagai proses mendapatkan kondisi yang memberikan hasil maksimum atau minimum dari suatu fungsi. Jadi optimasi adalah
mencari hasil yang paling optimum untuk suatu kondisi tertentu, sehingga hasil yang paling optimum dapat maksimum atau minimum seperti terlihat dalam gambar 3.7
Gambar 3.8 Diagram Fungsi Maksimum = f(x), Minimum= – f(x)
Dalam disain suatu sistem struktur terdapat besaran yang nilainya tidak berubah selama proses optimasi, besaran ini disebut parameter tetap (preassigned
parameter) sedangkan besaran yang nilainya berubah selama proses optimasi disebut variable disain. Setelah itu tujuan optimasi ditentukan.
Biasanya dalam bidang teknik sipil tujuan tersebut adalah untuk menmdapatkan minimumdari biaya. Kemudian rumus matematisnya dapat disusun dengan melibatkan parameter tetap dan variable disain dan dibatasi oleh fungsi
Formulasi problem optimasi struktur umnumnya dapat dituliskan sebagai
berikut :
MIN F(x) (3.2)
x ∈ X
yang memenuhi
gj (x) ≤ 0 j = 1,2, . . . m (3.3)
gk (x) ≤ 0 k = m+1, m+2, . . . n (3.4) dimana : x = vector variable disain
X = ruang (space) dari variable disain
F(x) = fungsi tujuan
gj (x) = fungsi kendala pertaksamaan
gk (x) = fungsi kendala persamaan m = jumlah kendala pertaksamaan n = jumlah kendala persamaan
1. Variable Disain
Di dalam proses optimasi struktur biasanya variable disain x terdiri dari besaran mengenai ukuran komponen striktur, misalnya tebal batang, luas
penampang, panjang komponen dan lain – lain. Seringkali dikehendaki variable disain harus memenuhi syarat – syarat tertentu, misalnya tidak diijinkan menjadi nol atau menjadi negative. Nilai ≤ 0 bagi tebal suatu komponen struktur tidak ada
artinya. Bila x mewakili luas penampang maka nilai x = 0 berarti komponen tersebut lenyap dari sistem struktur, dalam hal ini dapat menyebabkan struktur menjadi tidak
untuk menjamin bahwa hal tersebut tidak terjadi dengan memberikan kendala x ≥ a
≠ 0 dimana a adalah suatu konstanta.
2. Fungsi Kendala
Fungsi kendala merupakan fungsi yang memberikan batasan daerah layak
(feasible region). Dalam problem teknik, kendala dibagi menjadi dua jenis, yaitu kendala rencana (design constraint, side constraint) dan kendala sifat (behavior
constraint).
Kendala rencana adalah kendala yang diberikan karena alasan fungsional, fabrikasi atau estetika. Sedangkan kendala sifat adalah kendala yang membatasi
perilaku dari sistem seperti terlihat pada gambar di bawah ini :
Gambar 3.9 Kendala Permukaan Bidang
fungsi kendala yang sedemikian rupa menjadi suatu fungsi implicit dari variable disain x . Maka untuk mengevaluasi nilai fungsi kendala tersebut harus dilaksanakan terlebih dahulu analisis struktur.
Dalam kasus demikian menjadi sulit untuk menyatakan apakah kendala
merup-akan fungsi linier atau non linier dari variable x. kecuali tegangan atau perpindahan, kendala dapat pula berupa stabilitas struktur terhadap tekuk.
3. Fungsi Tujuan
Tujuan dalam optimasi terutama dalam teknik sipil adalah mencari struktur paling ringan, paling aman, paling murah dan lain – lain. Disain optimum mengendalikan faktor – faktor tersebut agar diperoleh suatu struktur dengan biaya total minimum. Setelah tujuan optimasi ditentukan, misalnya mencari struktur paling ringan, rumusan matematiknya dapat disusun dengan melibatkan parameter tetap dan variable disain dengan dibatasi fungsi kendala. Rumusan matematik ini disebut juga dengan fungsi tujuan (objective function, target function)
E. Metode Minimumisasi
Jika turunan dari f(x) dengan variable – variable x tidak ditemukan maka digunakan metode interpolasi kuadrat untuk mencari x minimum. Metode ini memerlukan langkah yangh panjang untuk meminimumisasikan harga x.
Fungsi f(x) diperkirakan sebagai fungsi kuadrat dan minimumnya x diperoleh sebagai turunan pertama persamaan kuadrat f(x). Persamaan f(x) dapat dirumuskan sebagai berikut :
f(x) = a + bx + cx² (3.5)
Kondisi yang dibutuhkan untuk mendapatkan minimu f(x) adalah :
dx x df( )
= b + 2cx
Yaitu x = -
c b
2 (3.6)
Syarat minimum f(x) adalah : 2 2 ) ( dx x f d
dimana : c > 0 (3.7)
Dalam upaya mengevaluasi konstanta – konstanta a, b, dan c kita harus mngevaluasi f(x) pada ketiga titik. Misalkan x = A, x = B dan x = C merupakan titik – titik dimana fungsi f(x) dievaluasi dengan memisalkan f(A), f(B), dan f(C) merupakan nilai – nilai fungsi sebagai berikut :
f(A) = a + b A + c A²
f(B) = a + b B + c B² (3.8)
f(C) = a + b C + c C² Sehingga menghasilkan persamaan
a =
(
)
(
)
(
)
(
)(
)(
)
− − − − + − + − A C C B B A A B AB f C A CA f B C BCfA B C
(3.9)
b =
(
) (
) (
)
(
)(
)(
)
− − − − + − + − A C C B B A B A f A C f C BfA 2 2 B 2 2 C 2 2
(3.10)
c =
(
)
(
)
(
)
(
)(
)(
)
− − −+ − + − − A C C B B A B A f A C f C BfA B C
(3.11)
Dari persamaan di atas diperoleh nilai minimum x sebagai berikut :
x = -
c b
2 (3.12)
(
) (
) (
)
BAB IV
PEMBAHASAN
A. Pendahuluan
Secara umum masalah desain dapat dikatakan sebagai kebalikan dari masalah analitis pada proses disain beban-beban yang bekerja telah diketahui dan akan ditentukan adalah berat elemen struktur agar mempunyai kekuatan yang cukup.
Dalam menentukan ukuran elemen-elemen struktur tersebut,perencana dihadapkan pada masalah disain struktur over designed yang berarti tidak ekonomis atau under
designed yang berarti tidak aman. Dalam hal ini, diinginkan desain yang “tepat’ memenuhi kekokohan minimum agar tercapai disain yang optimum. Untuk itu ada beberapa factor yang mesti ditinjau dalam desain optimum,dan yang terpenting adalah:
1. Bobot material total minimum
2. Dipenuhinya batas stabilitas terhadap tegangan ijin
Disain optimum mengendalikan factor-faktor tersebut agar diperoleh suatu struktur dengan biaya total yang minimum.
B. Batasan Stabilitas
Gelagar komposit memanjang dan melintang harus memenuhi syarat stabilitas tehadap tegangan ijin yaitu:
comp tbh comp
bg
pr bs
W M W
M
W M
'
+ +
Dimana :
Mbs = Momen akibat berat sendiri Mbg = Momen akibat muatan bergerak
Mtbh = Momen akibat beban tambahan Wpr = Momen tahanan baja
Wcomp = Momen tahanan komposit elastis
W’comp = Momen tahanan komposit plastis
Sedang untuk stabilitas terhadap rangka batang harus memenuhi syarat
batas menurut PPBBI : 1. Batang Tarik
a. Tegangan rata-rata pada batang tarik didapat dari gaya tarik yang bekerja dibagi luasan penampang bersih. Tegangan tersebut harus tidak boleh lebih
besar dari tegangan dasar untuk penampang tidak berlobang, dan tidak boleh lebih besar dari 0,75 kali tegangan dasar untuk penampang berlobang.
b. Kelangsingan batang tarik baja profil untuk konstruksi utama harus lebih kecil
dari 240, untuk konstruksi sekunder harus lebih kecil dari 300.
2. Batang Tekan
a. Batang tekan prismatic tersusun dihubungkan dengan plat kopel
1) Batang-batang yang tersusun yang terdiri dari beberapa elemen yang
3) Kelangsingan pada arah tegak lurus sumbu ( x – x ) dihitung dengan persamaan :
x kx x
I L
= λ
Dimana :
Lkx = Panjang tekuk batang tersusun pada arah tegak lurus sumbu (x-x) dengan memperhatikan penopang-penopang samping yang ada dan ujung-ujung batang.
Ix = Jari-jari kelembaban dari batang tersusun terhadap sumbu (x–x) 4) Pada arah tegak lurus sumbu bebas bahan ( y – y ) harus dihitung
kelangsingan idiil λiy dengan persamaan :
λiy =
2 2
) ( 2 )
(λy +m λi
λy = y ky
i L
λi = min
i Li
dimana :
m = jumlah tunggal yang membentuk batang tersusun
Lky = panjang tekuk batang tersusun pada arah tegak lurus sumbu (y-y ), dengan memperhatikan penopang-penopang samping yang ada dan ujung-ujung batang
iy = jari-jari kelembaban dari batang tersusun terhadap sumbu (y-y) L1 = jarak antara tengah-tengah plat kopel pada arah batang tekan
5) Kelangsingan batang tekan harus lebih kecil atau sama dengan 200
b. Batang tekan harus direncanakan sedemikian rupa sehingga terjamin stabilitasnya (tidak ada bahaya tekuk), hal ini harus diperhatikan dengan menggunakan persamaan :
ω .
F N
≤ σ
dimana :
N = Gaya tekan batang tersebut F = Luas Penampang
σ = Tegangan dasar dari baja
ω = factor tekuk yang tergantung dari kelangsingan (λ) dan macam bajanya
C. Prosedur
Dalam penyelesaian tulisan ini diambil data-data jembatan sebagai berikut: 1. Panjang bentang jembatan L = 48 meter
2. Lebar jembatan 8 meter, trotoir dan kanan masing-masing 1 meter 3. Jarak as ke as gelagar memanjang 2 meter
4. Tebal lantai kendaraan 15 meter 5. Tebal lapisan aus (aspal) 6 cm
6. Mutu baja diambil Fe 360 yang mempunyai tegangan dasar 1600 kg/cm² dan
tegangan leleh 1867 kg/cm² serta elastisitas E = 2,1 x 106kg/cm²
7. Mutu beton diambil K 225 σ’bk = 225 kg/cm² (tegangan karakteristik beton), dengan tegangan beton yang diijinkan σ’b = 0,33 σ’bk
1. Rencana Gelagar Memanjang
Panjang gelagar memanjang ditentukan dari jumlah medan yang dilakukan dengan cara coba-coba. Gelagar memanjang diberi beban berat sendiri yaitu pelat
lantai kendaraan, pembungkus beton dan berat sendiri gelagar memanjang. Akibat beban gerak diberi muatan PU 1987 yang terdiri dari muatan D atau muatan jalur,yaitu muatan terbagi rata q = 2,2 ton/meter untuk L≤ 30 meter m, dimana L
adalah panjang tinjauan, sedang muatan garis P = 12 ton.kedua muatan jalur ini diperhitungkan penuh untuk lebar jalur 5,5 meter dan selebihnya diperhitungkan 50
% dari muatan D tersebut. Sedang koefisien kejut di ambil rumus :
φ = 1+
L
+
50 20
akibat beban gerak trotoir diambil qtr = 500 kg/m² diperhitungkan hanya 60% bekerja terhadap perencanaan gelagar dari muatan trotoir tersebut.
Untuk beban tambahan yaitu muatan aspal diberi muatan terhadap gelagar memanjang, karena aspal dikerjakan setelah lantai beton mengeras. Dengan
demikian didapat momen-momen dari gelagar memanjang yaitu momen akibat beratn sendiri, momen bergerak dan momen tambahan. Kemudian dikontrol terhadap ijin dari baja dan beton.
2. Rencana Gelagar Melintang
Pengaruh gelagar memanjang terhadap gelagar melintang dimana beban gelagar memanjang dijadikan beban terpusat terhadap gelagar melintang. Sedang
beban tambahan sehingga didapat momen-momen gelagar melintang dan kemudian
dikontrol terhadap tegangan ijin beton dan baja.
3. Rencana Gelagar Induk
Berat sendiri gelagar induk ditaksir menurut rumus Prof Dr N E Kist :
Q =
L f t
L f L M V
. . 9
−
+
Dimana :
Q = Berat sendiri gelagar induk dalam satuan ton
V = Berat sendiri jembatan rangka (lantai + gelagar memanjang + gelagar
melintang dan lain-lain) dalam satuan ton L = Bentang jembatan dalam satuan meter
f = Koefisien jembatan rangka di atas dua perletakan (factor bentuk) berkisar 2,95 – 3,00 ( dipakai 2,97 untuk jembatan lalu lintas biasa)
M = Momen maksimum oleh beban bergerak pada pertengahan bentang dalam satuan ton meter
t = Tegangan ijin rata-rata dalam satuan kg/cm² dimana t = ½ [ σ + 1,172 x σ pada λ = 50]
untuk λ = 50 di dapat factor tekuk ω = 1,234 (PPBBI)
σ = σ
ω.
1
= .1600
234 , 1
1
Setelah estimasi gelagar induk didapat maka dilakukan pembebanan
terhadap rangka yang didistribusikan secara merata untuk tiap-tiap titik buhul. Untuk muatan bergerak terhadap gelagar rangka induk terdiri dari muatan
garis P = 12 ton dan muatan terbagi rata untuk 30 < L ≤ 60 m. q = 2,2 - 1,1 /60 ( L – 30 )
Sedang muatan bergerak trotoir diambil 500 kg/cm² diperhitungkan 60%
bekerja. Setelah beban bergerak ditotal maka dilakukan pembebanan terhadap rangka yang didistribusikan secara merata untuk tiap-tiap titik buhul.
Pengaruh tekanan angin diambil sebesar 100 kg/cm², dimana pengaruhnya terhadap gelagar induk adalah angin vertical yang tergantung pada tinggi jembatan, perhitungan angin terhadap rangka ditetapkan sebesar 1,5 kali jumlah luas bidang sisi rangka, sedangkan jumlah luas bidang sisi rangka diperhitungkan 30 % terhadap
luas bidang sisi jembatan. Kemudian dilakukan perhitungan statika, dimana dalam hal ini jembatan dalam keadaan berisi kendaraan, maka didapat beban total yang
dipikul rangka dan kemudian didistribusikan secara merata untuk tiap-tiap titik buhul.
Ketiga pembebanan untuk rangka yaitu berat sendiri, beban bergerak dan
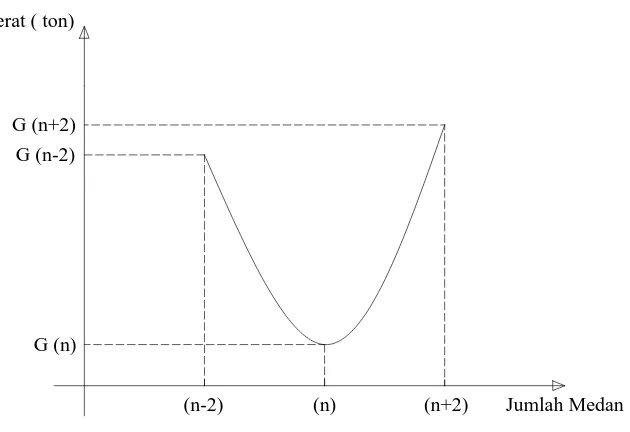
D. Penentuan Medan Ekonomis
Ekonomisasi dari suatu pembangunan jembatan tergantung dari berat konstruksi jembatan tersebut (makin berat bobotnya makin mahal pembangunannya
atau sebaliknya). Sehingga dengan demikian, maka berat sendiri gelagar induk suatu jembatan dengan bentang tertentu akan tergantung kepada berat sendiri gelagar memanjang, berat sendiri gelagar melintang dan berat sendiri berat lantai.
Dimana ukuran-ukuran (dimensi) profil yang dibutuhkan untuk suatu gelagar melintang atau gelagar memanjang tergantung kepada bentang (disebut
medan). Oleh karena itu, bentang gelagar memanjang tergantung kepada jarak gelagar melintang maka :
1. Bertambah banyak jumlah medan, maka bentang gelagar memanjang
bertambah kecil yang akan memberikan dimensi gelagar memanjang
semakin kecil, juga dimensi gelagar melintang semakin kecil sehingga berat sendiri semakin kecil, tetapi jumlah gelagar melintang semakin banyak. 2. Berkurang jumlah medan, maka bentang gelagar memanjang bertambah
besar, sehingga dimensi gelagar memanjang bertambah besar pula, tatapi dimensi setiap gelagar melintang bertambah besar dan berat sendirinya
bertambah besar hanya gelagar melintang berkurang.
Jadi akibat hal di atas, maka untuk merencanakan suatu jembatan berdinding penuh terlebih dahulu kita harus menghitung medan ekonomisnya
(jumlah medan yang memberikan berat sendiri jembatan yang terkecil)
(n-2) (n) (n+2) Jumlah Medan G (n)
G (n+2) Berat ( ton)
G (n-2)
memperoleh grafik hubungan antara berat (lantai, gelagar memanjang, dan gelagar
[image:68.595.161.476.134.350.2]melintang) dengan jumlah medan.
Gambar 4.1 Grafik Hubungan Berat dengan Jumlah Medan
E. Hasil
Hasil perhitungan momen dan tegangan beserta bobot total gelagar
F. Contoh Perhitungan
1. Sistem Pembebanan Lantai kendaraan
[image:69.595.98.522.181.660.2]Panjang Bentang Jembatan (L) = 48 meter dengan Jumlah medan (n) = 8
RBV
RAV
RBV
RAV
q eq
q total
RBV
RAV
Mencari qeq pada gelagar memanjang
RBV = RBV = ½ (6+4) 1,0 ½ = 2,5 M²
Mmax = RAV x (½L) - ½ x 1 x 1 x (⅓ x 1 x 4/2) – 1 x 2 x (2/2) = 2,5 (6/2) – (1,1667) – 2
= 4,333 M³
Mmax = ⅛ qeq L²
= ⅛ qeq L²
= 4,5 qeq M²
qeq = 2
3 5 , 4
333 , 4
M M
= 0,9630 M
2. Perhitungan Gelagar Memanjang a) Akibat Berat Sendiri
Akibat berat sendiri lantai beton = (0,15) (2,4) (0,963) = 0,347