SCRAMBLING INDEX DARI KELAS DIGRAF HAMILTON DWIWARNA DENGAN N TITIK GANJIL
SKRIPSI
MERRYANTY LESTARI P 110803067
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
SCRAMBLING INDEX DARI KELAS DIGRAF HAMILTON DWIWARNA DENGAN N TITIK GANJIL
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
MERRYANTY LESTARI P 110803067
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : Scrambling Index dari Kelas Digraf Hamilton Dwiwarna dengan n Titik Ganjil
Kategori : Skripsi
Nama : Merryanty Lestari P
Nomor Induk Mahasiswa : 110803067
Program Studi : Sarjana (S1) Matematika
Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara
Disetujui di Medan, Juli 2015
Komisi Pembimbing:
Pembimbing 2, Pembimbing 1,
Dr. Mardiningsih, M.Si Prof. Dr. Saib Suwilo, M.Sc NIP. 19630405 198811 2 001 NIP. 19640109 198803 1 004
Disetujui Oleh
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
SCRAMBLING INDEX DARI KELAS DIGRAF HAMILTON DWIWARNA DENGAN N TITIK GANJIL
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil karya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juli 2015
MERRYANTY LESTARI P 110803067
PENGHARGAAN
Segala puji hanya bagi Allah SWT yang senantiasa memberikan pertolongan dan rahmat-Nya sehingga penulis dapat menyelesaikan skripsi yang berjudul ”SCRAMBLING INDEX DARI KELAS DIGRAF HAMILTON DWI-WARNA DENGAN N TITIK GANJIL”ini dengan baik. Shalawat beriring salam kepada Nabi Muhammad SAW beserta keluarga dan para sahabat.
Dalam penulisan skiripsi ini penulis banyak mendapatkan bimbingan, moti-vasi dan bantuan dari berbagai pihak. Pada kesempatan ini penulis mengucapkan terima kasih kepada:
1. Ibunda Tetti Mahrani Lubis, AMS dan Ayahanda Anwar Pasaribu, S.Hut serta Kakanda Rahmelya Oktari, S.IA yang telah mendo’akan, memotivasi, dan memberikan dukungan selama penulisan skripsi ini.
2. Bapak Prof. Dr. Saib Suwilo, M.Sc, selaku Dosen Pembimbing I, dan Ibu Dr. Mardiningsih, M.Si, selaku Dosen Pembimbing II dan Sekretaris Departemen Matematika FMIPA USU Medan, yang telah banyak mem-bantu penulis dan memberikan dukungan baik berupa nasihat, motivasi maupun ilmu pengetahuan kepada penulis dalam menyelesaikan penelitian ini.
3. Bapak Prof. Dr. Tulus, M.Si, selaku Dosen Pembanding I dan Ketua Departemen Matematika FMIPA USU Medan, dan Bapak Dr. Suwarno Ariswoyo, M.Si, selaku Dosen Pembanding II, yang telah memberikan nasi-hat, kritik dan saran yang membangun selama penelitian ini.
4. Seluruh staf pengajar dan staf administrasi Departemen Matematika, Fakul-tas Matematika dan Ilmu Pengetahuan Alam, UniversiFakul-tas Sumatera Utara, Medan.
mengucapkan terima kasih kepada seluruh rekan-rekan Matematika 2011 terkhu-sus kepada Matematika Murni 2011 yang telah memberikan bantuan moril kepada penulis. Semoga Allah SWT memberikan balasan atas bantuan yang diberikan kepada penulis.
Penulis menyadari skripsi ini jauh dari kesempurnaan, untuk itu penulis mengharapkan kritik dan saran dari berbagai pihak untuk penyempurnaan skripsi ini. Semoga skripsi ini dapat bermanfaat bagi pembaca.
SCRAMBLING INDEX DARI KELAS DIGRAF HAMILTON DWIWARNA DENGAN N TITIK GANJIL
ABSTRAK
Scrambling index dari digraf dwiwarnaD(2) primitif adalah bilangan bulat positif
terkecil h+ℓ dari seluruh pasangan bilangan bulat tak negatif (h, ℓ) sedemikian hingga untuk setiap pasangan titikudanv diD(2) terdapat sebuah titikwdiD(2)
dengan sifat bahwa terdapat sebuah (h, ℓ)-walkdari titikuke titikwdan sebuah (h, ℓ)-walk dari titik v ke titik w. Tulisan ini membahas mengenai scrambling index dari kelas digraf Hamilton dwiwarna atas n ≥ 5 titik ganjil yang terdiri dari dua cycle dengan panjang n dan (n−1)/2. Pertama, tulisan ini membahas primitifitas dari sebuah digraf dwiwarna D(2) dan selanjutnya memperlihatkan
rumus scrambling index yang bergantung pada n titik dan posisi arc biru yang relatif terhadap titik berderajat masuk dua.
SCRAMBLING INDEX OF A CLASS OF TWO-COLORED HAMILTONIAN DIGRAPH WITH N ODD VERTICES
ABSTRACT
The scrambling index of a primitive two-colored digraph D(2) is the least positive
integer h+ℓ over all pairs of nonnegative integers (h, ℓ) such that for each pair of vertices u andv in D(2) there is a vertex win D(2) with the property that there
is an (h, ℓ)-walk from u to w and an (h, ℓ)-walk from v to w. This paper discuss the scrambling index of a class of two-colored Hamiltonian digraph on n ≥5 odd vertices consist of two cycles of length n and (n−1)/2, respectively. First, this paper discuss the primitivity of a two-colored digraph D(2) and then present
for-mulae for scrambling index that depend on n vertex and the position of the blue arcs relative to the vertex of indegree two.
Keywords: Primitive, two-colored digraph, Hamiltonian digraph, scrambling index.
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii
PENGHARGAAN iii
ABSTRAK v
ABSTRACT vi
DAFTAR ISI vii
DAFTAR GAMBAR viii
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 4
1.3 Tujuan Penelitian 4
1.4 Manfaat Penelitian 4
BAB 2 DIGRAF DWIWARNA PRIMITIF 5
2.1 Definisi Digraf Dwiwarna 5
2.2 Matriks Ketetanggaan Digraf Dwiwarna 7
2.3 Primitifitas Digraf Dwiwarna 8
2.4 Scrambling Index Digraf Dwiwarna 11
2.5 Batas Scrambling Index Digraf Dwiwarna 16
BAB 3 METODOLOGI PENELITIAN 19
BAB 4 SCRAMBLING INDEX DIGRAF HAMILTON DWIWARNA 21
BAB 5 KESIMPULAN DAN SARAN 41
5.1 Kesimpulan 41
5.2 Saran 41
DAFTAR GAMBAR
Nomor Judul Halaman
1.1 Digraf Wielandt Wn 3
1.2 (a) D(2) dengan 2 arc biru dan (b) D(2) dengan 3 arc biru 4
2.1 Digraf dwiwarna dengan 4 titik dan 5 arc 6
2.2 Digraf dwiwarna dengan 7 titik dan 10 arc 8
2.3 (a) D(2) terhubung kuat, (b) D(2) tidak terhubung kuat 9
2.4 Digraf dwiwarnaD(2) terhubung kuat primitif 10
2.5 Digraf dwiwarnaD(2) primitif 13
SCRAMBLING INDEX DARI KELAS DIGRAF HAMILTON DWIWARNA DENGAN N TITIK GANJIL
ABSTRAK
Scrambling index dari digraf dwiwarnaD(2) primitif adalah bilangan bulat positif
terkecil h+ℓ dari seluruh pasangan bilangan bulat tak negatif (h, ℓ) sedemikian hingga untuk setiap pasangan titikudanv diD(2) terdapat sebuah titikwdiD(2)
dengan sifat bahwa terdapat sebuah (h, ℓ)-walkdari titikuke titikwdan sebuah (h, ℓ)-walk dari titik v ke titik w. Tulisan ini membahas mengenai scrambling index dari kelas digraf Hamilton dwiwarna atas n ≥ 5 titik ganjil yang terdiri dari dua cycle dengan panjang n dan (n−1)/2. Pertama, tulisan ini membahas primitifitas dari sebuah digraf dwiwarna D(2) dan selanjutnya memperlihatkan
rumus scrambling index yang bergantung pada n titik dan posisi arc biru yang relatif terhadap titik berderajat masuk dua.
SCRAMBLING INDEX OF A CLASS OF TWO-COLORED HAMILTONIAN DIGRAPH WITH N ODD VERTICES
ABSTRACT
The scrambling index of a primitive two-colored digraph D(2) is the least positive
integer h+ℓ over all pairs of nonnegative integers (h, ℓ) such that for each pair of vertices u andv in D(2) there is a vertex win D(2) with the property that there
is an (h, ℓ)-walk from u to w and an (h, ℓ)-walk from v to w. This paper discuss the scrambling index of a class of two-colored Hamiltonian digraph on n ≥5 odd vertices consist of two cycles of length n and (n−1)/2, respectively. First, this paper discuss the primitivity of a two-colored digraph D(2) and then present
for-mulae for scrambling index that depend on n vertex and the position of the blue arcs relative to the vertex of indegree two.
Keywords: Primitive, two-colored digraph, Hamiltonian digraph, scrambling index.
SCRAMBLING INDEX DARI KELAS DIGRAF HAMILTON DWIWARNA DENGAN N TITIK GANJIL
SKRIPSI
MERRYANTY LESTARI P 110803067
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
SCRAMBLING INDEX DARI KELAS DIGRAF HAMILTON DWIWARNA DENGAN N TITIK GANJIL
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
MERRYANTY LESTARI P 110803067
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : Scrambling Index dari Kelas Digraf Hamilton Dwiwarna dengan n Titik Ganjil
Kategori : Skripsi
Nama : Merryanty Lestari P
Nomor Induk Mahasiswa : 110803067
Program Studi : Sarjana (S1) Matematika
Departemen : Matematika
Fakultas : Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara
Disetujui di Medan, Juli 2015
Komisi Pembimbing:
Pembimbing 2, Pembimbing 1,
Dr. Mardiningsih, M.Si Prof. Dr. Saib Suwilo, M.Sc NIP. 19630405 198811 2 001 NIP. 19640109 198803 1 004
Disetujui Oleh
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
SCRAMBLING INDEX DARI KELAS DIGRAF HAMILTON DWIWARNA DENGAN N TITIK GANJIL
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil karya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juli 2015
MERRYANTY LESTARI P 110803067
PENGHARGAAN
Segala puji hanya bagi Allah SWT yang senantiasa memberikan pertolongan dan rahmat-Nya sehingga penulis dapat menyelesaikan skripsi yang berjudul ”SCRAMBLING INDEX DARI KELAS DIGRAF HAMILTON DWI-WARNA DENGAN N TITIK GANJIL”ini dengan baik. Shalawat beriring salam kepada Nabi Muhammad SAW beserta keluarga dan para sahabat.
Dalam penulisan skiripsi ini penulis banyak mendapatkan bimbingan, moti-vasi dan bantuan dari berbagai pihak. Pada kesempatan ini penulis mengucapkan terima kasih kepada:
1. Ibunda Tetti Mahrani Lubis, AMS dan Ayahanda Anwar Pasaribu, S.Hut serta Kakanda Rahmelya Oktari, S.IA yang telah mendo’akan, memotivasi, dan memberikan dukungan selama penulisan skripsi ini.
2. Bapak Prof. Dr. Saib Suwilo, M.Sc, selaku Dosen Pembimbing I, dan Ibu Dr. Mardiningsih, M.Si, selaku Dosen Pembimbing II dan Sekretaris Departemen Matematika FMIPA USU Medan, yang telah banyak mem-bantu penulis dan memberikan dukungan baik berupa nasihat, motivasi maupun ilmu pengetahuan kepada penulis dalam menyelesaikan penelitian ini.
3. Bapak Prof. Dr. Tulus, M.Si, selaku Dosen Pembanding I dan Ketua Departemen Matematika FMIPA USU Medan, dan Bapak Dr. Suwarno Ariswoyo, M.Si, selaku Dosen Pembanding II, yang telah memberikan nasi-hat, kritik dan saran yang membangun selama penelitian ini.
4. Seluruh staf pengajar dan staf administrasi Departemen Matematika, Fakul-tas Matematika dan Ilmu Pengetahuan Alam, UniversiFakul-tas Sumatera Utara, Medan.
mengucapkan terima kasih kepada seluruh rekan-rekan Matematika 2011 terkhu-sus kepada Matematika Murni 2011 yang telah memberikan bantuan moril kepada penulis. Semoga Allah SWT memberikan balasan atas bantuan yang diberikan kepada penulis.
Penulis menyadari skripsi ini jauh dari kesempurnaan, untuk itu penulis mengharapkan kritik dan saran dari berbagai pihak untuk penyempurnaan skripsi ini. Semoga skripsi ini dapat bermanfaat bagi pembaca.
SCRAMBLING INDEX DARI KELAS DIGRAF HAMILTON DWIWARNA DENGAN N TITIK GANJIL
ABSTRAK
Scrambling index dari digraf dwiwarnaD(2) primitif adalah bilangan bulat positif
terkecil h+ℓ dari seluruh pasangan bilangan bulat tak negatif (h, ℓ) sedemikian hingga untuk setiap pasangan titikudanv diD(2) terdapat sebuah titikwdiD(2)
dengan sifat bahwa terdapat sebuah (h, ℓ)-walkdari titikuke titikwdan sebuah (h, ℓ)-walk dari titik v ke titik w. Tulisan ini membahas mengenai scrambling index dari kelas digraf Hamilton dwiwarna atas n ≥ 5 titik ganjil yang terdiri dari dua cycle dengan panjang n dan (n−1)/2. Pertama, tulisan ini membahas primitifitas dari sebuah digraf dwiwarna D(2) dan selanjutnya memperlihatkan
rumus scrambling index yang bergantung pada n titik dan posisi arc biru yang relatif terhadap titik berderajat masuk dua.
SCRAMBLING INDEX OF A CLASS OF TWO-COLORED HAMILTONIAN DIGRAPH WITH N ODD VERTICES
ABSTRACT
The scrambling index of a primitive two-colored digraph D(2) is the least positive
integer h+ℓ over all pairs of nonnegative integers (h, ℓ) such that for each pair of vertices u andv in D(2) there is a vertex win D(2) with the property that there
is an (h, ℓ)-walk from u to w and an (h, ℓ)-walk from v to w. This paper discuss the scrambling index of a class of two-colored Hamiltonian digraph on n ≥5 odd vertices consist of two cycles of length n and (n−1)/2, respectively. First, this paper discuss the primitivity of a two-colored digraph D(2) and then present
for-mulae for scrambling index that depend on n vertex and the position of the blue arcs relative to the vertex of indegree two.
Keywords: Primitive, two-colored digraph, Hamiltonian digraph, scrambling index.
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii
PENGHARGAAN iii
ABSTRAK v
ABSTRACT vi
DAFTAR ISI vii
DAFTAR GAMBAR viii
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 4
1.3 Tujuan Penelitian 4
1.4 Manfaat Penelitian 4
BAB 2 DIGRAF DWIWARNA PRIMITIF 5
2.1 Definisi Digraf Dwiwarna 5
2.2 Matriks Ketetanggaan Digraf Dwiwarna 7
2.3 Primitifitas Digraf Dwiwarna 8
2.4 Scrambling Index Digraf Dwiwarna 11
2.5 Batas Scrambling Index Digraf Dwiwarna 16
BAB 3 METODOLOGI PENELITIAN 19
BAB 4 SCRAMBLING INDEX DIGRAF HAMILTON DWIWARNA 21
BAB 5 KESIMPULAN DAN SARAN 41
5.1 Kesimpulan 41
5.2 Saran 41
DAFTAR GAMBAR
Nomor Judul Halaman
1.1 Digraf Wielandt Wn 3
1.2 (a) D(2) dengan 2 arc biru dan (b) D(2) dengan 3 arc biru 4
2.1 Digraf dwiwarna dengan 4 titik dan 5 arc 6
2.2 Digraf dwiwarna dengan 7 titik dan 10 arc 8
2.3 (a) D(2) terhubung kuat, (b) D(2) tidak terhubung kuat 9
2.4 Digraf dwiwarnaD(2) terhubung kuat primitif 10
2.5 Digraf dwiwarnaD(2) primitif 13
BAB 1 PENDAHULUAN
1.1 Latar Belakang
Matriks stochasticS adalah sebuah matriks bujursangkar berordo n yang setiap entri memenuhi 0< sij <1 dan jumlah entri setiap baris dan kolom sama dengan
1. Andaikan matriksstochastic S memenuhi sifat koefisien ergodicity τ1(S)<1,
dimana
τ1(S) =
1 2
{
max
ij n ∑
l=1
|sil−sjl| }
.
Matriksstochastic S disebut matriks scrambling jika dan hanya jika untuk setiap dua baris dari matriks stochastic S memiliki paling sedikit satu entri positif pada kolom yang sama (Seneta, 1979). Matriks tak negatif A adalah sebuah matriks persegi berordo n yang setiap entri aij ≥ 0. Matriks tak negatif A
dikatakan primitif jika terdapat bilangan bulat positif k sehingga Ak bernilai
positif. Scrambling index dari matriks tak negatif A primitif adalah bilangan bulat positif terkecil k sedemikian hingga Ak merupakan matriks scrambling.
Termotivasi dari gagasan Seneta diatas, Akelbek dan Kirland memperke-nalkan scrambling index dari digraf primitif D. Suatu digraf primitif D dengan n titik dapat direpresentasikan dalam bentuk matriks ketetanggaan A(D), yaitu matriks berukuran n×n yang setiap entrinya didefinisikan dengan aij = 1 jika
terdapat walk berarah dari titik vi ke titik vj dan aij = 0 jika tidak terdapat
walk berarah dari titik vi ke titik vj. Berdasarkan definisi matriks ketetanggaan
A(D) dapat dilihat bahwa A(D) adalah sebuah matriks tak negatif. Scrambling index dari digraf primitif D bernilai sama dengan scrambling index dari matriks tak negatif A(D).
2
Setelah diperkenalkannya definisi scrambling index, mulai banyak pengem-bangan penelitian mengenai scrambling index. Diawali Akelbek dan Kirland (2009a) mengemukakan batas atas scrambling index dari digraf primitif dengann titik dangirth s. Andaikan D adalah digraf primitif dengann titik dan girth s. Maka k(D) ≤ K(n, s) terpenuhi, jika D = Ds,n dan gcd(s, n) = 1, dimana Ds,n
adalah sebuah digraf dengan sebuah cycle Hamilton v1 → vn → vn−1 → · · · →
v2 → v1 dan sebuah cycle v1 → vs → vs−1 → · · · →v2 → v1 dengan panjang s,
K(n, s) =n−s+k(n, s) dan
k(n, s) =
{
((s−1)/2)n, ketika s ganjil, ((n−1)/2)s, ketika s genap.
Akelbek dan Kirland (2009b) menjelaskan karakteristik dari digraf-digraf primitif dengan scrambling index terbesar. Andaikan D adalah digraf primitif dengan n titik, girth s ≥ 2 dan k(D) = K(n, s), maka memenuhi sifat berikut ini.
1. Tidak terdapatcycle dengan panjang p, s < p < n, sehingga gcd(s, p) = 1.
2. D memuat Ds,n sebagai subgraf dan gcd(s, n) = 1.
Chen dan Liu (2010) menentukan hubungan antara scrambling index dan ekspo-nen dari digraf simetrik primitif D dengan n ≥ 2 titik. Andaikan titik u dan v berada di D, maka ku,v(D) ≤
⌈
expD(u, v)/2⌉
dan k(D) = ⌈
exp(D)/2⌉
, dimana
⌈
a⌉
adalah bilangan bulat terkecil yang tidak kurang dari a.
Liu dan Huang (2010) menentukan scrambling index dari digraf-digraf pri-mitif yang salah satunya adalah digraf pripri-mitif dengan d loop. Andaikan Ln,d
adalah digraf dengan himpunan titik V ={1,2,· · · , n} dan himpunan arc A = {(i, i+ 1)|1 ≤ i ≤ n −1} ∪ {(n,1)} ∪ {(i, i)|n−d ≤ i ≤ n}, dimana n, d ada-lah bilangan bulat dengan n ≥ 2 dan 1 ≤ d ≤ n, maka k(Ln,d) = n−
⌈
d/2⌉
. Selanjutnya, Gao dan Shao (2013) mengemukakan scrambling index dari digraf primitif dengancycle ganjilCn, dimana n≡1 (mod 2), maka k(Cn) = (n−1)/2.
Terlihat bahwa penelitian terdahulu pada umumnya membahas mengenai srcam-bling index dari digraf primitif. Kemudian, Mulyono dan Suwilo (2014) memper-kenalkan gagasan scrambling index dari digraf dwiwarna primitif.
Digraf dwiwarnaD(2) adalah digraf yang mana setiap arcnya diberi warna
merah atau biru (Fornasini dan Valcher, 1997). Digraf dwiwarna D(2) dikatakan
3
b
b b
b
b
b
b
b
b
b
vn
v1
v2
v3
vn−1
vn−2
[image:25.595.231.410.79.244.2]vn−3
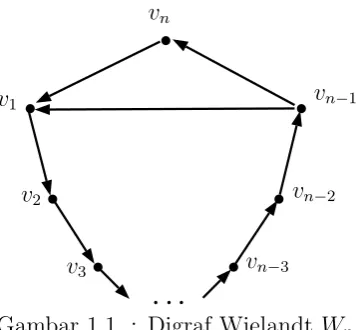
Gambar 1.1 : Digraf Wielandt Wn
terdapat walk berarah dari titik u ke titik v dan walk berarah dari titik v ke titik u. Digraf dwiwarna D(2) terhubung kuat dikatakan primitif dengan syarat
terdapat bilangan bulat tak negatifh danℓ sehingga untuk setiap pasangan titik u dan v di D(2) terdapat walk berarah dari titik u ke titik v dan walk berarah
dari titikv ke titik u dengan panjang h+ℓ. Bilangan bulat positif terkecil h+ℓ merupakan eksponen dari D(2), dinotasikan denganexp(D(2)).
Mulyono dan Suwilo (2014) membahas tentang scrambling index dari digraf Wielandt dwiwarna, yaitu sebuah digraf Hamilton dwiwarna yang terdiri dari cycle Hamilton v1 → v2 → v3 → · · · → vn−1 → vn → v1 dan cycle v1 → v2 →
v3 → · · · →vn−1 →v1 dengan panjangn−1. Representasi grafis digraf Wielandt
Wn dapat dilihat pada Gambar 1.1. AndaikanWn(2) adalah digraf Wielandt
dwi-warna dengan n titik. Scrambling index dari Wn(2) dengan n ≥ 4 ditentukan
berdasarkan posisi dan jumlah arc biru pada Wn(2), diperoleh sebagai berikut:
1. Jika Wn(2) memiliki satu arc biru vx →vx+1, dimana 1≤x ≤n−2, maka
k(Wn(2)) =n2 −2n+ 1−x.
2. Jika Wn(2) memiliki dua arc biru vn−1 → v1 dan vn →v1, maka k(Wn(2)) =
n2 −2n+ 1.
3. JikaWn(2) memiliki duaarcbiruvn−1 →v1 danvn−1 →vn, maka k(Wn(2)) =
n2 −2n+ 2.
Lebih lanjut, penulis akan membahas mengenai scrambling index dari kelas digraf Hamilton dwiwarna dengan n titik ganjil yang terdiri dari cycle Hamilton v1 → v2 → v3 → · · · → vn−1 → vn → v1 dan cycle v1 → v2 → v3 → · · · →
4
1.2 Perumusan Masalah
AndaikanD(2) adalah digraf Hamilton dwiwarna dengann ≥5 titik ganjil terdiri
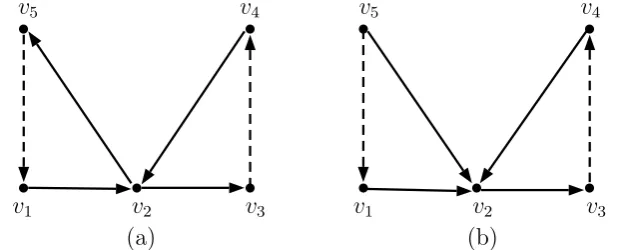
atas cycle Hamilton dan cycle dengan panjang n dan (n−1)/2. Penelitian ini membahas mengenaiD(2)memiliki duaarcbiru, yaituv
x →vx+1dimana 1≤x≤
(n−3)/2 danvy →vy+1dimana (n−1)/2≤y≤ndanD(2)memiliki tigaarcbiru,
yaitu v(n−1)/2 → v1, vx → vx+1, dan vy → vy+1 dimana (n−1)/2≤ x < y ≤ n,
seperti pada Gambar 1.2. Masalah penelitian ini adalah menentukan formula scrambling index yang bergantung pada n titik dan posisi arc biru yang relatif terhadap titik berderajat masuk dua atau v1.
b b b b
b
b
b
b b b b
b
b
b
b
b
b b b b
b b b b b b b b
bb b
bbb
bb b
b b b
v1
v2
v3 v4 vn−7
2 vx
vx+1
vn−1
2
vn+1 2
vy
vy+1
vn−2
vn−1
vn
v1
v2
v3 v4 vn−7
2 v
n−5
2
vn−3
2
vn−1
2
vx
vx+1
vy
vy+1
vn
(a) (b)
[image:26.595.140.502.285.494.2]: arc merah : arc biru
Gambar 1.2 : (a) D(2) dengan 2 arc biru dan (b) D(2) dengan 3 arc biru
1.3 Tujuan Penelitian
Tujuan penelitian ini adalah untuk menentukan scrambling index dari kelas digraf Hamilton dwiwarna dengan n ≥ 5 titik ganjil terdiri atas cycle Hamilton v1 →
v2 → v3 → · · · → vn−1 → vn → v1 dan cycle v1 →v2 →v3 → · · · → v(n−3)/2 → v(n−1)/2 →v1 dengan panjang (n−1)/2.
1.4 Manfaat Penelitian
BAB 2
DIGRAF DWIWARNA PRIMITIF
Pada bab ini akan dibahas mengenai teori-teori yang berhubungan dengan peneli-tian digraf Hamilton dwiwarna dan menjadi landasan berfikir untuk mempermu-dah dalam pembahasan hasil pada bab berikutnya. Adapun teori-teori yang akan dibahas mencakup definisi, primitifitas, scrambling index dan batas scrambling index digraf dwiwarna.
2.1 Definisi Digraf Dwiwarna
Pada subbab ini akan dipaparkan definisi digraf dwiwarna, notasi dan terminologi yang akan digunakan pada pembahasan selanjutnya.
Secara sederhana, suatu digrafD didefinisikan sebagai kumpulan titik ber-hinggaV dan sisi berarah atauarc A. Secara matematika, suatu digrafDadalah sebuah objek yang terdiri atas dua himpunan, yaitu
1. Himpunan berhingga dan tak kosong V = {v1, v2, v3,· · · , vn}, dimana vi
dengani= 1,2,3,· · · , n disebut titik dari digraf D.
2. Himpunan A yang merupakan himpunan bagian dari himpunan V × V. Unsur himpunan A disebut sisi berarah atau arc dari digraf D.
Suatu digraf dwiwarna, dinotasikan dengan D(2), adalah sebuah digraf D yang
setiap arc-nya diberi warna merah atau biru (Fornasini dan Valcher, 1997). Bila a = (vi, vj) ∈ V ×V adalah sebuah arc pada digraf dwiwarna D(2), maka titik
vi disebut sebagai titik asal dan titikvj disebut titik terminal. Suatu a= (vi, vj)
dikatakan arcmerah dinotasikan dengan vi −→vj dana = (vi, vj) dikatakanarc
biru dinotasikan dengan vi − →vj.
Contoh 2.1.1. Himpunan titik V = {v1, v2, v3, v4} bersama dengan himpunan
arc yang terdiri dari himpunan arc merah R = {(v1, v2),(v3, v4),(v4, v1)} dan
himpunan arc biru B = {(v2, v3),(v4, v1)} merupakan sebuah digraf dwiwarna
D(2) dengan 4 titik dan 5 arc. Representasi grafis dari digraf dwiwarna D(2)
6
bc
bc
bc
bc
v1
v2
v3
[image:28.595.248.394.82.199.2]v4
Gambar 2.1 : Digraf dwiwarna dengan 4 titik dan 5arc
Konsep insidensi antara titik dengan arc pada digraf dwiwarna D(2)
di-definisikan sama dengan konsep insidensi pada digraf D. Andaikan a = (vi, vj)
adalah sebuaharcpada digraf dwiwarnaD(2). Titikv
i dikatakan insiden kearc a
dan titikvj dikatakan insiden dariarc a. Sedangkan,arc adikatakan insiden dari
titik vi dan arc a dikatakan insiden ke titik vj. Derajat masuk (indegree) dari
sebuah titik vi, dinotasikan dengan id(vi), adalah banyaknya arc yang insiden
ke titik vi. Derajat keluar (outdegree) dari sebuah titik vi, dinotasikan dengan
od(vi), adalah banyaknya arcyang insiden dari titik vi. Pada Gambar 2.1
perha-tikanarc(v1, v2), maka titikv1insiden ke (v1, v2) dan titikv2 insiden dari (v1, v2).
Selain itu, diperoleh bahwa id(v1) = 2 dan od(v1) = 1, sedangkan id(v2) = 1 dan
od(v2) = 1.
Sebuah (h, ℓ)-walk berarah pada digraf dwiwarna D(2) adalah sebuahwalk
berarah dengan panjangh+ℓyang terdiri darih arcmerah danℓ arcbiru. Notasi vi
(h,ℓ)
−→ vj digunakan untuk menyatakan sebuah (h, ℓ)-walk berarah dari titik vi
ke titik vj. AndaikanW adalah sebuahwalk berarah, banyaknyaarcmerah dari
W dinotasikan dengan r(W) dan banyaknyaarcbiru dariW dinotasikan dengan b(W). Panjang dariW adalahℓ(W) = r(W)+b(W) dan vektor
[
r(W) b(W)
]
adalah
komposisi dari W.
Sebuahwalk berarah yang memuat setiap titik berbeda kecuali pada titik awal dan titik akhir disebut path. Sebuah (h, ℓ)-path adalah sebuah path yang terdiri dari h arc merah dan ℓ arc biru. Notasi Pvi,vj menyatakan terdapat path
dari titikvike titikvj. AndaikanPvi,vj adalah sebuahpath, banyaknyaarcmerah
dari Pvi,vj dinotasikan dengan r(Pvi,vj) dan banyaknya arc biru dari Pvi,vj
dino-tasikan dengan b(Pvi,vj). Vektor [
r(Pvi,vj)
b(Pvi,vj) ]
adalah komposisi dariPvi,vj. P ath
7
Perhatikan Gambar 2.1, akan diperlihatkanwalk,path, dan cycleyang ada pada digraf dwiwarna D(2) tersebut.
1. v1 −→ v2 − → v3 −→ v4 − → v1 −→ v2 − → v3 adalah walk berarah
dengan komposisi
[
3 3
]
dan bukan path karena titik v1, v2, v3 muncul 2
kali.
2. v1 −→v2 − →v3 −→v4 adalahpath dengan komposisi
[
2 1
]
.
3. v1 −→v2 − →v3 −→v4 −→v1 adalah cycle dengan komposisi
[
3 1
]
.
Definisi 2.1.2. Path Hamilton adalah path yang memuat setiap titik yang ada pada digraf dwiwarna D(2) tepat satu kali. Cycle Hamilton adalah cycle yang
melalui setiap titik yang ada pada digraf dwiwarna D(2) tepat satu kali, kecuali
pada titik awal dan titik akhir.
Suatu digraf dwiwarna D(2) yang memuat cycle Hamilton disebut digraf
Hamilton dwiwarna, sedangkan digraf dwiwarna D(2) yang memuat path Hamil-ton disebut digraf semi-HamilHamil-ton dwiwarna.
2.2 Matriks Ketetanggaan Digraf Dwiwarna
Suatu digraf dwiwarna D(2) atas n titik dapat direpresentasikan dalam bentuk
matriks ketetanggaan(adjacency matrix). Matriks ketetanggaan dari suatu digraf dwiwarna D(2) terbagi menjadi dua, yaitu matriks ketetanggaan merah R dan
matriks ketetanggaan biru B.
Matriks ketetanggaan merah dari D(2) adalah matriks bujursangkar R =
(rij) berordon didefinisikan sebagai
rij =
1, jika (vi, vj) adalah arc merah,
0, jika sebaliknya.
Matriks ketetanggaan biru dariD(2) adalah matriks bujursangkarB = (b
ij)
berordo n didefinisikan sebagai
bij =
1, jika (vi, vj) adalah arc biru,
8
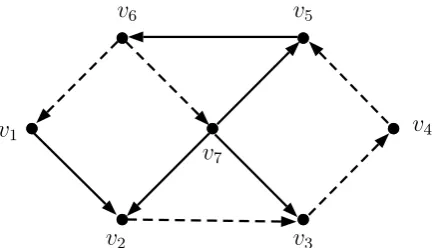
Contoh 2.2.1. Perhatikan digraf dwiwarna D(2) dengan 7 titik dan 10arc
beri-kut ini. bc bc bc bc bc bc bc v1
v2 v3
v4
v5
v6
[image:30.595.212.430.123.247.2]v7
Gambar 2.2 : Digraf dwiwarna dengan 7 titik dan 10 arc
Matriks ketetanggaan merah dan biru dari Gambar 2.2 adalah sebagai berikut. R =
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0
dan B =
0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0
.
Suatu matriks bujursangkarM = (mij) berordon, untuk setiap i, j = 1,2, . . . , n,
dikatakan matriks tak negatif jikamij merupakan bilangan bulat tak negatif dan
dikatakan matriks positif jika mij merupakan bilangan bulat positif.
Contoh 2.2.2. Berikut diperlihatkan contoh matriks tak negatif dan matriks positif.
Matriks M =
1 0 5 3 2 7 6 0 9
adalah matriks tak negatif.
Matriks M =
2 3 5 1 9 6 8 7 4
adalah matriks positif.
2.3 Primitifitas Digraf Dwiwarna
Suatu digraf dwiwarna D(2) dikatakan terhubung kuat (strongly connected)
apa-bila digraf dari D(2), tanpa memperhatikan warna setiap arc, adalah terhubung
9
dan titik vj terdapatwalk berarah dari titikvi ke titikvj dan walk berarah dari
titik vj ke titik vi. Terdapat sifat khusus dari digraf dwiwarna D(2) terhubung
kuat yang berkaitan dengan keberadaan cycle.
Proposisi 2.3.1. AndaikanD(2) adalah sebuah digraf dwiwarna terhubung kuat.
Setiap titik di D(2) terletak pada sebuah cycle.
Bukti. Andaikan vi adalah sebarang titik di D(2). Dapat dibentuk sebuah cycle
yang memuat titikvi. KarenaD(2) terhubung kuat, maka terdapat titikvj diD(2)
sehingga (vi, vj) adalah sebuaharcdiD(2). KarenaD(2)terhubung kuat, terdapat
sebuahpath Pvi,vj dari titikvike titikvj. Sekarangarc(vi, vj) dilanjutkan dengan
path Pvi,vj adalah sebuah cycle yang memuat titik vi.
Berikut diperlihatkan contoh digraf dwiwarna D(2) terhubung kuat dan
tidak terhubung kuat.
b
b b b
b b
b b b
b
v1 v2 v3 v1 v2 v3
v4
v5 v5 v4
[image:31.595.165.475.340.465.2](a) (b)
Gambar 2.3 : (a) D(2) terhubung kuat, (b) D(2) tidak terhubung kuat
Gambar 2.3(a) merupakan digraf dwiwarna D(2) terhubung kuat karena
terdapat walk berarah yang menghubungkan setiap pasangan titik di D(2) atau
berdasarkan Proposisi 2.3.1 setiap titik berada pada sebuah cycle, sedangkan Gambar 2.3(b) merupakan digraf dwiwarna D(2) tidak terhubung kuat karena
tidak terdapat walk berarah yang menghubungkan titik v2 ke titikv5 atau
ber-dasarkan Proposisi 2.3.1 titik v1 dan v5 tidak berada pada sebuah cycle.
Suatu digraf dwiwarnaD(2) terhubung kuat dikatakan primitif dengan
sya-rat terdapat bilangan bulat tak negatif h dan ℓ sehingga untuk setiap pasangan titik vi dan vj di D(2) terdapat vi
(h,ℓ)
−→vj walk dan vj
(h,ℓ)
−→vi walk. Bilangan
bu-lat tak negatif h+ℓ terkecil merupakan eksponen dari D(2), dinotasikan dengan
exp(D(2)).
Andaikan D(2) adalah digraf dwiwarna dan andaikan C ={C
10
sebagai matriks 2×q yang mana kolom ke-i adalah komposisi dari cycle Ci, i=
1,2, . . . , q yaitu sebagai berikut
M =
[
r(C1) r(C2) · · · r(Cq)
b(C1) b(C2) · · · b(Cq) ]
.
Jika M memiliki rank 1, maka content dari M adalah 0 dan content dari M didefinisikan sebagai pembagi bersama terbesar dari determinan submatriks 2× 2 dari M. Berikut diberikan karakteristik dari sebuah digraf dwiwarna D(2)
primitif.
Teorema 2.3.2. (Fornasini dan Valcher, 1998) AndaikanD(2) adalah digraf
dwiwarna terhubung kuat dengan paling sedikit satuarcsetiap warna dan andaikan M adalah matriks cycle dari D(2). Digraf dwiwarna D(2) dikatakan primitif jika
dan hanya jika content dari M adalah 1.
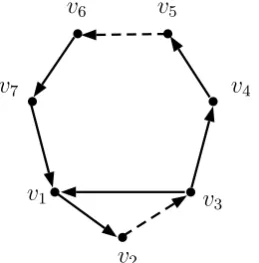
Contoh 2.3.3. Perhatikan digraf dwiwarna D(2) terhubung kuat pada Gambar
2.4. Digraf dwiwarna D(2) tersebut terdiri atas dua cycle sehingga diperoleh
matriks cycle M sebagai berikut.
M =
[
r(C1) r(C2)
b(C1) b(C2)
]
=
[
5 2 2 1
]
karena det(M) = 1, berdasarkan Teorema 2.3.2 maka digraf dwiwarna D(2)
ter-sebut adalah primitif.
b b
b
b
b
b
b
v1
v2
v3
v4
v5
v6
[image:32.595.257.387.500.632.2]v7
Gambar 2.4 : Digraf dwiwarna D(2) terhubung kuat primitif
AndaikanD(2) adalah digraf dwiwarna terhubung kuat dengan n titik.
Un-tuk sebarang pasangan matriks tak negatif (A, B) berukuran n×n dapat dite-mukan digraf dwiwarnaD(2)atasntitik yang berhubungan dengan (A, B) sebagai
berikut. Sebuah (vi, vj) diD(2) adalaharcmerah jika dan hanya jika aij >0 dan
11
Untuk sebarang pasangan matriks tak negatif (A, B), suatu (h, ℓ)-Hurwitz productdari matriksAdanB, dinotasikan dengan (A, B)(h,ℓ), didefinisikan secara
rekursif sebagai berikut. Untuk sebarang bilangan bulat tak negatif h ≥ 1 dan ℓ≥1, (A, B)(h,0) =Ah,(A, B)(0,ℓ) =Bℓ, dan
(A, B)(h,ℓ) =A(A, B)(h−1,ℓ)+B(A, B)(h,ℓ−1).
Lemma 2.3.4. AndaikanD(2)adalah digraf dwiwarna denganntitik dan andaikan
R danB adalah matriks ketetanggaan merah dan biru dariD(2). Maka entri (i, j)
dari (R, B)(h,ℓ) adalah banyaknya (h, ℓ)-walk dari titik v
i ke titik vj.
Bukti. Akan dibuktikan induksi pada (h+ℓ) dan (h+ℓ+ 1), jika h = 0 maka ℓ= 1 atau jikah= 1 makaℓ = 0. Jikah= 0 maka entri (i, j) dari (R, B)(0,1) =B
adalah walk dengan kompisisi
[
0 1
]
. Dengan cara yang sama, jika ℓ = 0 maka
entri (i, j) dari (R, B)(1,0) =R adalah walk dengan kompisisi
[
1 0
]
diD(2).
Asumsikan Lemma 2.3.4 adalah benar untuk bilangan bulat tak negatif h′ dan ℓ′
dengan h′ +ℓ′
≤ h+ℓ, akan diperlihatkan untuk h+ℓ+ 1 adalah benar dengan catatan sebagai berikut.
(R, B)(h+1,ℓ)=R(R, B)(h,ℓ)+B(R, B)(h+1,ℓ−1).
Berdasarkan hipotesis induksi, entri (i, j) pada R(R, B)(h,ℓ) adalah walk dari
ti-tik vi ke titikvj yang dimulai denganarc merah dan diikuti oleh (h, ℓ)-walk dan
entri (i, j) padaB(R, B)(h+1,ℓ−1) adalahwalk dari titikv
i ke titikvj yang dimulai
denganarcbiru dan diikuti oleh (h+ 1, ℓ−1)-walk sedemikian hingga entri (i, j) dariR(R, B)(h+1,ℓ) adalah banyaknya (h+ 1, ℓ)-walk dari titikv
i ke titikvj. Jadi,
entri (i, j) pada (R, B)(h,ℓ)adalah banyaknya (h, ℓ)-walkdari titikv
i ke titikvj.
2.4 Scrambling Index Digraf Dwiwarna
AndaikanD(2)adalah digraf dwiwarna primitif dan andaikan titikv
idanvj adalah
dua titik berbeda di D(2). Scrambling index lokal dari titik v
i dan vj di titik
vt ∈ V(D(2)), kvi,vj(vt), adalah bilangan bulat positif terkecil h+ℓ dari seluruh
pasangan bilangan bulat tak negatif (h, ℓ) sedemikian hingga terdapat sebuah vi
(h,ℓ)
−→vt walk dan vj
(h,ℓ)
12
D(2) didefinisikan sebagai,
kvi,vj(D
(2)) = min
vt∈V(D(2)){kvi,vj(vt)}.
Scrambling index dari D(2), dinotasikan dengan k(D(2)), adalah bilangan bulat
positif terkecil h+ℓ dari seluruh pasangan bilangan bulat tak negatif (h, ℓ) se-demikian hingga untuk setiap pasangan titik vi dan vj di D(2) terdapat sebuah
titik vt dengan sifat bahwa terdapat vi
(h,ℓ)
−→vt walk dan vj
(h,ℓ)
−→vt walk.
Berdasarkan definisi scrambling index, diperoleh hubungan sebagai berikut
max
vi,vj∈V(D(2)){kvi,vj(D
(2))} ≤k(D(2)).
Contoh 2.4.1. Representasi digraf dwiwarnaD(2) primitif dengan 3 titik, 2arc
merah, dan 2 arc biru seperti pada Gambar 2.5. Scrambling index lokal dari digraf dwiwarna D(2) tersebut sebagai berikut.
kv1,v2(D
(2)) = min{k
v1,v2(v1), kv1,v2(v2), kv1,v2(v3)}
= min{(1,1),(2,1),(3,1)}= min{2,3,4}= 2, kv1,v3(D
(2)) = min{k
v1,v3(v1), kv1,v3(v2), kv1,v3(v3)}
= min{(2,2),(3,2),(4,2)}= min{4,5,6}= 4, kv2,v3(D
(2)) = min{k
v2,v3(v1), kv2,v3(v2), kv2,v3(v3)}
= min{(0,1),(1,1),(2,1)}= min{1,2,3}= 1.
Dari definisi, maka diperolehk(D(2))≥max{k
v1,v2(D
(2)), k
v1,v3(D
(2)), k
v2,v3(D
(2))}
= max{2,4,1}= 4 dengan komposisi 2 arc merah dan 2 arc biru.
Selanjutnya, akan diperlihatkan bahwak(D(2))≤4 dengan komposisi 2arc
merah dan 2 arc biru, yaitu akan diperlihatkan untuk setiap dua pasang titik (vi, vj) yang berbeda diD(2) terdapat titikvtdiD(2) sedemikian hingga terdapat
vi
(2,2)
−→ vt walk dan vj
(2,2)
−→ vt walk. Pada Contoh 2.4.1, diperoleh setiap dua
pasang titik yang berbeda, yaitu (v1, v2),(v2, v3),(v1, v3) di D(2).
1. Untuk pasangan titik (v1, v2) terdapatv1sedemikian hingga terdapatv1 (2,2)
−→ v1 walk dan v2
(2,2)
−→v1 walk, yaitu
v1 −→v2 − →v1 −→v2 − →v1 dan v2 −→v3 − →v1 −→v2 − →v1.
2. Untuk pasangan titik (v1, v3) terdapatv1sedemikian hingga terdapatv1 (2,2)
−→ v1 walk dan v3
(2,2)
−→v1 walk, yaitu
13
b
b
b
v1 v2
v3
Gambar 2.5 : Digraf dwiwarna D(2) primitif
3. Untuk pasangan titik(v2, v3) terdapatv1 sedemikian hingga terdapatv2 (2,2)
−→ v1 walk dan v3
(2,2)
−→v1 walk, yaitu
v2 −→v3 − →v1 −→v2 − →v1 dan v3 − →v1 −→v2 −→v3 − →v1.
Telah diperlihatkan bahwak(D(2))≤4 dan k(D(2))≥4 dengan kompisisi 2
arc merah dan 2 arc biru. Jadi, dapat disimpulkan scrambling index dari digraf dwiwarna D(2) primitif pada Gambar 2.5 adalah 4.
Berdasarkan Lemma 2.3.4, scrambling index dari suatu digraf dwiwarna D(2) primitif dapat dicari dengan menggunakan (h, ℓ)-Hurwitz productdari
mat-riks ketetanggaan merah R dan matriks ketetanggaan biru B. Jika untuk setiap dua baris pada (R, B)(h,ℓ) terdapat paling sedikit satu entri bernilai positif pada
kolom yang sama, maka k(D(2)) =h+ℓ.
Contoh 2.4.2. Matriks ketetanggaan merah dan biru dari digraf dwiwarna D(2)
primitif pada Gambar 2.5 diberikan sebagai berikut.
R =
0 1 0 0 0 1 0 0 0
dan B =
0 0 0 1 0 0 1 0 0
,
maka untuk h+ℓ= 1, diperoleh
1. (R, B)(1,0) =R=
0 1 0 0 0 1 0 0 0
.
Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama
dengan 1 karena baris pertama dan baris kedua pada matriks (R, B)(1,0)
tidak memiliki entri positif pada kolom yang sama.
2. (R, B)(0,1) =B =
0 0 0 1 0 0
14
Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama
dengan 1 karena baris pertama dan baris kedua pada matriks (R, B)(0,1)
tidak memiliki entri positif pada kolom yang sama.
Untuk h+ℓ= 2, diperoleh
1. (R, B)(2,0) =R2 =
0 0 1 0 0 0 0 0 0
.
Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama
dengan 2 karena baris pertama dan baris kedua pada matriks (R, B)(2,0)
tidak memiliki entri positif pada kolom yang sama.
2. (R, B)(0,2) =B2 =
0 0 0 0 0 0 0 0 0
.
Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama
dengan 2 karena untuk setiap dua baris pada matriks (R, B)(0,2) tidak memiliki entri positif pada kolom yang sama.
3. (R, B)(1,1) =R(R, B)(0,1)+B(R, B)(1,0) =
1 0 0 1 1 0 0 1 0
.
Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama dengan 2 karena baris pertama dan baris ketiga pada matriks (R, B)(1,1)
tidak memiliki entri positif pada kolom yang sama.
Untuk h+ℓ= 3, diperoleh
1. (R, B)(3,0) =R3 =
0 0 0 0 0 0 0 0 0
.
Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama
dengan 3 karena untuk setiap dua baris pada matriks (R, B)(3,0) tidak
memiliki entri positif pada kolom yang sama.
2. (R, B)(0,3) =B3 =
0 0 0 0 0 0 0 0 0
.
Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama
dengan 3 karena untuk setiap dua baris pada matriks (R, B)(0,3) tidak
15
3. (R, B)(2,1) =R(R, B)(1,1)+B(R, B)(2,0) =
1 1 0 0 1 1 0 0 1
.
Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama
dengan 3 karena baris pertama dan baris ketiga pada matriks (R, B)(2,1)
tidak memiliki entri positif pada kolom yang sama.
4. (R, B)(1,2) =R(R, B)(0,2)+B(R, B)(1,1) =
0 0 0 1 0 0 1 0 0
.
Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama
dengan 3 karena baris pertama dan baris kedua pada matriks (R, B)(1,2)
tidak memiliki entri positif pada kolom yang sama.
Untuk h+ℓ= 4, diperoleh
1. (R, B)(4,0) =R4 =
0 0 0 0 0 0 0 0 0
.
Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama
dengan 4 karena untuk setiap dua baris pada matriks (R, B)(4,0) tidak
memiliki entri positif pada kolom yang sama.
2. (R, B)(0,4) =B4 =
0 0 0 0 0 0 0 0 0
.
Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama
dengan 4 karena untuk setiap dua baris pada matriks (R, B)(0,4) tidak
memiliki entri positif pada kolom yang sama.
3. (R, B)(3,1) =R(R, B)(2,1)+B(R, B)(3,0) =
0 1 1 0 0 1 0 0 0
.
Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama
dengan 4 karena baris pertama dan baris ketiga pada matriks (R, B)(3,1) tidak memiliki entri positif pada kolom yang sama.
4. (R, B)(1,3) =R(R, B)(0,3)+B(R, B)(1,2) =
0 0 0 0 0 0 0 0 0
.
Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama dengan 4 karena untuk setiap dua baris pada matriks (R, B)(1,3) tidak
16
5. (R, B)(2,2) =R(R, B)(1,2)+B(R, B)(2,1) =
1 0 0 2 1 0 1 1 0
.
Scrambling index dari digraf dwiwarnaD(2) pada Gambar 2.5 sama dengan
4 karena untuk setiap dua baris pada (R, B)(2,2) terdapat paling sedikit satu
entri positif pada kolom yang sama. Jadi, diperoleh k(D(2)) = 4 dengan
komposisi [ 2 2 ] .
2.5 Batas Scrambling Index Digraf Dwiwarna
Pada subbab ini akan dibahas mengenai batas atas dan batas bawah untuk scram-bling index dari digraf dwiwarna D(2) primitif, terkhusus digraf dwiwarna D(2)
primitif yang terdiri atas dua cycle (Mulyono dan Suwilo, 2014).
Setiapwalkberarah pada suatu digraf dwiwarnaD(2) dapat diuraikan
men-jadi sebuahpath dan beberapacycle. Hal ini berarti untuk setiapvi
(h,ℓ)
−→vj walk
memiliki hubungan sebagai berikut.
[ h ℓ ] = [
r(Pvi,vj)
b(Pvi,vj) ]
+z1
[
r(C1)
b(C1)
]
+z2
[
r(C2)
b(C2)
]
+· · ·+zq [
r(Cq)
b(Cq) ]
=
[
r(Pvi,vj)
b(Pvi,vj) ]
+Mz
untuk beberapa path Pvi,vj dari titik vi ke titik vj dan beberapa vektor bilangan
bulat tak negatif z.
Proposisi berikut ini digunakan untuk menentukan batas atas scrambling index digraf dwiwarna.
Proposisi 2.5.1. (Mulyono dan Suwilo, 2014) Andaikan D(2) adalah digraf
dwiwarna primitif yang terdiri atas dua cycle C1 dan C2. Andaikan vj adalah
sebuah titik yang berada pada kedua cycle. Jika untuk beberapa bilangan bulat positif h dan ℓ, terdapat sebuah path Pvi,vj dari titik vi ke titik vj sedemikian
hingga sistem
Mz+
[
r(Pvi,vj)
b(Pvi,vj) ] = [ h ℓ ] (2.1)
17
Bukti. Asumsikan bahwa solusi dari sistem (2.1) adalah z =
[
z1
z2
]
. Terdapat
empat kemungkinan nilai z1 dan z2 sebagai berikut.
Jika z1 > 0 dan z2 >0, maka walk berarah bergerak mulai dari titik vi ke
vj melalui sepanjang (r(Pvi,vj), b(Pvi,vj))-path Pvi,vj dan akhirnya bergerak
meng-elilingicycle C1 sebanyak z1 kali dan bergerak mengelilingi cycle C2 sebanyak z2
kali, dan kembali ke titikvj adalah sebuah (h, ℓ)-walk berarah dari titikvi kevj.
Jika z1 = 0 dan z2 >0, maka walk berarah bergerak mulai dari titik vi ke
vj melalui sepanjang (r(Pvi,vj), b(Pvi,vj))-path Pvi,vj dan akhirnya bergerak
meng-elilingi cycle C2 sebanyak z2 kali. Dengan cara yang sama, Jika z1 > 0 dan
z2 = 0, maka walk berarah bergerak mulai dari titik vi ke vj melalui sepanjang
(r(Pvi,vj), b(Pvi,vj))-path Pvi,vj dan akhirnya bergerak mengelilingi cycle C1
seba-nyak z1 kali dan kembali ke titikvj adalah sebuah (h, ℓ)-walk berarah dari titik
vi ke vj.
Jika z1 = z2 = 0, maka (r(Pvi,vj), b(Pvi,vj))-path Pvi,vj dari titik vi ke vj
adalah sebuah (h, ℓ)-walk berarah.
Lemma berikut ini digunakan untuk menentukan batas bawah scrambling index digraf dwiwarna. Didefinisikan bahwa ℓ(C1) adalah panjang dari cycle C1
dan ℓ(C2) adalah panjang dari cycle C2.
Lemma 2.5.2. (Mulyono et al. 2015) AndaikanD(2) adalah digraf dwiwarna
primitif yang terdiri atas dua cycle C1 dan C2 dengan matriks cycle
M =
[
r(C1) r(C2)
b(C1) b(C2)
]
,
dan andaikan vi dan vj adalah sebarang dua titik yang berbeda di D(2). Jika
kvi,vj(vt) diperoleh dari sebuah (h, ℓ)-walk berarah, maka
[
h ℓ
]
≥M
[
b(C2)r(Pvi,vt)−r(C2)b(Pvi,vt)
r(C1)b(Pvj,vt)−b(C1)r(Pvj,vt) ]
.
Oleh karena itu,
kvi,vj(vt)≥ℓ(C1)[b(C2)r(Pvi,vt)−r(C2)b(Pvi,vt)]+ℓ(C2)[r(C1)b(Pvj,vt)−b(C1)r(Pvj,vt)]
18
Bukti. KarenaD(2) adalah primitif, maka berdasarkan Teorema 2.3.2 diperoleh
det(M) = 1 atau det(M) = −1. Tanpa menghilangkan keumuman diasumsikan bahwa det(M) = 1. Karena det(M) = 1, terdapat bilangan bulat e1 dan e2
sedemikian hingga [ h ℓ ] =M [ e1 e2 ] . (2.2)
Karena setiap walk berarah dapat diuraikan menjadi sebuah path dan beberapa cycle, maka [ h ℓ ] = [
r(Pvi,vt)
b(Pvi,vt) ]
+Mz, (2.3)
untuk beberapa path Pvi,vt dari titik vi kevt dan beberapa vektor bilangan bulat
tak negatif z. Bandingkan persamaan (2.2) dan (2.3), maka diperoleh
z=
[
e1
e2
]
−M−1
[
r(Pvi,vt)
b(Pvi,vt) ]
≥0.
Oleh karena itu,
[
e1
e2
]
≥M−1
[
r(Pvi,vt)
b(Pvi,vt) ]
=
[
b(C2)r(Pvi,vt)−r(C2)b(Pvi,vt)
r(C1)b(Pvi,vt)−b(C1)r(Pvi,vt) ]
.
Sehingga, diperolehe1 ≥b(C2)r(Pvi,vt)−r(C2)b(Pvi,vt) untuk beberapapath Pvi,vt
dari titik vi ke vt dan e2 ≥ r(C1)b(Pvj,vt)−b(C1)r(Pvj,vt) untuk beberapa path
Pvj,vt dari titikvj ke vt. Jika kvi,vj(vt) diperoleh dari sebuah (h, ℓ)-walk berarah,
maka [ h ℓ ] =M [ e1 e2 ] ≥M [
b(C2)r(Pvi,vt)−r(C2)b(Pvi,vt)
r(C1)b(Pvj,vt)−b(C1)r(Pvj,vt) ]
dan diperoleh
kvi,vj(vt)≥ℓ(C1)[b(C2)r(Pvi,vt)−r(C2)b(Pvi,vt)]+ℓ(C2)[r(C1)b(Pvj,vt)−b(C1)r(Pvj,vt)]
BAB 3
METODOLOGI PENELITIAN
Metodologi penelitian yang dilakukan untuk mendapatkan scrambling index dari digraf Hamilton dwiwarnaD(2) adalah dengan studi penelahaan terhadap
jurnal-jurnal dan buku yang berkaitan dengan teori graf dan scrambling index. Adapun langkah-langkah yang dilakukan dalam penelitian ini sebagai berikut.
1. Menentukan primitifitas digraf dwiwarna
Penelitian ini membahas digraf Hamilton dwiwarna D(2) terdiri atas dua
cycle dengan panjang n dan (n−1)/2. Akan dicari matriks cycle M dari D(2)
sehingga berdasarkan Teorema 2.3.2 content dari matriks cycle M adalah 1. Dengan kata lain, diketahui
M =
[
n−a (n−1)/2−b
a b
]
akan ditentukan nilai a danb sedemikian hingga det(M) = 1 atau det(M) =−1.
2. Komputasi nilai scrambling index
Terdapat dua cara untuk menghitung scrambling index dariD(2). Pertama,
dengan menggunakan sof twareMATLAB akan diperolehh+ℓ, sehinggak(D(2))
= h+ℓ. Berikut algoritma program scrambling index dari D(2) dengan n ≥ 5
titik ganjil.
1. Menginput matriks ketetanggaan dari D(2), yaitu matriks ketetanggaan
merah R dan matriks ketetanggaan biru B.
2. Menghitung (h, ℓ)-Hurwitz product, (R, B)(h,ℓ), dari matriks ketetanggaan
merah R dan matriks ketetanggaan biru B.
3. Jika untuk setiap dua baris pada (R, B)(h,ℓ) sedikitnya terdapat satu entri
bernilai positif pada kolom yang sama, makak(D(2)) =h+ℓ.
20
Lemma 2.5.2, diketahui bahwa
[
h ℓ
]
≥M
[
b(C2)r(Pvi,vt)−r(C2)b(Pvi,vt)
r(C1)b(Pvj,vt)−b(C1)r(Pvj,vt) ]
dengane1 =b(C2)r(Pvi,vt)−r(C2)b(Pvi,vt) dane2 =r(C1)b(Pvj,vt)−b(C1)r(Pvj,vt),
agar mendapatkanh+ℓ, maka harus dicari nilaie1 dan e2 yaitu dengan mencari
path Pvi,vt dari titik vi ke titik vt yang memuat arc merah paling banyak dan
sedikit arc biru dan mencaripath Pvj,vt dari titik vj ke titikvt yang memuatarc
biru paling banyak dan sedikit arc merah. Karena digraf Hamilton dwiwarna D(2) memuat dua cycle, maka terdapat paling banyak dua kemungkinan path
Pvi,vt dan path Pvj,vt. Apabila terdapat dua path Pvi,vt dari titik vi ke titik vt,
maka e1 = min{b(C2)r(Pvi,vt)−r(C2)b(Pvi,vt)}. Apabila terdapat dua path Pvj,vt
dari titik vj ke titik vt, maka e2 = min{r(C1)b(Pvj,vt)−b(C1)r(Pvj,vt)}. Karena
nilai e1 dan e2 yang dipilih bernilai kecil, maka akan menghasilkan h+ℓ yang
bernilai kecil. Setelah diperolehkvi,vj(vt) = h+ℓuntuk setiap titik vt∈V(D
(2)),
maka k(D(2)) = min{k
vi,vj(vt)}.
Selanjutnya, menentukan bentuk umum formula scrambling index dari digraf Hamilton dwiwarna D(2) dengan n ≥ 5 titik ganjil berdasarkan komputasi nilai
scrambling index yang diperoleh.
3. Pembuktian formula scrambling index
Pembuktian formula scrambling dengan cara menentukan batas atas dan batas bawah dari dcrambling index tersebut. Berdasarkan Proposisi 2.5.1 akan diperlihatkan bahwak(D(2))≤h+ℓ dan berdasarkan Lemma 2.5.2 akan
BAB 4
SCRAMBLING INDEX DIGRAF HAMILTON DWIWARNA
Pada bab ini akan dipaparkan hasil dari penelitian ini, yaitu primitifitas dari digraf Hamilton dwiwarna yang terdiri atas dua cycle dan formula scrambling index yang bergantung pada n titik dan posisi arc biru yang relatif terhadap titik berderajat masuk dua atau v1.
Andaikan D(2) adalah digraf Hamilton dwiwarna primitif dengan n titik
ganjil yang memuat cycle Hamilton v1 → v2 → · · · → vn−1 → vn → v1 dan cycle v1 → v2 → · · · → v(n−3)/2 → v(n−1)/2 → v1 dengan panjang (n− 1)/2. AndaikanC1 dan C2 adalah duacycleyang terdapat padaD(2). Didefinisikan C1
adalah cycle Hamilton v1 → v2 → · · · → vn−1 → vn → v1 dan C2 adalah cycle
v1 →v2 → · · · →v(n−3)/2 →v(n−1)/2 →v1. Akibat dari Teorema 2.3.2, diperoleh
karakteristik primitifitas dari D(2) sebagai berikut.
Corollary 4.1. Andaikann ≥5adalah bilangan ganjil dan andaikanD(2) adalah
digraf Hamilton dwiwarna primitif atas n titik yang memuat C1 dan C2 dengan
panjang n dan(n−1)/2. Matrikscycle M dariD(2) adalah salah satu dari kedua
bentuk berikut.
M =
[
n−2 (n−3)/2
2 1
]
atau M =
[
2 1
n−2 (n−3)/2
]
.
Bukti. Matriks cycle dari D(2) adalah M =
[
n−a (n−1)/2−b
a b
]
dimana
0 ≤ a ≤ n dan 0 ≤ b ≤ (n −1)/2. Berdasarkan asumsi D(2) adalah primitif,
maka det(M) = 1 atau det(M) =−1.
1. Jika det(M) = 1 diperoleh ((2b−a)n+a)/2 = 1, agar memenuhi 0≤a≤n, maka 2b−a = 0. Oleh karena itu, diperoleh a= 2 danb = 1.
2. Jika det(M) = −1 diperoleh ((2b − a)n +a)/2 = −1, agar memenuhi 0 ≤ a ≤ n, maka 2b−a = −1. Oleh karena itu, diperoleh a = n−2 dan b= (n−3)/2.
mat-22
M =
[
n−2 (n−3)/2
2 1
]
atau M =
[
2 1
n−2 (n−3)/2
]
.
Pada dasarnya, kedua matriks cycle M yang diperoleh pada Corollary 4.1 hanya mengganti arc merah dengan arc biru dan arc biru dengan arc merah. Scrambling index merupakan jumlahan dari banyak arc merah dan banyak arc biru sehingga mempertukarkanarc merah denganarcbiru atau sebaliknya tidak akan mempengaruhi nilai scrambling index yang diperoleh. Oleh karena itu, kedua matriks cycle M tersebut memiliki scrambling index yang sama. Pada pe-nelitian ini, matrikscycle M yang digunakan adalahM =
[
n−2 (n−3)/2
2 1
]
.
Corollary 4.1 menyatakan bahwa D(2) memiliki dua arc biru atau tiga arc
biru. Scrambling index dari D(2) ditentukan berdasarkan jumlah arc biru yang
terdapat pada digraf dwiwarna tersebut. Pertama, akan dibahas D(2) memiliki
dua arcbiru yang didefinisikan sebagaivx →vx+1 dimana 1≤x≤(n−3)/2 dan
vy →vy+1 dimana (n−1)/2≤y≤n, seperti pada Gambar 1.2(a). Didefinisikan
d(vi, vj) adalah panjang walk berarah terpendek dari titik vi ke titik vj. Pada
penelitian ini, didefinisikan d1 =d(vy+1, v1) dan d2 = (vx+1, v1) dan diasumsikan
vn+1 =v1.
Teorema 4.2. Andaikan D(2) adalah digraf Hamilton dwiwarna primitif dengan
n ≥ 5 titik ganjil terdiri atas cycle Hamilton v1 →v2 → · · · → vn−1 → vn → v1
dan cycle v1 → v2 → v3 → · · · → v(n−3)/2 → v(n−1)/2 → v1 dengan panjang
(n−1)/2. Jika D(2) memiliki dua arc biru, maka
1. k(D(2)) = (n2+n(2d
1−2d2−4) + 2d2+ 3)/2 ketika d1 > d2.
2. k(D(2)) = (n2+n(2d
2−2d1−3) + 2d1+ 2)/2 ketika d1 ≤d2.
Bukti. Terdapat dua keadaan kasus dimana d1 > d2 dan d1 ≤d2.
Kasus 1. d1 > d2
Berikut ini akan dibuktikan bahwak(D(2)) = (n2+n(2d
1−2d2−4) + 2d2+ 3)/2.
Pertama, akan diperlihatkan bahwak(D(2))≥(n2+n(2d
1−2d2−4) + 2d2+ 3)/2.
Asumsikan bahwa kvy+1,vx(vt) diperoleh dari (h, ℓ)-walk berarah dan asumsikan
terdapat vy+1 (h,ℓ)
−→vt walk dan vx
(h,ℓ)
−→vt walk. Andaikan
23
dan
e2 =r(C1)b(Pvx,vt)−b(C1)r(Pvx,vt). (4.2)
Terdapat tiga kemungkinan posisi titik vt sebagai berikut.
1. Titikvt terletak padav1 →vx path.
Terdapat sebuahpathPvy+1,vt dari titikvy+1ke titikvtyaitu (d1+d(v1, vt),0)-path.
Dengan menggunakan path ini dan persamaan (4.1), diperoleh
e1 = (1)(d1+d(v1, vt))−((n−3)/2)(0) =d1+d(v1, vt). (4.3)
Terdapat dua path Pvx,vt dari titik vx ke titik vt yaitu (d2+d(v1, vt),1)-path dan
((n−1)/2 +d2+d(v1, vt),2)-path. Dengan menggunakan (d2 +d(v1, vt),1)-path
dan persamaan (4.2), diperoleh
e2 = (n−2)(1)−(2)(d2+d(v1, vt)) =n−2−2d2−2d(v1, vt). (4.4)
Dengan menggunakan ((n−1)/2 + d2 +d(v1, vt),2)-path dan persamaan (4.2),
diperoleh
e2 = (n−2)(2)−(2)((n−1)/2 +d2+d(v1, vt))
=n−3−2d2−2d(v1, vt). (4.5)
Pilih nilai e2 yang lebih kecil yaitu pada persamaan (4.5). Berdasarkan Lemma
2.5.2, diperoleh
kvy+1,vx(vt)≥ℓ(C1)e1+ℓ(C2)e2
= (n)(d1+d(v1, vt)) + ((n−1)/2)(n−3−2d2−2d(v1, vt))
= (n2+n(2d1−2d2−4) + 2d2+ 3)/2 +d(v1, vt) (4.6)
untuk setiap titik vt terletak pada v1 →vx path.
2. Titikvt terletak padavx+1 →vy path.
Terdapat sebuahpath Pvy+1,vt dari titikvy+1ke titikvtyaitu (d1+d(v1, vt)−1,
1)-path. Dengan menggunakanpath ini dan persamaan (4.1), diperoleh
e1 = (1)(d1+d(v1, vt)−1)−((n−3)/2)(1)
24
Terdapat sebuah path Pvx,vt dari titik vx ke titik vt yaitu (d2+d(v1, vt)−(n−
1)/2,1)-path. Dengan menggunakan path ini dan persamaan (4.2), diperoleh
e2 = (n−2)(1)−(2)(d2+d(v1, vt)−(n−1)/2)
= 2n−3−2d2−2d(v1, vt). (4.8)
Berdasarkan Lemma 2.5.2, diperoleh
kvy+1,vx(vt)≥ℓ(C1)e1+ℓ(C2)e2
= (n)(d1+d(v1, vt)−(n−1)/2) + ((n−1)/2)(2n−3−2d2−2d(v1, vt))
= (n2+n(2d1−2d2−4) + 2d2+ 3)/2 +d(v1, vt) (4.9)
untuk setiap titik vt terletak pada vx+1 →vy path.
3. Titikvt terletak padavy+1 →vn path.
Terdapat sebuahpathPvy+1,vt dari titikvy+1ke titikvtyaitu (d1+d(vt, v1),0)-path.
Dengan menggunakan path ini dan persamaan (4.1), diperoleh
e1 = (1)(d1+d(vt, v1))−((n−3)/2)(0) =d1+d(vt, v1). (4.10)
Terdapat sebuah path Pvx,vt dari titik vx ke titik vt yaitu (d2 +d(vt, v1) + (n−
1)/2,2)-path. Dengan menggunakan path ini dan persamaan (4.2), diperoleh
e2 = (n−2)(2)−(2)(d2+d(vt, v1) + (n−1)/2)
=n−3−2d2+ 2d(vt, v1). (4.11)
Berdasarkan Lemma 2.5.2, diperoleh
[
h ℓ
]
≥
[
(n2+n(2d
1−2d2−6)−4d1 + 6d2+ 9)/2−d(vt, v1)
n−3 + 2d1−2d2
]
.
Perhatikanvy+1 →vtwalk. Karena menggunakan (d1−d(vt, v1),0)-pathdiperoleh
solusi dari sistem
Mz+
[
r(Pvy+1,vt)
b(Pvy+1,vt) ]
=
[
(n2+n(2d
1−2d2−6)−4d1+ 6d2+ 9)/2−d(vt, v1)
n−3 + 2d1−2d2
]
adalahz1 = 0 danz2 =n−3 + 2d1−2d2. Andaikanm = (n2+n(2d1−2d2−6)−
4d1+ 6d2+ 9)/2−d(vt, v1) danp=n−3 + 2d1−2d2. Karenapath Pvy+1,vt terletak
padaC1, maka tidak terdapatvy+1 (m,p)
25
terpendek dari titikvy+1 ke titik vt yang memuat paling sedikitm arcmerah dan
paling sedikitp arcbiru adalahwalk berarah yang dimulai dari titikvy+1 sampai
ke titikv1kemudian mengelilingiC2 sebanyakn−3+2d1−2d2 kali dan kembali ke
titikv1dan selanjutnya bergerak sampai ke titikvt. W alkberarah yang demikian
adalahwalk berarah dengan (n2+n(2d
1−2d2−4)−4d1+ 6d2+ 5)/2−d(vt, v1)
arc merah dann−1 + 2d1−2d2 arc biru. Karena d(v1, vt) +d(vt, v1) =n, maka
dapat disimpulkan bahwa
kvy+1,vx(vt)≥(n
2+n(2d
1−2d2−4) + 2d2+ 3)/2 +d(v1, vt) (4.12)
untuk setiap titik vt terletak pada vy+1 →vn path.
Berdasarkan persamaan (4.6), (4.9), dan (4.12) dapat disimpulkan bahwa
kvy+1,vx(vt)≥(n
2+n(2d
1−2d2−4) + 2d2+ 3)/2 +d(v1, vt)
untuk setiap t = 1,2, . . . , n. Oleh definisi scrambling index lokal dari titik vy+1
dan vx di D(2) yaitu kvy+1,vx(D
(2)) = min
vt∈D(2){kvy+1,vx(vt)}, diperoleh
kvy+1,vx(D
(2)) = min
vt∈D(2){(n
2+n(2d
1−2d2−4) + 2d2+ 3)/2 +d(v1, vt)}.
Nilai kvy+1,vx(D(2)) akan bernilai minimum ketika d(v1, vt) = 0 yaitu ketika t= 1
atau vt=v1 sehingga diperoleh
kvy+1,vx(D
(2)) = (n2 +n(2d
1−2d2−4) + 2d2 + 3)/2.
Berdasarkan hubungan k(D(2))≥max
vi,vj∈D(2){kvi,vj(D(2))}, maka diperoleh
k(D(2))≥ max
vi,vj∈D(2){kvi,vj(D
(2))} ≥k
vy+1,vx(D
(2)) = (n2+n(2d
1−2d2−4)+2d2+3)/2.
Oleh karena itu, dapat disimpulkan bahwa k(D(2)) ≥ (n2 +n(2d
1 −2d2 −4) +
2d2+ 3)/2.
Kedua, akan diperlihatkan bahwak(D(2))≤(n2+n(2d
1−2d2−4) + 2d2+
3)/2. Hal ini berarti, akan ditunjukkan bahwa untuk setiap titik vt dimana t =
1,2,3, . . . , n diD(2) sistem
Mz+
[
r(Pvt,v1)
b(Pvt,v1)
]
=
[
(n2+n(2d
1−2d2−6)−4d1+ 6d2+ 9)/2
n−3 + 2d1−2d2
]
26
memiliki solusi bilangan bulat tak negatif untuk beberapapath Pvt,v1 dari titikvt
ke titik v1. Perhatikan bahwa dari sistem (4.13) diperoleh
Mz=
[
(n2+n(2d
1−2d2−6)−4d1+ 6d2+ 9)/2
n−3 + 2d1−2d2
]
−
[
r(Pvt,v1)
b(Pvt,v1)
]
Mz=
[
(n2+n(2d
1−2d2−6)−4d1+ 6d2+ 9)/2−r(Pvt,v1)
n−3 + 2d1−2d2−b(Pvt,v1)
]
z=M−1
[
(n2+n(2d
1−2d2 −6)−4d1+ 6d2+ 9)/2−r(Pvt,v1)
n−3 + 2d1−2d2−b(Pvt,v1)
]
z=
[
1 (3−n)/2 −2 n−2
] [
(n2+n(2d
1−2d2−6)−4d1+ 6d2+ 9)/2−r(Pvt,v1)
n−3 + 2d1−2d2−b(Pvt,v1)
]
z=
[
((n−3)/2)b(Pvt,v1) +d1−r(Pvt,v1)
(1−b(Pvt,v1))n+ 2(r(Pvt,v1) +b(Pvt,v1)−d2)−3
]
,
maka solusi dari sistem (4.13) adalah sebagai berikut.
z1 = ((n−3)/2)b(Pvt,v1) +d1−r(Pvt,v1) (4.14)
dan
z2 = (1−b(Pvt,v1))n+ 2(r(Pvt,v1) +b(Pvt,v1)−d2)−3. (4.15)
Jika 1≤t≤x−1, maka terdapat sebuah (r(Pvt,v1),1)-path dari titikvt ke
titik v1 dengan d2 + 1 ≤ r(Pvt,v1) ≤ (n −3)/2. Dengan menggunakan path ini
dan persamaan (4.14), diperolehz1 = (n−3)/2 +d1−r(Pvt,v1) karenar(Pvt,v1)≤
(n−3)/2, maka z1 ≥ d1. Dengan menggunakan path ini dan persamaan (4.15),
diperoleh z2 = 2(r(Pvt,v1)−d2)−1 karena r(Pvt,v1)≥d2+ 1, maka z2 ≥1.
Jika t=x, maka terdapat sebuah (r(Pvt,v1),2)-path dari titik vt ke titik v1
denganr(Pvt,v1)≤d2+ (n−1)/2. Dengan menggunakanpath ini dan persamaan
(4.14), diperoleh z1 = n−3 +d1 −r(Pvt,v1) karena r(Pvt,v1) ≤ d2 + (n−1)/2,
diperoleh z1 ≥ (n−5)/2 + d1 −d2 dan karena d1 > d2, maka z1 ≥ (n−3)/2.
Dengan menggunakanpath ini dan persamaan (4.15), diperolehz2 = 2(r(Pvt,v1)+
b(Pvt,v1)−d2)−(n+ 3) karena r(Pvt,v1) +b(Pvt,v1)≥d2+ (n+ 3)/2, makaz2 ≥0.
Jika x+ 1 ≤ t ≤ (n −1)/2, maka terdapat sebuah (r(Pvt,v1),0)-path dari
titik vt ke titik v1 dengan 1≤r(Pvt,v1)≤d2. Dengan menggunakan path ini dan
persamaan (4.14), diperolehz1 =d1−r(Pvt,v1) karenar(Pvt,v1)≤d2 dan d1 > d2,
maka z1 ≥ 1. Dengan menggunakan path ini dan persamaan (4.15), diperoleh
27
karena d2 ≤(n−3)/2, maka z2 ≥2.
Jika (n+ 1)/2 ≤ t ≤ y, maka terdapat sebuah (r(Pvt,v1),1)-path dari titik
vt ke titik v1 dengan d1 ≤ r(Pvt,v1) ≤ (n −1)/2 −d1. Dengan menggunakan
path ini dan persamaan (4.14), diperoleh z1 = (n−3)/2 +d1−r(Pvt,v1) karena
r(Pvt,v1) ≤ (n − 1)/2− d1, diperoleh z1 ≥ 2d1 −1 dan karena d1 > d2 ≥ 1,
maka z1 ≥ 3. Dengan menggunakan path ini dan persamaan (4.15), diperoleh
z2 = 2(r(Pvt,v1)−d2)−1 karena r(Pvt,v1)≥d1, diperoleh z2 ≥2d1−2d2−1 dan
karena d1 > d2, maka z2 ≥1.
Jikay+ 1 ≤t ≤n, maka terdapat sebuah (r(Pvt,v1),0)-path dari titikvt ke
titikv1 dengan 1 ≤r(Pvt,v1)≤d1. Dengan menggunakanpath ini dan persamaan
(4.14), diperoleh z1 =d1−r(Pvt,v1) karena r(Pvt,v1)≤ d1, maka z1 ≥ 0. Dengan
menggunakanpathini dan persamaan (4.15), diperolehz2 =n−3+2r(Pvt,v1)−2d2
karena r(Pvt,v1) ≥ 1, kita peroleh z2 ≥ n−1−2d2 dan karena d2 ≤ (n−3)/2,
maka z2 ≥2.
Oleh karena itu, untuk setiap t = 1,2, . . . , n, terdapat sebuah path Pvt,v1
dari titik vt ke titik v1 sedemikian hingga sistem (4.13) memiliki solusi bilangan
bulat tak negatif. Berdasarkan Proposisi 2.5.1, terdapat sebuah vt
(m,p)
−→ v1 jalan
denganm = (n2+n(2d
1−2d2−6)−4d1+ 6d2+ 9)/2 danp=n−3 + 2d1−2d2
sehingga
k(D(2))≤(n2+n(2d1−2d2−4) + 2d2+ 3)/2.
Jadi, dapat disimpulkan bahwa
k(D(2)) = (n2+n(2d1−2d2−4) + 2d2+ 3)/2
ketika d1 > d2.
Kasus 2. d1 ≤d2
Berikut ini akan dibuktikan bahwak(D(2)) = (n2+n(2d
2−2d1−3) + 2d1+ 2)/2.
Pertama, akan diperlihatkan bahwak(D(2))≥(n2+n(2d
2−2d1−3) + 2d1+ 2)/2.
Asumsikan bahwa kvx+1,vy(vt) diperoleh dari (h, ℓ)-walk berarah dan asumsikan
terdapat vx+1 (h,ℓ)
−→vt walk dan vy
(h,ℓ)
−→vt walk. Andaikan
e1 =b(C2)r(Pvx+1,vt)−r(C2)b(Pvx+1,vt) (4.16)
dan
28
Terdapat tiga kemungkinan posisi titik vt sebagai berikut.
1. Titikvt terletak padav1 →vx path.
Terdapat dua path Pvx+1,vt dari titik vx+1 ke titik vt yaitu (d2 +d(v1, vt) + (n−
1)/2,1)-path dan (d2+d(v1, vt),0)-path. Dengan menggunakan (d2 +d(v1, vt) +
(n−1)/2,1)-path dan persamaan (4.16), diperoleh
e1 = (1)(d2+d(v1, vt) + (n−1)/2)−((n−3)/2)(1)
=d2+d(v1, vt) + 1. (4.18)
Dengan menggunakan (d2+d(v1, vt),0)-path dan persamaan (4.19), diperoleh
e1 = (1)(d2+d(v1, vt))−((n−3)/2)(0) =d2+d(v1, vt). (4.19)
Pilih nilaie1 yang lebih kecil yaitu p