VIBRACIONES UI

UNIDAD I.- CINEMÁTICA DE LA VIBRACIÓN.

INTRODUCCIÓN.

El estudio de las vibraciones se refiere a los movimientos oscilatorios de los cuerpos y a las fuerzas asociadas con ellos.

Dado que los cuerpos poseen masa y elasticidad, son capaces de vibrar. La mayoría de las máquinas y estructuras experimentan efectos vibratorios hasta cierto grado, y su diseño requiere de la consideración de su comportamiento oscilatorio.

En general los efectos de las vibraciones son perjudiciales para el buen funcionamiento de una máquina o de un elemento en particular de la misma, por lo que resulta muy importante mantener niveles de vibración relativamente bajos para un funcionamiento favorable y prevenir paros repentinos.

Un sistema vibratorio se puede comportar en forma lineal o en forma no lineal. Un sistema lineal se rige por el principio de superposición y puede representarse mediante una ecuación diferencial lineal.

Un sistema no lineal es muy difícil de analizar, sin embargo su conocimiento es deseable debido a que todos los sistemas lineales tienden a volverse no lineales cuando crece la amplitud de la vibración.

Clasificación de las vibraciones.

Existen dos clases generales de vibraciones:

a).- Vibraciones libres b).- Vibraciones forzadas

La vibración libre ocurre cuando un sistema oscila bajo la acción de fuerzas inherentes al sistema mismo (no existen fuerzas externas). La frecuencia de oscilación de este tipo de sistemas se conoce como frecuencia natural, la cual depende de la rigidez y la distribución de la masa del sistema.

1.1.- Grados de libertad (GL) de un sistema oscilatorio.

Es el número de coordenadas linealmente independientes que se requieren para describir su movimiento. Por ejemplo

Una partícula libre en tres dimensiones tiene tres grados de libertad (3 GL).

Un cuerpo rígido en tres dimensiones tiene seis grados de libertad (6 GL).

Un cuerpo flexible posee un número infinito de grados de libertad, ya que posee un número infinito de puntos.

1.2.- Movimiento armónico y su representación.

Este es el tipo de movimiento oscilatorio más simple, y se puede definir mediante la relación

x Asen t  --- (1.1)

en donde A= amplitud de la oscilación (cm, pul, etc.) = frecuencia circular (rad/s)

2

f  _ --- (1.2) (frecuencia del movimiento armónico en cps o Hz)

1



El movimiento armónico puede representarse como la proyección sobre una línea recta tal como se representa en la siguiente figura:

Figura (1.2).- Movimiento armónico como proyección de un punto que se mueve en una Circunferencia.

El movimiento armónico puede ser representado por medio de un vector de magnitud A a una velocidad angular constante . En la figura (1.2) el vector puede darse en función de sus proyecciones horizontal y vertical por

--- (1.4)

Cuando el tiempo se mide desde la posición horizontal del vector como punto de partida, la proyección horizontal del vector se escribe como Acost, y la proyección vertical como

Asen t . Cualquiera de las dos proyecciones puede tomarse como representativas de un movimiento armónico, sin embargo en muchas ocasiones se toma en cuenta la componente

Asen t .

La velocidad y aceleración del movimiento armónico puede obtenerse simplemente por diferenciación como sigue:

x Asen t 



2



cos

x&A  t Asen t





2 2

x  Asen t  Asen  t &&

Si graficamos las ecuaciones anteriores podemos observar que la velocidad y la aceleración preceden a x en 90o _{y 180}o _{respectivamente.}

[image:3.595.125.476.101.239.2]

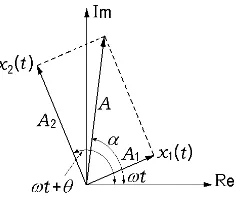
En forma vectorial se tiene lo siguiente:

Aunque el uso de vectores para visualizar movimientos armónicos es un criterio muy simple, para cálculos numéricos no está bien adaptado debido a que es necesario descomponer los vectores en sus componentes vertical y horizontal, resultando un método sumamente largo y tedioso.

1.3.- Uso de fasores para la suma, resta, multiplicación y división de movimiento armónico.

Un fasor es un vector en rotación bidimensional que se utiliza para representar una onda en movimiento armónico simple. Una forma de representarlo es mediante números complejos.

Un vector _Xr en el plano xy puede ser representado como un número complejo

Xr  a jb

donde j 1

a y b son las componentes de x y y de _Xr respectivamente

Figura (1.3).- Representación de un número complejo.

Si A representa la magnitud del vector _Xr , y  representa el argumento o ángulo entre el vector y el eje x, entonces _Xr puede ser expresado también como

cos j

Xr A  jAsen Ae 

(cos ) j

Xr  A  jsen Ae  --- (1.5)

donde _{A a}2_b2 _{y tan} 1b

a

1.3.1.- Operaciones con números complejos. Dados los números complejos 1

1 1 1 1 j

z  a jb A e  y 2

2 2 2 2 j

z a  jb  A e  entonces

a).- z₁�z₂ (a₁�a₂) j b( ₁�b₂)

b).- ( 1 2)

1 2 ( 1 1)( 2 2) ( 1 2 1 2) ( 1 2 2 1) 1 2 j

z zg  a  jb a  jb  a a b b  j a b a b  A A e  

c).- 1 1 1 1 1 2 2 1 2 1 2 1 2 2 1 1 1 2 2 2

2 2 2 2 2 2 2 _{2 2} 2

( )( ) ( ) ( ) ( )

( )( )

z a jb a jb a jb a a b b j a b a b A j

z a jb a jb a jb _{a b} A e  

      

   _

   

1.3.2.- Suma de movimientos armónicos.

Para sumar dos movimientos armónicos x t1( )A1cost y x t2( )A2cos( t ) de la misma frecuencia circular, en donde A1,A2 y  son valores conocidos, se pueden utilizar los métodos siguientes:

a).- Usando relaciones trigonométricas:

1 2

( ) cos( ) ( ) ( )

x t A  t x t x t

1 2

(cos cos ) cos (cos )

A t sen t sen   A t A  t 

1 2

( cos ) cosA  t(Asen sen t)  A cost A (costcos sen t sen ) --- (i)

De la relación (i) se obtienen las siguientes relaciones:

1 2

cos cos

A   A A  --- (ii)

2

Asen A sen --- (iii)

Resolviendo el sistema anterior se obtienen los valores correspondientes deA y .

b).- Usando vectores.

Para un valor arbitrario de t, los movimientos armónicos x t1( ) y x t2( )pueden representarse gráficamente como se muestra el la figura (1.4). Sumando vectorialmente los movimientos armónicos representados por x t1( ) y x t2( ), se obtiene el vector resultante dado por

( ) cos( )

x t A  t .

Figura (1.4).- Suma de movimientos armónicos.

[image:5.595.240.359.586.685.2]

Los dos movimientos armónicos pueden ser representados en forma compleja por:

1( ) Re 1 j t

x t  �_�A e  �_� --- (iv)

( )

2( ) Re 2 j t

x t  �_�A e   �_�--- (v)

La suma de x t1( ) y x t2( )puede ser expresada como

( )

( ) Re j t

x t  �_�Ae   �_� --- (1.6)

Ejemplo 1.1.- Encontrar la suma de los movimientos armónicos x t1( ) 5cos(3 1) t y

2( ) 10cos(3 2)

x t  t , utilizando

a).- Relaciones trigonométricas b).- Suma de vectores

c).- Números complejos

Solución:

a).- x t( ) Acos( t ) x t1( )x t2( ) 5cos(3 1) 10cos(3 t  t 2)

A(cos3t_) 5 cos 3 cos_{ �} t

 

1 180�_{ }sen t sen3

 

1 180�_{ �}

� �

10 cos3 cos_�� t



2 180�_



sen t sen3



2 180�_



�_�

Acos3 cost  Asen t sen3   1.45648cos3 13.30031t sen t3 

Acos  1.45648 --- (i) Asen 13.3001 --- (ii)

Dividiendo (ii) entre (i) se obtiene

13.30031 1.45648

tan _  9.1318_{  83.75}o _{180 83.75} o _96.25o _{1.68 rad}

En (i) se tiene que A_cos96.251.45648o 13.38

( ) 13.38cos(3 1.68)

x t  t

Angulo entre x t1( ) y x t2( ):  1.68 1 0.68 rad = 38.96  o

c).- Usando números complejos.



(3 1)



1( ) Re 5 j t

x t  e 



(3 2)



2( ) Re 10 j t

x t  e 

x t( ) Re



Aej t(3)



Re 5



ej t(3 1)

 

Re 10ej t( 2)



--- (iii)

Desarrollando y resolviendo (iii) se obtiene



(3 1.68)



( ) Re 13.38 j t

x t  e 

Cuando se suman dos movimientos armónicos, con frecuencias muy cercanas entre si, el movimiento resultante representa un fenómeno conocido como “pulsación”. Por ejemplo, si

1( ) cos

x t X t y x t₂( )Xcos(  )t, donde  es una cantidad pequeña, la suma de estos movimientos es





1 2

( ) ( ) ( ) cos cos( )

x t x t x t  X t   t --- (1.7)

Usando la relación cosAcosB2cos

   

A B₂ cos A B₂ , la ecuación (1.7) se puede escribir como





2 2

( ) 2 cos tcos

x t  X   --- (1.8)

1.4.- Serie de Fourier aplicada al movimiento armónico.

1.4.1.- Movimiento periódico.

Un movimiento periódico tiene la propiedad de repetirse íntegramente después de un cierto intervalo de tiempo llamado periodo del movimiento . Todos los movimientos armónicos son periódicos, pero no todos los movimientos periódicos son armónicos. Por ejemplo la figura que se muestra a continuación, representa el movimiento de la ecuación

2

( ) a 2

x t a sen t  sen t

Fourier demostró que éste tipo de movimiento puede ser representado mediante una serie de senos y cosenos de la forma

1 2 1 2

2

( ) ao cos cos 2 2

x t  a t a t L b sen t b sen  t L





2 1

( ) ao cos

n n n n

n

x t � a _ t b sen t_



 

�

 --- (1.9)

en donde n n --- (1.10)

 2_ --- (1.11)

,

o n

2

2

2 _{( )}

o

a _ _ x t dt





�

--- (1.12)

2

2

2 _{( ) cos}

n n

a _ _ x t  t dt





�

--- (1.13)

2

2

2 _{( )}

n n

b _ _ x t sen t dt_





�

--- (1.14)

La serie anterior puede representarse también en términos de la función exponencial, sustituyendo





1 2

cos j tn j tn

nt e  e 

    --- (a)





1

2 n n

j t j t

n

sen t  e  e  --- (b)

Sustituyendo (a) y (b) en (1.9) se obtiene:



 







2 2 2

1

( ) ao an j tn j tn bn j tn j tn

j n

x t � e  e  e  e 



 

�

   











1 1



2 2 2

1

( ) ao j tn j tn

n n n n

n

x t � a jb e  a jb e 



 

�

   





1

( ) j tn j tn j tn

o n n n

n n

x t c � c e  c e   � c e 

 �

 

�

 

�

--- (1.15)

en donde c_o 1₂a_o

c_n 1₂



a_n jb_n



c_n 1₂



a_n jb_n



Sustituyendo a_n y b_n en c_n encontramos que

2

2

1 _{( )} j tn n

c _ _ x t e  dt





�

--- (1.16)

Podemos graficar los coeficientes de Fourier contra n, lo que da como resultado una serie de

líneas discretas que constituyen el llamado “espectro de Fourier” o espectro de frecuencias. Generalmente se grafican el valor absoluto 2c_n  a_n2b_n2 y la fase tan 1 n

n

b

n _a

   .

Algunos términos importantes usados en vibraciones son:

Valor pico.- Indica generalmente el esfuerzo máximo que está sufriendo la parte vibrante.

Valor medio.- Indica un valor estático o estacionario. Se determina mediante la expresión

lim _T1 ₀T ( )

T

x x t dt

��



�

--- (1.17)

Valor cuadrático medio.- Se determina a partir del promedio de los valores cuadráticos, integrando sobre el intervalo T del tiempo. Su expresión es

2 lim _T1 ₀T 2( )

T

x x t dt

��



�

--- (1.18)

Valor de la raíz cuadrática media (rms).- Es la raíz cuadrada del valor medio cuadrado; esto es

_{rms x}2 _{--- (1.19)}

Decibel.- Es una unidad de medida que se utiliza frecuentemente en vibraciones. Se le define como una razón de potencias

 

1 2 10 log _PP

dB --- (1.20)

En función de los desplazamientos la ecuación anterior de expresa como sigue:

 

1

 

1

2 2

2

10 log _XX 20 log _XX

Problema 1.2.- Para la función diente de sierra que se muestra a continuación, determinar:

a).- La serie de Fourier en forma trigonométrica. b).- La serie de Fourier en forma exponencial. c).- La rms de la onda mostrada.

d).- El espectro de amplitud.

Solución.- De la figura tenemos que  2,   2_ 1, m₂1_ , x t( ) ₂1_t.

a).- Forma trigonométrica:

 

 

 

2 2 2 2 2 ₂

2 2 1 1 1

2 ₀ 2 ₂ 2 ₀

( ) 1

o

a _ _ x t dt _  _ tdt t 

  

�



�

 





2 2 2 2 2 2 2

2 1 1 1

0 0 0

2 2

( ) cos cos t 0

n n _{n n}

a _ _ x t t dt t nt dt sen nt  sen ntdt

    � �    _�  _� � �

�

�

�





2 2 2 2 2 2 2

2 1 1 1

0 0 0

2 2

( ) t cos cos

n n _{n n}

b _ _ x t sen t dt t sen nt dt nt   ntdt

    � �    _�  _� � �

�

�

�





2 2 2

2

2 1 1 1

2 2 ₀

n _{n n n}

b  sennt  _

 

    

La serie trigonométrica de Fourier es 1₂ 1 1 1

( ) _n

n

x t _ � sen nt



 

�

b).- Forma exponencial:

 





2 2 2 2 2 2

1 1 1 1 1

2 2 _{0 4 0 0}

( ) j tn jnt t jnt jnt

n _{jn jn}

c _ _x t e  dt _{ } te dt e  e dt

      � �    _�  _� � �

�

�

�

2 j n _n

c  _

La serie de Fourier en forma exponencial es ( ) ₂j 1_n jnt

n

x t _ e

�

�

c).- Cálculo de la rms.

2 2

1 1

2 ₄

( ) ( )

x t _ t x t



 � 

 

2 3

2 2

2 1 2 1 1 2 1 1 3 1

2 3 3

0 0 4 8 0

lim _T T ( )

x

x x t dt _  t dt t 

 

��



�



�

 

2 1

3

rms x 

d).- Espectro de amplitud.

1 2c_n  _n

n ₂

n c

1 0.31831 2 0.15951 3 0.10610 4 0.07957 5 0.06366 6 0.05305 7 0.04547 8 0.03978 9 0.03536 10 0.03183

1.5.- Diagnóstico de fallas en la maquinaria rotatoria a partir del registro de la vibración. La finalidad de un diagnóstico es la de establecer las causas de una vibración. Para tal fin, la información que se obtiene por medio de sensores deberá ser comparada con mediciones de referencia o con características de fenómenos vibratorios conocidos. Por medio de las mediciones y el análisis de las vibraciones, tenemos un método no destructivo y de costo efectivo de diagnóstico para establecer condiciones de falla.

Algunas fallas que pueden detectarse mediante un análisis de vibraciones son:

a).- Ausencia de lubricación. b).- Ejes flexionados. c).- Alabes rotos.

d).- Daño o desalineamiento de transmisiones flexibles. e).- Cojinetes dañados o desgastados.

f).- Excentricidad.

g).- Corrosión por frotamiento. h).- Montaje incorrecto. i).- Componentes inseguros. J).- Aflojamiento mecánico. k).- Inicios de cavitación.

l).- Engranes desgastados o dañados. m).- Desbalance estático o dinámico.

n).- Presencia de cuerpos sólidos (transmisión de fluidos).

En el análisis de vibraciones, la frecuencia es la clave para diagnosticar fuentes de vibración. Al caracterizar una fuente de vibración se debe conocer la naturaleza del fenómeno que causa esa vibración. Es fundamental establecer un modelo para conocer los síntomas que caracterizan un determinado problema, los cuales se comprueban con la evidencia experimental.

El proceso de diagnóstico involucra un análisis de señales que puede ir desde una medición simple de amplitudes rms, hasta un análisis espectral que incluya posiblemente trazos en forma de onda con extensión a formas más sofisticadas de procesamiento de señales en un rango de conceptos físico-matemáticos.

Los defectos que se pueden presentar durante la rotación de un eje, y que son posibles de detectar mediante un análisis orbital son:

a).- Fase orbital de un eje. b).- Vórtice y/o chicoteo de aceite. c).- Eje con precarga.

d).- Frotamiento o chicoteo seco.

CAUSA AMPLITUD FRECUENCIA FASE

Desequilibrio

Es proporcional

al desequilibrio 1xRPM

Marca de referencia simple Desalineamiento

de coples y chumaceras

Grande en la dirección axial, 50% o más de la vibración radial

Generalmente 1xRPM. En ocasiones 2 y 3 veces RPM

Sencilla, doble o triple

Chumaceras en mal estado del tipo antifricción

Inestable. Usar la medición de velocidad si es posible

Muy alta. Es muchas veces un múltiplo de las RPM

Errática

Muñones excéntricos

Generalmente no es grande

1xRPM Marca

sencilla Engranes

defectuosos o ruido en los mismos

Es baja. Usar la medición de velocidad si es posible 2XRPM Errática Desajuste mecánico ---2xRPM

Dos marcas de

referencia. Ligeramente errática Bandas de

accionamiento defectuosas

Errática

o pulsativa 1,2,3,4 xRPMde las bandas Una o dos,dependiendo

de la

frecuencia

Eléctrica

Desaparece

cuando se

desconecta el suministro de energía

1xRPM o 1 o 2xfrecuencia sincrónica Marca simple o rotatoria Fuerzas aerodinámicas o hidráulicas

---1xRPM o número de aspas de ventilador o de impelentes xRPM

---Fuerzas

reciprocantes

---1,2 y múltiplos mayores