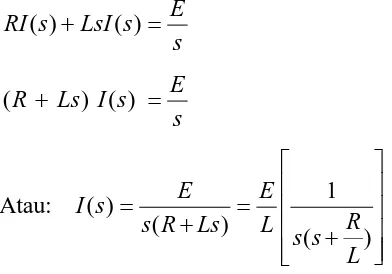Informasi Dokumen
- Penulis:
- Chandra L. P. Simbolon
- Pengajar:
- Drs. Ujian Sinulingga, M.Si
- Dra. Mardiningsih, M.Si
- Sekolah: Universitas Sumatera Utara
- Mata Pelajaran: Matematika
- Topik: Uji Kestabilan Arus Listrik Pada Rangkaian Arus Searah Dengan Metode Transformasi Laplace Routh-Hurwitz
- Tipe: Skripsi
- Tahun: 2008
- Kota: Medan
Ringkasan Dokumen
I. Pendahuluan
Pendahuluan dalam skripsi ini memberikan konteks penting mengenai kestabilan arus listrik dalam rangkaian arus searah. Latar belakang menjelaskan bahwa dalam sistem listrik, kestabilan arus sangat penting untuk memastikan bahwa perangkat berfungsi dengan baik dan aman. Penelitian ini bertujuan untuk menggunakan metode transformasi Laplace dan Routh-Hurwitz untuk menganalisis kestabilan tersebut. Dengan memahami kestabilan arus, mahasiswa dapat mengaplikasikan teori ini dalam praktik teknik elektro dan sistem kontrol, yang merupakan bagian penting dari kurikulum teknik.
1.1 Latar Belakang
Latar belakang menjelaskan pentingnya kestabilan arus listrik dan kebutuhan untuk mengontrol arus dalam rangkaian. Dalam konteks ini, penulis menunjukkan bahwa metode transformasi Laplace dapat digunakan untuk menyelesaikan persamaan diferensial yang menggambarkan sistem listrik. Hal ini relevan untuk pendidikan teknik elektro, di mana pemahaman tentang kestabilan dan kontrol arus adalah fundamental.
1.2 Perumusan Masalah
Perumusan masalah menjelaskan fokus penelitian, yaitu bagaimana mentransformasikan persamaan fungsi arus ke dalam bentuk transformasi Laplace dan menganalisis kestabilan menggunakan metode Routh-Hurwitz. Ini memberikan gambaran jelas tentang tujuan akademis dan relevansi metodologi yang digunakan dalam penelitian ini.
1.3 Pembatasan Masalah
Pembatasan masalah menjelaskan bahwa penelitian ini hanya menggunakan dua metode, yaitu Routh dan Hurwitz. Hal ini penting untuk menjaga fokus penelitian dan memberikan batasan yang jelas, yang akan membantu mahasiswa dalam memahami ruang lingkup analisis kestabilan dalam sistem listrik.
1.4 Tujuan Penelitian
Tujuan penelitian adalah untuk mendeteksi kestabilan arus listrik dalam rangkaian. Ini menunjukkan aplikasi praktis dari teori yang dipelajari di kelas, dan penting untuk tujuan pembelajaran mahasiswa dalam memahami analisis sistem dinamik.
II. Landasan Teori
Bab ini menjelaskan konsep-konsep dasar yang menjadi landasan bagi analisis kestabilan arus listrik. Teori yang dibahas mencakup arus listrik, persamaan diferensial, dan transformasi Laplace. Pemahaman tentang teori ini sangat penting bagi mahasiswa untuk dapat menerapkan pengetahuan mereka dalam konteks praktis dan penelitian.
2.1 Arus Listrik
Penjelasan mengenai arus listrik dan komponennya, termasuk resistor, kapasitor, dan induktor, memberikan pemahaman dasar yang diperlukan untuk analisis lebih lanjut. Hukum Kirchoff dan hukum Ohm juga dibahas, yang merupakan fondasi penting dalam studi listrik dan teknik elektro.
2.2 Persamaan Diferensial
Bab ini membahas persamaan diferensial yang digunakan untuk menggambarkan sistem listrik. Pemahaman tentang jenis-jenis persamaan diferensial dan cara menyelesaikannya sangat penting dalam analisis sistem dinamik, yang merupakan bagian dari kurikulum teknik.
2.3 Transformasi Laplace
Transformasi Laplace adalah alat penting dalam analisis sistem. Penggunaan transformasi ini memungkinkan mahasiswa untuk menyelesaikan persamaan diferensial dengan lebih mudah dan efektif. Ini merupakan keterampilan yang sangat berguna dalam bidang teknik dan sains.
2.4 Teori Kestabilan
Teori kestabilan menjelaskan bagaimana sistem dapat dianalisis untuk menentukan apakah sistem tersebut stabil atau tidak. Ini adalah konsep kunci dalam rekayasa kontrol dan penting untuk memastikan bahwa sistem beroperasi dengan aman dan efisien.
III. Pembahasan
Pembahasan dalam skripsi ini mencakup penerapan teori yang telah dibahas sebelumnya untuk menganalisis kestabilan arus listrik dalam rangkaian. Melalui contoh kasus, mahasiswa dapat melihat bagaimana teori diterapkan dalam praktik, yang sangat penting untuk pembelajaran dan pemahaman yang lebih dalam.
3.1 Solusi Komplementer
Bagian ini menjelaskan bagaimana solusi komplementer untuk sistem listrik dapat diperoleh. Ini memberikan wawasan praktis tentang bagaimana teori diterapkan dalam analisis sistem nyata, yang merupakan keterampilan penting bagi mahasiswa teknik.
3.2 Pemakaian Transformasi Laplace
Diskusi mengenai langkah-langkah pemakaian transformasi Laplace dalam analisis sistem listrik menunjukkan penerapan praktis dari teori yang dipelajari. Ini membantu mahasiswa memahami bagaimana teori dapat digunakan untuk menyelesaikan masalah nyata dalam sistem listrik.
3.3 Contoh Kasus
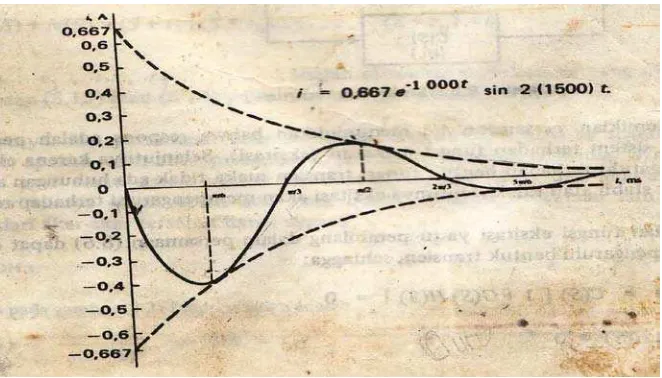
Contoh kasus yang diberikan menunjukkan penerapan metode yang telah dibahas sebelumnya. Ini memberikan mahasiswa kesempatan untuk melihat bagaimana teori dan praktik saling terkait dan bagaimana analisis kestabilan dapat dilakukan secara sistematis.
IV. Kesimpulan dan Saran
Kesimpulan dari penelitian ini merangkum temuan utama dan memberikan saran untuk penelitian lebih lanjut. Ini penting untuk mendorong mahasiswa berpikir kritis dan mempertimbangkan bagaimana penelitian ini dapat diperluas atau diterapkan dalam konteks lain.
4.1 Kesimpulan
Kesimpulan memberikan ringkasan dari hasil analisis dan pentingnya kestabilan arus listrik dalam rangkaian. Ini membantu mahasiswa memahami nilai dari penelitian ini dalam konteks yang lebih luas.
4.2 Saran
Saran untuk penelitian lebih lanjut memberikan arahan bagi mahasiswa untuk mengeksplorasi lebih dalam topik ini. Ini mendorong pengembangan pemikiran kritis dan penelitian independen di kalangan mahasiswa.
Referensi Dokumen
- Persamaan Diferensial dan Matematika Model ( Baiduri )
- Rangkaian Listrik ( Durbin M. Steven )
- Physic for Scientist and Engineers with Modern Physic ( Kanginan )
- Matematika Untuk Tekhnik Edisi Ketiga ( Kastroud )
- Penerapan Teori Kontrol - cetakan kedua ( Pakpahan. Sahat )
- Transformasi Laplace ( Spiegel. Murray. R. )